The Impact of Environmental Risk on Business Failure: A Fuzzy-Set Qualitative Comparative Analysis Approach with Extreme Gradient Boosting Feature Selection

Abstract

Corporate performance is increasingly impacted by environmental issues, but their specific role in business failure remains underexplored, which leads to a gap in research that is often focused exclusively on financial metrics. By investigating the relationship between environmental financial exposure and business failure, this study addresses this gap, integrating financial ratios and environmental variables to understand how environmental performance affects financial viability. A novel dual-stage methodology was employed, first using Extreme Gradient Boosting (XGBoost) for feature selection to identify the most significant predictors of failure from a dataset of Spanish companies (N = 38,456) using 2022 ORBIS data. Next, a fuzzy-set qualitative comparative analysis (fsQCA) was applied to analyze the sufficient causal configurations leading to a high propensity for business failure. The analysis identified three distinct causal configurations associated with failure. All highlighted poor financial performance indicators, such as low results per employee and low profit per employee. Notably, one configuration identified high environmental risk (measured by TRUCAM) as a core condition contributing significantly to financial distress. These findings highlight the critical link between environmental responsibility and financial health, demonstrating the benefits of combining fsQCA with machine learning to identify intricate causal configurations and providing information to companies and governments who want to support long-term financial stability and corporate sustainability.

1. Introduction

Environmental issues have gained prominence in the context of economic activity in recent years. In response to mounting data on pollution, climate change, and resource depletion, businesses and policymakers have adopted more creative sustainability strategies and increasingly stringent regulations [1,2]. New frameworks, such as enhanced emissions standards, incentives for renewable energy adoption, and comprehensive waste management policies, reflect a contemporary understanding of the risks associated with unsustainable practices [3].

It is widely acknowledged that environmental factors are essential to the long-term sustainability of businesses. Firms that fail to meet updated environmental standards face not only reputational risks but also significant financial penalties, which can adversely affect their operational performance [4,5]. This shift in the regulatory landscape has heightened the importance of integrating environmental performance into corporate financial strategies.

This study examines how environmental risks interact with financial metrics to influence business failure in Spanish firms. Prior studies highlight standalone financial predictors [6]; however, emerging evidence suggests that environmental factors augment financial distress through regulatory penalties [7] and consumer backlash [8]. Our analysis addresses this gap by integrating machine learning (XGBoost) and fuzzy-set qualitative comparative analysis (fsQCA) to identify failure pathways involving environmental risk.

This study begins with a brief introduction and a review of relevant literature, underscoring key contributions related to the research focus. We then outline the study’s objectives, describe the sample and data sources, and define the variables employed in the analysis. After providing a thorough description of the methodology, we provide the research findings, the key conclusions, and offer ideas for further study.

2. Literature Review

This study examines environmental risk and business failure. This relationship is receiving increased attention in academic research. Research on business failure has focused recently on the development of predictive models that incorporate methodological advances and artificial intelligence techniques [9,10,11]. These models have evolved to integrate new variables and approaches that reflect contemporary business realities and improve predictive capabilities. While traditional studies have often focused on financial ratios and operational metrics, the significance of including environmental considerations in these models is becoming more widely acknowledged [12,13]. Firstly, this section will review the literature on the relationship between environmental risk and business performance, then it will cover studies on the methodological tools used in this study.

Environmental risk, also known as environmental financial exposure, is defined as the potential percentage of a company’s revenue that is at risk due to the environmental damage it causes. This idea covers a wider spectrum of risks, which goes beyond conventional cost measurements, including remediation expenses, regulatory fines, and reputational damage [4,5]. Therefore, environmental risk has become a critical factor in assessing corporate risk and financial stability, influencing both operational performance and long-term viability.

The literature review on the environment and economic activity reveals that many studies have explored the relationship between environmental factors and economic growth, particularly observing the impact of economic growth on carbon intensity. For example, studies have generally concluded that both economic growth and carbon intensity tend to increase in parallel [14,15,16,17]. Although these findings provide important context, they primarily address macroeconomic scenarios rather than the direct financial implications for individual companies. Further research has emphasized the influence of industrialization on environmental outcomes, underlining the significant impact of industrialization on carbon emission intensity [18,19,20]. Although these studies contribute valuable insights into the environmental consequences of economic development, they are more focused on aggregate emissions than on the financial risks faced by firms.

Numerous studies have advocated for strategies aimed at mitigating these effects, as they recognize the environmental impact of economic development. Researchers have suggested measures such as reducing global energy consumption, investing in renewable energy, and promoting technological advancements [21,22,23]. In addition, some have highlighted the vital role of governments in creating regulations and institutional frameworks that nurture a clean economy [24,25,26]. These initiatives are essential for reducing environmental risk and ensuring that companies remain financially resilient in the face of environmental challenges.

Recent research has concentrated on the direct relationship between environmental risk and business performance, particularly financial sustainability, which is in line with our study’s goal of identifying the configurations and factors that contribute to business failure, particularly the role of environmental risk. It has been shown that firms experiencing raised levels of environmental risk tend to see noteworthy declines in profitability, which implies that high environmental financial exposure may serve as a precursor to operational inefficiencies and liquidity constraints [12]. This study supports the idea that financial instability can worsen if environmental risk is not given enough consideration. Similarly, the integration of sustainable practices has been shown to mitigate adverse financial impacts; for instance, a study on the green value chain revealed its effectiveness in reducing the costs associated with environmental failures, thereby improving operational efficiency and long-term viability [27]. These results suggest that proactive environmental initiatives improve organizational resilience in competitive markets while also lessening financial issues.

The dynamic relationship between environmental performance, risk, and financial outcomes has also been a focal point in recent literature. Some examined this relationship and found that costs associated with environmental prevention and failure activities directly influence profitability metrics [28]. Their findings underscore the necessity for firms to internalize environmental considerations as part of their financial planning processes. By allocating resources toward sustainable practices, companies can mitigate risks related to regulatory penalties and reputational damage, thereby safeguarding their financial performance.

Moreover, a study about emerging markets discovered that higher environmental risk negatively impacts profitability, especially the return on equity, in resource-constrained environments [13]. This indicates that businesses that operate in these environments struggle to strike a balance between their financial goals and their environmental responsibilities. This reinforces the need for robust environmental risk management strategies.

Despite the role of environmental factors in causing economic development becoming increasingly acknowledged, a critical gap remains in understanding how environmental financial exposure directly contributes to financial distress or business failure. Few studies have fully investigated the intricate relationships between environmental risk and financial performance indicators at the firm level, despite the fact that previous research has shown correlations between high exposure levels and adverse financial outcomes. This study addresses this gap by investigating whether a causal relationship exists between environmental financial exposure and business failure, motivated by the increasing importance of environmental sustainability and the potential financial risks for companies that do not pay enough attention to sustainable practices.

To address the research gap, this study employs a two-stage methodological approach. The first stage utilizes XGBoost, a machine-learning algorithm, for feature selection. The second stage employs fsQCA to analyze causal configurations.

Previous research has demonstrated the effectiveness of XGBoost in predicting business failure [9,10,11,29], confirming its capacity to assess both the sign and magnitude of each variable’s impact on the prediction [30]. XGBoost computes feature importance scores during training, allowing researchers to identify the most critical variables influencing business failure [31].

FsQCA complements machine learning by providing configurational insights that improve the explanatory depth of the study. As a methodological approach that combines qualitative and quantitative analysis, it has demonstrated efficacy in identifying combinations of elements linked to company failure [32,33,34,35], and scholars are increasingly employing fsQCA to examine environmental problems [36]. This method is particularly well-suited for exploring outcomes resulting from complex interactions, as it enables researchers to identify combinations of conditions associated with specific outcomes [37].

3. Dataset and Variables

We analyze financial data from a sample of active Spanish companies in 2022, obtained from the ORBIS database [38]. The data include financial ratios and two key variables: VADIS, a financial strength indicator used to assess the propensity for business failure; and TRUCAM, which quantifies the costs associated with a company’s environmental impact.

We employed an XGBoost machine learning model for feature selection to identify the most important variables associated with business failure. These variables were then used in the fsQCA to determine the existence of sufficient causal relationships between environmental risk and business failure.

3.1. Financial Strength and Environmental Indicators: VADIS and TRUCAM

The ORBIS database [38] provides a range of financial strength indicators for analyzing various aspects of company viability. This study focuses on the VADIS indicator, which assesses a company’s evolution by considering a multitude of factors (approximately 15,000 per company). Based on this comprehensive assessment, the VADIS indicator offers several key insights, including:

• Probability of Business Bankruptcy (P2BB):

  -

  This metric assesses the likelihood that a company will declare bankruptcy in the next 18 months.

• Probability of Business Sale (P2BSold):

  -

  Measures the likelihood that a company will be sold in the next 18 months.

• Estimated Value of Company Operation (VPI EDV):

  -

  Estimates the value of the future operation of companies associated with a P2Bsold indicator and is expressed in terms of a confidence interval (i.e., it has upper and lower limits).

This study utilizes the VADIS indicator (P2BB), which assigns companies an integer value ranging from 1 to 9 to represent their propensity for failure. A value of 1 indicates a low propensity for bankruptcy, while a value of 9 indicates a high propensity.

Table 1. Scale of the VADIS financial strength indicator on the propensity for bankruptcy.

Value	Risk of Bankruptcy for the Company in the Next 18 Months Is as Follows:
9	More than 10 times the average of its country
8	Between 5 and 10 times the average of its country
7	Between 3 and 5 times the average of its country
6	Between 2 and 3 times the average of its country
5	Between 1 and 2 times the average of its country
4	Between 1/2 and 1 time the average of its country
3	Between 1/5 and 1/2 times the average of its country
2	Between 1/10 and 1/5 times the average of its country
1	Less than 1/10 times the average of its country

Source: Own elaboration based on information from the ORBIS database (2022).

provides a detailed overview of the VADIS scale.

This study incorporates the environmental indicator TRUCAM, derived from the Trucost environmental risk rating developed by S&P Global Trucost, a leading UK-based environmental consultancy. TRUCAM values were obtained from the ORBIS database [38]. TRUCAM quantifies the potential percentage of a firm’s revenue at risk due to environmental damage. This involves costs associated with remediation, pollution mitigation, supply chain disruptions, and resource dependencies. When evaluating the possible financial risk that a business may incur as a result of its environmental impact, this variable is important.

The environmental risk score of the TRUCAM indicator comprises a company’s total direct environmental costs and supply chain costs associated with resource use and pollution, expressed as a percentage of revenue. Consequently, companies with higher environmental risk scores relative to their industry peers demonstrate greater environmental intensity and may face increased exposure to environmental costs.

The combined use of VADIS and TRUCAM facilitates an in-depth analysis of the interaction between financial strength and environmental impact. These metrics are essential to our research because they allow us to examine possible causal links between environmental risk and the likelihood of business failure.

3.2. Data Selection

Financial data for active Spanish companies across all non-financial sectors was extracted from the ORBIS database for the fiscal year 2022. The reliance on this database may be limiting due to the presence of companies with incomplete financial information, a problem we mitigated by excluding companies lacking the necessary data. After removing companies with excessive missing values, we collected annual data and financial ratios from 38,456 companies, including information on the financial strength indicator (VADIS) and the environmental indicator (TRUCAM). The sectoral composition of these companies is shown in

Table 2. Sectoral composition of the companies in the sample.

Sector	Percentage	Section–Nace Rev. 2 (2008)
PRIMARY	3.25%	A B
SECONDARY	37.30%	C D E F
Manufacturing	27.61%	C
Energy and water	1.60%	D E
Construction	8.09%	F
TERTIARY	59.45%	G H I J L M N O P Q R S T U
Commerce	30.81%	G
Transportation	6.67%	H
Hospitality	5.07%	I
Information and communication	3.31%	J
Professional services	8.58%	L M N
Education, healthcare, and others	5.01%	O P Q R S T U

Source: Author’s calculations based on data from the ORBIS database [38] and the NACE Rev. 2 classification [39]. Note: NACE Rev. 2 (Statistical Classification of Economic Activities in the European Community) is the standard classification system used in the European Union to categorize economic activities.

according to the NACE Rev. 2 [39] classification criteria.

Companies were categorized based on their propensity for failure using the VADIS indicator, a discrete variable with values ranging from 1 to 9. As previously noted, a value of 1 represents a low propensity for failure, while a value of 9 represents a high propensity.

3.3. Selection and Definition of Explanatory Variables

One of the most important factors in creating prediction or classification models for business failure is the use of independent or explanatory variables. This study focuses on economic and financial ratios as key predictors, following the line established by influential works [6,40,41] that introduced key concepts and methodologies for predicting business failure using financial ratios.

One acknowledged limitation is the lack of a clear theoretical foundation for choosing predictor variables in business failure models. To address this, we rely on comprehensive bibliographic reviews [42,43], which meticulously analyzed the variables employed in leading studies on business failure prediction. The diversity of methods and variables included in the literature emphasizes the complexity of this problem and how much more research is required to determine which factors are most important and to create more reliable and accurate models. Thus, the selection of variables was systematically derived from existing bibliographic sources, ensuring that the model incorporates predictors supported by empirical evidence within the field.

Accordingly, we initially considered all 25 economic and financial variables available in the ORBIS database, as these variables are commonly examined in previous literature. We employed the XGBoost algorithm to identify the key variables that are most strongly associated with business failure. XGBoost is a widely recognized machine learning technique for feature selection [31], known for its high accuracy and efficiency in predictive tasks. It belongs to the family of ensemble methods, specifically gradient boosting, which combines multiple weak learners (typically decision trees) to create a strong predictive model. This feature selection process helps to reduce the number of variables included in the subsequent fsQCA, ensuring a more parsimonious and interpretable model. (For a detailed explanation of the XGBoost algorithm and its application as a feature selection method, readers may refer to a previous study [31] and https://xgboost.readthedocs.io/en/stable/ [accessed on 5 April 2024] [44]).

Figure 1 illustrates the ten most relevant predictors identified by the XGBoost algorithm, from which we have selected the top six:

• SOLL: Indicative of the solvency of the entity, reflecting its capacity to meet payments arising from debts.
• GEAR: Provides a measure of the entity’s level of indebtedness.
• RTAS and ROA: Representative of the company’s profitability in relation to its size.
• TPR and PPE: Reflect returns per employee.

These variables provide insights into the financial health, profitability, and efficiency of the companies, thereby contributing to the prediction of business failure propensity (see

Table 3. Description of the most important financial variables.

Key	Variables
PROFITABILITY RATIOS
RTAS	ROA (Pre-tax profit) (%) = (Pre-tax profit/Total Assets) × 100
ROA	ROA (Net income) (%) = (Net income/Total Assets) × 100
CFOP	Operating cash Flow (%) = (Cash Flow/Operating revenue) × 100
STRUCTURAL RATIOS
SOLL	Solvency ratio (%) = (Equity/Total Assets) × 100
GEAR	Indebtedness Ratio (%) = [(Non-current liabilities + Loans)/Equity] × 100
LIQR	Liquidity Ratio = (Current assets -Stocks)/Current liabilities
OPERATIONAL RATIOS
COLL	Collection Period (days) = (Debtors/Operating revenue) × 360
EMPLOYEE-BASED RATIOS
PPE	Profit per Employee = EBT/Number of employees
TPR	Operating revenue per employee = Profit before taxes/Number of employees
WCPE	Working capital per employee = Working capital/Number of employees

Note: Key based on the reference in the ORBIS database [38].

for details).

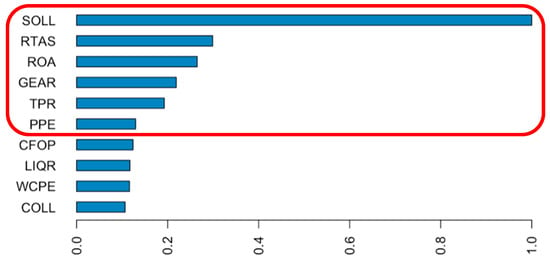
Figure 1. The ten most relevant variables identified by the XGBoost algorithm. Notes: The figure shows the relative importance of the predictors or features. The solvency ratio (SOLL) is identified as the most important feature, with all other features ranked relative to its importance. The relative values of the other features are scaled in comparison to SOLL, highlighting their proportional significance in predicting business failure. From the ten most relevant predictors identified by the XGBoost algorithm, we have selected the top six (indicated by the red rectangle).

Figure 1. The ten most relevant variables identified by the XGBoost algorithm. Notes: The figure shows the relative importance of the predictors or features. The solvency ratio (SOLL) is identified as the most important feature, with all other features ranked relative to its importance. The relative values of the other features are scaled in comparison to SOLL, highlighting their proportional significance in predicting business failure. From the ten most relevant predictors identified by the XGBoost algorithm, we have selected the top six (indicated by the red rectangle).

The selected variables were then completed with the TRUCAM variable, which quantifies the financial impact of a company’s environmental footprint. We employed fsQCA to analyze this set of variables, specifically examining the role of environmental risk in contributing to business failure. This analysis focused on identifying causal configurations that incorporate the TRUCAM variable, indicating the potential for environmental risk to influence business failure. The objective is to understand how a company’s environmental impact can lead to adverse financial outcomes, using fsQCA to identify the specific combinations of factors that contribute to a high propensity for business failure. Thus, the inclusion of the TRUCAM variable is essential to this investigation.

FsQCA is particularly beneficial for examining a restricted number of variables or conditions, as it allows for the examination of complicated causal relationships and exposes how different combinations of conditions can lead to specific outcomes [45]. However, employing many conditions or variables in fsQCA can result in overly complex solutions that may make their interpretation difficult [46]. Researchers must carefully balance model complexity and explanatory power when determining the appropriate number of conditions to include in an fsQCA study. In this study, as explained, we have selected seven variables, achieving a balance between complexity and explanatory power.

4. Methodology

As mentioned earlier, this study integrates two methodologies to identify the key factors and causal configurations associated with business failure: Extreme Gradient Boosting (XGBoost), a machine learning technique for feature selection, and fuzzy-set qualitative comparative analysis (fsQCA) for analyzing causal relationships or configurations.

By first employing XGBoost to identify key financial variables and then using fsQCA to analyze the configurational effects of these variables in conjunction with the TRUCAM indicator, the methodology provides a comprehensive understanding of how environmental financial exposure interacts with traditional financial measures to influence business failure. This integrated approach ensures that both the predictive power and the causal complexity underlying business performance are adequately captured.

4.1. Feature Selection Using XGBoost

The first phase of the analysis involves the application of the XGBoost algorithm to identify the most significant predictors of business failure. XGBoost is a machine-learning technique that employs gradient boosting to improve predictive accuracy through an ensemble of decision trees [47]. The process proceeds as follows:

• Variable Ranking: XGBoost is applied to the full set of 25 variables, generating importance scores for each predictor.
• Selection Criteria: Variables are ranked based on their contribution to model performance, and those with the highest scores are retained. In this study, the top financial predictors are selected (see Figure 1), and the TRUCAM variable is added, given its central role in representing environmental financial exposure.
• Model Parsimony: This feature selection step not only enhances the predictive capability of the model but also reduces the complexity of subsequent analyses, ensuring that only the most relevant variables are carried forward.

This initial screening provides a robust set of predictors that form the basis for further causal analysis using fsQCA.

XGBoost is robust to issues related to endogeneity and multicollinearity, which are common concerns in traditional econometric analyses. Unlike parametric models that rely on strict assumptions about variable independence and linear relationships, XGBoost is a non-parametric machine learning algorithm that iteratively builds decision trees to optimize predictive accuracy [48]. Its use of regularization techniques, such as L1 and L2 penalties, helps prevent overfitting and minimizes the influence of spurious correlations [30]. Additionally, XGBoost’s ability to handle complex and nonlinear interactions among variables ensures that the presence of correlated predictors does not undermine its predictive power. This makes it particularly well-suited for analyzing complex datasets, where endogeneity and multicollinearity might otherwise create significant challenges. As XGBoost prioritizes prediction rather than causal inference, it reduces the risk of biased estimates arising from endogeneity concerns.

An important characteristic of XGBoost is its ability to perform feature selection. The algorithm can identify the most relevant subset of features that contribute the most to the prediction accuracy of the model. This is carried out by assigning a score to each feature based on its importance in the prediction problem. The higher the score, the more important the feature [31].

4.2. Causal Configuration Analysis Using fsQCA

Following feature selection, fsQCA is applied to explore the complex causal pathways that lead to a high propensity for business failure. FsQCA is well suited for handling configurational complexity and identifying multiple causal recipes that yield the same outcome [45].

FsQCA is particularly well-suited for exploring outcomes arising from complex interactions, as it enables researchers to identify combinations of conditions associated with specific outcomes [37].

The key steps in the fsQCA process include the following:

• Calibration of variables: Data are calibrated or assigned membership scores using established methods to determine the degree to which each case exhibits the conditions under study.
• Truth table construction: A truth table is constructed to analyze the different combinations of conditions and their association with the outcome.
• Logical minimization: Logical minimization techniques are employed to identify the most essential combinations of conditions that explain the outcome.
• Solution assessment: The solutions are assessed using measures of consistency and coverage to evaluate their empirical validity.

Calibration

The initial step in fsQCA involves transforming variables into “fuzzy sets” [49], representing the degree to which each case belongs to a set—the calibration of raw data. These sets are referred to as “conditions” (analogous to independent variables in regression) and “outcome” (analogous to the dependent variable). By analyzing these fuzzy sets, researchers can identify the combinations of conditions, or “configurations”, that are sufficient for producing a specific outcome [50]. These configurations, also known as “causal recipes”, reveal the complex interplay of conditions that lead to the outcome of interest.

This calibration process involves establishing three thresholds: full membership (1.0), full non-membership (0.0), and a crossover point (0.5) where a case is equally in and out of the set. This is similar to normalizing data [49]. Following [51], we calibrated our variables using a cluster-based approach with Euclidean distance to determine these thresholds.

Truth Table Construction

After calibration, the fsQCA method constructs a “truth table” that systematically analyzes all possible combinations of conditions and their relationship to the outcome. Each row in the truth table represents a unique combination of conditions, with “1” indicating the presence of a condition and “0” indicating its absence. The truth table also includes measures of consistency and coverage for each configuration. Consistency, in the context of sufficiency, assesses the degree to which a configuration is consistently associated with the outcome. Coverage, on the other hand, measures the extent to which a specific configuration accounts for the occurrence of the outcome. Analyzing the truth table, it is possible to identify the combinations of conditions, or “configurations”, that are sufficient for producing the outcome. These configurations reveal complex causal relationships and provide insights into the combinations of conditions (variables) that lead to the outcome of interest—in this study, a high propensity for business failure.

Logical Minimization

Logical minimization is a core procedure in fsQCA that simplifies the results obtained from the truth table. This step aims to identify the essential combinations of conditions that are sufficient for the outcome to occur [52]. It involves applying Boolean algebra rules and logical reduction techniques, such as the Quine–McCluskey algorithm, to simplify complex logical expressions [45]. This simplification process helps to:

• Enhance interpretability: By reducing the number of conditions and configurations, logical minimization makes the results more manageable and easier to understand [46].
• Identify core causal conditions: It highlights the most critical conditions that are consistently associated with the outcome [53].
• Improve generalizability: Simpler solutions may be more generalizable to other contexts and datasets [54].

Solution Assessment

FsQCA uses measures such as consistency and coverage to evaluate the relationships between causal conditions and outcomes [37]. Consistency, in the context of sufficiency, measures the degree to which a causal condition or configuration is consistently associated with the outcome [55]. It quantifies the degree to which cases sharing a particular configuration of conditions also exhibit the outcome.

Coverage, on the other hand, indicates the degree to which a configuration accounts for the instances of an outcome. It reflects the empirical relevance of the configuration or its ability to explain the outcome. A higher coverage value suggests a greater importance of the configuration in producing the outcome. In an extreme case where a configuration covers 100% of the outcome, it would be both sufficient and necessary. In [37], the authors suggest that consistency is analogous to Pearson’s correlation coefficient (r), while coverage is analogous to the coefficient of determination (R²).

Unlike traditional statistical methods that focus on isolated effects of conditions or independent variables, fsQCA identifies “causal recipes”—combinations of conditions associated with a specific outcome or dependent variable [49]. This approach offers a more comprehensive understanding of causality by considering the interaction of multiple conditions. In [56], the authors explain that fsQCA identifies patterns by grouping observations based on potential causal relationships that led to a specific outcome. These relationships are interpreted using Boolean algebra, a mathematical framework for analyzing logical relationships.

Business failure is rarely a consequence of a single isolated cause; rather, it typically arises from the complex interaction of multiple factors, including financial strain, managerial decisions, and environmental pressures. Moreover, the relationship between these factors and the outcome of failure is often nonlinear [57].

4.3. Integration and Sequential Application

The sequential application of XGBoost and fsQCA forms a comprehensive analytical framework. Initially, XGBoost refines the predictor set by highlighting the most relevant variables through a data-driven approach. Subsequently, fsQCA leverages these predictors to identify distinct causal configurations that explain the occurrence of business failure.

The combination of machine learning and set-theoretic methods provides both a predictive and explanatory perspective, offering insights into how environmental financial exposure interacts with financial performance. While XGBoost ensures that the model is parsimonious and focused on the most influential variables, fsQCA explains the complex interdependencies and multiple causal pathways of business failure.

4.4. Complexity, Equifinality, and Asymmetry

Guided by the principles of complexity, equifinality, and asymmetry, we employ fsQCA to identify the combinations of financial and environmental variables that are sufficient for predicting a high propensity for business failure. This approach acknowledges the complex interaction of factors contributing to business failure and allows for the identification of multiple causal pathways.

The principle of equifinality recognizes that multiple pathways, or configurations of conditions, can lead to the same outcome [58]. In other words, there are multiple, equally valid solutions for achieving a desired result. A specific outcome, such as the propensity for business failure, may be reached through multiple pathways, each involving a different configuration of conditions.

Conjunctural causality or complexity emphasizes that the effect of conditions on an outcome is determined by their combination, not by their individual magnitudes [59]. Conditions operate interdependently, and their combined effect may differ from the sum of their individual effects. It also emphasizes the nonlinearity of relationships within complex systems, recognizing that certain conditions may only contribute to an outcome when acting in combination with others [60].

The principle of asymmetry acknowledges that a condition may be causally relevant in one configuration but irrelevant, or even have an opposite effect, in another configuration [61]. This highlights the context-dependent nature of causal relationships.

4.5. Model Formulation

As previously noted, all financial variables from the ORBIS database were included in the initial analysis, along with the VADIS financial strength indicator, which measures a company’s propensity for failure. We utilized the XGBoost machine learning algorithm as a feature selection method to identify the six most relevant variables for predicting the propensity for business failure (see Figure 1).

The TRUCAM variable was added to the set of six key predictors identified with the XGBoost algorithm, bringing the total number of predictors to seven. This inclusion allows us to examine whether environmental risk, as measured by TRUCAM, contributes to a company’s propensity for failure. The presence of causal configurations that incorporate TRUCAM would underscore the potential influence of environmental impact on a company’s financial viability.

Therefore, we considered a total of seven variables (see Table 3 for detailed variable names) as antecedents to a company’s failure, aiming to identify the causal recipes or configurations that lead to a high propensity for business failure.

Propensity of failure = f(SOLL, RTAS, ROA, GEAR, TPR, PPE, TRUCAM)

The propensity for failure assesses the likelihood that a company will declare bankruptcy in the next 18 months. This variable takes values between 1 and 9. A value of 1 indicates a low propensity for bankruptcy, while a value of 9 indicates a high propensity (see Table 1).

All models were fitted using version 4.3.0 of the R statistical package [62], and the fsQCA was conducted using version 3.22 of the QCA package [55].

4.6. Methodology Generalization

The integrated methodology combining Extreme Gradient Boosting (XGBoost) for feature selection and fuzzy-set qualitative comparative analysis (fsQCA) for causal configuration analysis is adaptable to a variety of datasets. In the first step, XGBoost is employed to identify the most influential predictors for the outcome under investigation. Researchers should begin by ensuring the dataset is rigorously pre-processed to address issues of data quality and consistency. Feature selection via XGBoost can be optimized by adjusting model parameters and incorporating context-specific variables that reflect the characteristics of the new dataset. This data-driven approach results in a parsimonious set of variables that are prepared for further causal analysis.

Following the feature selection, fsQCA is applied to examine the combinations of conditions that lead to the outcome of interest. The selected variables are calibrated into fuzzy sets using established thresholds—full membership, crossover, and full non-membership—that are tailored to the specific data distributions and contextual characteristics of the new dataset. By analyzing the interaction of these calibrated variables, fsQCA uncovers multiple causal pathways, thereby demonstrating the method’s ability to handle complexity and equifinality in causal relationships. This sequential approach, beginning with XGBoost and followed by fsQCA, ensures that the methodology is robust and generalizable across diverse datasets.

5. Results and Robustness Analysis

5.1. Results

As described above, the first step in fsQCA is calibration, which involves transforming variables into fuzzy sets. This process assigns a degree of membership to each case, indicating the extent to which it belongs to a particular set. These sets are referred to as “conditions”, analogous to independent variables, and “outcome”, analogous to the dependent variable. Therefore, the raw data were transformed into fuzzy sets with membership values ranging from 0 to 1, representing the degree to which each case belongs to a set. In this study, we implemented a clustering approach to establish the thresholds, specifically employing the Euclidean distance method. In [55], the author notes that cluster analysis is instrumental in identifying the optimal cutoff points, as it efficiently partitions the scores into distinct groups, thereby segmenting the original data into the most meaningful clusters. This process enables us to identify the three thresholds required for calibration: full membership (1.0), full non-membership (0.0), and a crossover point (0.5), where a case is equally in and out of the set.

FsQCA produces three types of solutions: complex, intermediate, and parsimonious. Each solution represents a different level of simplification, with the complex solution being the most comprehensive and the parsimonious solution being the most simplified [45]. All solutions adhere to Boolean logic and are free of contradictions. The complex solution, which includes all possible configurations of conditions sufficient for the outcome, offers a detailed but potentially unmanageable picture of causal relationships. Its complexity can make interpretation challenging, particularly when numerous conditions are involved.

In contrast to the complex solution, the parsimonious solution simplifies causal configurations by retaining only the prime implicants, which are the minimal combinations of conditions indispensable for the outcome to occur. However, this simplification involves making assumptions about logical remainders, potentially leading to conclusions not fully supported by empirical evidence or theoretical understanding. In [45], the author does not recommend relying on these simplification mechanisms and proposes focusing on the complex or intermediate solutions, which are more closely grounded in the empirical data.

The intermediate solution offers a balance between complexity and parsimony by incorporating theoretical expectations to simplify the causal analysis. These expectations, supported by existing research and knowledge, guide the selection of specific causal configurations. Effectively utilizing the intermediate solution requires a strong theoretical understanding of the relationships between the conditions and the outcome.

This study focuses on the intermediate solution, and results are presented according to this type of solution. This solution balances comprehensiveness and interpretability, avoiding the potential oversimplification of the parsimonious solution and the complexity of the complex solution. By incorporating theoretically informed assumptions, the intermediate solution provides a manageable set of causal configurations that are both empirically grounded and theoretically meaningful.

Table 4. Expectations between causal conditions and propensity for failure.

Condition	Expected Sign
SOLL	Negative
RTAS	Negative
ROA	Negative
GEAR	Positive
TPR	Negative
PPE	Negative
TRUCAM	Negative

Notes: The “negative” sign indicates that the condition is expected to contribute to a low score on the outcome (propensity for business failure), and the “positive” sign indicates that the condition is expected to contribute to a high score on the outcome (propensity for business failure). Table 3 contains the definition of the variables.

outlines the specific assumptions employed to derive the intermediate solution—the estimated relationships or expectations between causal conditions and a situation of high propensity for business failure. The intermediate solution is derived by incorporating theoretically informed assumptions to identify causal configurations that are both empirically and theoretically meaningful. The “Positive” and “Negative” signs in Table 4 reflect these theoretically informed assumptions. A “Positive” sign signifies that the presence or high value of the condition aligns with a high likelihood of the outcome (propensity for failure), while a “Negative” sign indicates that the presence or high value of the condition aligns with a low likelihood of the outcome (no propensity for failure).

As already mentioned, a key tool in fsQCA is the truth table, which systematically analyzes all possible combinations of conditions and their relationship to the outcome. A condition is considered sufficient if it consistently leads to the outcome, meaning that cases exhibiting that condition also exhibit the outcome [63]. The truth table lists all possible configurations of conditions, with each row representing a unique combination. Cases are assigned to the configuration with the highest membership score (above 0.5). These configurations are then analyzed using Boolean algebra to identify simplified expressions that capture the key causal relationships. This process often involves logical minimization techniques such as the Quine–McCluskey algorithm [58]. With seven conditions in this study, the truth table comprises 128 rows, representing all possible causal configurations (2n rows).

Once we have obtained the truth table of all possible causal configurations leading to a high propensity for business failure, the next step is to measure the solutions using consistency and coverage to evaluate their empirical validity. Consistency evaluates the degree to which a causal condition or configuration is consistently associated with the presence of an outcome. Coverage, on the other hand, measures the extent to which that condition or configuration accounts for the occurrence of the outcome across all cases where the outcome is present.

Table 5 presents the results of the sufficiency analysis conducted using fsQCA, examining the conditions associated with a high propensity for business failure. The sufficiency analysis aims to identify the combinations of conditions that are sufficient for producing a particular outcome. A condition is considered sufficient if its presence consistently leads to the outcome; in other words, whenever the condition is present, the outcome is also present. This analysis, which included seven potential antecedent conditions, yielded three causal configurations associated with the outcome, derived from the truth table and the logical minimization process described previously. The overall solution demonstrates reasonable consistency (0.802) and coverage (0.223). Three possible solutions or causal configurations lead to the outcome (a high propensity for business failure):

• First solution: Low values of solvency ratio (SOLL) and low values of profit per employee ratio (TPR) and low values of benefit per employee ratio (PPE).
• Second solution: High values of debt ratio (GEAR), and low values of profit per employee ratio (TPR) and low values of benefit per employee ratio (PPE).
• Third solution: Low values of economic profitability ratio (RTAS) and low values of profit per employee ratio (TPR) and low values of benefit per employee ratio (PPE) and high values of environmental impact on results (TRUCAM).

Table 5. Sufficiency analysis of conditions for high propensity for failure.

Solution: → ~F.SOLL*~F.TPR*~F.PPE + F.GEAR*~F.TPR*~F.PPE + ~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM → F.VADISP2BB
	Consistency	Coverage
~F.SOLL*~F.TPR*~F.PPE	0.867	0.181
F.GEAR*~F.TPR*~F.PPE	0.734	0.085
~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM	0.890	0.022
Total minimum	0.802	0.223

Notes: Sample size = 38,456. The symbol ~ indicates the absence of the condition (or low values), and its omission indicates its presence (or high values of the condition). The asterisk symbol (*) represents the logical “and” operator, while the plus symbol (+) represents the logical “or” operator, consistent with standard Boolean algebra. “F.” denotes that variables have been transformed into conditions (fuzzified). Variable definitions are provided in Table 3.

Table 5. Sufficiency analysis of conditions for high propensity for failure.

Solution: → ~F.SOLL*~F.TPR*~F.PPE + F.GEAR*~F.TPR*~F.PPE + ~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM → F.VADISP2BB
	Consistency	Coverage
~F.SOLL*~F.TPR*~F.PPE	0.867	0.181
F.GEAR*~F.TPR*~F.PPE	0.734	0.085
~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM	0.890	0.022
Total minimum	0.802	0.223

Notes: Sample size = 38,456. The symbol ~ indicates the absence of the condition (or low values), and its omission indicates its presence (or high values of the condition). The asterisk symbol (*) represents the logical “and” operator, while the plus symbol (+) represents the logical “or” operator, consistent with standard Boolean algebra. “F.” denotes that variables have been transformed into conditions (fuzzified). Variable definitions are provided in Table 3.

In this analysis, the symbol “~” is used to represent the absence of a specific condition or variable (or low values). This notation is frequently employed in fsQCA studies to denote the non-existence or lack of a particular factor or condition within a given configuration. By utilizing this symbol, we can effectively distinguish between the presence and absence of conditions, allowing for a more precise analysis of the complex relationships between variables and outcomes.

In fuzzy-set qualitative comparative analysis (fsQCA), causal conditions are classified as either core or peripheral based on their relative importance and stability across different solution types [45,53]. Core conditions are those that consistently appear in both parsimonious and intermediate solutions, demonstrating a robust and central influence on the outcome. Their inclusion is critical; omitting a core condition generally leads to significant alterations in the overall configuration, underscoring its essential role in the causal recipe. Peripheral conditions, by contrast, tend to emerge only in the intermediate solution. They are considered less central and often represent context-specific factors or modifiers that enrich the explanation of the outcome without being indispensable. While peripheral conditions contribute to the complexity of the causal pathways, their absence does not typically disrupt the fundamental structure of the solution. This distinction between core and peripheral conditions enables the explanation of the most critical causal factors and those that offer additional contextual insights [45,53].

To enhance the clarity of the findings, we have transformed the solutions from Table 5 into a more reader-friendly table (

Table 6. Sufficiency analysis of conditions for high propensity for failure (transformed solution).

Antecedents	Configuration I		Configuration II	Configuration III
Solvency ratio (SOLL)
Operating revenue per employee (TPR)	⨂		⨂	⨂
Profit per employee (PPE)	⨂		⨂	⨂
GEAR (Indebtedness)
RTAS (Pre-tax profit)				⨂
Environmental impact (TRUCAM)
Net income (ROA)
Consistency	0.867		0.734	0.890
Coverage	0.181		0.085	0.022
Overall solution consistency		0.802
Overall solution coverage		0.223

Notes: Black circles (●) indicate the presence of a condition, and circles with x (⨂) indicate its absence. Large circles: core condition. Small circles: peripheral condition. Blank space: “don’t care” condition.

). Conventionally, a black circle (●) denotes the presence of a condition, a crossed-out circle (⊗) indicates its absence or negation, and a blank space represents a “do not care” condition [63]. Additionally, core conditions are distinguished using large circles, while peripheral conditions are indicated with smaller circles.

The three solutions identified reveal a consistent pattern: Low values for both results per employee and profit per employee are associated with a high propensity for business failure. This suggests that poor financial performance, as indicated by these ratios, is a key determinant of business failure. Notably, one of the solutions includes the environmental impact variable, which is considered a core condition. This finding indicates that high environmental risk can contribute to a higher propensity for business failure, highlighting the potential impact of environmental performance on a company’s financial viability (see third causal configuration in Table 5 and Table 6).

Therefore, one of the three identified solutions highlights the crucial role of the environmental condition. The presence of high values for this variable is associated with an increased propensity for business failure. This finding underscores the harmful impact of environmental risk on a company’s financial health, suggesting that poor environmental performance can contribute significantly to financial distress and ultimately, business failure.

This finding underscores the critical link between a company’s environmental performance and its financial health. The negative impact of environmental risk extends beyond ecological concerns, influencing a company’s financial performance and increasing its vulnerability to business failure. This interrelation highlights the need for a full approach to corporate sustainability, recognizing that environmental responsibility is not merely an ethical imperative but also a strategic imperative for long-term financial viability and success.

5.2. Robustness Analysis

To assess the robustness of our findings, we conducted a contradiction test, as recommended by Duşa and Alrik [64]. This test involves applying the fsQCA algorithm to the negation of the outcome (i.e., a low propensity for failure) using the same solutions or causal configurations identified for the original outcome (a high propensity for failure). If a condition or configuration is sufficient for both the outcome and its negation, it indicates a contradictory or paradoxical relationship, potentially undermining the validity of the analysis. As shown in

Table 7. Sufficiency analysis of conditions for a low propensity for failure.

Solution: → ~F.SOLL*~F.TPR*~F.PPE + F.GEAR*~F.TPR*~F.PPE + ~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM → ~F.VADISP2BB
	Consistency	Coverage
~F.SOLL*~F.TPR*~F.PPE	0.611	0.052
F.GEAR*~F.TPR*~F.PPE	0.548	0.012
~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM	0.745	0.004
Total minimum	0.544	0.001

Notes: Sample size = 38,456. The symbol ~ indicates the absence of the condition (or low values), and its omission indicates its presence (or high values of the condition). The asterisk symbol (*) represents the logical “and” operator, while the plus symbol (+) represents the logical “or” operator, consistent with standard Boolean algebra. “F.” denotes that variables have been transformed into conditions (fuzzified). Variable definitions are provided in Table 3.

, the consistency and coverage values for the negation of the outcome are low, confirming the absence of contradictory relationships and supporting the robustness of our findings.

A further robustness check, as suggested by Duşa and Alrik [64], involves examining whether the negation of the identified causal configurations or solutions leads to the same outcome. If both a configuration and its negation are sufficient for the outcome, it indicates a potential contradiction or paradoxical relationship.

Table 8. Analysis of the sufficiency of the negation of conditions for a high propensity for failure.

Solution: → negation (~F.SOLL*~F.TPR*~F.PPE + F.GEAR*~F.TPR*~F.PPE + ~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM) → ~F.VADISP2BB
	Consistency	Coverage
negation (~F.SOLL*~F.TPR*~F.PPE)	0.575	0.003
negation (F.GEAR*~F.TPR*~F.PPE)	0.575	0.003
negation (~F.RTAS*~F.TPR*~F.PPE*F.TRUCAM)	0.575	0.003
Total minimum	0.575	0.003

Notes: Sample size = 38,456. The symbol ~ indicates the absence of the condition (or low values), and its omission indicates its presence (or high values of the condition). The asterisk symbol (*) represents the logical “and” operator, while the plus symbol (+) represents the logical “or” operator, consistent with standard Boolean algebra. “F.” denotes that variables have been transformed into conditions (fuzzified). Variable definitions are provided in Table 3.

presents the results of this analysis, demonstrating that the negation of the configurations associated with a high propensity for failure does not lead to the same outcome. The low consistency and coverage values observed for the negated configurations further support the robustness of our findings and confirm the absence of contradictory relationships.

5.3. Exploring Asymmetry Through the Analysis of “Low Propensity for Business Failure”

To explore the asymmetric nature of causality in business failure, we conducted an additional fsQCA using “low propensity for business failure” as the outcome.

This approach allows us to examine the configurations of conditions that are associated with the absence of business failure, providing a contrast to the configurations that lead to its occurrence.

The analysis involved the same set of predictor variables identified in the original analysis (SOLL, RTAS, ROA, GEAR, TPR, PPE, and TRUCAM). We applied the fsQCA methodology to the new outcome (low propensity for business failure) as described in Section 4.

The results of this analysis revealed a distinct causal configuration associated with “low propensity for business failure”, which differs from those found in the original analysis. The solution is displayed in

Table 9. Sufficiency analysis of conditions for low propensity for failure.

Solution: F.SOLL*~F.GEAR*~F.TPR*~F.PPE*F.TRUCAM → F.LOW_VADISP2BB
	Consistency	Coverage
F.SOLL*~F.GEAR*~F.TPR*~F.PPE*F.TRUCAM	0.944	0.120
Total minimum	0.944	0.120

Notes: Sample size = 38,456. The symbol ~ indicates the absence of the condition (or low values), and its omission indicates its presence (or high values of the condition). The asterisk symbol (*) represents the logical “and” operator, while the plus symbol (+) represents the logical “or” operator, consistent with standard Boolean algebra. “F.” denotes that variables have been transformed into conditions (fuzzified). LOW_VADISP2BB: Low Propensity for Failure. The remaining variable definitions are provided in Table 3.

.

This solution suggests that a combination of high solvency (F.SOLL), low indebtedness (~F.GEAR), high returns per employee (~F.TPR, ~F.PPE), and low environmental risk (~F.TRUCAM) is associated with a low propensity for business failure (F.LOW_VADISP2BB).

In contrast, the original analysis, where the outcome was “business failure” (Table 5), identified three different causal configurations:

The differences between these results and the original analysis highlight the asymmetry of causality in business failure. Conditions that contribute to failure do not simply have the opposite effect on “no failure”, indicating that different causal pathways imply separate causal dynamics. This underscores the importance of examining both outcomes to gain a better understanding of the factors influencing business success and failure.

6. Discussion

This study aimed to explain the causal configurations underlying business failure, with a specific focus on environmental financial exposure—that is, the proportion of a company’s revenue at risk due to the environmental damage it causes. By integrating Extreme Gradient Boosting (XGBoost) for feature selection with fuzzy-set qualitative comparative analysis (fsQCA) for identifying causal configurations, our analysis provides an understanding of how traditional financial indicators and environmental risk interact.

Prior studies have established a link between high environmental risk and negative financial outcomes, such as decreased profitability and increased operational inefficiencies [12]. Our findings corroborate this, showing that environmental financial exposure (TRUCAM) is a core condition in one of the causal configurations leading to a high propensity for business failure. This directly supports the idea that environmental risk is not just an ethical concern but a tangible financial threat.

Likewise, previous research often focused on the independent effects of either environmental risk or financial factors [6,7,8]. The use of fsQCA enables a more comprehensive examination. We identify specific combinations of conditions, including environmental risk, that are sufficient for business failure. This reveals the complex interaction between environmental and financial factors. For example, the third solution in Table 6 shows that high environmental risk (TRUCAM), in conjunction with low economic profitability (RTAS) and low returns per employee (TPR and PPE), leads to a high propensity for failure. This configurational approach provides a better understanding than simply correlating environmental risk with negative financial performance.

The application of fsQCA revealed multiple causal pathways (equifinality) that lead to business failure [58]. The configurations that explain a high propensity for failure exhibit greater overall consistency and coverage compared to those explaining the robustness analysis. These results support the argument that incorporating environmental financial exposure into traditional financial risk assessments enhances the explanatory power of such models [28].

Our study focuses on environmental financial exposure or environmental risk. This focus is critical, as recent reports emphasize that environmental risk factors are becoming increasingly integral to assessing corporate performance and sustainability [4,5]. The findings contribute to this ongoing debate by demonstrating that it is not merely the direct costs of environmental damage but the associated financial exposure that significantly raises the risk of business failure.

From a methodological perspective, the integration of XGBoost and fsQCA offers a complementary approach. XGBoost ensures that only the most influential predictors are considered, thereby simplifying the model and enhancing interpretability [31]. Meanwhile, fsQCA captures the complexity of the causal relationships, offering a clear representation of how various combinations of financial and environmental conditions can lead to similar outcomes [45,56].

Several limitations should be acknowledged. The study’s reliance on the ORBIS database may limit generalizability. The findings are based on Spanish companies, and the results may not be generalizable to other countries. The study did not explore dynamic or temporal changes in these factors over time. This study’s reliance on a single-year dataset may not fully capture the dynamic interaction between financial variables, environmental risk, and business failure. Ongoing research could benefit from employing a longitudinal approach.

Additionally, the study acknowledges limitations in coverage and consistency values for some configurations. As Ragin noted [45], fsQCA prioritizes identifying sufficient causal pathways over maximizing variance explanation, often resulting in lower coverage. While coverage values in this study are modest (0.223 total coverage), they are consistent with prior fsQCA research in finance, where low coverage is typical [54,63]. These limitations are balanced by the method’s ability to reveal pathways involving environmental risk, which linear models might overlook. The findings remain theoretically meaningful, adhering to fsQCA’s principles of causal asymmetry and configurational logic.

Future research should explore the relationship between environmental risk and business failure in diverse contexts, considering factors such as industry, regulatory environment, and cultural norms. Further investigation is also needed to examine the specific mechanisms through which environmental costs contribute to business failure.

In summary, our study provides evidence that high environmental financial exposure, when combined with poor financial performance, is associated with an increased propensity for business failure. This finding underscores the necessity for integrating environmental risk metrics into financial analyses and strategic decision-making processes.

7. Conclusions

Addressing a gap in the literature, this study employed fuzzy-set qualitative comparative analysis (fsQCA) and Extreme Gradient Boosting (XGBoost) to identify key factors and configurations contributing to business failure, with a particular focus on the role of environmental risk. Our primary objective was to integrate these methods to uncover both the causal pathways leading to business failure and the most influential variables in predicting such outcomes. In doing so, we contribute to the understanding of business failure by demonstrating how environmental financial exposure impacts a company’s financial viability. While previous studies have primarily focused on traditional financial factors, our analysis underscores the importance of incorporating environmental risk as a critical determinant of business success.

XGBoost enabled us to identify the most relevant financial predictors from a wide range of variables. FsQCA was employed to identify causal configurations that lead to business failure. This method revealed three different causal configurations, each emphasizing the role of poor performance indicators such as low profit per employee and low result-per-employee ratios. Notably, one configuration highlighted the significant impact of environmental risk, with high values in the TRUCAM indicator being strongly associated with an increased likelihood of failure.

The findings demonstrate the complexity of business failure. They show that environmental financial exposure, when combined with weak financial performance, enhances the understanding of corporate vulnerability. By using advanced analytical techniques, we provide a comprehensive framework that can guide business leaders and policymakers.

To ensure the robustness of our findings, we conducted extensive analyses to detect any contradictions or inconsistencies in the causal configurations identified. These analyses confirmed that the configurations leading to a high propensity for business failure are robust, reinforcing the reliability and validity of our results.

In summary, our study demonstrates that environmental financial exposure is a significant factor in business failure, particularly when it coincides with poor financial performance. This research highlights the necessity of integrating environmental risk considerations into financial analyses and strategic decision-making processes. The insights gained from this study provide a strong foundation for future research and practical applications aimed at enhancing corporate sustainability and financial resilience.