Abstract
This work deals with switching structured linear systems, a class of structured linear systems whose existing links between the state, input, and output variables have unknown numerical values and, in addition, are subject to change according to an exogenous, time-dependent signal. Geometric methods and computational tools developed to solve control and observation problems stated for this class of structured linear systems are presented. In particular, this work delves into the notions of invariance, controlled invariance, and conditioned invariance and focuses on their use in the statement and proof of conditions for the solvability of the disturbance decoupling problem, both by state feedback and by output feedback, and of the unknown-input state observation problem. The fundamental concepts and the main results are explained using handy examples, with visual aid provided by directed graphs.
1. Introduction
Switching structured linear systems are dynamical systems that can be described by a family of structured linear systems with the same dimension, the modes, and by a time-dependent signal, the switching signal, that determines the active mode at each time instant. Each mode, as a structured linear system, is such that the direct relations between its variables are described either by fixed zeros or by real parameters whose value (possibly including zero) is unknown. In particular, the switching from one structured linear system of the family to another enables the direct relations between the variables to change from non-existent (fixed zeros) to existent (unknown real parameters) and vice versa. Therefore, the interconnections between the variables of switching structured linear systems are not only described by unknown real values wherever they exist, but they also exhibit a topology subject to change. The main motivation for introducing and studying this class of dynamical systems is that they are a powerful means to model multiagent systems whose network features an evolving topology, as is explained through the literature review that follows.
Structured linear systems were introduced in the mid-seventies by Lin [1]. In the following two decades, they were extensively studied and the literature of those years mainly emphasizes their role in coping with model uncertainties. Since the state-space representation of a structured linear system consists of linear maps whose entries are either fixed zeros or unknown real parameters, a single structured linear system is, actually, representative of a family of classic linear time-invariant systems. For this reason, many authors resorted to structured linear systems to investigate systems’ properties featuring some robustness to parameter variations (see, e.g., [2,3,4]) or, as was more precisely pointed out by Dion and coauthors in their survey paper [5], properties that hold true for almost any value of the parameters, briefly referred to as generic properties.
More recently, structured linear systems have received renewed attention, as is well-documented by another survey paper [6]. However, in the latest years, the focus of interest for structured linear systems has turned to their use in the study of complex systems and networked systems (see, e.g., [7,8,9,10,11]). Indeed, a consolidated approach to the study of networked systems leverages the network topology (i.e., the map of the interconnections between the agents) to investigate the network properties, whereas the behavior of each agent is modeled by quite simple dynamics—in the most elementary case, the agents are described by single integrators [12].
The widespread use of structured linear systems in the investigation of the properties of networked systems has led to various generalizations of the original paradigm, such as switching structured linear systems [13,14], structured switching descriptor linear systems [15], and structured linear systems with pattern matrices [16,17,18]. In particular, switching structured linear systems were introduced in [13], while in [14] they were considered in connection with electrical networks and complex systems, like the glucose metabolism in the human body, as a means to model networked systems where the topology of the respective interconnections is subject to change.
Since, as mentioned earlier, switching structured linear systems consist of a family of modes, which are structured linear systems, and of an exogenous signal, which rules the switching from one mode to another, the system properties worth investigating are those that are true not only for almost any value of the parameters, but also for any admissible switching sequence. The study of such properties was first approached with geometric methods in [14], where the notion of controlled invariance was introduced in connection with disturbance decoupling, and in [19], where the notion of conditioned invariance was presented in connection with unknown-input state observation.
The geometric notions introduced in [14,19] for switching structured linear systems were also illustrated by directed graphs. As a matter of fact, graph theory has often been used to analyze the properties of structured linear systems, and its extension to switching structured linear systems is quite natural, although not completely straightforward. Several of the classic control problems addressed in the papers mentioned earlier [1,2,3,4] were modeled and solved by graph-theoretic methods, and those methods have been developed further with the broad employment of structured linear systems in the study of networked systems [20,21,22,23,24].
This work is organized as follows. In Section 2, the class of dynamical systems dealt with is introduced. A state-space representation and a graph representation are given and the main assumptions are elucidated. Section 3 delves into the geometric notions of invariance, controlled invariance, and conditioned invariance for switching structured linear systems. In Section 4, these notions are shown to be essential to the solution of the disturbance decoupling problem and of the unknown-input state-observation problem. The proofs of the solvability conditions given for disturbance decoupling by state feedback and for unknown-input state observation can be found in [14,19], where those problems were tackled first. The discussion of the disturbance decoupling problem by output feedback is new in the literature, although it was included in a preliminary version, by the same authors, of [14]. Section 5 contains some concluding remarks.
Notation. and stand for the sets of real numbers and nonnegative real numbers, respectively. Linear maps and matrices are denoted by slanted capital letters like A. Let , where is either a fixed zero or an unknown real parameter; the notation means that the entry of matrix A is not a fixed zero. Given two sets A and B, the symbol denotes the set difference between A and B: i.e., . Given a set A, the notation stands for the cardinality of A.
2. Switching Structured Linear Systems
A switching structured linear system has a state-space representation of the form
where is the time variable, is the state, is the input, and is the output. Moreover, is a piecewise-constant left-continuous function, defined by , where is a finite index set, and is a finite indexed family of structured linear systems of the form
where , , and are matrices of appropriate dimensions whose entries are either fixed zeros or unknown real parameters. It is assumed that each column of , and, respectively, each row of has one and only one entry that is different from a fixed zero. This assumption simplifies the treatment with respect to the general case considered, e.g., in [5]. However, this assumption is often encountered in the literature, since it is satisfied by many real systems that can be effectively modeled as structured linear systems: e.g., multiagent networks [20,25,26], quantum systems [27], and biological systems [28]. The systems of the family are called modes of the switching structured linear system. The function is called the switching signal and each discontinuity of defines a change of the active mode. It is assumed that presents only a finite number of discontinuity in any finite time interval. This assumption is aimed at avoiding undesired behaviors, like Zeno behaviors in particular.
The state-space representation (1) is associated with the graph representation
where is the piecewise-constant left-continuous function considered above, and
is a family of triplets whose elements are defined as follows. The pair consists of the finite set of vertices and of the h-th set of edges , where means that the edge with the tail in and the head in belongs to . Note that all of the pairs of the family have the same set of vertices G, while they differ from each other for the set of edges . Moreover, is the h-th subset of vertices directly connected to the inputs, while is the h-th subset of vertices directly connected to the outputs. In particular, the family of structured linear systems (2) and the family of triplets (4) are associated with each other through the simple rules illustrated below. For any , the structured linear system , with
and the triplet , with , , and , are associated with each other according to the following rules:
- ;
- , with and ;
- , with and .
Consistently with the assumption made with reference to the state-space representation, from the correspondences above it ensues that, for any , each vertex is directly connected to one input at most, while each input is directly connected to only one vertex. Likewise, it ensues that, for any , each vertex is directly connected to one output at most, while each output is directly connected to only one vertex.
In the directed graph corresponding to the h-th triplet, the edge is represented by an arrow with the tail in and the head in ; the vertices belonging to are marked by ingoing arrows; the vertices belonging to are marked by outgoing arrows. An example of a directed graph is shown in Figure 1.
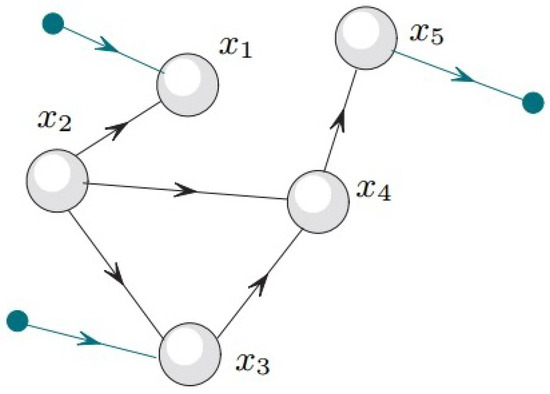
Figure 1.
Directed graph of , where , , , .
From the above discussion, it ensues that a switching structured linear system can be equivalently represented by its state-space representation or by its graph representation. Henceforth, the notation
will be adopted to refer to both representations.
In this context, it is worth reviewing the notion of a switching path that will play a role in the formulation of the disturbance decoupling problems and of the unknown-input state reconstruction problem (see Section 4). An example of a switching path is shown in Figure 2. The formal definition follows.
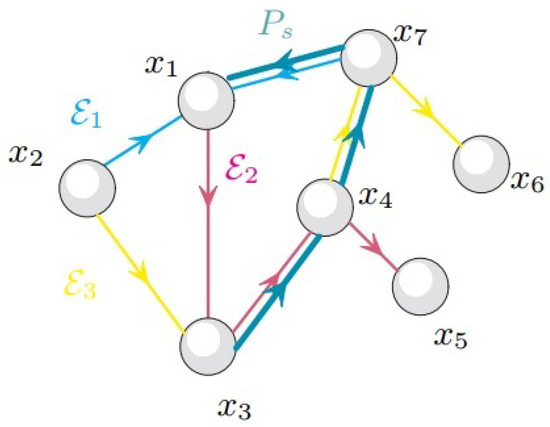
Figure 2.
The switching path in , with , , .
Let be a switching structured linear system. A switching path in is a finite ordered sequence of edges , such that the head of the edge is the tail of the edge , with . The tail of the first edge of the switching path is called the tail of the switching path . The head of the last edge of the switching path is called the head of the switching path .
3. Invariance, Controlled Invariance, and Conditioned Invariance in Switching Structured Linear Systems
This section presents the definitions and the main properties of the fundamental geometric notions of invariance, controlled invariance, and conditioned invariance extended to the context of switching structured linear systems. These notions were first introduced in [14,19].
Definition 1.
A switching invariant subset of the switching structured linear system is a subset such that, for any ,
Figure 3 shows an example of a switching invariant subset.
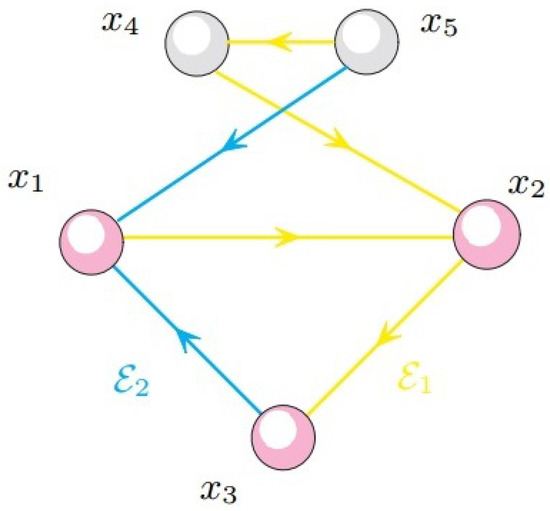
Figure 3.
The switching invariant subset .
Definition 2.
A switching controlled invariant subset of the switching structured linear system is a subset such that, for any ,
Figure 4 shows an example of a switching controlled invariant subset.
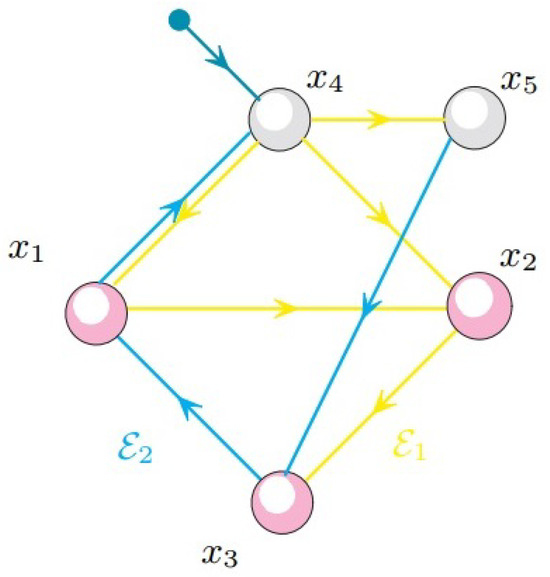
Figure 4.
The switching controlled invariant subset .
Definition 3.
A switching conditioned invariant subset of the switching structured linear system is a subset such that, for any ,
where the symbol stands for the set difference of G and .
Figure 5 shows an example of a switching conditioned invariant subset.
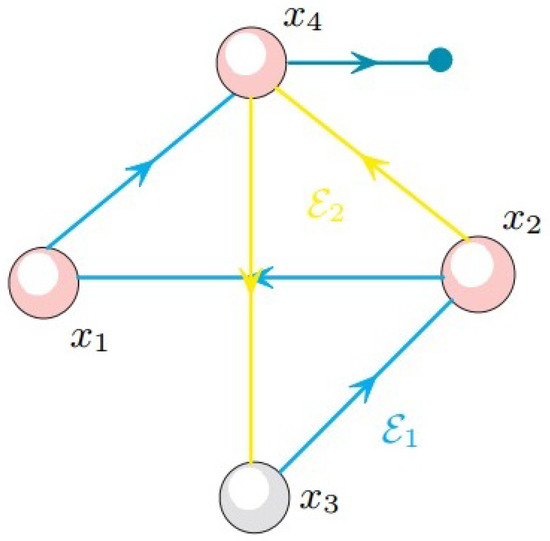
Figure 5.
The switching conditioned invariant subset .
The following definitions are aimed at establishing the equivalence between switching controlled invariance and switching invariance by essential state feedback.
A switching essential state feedback for the switching structured linear system is formed by a family of essential state feedbacks for the family of triplets and by the switching signal . A family of essential state feedbacks for the family of triplets is a family of sets of edges such that, for any ,
The application of to the family of triplets leads to the family of compensated triplets
where the symbol stands for the set difference . For any , the linear map
and the essential state feedback are associated with each other according to the following rule:
and, in particular,
By applying to , one obtains the compensated switching structured linear system
whose state-space representation is
Hence, the anticipated equivalence between switching controlled invariance and switching invariance by essential state feedback can be stated as follows.
Property 1.
Let be a switching structured linear system. The following statements are equivalent:
- A subset is a switching controlled invariant subset of ;
- There exists a switching essential state feedback such that V is a switching invariant subset for .
Figure 6 shows an example of how a suitable choice of the switching essential state feedback turns a switching controlled invariant subset for into a switching invariant subset for .
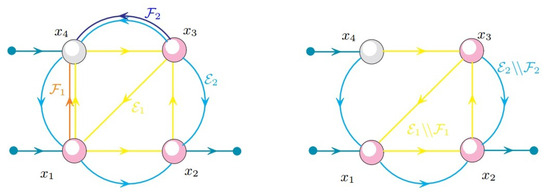
Figure 6.
The subset is a switching controlled invariant of (left) and is a switching invariant for (right), with , .
The arguments developed for switching controlled invariant subsets and switching essential state feedbacks as well as the equivalence between switching controlled invariance and switching invariance by essential state feedback find a counterpart in the context of switching conditioned invariance and switching essential output injections.
A switching essential output injection for the switching structured linear system is formed by a family of essential output injections for the family of triplets and by the switching signal . A family of essential output injections for the family of triplets is a family of sets of edges such that, for any ,
The application of to the family of triplets leads to the family of compensated triplets
where the symbol stands for the set difference . For any , the linear map
and the essential output injection are associated with each other according to the following rule:
and, in particular,
By applying to , one obtains the compensated switching structured linear system
whose state-space representation is
Property 2.
Let be a switching structured linear system. The following statements are equivalent:
- A subset is a switching conditioned invariant subset of ;
- There exists a switching essential output injection such that S is a switching invariant subset for .
Figure 7 shows how an appropriate switching essential output injection turns a switching conditioned invariant subset for into a switching invariant subset for .
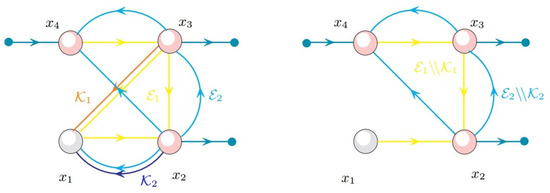
Figure 7.
The subset is a switching conditioned invariant of (left) and is a switching invariant for (right), with and .
In addition to switching essential state feedback and switching essential output injection, it is worth introducing a further compensation scheme, which is called switching essential output feedback and that is exploited in the solution of the problem of disturbance decoupling by output feedback (Section 4).
A switching essential output feedback for the switching structured linear system is formed by a family of essential output feedbacks for the family of triplets and by the switching signal . A family of essential output feedbacks for the family of triplets is a family of sets of edges such that, for any ,
The application of to the family of triplets leads to the family of compensated triplets
where the symbol stands for the set difference . For any , the linear map
and the essential output feedback are associated with each other according to the following rule:
and, in particular,
By applying to , one obtains the compensated switching structured linear system
whose state-space representation is
The following results are relevant to the application of the notion of switching controlled invariance to the solution of the disturbance decoupling problems (Section 4), since they indicate the existence of a switching controlled invariant subset with certain essential properties and they provide a recursive algorithm for its computation.
Proposition 1.
Let be a switching structured linear system and Q a subset of G. The set of all switching controlled invariant subsets of contained in Q has a maximal element.
The symbol is used to denote the maximal switching controlled invariant subset of contained in Q.
Algorithm 1.
The subset is the last term of the monotone nonincreasing sequence
where is the least integer such that .
Likewise, the following results enable the statement of necessary and sufficient solvability conditions for the unknown-input state observation problem and for the disturbance decoupling problem by output feedback grounded on the notion of switching conditioned invariance.
Proposition 2.
Let be a switching structured linear system and D a subset of G. The set of all switching conditioned invariant subsets of containing D has a minimal element.
The symbol is used to denote the minimal switching conditioned invariant subset of containing D.
Algorithm 2.
The subset is the last term of the monotone nondecreasing sequence
where is the least integer such that .
4. Control and Observation Problems
This section deals with the problem of disturbance decoupling by state feedback, the problem of unknown-input state observation, and the problem of disturbance decoupling by output feedback, for switching structured linear systems (the former two were first investigated and solved in [14,19], respectively).
4.1. Disturbance Decoupling by State Feedback
The problem of disturbance decoupling by state feedback concerns a switching structured linear system whose state-space representation is
where is the control input, is the disturbance input, and is the to-be-decoupled output (i.e., the output to be made insensitive to the disturbance). With the obvious meaning of the symbols, one can also refer to the graph representation
and, therefore, adopt the unifying notation
Hence, the disturbance decoupling problem by state feedback is stated as follows.
Problem 1.
Let be a switching structured linear system affected by the disturbance input d. The problem of disturbance decoupling by state feedback consists in finding a switching essential state feedback such that the compensated switching structured linear system does not exhibit any switching path in whose tail and head are in and , respectively, for any .
Theorem 1.
The following statements are equivalent:
- Problem 1 is solvable;
- .
A proof of Theorem 1 was given in [14].
Remark 1.
The formulation of disturbance decoupling given in Problem 1, which requires that there are no switching paths connecting the disturbance input to the output, is stronger (i.e., more demanding) than a formulation that requires that the output is insensitive to the disturbance for almost any instance of the parameters. In fact, the latter formulation includes the case where there may be different paths from the disturbance input to the output, but these paths are such that the effects on the output of the disturbance through each one of them compensate for one another. As will be shown in the following example, the condition of Theorem 1 is necessary and sufficient for the solvability of the disturbance decoupling problem as stated in Problem 1, while it is not necessary for the weaker formulation mentioned in this remark (the issue dealt with in this remark and in the following illustrative example has been clarified thanks to profitable discussions held with Prof. M.K. Camlibel).
Example 1.
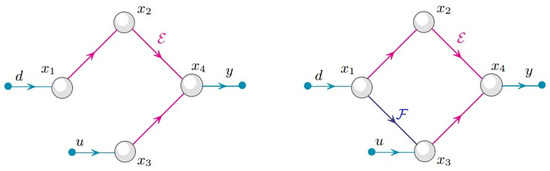
To illustrate the content of Remark 1 with an example, a classic (i.e., non-switching) structured linear system is considered and the notation is simplified consequently.
Let Problem 1 be stated for a structured linear system , where , , , , and .
The computation of , performed according to Algorithm 1, gives . In fact, , , and . Hence, the condition of Theorem 1 is not satisfied and Problem 1 is not solvable. Indeed, from the direct inspection of the digraph of system shown in Figure 8 (left), it is easy to see that there is no essential state feedback achieving the cancellation of any edge of the path from d to y.

Figure 8.
The given structured linear system (left). The compensated structured linear system (right).
Nevertheless, considering the state space representation of , which is of the form (5) with
one can see that the essential state feedback , with
makes the output y insensitive to the disturbance input d for almost any value of the parameters (namely, for all values except those that make the denominator of equal to zero). In fact, simple computations show that , and for all , where the latter implies that for all . As a matter of fact, the essential state feedback introduces an edge from to whose value depends on the values of the parameters of the given system and that gives rise to a new path from d to y whose aim is to annihilate the effect of the existing path in the given system. This fact is illustrated in Figure 8 (right). To complete for this reasoning, it is worth mentioning that, with reference to the parametric state-space representation (5) with (6), the computation of the maximal -controlled invariant subspace contained in , where and , briefly denoted by , according to the classic recursive algorithm (see, e.g., [29], Algorithm 4.1-2), gives
Hence, the classic condition for disturbance decoupling consisting in the inclusion of subspaces is satisfied.
4.2. Unknown-Input State Observation
The unknown-input state observation problem is formulated for a switching structured linear system whose state-space representation is of the form
where is the unknown input, is the measured output, and is the to-be-observed (partial) state. With the obvious meaning of the symbols, the corresponding graph representation is
and the compact notation
can be adopted. Hence, the unknown-input state observation problem is stated as follows.
Problem 2.
Let be a switching structured linear system. The problem of observing the subset of states in the presence of the unknown input directly affecting the subset of states consists in finding a switching essential output injection , with for all , such that, having constructed the switching structured state observer , where for all , the switching structured linear system , which models the evolution of the observation error, does not exhibit any switching path in with the tail and the head in and , respectively, for any .
Theorem 2.
The following statements are equivalent:
- Problem 2 is solvable;
- .
A proof of Theorem 2 was given in [19].
4.3. Disturbance Decoupling by Output Feedback
The problem of disturbance decoupling by output feedback is considered last, since, as will be shown, the necessary and sufficient solvability condition involves both a maximal switching controlled invariant subset and a minimal switching conditioned invariant subset—namely, both of the geometric objects that, so far, have been separately considered in disturbance decoupling and unknown-input state observation, respectively.
The problem of disturbance decoupling by output feedback concerns a switching structured linear system whose state-space representation is of the form
where is the control input, is the disturbance input, is the measurable output, and is the to-be-decoupled output. With the obvious meaning of the symbols, one can also refer to the graph representation
and, therefore, adopt the unifying notation
Hence, the disturbance decoupling problem by output feedback is formulated as follows.
Problem 3.
Let be a switching structured linear system affected by the disturbance input d, with measurable output y and to-be-decoupled output z. The problem of disturbance decoupling by output feedback consists in finding a switching essential output feedback such that the compensated switching structured linear system does not exhibit any switching path in whose tail and head are in and , respectively, for any .
Theorem 3.
The following statements are equivalent:
- Problem 3 is solvable;
- .
Proof.
The condition of the theorem is equivalent to the fact that any switching path in , whose tail and head are in and , respectively, for some , contains at least one edge , for some , whose tail and head are in and . Then, a solution of the problem consists in a switching essential output feedback that removes all the edges of this kind. □
Example 2.
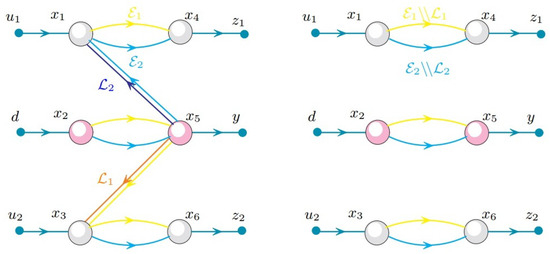
Let Problem 3 be stated for a switching structured linear system with two modes, where , , , , , , and .
The computation of and , performed according to Algorithm 1 and Algorithm 2, respectively, gives
Hence, the condition of Theorem 3 is satisfied and the problem is solvable. A switching essential output feedback , with and , achieves disturbance decoupling, since it cancels those edges with the tail in vertices connected to the measurable output and the head connected to the control inputs contained in the paths originally connecting the disturbance input with the to-be-decoupled output.
The directed graph of the given system and of the devised switching essential output feedback are shown in Figure 9 (left). The directed graph of the compensated system is shown in Figure 9 (right).

Figure 9.
An illustrative example for disturbance decoupling by output feedback.
5. Conclusions
This work has considered in a unified setting the geometric methods and the computational tools recently developed for the study of switching structured linear systems and for the solution of the disturbance decoupling problem (by state feedback and by output injection, respectively) and of the unknown-input state observation problem.
Author Contributions
Conceptualization, E.Z., A.M.P. and G.C.; methodology, E.Z., A.M.P. and G.C.; formal analysis, E.Z., A.M.P. and G.C.; investigation, E.Z., A.M.P. and G.C.; resources, E.Z., A.M.P. and G.C.; writing—original draft preparation, E.Z., A.M.P. and G.C.; writing—review and editing, E.Z., A.M.P. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, C.T. Structural controllability. IEEE Trans. Autom. Control 1974, 19, 201–208. [Google Scholar] [CrossRef]
- van der Woude, J.W. On the structure at infinite of a structured system. Linear Algebra Its Appl. 1991, 148, 145–169. [Google Scholar] [CrossRef]
- Dion, J.M.; Commault, C. Feedback decoupling of structured systems. IEEE Trans. Autom. Control 1993, 38, 1132–1135. [Google Scholar] [CrossRef]
- Commault, C.; Dion, J.M.; Hovelaque, V. A geometric approach for structured systems: Application to disturbance decoupling. Automatica 1997, 33, 403–409. [Google Scholar] [CrossRef]
- Dion, J.M.; Commault, C.; van der Woude, J. Generic properties and control of linear structured systems: A survey. Automatica 2003, 39, 1125–1144. [Google Scholar] [CrossRef]
- Ramos, G.; Aguiar, A.P.; Pequito, S. An overview of structural systems theory. Automatica 2022, 140, 110229. [Google Scholar] [CrossRef]
- Conte, G.; Perdon, A.M.; Zattoni, E.; Moog, C.H. Invariance, controlled invariance and conditioned invariance in structured systems and applications to disturbance decoupling. IOP Conf. Ser. Mater. Sci. Eng. 2019, 707, 012010. [Google Scholar] [CrossRef]
- Commault, C. Structural controllability of networks with dynamical structured nodes. IEEE Trans. Autom. Control 2020, 65, 2736–2742. [Google Scholar] [CrossRef]
- Commault, C.; van der Woude, J.; Frasca, P. Functional target controllability of networks: Structural properties and efficient algorithms. IEEE Trans. Netw. Sci. Eng. 2020, 7, 1521–1530. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Kouvelas, A. Strong structural functional controllability of networks. In Proceedings of the 2021 European Control Conference, Delft, The Netherlands, 29 June–2 July 2021; pp. 1509–1514. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, Y.; Zhai, D.H. Structural controllability of networked relative coupling systems. Automatica 2021, 128, 109547. [Google Scholar] [CrossRef]
- Commault, C.; Kibangou, A. Generic controllability of networks with identical SISO dynamical nodes. IEEE Trans. Control Netw. Syst. 2020, 7, 855–865. [Google Scholar] [CrossRef]
- Boukhobza, T.; Hamelin, F. Observability of switching structured linear systems with unknown input. A graph-theoretic approach. Automatica 2011, 47, 395–402. [Google Scholar] [CrossRef]
- Conte, G.; Perdon, A.M.; Zattoni, E.; Moog, C.H.; Scharbarg, E. Invariance and controlled invariance in switching structured systems with application to disturbance decoupling. IOP Conf. Ser. Mater. Sci. Eng. 2020, 922, 012002. [Google Scholar] [CrossRef]
- Boukhobza, T.; Hamelin, F. Discrete mode observability of structured switching descriptor linear systems: A graph-theoretic approach. Automatica 2013, 49, 3042–3048. [Google Scholar] [CrossRef][Green Version]
- Jia, J.; Trentelman, H.L.; Charalampidis, N.; Camlibel, M.K. Strong structural controllability of colored structured systems. Syst. Control Lett. 2021, 152, 104924. [Google Scholar] [CrossRef]
- Jia, J.; Shali, B.M.; van Waarde, H.J.; Camlibel, M.K.; Trentelman, H.L. Scalable controllability analysis of structured networks. IEEE Trans. Control Netw. Syst. 2022, 9, 891–903. [Google Scholar] [CrossRef]
- Shali, B.M.; VanWaarde, H.J.; Camlibel, M.K.; Trentelman, H.L. Properties of pattern matrices with applications to structured systems. IEEE Control Syst. Lett. 2022, 6, 9319174. [Google Scholar] [CrossRef]
- Zattoni, E.; Perdon, A.M.; Conte, G. Unknown-input state observers for switching linear structured systems. IFAC-PapersOnLine 2022, 55, 25–30. [Google Scholar] [CrossRef]
- van Waarde, H.J.; Monshizadeh, N.; Trentelman, H.L.; Camlibel, M.K. Strong structural controllability and zero forcing. In Structural Methods in the Study of Complex Systems; Lecture Notes in Control and Information Sciences; Springer: Cham, Switzerland, 2020; Volume 482, pp. 91–112. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; Pequito, S.; Pappas, G.J.; Preciado, V.M. On the structural target controllability of undirected networks. IEEE Trans. Autom. Control 2021, 66, 4836–4843. [Google Scholar] [CrossRef]
- Jia, J.; Van Waarde, H.J.; Trentelman, H.L.; Camlibel, M.K. A unifying framework for strong structural controllability. IEEE Trans. Autom. Control 2021, 66, 391–398. [Google Scholar] [CrossRef]
- Zattoni, E.; Perdon, A.M.; Conte, G. Stability and stabilizability of discrete-time structured linear systems. IFAC-PapersOnLine 2022, 55, 90–95. [Google Scholar] [CrossRef]
- Boukhobza, T.; van der Woude, J.; Commault, C.; Millérioux, G. A graph-oriented approach to address generically flat outputs in structured LTI discrete-time systems. Automatica 2022, 142, 110344. [Google Scholar] [CrossRef]
- Monshizadeh, N.; Zhang, S.; Camlibel, M.K. Zero forcing sets and controllability of dynamical systems defined on graphs. IEEE Trans. Autom. Control 2014, 59, 2562–2567. [Google Scholar] [CrossRef]
- Trefois, M.; Delvenne, J.C. Zero forcing number, constrained matchings and strong structural controllability. Linear Algebra Its Appl. 2015, 484, 199–218. [Google Scholar] [CrossRef]
- Burgarth, D.; D’Alessandro, D.; Hogben, L.; Severini, S.; Young, M. Zero forcing, linear and quantum controllability for systems evolving on networks. IEEE Trans. Autom. Control 2013, 58, 2349–2354. [Google Scholar] [CrossRef]
- Califano, C.; Scharbarg, E.; Magdelaine, N.; Moog, C.H. Diabetic gastroparesis modeling and observer design. IFAC-PapersOnLine 2018, 51, 97–102. [Google Scholar] [CrossRef]
- Basile, G.; Marro, G. Controlled and Conditioned Invariants in Linear System Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).