1. Introduction
The Lasso model performs automatic feature selection by shrinking some coefficients to exactly zero. This mechanism prunes irrelevant features while retaining statistically significant predictors, thereby constructing a streamlined model with enhanced interpretability [
1]. Consequently, the Lasso model has emerged as one of the most widely adopted tools for linear regression and finds applications across diverse domains including statistical and machine learning [
2,
3,
4,
5,
6,
7], image and signal processing [
8,
9,
10,
11].
Specifically, for
n random observations
and
p fixed covariates
. This high-dimensional linear model is defined as
where
is the vector of observations,
is the unknown parameter of interest,
is a deterministic design matrix (for without loss of generality, we assume
for all
,
is the noise vector with identically and independently distributed (i.i.d.) Gaussian entries with variance
, and
denotes the identity matrix in
. In general, we assume
, and our goal is to accurately estimate
.
The Lasso model is a type of linear regression model utilized for estimating
and can be formulated as the following optimization problem [
12]
where
is the mean squared error (MSE) loss and the
norm
is the regularizer,
is a predefined tuning parameter that controls the level of regularization. The prediction performance of the Lasso model refers to how well it predicts outcomes or responses based on input features and depends on its ability to strike a balance between regularization and feature selection. The prediction performance of the Lasso model plays a crucial role in understanding its effectiveness [
12,
13,
14].
The
norm in Equation (
2) is the most popular regularization because of its outstanding ability to induce sparsity among convex regularization methods. However, it has been observed that this formal approach often underestimates the high-amplitude components of
[
15]. In contrast, non-convex regularizations in the Lasso model have also made significant progress [
6,
10,
16,
17]. For instance, the smoothly clipped absolute deviation (SCAD) penalty [
18] and the minimax concave penalty (MCP) [
15], as well as
and other non-convex regularization terms, can more accurately estimate high-amplitude components. However, due to their non-convex nature, the objective function is prone to getting stuck in local optima, which poses additional challenges to the solution process.
To utilize the advantages of both non-convex regularization and convex optimization methods, Selesnick et al. introduced the CNC strategy, which involves constructing a non-convex regularizer by subtracting the smooth variation from its convex sparse counterpart [
19,
20,
21,
22]. Under specific conditions, the proposed regularization ensures global convexity of the objective function. Due to its global convexity, CNC sparse regularization can effectively avoid local optima and overcome the biased estimation associated with nonconvex sparse regularization. As a result, it has gained widespread usage in image processing and machine learning applications [
23,
24,
25,
26,
27,
28]. However, to the best of the authors’ knowledge, most of the research on CNC sparse regularization focuses on algorithm design and applications and the theoretical analysis is lacking. This motivates us to conduct an analysis on the prediction performance of the Lasso model with CNC sparse regularization, thereby substantiating that CNC sparse regularization outperforms
regularization.
In this paper, we consider the following Lasso model with CNC sparse regularization
where the non-convex regularization term
is parameterized by a matrix
B, and the global convexity of the objective function in (
3) can also be guaranteed by adjusting
B.
Through rigorous theoretical analysis and comprehensive experimental evaluations, we demonstrate that the utilization of non-convex regularization significantly enhances the prediction performance of the Lasso model, enabling accurate estimation of unknown variables of interest. Our contributions can be summarized as follows
Theoretically, for the Lasso model with a specific CNC sparse regularization, we establish the conditions necessary to ensure global convexity of the objective function. Subsequently, by leveraging oracle inequality, we derive an improved upper bound on prediction performance compared to that of the Lasso model with regularization.
Algorithmically, we derive an ADMM algorithm that ensures convergence to a critical point for the proposed Lasso model with CNC sparse regularization.
Empirically, we demonstrate that the proposed Lasso model with generalized minimax concave (GMC) regularization outperforms regularization in both synthetic data and MRI reconstruction experiments, owing to its utilization of non-convex regularization.
The subsequent sections of this paper are arranged as follows.
Section 2 presents some preliminary and related work concerning CNC sparse regularization, predictive performance results, and convex optimization. In
Section 3, we give theoretical analysis on the prediction performance of the Lasso model with CNC sparse regularization and further propose an effective ADMM algorithm to solve it. In
Section 4, we verified the superiority of the proposed model through synthetic datasets and real datasets. Finally, the conclusions are summarized in
Section 5.
Notation
Throughout this paper, the , , and norms of are defined , , and ; meanwhile, represents the number of non-zero elements in and is the support of . For any given set T, we use and to respectively represent its complement and cardinality . For matrix A, we denote its maximum eigenvalue and minimum eigenvalue as and , respectively. The transpose and the pseudo-inverse of a matrix X are defined as and respectively. For any given subset T of p in a matrix , we denote as the resulting matrix obtained by excluding all columns belonging to the complement of T from X. For the design matrix X, we denote the orthogonal projection onto by . In addition, for the sake of convenience, we denote the prediction loss of two vectors by .
3. Lasso with CNC Sparse Regularization
In this section, we will analyze the Lasso model with CNC sparse regular terms both theoretically and algorithmically. In particular, we will consider the following Lasso model with the non-separable non-convex GMC regularization
where the GMC regularization is defined as (
7), and the matrix parameter
B can influence the non-convexity of
.
3.1. Convex Condition
In this subsection, we explore the adjustment of GMC regularization to preserve the overall convexity of the Lasso model (
14).
Theorem 2. Let , , and . Define the objection function of (14) asthen is convex if and is strictly convex if . By constructing the matrix parameter
B, we can ensure that the convexity conditions mentioned above are maintained. Similar to [
23], when
X and
are specified, a straightforward method to determine the parameter
B is
Then,
which satisfies Theorem 2 when
. The parameter
controls the non-convexity of the
. When
,
and the penalty reduces to the
norm. When
, (
15) is satisfied with equality, resulting in a ’maximally’ non-convex penalty.
According to Theorem 2, we can deduce the following corollary, which is useful in our proof of algorithm convergence.
Corollary 1. For all , is convex, where is the largest eigenvalue of .
By replacing
with
in (
A14), we can draw Corollary 1 from the proof of the Theorem 2.
3.2. Prediction Performance
In this subsection, we analyze the prediction performance of the Lasso model with GMC regularization (
14) and use the oracle inequality to obtain an upper bound on the prediction performance that is better than the upper bound of Lasso model with
regularization.
We consider a general Lasso model with GMC regularization (
14), that is, the GMC regularization term is non-convex and does not necessarily satisfy the convexity condition given by Theorem 2. Due to the non-convexity, it is possible that the global minimum of the proposed Lasso model cannot be achieved. Hence, it becomes crucial to find a stable point that satisfies the conditions. We define
as a stationary point of
when it fulfills
Based on Definition 1, the compatibility factor enables us to establish a subsequent oracle inequality, which is applicable to the stationary points of the Lasso estimator with GMC regularization.
Theorem 3 (Oracle inequality of the Lasso model with GMC regularization).
Assume . Let be a fixed tolerance level and . Let be a stationary point of (14) and is the smallest eigenvalue of . Set the regularization parameter as ; then, the estimation error satisfieswith probability at least for any .
The oracle inequality holds for any
that meets the first-order optimality condition, regardless of whether the regularization is non-convex. This mild condition imposed on
represents a significant divergence from previous findings, such as Theorem 2 of [
12], which is suitable for global minimization but challenging to ensure when employing non-convex regularizations.
Theorem 3 enables the optimization of the error bounds on the right-hand side of (
17) by allowing the selection of suitable values for
and
T. For instance, choose
in (
17) (hence an ‘oracle’), then
; therefore, the (
17) can be rewritten as
Furthermore, if
T is set as the empty set, then
In contrast, if
T is set as the support of
, then
which increases linearly with the sparsity level
.
We compare the prediction error bounds of Theorem 3 with Theorem 1, which is obtained for a Lasso model with the
regularization. We note that the upper bounds of terms within the lower bound in inequality (
17) are limited by the upper bounds of terms within the lower bound in Theorem 1. When
contains larger coefficients, non-convex regularization leads to more stringent bound, hence
. Furthermore, the error bound in Equation (
17) includes
in the denominator, which makes it an upper bound for Theorem 1. This gap can be mitigated by adjusting the matrix parameter
B in
, specifically by selecting a smaller value for
in (
16). However, when
, the non-convex GMC regularization
also tends to
, eliminating the improvement brought by using a non-convex regularization in the first term of the bound. This means that the overall error bound can be adjusted by tuning
, thereby enabling a trade-off with the non-convexity of the regularization.
In summary, despite the non-convex of the regularization term, we can ensure that any stationary point of the proposed Lasso model with GMC regularization possesses a strong statistical guarantee.
3.3. ADMM Algorithm
In this subsection, we will consider using the ADMM algorithm to solve the Lasso model with GMC regularization (
14). Boyd et al. introduced a generalized ADMM framework for addressing sparse optimization problems [
42]. The basic idea is to transform unconstrained optimization problems into constrained ones by splitting variables and then iteratively solve them. ADMM proves to be particularly efficient when the sparse regularization term possesses a closed-form proximal operator. The main challenge in solving (
14) by ADMM lies in how to obtain the proximal operator of the GMC regularization.
The augmented Lagrange form of (
14) can be written as follows by setting
.
where
u represents the Lagrange multiplier and
denotes the penalty parameter. We then update
and
u in an alternating manner.
The objective function in Equation (
22) is differentiable with respect to
. As a result,
can be obtained by utilizing the first-order optimality condition
Equation (
24) serves as the proximal operator for
, although it lacks a closed-form solution. Despite this limitation, the PGD algorithm can be employed to iteratively address Equation (
24).
The substitution of
with (
7) allows us to reformulate Equation (
24) as
Let
and
. The update of
of (
25) can be obtained through PGD algorithm as follows:
where
is the iteration step size. The main challenge of (
26) is solving the gradient
.
According to Lemma 3 in [
24], the last term of
is a differentiable with respect to
. Furthermore, the gradient of
can be expressed as
Note that (
27) contains an
-regularization problem
, which can be viewed as a proximal operator associated with the
, i.e.,
where
can be easily addressed by employing the soft-thresholding function (
13).
Then, by substituting (
28) and (
27) to (
26) and sorting them out, the update of
can be summarized as follows
Finally, the ADMM algorithm for the Lasso model with convex non-convex sparse regularization can be derived by integrating Equations (
23), (
29), and (
30). This derivation is presented as Algorithm 1.
| Algorithm 1 ADMM for solving (14) |
- Require:
. - Ensure:
.
while “stopping criterion is not met” do ; ; . end while |
Furthermore, we provide the following convergence guarantee for Algorithm 1.
Theorem 4. Through proper selection of the penalty parameter ρ, the primal residual , and the dual residual , Algorithm 1 satisfies and .
Theorem 4 illustrates that Algorithm 1 ultimately converges to satisfy both primal and dual feasibility conditions. Additionally, it confirms the equivalence between the augmented Lagrangian formulation (
21) with constant
z and
u values and the original Lasso problem (
14). During each iteration of Algorithm 1, a stationary point
is generated for the augmented Lagrangian formulation (
21) when
z and
u are fixed, which indicates that
also serves as a stationary point for (
14).
4. Numerical Experiment
In this section, we present the efficacy of the proposed Lasso model that incorporates GMC sparse regularization through numerical experiments conducted on synthetic and real-world data. All experiments are demonstrated on MATLAB R2020a on a PC equipped with a 2.5 GHz CPU and 16 GB memory.
4.1. Synthetic Data
The data in this experiment are simulated with
samples and
features, where the correlation between features
j and
is equal to
. The true vector
consists of 800 non-zero entries, all equal to 1. The observations are obtained through the linear model
, where
is Gaussian noise with variance such that
(
). The parameter
is expressed as a fraction of
. The objective function incorporates a maximum penalty
for regularization, which will give the maximum sparse solution, i.e.,
. Then, the range of
values can be set to vary between
in order to obtain a regular path graph. For the GMC regularization, it is necessary to explicitly specify matrix
B we set it by using (
16) and
.
In this experiment, F1-score and root mean square error (RMSE) were chosen as evaluation metrics to assess the predictive performance of model (
14).
The F1 score is the harmonic mean of precision and recall, offers a more comprehensive perspective for assessing model performance in comparison to solely considering precision and recall metrics. Specifically, the precision and recall are defined as
where
and
respectively represent the estimated value and the true value. Then, the F1 score is defined as
The range of F1 score is between 0 and 1, where an F1 score of 1 indicates complete support for recovery, meaning the model accurately estimates sparse vectors; while an F1 score of 0 means no support for recovery, indicating zero estimation capability. Thus, a higher F1 score signifies stronger predictive performance demonstrated by the model.
The RMSE is an important indicator in regression model evaluation, which can be used to measure the magnitude of prediction errors. Its definition is as follows
where
is the
i-th predicted value,
is the
i-th actual observed value,
n is the number of observations. A smaller RMSE value indicates a higher predictive capability and better model fit.
We compared the GMC sparse regularization (
14) with the traditional
and
regularizations. To obtain typical conclusions, we conducted 100 Monte Carlo experiments using random noise with
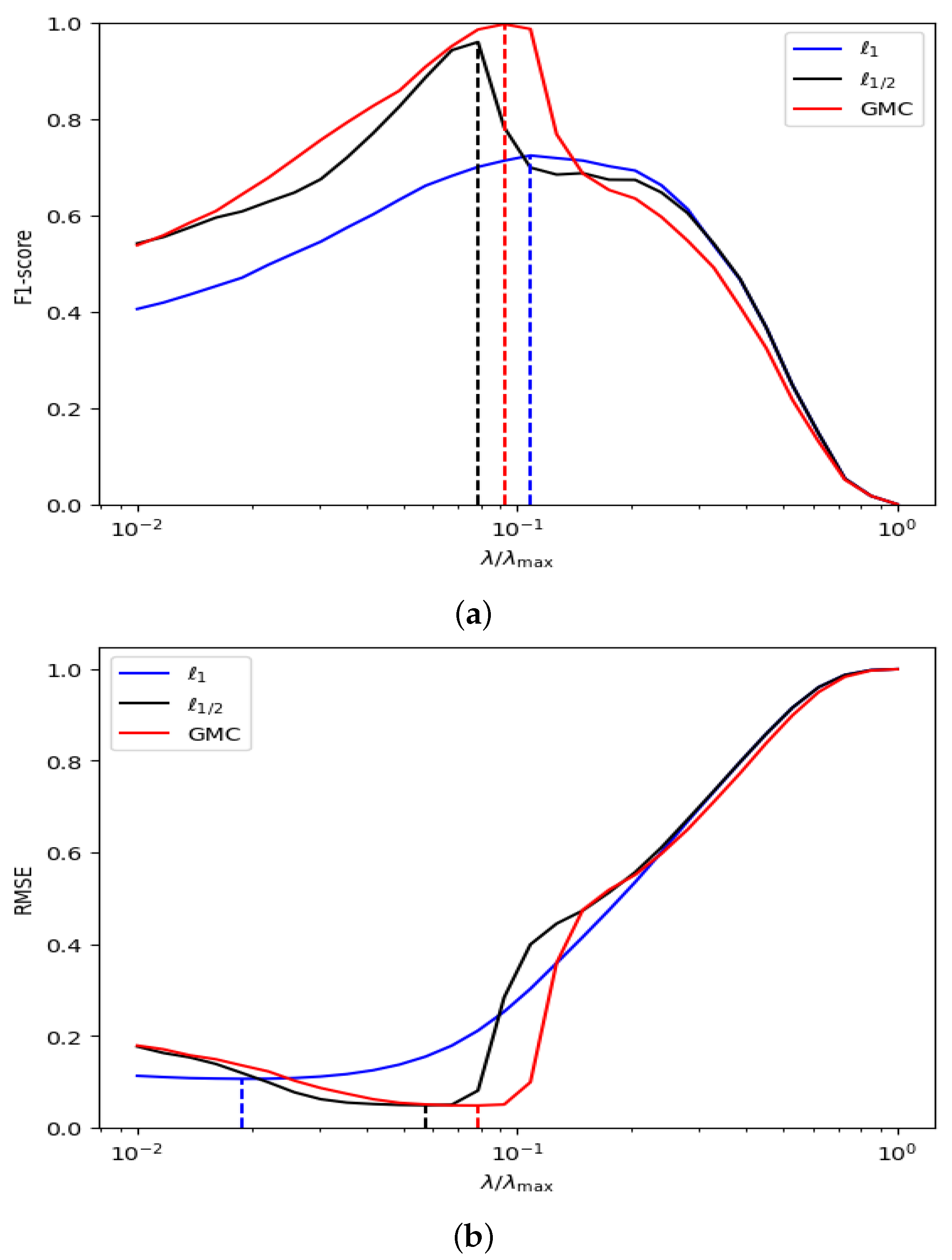
and calculated the average F1 and RMSE values. As shown in
Figure 1a, when an appropriate
value is selected, the F1 score of the GMC sparse regularization reaches the maximum value of 1. In contrast, the F1 scores of the
and
regularizations are approximately 0.7 and 0.95, respectively, both lower than the performance of the GMC regularization. Additionally, it can be clearly observed from
Figure 1b that in the sparse vector prediction task, the minimum RMSE of the GMC sparse regularization is significantly lower than that of the
and
regularizations. This result further validates the superior accuracy of the GMC sparse regularization in sparse vector prediction. On the other hand,
Figure 1 shows that when estimating sparse vectors, the difference between the
values corresponding to the maximum F1 score and the minimum RMSE in the Lasso model based on GMC sparse regularization is relatively small. In contrast, this difference is larger in the
regularization, indicating that GMC sparse regularization (
14) outperforms the
and
regularizations in terms of prediction performance when choosing an appropriate
value.
The conclusion of our study highlights the exceptional predictive performance of our model (
2) in estimating sparse vectors, surpassing the
regularization approach employed by the Lasso model. Additionally, although the Lasso model with
regularization also performs well in prediction tasks, its non-convexity poses challenges for the algorithms solving the objective function. In contrast, our model not only has excellent predictive ability but also ensures the overall convexity of the objective function, thereby providing convenient conditions for the design and implementation of optimization algorithms. In summary, the model proposed in this study has significant advantages in both predictive performance and optimization characteristics, effectively avoiding the computational difficulties brought by non-convex regularization methods.
4.2. MRI Reconstruction
The utilization of high-dimensional sparse linear regression serves as the foundation for numerous signal and image processing techniques, including MRI reconstruction [
43,
44,
45]. The MRI is a powerful medical imaging technique, featuring high soft tissue contrast and the advantage of being radiation-free. It is widely used in clinical diagnosis and scientific research fields. In this experimental, we employ GMC sparse regularization (
15) for MRI reconstruction and compare its performance against
and
regularization.
To make the statement clear, we define the design matrix
, where
is the sampling template, and
is the sparse Fourier operator. We tested different reconstruction models on three MRI images with variable density sampling and Cartesian sampling templates, respectively. For comparison, all images are set to
pixels, with grayscale values ranging from 0 to 255. The parameters were
,
, the iteration step size
was chosen
. For the GMC regularization, it is necessary to explicitly specify matrix
B and set it using (
16) with
.
In this experiment, we selected relative error (RE) and peak signal-to-noise ratio (PSNR) as evaluation metrics to quantitatively assess the quality and accuracy of reconstructed images.
The RE is defined as
where
and
are the original and reconstructed images, respectively.
The PSNR is defined as
where
,
, and
,
are the reconstructed, and the original image, respectively.
For these two types of quantitative evaluation criteria, the lower the RE value, the more superior the reconstruction effect, while for PSNR, an increase in numerical value indicates a more outstanding reconstruction ability.
To further enhance the visual contrast effect, we calculated the difference between the reconstructed image and the original image. Furthermore, we magnified a small portion of the local image to show more details. The reconstruction results of three regularizations are shown in
Figure 2,
Figure 3 and
Figure 4. It can be found that the reconstructed images based on
regularization have problems such as blurred edges and residual shadows, and the
regularization reconstruction model also shows similar phenomena. In contrast, the reconstructed images based on GMC sparse regularization are closer to the original images and exhibit higher reconstruction quality.
Additionally, we conducted a quantitative evaluation of the reconstruction results in
Table 1. It is obvious that compared with
and
regularization, GMC sparse regularization has the best performance in MRI reconstruction and can obtain the lowest RE and highest PSNR.
5. Conclusions
In this paper, we propose CNC sparse regularization as a valuable alternative to the regularization used in Lasso regression. This approach effectively addresses the issue of underestimation for high-amplitude components while ensuring the global convexity of the objective function. Our theoretical analysis demonstrates that the prediction error bound associated with CNC sparse regularization is smaller than that of regularization, which provides theoretical support for the practical application of the CNC regularization. Additionally, we demonstrate that the Lasso model with CNC regularization exhibits superior performance on both synthetic and real-world datasets. These findings suggest its potential significance in future applications such as image denoising, image reconstruction, seismic reflection analysis, etc.
Additionally, given that the oracle inequality of the Lasso model relies on the restricted eigenvalue condition, future research directions may include exploring theoretical guarantees under more relaxed assumptions, such as the oracle inequality based on weak correlation or unconstrained design matrices, and experimentally verifying the practical effectiveness of the restricted eigenvalue condition (such as calculating the specific value of ), and further analyzing its impact on model performance.