Adaptive Reconfigurable Learning Algorithm for Robust Optimal Longitudinal Motion Control of Unmanned Aerial Vehicles
Abstract
1. Introduction
1.1. Literature Review
1.2. Main Contributions
- Constitution of a baseline LQI control law for the longitudinal motion control of a UAV. The asymptotic stability of the baseline LQI tracking controller is analyzed in a subsequent discussion.
- Formulation of the proposed RLCA framework that synergistically combines the dissipative, anti-dissipative term, and model-reference tracking control action in the learning control law.
- Augmentation of the RLCA with a superior layer of state-error-driven hyperbolic scaling functions to autonomously modify the learning gains, ensuring robustness against disturbances.
- Validation of the enhanced performance of the adaptive RLCA scheme over the baseline LQI controller via customized MATLAB simulations.
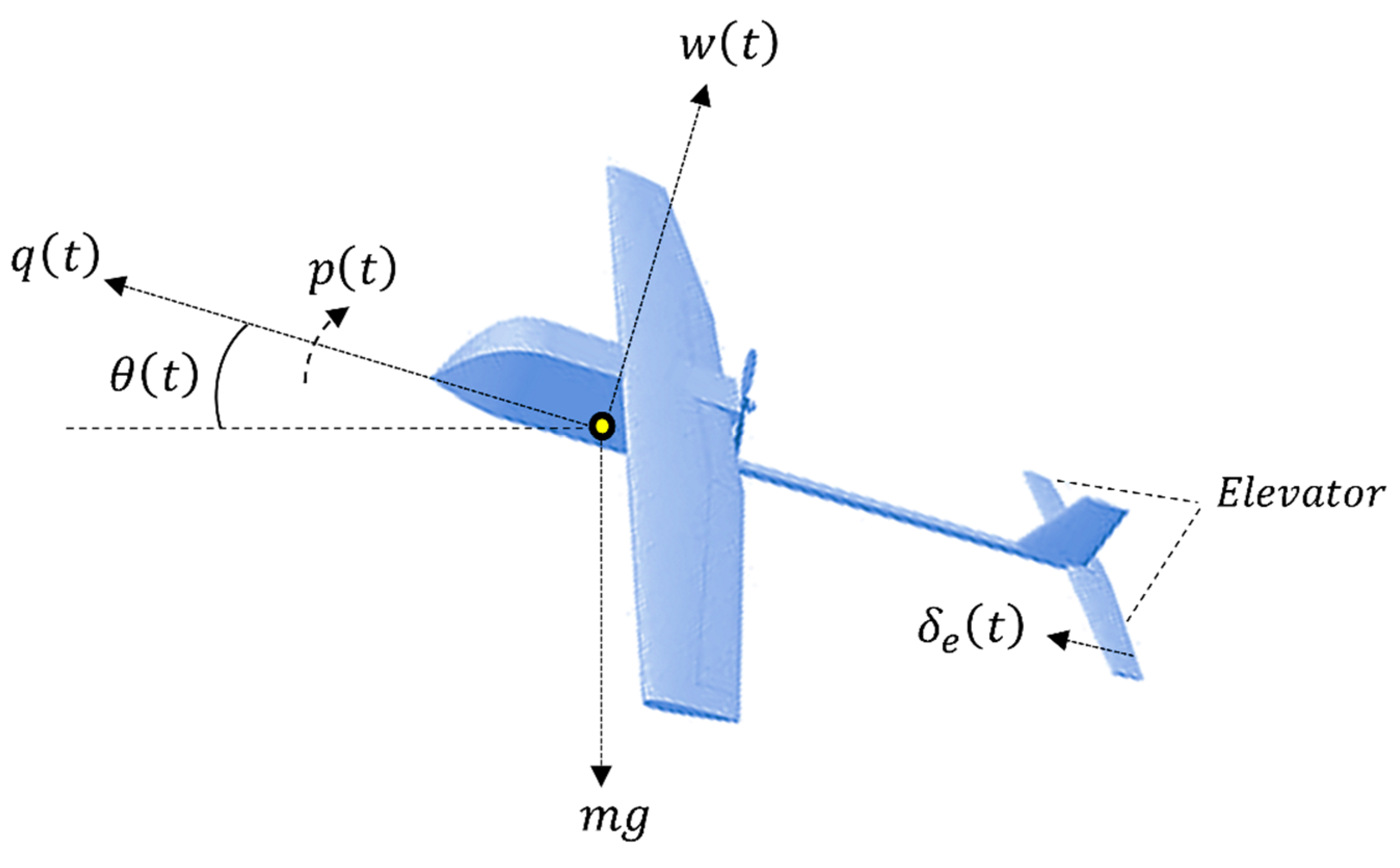
2. System Description
2.1. State Space Model
2.2. Baseline LQI Controller
3. Proposed Control Methodology
3.1. Learning Control Algorithm (LCA)
3.2. Reconfigurable Learning Control Algorithm (RLCA)
- For small errors, the adaptation law intensifies the dissipative control action, applying minimal corrective control.
- For moderate errors, a combination of dissipative and model-reference tracking terms is deployed to ensure optimal state regulation without excessive control input.
- For large errors, the anti-dissipative term is activated to intensify the (phase-informed) control actions for robust disturbance rejection, followed by a gradual transition back to nominal conditions.
4. Parameter Optimization Procedure
5. Simulations and Results
5.1. Simulation Setup
5.2. Simulation Results
- A.
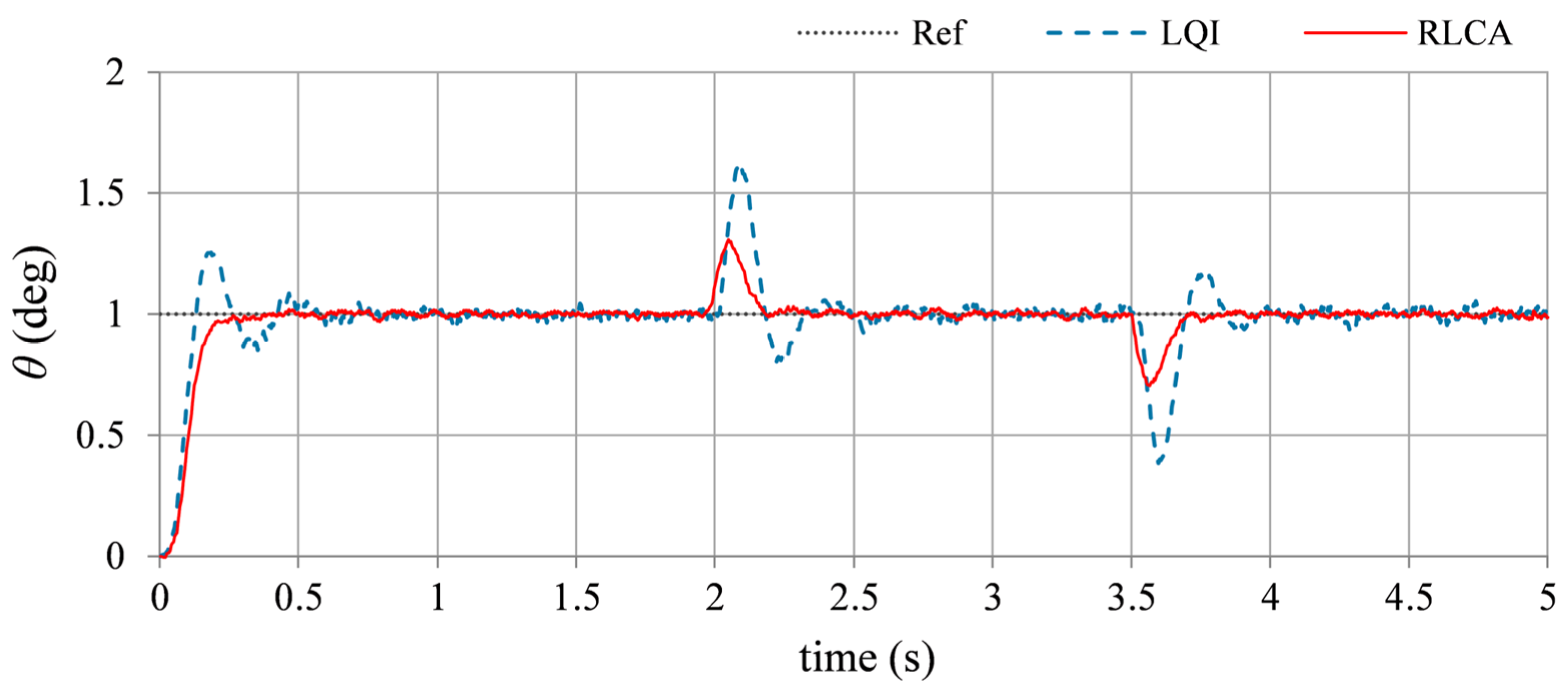
- Step reference tracking: This simulation case is used to evaluate the controller’s ability to track step changes in altitude under nominal (disturbance-free) conditions. The UAV longitudinal model with nominal parameters is used. The test is performed by tasking the UAV to track a step reference trajectory of +1.0 deg. The variations in the pitch angle of the LQI controller and the RLCA are shown in Figure 9.
- B.
- Ramp reference tracking: This test case assesses the UAV’s ability to follow continuously changing altitude as a result of cruise altitude adjustments for steady ascent (or descent) during long-range flights. A ramp trajectory closely mimics how a UAV’s autopilot system adjusts altitude smoothly during the takeoff phase or the landing phase. Hence, this test is performed by tasking the UAV model to track the ramp reference trajectory of 4.0 deg. peak-to-peak amplitude, +3.0 deg. offset, and a frequency of 0.1 Hz to represent a gradual altitude climb and descent. The reference tracking accuracy (or lag) manifested by each controller is presented in Figure 10.
- C.
- Impulsive disturbance suppression: This simulation is used to test the UAV’s disturbance rejection ability against sudden external forces caused by wind gusts or mid-air collision with flying objects. The test is performed by introducing an external pulse of ±2.0 V magnitude and 100 ms duration in the control input signal at t = 2.0 s and t = 3.5 s, respectively, to observe the system’s transient response. This arrangement emulates the application of a short-duration impulsive force under steady flight conditions of the UAV. The time domain profiles of the UAV’s pitch angle, under the influence of each controller, are shown in Figure 11.
- D.
- Step disturbance rejection: This simulation case examines the UAV’s response to sustained external disturbances, such as constant wind disturbance or a sudden change in elevator deflection. The test is performed by introducing an external step signal of +1.0 V magnitude and 100 ms duration in the control input signal at t = 2.0 s to observe the system’s disturbance recovery response. This arrangement emulates the application of a constant external force under steady flight conditions of the UAV. The time domain profiles of the UAV’s pitch angle, under the influence of each controller, are shown in Figure 12.
- E.
- Model uncertainties compensation: This simulation evaluates the UAV’s ability to compensate for model uncertainties resulting from variations in actuator dynamics. This scenario captures a critical aspect of uncertainty compensation—adjustments in control system dynamics due to actuator nonlinearities or miscalibrations. The test is conducted by increasing the servomotor gain by 20% at t = 2.0 s, simulating the actuator’s sensitivity to hardware inconsistencies or miscalibrations. The sudden increment in modifies the UAV’s state-space model by changing key system parameters, and altering the elevator’s control response characteristics, which potentially affects the UAV’s pitch stability and tracking accuracy. The time-domain responses of the UAV’s pitch angle, under the influence of each controller, are presented in Figure 13.
- F.
- Performance under extreme conditions: To rigorously assess the robustness of the UAV’s control algorithm in extreme real-world conditions, a test case is designed with simultaneous dynamic variations, external disturbances, and sensor noise. The UAV follows a continuous ramp reference trajectory, challenging its tracking performance under changing setpoints. Sudden impulsive disturbances of ±2.0 V magnitude and 100 ms duration are injected at discrete intervals to simulate wind gusts or mid-air collisions, while band-limited white noise is added to the control input to replicate turbulence and sensor noise. Additionally, a 20% increment in the UAV’s servomotor gain at t ≈ 8.0 s is introduced to assess robustness against model-induced parametric uncertainties. The time-domain responses of the UAV’s pitch angle, under the influence of each controller, are presented in Figure 14.
5.3. Performance Evaluation and Discussion
- RMSEθ: The root mean squared value of the tracking error , calculated as follows:where represents the total number of samples.
- OS: The peak deviation observed during the start-up phase of the response;
- Tset: The duration required for the system response to settle within ±2% of the reference value;
- Mpeak: The maximum deviation (overshoot or undershoot) that occurs following a disturbance;
- Trec: The time taken for the response to stabilize within ±2% of the reference value after experiencing a disturbance.
- Dissipative control component: Under small error conditions, the dissipative term ensures controlled energy dissipation, preventing excessive control input fluctuations that could lead to oscillations or overshoot. This mechanism exponentially attenuates the applied control action as the system state approaches equilibrium, ensuring a smooth and stable convergence.
- Model-reference tracking component: The RLCA employs an LQI-derived model-reference tracking term, which acts as a baseline controller under nominal conditions. By maintaining alignment with the LQI control law when disturbances are absent, the RLCA preserves steady-state accuracy while minimizing unnecessary control effort. This ensures that the system operates optimally without excessive control actions that could compromise stability.
- Anti-dissipative control component: In contrast to the LQI controller, which lacks a real-time adaptive response to exogenous perturbations, the RLCA leverages an anti-dissipative term informed by the phase of the system’s state error. This term intensifies control actions under large error conditions, ensuring rapid disturbance rejection. The inclusion of an error cube polynomial further amplifies corrective control inputs when the system deviates significantly from the reference trajectory, accelerating transient recovery while maintaining stability.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Irfan, S.; Zhao, L.; Ullah, S.; Javaid, U.; Iqbal, J. Differentiator- and observer-based feedback linearized advanced nonlinear control strategies for an unmanned aerial vehicle system. Drones 2024, 8, 527. [Google Scholar] [CrossRef]
- Sonugür, G. A Review of quadrotor UAV: Control and SLAM methodologies ranging from conventional to innovative approaches. Robot. Auton. Syst. 2023, 161, 104342. [Google Scholar]
- Asadzadeh, S.; de Oliveira, W.J.; de Souza Filho, C.R. UAV-based remote sensing for the petroleum industry and environmental monitoring: State-of-the-art and perspectives. J. Petroleum Sci. Eng. 2022, 208, 109633. [Google Scholar]
- Li, H.; Wang, C.; Yuan, S.; Zhu, H.; Li, B.; Liu, Y.; Sun, L. Energy Scheduling of Hydrogen Hybrid UAV Based on Model Predictive Control and Deep Deterministic Policy Gradient Algorithm. Algorithms 2025, 18, 80. [Google Scholar] [CrossRef]
- Tutsoy, O.; Hendoustani, D.; Ahmadi, K.; Nabavi, Y.; Iqbal, J. Minimum distance and minimum time optimal path planning with bioinspired machine learning algorithms for impaired unmanned air vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9069–9077. [Google Scholar]
- Liu, C.; Chen, W. Disturbance Rejection Flight Control for Small Fixed-Wing Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2016, 39, 2810–2819. [Google Scholar]
- Ducard, G.; Carughi, G. Neural Network Design and Training for Longitudinal Flight Control of a Tilt-Rotor Hybrid Vertical Takeoff and Landing Unmanned Aerial Vehicle. Drones 2024, 8, 727. [Google Scholar] [CrossRef]
- Yang, Y.; Kim, S.; Lee, K.; Leeghim, H. Disturbance Robust Attitude Stabilization of Multirotors with Control Moment Gyros. Sensors 2024, 24, 8212. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, D.; Di Gennaro, S.; Di Ferdinando, M.; Acosta Lùa, C. Robust Control of UAV with Disturbances and Uncertainty Estimation. Machines 2023, 11, 352. [Google Scholar] [CrossRef]
- Yit, K.K.; Rajendran, P. Enhanced Longitudinal Motion Control of UAV Simulation by Using P-LQR Method. Int. J. Micro Air Vehicle 2015, 7, 203–210. [Google Scholar] [CrossRef]
- Li, J.; Liu, X.; Wu, D.; Pi, Z.; Liu, T. A High Performance Nonlinear Longitudinal Controller for Fixed-Wing UAVs Based on Fuzzy-Guaranteed Cost Control. Drones 2024, 8, 661. [Google Scholar] [CrossRef]
- Sree Ezhil, V.R.; Rangesh Sriram, B.S.; Christopher Vijay, R.; Yeshwant, S.; Sabareesh, R.K.; Dakkshesh, G.; Raffik, R. Investigation on PID controller usage on Unmanned Aerial Vehicle for stability control. Mater. Today: Proc. 2022, 66, 1313–1318. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Lowenberg, M.H.; Neild, S.A. Identifying limits of linear control design validity in nonlinear systems: A continuation-based approach. Nonlinear Dyn. 2021, 104, 901–921. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Zeb, A.A.; Ali, A.H.; Saleem, M.A. Online adaptive PID tracking control of an aero-pendulum using PSO-scaled fuzzy gain adjustment mechanism. Soft Comput. 2020, 24, 10629–10643. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhang, Y. A Fast-Convergent Hyperbolic Tangent PSO Algorithm for UAVs. IEEE Access 2020, 8, 132456–132465. [Google Scholar]
- Wang, J.; Zhang, L.; Liu, Y. Parameter Adaptation-Based Ant Colony Optimization with Dynamic Hybrid Mechanism. Int. J. Comput. Intell. Appl. 2020, 19, 215–230. [Google Scholar]
- Zhang, L.; Wang, X.; Li, Y. Application of Hybrid Algorithm Based on Ant Colony Optimization and Particle Swarm Optimization in UAV Path Planning. J. Intell. Robot. Syst. 2023, 101, 635–648. [Google Scholar]
- Perrusquía, A.; Yu, W. dentification and optimal control of nonlinear systems using recurrent neural networks and reinforcement learning: An overview. Neurocomput 2021, 438, 145–154. [Google Scholar]
- Wang, H.; Xu, K.; Liu, P.X.; Qiao, J. Adaptive Fuzzy Fast Finite-Time Dynamic Surface Tracking Control for Nonlinear Systems. IEEE Trans. Circuit Syst. 2021, 68, 4337–4348. [Google Scholar] [CrossRef]
- Moali, O.; Mezghani, D.; Mami, A.; Oussar, A.; Nemra, A. UAV Trajectory Tracking Using Proportional-Integral-Derivative-Type-2 Fuzzy Logic Controller with Genetic Algorithm Parameter Tuning. Sensors 2024, 24, 6678. [Google Scholar] [CrossRef]
- Kuang, J.; Chen, M. Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances. Drones 2024, 8, 614. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, X.; Yang, D. Double-layer fuzzy adaptive NMPC coordinated control method of energy management and trajectory tracking for hybrid electric fixed wing UAVs. Int. J. Hydrogen Energy 2022, 47, 39239–39254. [Google Scholar]
- Kanokmedhakul, Y.; Bureerat, S.; Panagant, N.; Radpukdee, T.; Pholdee, N.; Yildiz, A.R. Metaheuristic-assisted complex H-infinity flight control tuning for the Hawkeye unmanned aerial vehicle: A comparative study. Expert. Syst. Appl. 2024, 248, 123428. [Google Scholar]
- Yanez-Badillo, H.; Beltran-Carbajal, F.; Tapia-Olvera, R.; Favela-Contreras, A.; Sotelo, C.; Sotelo, D. Adaptive robust motion control of quadrotor systems using artificial neural networks and particle swarm optimization. Mathematics 2021, 9, 2367. [Google Scholar] [CrossRef]
- Flores, G. Longitudinal modeling and control for the convertible unmanned aerial vehicle: Theory and experiments. ISA Trans. 2022, 122, 312–335. [Google Scholar] [PubMed]
- Madeiras, J.; Cardeira, C.; Oliveira, P.; Batista, P.; Silvestre, C. Saturated Trajectory Tracking Controller in the Body-Frame for Quadrotors. Drones 2024, 8, 163. [Google Scholar] [CrossRef]
- Liang, X.; Zheng, M.; Zhang, F. A Scalable Model-Based Learning Algorithm with Application to UAVs. IEEE Control Syst. Lett. 2018, 2, 839–844. [Google Scholar] [CrossRef]
- Lwin, N.; Tun, H.M. Implementation of flight control system based on Kalman and PID controller for UAV. Int. J. Sci. Technol. Res. 2014, 3, 309–312. [Google Scholar]
- Rahimi, M.R.; Hajighasemi, S.; Sanaei, D. Designing and simulation for vertical moving control of UAV system using PID, LQR and Fuzzy Logic. Int. J. Elect. Comput. Eng. 2013, 3, 651. [Google Scholar]
- Zhao, X.; Yuan, M.; Cheng, P.; Xin, L.; Yao, L. Robust H∞/S-plane Controller of Longitudinal Control for UAVs. IEEE Access 2019, 7, 91367–91374. [Google Scholar]
- Maqsood, A.; Hiong Go, T. Longitudinal flight dynamic analysis of an agile UAV. Aircr. Eng. Aerosp. Technol. 2010, 82, 288–295. [Google Scholar]
- Saleem, O.; Kazim, M.; Iqbal, J. Robust Position Control of VTOL UAVs Using a Linear Quadratic Rate-Varying Integral Tracker: Design and Validation. Drones 2025, 9, 73. [Google Scholar] [CrossRef]
- Saleem, O.; Iqbal, J. Blood-glucose regulator design for diabetics based on LQIR-driven Sliding-Mode-Controller with self-adaptive reaching law. PLoS ONE 2024, 19, e0314479. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Saleem, O.; Iqbal, J.; Afzal, M.S. A robust variable-structure LQI controller for under-actuated systems via flexible online adaptation of performance-index weights. PLoS ONE 2023, 18, e0283079. [Google Scholar]
- Saleem, O.; Iqbal, J. Phase-Based Adaptive Fractional LQR for Inverted-Pendulum-Type Robots: Formulation and Verification. IEEE Access 2024, 12, 93185–93196. [Google Scholar]
- Alagoz, B.B.; Ates, A.; Yeroglu, C.; Senol, B. An experimental investigation for error-cube PID control. Trans. Inst. Meas. Control 2015, 37, 652–660. [Google Scholar]
- Hassan, M.A.; Cao, Z.; Man, Z. Hyperbolic-Secant-Function-Based Fast Sliding Mode Control for Pantograph Robots. Machines 2023, 11, 941. [Google Scholar] [CrossRef]












| Control Term | Mathematical Expression |
|---|---|
| Dissipative term | |
| Model-reference tracking term | |
| Anti-dissipative term |
| Experiment | Performance Index | Control Procedure | ||
|---|---|---|---|---|
| Symbol | Unit | LQI | RLCA | |
| A | RMSEθ | deg. | 0.017 | 0.013 |
| OS | deg. | 0.246 | 0.027 | |
| Tset | sec. | 0.516 | 0.296 | |
| B | RMSEθ | deg. | 0.127 | 0.026 |
| OS | deg. | 1.537 | 0.217 | |
| Tset | sec. | 0.514 | 0.288 | |
| C | RMSEθ | deg. | 0.027 | 0.019 |
| OS | deg. | 0.255 | 0.020 | |
| Tset | sec. | 0.524 | 0.252 | |
| Mpeak | deg. | 0.63 | 0.31 | |
| Trec | sec. | 0.305 | 0.211 | |
| D | RMSEθ | deg. | 0.023 | 0.017 |
| OS | deg. | 0.247 | 0.025 | |
| Tset | sec. | 0.520 | 0.204 | |
| Mpeak | deg. | 0.333 | 0.145 | |
| Trec | sec. | 1.292 | 0.815 | |
| E | RMSEθ | deg. | 0.028 | 0.015 |
| OS | deg. | 0.250 | 0.010 | |
| Tset | sec. | 0.517 | 0.288 | |
| Mpeak | deg. | 0.735 | 0.270 | |
| Trec | sec. | 0.427 | 0.403 | |
| F | RMSEθ | deg. | 0.263 | 0.081 |
| OS | deg. | 1.193 | 0.046 | |
| Tset | sec. | 0.496 | 0.302 | |
| Mpeak | deg. | 2.958 | 1.709 | |
| Trec | sec. | 0.344 | 0.235 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, O.; Tanveer, A.; Iqbal, J. Adaptive Reconfigurable Learning Algorithm for Robust Optimal Longitudinal Motion Control of Unmanned Aerial Vehicles. Algorithms 2025, 18, 180. https://doi.org/10.3390/a18040180
Saleem O, Tanveer A, Iqbal J. Adaptive Reconfigurable Learning Algorithm for Robust Optimal Longitudinal Motion Control of Unmanned Aerial Vehicles. Algorithms. 2025; 18(4):180. https://doi.org/10.3390/a18040180
Chicago/Turabian StyleSaleem, Omer, Aliha Tanveer, and Jamshed Iqbal. 2025. "Adaptive Reconfigurable Learning Algorithm for Robust Optimal Longitudinal Motion Control of Unmanned Aerial Vehicles" Algorithms 18, no. 4: 180. https://doi.org/10.3390/a18040180
APA StyleSaleem, O., Tanveer, A., & Iqbal, J. (2025). Adaptive Reconfigurable Learning Algorithm for Robust Optimal Longitudinal Motion Control of Unmanned Aerial Vehicles. Algorithms, 18(4), 180. https://doi.org/10.3390/a18040180







