Abstract
The Euler-Type Universal Numerical Integrator (E-TUNI) is a discrete numerical structure that couples a first-order Euler-type numerical integrator with some feed-forward neural network architecture. Thus, E-TUNI can be used to model non-linear dynamic systems when the real-world plant’s analytical model is unknown. From the discrete solution provided by E-TUNI, the integration process can be either forward or backward. Thus, in this article, we intend to use E-TUNI in a backward integration framework to model autonomous non-linear dynamic systems. Three case studies, including the dynamics of the non-linear inverted pendulum, were developed to verify the computational and numerical validation of the proposed model.
1. Introduction
The Euler-Type Universal Numerical Integrator (E-TUNI) is a particular case of a Universal Numerical Integrator (UNI). In turn, the UNI is the coupling of a conventional numerical integrator (e.g., Euler, Runge–Kutta, Adams-Bashforth, Predictive-Corrector, among others) with some kind of universal approximator of functions (e.g., MLP neural networks, SVM, RBF, wavelets, fuzzy inference systems, among others). Furthermore, UNIs generally work exclusively with neural networks with feed-forward architecture through supervised learning with input/output patterns.
In [1], the first work involving the mathematical modelling of an artificial neuron is presented. In [2,3], it is mathematically demonstrated, independently, that feed-forward neural networks with Multi-Layer Perceptron (MLP) architecture are universal approximators of functions. For the mathematical demonstration of the universality of feed-forward networks, a crucial starting point is the Stone-Weierstrass theorem [4]. An interesting work on the universality of neural networks involving the ReLU neuron can be found in [5]. In summary, many neural architectures were developed in the last half of the twentieth century, involving shallow neural networks [6]. On the other hand, in this century, many architectures of deep neural networks demonstrated the great power of neural networks [7].
So, artificial neural networks solve an extensive range of computational problems. However, in this article, we limit the application of artificial neural networks with feed-forward architecture in the resolution of mathematical problems involving modelling autonomous non-linear dynamic systems governed by a system of ordinary differential equations. With the neural networks, it is possible to solve the inverse problem of modelling dynamical systems, i.e., given the solution of the dynamical system, then obtain the instantaneous derivative functions or the mean derivative functions of the system.
The starting point for the proper design of a Universal Numerical Integrator (UNI) is the conventional numerical integrators [8,9,10,11,12,13,14,15]. In [16], a qualitative and very detailed description of the design of a UNI is presented. Also, in [16], an appropriate classification is given for the various types of Universal Numerical Integrators (UNIs) found in the literature.
According to these authors, the UNIs can be divided into three large groups, giving rise to three different methodologies, namely: (i) the NARMAX methodology (Nonlinear Auto Regressive Moving Average with Exogenous input); (ii) the instantaneous derivatives methodology (e.g., Runge–Kutta neural network, Adams-Bashforth neural network, Predictive-Corrector neural network, among others), and (iii) mean derivatives methodologies or E-TUNI. For a detailed understanding of the similarities and differences between the existing UNIS types, see again [16].
In practice, the leading scientific works involving the proper design of a UNI are: (i) the NARMAX methodology in [17,18,19,20,21]; (ii) the Runge–Kutta neural network in [22,23,24,25]; (iii) the Adams-Bashforth neural network in [26]; and (iv) the E-TUNI in [27,28]. For this article, it should be noted that E-TUNI works exclusively with mean derivative functions instead of instantaneous derivative functions. Furthermore, the NARMAX and mean derivative methodologies are of fixed steps in the simulation phase, while the instantaneous derivative methodologies are of varied integration steps in the simulation phase [16]. However, all of them are fixed steps in the training phase.
In this paragraph, we briefly describe existing work on E-TUNI. In [27], it is a technological application of E-TUNI using neural networks with MLP architecture. In [28], it is a technological application of E-TUNI using fuzzy logic and genetic algorithms. Still in [28], the fuzzy membership functions are adjusted automatically, using genetic algorithms through supervised learning using input/output patterns.
However, none of the previous works used E-TUNI with backward integration. Therefore, this article’s originality lies in using E-TUNI in a backward integration process coupled with a shallow neural network with MLP architecture. As far as we know, this has not yet been done.
This article is divided as follows: Section 2 briefly describes the symbology and notation adopted in this paper. Section 3 describes the context in which this work can be applied to real-world problems. Section 4 briefly describes the basic structure of a Universal Numerical Integrator (UNI). Section 5 describes the detailed mathematical development of E-TUNI, designed with backward integration. Section 6 analyzes the numerical accuracy of E-TUNI using Landau symbols. Section 7 presents the numerical and computational results validating the proposed model. Section 8 presents the main conclusions of this work.
2. Symbols and Notations Adopted
For a more detailed understanding of the theoretical development presented in this paper, we define all the symbols and variables used in this work. The proposed method is called Euler-Type Universal Numerical Integrator (E-TUNI) and uses backward integration. This method is discrete. Thus, we propose a discrete method to approximate a continuous system of autonomous ordinary differential equations. Therefore, below, we present all the symbologies and variables used here. They are divided into two groups: (i) continuous variables and (ii) discrete variables.
- (i)
- Continuous Variables
- —System of continuous differential equations.
- —State Variables.
- —Instantaneous derivative functions.
- d—Plant noise.
- —Measuring instrument noise.
- —Particular continuous and differentiable curve of a family of solution curves of the dynamical system .
- —First derivative of .
- (ii)
- Discrete Variables
- —Vector of state variables at time .
- —Scalar state variable for at time . It is a generic discretization point of the state variables generated by the integers i, j, and k.
- n—Total number of state variables.
- —Vector of control variables at time .
- —Scalar control variable for at time .
- m—Total number of control variables.
- —Exact vector of state variables at time .
- —Exact scalar state variable for at time .
- —Estimated Vector of state variables by UNI or E-TUNI at time .
- —Scalar state variable estimated by UNI or E-TUNI for at time .
- —Estimated Vector of state variables when using only the integrator and without using the neural network at time .
- —Exact vector of positive mean derivative functions at time .
- —Scalar positive mean derivative functions for at time .
- —Estimated vector of positive mean derivative functions by the E-TUNI at time .
- —Exact vector of negative mean derivative functions at time .
- —Scalar negative mean derivative functions for at time .
- —Estimated vector of negative mean derivative functions by the E-TUNI at time .
- —Vector of positive instantaneous derivatives at time .
- —Scalar positive instantaneous derivative for at instant .
- —Vector of negative instantaneous derivatives at instant .
- —Scalar negative instantaneous derivative for at time .
- —Time instant .
- —Time instant .
- —Integration step.
- i—Over-index that enumerates a particular curve from the family of curves of the dynamical system to be modelled ().
- j—Under-index that enumerates the state and control variables.
- k—Over-index that enumerates the discrete time instants ().
- r—Total number of horizons of the time variable.
- q—Total number of curves from the family of curves curves of the dynamic system to be modelled.
- —Instant of time within the interval as a result of the Differential Mean Value Theorem (see Theorem 2).
- —Instant of time within the interval as a result of the Integral Mean Value Theorem (see Theorem 3).
To understand this symbology, the first step is to understand the difference between , , and . The vector variable is the exact value of the state variables at time . The vector variable is the estimated value of the state variables using only the numerical integrator. Finally, the vector variable is the estimated value of the state variables using the numerical integrator coupled with an artificial neural network. Figure 1, Figure 2, Figure 3 and Figure 4 follow this convention for a better understanding of the model proposed in this work. Additionally, it is important to understand the meaning of the auxiliary variables i, j, and k. This is described in the next paragraph.
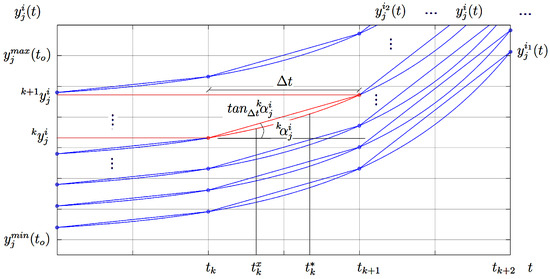
Figure 1.
Symbology and notation used in this article.
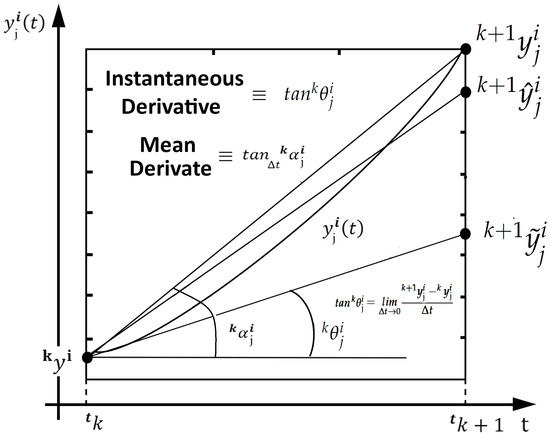
Figure 2.
Basic difference between the instantaneous derivative and the mean derivative (Source: [16]).
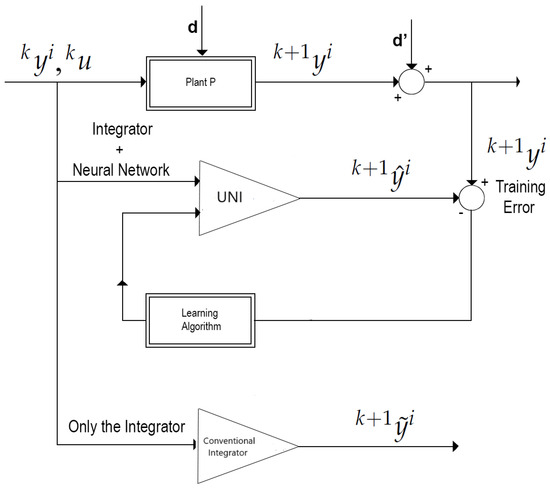
Figure 3.
General graphic diagram of the operation of a Universal Numerical Integrator (UNI) (Source: [16]).
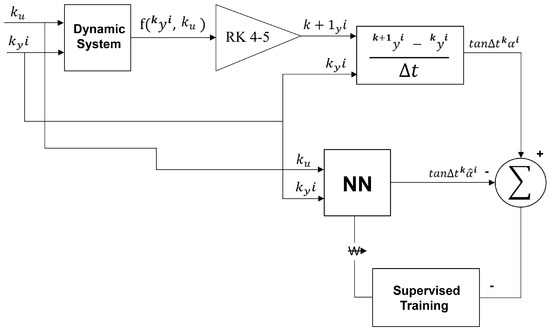
Figure 4.
The E-TUNI designed according to the direct approach (Source: [16,27]).
Here, an important issue is to elucidate the use of the over-indexes k and i and the sub-index j in the variables and . Figure 1 will help in this explanation. When the auxiliary variables i, j, and k are used simultaneously, they uniquely identify the secant () at the point . Notice that the over-index k indicates the time instant of the secant, the sub-index j indicates the state variable in question, where , and the over-index i indicates the particular curve, where the respective secant is located, of the family of possible curves of the system of differential equations considered. The value of q can be as large as one wants. The larger the value of q the more different curves will be trained by the neural network, and the better its generalization will be.
This unique mapping of the secant will be of fundamental importance for the demonstration of Theorem 4 that will be presented and demonstrated in Section 5. This theorem establishes that if the Euler integrator uses the secant instead of the instantaneous derivatives, it will be a discrete and exact solution for a system of ordinary and autonomous differential equations. Furthermore, the mapping mentioned above is unique because of the uniqueness theorem for systems of ordinary differential equations. Finally, an artificial neural network will be used to learn the secants of the considered dynamic system through supervised learning using input/output training patterns.
3. Contextualization
This section clarifies some critical issues regarding using the E-TUNI in mathematics, physics, and engineering problems. These issues will help provide a better theoretical and practical understanding of the method proposed in this article. To this end, in the following, we formulate five essential questions regarding the proper design of E-TUNI and give succinct and objective answers to all of them.
What is the difference between E-TUNI and the Conventional Euler method? The traditional Euler method works with instantaneous derivative functions, and the E-TUNI works with mean derivative functions. Although this difference may seem insignificant, in reality, it is not. We also can refer to Figure 2 to answer this question. In this figure, , , and are, respectively, the solution obtained by conventional Euler, the solution obtained by E-TUNI, and the exact solution of the dynamical system at time . As can be seen, the mean derivative gives a more accurate solution than the instantaneous derivative. Another advantage of E-TUNI is that it can be designed using real-world training patterns through supervised learning. To this end, E-TUNI uses an artificial neural network to learn the mean derivative functions with high precision. Notice also a difference between the values and . This difference is caused by the training of the neural network since the error generated by this same neural network is non-zero.
What are the advantages of E-TUNI with backward integration compared to other conventional numerical integration methods? Since E-TUNI uses a neural network, its accuracy is equivalent to any other higher-order numerical integrator. This property is because artificial neural networks are universal approximators of functions [2,3,4,5]; that is, the training error of the neural network can be as small as desired. The other advantage of E-TUNI is that it has a mathematical structure only of the first-order, which means it is much simpler than higher-order integrators. The disadvantage of E-TUNI, concerning higher-order integrators, is that the former has a fixed step, and the latter has a variable step. This difference means that if it is desired to vary the integration step of E-TUNI, a new neural training will be necessary. Furthermore, as previously mentioned, E-TUNI can work with real-world data and not only with theoretical models.
How does the algorithm guarantee accuracy and stability when finding the endpoints of the integration interval during the backward integration process? In this paper, we only empirically verify that this is possible through the practical examples presented in the numerical results section at the end of this paper. However, a convergence proof of the numerical stability of the proposed model is left for future work. However, here, we prove that the general expression of E-TUNI (which works with mean derivative functions) is an exact solution for a system of Ordinary Differential Equations (ODEs) and as demonstrated by Theorem 4.
Is this valuable method for dynamical systems of nonlinear differential equations of any dimension n? As exemplified by Equations (1)–(3), E-TUNI is capable of solving a non-linear dynamic modelling problem of any order. However, it seems reasonable to assume that the larger the dimension n of the proposed problem, the greater the computational effort required to train the neural network used. This article exemplifies its technological application with physics problems of up to four state variables.
Does the E-TUNI model have application value for new problems in a specific discipline such as Physics or Engineering? Yes, this method can be applied to any physical problem governed by an autonomous non-linear ordinary differential equation with n state variables and m control variables. However, its use in partial differential equations requires further studies. A good application of the proposed method would be, for example, forecasting the stock market, forecasting river flows in hydro-graphic basins, control problems applied to aerospace engineering, among others. The E-TUNI models for forward and backward integration can also be used in optimal control to solve problems involving Pontryagin’s principle. Additionally, the E-TUNI can be an alternative to the traditional NARMAX model and Recurrent Neural Networks (RNNs). Finally, Figure 3 graphically schematizes the coupling of an E-TUNI model to any real-world plant, which can be learned through supervised learning with input/output training patterns.
4. Universal Numerical Integrator (UNI)
Figure 3 illustrates a general scheme for adequately designing a Universal Numerical Integrator (UNI). Notice that in Figure 3, when one couples a conventional numerical integrator (e.g., Euler, Runge–Kutta, Adams-Bashforth, predictive-corrector, among others) to some kind of universal approximators of functions (e.g., MLP neural networks, RBF, SVM, fuzzy inference systems, among others), the UNI design can be achieved high numerical accuracy through supervised learning using input/output training patterns. This allows for solving real-world problems involving the modeling of non-linear dynamic systems.
Still, regarding Figure 3, note that is the prediction made at instant by the UNI used and is the real value generated by the plant at the same instant. Note that these two values are compared in the “Training Error” block, and the weights present in the UNI are updated through supervised learning with input/output training patterns. Since artificial neural networks are considered universal approximators of functions, the neural training error can be as small as desired. Notice that is the output generated if only the conventional numerical integrator is used. However, in the latter case, training it with real-world training patterns is impossible.
As previously mentioned, a Universal Numerical Integrator (UNI) can be of three types, thus giving rise to three distinct methodologies, namely: (i) NARMAX model, (ii) instantaneous derivatives methodology (e.g., Runge–Kutta neural network, Adams-Bashforth neural network, predicted-corrector neural network, among others), and (iii) mean derivatives methodology or E-TUNI. The three types of universal numerical integrators are equally precise, as the Artificial Neural Network (ANN) is a universal approximator of functions [2,3,4,5], every UNI can have its approximation error as close to zero, as much as one likes.
To fully understand the difference between the instantaneous and mean derivative methodologies, see Figure 2 again. This figure presents the geometric difference between the instantaneous and mean derivative functions. It is well-known that the mean derivative () is the tangent of the angle of the secant line connecting two distinct points of a mathematical function. On the other hand, the instantaneous derivative () is the tangent of the angle of the tangent line to any given point of a mathematical function.
The mean derivatives methodology occurs when a universal approximator of functions is coupled to the Euler-type first-order integrator. In this case, the first-order integrator would have a substantial error if instantaneous derivative functions were used. However, when the mean derivative functions replace the instantaneous derivative functions, the integrator error is reduced to zero [16,27]. In this way, it is possible to train an artificial neural network to learn the mean derivative functions through two possible approaches [16]: (i) the direct approach and (ii) the indirect or empirical approach.
Figure 4 schematically represents the direct approach. Figure 5 schematically represents the indirect or empirical approach. In the direct approach, the artificial neural network is trained separately from the first-order integrator. The artificial neural network is trained and coupled to the first-order integrator in the indirect or empirical approach. Both approaches are equivalent to each other. However, the back-propagation algorithm must be recalculated using the indirect or empirical approach. In the direct approach, this is unnecessary [16].
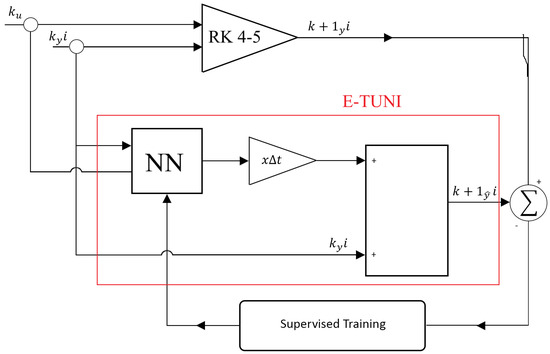
Figure 5.
The E-TUNI designed according to the indirect or empirical approach (Source: [16]).
However, in this article, only the direct approach will be used to train the neural network with the mean derivative functions. In this sense, giving a more detailed explanation of Figure 4 is useful. The “Dynamic System” block is the state equations of the dynamic system that we want to reproduce through E-TUNI. A higher-order numerical integrator solves the theoretical dynamical system (e.g., Runge–Kutta 4-5, among others). After this, the values and are used to calculate the mean derivative of this theoretical system, i.e., . In parallel, the “NN” block contains the neural network. The neural network inputs will be (state variable) and (control variable), calculated at time . The output of the neural network will be the mean derivative . Notice that the same inputs and are simultaneously stimulated in the original theoretical dynamical system and the neural network. Thus, after the dynamical system is adequately trained, the output variable of the neural network () should be the same as the output variable of the original dynamical system (), at least for a small residual error. Furthermore, if we want to learn a real-world plant, we must only replace the theoretical model with a computational data acquisition system.
The same explanation applies to Figure 5. However, since the integrator is trained with the neural network in this case, the reference value in training will not be the mean derivative functions but an instant future ahead of state variables, i.e., .
Additionally, in the remainder of this article, although the dynamical system can be used with both state variables and control variables, we will consider dynamical systems with only state variables. It is also essential to note that in the E-TUNI, the integration step () can be any (it does not need to be infinitesimal). It should be small only in the case where control variables are used.
This difference between the direct and indirect approach also applies to the instantaneous derivatives methodology. However, in this case, the direct approach only applies to theoretical models, as instantaneous derivative functions cannot be determined directly in real-world problems [16]. Furthermore, this difference between the direct and indirect approach does not apply to the NARMAX model. However, the NARMAX model is also a particular case of UNI. This is because, although a conventional integrator is not coupled to the NARMAX model, the universal approximator of functions behaves as if it were a numerical integrator [16].
5. The Euler-Type Universal Numerical Integrator (E-TUNI)
Firstly, in this section, we briefly introduce the Euler-Type Universal Numerical Integrator (E-TUNI) and present the general expression of this unique type of Universal Numerical Integrator (UNI). Next, we present the mathematical foundations of E-TUNI with forward and backward integrations. It is also important to highlight that this integrator is inherently of first-order.
As a result, Equation (1) mathematically represents a system of n autonomous non-linear ordinary differential equations with dependent variables . Based on this, it is possible to establish an initial value problem for a first-order system, also described by (1):
The system represented by Equation (1) is a non-linear and autonomous (time-invariant) system of ordinary differential equations. It is important to notice that the method presented here will be limited to this type of equation. Thus, neither non-autonomous systems nor Partial Differential Equations (PDEs) will be considered here.
Additionally, the solution of the differential Equation (1) can be obtained through a first-order approximation. Such a solution was obtained by the mathematician Leonard Euler in 1768. This solution, keeping the convention described by Figure 2, is given by Equation (2):
However, it is essential to notice that the accuracy of Equation (2) is awful. Because of this, if the mean derivative functions replace the instantaneous derivative functions, then the Euler-type first-order integrator becomes precise (see demonstration of Theorem 4). This new solution is given by Equation (3):
for
Note that Equation (3) is straightforward to obtain, as the mean derivative functions sound easily computable, for real-world problems, via Equation (4), for . Here, the variable n is the total number of state variables of the dynamical system given by (1).
Before we proceed with the rest of this article, we will give an intuitive justification for the passage from Equation (2) to Equation (3), with the help of Figure 2. If an artificial neural network is trained to learn the instantaneous derivative function () of any non-linear dynamical system and this neural network is subsequently coupled to the first-order Euler integrator, then the output of this model will be (see Figure 2 again). Therefore, this value is very different from the real value . However, if the neural training on the Euler integrator, mentioned above, is continued through the indirect approach, its training error will be reduced to almost zero, since the neural network is a universal approximator of functions. Therefore, the new output will be . Notice that graphically, the instantaneous derivative function has been forced to converge to the mean derivative function to reduce the integrator error to almost zero. Additionally, by the uniqueness theorem (Theorem 1 which will be presented later) there is no other way for this problem to converge.
Finally, it is crucial to notice that a neural network can compute the mean derivative functions, as schematized by Figure 6. In this way, the E-TUNI works with a first-order numerical integrator coupled to a neural network with any feed-forward architecture (e.g., MLP neural network, RBF, SVM, wavelets, fuzzy inference systems, Convolutional Neural Network (CNN), among others).
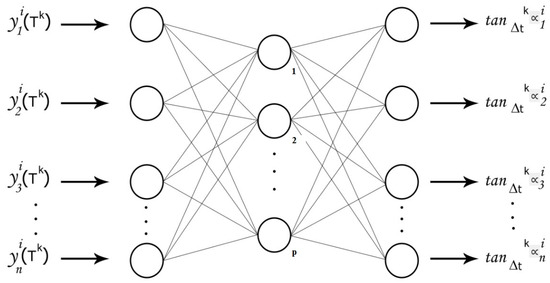
Figure 6.
A MLP neural network designed with the concept of mean derivative functions.
5.1. Fundamental Theorem
In this section, the general expression of E-TUNI is demonstrated. For this purpose, let the system of non-linear differential Equations (5) be:
where, and . The uniqueness theorem is a fundamental theorem about Equation (5).
Theorem 1
(T1). Assume that each of the functions has continuous partial derivatives with respect to . So the known initial value problem for has one and only one solution in , starting from each . If two solutions have a common point, they must be identical.
For the formal demonstration of the general expression of E-TUNI, which will numerically and discretely solve Equation (5), two hypotheses will be assumed: (i) a set of points that is an exact solution of the dynamical system (5) is known and which we will call and (ii) the existence of two sets of continuous and differentiable functions that pass through these points is assumed, namely, and . Figure 7 mathematically illustrates these two hypotheses when , , and . The meanings of the auxiliary variables i, j, and k are the same as those described in Figure 1. Furthermore, only the points must be known. The functions and just need to exist; that is, it is not necessary to know them.

Figure 7.
Example of numerical discretization of the solution of the differential Equation (5).
What do the matrices mean in Figure 7? The first line of these point matrices represents a set of exact points belonging to the first curve of the family of solution curves of the considered system, and so on. For example, all points , , , , and pass through the continuous and differentiable function , and so on. Since , the family of curves, in this case, is composed of four curves. Based on the continuous hypothesis, i can be as large as one wants. Since the neural network, responsible for modelling the system (5), will be designed with the supervised learning approach through input/output training patterns, knowing in advance the discrete solution of the system (5), is not absurd. Thus, the system (5) can be replaced by the following set of solutions (6):
where ; ; . It is essential to note that changing the values of q, n, r, and can obtain any finite density of discrete point solutions of (5) over a finite domain. Thus, the great advantage of Equation (6) concerning Equation (5) is that the former is an explicit function only of the variable t. Thus, the differential and integral mean value theorems can be applied in (6) to arrive at the general expression of E-TUNI, which uses the functions of mean derivatives. The differential and integral mean value theorems cannot be applied in (5) because, in this case, the system in question is an explicit function of y and not of t.
Theorem 2
(The Differential Mean Value Theorem). If a function for is a continuous function and defined over the closed interval is differentiable over the open interval , then there exists at least one number with such that, .
Theorem 3
(The Integral Mean Value Theorem). If a function for is a continuous function and defined over the closed interval , then there exists at least one internal point in such that, .
The notation used to represent is sufficient to map it uniquely to its respective region of interest, where its associated characteristic secant is confined. Thus, it can be stated that for the state , we have a single characteristic secant associated with it and given by . The existence of a unique secant associated with each point is an immediate consequence of the uniqueness theorem (Theorem 1).
Consider also for a particular trajectory of a family of solutions of the system of differential equations passing through at time , i.e., initializing within a finite domain of interest .
In [29,30], by definition, the secant curve between two points and belonging to the curve for is the straight line segment that joins these two points. Thus, the tangents of the secants between the points and , and , …, and are defined as:
where for .
Property 1.
Applying Theorem 2 on the curve is equivalent to applying Theorem 1 on the curve both on the same interval closed , i.e., .
Proof.
If one applies Theorem 2 to the continuous curve , this results in a for such that as a result of the fundamental theorem of calculus. This way, . On the other hand, the application of Theorem 1 on the continuous and differentiable curve implies the existence of a for , such that . This way, . However, this demonstration does not prove that . □
Theorem 4.
The general discrete and exact solution for of the autonomous system of nonlinear differential equations of the type can be established through the first-order Euler relation of the type for a given and fixed, since the general solution of this dynamical system, given by, and are previously known for ; and tϵ.
Proof.
Let the first-order non-linear and autonomous dynamical system be given by for and . If the solution of the dynamical system is known and equal to , then the function can be replaced by , i.e., . In this way, we can write that . Note that the indices i, j, and k uniquely map the secant we are interested in and in accordance with Figure 1. This last integral can still be simplified as . Thus, applying the mean integral value theorem, in this last expression, we obtain where and for . On the other hand, applying the differential mean value theorem on the function for in the interval we obtain that . Thus, by Property 1 we have that for . Therefore, for or, in vector form, it turns out that . □
Note that the functions and , used in the previous demonstration, need to be continuous and differentiable because of Theorems 2 and 3, but they do not need to be known. Their existence is enough. What needs to be known are the points . Finally, through a mathematical demonstration, very similar to Theorem 4, one can demonstrate the general expression of E-TUNI with backward integration, i.e., for and . For more details on E-TUNI and its relationship with other types of UNIs, see [16,31].
5.2. General E-TUNI Algorithm with Forward and Backward Integrations
This section describes first-order Euler integrators with forward and backward integration. They are divided into two classes: (i) the conventional Euler integrator, which works with instantaneous derivative functions (low numerical precision and variable step), and (ii) the E-TUNI type integrator, which works with mean derivative functions (high numerical precision and fixed step).
Therefore, it is important to mathematically relate the mean derivatives functions with the instantaneous derivatives functions (see again Figure 2). Thus, it is easily seen that if then,
or
Figure 2 graphically illustrates the convergence of mean derivatives functions to instantaneous derivatives functions when tends to zero. Based on this, it is possible to enunciate two basic types of first-order numerical integrators or Euler integrators. An Euler integrator that uses instantaneous derivatives functions, given by for and an Euler integrator that uses mean derivatives functions, given by .
A significant difference between the mean derivatives functions and the instantaneous derivatives functions is that the instantaneous derivatives functions for is only dependent on , but the mean derivatives functions for is dependent on , and at the point . As will be seen later, this difference is significant.
The first important point to be considered here is the possibility of carrying out both forward and backward integration of the Euler Integrator with instantaneous derivatives. So, the instantaneous derivative functions at the points for can be defined in two different ways:
or
However, if the instantaneous derivatives functions exist at the point , then necessarily or (see Figure 8). In this way, the expressions of forward and backward propagating Euler integrators, necessarily designed with the instantaneous derivative functions, are given, respectively, by (i.e., with low numerical precision):
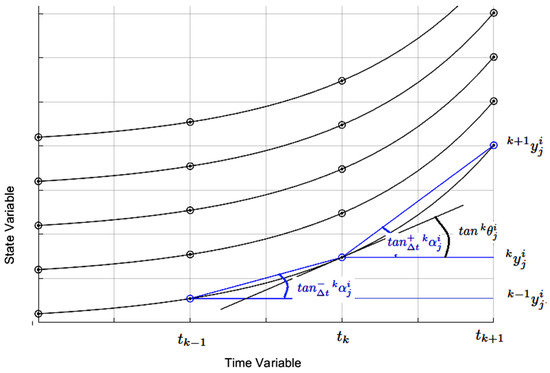
Figure 8.
Geometric finding that instantaneous derivative functions are symmetric, but mean derivative functions are not.
Note that Equation (13) can also be obtained directly from Equation (12) by making the substitution of the variable .
Additionally, like , the Euler integrator with instantaneous derivatives functions has a symmetric solution between intervals and , thus implying low numerical precision, for the outputs and for . To say that a solution is symmetric at the point k means to say that to .
This Euler integrator symmetry property only occurs when instantaneous derivative functions are used. However, in Euler’s integrator, designed with the mean derivatives functions, this symmetry of the solution around the point is not verified (see Figure 8 again). This is important because in Euler’s integrator, designed with mean derivatives functions, the backward solution does not necessarily decrease when the forward solution grows.
In [32], several difference operators can be applied to a function for . However, the two operators that interest us are the forward difference and the backward difference, given below, respectively:
Thus, using the finite difference operators, there are two different ways to represent the secant at the point and with integration step :
Comparing Equation (16) with the result of Theorem T4, one can obtain the following recursive and exact equation to represent the solution of autonomous non-linear ordinary differential equations system for a forward integration process (i.e., with high numerical accuracy):
or
Equations (18) and (19) represent an Euler-type integrator, which uses mean derivatives functions and forward integration. However, to obtain the Euler integrator with backward recursion, it is enough to analyze the asymmetry of the mean derivative functions at the point and as is illustrated in Figure 8. In this way, we can obtain the following equation to perform the backward integration of E-TUNI (i.e., with high numerical precision):
or
Thus, the iterative equations of the first-order Euler integrator, using mean derivatives, which perform forward and backward recursions, are, respectively, Equations (18) and (20). The negative sign that appears in Equation (20) means, not necessarily, that when increases, then decreases, because they are two neural networks independent of each other. Therefore, it is observed that, in general, , and therefore Euler integrators with mean derivatives functions do not have a symmetric solution, i.e., in general, for . As can be easily seen in Figure 8, the negative mean derivative has a different slope than the positive mean derivative for the same point in .
It is interesting to note that the negative sign that appears in Equations (13), (20) and (21) is because of the inverted direction of the flow of time (from present to past) in backward integration.
Additionally, the following algorithm is proposed to determine the mean derivatives through the direct methodology involving both forward and backward integrations in the Universal Numerical Integrator (UNI) of the E-TUNI type. This approach requires five steps.
1. Given a finite domain of interest computed at time for state variables, generate, according to a uniform probability distribution, q initial conditions such that,
and
which are the E-TUNI’s input training patterns at time for both the forward and backward integrators. The number q of training patterns should be large enough to ensure adequate supervised training. To this end, the training patterns should be appropriately divided, with one portion for training and another for testing.
2. Using a high-order integrator, propagate all initial conditions to obtain the corresponding states at time and at time . Thus, assemble the output patterns and to train the positive and negative mean derivatives.
and
Note: Alternatively, in this step, a data acquisition system could capture real-world dynamic systems’ behavior.
3. Once input vectors P and output vectors and are required by the universal approximator of functions, train two neural networks through supervised learning. One training pair to learn the positive mean derivative function and one training pair to learn the negative mean derivative function. These two neural networks will look similar to the one in Figure 6.
4. When the two supervised trainings are consolidated, it is possible to simulate the dynamics of the system through the following discrete recursive expressions:
and
5. Using the E-TUNI expression to propagate the positive mean derivative, integrate the dynamical system from the initial instant to the final instant . Then, integrate the E-TUNI expression from to using the negative mean derivative. By the uniqueness theorem, the initial starting point of the first integration must coincide with the final arrival point of the second integration.
6. Analysis of the Numerical Accuracy of E-TUNI Using Landau Symbols
In this section, an analysis of the accuracy of the E-TUNI solution is performed. For this purpose, the numerical accuracy of the conventional Euler method, which works with instantaneous derivative functions, is initially analyzed. Next, an analysis of the accuracy of the E-TUNI solution, i.e., the Euler method that works with mean derivative functions, is performed. It is essential to note that the mean derivative functions will be obtained through an artificial neural network.
6.1. Numerical Accuracy of the Conventional Euler Method
The explicit Euler method is a numerical integration technique for solving ordinary differential equations of the form:
The formula for the method is:
where h is the integration step; is the approximation of the exact solution ; is the instantaneous derivative of the solution at the point . Therefore, it is a well-known result that the difference between the exact solution and the Euler approximation is given by:
Therefore, the accuracy of the method is evaluated by two errors: (i) The local truncation error and (ii) the global truncation error . Understanding the global error is quite simple; since the Euler method performs steps to integrate up to a time T, the global error is obtained by adding the local errors over this interval. Finally, the accuracy of the Euler method is first order since the global error is . This result shows that the Euler method is accurate only for small steps, and higher-order methods such as Runge–Kutta are preferable to obtain greater accuracy.
6.2. The E-TUNI Numerical Accuracy
In the modified Euler method, i.e., in E-TUNI, we employ the mean derivative functions , which can be obtained by an Artificial Neural Network (ANN):
where the mean derivative is defined as:
If the mean derivative is estimated by an Artificial Neural Network (ANN), we will have:
where represents the error of the neural network. Expanding the exact solution around , we have that:
The mean derivative can be approximated by expanding :
Thus, substituting Equation (29) into the integral (26) and integrating over the interval , we have:
Thus, substituting the mean derivative Equation (30) into the modified Euler method, we finally have:
Equation (31) shows that the local error of the method has increased to , improving accuracy. On the other hand, if the mean derivative is approximated by an Artificial Neural Network (ANN):
So, the modified method becomes:
So, the total error will be:
Thus, if the artificial neural network is accurate enough, we can make , making the integration error close to . Thus, the local error being equal to will make the global error, summed over steps, equal to . Therefore, the modified Euler method with mean derivatives improves the global accuracy to . If an artificial neural network is used to estimate the mean derivative, its error can be reduced to a minimum, making the method highly accurate. Thus, this method can be seen as a transition to higher-order Runge–Kutta methods.
7. Results and Analysis
In this section, we perform a numerical and computational analysis of the Universal Numerical Integrator (UNI), which exclusively uses mean derivative functions. As previously described, this is the Euler-Type Universal Numerical Integrator (E-TUNI). Therefore, we present here three case studies: (i) a one-dimensional simple case, (ii) the non-linear simple pendulum (two state variables), and (iii) the non-linear inverted pendulum (four state variables).
Thus, for all experiments that it is presented below, the use of MLP neural networks was standardized with the traditional Levenberg–Marquardt training algorithm [33] from 1994. Concerning the architecture of the neural network used, all experiments were trained using only one inner layer (with thirty neurons with tangent hyperbolic activation function) in an artificial neural network of the Multi-Layer Perceptron (MLP) type. In all experiments, of the total patterns were left for training the MLP neural network, of the patterns for testing, and for validation. Concerning the architecture of E-TUNI, the direct approach was exclusively used. However, it must be said that the indirect or empirical approach of E-TUNI was not tested in this article. Thus, the general algorithm for training and testing the methodology presented in this article can be briefly described as follows:
Step 1. Using a high-order 4-5 Runge–Kutta integrator, over the considered autonomous non-linear ordinary differential equation system, randomly generate p training patterns input/output for E-TUNI concerning the initial instant . Perform both forward and backward integration.
Step 2. Determine both the values of the positive mean derivatives , as well as the values of the negative mean derivatives in relation to initial instants for .
Step 3. Train two distinct neural networks. One is to output positive mean derivative functions, and the other is to output negative mean derivative functions. Do this following the graphic diagram in Figure 6.
Step 4. Simulate, for several different integration steps, the performance of E-TUNI both with forward and backward integration. Observe that if starting from an initial instant , the solution is propagated in n distinct instants forward and, after that, one returns to the same n instants with backward integration because of the uniqueness theorem, one returns perfectly to the original initial instant . This trick will be used to test the efficiency of E-TUNI when it is propagated backward.
Step 5. Do the same, using the Euler-type first-order integrator, but now using the original instantaneous derivative functions of the dynamical system in question. Then, compare E-TUNI with conventional Euler. Thus, to verify the superiority of E-TUNI concerning the conventional Euler, the accuracy of the discrete numerical solutions obtained must be verified.
Therefore, next, we briefly describe the systems of non-linear differential equations of the three dynamical systems considered here to test the proposed algorithm to perform the backward integration of E-TUNI. Table 1 also summarizes the training data of the eight experiments conducted here to test the proposed methodology.
Example 1.
Simulate the one-dimensional non-linear dynamics problem, given by Equation (35). The variable y was trained on the range . Note that this dynamic has infinite stability points since has infinitely many solutions. Note that the points of stability recovering the initial condition through backward integration is very difficult for any integrator.
Example 2.
Simulate the non-linear simple pendulum problem given by the system of differential Equations (36). Note that this example does not involve control variables. The acceleration values due to gravity constants and the pendulum’s length are, respectively, given by and . The variable θ was trained on the range and the variable was trained on the range .
Example 3.
Do the same for the non-linear inverted pendulum problem described by the system of differential Equations (37). The constants adopted for this problem were , , , , , , e . This problem has four state variables (, , , and ) and a constant control (). The state variables were trained on the intervals between , between , between , and between .
Figure 9 graphically illustrates the numerical simulation obtained for Example 1. This figure is not yet the result obtained by E-TUNI, but by Runge–Kutta 4-5, available in Matlab, to numerically solve Equation (35). Therefore, the result obtained by E-TUNI will be compared later, numerically and graphically, with the graphic result of this figure. Also, in Figure 9, the following convention was used: (i) the blue dots in “x” represent the forward propagation, in high precision, of Runge–Kutta 4-5 over the dynamics of Equation (35), (ii) the blue dots in “o” represent the high precision backward propagation of Runge–Kutta 4-5 over the same dynamics, and (iii) the solid red lines represent the slope of the mean derivatives functions between two consecutive points.
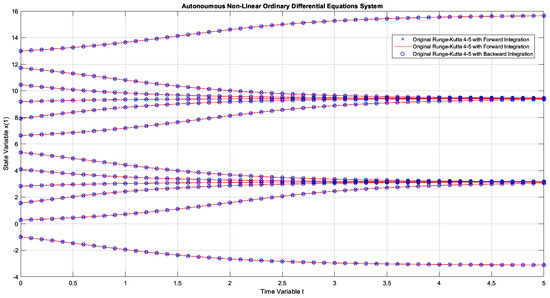
Figure 9.
The dynamics of Example 1 solved with Runge–Kutta 4-5, available in Matlab with step automation through the “ode45.m” function, using forward and backward integrations.
Note that the integration step, as graphically presented, was . However, it is essential to notice that the Runge–Kutta 4-5 works internally with a varied integration step much smaller than this one to achieve the high numerical accuracy shown in Figure 9. So, both forward and backward integration were performed from to . In this case, as can be seen, the result obtained is perfect, as the points obtained by backward integration overlapped perfectly over the points with forward integration.
Figure 10 presents the first graphic result of E-TUNI, for the dynamics given by Equation (35). The blue dots represent the results obtained by E-TUNI and follow the same convention as in the previous figure. The green dots represent the results obtained by the conventional Euler Integrator, using the instantaneous derivative functions, also given by Equation (35). The two black dash-dot horizontal lines delimit the E-TUNI training range. Note that within the training range, the E-TUNI result was perfect, with both forward and backward integration. The line in Table 1 with the indicates the training data obtained for this case. In this way, 400 training patterns were generated, and of them, 320 patterns, were effectively left for training. Note that in Table 1 the symbols and represent, respectively, the mean square error of forward integration and the mean square error of backward integration.
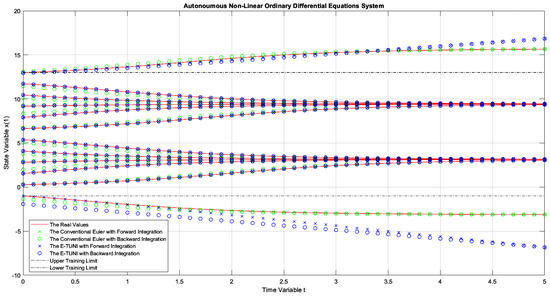
Figure 10.
The dynamics of Example 1, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .
Note that outside the training region, E-TUNI has become inaccurate. However, to solve this problem, the training domain of the state variable should be increased. Note also that the conventional Euler presented a slight deviation in the backward integration concerning the forward integration in the given domain. Thus, in conventional Euler, this deviation becomes more critical and accentuated, which increases the integration step. However, in E-TUNI, the result does not deteriorate with the increase of the integration step.
Figure 11 presents the same result as the previous figure, but now using an integration step . The E-TUNI result was perfect, but the conventional Euler result was even worse. This confirms what was said in the previous paragraph. See Table 1 again in line to find out about the main parameters used in this training. Figure 12 presents the same result as the previous figure, but now using an integration step . In this case, the result achieved by E-TUNI is still perfect, and the result by conventional Euler is as well. The result, obtained by conventional Euler, was perfect in this case because a tiny integration step was used and equal to . Figure 13 presents a simulation using the integration step . Again, E-TUNI presented a perfect result, but the conventional Euler degenerated its solution.
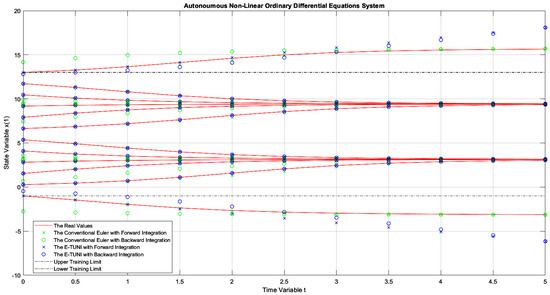
Figure 11.
The dynamics of Example 1, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .
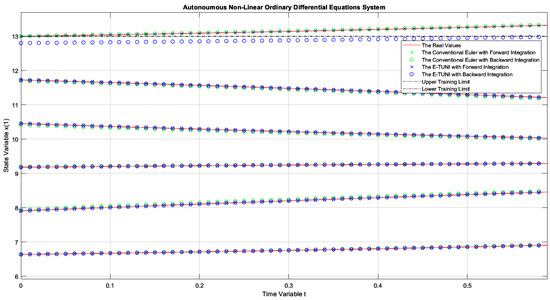
Figure 12.
The dynamics of Example 1, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .
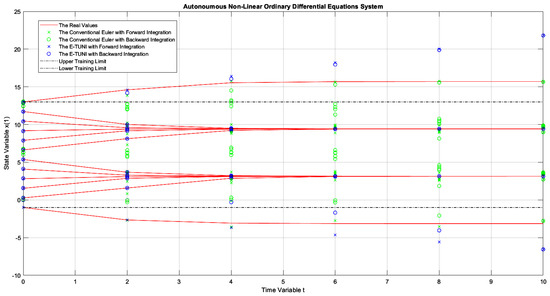
Figure 13.
The dynamics of Example 1, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with and being integrated up to .
Figure 14 and Figure 15 deserve a little more attention. In Figure 14, as can be seen, the solution obtained by E-TUNI, through backward integration, was degenerate (see the zoom). In this case, the blue circle should lie perfectly on the solid red line. In Figure 15, the backward integration solution obtained by Runge–Kutta 4-5 was also degenerate. Both solutions turned out bad because the integration process was conducted for too long, over a point of stability. The zoom made in Figure 14 will be used to better explain this.
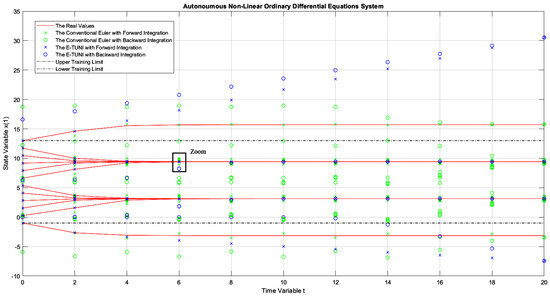
Figure 14.
The dynamics of Example 1, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with and being integrated up to .
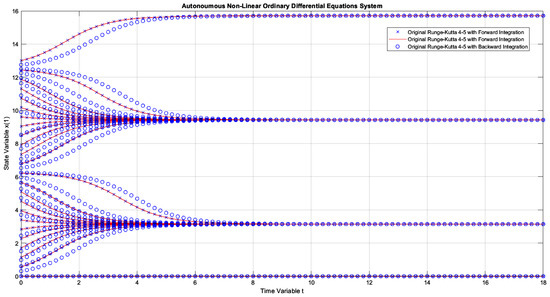
Figure 15.
The same example as in Figure 9, but instead of being integrated up to , it was integrated up to (notice the dissolution of the solution).
What is explained for Figure 14 is also valid for Figure 15. In Figure 14, the integration process was conducted from to . The biggest problem occurred when returning from to . For example, all families of curves confined between and at the initial instant were confined in a much smaller interval than this one at the instant . Therefore, to work properly, backward integration would have to be trained with a much smaller mean squared error than the one achieved in Table 1 (line ). However, this is impossible to achieve using just the algorithm in [33]. Note that this task was also impossible for Runge–Kutta 4-5, as schematized in Figure 15. Therefore, the problem presented here is critical, regardless of the integrator used.
Figure 16 presents the first graphic result of E-TUNI for the dynamics given by Equation (36), which represents the dynamics of the non-linear simple pendulum. In this case, the superiority of E-TUNI over the conventional Euler is evident. An integration step was used in this case. Figure 17 concerns the same previous example, but using an integration step . The conventional Euler was not presented in this figure because its result was bad, which would impair, therefore, the scale of the graph. Still referring to Figure 17, the main reason the backward integration turned out to be a bit bad at the end of the integration process is that the average training error became slightly oversized (see Table 1 in cell ). To solve this problem, it is enough to reduce the average training error of the artificial neural network used, but that is not always an easy task. Figure 18 demonstrates that, even for Runge–Kutta 4-5, the backward integration process of the simple pendulum can also be imperfect (see blue circles misaligned with the blue “x”).
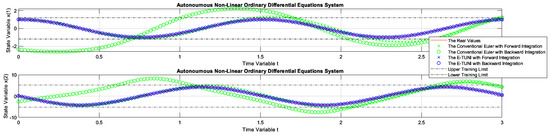
Figure 16.
The dynamics of Example 2, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .
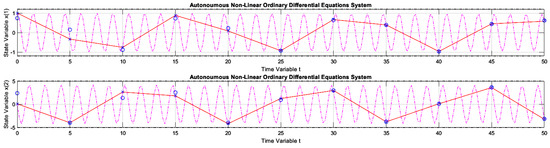
Figure 17.
The dynamics of Example 2, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .
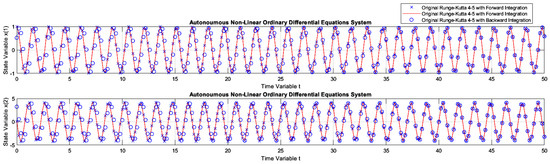
Figure 18.
The dynamics of Example 2 solved with Runge–Kutta 4-5, available in Matlab with step automation through the “ode45.m” function, using forward and backward integrations.
Note that the solution from Equation (36), graphically presented in Figure 17, was much worse than the other solutions given in Table 1 (compare lines 6 and 7). This fact can be seen by checking the training mean square errors in Table 1 (line ), which were too high. This was most likely caused by two fundamental reasons. The first reason is that the E-TUNI local error is amplified by the square of the Integration step. However, the analysis of the global error would require further studies. The other reason, which is purely speculative, is the following: it is believed that when the E-TUNI integration step is very large if the solution of the real dynamical system becomes a non-convex function (concerning the line of mean derivatives in this same interval ), then the training becomes more difficult. However, this last argument still needs to be verified empirically and theoretically.
Figure 19 presents the first graphic result of E-TUNI, for the dynamics given by Equation (37), which represents the dynamics of the non-linear inverted pendulum. As can be seen, in this figure, Runge–Kutta 4-5 perfectly simulated this dynamic, both for forward and backward integrations. Figure 20 is the same case simulation but performed by E-TUNI. Theoretically, Figure 20 is the same as Figure 19. They are just on different scales. Notice that in Figure 20 the E-TUNI simulation was perfect. However, the conventional Euler simulation (green dots) became confusing due to the numerical imprecision achieved by it. Furthermore, this caused an exaggerated change in the scale of the figure.
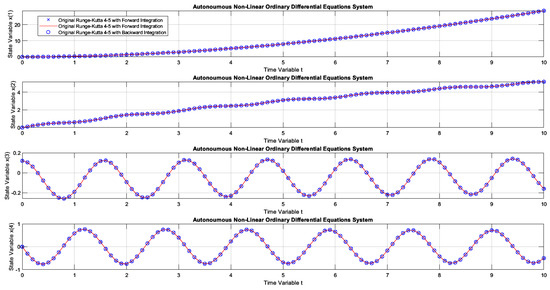
Figure 19.
The dynamics of Example 3 solved with Runge–Kutta 4-5, available in Matlab with step automation through the “ode45.m” function, using forward and backward integrations.
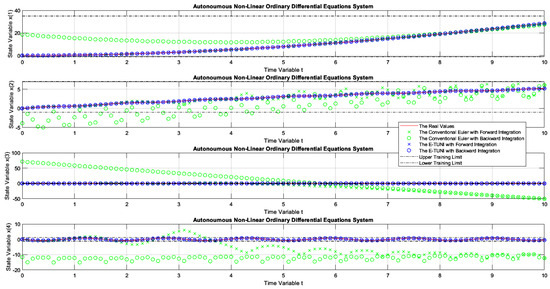
Figure 20.
The dynamics of Example 3, comparing the conventional Euler integrator with E-TUNI, using forward and backward integrations with .

Table 1.
Training data summary.
8. Conclusions
As far as we know, all previous work on E-TUNI was developed using only forward integration. Therefore, we present here, for the first time, a work that uses E-TUNI in a backward integration process. Three case studies were carried out. Non-linear and autonomous ordinary differential equations govern all three dynamical systems considered in this study.
The Euler-type Integrator designed with instantaneous derivatives is not very accurate. However, the E-TUNI has numerical precision equivalent to that of the highest-order integrators. It is interesting to note that the elegance of the theory of ordinary differential equations can be improved when combined with the theory of universal approximator of functions. This propriety is possible because artificial neural networks allow working with real-world input/output training patterns. This fact enables refining the final solution obtained by the first-order Euler integrator and estimator. Because of this, the E-TUNI can also be used to predict real-world dynamics (e.g., river flow and stock market forecasts, among others).
Additionally, we can call the forward mean derivatives functions positive mean derivatives functions. Equivalently, we can call the backward mean derivatives functions negative mean derivatives functions. Thus, we also conclude that the mean derivative functions depend on the integration step and are asymmetric. This propriety means training two distinct neural networks to simultaneously perform forward and backward integration. Unfortunately, the positive and negative instantaneous derivative functions are symmetric to each other.
Additionally, it would be interesting to carry out a future study of E-TUNI using deep neural networks instead of shallow neural networks, aiming to reach two essential points: (i) to be able to increase the number of training patterns (and, consequently, the domain of state variables) and (ii) try to reduce the training mean squared error, as this quantity is critical, in the case of modeling non-linear dynamic systems designed through artificial neural networks. Interestingly, E-TUNI is an excellent option to replace the NARMAX model and even the Runge–Kutta Neural Network (RKNN).
Finally, as another future contribution, one could consider changing the notation used in this article to something more straightforward, as explained in [34,35]. It is essential to notice that the same notation used in articles [16,26,27,28,31] was used here. In this sense, the most significant criticism would be not using the over-index i in the algebraic development of E-TUNI. However, in [31], the over-index i was used to help demonstrate the general expression of E-TUNI. Furthermore, E-TUNI could also be tested for dynamic systems using control variables.
Author Contributions
P.M.T. designed the proposed model and wrote the main part of the mathematical model. J.C.M., L.A.V.D. and A.M.d.C. supervised the writing of the paper and its technical and grammatical review. P.M.T. and G.S.G. (supervised by J.C.M., L.A.V.D. and A.M.d.C.) developed the software and performed several computer simulations to validate the proposed model. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
I would like to thank my great friend Atair Rios Neto for his valuable tips for improving this article. Finally, I would also like to thank the valuable improvement tips given by the good reviewers of this journal. The authors of this article would also like to thank God for making all of this possible.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABNN | Adams-Bashforth Neural Network |
| E-TUNI | Euler-Type Universal Numerical Integrator |
| L-MTA | Levenberg–Marquardt Training Algorithm |
| MSE | Mean Square Error |
| MLP | Multi-Layer Perceptron |
| NARMAX | Nonlinear Auto Regressive Moving Average with eXogenous inputs |
| PCNN | Predictive-Corrector Neural Network |
| RBF | Radial Basis Function |
| RKNN | Runge–Kutta Neural Network |
| SVM | Support Vector Machine |
| UNI | Universal Numerical Integrator |
References
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Cotter, N.E. The Stone-Weierstrass and its application to neural networks. IEEE Trans. Neural Netw. 1990, 1, 290–295. [Google Scholar] [CrossRef]
- Hanin, B. Universal function approximation by deep neural nets with bounded width and ReLU activations. Mathematics 2019, 7, 992. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Henrici, P. Elements of Numerical Analysis; John Wiley and Sons: New York, NY, USA, 1964. [Google Scholar]
- Lapidus, L.; Seinfeld, J.H. Numerical Solution of Ordinary Differential Equations; Academic Press: New York, NY, USA; London, UK, 1971. [Google Scholar]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; John Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis; Electrical Engineering Series; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1978. [Google Scholar] [CrossRef]
- Chen, D.J.L.; Chang, J.C.; Cheng, C.H. Higher order composition Runge-Kutta methods. Tamkang J. Math. 2008, 39, 199–211. [Google Scholar] [CrossRef]
- Misirli, E.; Gurefe, Y. Multiplicative Adams Bashforth-Moulton methods. Numer. Algor. 2011, 57, 425–439. [Google Scholar] [CrossRef]
- Ming, Q.; Yang, Y.; Fang, Y. An optimized Runge-Kutta method for the numerical solution of the radial Schrödinger equation. Math. Probl. Eng. 2012, 2012, 867948. [Google Scholar] [CrossRef]
- Polla, G. Comparing accuracy of differential equation results between Runge-Kutta Fehlberg methods and Adams-Moulton methods. Appl. Math. Sci. 2013, 7, 5115–5127. [Google Scholar] [CrossRef]
- Tasinaffo, P.M.; Gonçalves, G.S.; Cunha, A.M.; Dias, L.A.V. An introduction to universal numerical integrators. Int. J. Innov. Comput. Inf. Control 2019, 15, 383–406. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A. Representations of nonlinear systems: The NARMAX model. Int. J. Control 1989, 49, 1013–1032. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A.; Cowan, C.F.N.; Grant, P.M. Practical identification of NARMAX models using radial basis functions. Int. J. Control 1990, 52, 1327–1350. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef]
- Hunt, K.J.; Sbarbaro, D.; Zbikowski, R.; Gawthrop, P.J. Neural networks for control systems—A survey. Automatica 1992, 28, 1083–1112. [Google Scholar] [CrossRef]
- Norgaard, M.; Ravn, O.; Poulsen, N.K.; Hansen, L.K. Neural Networks for Modelling and Control of Dynamic Systems; Springer: London, UK, 2000. [Google Scholar]
- Wang, Y.-J.; Lin, C.-T. Runge-Kutta neural network for identification of dynamical systems in high accuracy. IEEE Trans. Neural Netw. 1998, 9, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Uçak, K. A Runge-Kutta neural network-based control method for nonlinear MIMO systems. Soft Comput. 2019, 23, 7769–7803. [Google Scholar] [CrossRef]
- Uçak, K.; Günel, G.O. An adaptive state feedback controller based on SVR for nonlinear systems. In Proceedings of the 6th International Conference on Control Engineering and Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 25–27. Available online: https://api.semanticscholar.org/CorpusID:195775331 (accessed on 20 November 2024).
- Uçak, K. A novel model predictive Runge-Kutta neural network controller for nonlinear MIMO systems. Neural Process. Lett. 2020, 51, 1789–1833. [Google Scholar] [CrossRef]
- Tasinaffo, P.M.; Rios Neto, A. Adams-Bashforth neural networks applied in a predictive control structure with only one horizon. Int. J. Innov. Comput. Inf. Control 2019, 15, 445–464. [Google Scholar] [CrossRef]
- Tasinaffo, P.M.; Rios Neto, A. Mean derivatives based neural Euler integrator for nonlinear dynamic systems modeling. Learn. Nonlinear Model. 2005, 3, 98–109. [Google Scholar] [CrossRef]
- de Figueiredo, M.O.; Tasinaffo, P.M.; Dias, L.A.V. Modeling autonomous nonlinear dynamic systems using mean derivatives, fuzzy logic and genetic algorithms. Int. J. Innov. Comput. Inf. Control 2016, 12, 1721–1743. [Google Scholar] [CrossRef]
- Munem, M.A.; Foulis, D.J. Calculus with Analytic Geometry (Volumes I and II); Worth Publishers, Inc.: New York, NY, USA, 1978. [Google Scholar]
- Wilson, E. Advanced Calculus; Dover Publication: New York, NY, USA, 1958. [Google Scholar]
- Tasinaffo, P.M.; Dias, L.A.V.; da Cunha, A.M. A Survey About Universal Numerical Integrators (UNIs): Part II or Quantitative Approach. Hum.-Centric Intell. Syst. (Preprint) 2024, 4, 1–20. [Google Scholar] [CrossRef]
- Ames, W.F. Numerical Methods for Partial Differential Equations, 2nd ed.; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Cheney, W.; Kincaid, D. Numerical Mathematics and Computing, 6th ed.; Thonson Brooks/Cole: Belmont, CA, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).