Abstract
For networks that process 3D data, estimating the orientation and position of 3D objects is a challenging task. This is because the traditional networks are not robust to the rotation of the data, and their internal workings are largely opaque and uninterpretable. To solve this problem, a novel equivariant self-supervised vector network for point clouds is proposed. The network can learn the rotation direction information of the 3D target and estimate the rotational pose change of the target, and the interpretability of the equivariant network is studied using information theory. The utilization of vector neurons within the network lifts the scalar data to vector representations, enabling the network to learn the pose information inherent in the 3D target. The network can perform complex rotation-equivariant tasks after pre-training, and it shows impressive performance in complex tasks like category-level pose change estimation and rotation-equivariant reconstruction. We demonstrate through experiments that our network can accurately detect the orientation and pose change of point clouds and visualize the latent features. Moreover, it performs well in invariant tasks such as classification and category-level segmentation.
1. Introduction
With the rapid development of autonomous driving [1,2], virtual reality [3], and robot interaction [4,5], the processing of 3D data is becoming increasingly important [6], and the equivariant network has a good performance in processing transformed stereoscopic data. Three-dimensional data contain depth information that is unavailable in 2D planar data, allowing machines to perform more advanced tasks, such as robotic arm manipulation [7] using a point cloud. In this task, the neural network is required to consistently provide pose information for varying object poses equivariantly, facilitating precise object grasping by the robotic arm. This requires the network to be able to effectively learn the pose information in objects, that is, the network needs to have equivariance.
If a neural network has equivariance, it means that the representations it produces transform under transformations of the input [8]. The traditional neural network, which does not consider the transformation of data, is not sensitive to the transformation of 3D data in space [9]. Equivariant networks for 3D data show more rotation equivariance. If a network has rotation equivariance, it actively learns the rotational operations within the data, where rotations in the Euclidean space drive the rotation of features in the latent space. Therefore, rotation-equivariant networks can perceive the transformation of data and conveniently learn deeper spatial geometric features. Rotation invariance is a special case of rotation equivariance. Rotation-invariant networks handle rotated data robustly, and the rotation operation applied to the data does not impact the learning of the network’s latent features. It abstracts the same invariant information from the geometric characteristics of the same class of rotation data. Recent works [10,11,12,13] have looked into more efficient equivariant networks, but these equivariant networks can be complex [14] or involve complex formulations and are difficult to incorporate into existing pipelines [15]. Therefore, it is hard to apply them to 3D point cloud processing networks with excellent performance [16,17,18,19,20].
Self-supervised learning leverages unlabeled data to learn latent features, eliminating the need for human-defined annotations when constructing representations [20]. It has demonstrated promising outcomes in the domains of natural language processing and computer vision, yielding notable achievements. Among them, the masked autoencoder [21,22,23] is a promising scheme for both languages and images. In point cloud networks, there are also advanced masked self-supervised learning frameworks such as Point-Bert [19] and Point-Mae [20]. However, due to the lack of interpretability, the internal mechanism of the network remains a black box [24], and it is hard to visualize its learned features and enhance them.
In this paper, we propose an equivariant self-supervised vector network to handle pose variation information in 3D point clouds, enhance the network’s generality for rotated point clouds, and conduct a theoretical analysis of the network’s interpretability using information theory. We design a simple and efficient masked self-supervised learning scheme to guide the model to map the input into the latent space in an equivariant way and reconstruct the original input from the latent features equivariantly, to achieve the reconstruction of point clouds in any direction in 3D space. For the equivariance of the network, we adopt the idea of vectorization [15] and use vector neural layers in the network to achieve the transmission of equivariant features. In our self-supervised learning framework, we integrate vector neurons and innovatively extend them to the Transformer architecture of the autoencoder to construct a vector attention calculation mechanism. This enables the seamless transfer of vector information throughout the entire network. Moreover, we refer to the theoretical analysis on the interpretability of Transformers in information theory [24,25,26] and describe the interpretability of our equivariant self-supervised vector network, which is used as inspiration to explain the equivariance and masked self-supervised learning in the network. Our network can effectively learn the deep latent features of the original data samples even when trained on incomplete data. Furthermore, we provide visualizations of the features generated by the encoder, offering a more intuitive elucidation of the network’s equivariance. On downstream tasks, we extend equivariant networks [27,28,29,30,31] to both rotation-invariant and rotation-equivariant tasks, and mainly focus on equivariant reconstruction and pose change estimation in rotation equivariant tasks. It can realize not only rotation-invariant classification and segmentation tasks but also rotation-equivariant reconstruction and pose change estimation tasks, which are more complex. At the same time, it has good performance in few-shot classification learning, which reflects the good generalization ability and inclusiveness of the network.
In summary, our main contributions are as follows:
- We propose an equivariant self-supervised vector network for point clouds. The network with a novel structure has better robustness to rotated data and can reconstruct the point cloud under arbitrary rotation in 3D space.
- Our network can deal with more rotation-equivariant tasks like pose change estimation and rotation-invariant tasks like classification, segmentation, and few-shot learning. It means our network has high generalization ability.
- We perform an interpretability analysis of equivariant and self-supervised learning architectures in the network and visualizations to demonstrate that it is equivariant.
2. Related Work
2.1. Transformer for Point Clouds
The Transformer [32] and its self-attention mechanism have achieved remarkable achievements in the fields of natural language processing [22] and computer vision [18,33,34,35,36]. Most point cloud networks use convolution or graph structures like PointNet++ [16], DGCNN [17], ShellNet [37], etc. [38,39,40,41,42], and the Transformer architecture for point cloud data is less common. Considering that the point cloud is a type of set, the self-attention mechanism is very suitable for dealing with this type of data [18]. Consequently, networks employing Transformer structures for point clouds have demonstrated remarkable performance and achieved noteworthy results. PCT [43] and PointTransformer [18] have a modified Transformer structure to better fit point cloud processing. GPSFormer [42] combines the Transformer structure with graph convolution and achieves good results. Point-BERT [19] and Point-MAE [20] introduce the standard Transformer architecture to process point clouds and achieve advanced results.
Although the current Transformer-based point cloud processing methods are widely used, these methods still use the traditional scalar neuron structure, which makes it difficult to effectively process vector information with directional characteristics. This paper introduces vector neurons and vectorizes the Transformer architecture, enabling it to directly process vector information and improve the robustness of the network when processing rotated point clouds.
2.2. Self-Supervised Learning
Self-supervised learning [44] is a type of unsupervised learning where the labels used for learning can be generated from the data themselves. It is usually pre-trained on a large dataset using a pretext task such as a reconstruction or puzzle, then fine-tuned to generalize its learned representations to other datasets for various tasks. It does not require labels during pre-training, which alleviates the high demand for manually labeled data [20].
Self-Supervised Learning for Point Clouds: Self-supervised learning has also been extensively studied for point cloud networks. Most of them adopt the idea of mask reconstruction [19,20,45,46]. OcCo [45] attempts to recover the original point cloud from the occluded point cloud in camera views. As a BERT-style self-supervised framework, Point-BERT [19] employs a two-stage pre-training process where it predicts latent representations learned by an offline tokenizer. However, it is important to note that directly recovering raw point clouds can potentially result in information leakage due to the positional encoding of masked tokens. To alleviate the above problem, Point-MAE [20], which adopts the MAE [23] idea, was proposed to only input unmasked tokens into the encoder and add the masked tokens to the decoder for reconstructing.
Information Theory in Self-Supervised Learning: Self-supervised learning models demonstrate that the intrinsic representations derived from pre-training exhibit strong generalization capabilities across various downstream tasks, yielding favorable performance outcomes. However, their internal workings remain opaque. In recent years, scholars have made attempts at interpretability [47]. From the perspective of information theory, Ma Yi et al. explain modern deep networks using the principles of data compression and discriminant representation [24,25,26], and also offer a fresh perspective to explain the quality of learning in the self-supervised learning framework and theoretically guide the optimization direction of self-supervised learning.
While these methods showcase strong performance in point cloud processing, they often lack ample sensitivity to the intrinsic features embedded in rotated point clouds due to insufficient consideration of rotation equivariance. This paper introduces a network framework leveraging a masked autoencoder to effectively capture the intrinsic representations of point clouds through self-supervised learning, without relying on labeled data. Additionally, by vectorizing the network, it acquires rotation equivariance, empowering it to handle more complex rotations of point clouds. Furthermore, the adoption of pre-training and fine-tuning strategies further broadens the network’s applicability, enabling it to tackle various tasks such as classification, segmentation, and pose change estimation.
2.3. Equivariant Network
Equivariant network research mainly focuses on two types of methods: steerable kernel-based methods that construct group convolutions, and vector network methods that use vector representations. In steerable kernel-based methods, Cohen et al. introduced networks using group equivariant convolutional [8,48,49,50,51] that learn the directional information in the input data by group convolutions, and mapped the 3D data to the sphere by applying spherical convolutions [52,53]. By employing this approach, they could process 3D data in an equivariant manner. In vector-based networks, Hinton et al. target the CNN pooling operation to destroy the rotation and other characteristics of the network, design the capsule network [54,55,56,57,58], which uses capsules to store vector information, and design a dynamic routing mechanism so that direction information can be transmitted in the network. The equivariance embedded in the aforementioned networks is beneficial for processing the information of the 3D data. When it comes to tasks, they can be divided into the following two categories:
Rotation Invariant: Rotation invariance is a desirable property for label-class tasks such as classification and segmentation, and many rotation-invariant architectures have been proposed to solve these problems [27,28,29,30,31]. For example, GC-Conv [29] relies on PCA-based multi-scale reference frames; SFCNN [30] is a method similar to multi-view, which maps the point cloud to a sphere and relies on spherical convolution to achieve the property of rotation invariance; ClusterNet [27] uses hierarchical clustering to explore the geometric structure of point clouds in hierarchical trees; and Deltaconv [31] employs a two-stream structure of a vector and scalar to capture the surface invariant information of point clouds, and makes the point cloud from all angles output the same feature through the construction of a basis vector.
Rotation Equivariant: Rotation-equivariant deep learning frameworks [59,60,61] have mostly relied on the notion of steerable kernel-based convolution. For example, spherical CNNs [52,53] convert the input point cloud into a spherical signal and use spherical harmonic filters that produce features in spherical space. However, these methods require a specific architecture to match the specially processed data which has good performance but also limits the applicability and adaptability of the network. The VNN [15] is a concise SO(3) equivariant framework with good accessibility and generality, where SO(3) denotes any rotation in 3D space. Conceptually, any standard point cloud processing network can be promoted to an SO(3) equivariant network while maximally retaining the original architecture.
Although the above methods improve the network’s ability to process rotated point clouds, most networks do not have expanded capabilities. Even some rotation-equivariant networks limit their tasks to rotation-invariant tasks like classification, and the complex structures of most networks make it difficult to adapt to different tasks. The method in this paper retains the vector information contained in the 3D data by constructing vector neurons and trains the network using self-supervised learning, making the network have excellent transferability and exploring both rotation-equivariant and rotation-invariant tasks.
3. The Equivariant Vector Network with Self-Supervised Learning
We have devised a self-supervised learning network that effectively learns from point clouds, enabling it to acquire an intrinsic representation that exhibits rotation equivariance. This characteristic enhances its applicability and versatility. To this end, we constructed a masked autoencoder self-supervised learning framework with high mutual information based on information theory. We then vectorized it to make it equivariant and learn deeper equivariant features of point clouds. This approach can be extended to both rotation-invariant and rotation-equivariant tasks. At the same time, the interpretability of the network is elaborated by using information theory, and the possibility of obtaining equivariance is theoretically verified.
3.1. The Theory of Equivariant Networks
To realize the equivariant and universality of point cloud networks, our network adopts an SO(3) equivariant network framework with good performance and portability at the present stage which is called the Vector Neural Network (VNN) [15]. The VNN achieves equivariance on the 3D rotation by lifting the representation of the neurons in the network from a scalar to a vector . In this way, the equivariance of the whole network is realized. The network’s learned mapping function f satisfies the following property: for any rotation matrix ,
holds true.
The in the formula is the vector feature generated by the original scalar feature in the data. The original scalar feature in the input sample can be lifted into a vector feature after the vectorization operation in the data processing stage so that information can be transmitted equivariantly in the network. This vector list feature is similar to standard latent representations and can be used to encode entire 3D shapes, parts, or individual points. The number of potential channels of can be mapped from layer to layer similarly to a standard neural network:
Through the use of vector neurons, the rotation action in the data sample can be expressed in the network so that the network can not only encode the entire 3D shape but also learn the direction information of it. The theory of vector neurons also inspired us to vectorize the Transformer architecture, which is also a scalar computation architecture, so it can also be vectorized to transfer vector information.
3.2. Information Theory in Masked Autoencoder
A popular way to interpret the role of deep networks is to view the output of intermediate layers of the network as some kind of latent feature [25]. Each deep network tries to learn useful features z from a randomly distributed set of data samples . We can generally represent this learning process as a continuous mapping, , where the is the parameters of the mapping function f. The learned internal feature z is a compressed representation of X in the latent space, after which the internal feature z can be used to learn the subsequent task y by the head . It is expressed as follows:
According to the hypothesis of Information Bottleneck theory [25], mutual information is the index to measure the quality of network learning in the process of learning, where represents the Shannon entropy of x. In the stepwise training process, the network will tend to maximize the mutual information between the internal representation z and the learning target y while minimizing the mutual information between the z and the learning sample x.
Therefore, the neural network has been a task-driven model before. The hidden feature z in the network will continuously increase the mutual information with the training target y during the training process, thereby obtaining better learning results. However, if a new learning task is replaced, the effect will be unsatisfactory and re-training is required. It is for this reason that the robustness, generalization, and transfer of neural networks are difficult to improve. In order to improve the generalization and robustness of the network, scholars have proposed self-supervised learning methods, which let the internal feature of the network learn enough until it can regenerate the original data x and then reconstruct x through some decoding generators . This framework is called an autoencoder. The expression is as follows:
Mappings f and g in the formula are called the encoder and decoder, respectively. Meanwhile, to further improve the encoder’s ability to learn the latent features of sample data, some scholars have proposed a mask learning method. The main idea of it is to partially mask the original data, that is, to divide the original sample data x into two parts, the visible part and invisible part , then input as learning sample data into the framework of the autoencoder and change the target of network reconstruction from x to . Then, the framework of the network framework takes the following form:
It is called a masked autoencoder (MAE) [23] because of its use of masks. Through this construction, even if the network is still limited by the Information Bottleneck theory, its internal representation of z will learn the information of as much as possible, where is originally a subset of the original data x. This approach provides an excellent method for learning features from original data. In addition, the mask operation disrupts the original data structure of the input data x, allowing the latent feature z to more effectively learn the depth characteristics of the sample data x through the visualized subset . Information theory can also provide an explanation for the improved learning effect as the mask rate increases within a certain interval in the MAE. As the mask rate increases and the subset expands, the latent feature z becomes more capable of learning information specific to the network’s target subset . This results in better learning outcomes.
Simultaneously, it is worth noting that both the input and output of the network constitute a subset of the original sample data distribution x, and the goal of the MAE can be regarded as the optimal estimation of . The general form of the MAE loss function can be easily obtained, and this general form also has better generalization. Its expression is as follows:
If the encoder and the decoder in the MAE network framework have equivariance, the latent feature z can be equally rotated with the rotation of the input data , and the MAE of features learned in this way can realize the equivariant reconstruction.
When encoder and decoder have equivariance, so that it meets , , the equivariance is as follows. For any rotation matrix , there is
In this case, the overall framework of the MAE is equivariant:
The rotation R performed on the input data is passed through the network to the latent feature z, and then to the final reconstruction result. Finally, the network can be implemented for equivariant feature learning and rotated data reconstruction.
The above theory illustrates that the internal representation learned through the MAE framework can regenerate the data if it is rich enough. Of course, this is also well demonstrated by the original MAE experiment. At the same time, if the encoder and the decoder are equivariant, the MAE framework will be equivariant. The network architecture design in this paper extends the MAE. While retaining its original excellent internal representation learning ability, it is endowed with the learning of equivariant features. Following the above ideas, if constructed in an equivariant way, the network can be applied to a wider range of learning tasks, achieving better generalization and robustness. It can realize the equivariant reconstruction of point clouds and the learning of equivariant features.
3.3. Network Overview
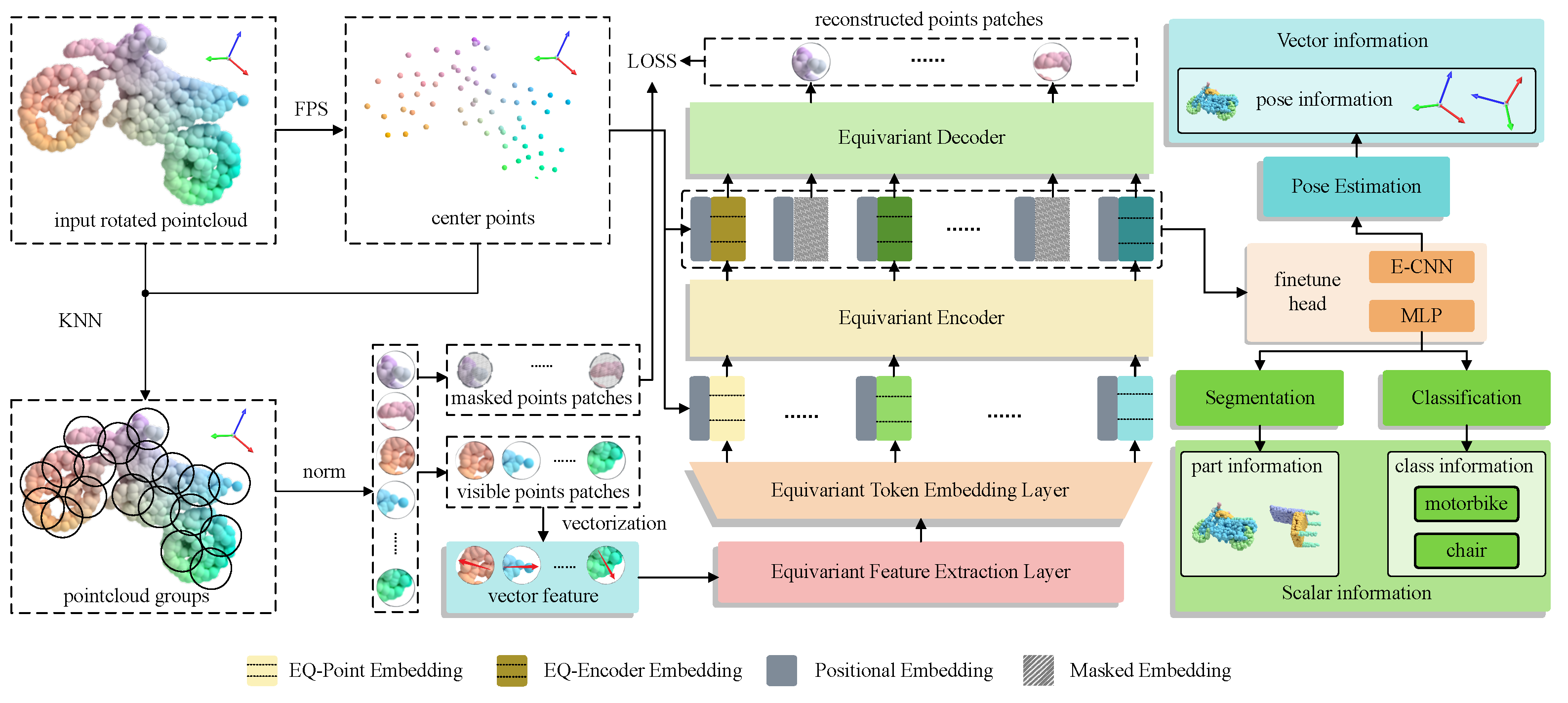
Our equivariant self-supervised vector network is an efficient autoencoder that reconstructs the original signal for arbitrarily rotated point clouds. Figure 1 illustrates the general framework of our approach. To address the challenges posed by the vast number of data and the inherent disorder in point clouds, an initial step involves partitioning the input point cloud into patches. This process aims to decrease the information density of the point cloud and alleviate the sensitivity of latent features to variations in point cloud density. This reduction in density helps facilitate subsequent processing of the point cloud data. At the same time, during patching, local vector features are also initialized in patches for the subsequent processing of our vector network. When the input data become point groups with a uniform scale, we mask them, and then only the visible point groups are processed, and a series of data processing steps such as vectorization, extraction of equivariant features, and feature embedding is carried out. Afterward, a Transformer-based autoencoder framework is employed to train and learn the embedding of the processed data. This learned embedding is then utilized to reconstruct the obscured point patches within the input point cloud. The above operations belong to the part of pre-training in the proposed scheme, and the decoder module is only used in the pre-training process. In downstream fine-tuning tasks, we combine the encoder module with different fine-tuning heads so that the network can be applied to different downstream tasks, such as rotation-invariant classification and segmentation or rotation-equivariant pose change estimation.
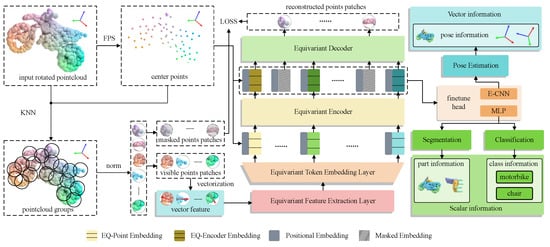
Figure 1.
Equivariant self-supervised vector network’s overall architecture. The input point cloud is divided into several point cloud patches, after which they are randomly masked, and then the point embed operation is carried out through the equivariant layer and token embed layer. Then, the obtained point embedding with vector information is fed into the autoencoder for pre-training. When the pre-training is finished, the decoder module will be abandoned and replaced by different fine-tuning heads. After connecting various fine-tuning heads to the front network, the network can be applied to different downstream tasks.
3.4. Network Backbone
3.4.1. Patch Generation of Point Clouds
When generating a 2D image patch, the inherent constraints and relatively square shape of a 2D image allow for a direct division of the patch in a checkerboard-like manner. However, as a point set in 3D space, the shape of each point cloud is different, and there is no uniform size constraint; therefore, this paper uses the Farthest Point Sampling (FPS) [20] method and the K-Nearest Neighbor (KNN) [20] algorithm to divide the point cloud into patches. Given point cloud data with N points, the role of FPS is to find the n center points that can most concisely describe the contour of this point cloud. Based on these n center points, the KNN algorithm finds the k closest points to each center point in the original point cloud data X. These point groups and the n center points together form n point patches, that is, .
In these point patches, each point within the patch undergoes coordinate normalization operations with respect to the central point of the patch, resulting in a well-converged group of points. In terms of mask operation, this study masks the generated patch with the mask rate of m. Visible patches will be used as input and sent into the later module, and masked patches are regarded as the ground truth for loss calculation with reconstructed patches, formed like . In the selection of the masking strategy, we adopt the effective random masking strategy, the same as for the MAE [23].
3.4.2. Initialization of Vector Features
The input point cloud only has 3D coordinate information, which is just some scalar property features . These scalar features are not significantly affected when implementing rotation transformation, so we follow the advice of the VNN [15] and carry out vectorization. For each point in each point patch, local vector features can be constructed with reference to the patch in which it is located so that it can integrate more dimensional vector information in the original data as much as possible. As each patch undergoes coordinate normalization, every point within a patch is vectorized based on its relative position to the center point of the corresponding patch. For each point in the patch , we have
The vector information obtained in this manner appears heterogeneous and lacks a simple structure, which poses challenges for subsequent operations. Therefore, the features are gathered into a vector matrix of after the convolution operation, which is used to combine into the initial vector feature list for later calculation in the vector equivariant network. Each V is aggregated from v as follows:
3.4.3. Equivariant Layers
The equivariant layer contains two layers; one is the equivariant feature extraction layer, and the other is the equivariant token embedding layer. These equivariant linear, nonlinear, and normalized layers are combined into the VN-MLP. Both the linear vector layer and the normalization vector layer are linear transformations that preserve the original directionality of the vector features. As a result, equivariant transmission between the two layers can be ensured after vectorization. However, the activation function in the nonlinear layer requires special treatment. The traditional ReLU function is an activation function for scalar features which does not apply to the vector features. This paper adopts a linear vector layer to predict the direction vector k that the vector V needs to activate. Then, the vector V is decomposed along the vector k to obtain a component vector which is parallel to the direction vector k and , which is perpendicular to the vector k. Then, the activation operation is performed on , and the vector ReLU is expressed as follows:
These vector layers are serially combined in the traditional structure of the MLP and finally stacked to form the VN-MLP. We denote the feature extraction network, the VN-MLP, as and the embedding layer for vector token as , so that we have
where is the input point cloud, is the vector feature list after vector initialization, is the vector token, and is the ordinary rotation matrix. Here, we can see that the rotation operations that were originally located at the input point cloud are transferred equivariantly to the subsequent vector features. The autoencoder backbone after the vector layers is also equivariant, embedding vector neurons in the Transformer.
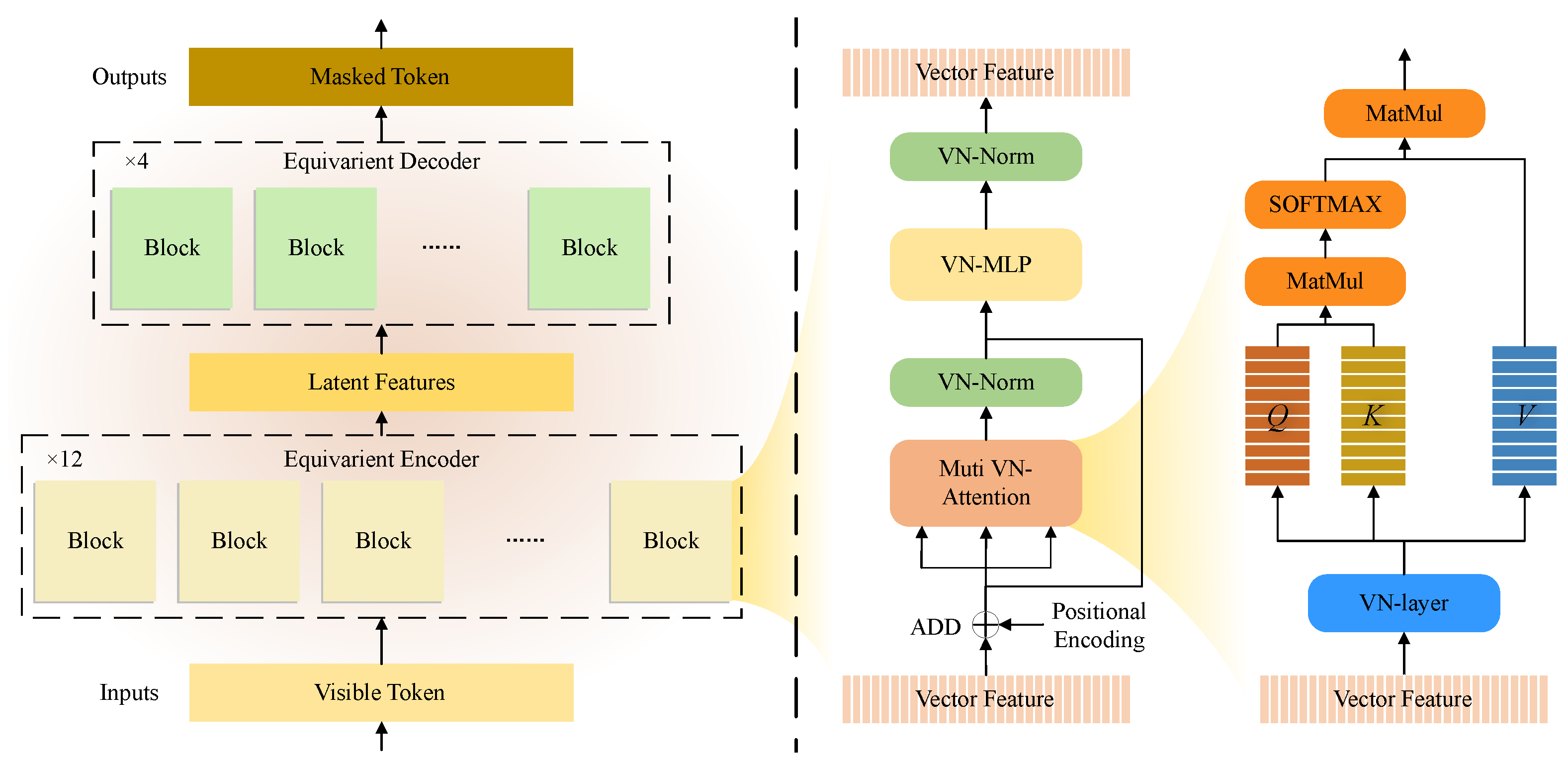
3.4.4. Autoencoder Backbone
In this study, the autoencoder backbone is based on the masked autoencoder with a Transformer structure. At the same time, it adopts an asymmetric encoder–decoder design, that is, the encoder has more layers than the decoder.
Encoder: In the encoder part, we follow the original MAE [23] practice that only takes the visible tokens, , as input. Embedding is applied individually to each position of the visible tokens, and the obtained position embeddings are , which will be fed into the encoder along with . This approach offers two advantages. Firstly, it helps to reduce the computational burden in the encoder part. Given that the encoder typically comprises more blocks than the decoder, reducing the input data volume in the encoder can substantially alleviate computational complexity and processing time. Second, it can reduce the correlation between the information of the input data. The complete absence of masked tokens can make the encoder better pay attention to the internal relationship between the visible tokens and learn the potential features in the data.
Decoder: For the decoder, the output tokens from the encoder module and the masked tokens will be combined as a completely new input. At the same time, for the processing of location information, the decoder takes all token location information embeddings, (including visible and masked tokens), as part of the input, which is learned together with , as input. The input , , and will be processed by the decoder, and only the masked tokens will be output as , which will be used as the input of the later reconstruction task and reshaped into the masked point patches in the later reconstruction module.
VN-Attention: Due to the conventional Transformer scalar structure, to ensure equivariant transmission, we also modify the structure of the Transformer to handle vector information. The most important thing in Transformers is the computation of attention, so we redesign the attention layer in the Transformer to enable operations on vectors. The calculation of attention in the Transformer is as follows:
We use vector neurons to change the original attention formula into VN-Attention, which does not change the calculation steps but can retain the direction in the data when calculating attention and make it equivariant. The formula is as follows:
We use the vector data Query , Key , and Value instead of using the scalar data in the calculation. In the new formula of VN-Attention, it can be found that the rotation of the input data is equivalent to the rotation of the output data after the attention calculation, that is, the attention calculation is equivariant. Other linear transformations in the Transformer architecture are also vectorized by vector neurons. Based on this, we construct the vector Transformer structure. It is used to ensure equivariant transmission in the autoencoder framework.
As shown in Figure 2 below, we retain the standard Transformer architecture to the greatest extent and replace scalar neurons with vector neurons to enable the transfer of vector information. We lift the original scalar matrix to a vector matrix in the attention calculation and transfer the original attention to VN−Attention so that it can perform the attention calculation of vector features. Instead of greatly modifying the calculation process and calculation method of the Transformer, we only replace the scalar flow calculated with a vector flow, which not only retains the feature extraction ability of the Transformer to the greatest extent but also realizes the equivariant calculation of vectors, to ensure the equivariant transmission throughout the network.
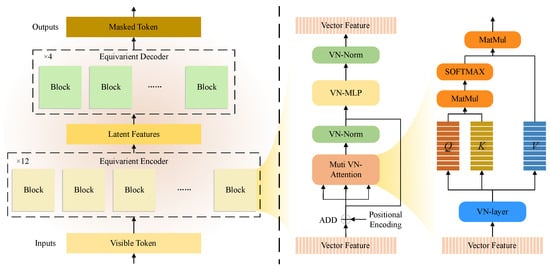
Figure 2.
A diagram of the framework of the VN-Transformer. Its structure is similar to the standard Transformer framework. The left is the flow of tokens in the whole autoencoder framework, and the right is the internal structure of each block and the calculation process of VN-Attention.
3.5. Implementation
3.5.1. Pre-Training Tasks
We combine all the previous modules for the pre-training task. The point clouds after preprocessing as input will be sent to equivariant layers for equivariant feature learning through patching, vector feature embedding, and masking, and then the autoencoder will finally receive the tokens . will be fed as input to the final reconstruction head reshaped into the shape of point patches, and finally the reconstruction results are obtained. The original masked point patches, , are used as the ground truth, that is, and are used to calculate the loss, which is used to realize the self-supervised training process. This whole training process can guide the network to learn equivariant features in the point cloud so that the latent features of the model can learn the intrinsic representation of the original point cloud sample X. For the calculation of the self-supervised loss, the regular point cloud employs the Chamfer Distance, which is formulated as follows:
3.5.2. Fine-Tuning Tasks
In the fine-tuning tasks, the decoder module is replaced by different fine-tuning heads. The input point cloud goes through the same process to obtain tokens, but this time the tokens are full tokens, shown by . Depending on the task, the is fed into different fine-tuning headers, such as the MLP or equivariant CNN, to output different structures of the data for different tasks.
4. Experiment
We evaluate our method on four core tasks of point cloud processing: reconstruction (Section 4.1), pose change estimation (Section 4.2), classification (Section 4.3), and segmentation (Section 4.4), and also test it on a classification task with few-shot learning (Section 4.5), which is used to demonstrate the robustness of our network. These tasks are not only rich and diverse but also encompass most of the different application scenarios of the equivariant framework. Reconstruction and pose change estimation are rotation-equivariant tasks, while classification and segmentation are rotation-invariant tasks. Moreover, the pose change estimation of 3D point clouds has been less explored in the previous research.
Dataset: We mainly use ShapeNet [62] and ModelNet40 [63] datasets for the evaluation. The ShapeNet dataset contains more than 50,000 different 3D models of point clouds, which can be divided into 55 categories. The ModelNet40 dataset consists of 12,311 3D point cloud models covering 40 object classes. For the segmentation task, we use the ShapeNetPart dataset for partial segmentation, which contains 16 shape classes and more than 30,000 models. Since there is currently no publicly available clean human point cloud dataset, we utilize point clouds sampled from the HumanBody dataset [64]. The HumanBody dataset comprises 399 meshes. For our study, we select 397 complex mesh models (two of the mesh models are too simple to sample effectively) and randomly sample 4096 points on each model. At the same time, we also add random noise perturbation during the sampling process.
Rotation Settings for Training/Testing: The three rotation settings in training and testing are i, z, and SO(3), where i means no rotation of the data, z means rotation only around the z-axis, and SO(3) means any rotation in 3D space. We test all tasks under the three rotation settings.
4.1. Reconstruction
The goal of pre-training in this paper is the reconstruction task, which can realize the reconstruction of incomplete point cloud data. The datasets adopted for this task are ShapeNet and point clouds sampled from the HumanBody dataset. For ShapeNet, we use an FPS operation to unify all point cloud models into 1024 points and divide them into 64 patches with 32 points in each patch, which are used as input. For point clouds sampled from the HumanBody dataset, we divide 4096 points into 256 patches with 32 points in each patch. Before the data are fed into the network, we randomly rotate it to ensure that each sample has a different rotation state each time.
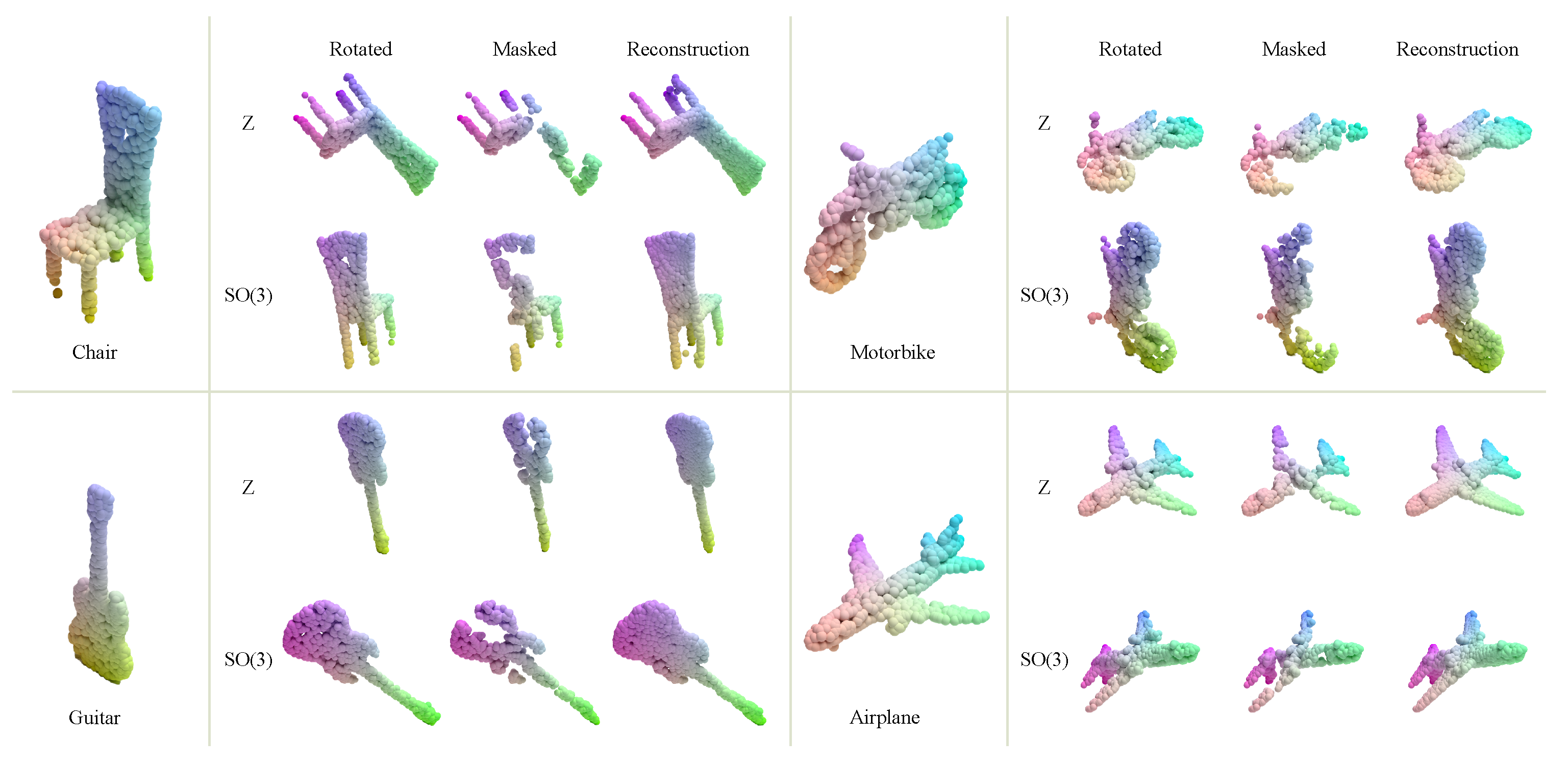
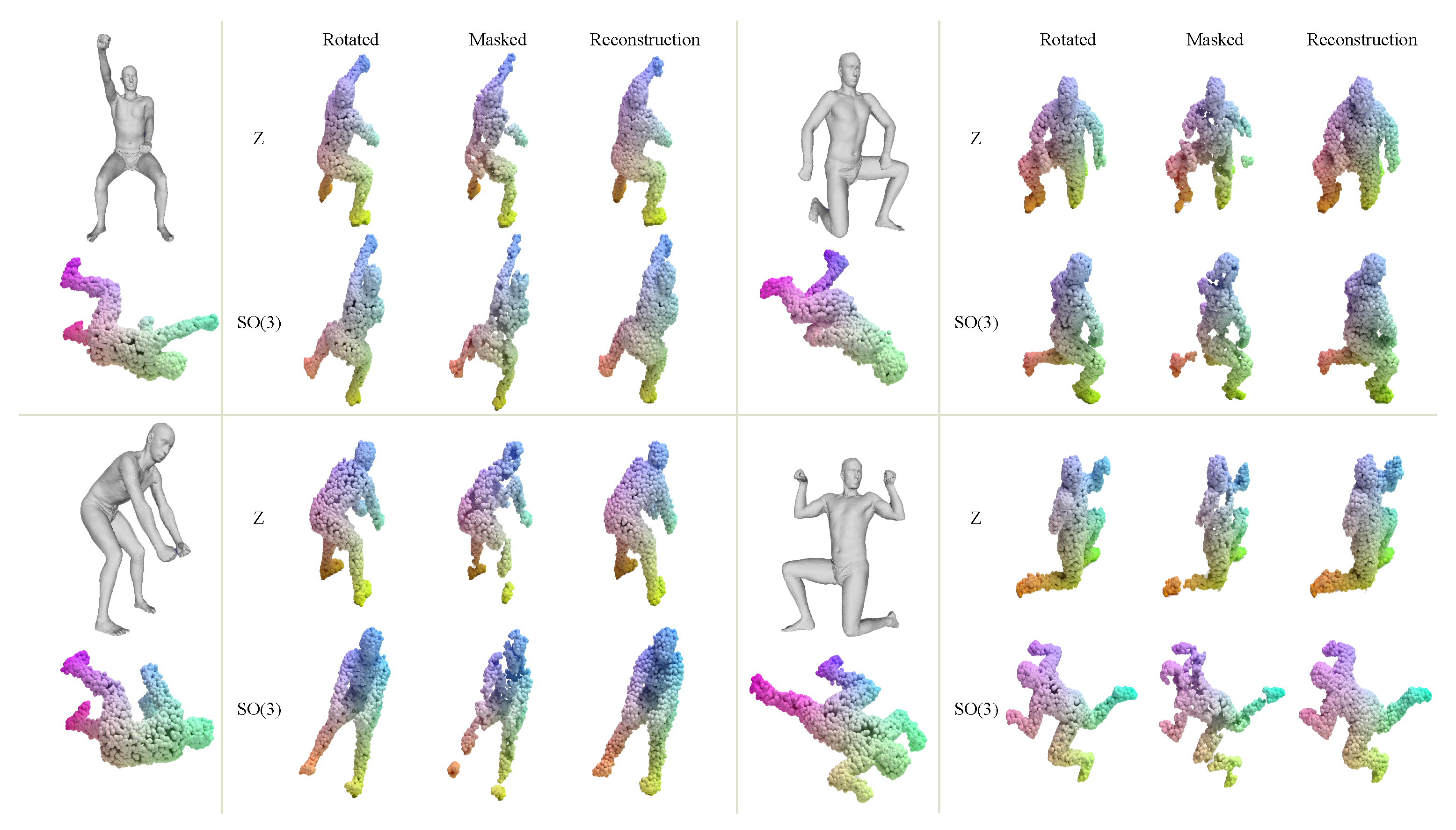
The network of the reconstruction is a complete network structure, including the equivariant vector layers at the beginning and the subsequent autoencoder module. In the end, all tokens are mapped and reconstructed into the ground truth shape through a simple MLP layer, and the output is , which is finally combined with the input visible point cloud patches to form a complete point cloud. Since our input is a randomly rotated point cloud, our reconstruction target should be a point cloud that is consistent with the rotated state of the input to verify the equivariance of our network. To demonstrate the effectiveness of our approach, we visualize [6] our reconstruction results on the ShapeNet dataset in Figure 3 and human point clouds in Figure 4. As we can see in Figure 3, the reconstruction effect of our network is very excellent. It can not only well reconstruct the point cloud under different rotation states, but also yield a reconstructed point cloud with less noise, and the reconstruction result is very simple and fits the original input. As for the human point clouds, we construct a clean human point cloud dataset from the HumanBody dataset. Our network also performs very well on complex human point clouds; there is no excessive adhesion, and the human limbs are relatively distinct. The network is pre-trained with a 60% mask rate, but it is also able to reconstruct the input with various masked ratios. This high generalization and strong robustness verify that our model can better learn advanced latent features and can be used as a good pre-trained model for downstream tasks.

Figure 3.
Rendering of the reconstruction effect of our network on ShapeNet. The network will reconstruct the visible point clouds under different rotation states. During training, the network only learns the non-rotated points, but, in the test, the network can also reconstruct the rotated point clouds under z and SO(3) conditions well. The training in the figure uses a 60% mask rate. Meanwhile, in order to better present the results, we render the point clouds in this figure and the later results presentation figure to some extent.
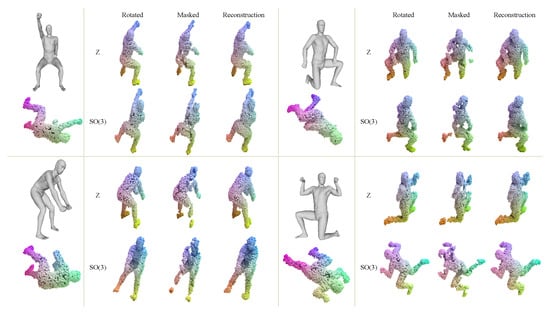
Figure 4.
Rendering of the reconstruction effect of our network on human point clouds. The human point clouds are trained in the same way as ShapeNet. These human point clouds were obtained by sampling on the mesh model of the HumanBody dataset. Since the initial pose in the original HumanBody dataset is confusing (i.e., the pose of the point cloud below the mesh is the origin pose), we manually adjusted the mesh to show its rough pose and appearance. The training in the figure uses a 60% mask rate.
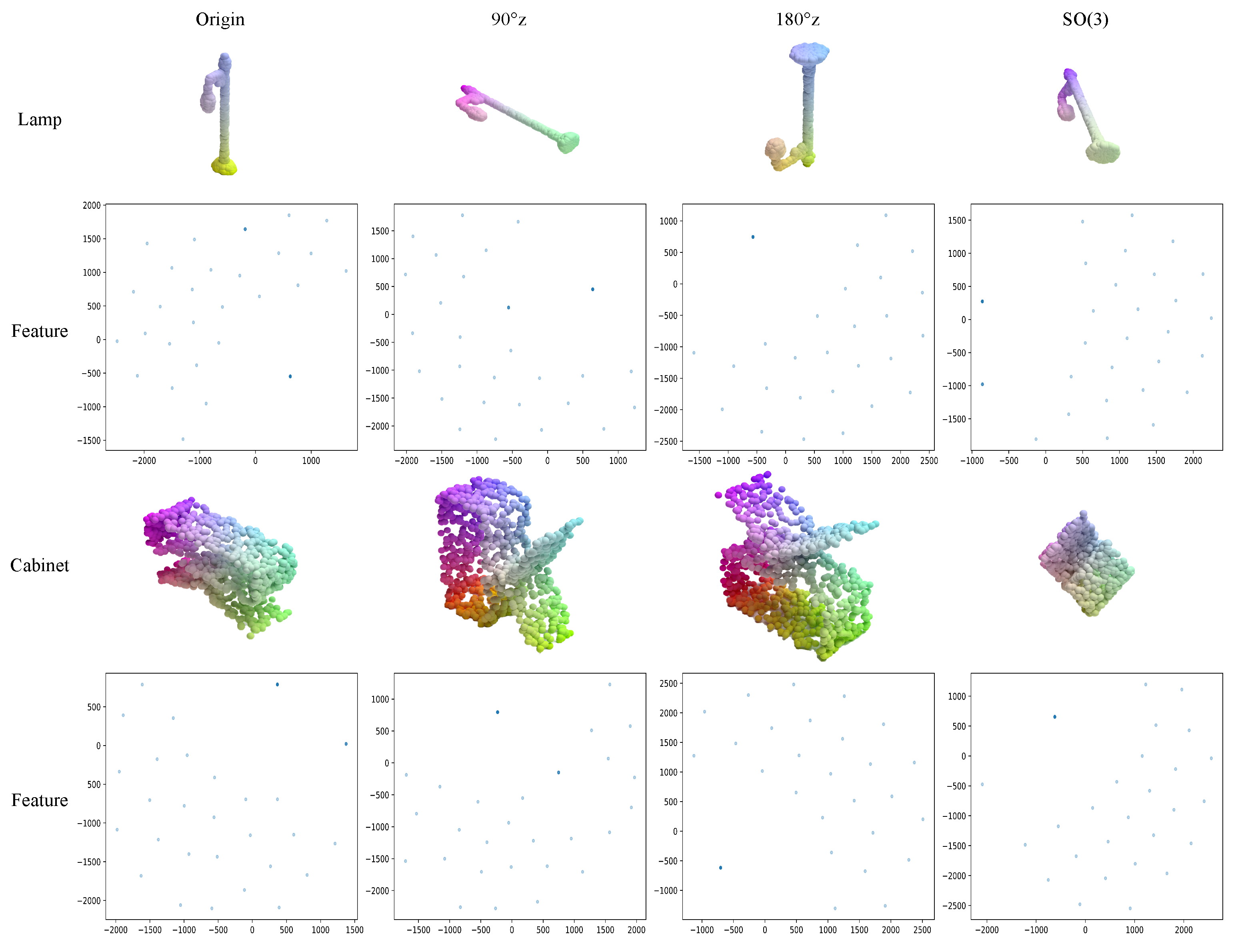
Meanwhile, we also study the latent features of our network. The MAE has been active in networks of various data types with excellent performance since its advent, but its performance in tasks of rotation equivariance and rotation invariance has not been well explored. And, because the neural network is a black box, its internal representation has always had a fuzzy existence that is difficult to express. We verify the interpretability and equivariance by visualizing the latent features generated by the encoder module. As depicted in Figure 5, we visualize the latent feature in our network. Remarkably, we observe that exhibits rotation congruent with the input as the data undergo rotation. This indicates that, after using vector neurons, our network possesses rotation equivariance, allowing the learned latent features from point clouds to transform along with the point cloud variations.
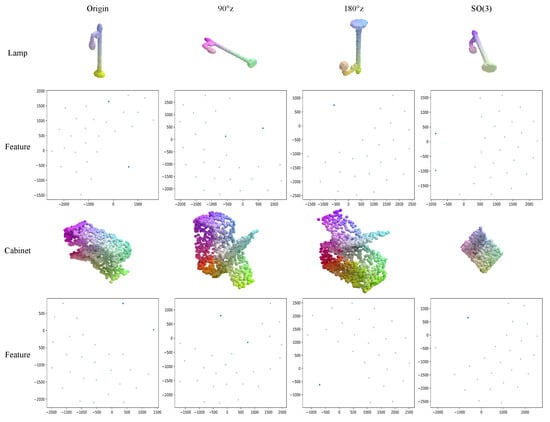
Figure 5.
Demonstration of the latent features of the network. The top of each row is the state of the input point cloud, and the bottom is the state of its corresponding latent feature, which can be seen to rotate with the rotation of the point cloud. The origin column is the point cloud without rotation, and the rest are the point clouds rotated by different angles, for example, 90°z means that the point cloud rotates 90 degrees around the z-axis.
For point clouds with different states, the network learns and maps it into the latent space, and we intercept its latent feature from the network after the encoder module. is a high-dimensional vector in the network, which is difficult to visualize through intuitive methods. Therefore, we use the T-SNE [65] method, which can project the features to a 2D plane according to the distance and distribution between the latent feature while preserving the original feature distribution to the greatest extent, so that it can be visualized intuitively in the 2D plane in the form of pictures. As you can see from Figure 5, the latent feature of our network is rotated as we rotate the input point cloud, with the rotation around the z-axis being more pronounced. The rotation angle of the original data can be well reflected from the features. Since SO(3) is a rotation of any angle in 3D space, it will rotate in three directions; therefore, it cannot fully reflect the rotation angle in the 2D plane. Although the 2D plane can reflect the 3D rotation less, we can see that the features rotate as the data rotate.
4.2. Pose Change Estimation
Our network shows excellent equivariant properties in the reconstructed task, so we set out to extend it to downstream tasks. We evaluate the pose change estimation ability of our pre-trained model on the ModelNet40 dataset. Our pose change estimation for the point cloud is mainly to predict the overall pose change direction of point clouds at the category level. When the point cloud is rotated, an isometric transformation is generated between the point cloud and the original state. This isometric rotation transformation can be expressed in the form of a rotation matrix, which is denoted as . The previous methods of pose estimation generally use quaternion to describe the rotation, which is more concise, but the description of rotation is too abstract to be expressed intuitively by images. While it is possible to convert it into a rotation matrix through formulaic calculations, this outcome does not align with our intended objective. We prefer to use the rotation matrix as an intuitive representation to express the pose change. The purpose of our fine-tuning head is therefore to directly predict this rotation matrix S, allowing the network to learn the pose information of the point cloud and visualize the rotation at the same time. Since this task is complex, not a simple classification and segmentation, and it needs to maintain equivariant transmission, we use a one-dimensional convolutional layer and a vn-pooling layer to replace the original linear layer fine-tuning head. The final designed network will directly output the predicted matrix . This task is not a normal classification and segmentation task that uses label loss, so we design a new loss for this task:
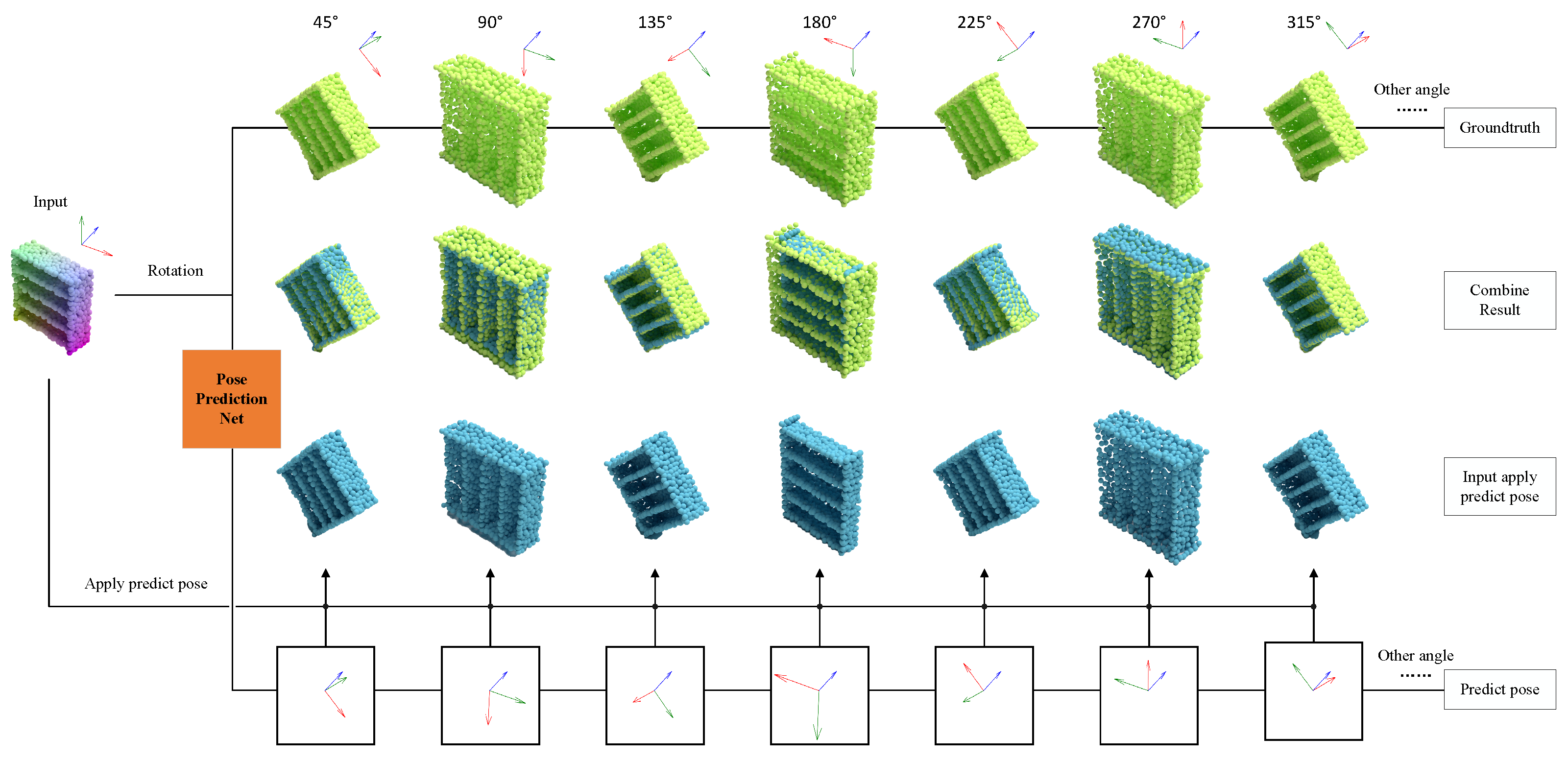
The function d computes the Euclidean distance between the corresponding vectors of the rotation matrix, and are the coefficients used to adjust the weights, and the right-hand side is the matrix regularization term for the rotation of the output. If the determinant of the rotation matrix is not 1, that is, the matrix is not orthogonal, then the affine transformation applied to the point cloud by the rotation matrix is not an isometric change. Consequently, the point cloud may undergo stretching or compression, resulting in deformation. To address this issue, it becomes essential to impose specific regularization constraints on the rotation matrix. To measure the final effect, we use the cosine similarity. When the cosine similarity between and each corresponding vector in S is larger, it means that each vector is closer in that direction, which also indicates that the prediction effect is better. Figure 6 is a visual presentation of the experiment.
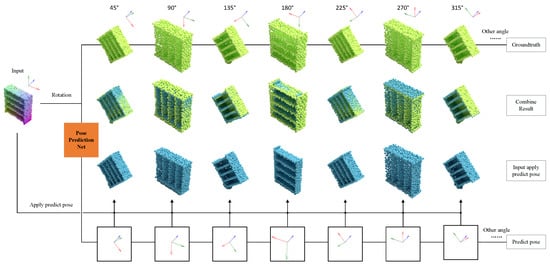
Figure 6.
Gradual rotation of point clouds and their corresponding output results. This figure shows how the network outputs different poses for different angles of the same point cloud around the same axis (z-axis). The top row is the input point cloud P after applying the rotation matrix S, and the bottom row is the predicted pose generated by the network based on the rotated point cloud , which is generated from the point cloud P after applying the rotation matrix S. The predicted pose is expressed as the rotation matrix . After reapplying to the origin point cloud P, a new rotation point cloud can be obtained, and whether the predicted pose is consistent can be judged by comparing with .
When the rotated point cloud is fed into the network, the network outputs its corresponding rotation matrix, which is the predicted pose change. We visualize this as the classic XYZ axis, which shows the pose of its output. Using the rotation matrix as the output allows us to visualize what each pose change looks like in a way that is difficult to visualize with quaternions, and our pose change estimation is much better than using quaternions alone. We can apply the predicted pose change to the original unrotated point cloud and compare it with the rotated point cloud. The middle row in Figure 6 shows the combined results. We can see that the final results of applying the original pose change rotation matrix S and applying the predicted pose change rotation matrix on the input point cloud are highly consistent.
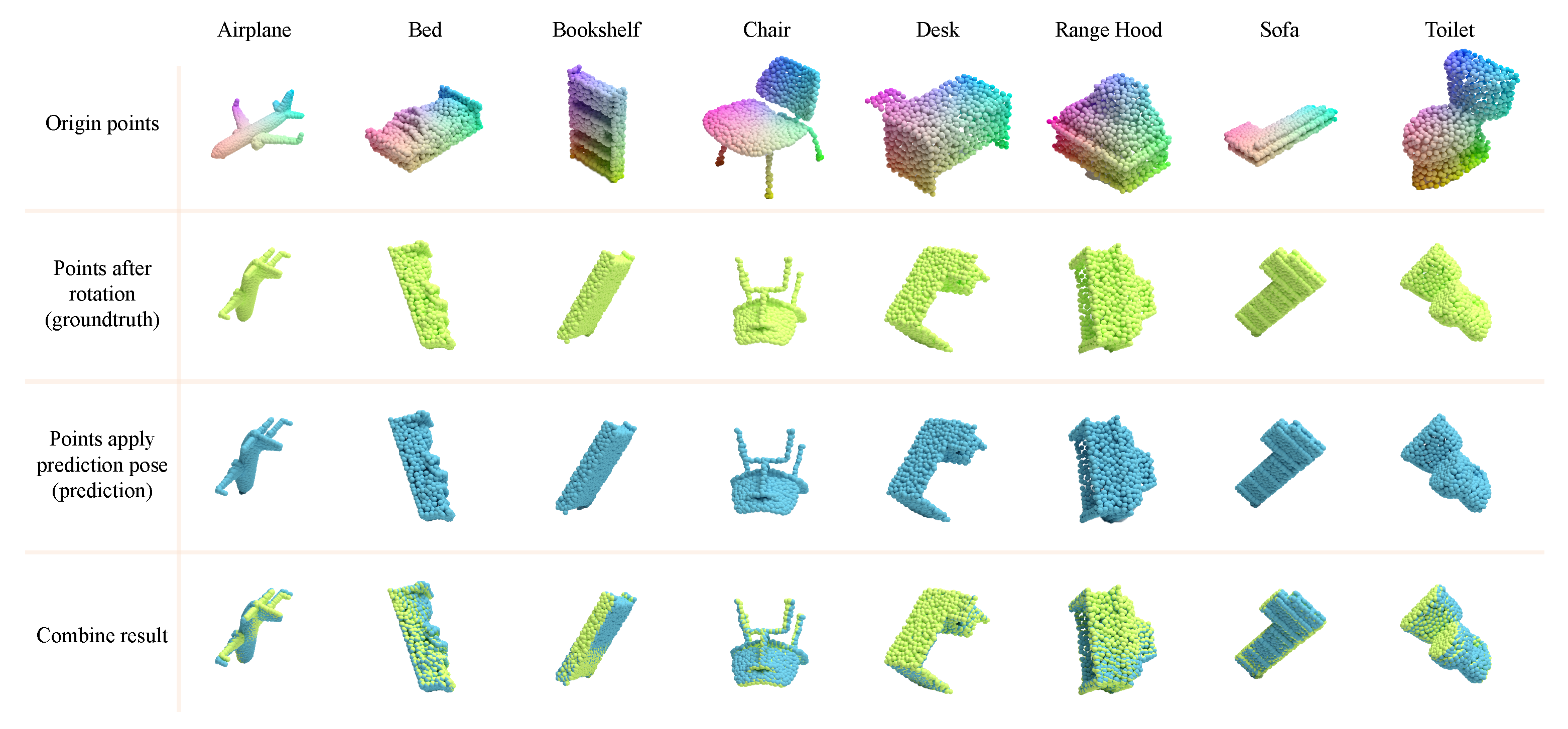
We also tested the network in SO(3). In Figure 7, we not only show the coincidence degree between the output pose and the original pose under random rotation but also compare the coincidence degree of different categories of point clouds. Due to the excellent rotation equivariance of vector neurons, our network efficiently learns vector information within point clouds. Among these, the pose information within point clouds is a key vector feature. Therefore, our network excels in handling pose variations of rotated point clouds, accurately estimating their pose changes under different rotation conditions. The experimental results demonstrate the network’s remarkable stability in pose change estimation tasks, accurately predicting pose changes in the SO(3) space. This not only proves the network’s strong adaptability in pose change estimation tasks but also showcases its efficient capture of equivariant features, further confirming the robustness and effectiveness of the network architecture.
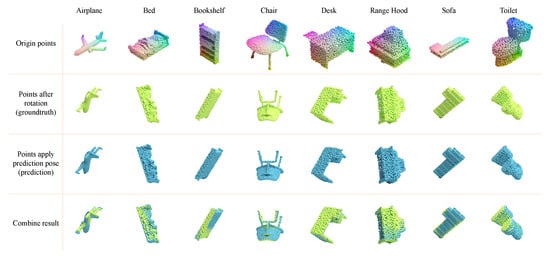
Figure 7.
Randomly rotated point cloud and their corresponding output results in 3D space. This figure shows the comparison between the pose output by the network and the origin point cloud for different point clouds rotated randomly under SO(3).
4.3. Classification
Regarding the task of rotation invariance, our network also demonstrates its strong performance. We conduct experiments on point cloud classification using the ModelNet40 dataset and compare the performance of our model with other networks under varying rotation conditions. The classification task inherently reflects the requirement of rotation invariance, and it serves as a valuable test for evaluating network performance. Table 1 presents the classification results of each model under different rotation settings.

Table 1.
Classification on ModelNet40. Test classification accuracy (%) on the ModelNet40 dataset in three train/test scenarios. We bolded the results of the best performing networks.
Due to the effective learning of intrinsic features in point clouds by vector neurons, our network not only exhibits the highest accuracy in non-rotated states but also demonstrates excellent recognition rates in rotated states. The best recognition results are achieved under rotations in SO(3), indicating the superior performance of our network and its robustness to rotated point clouds. The network’s performance is minimally impacted by rotated point clouds, showcasing its effectiveness in handling rotational variations.
4.4. Segmentation
We test the segmentation task of our network on the ShapeNetPart dataset, and, similarly, the segmentation also belongs to the task of rotation invariance. Our method also performs well in this task. Table 2 shows the segmentation results of each model for the ShapeNetPart dataset. Given the ability of vector neurons to learn invariant semantic information in point clouds, it can be seen that our network performs well in both rotated and non-rotated states. Although it does not achieve the best performance in the non-rotated state, it demonstrates strong adaptability in segmenting rotated point clouds. The vector information extracted by the network in the rotated point cloud helps the learning of the invariant semantic information in the rotated point cloud, thereby demonstrating strong generalization ability and performance. This enables our network to achieve the best performance in the segmentation task involving rotated point clouds.

Table 2.
Segmentation on ShapeNetPart. The results are reported in terms of the overall average category mean IoU (%) over 16 categories in three train/test scenarios. We bolded the results of the best performing networks.
Figure 8 shows the partial segmentation effect of our network for the ShapeNetPart dataset under different rotation states. It can be seen that our network adeptly segments various components of the point cloud across different rotation states, demonstrating its competence in the segmentation task and showcasing robust rotation invariance.

Figure 8.
Segmentation of rotated point clouds. This figure illustrates the comparison of segmentation results obtained from our network’s output for different point cloud rotation states, namely, Z and SO(3), in contrast to the original point cloud.
4.5. Few-Shot Learning
In order to reflect the powerful learning ability of our network, we conduct experiments with small samples on the ModelNet40 dataset. We follow the previous work and adopt the n-way, m-shot setting, where n is the number of randomly selected categories from the dataset and m is the number of randomly collected objects from the n classes. At training time, only these objects are used for training, i.e., there are only training samples. Then, in the subsequent testing session, we randomly select 20 unlearned objects from n classes for evaluation.
Table 3 shows the test results of different settings in and . Meanwhile, we perform 10 independent experiments for each setting, following the standard protocol, and report the average accuracy with standard deviation. Due to the excellent transfer capability of self-supervised learning, our network achieves significant improvements in accuracy and greatly reduced bias across three different settings. This indicates that our network can achieve the performance of other networks trained on a larger samples with only a small number of data. Furthermore, we further validate the network performance in a rotation scenario. The vector neurons in the network give it excellent rotation equivariance, which makes it lose only a small amount of accuracy when processing rotated data. This result fully proves that our network is extremely robust to rotated point clouds.

Table 3.
Few-shot object classification on ModelNet40. We conduct 10 independent experiments for each setting and report mean accuracy (%) with standard deviation. We bolded the results of the best performing networks.
4.6. Summary
The excellent performance in the few-shot experiment shows that our network only needs to learn a few samples to achieve better results, which shows the excellent generalization ability of our network. In addition, all our downstream task experiments are re-trained on the basis of the same pre-trained network, which has good performance in all downstream tasks, proving that our network has learned excellent latent features in the pre-training part, and thus it has good generalization ability and transferability. The introduction of vector neurons provides strong support for the network’s rotation equivariance. This characteristic enables the network to excel in handling various downstream tasks involving rotated point clouds, demonstrating outstanding performance and adaptability.
5. Limitations and Future Work
In this study, the self-supervised learning equivariant vector network proposed by us can effectively handle various tasks under point cloud rotations and demonstrate excellent performance across different tasks. However, the datasets we use are relatively clean. Although some datasets, such as the HumanBody dataset, contain some degree of noise, it is mild, and the network can still robustly reconstruct them. But, in some complex scenarios or directly collected raw point cloud data, there is a large amount of noise unrelated to the objects themselves, disrupting the semantic structure of the point cloud, which may reduce the network’s effectiveness in processing the point clouds. In the future, our method can be combined with denoising techniques by training diffusion models [66] to learn the noise in chaos point clouds and then denoise the point clouds to enhance the network’s robustness to the different data source. This will enable the network to handle more realistic point cloud data and expand its applicability.
6. Conclusions
In this paper, we propose a novel self-supervised learning scheme with equivariance for point clouds. Our method exhibits robust performance and demonstrates a high degree of sensitivity in effectively learning rotation information. At the same time, it also shows that our network has equivariance through the visualization of features. Our method has good results in rotation-invariant tasks such as object classification, part segmentation, and few-shot learning. In addition, we also verify that our network has a good ability to learn equivariant features in rotation-equivariant reconstruction and the pose change estimation tasks of point clouds, and is robust in rotation-invariant tasks such as classification and segmentation. At the same time, as a self-supervised learning scheme, our network can be fine-tuned to adapt to different downstream tasks after pre-training, which can better adapt it to more tasks. Our network can output some rotation-invariant label information and rotation-equivariant pose change information. The output of diversified information is more practical. For example, it can help visual equipment better identify object information in different poses, and it can also use pose change information to help robots better grasp scattered objects in 3D space.
Author Contributions
Conceptualization, K.S. and M.X.; methodology, K.S. and M.X.; software, K.S.; validation, K.S. and M.X.; formal analysis, K.S.; investigation, M.X.; resources, J.Z.; data curation, K.S.; writing—original draft preparation, K.S.; writing—review and editing, K.S., M.X. and J.Z.; visualization, K.S.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation of China under grant no. 62471266, the Natural Science Foundation of Zhejiang Province under grant no. LZ22F020001, and the 2025 Key Technological Innovation Program of Ningbo City under grant no. 2023Z224.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, J.; Zhao, W.; Deng, B.; Wang, Z.; Zhang, F.; Zheng, W.; Cao, W.; Nan, J.; Lian, Y.; Burke, A.F. Autonomous driving system: A comprehensive survey. Expert Syst. Appl. 2024, 242, 122836. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, M.; Xu, S.; Cao, T.; Chen, Q. Ppad: Iterative interactions of prediction and planning for end-to-end autonomous driving. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany; pp. 239–256. [Google Scholar]
- Liebers, C.; Prochazka, M.; Pfützenreuter, N.; Liebers, J.; Auda, J.; Gruenefeld, U.; Schneegass, S. Pointing it out! Comparing manual segmentation of 3D point clouds between desktop, tablet, and virtual reality. Int. J. Hum.-Interact. 2024, 40, 5602–5616. [Google Scholar] [CrossRef]
- Ding, X.; Qiao, J.; Liu, N.; Yang, Z.; Zhang, R. Robotic grinding based on point cloud data: Developments, applications, challenges, and key technologies. Int. J. Adv. Manuf. Technol. 2024, 131, 3351–3371. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X. A robust assessment method of point cloud quality for enhancing 3D robotic scanning. Robot. Comput.-Integr. Manuf. 2025, 92, 102863. [Google Scholar] [CrossRef]
- Chen, K.X.; Zhao, J.Y.; Chen, H. A vector spherical convolutional network based on self-supervised learning. Acta Autom. Sin. 2023, 49, 1354. [Google Scholar] [CrossRef]
- Simeonov, A.; Du, Y.; Tagliasacchi, A.; Tenenbaum, J.B.; Rodriguez, A.; Agrawal, P.; Sitzmann, V. Neural Descriptor Fields: SE(3)-Equivariant Object Representations for Manipulation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar] [CrossRef]
- Cohen, T.; Welling, M. Steerable CNNs. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Lin, C.E.; Song, J.; Zhang, R.; Zhu, M.; Ghaffari, M. Se (3)-equivariant point cloud-based place recognition. In Proceedings of the Conference on Robot Learning, Atlanta, GA, USA, 6–9 November 2023; PMLR: New York, NY, USA, 2023; pp. 1520–1530. [Google Scholar]
- Zhu, M.; Ghaffari, M.; Clark, W.A.; Peng, H. E2PN: Efficient SE (3)-equivariant point network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1223–1232. [Google Scholar]
- Yu, H.X.; Wu, J.; Yi, L. Rotationally equivariant 3D object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1456–1464. [Google Scholar]
- Wu, H.; Wen, C.; Li, W.; Li, X.; Yang, R.; Wang, C. Transformation-equivariant 3D object detection for autonomous driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 2795–2802. [Google Scholar]
- Fuchs, F.; Worrall, D.; Fischer, V.; Welling, M. SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; 33, pp. 1970–1981. [Google Scholar]
- Zhu, M.; Han, S.; Cai, H.; Borse, S.; Ghaffari, M.; Porikli, F. 4D panoptic segmentation as invariant and equivariant field prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 22488–22498. [Google Scholar]
- Deng, C.; Litany, O.; Duan, Y.; Poulenard, A.; Tagliasacchi, A.; Guibas, L. Vector Neurons: A General Framework for SO(3)-Equivariant Networks. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 5100–5109. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. Acm Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-BERT: Pre-training 3D Point Cloud Transformers with Masked Point Modeling. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 19291–19300. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, W.; Tay, F.E.; Liu, W.; Tian, Y.; Yuan, L. Masked autoencoders for point cloud self-supervised learning. In Proceedings of the Computer Vision—ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2022; pp. 604–621. [Google Scholar]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. Beit: Bert pre-training of image transformers. arXiv 2022, arXiv:2106.08254. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 3–5 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Chan, K.H.R.; Yu, Y.; You, C.; Qi, H.; Wright, J.; Ma, Y. ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction. J. Mach. Learn. Res. 2022, 23, 1–103. [Google Scholar]
- Yu, Y.; Chan, K.; You, C.; Song, C.; Ma, Y. Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Volume 33, pp. 9422–9434. [Google Scholar]
- Yu, Y.; Buchanan, S.; Pai, D.; Chu, T.; Wu, Z.; Tong, S.; Haeffele, B.D.; Ma, Y. White-Box Transformers via Sparse Rate Reduction. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Volume 36, pp. 9422–9457. [Google Scholar]
- Chen, C.; Li, G.; Xu, R.; Chen, T.; Wang, M.; Lin, L. ClusterNet: Deep Hierarchical Cluster Network with Rigorously Rotation-Invariant Representation for Point Cloud Analysis. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Li, X.; Li, R.; Chen, G.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. A Rotation-Invariant Framework for Deep Point Cloud Analysis. IEEE Trans. Vis. Comput. Graph. 2022, 28, 4503–4514. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Hua, B.S.; Chen, W.; Tian, Y.; Yeung, S.K. Global Context Aware Convolutions for 3D Point Cloud Understanding. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Fukuoka, Japan, 25–28 November 2020; pp. 210–219. [Google Scholar] [CrossRef]
- Yongming, R.; Jiwen, L.; Jie, Z. Spherical Fractal Convolutional Neural Networks for Point Cloud Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 452–460. [Google Scholar]
- Wiersma, R.; Nasikun, A.; Eisemann, E.; Hildebrandt, K. Deltaconv: Anisotropic operators for geometric deep learning on point clouds. ACM Trans. Graph. (TOG) 2022, 41, 1–10. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 6000–6010. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Awais, M.; Naseer, M.; Khan, S.; Anwer, R.M.; Cholakkal, H.; Shah, M.; Yang, M.H.; Khan, F.S. Foundation Models Defining a New Era in Vision: A Survey and Outlook. IEEE Trans. Pattern Anal. Mach. Intell. 2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Hua, B.S.; Yeung, S.K. ShellNet: Efficient Point Cloud Convolutional Neural Networks Using Concentric Shells Statistics. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Rpublic of Korea, 27 October–2 November 2019. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph Attention Convolution for Point Cloud Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, L.; Wang, P.S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point Transformer V3: Simpler Faster Stronger. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 4840–4851. [Google Scholar]
- Wang, C.; Wu, M.; Lam, S.K.; Ning, X.; Yu, S.; Wang, R.; Li, W.; Srikanthan, T. Gpsformer: A global perception and local structure fitting-based transformer for point cloud understanding. In Proceedings of the European Conference on Computer Vision, Paris, France, 26–27 March 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 75–92. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. PCT: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Gui, J.; Chen, T.; Zhang, J.; Cao, Q.; Sun, Z.; Luo, H.; Tao, D. A Survey on Self-supervised Learning: Algorithms, Applications, and Future Trends. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9052–9071. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, Q.; Yue, X.; Lasenby, J.; Kusner, M.J. Unsupervised Point Cloud Pre-Training via Occlusion Completion. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar] [CrossRef]
- Liu, H.; Cai, M.; Lee, Y.J. Masked discrimination for self-supervised learning on point clouds. In Proceedings of the European Conference on Computer Vision, Tel-Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 657–675. [Google Scholar]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A Survey on Neural Network Interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Cohen, T.S.; Welling, M. Group Equivariant Convolutional Networks. In Proceedings of the 33rd International Conference on Machine Learning: ICML 2016, New York, NY, USA, 19–24 June 2016; Volume 6, pp. 4375–4386. [Google Scholar]
- Cohen, T.S.; Geiger, M.; Weiler, M. A general theory of equivariant CNNs on homogeneous spaces. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. Available online: https://dl.acm.org/doi/abs/10.5555/3454287.3455107 (accessed on 10 February 2025).
- Chen, Z.; Chen, Y.; Zou, X.; Yu, S. Continuous Rotation Group Equivariant Network Inspired by Neural Population Coding. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–25 February 2024; Volume 38, pp. 11462–11470. [Google Scholar]
- Penaud-Polge, V.; Velasco-Forero, S.; Angulo-Lopez, J. Group equivariant networks using morphological operators. In Proceedings of the International Conference on Discrete Geometry and Mathematical Morphology, Firenze, Italy, 15–18 April 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 165–177. [Google Scholar]
- Cohen, T.S.; Geiger, M.; Köhler, J.; Welling, M. Spherical CNNs. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Cohen, T.; Weiler, M.; Kicanaoglu, B.; Welling, M. Gauge equivariant convolutional networks and the icosahedral CNN. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: New York, NY, USA, 2019; pp. 1321–1330. [Google Scholar]
- Hinton, G.E.; Krizhevsky, A.; Wang, S.D. Transforming auto-encoders. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2011: 21st International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 44–51. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G. Dynamic Routing Between Capsules. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 3859–3869. [Google Scholar]
- Hinton, G.; Sabour, S.; Frosst, N. Matrix capsules with EM routing. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Kosiorek, A.; Sabour, S.; Teh, Y.; Hinton, G. Stacked capsule autoencoders. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. Available online: https://dl.acm.org/doi/abs/10.5555/3454287.3455677 (accessed on 10 February 2025).
- McIntosh, B.; Duarte, K.; Rawat, Y.S.; Shah, M. Visual-Textual Capsule Routing for Text-Based Video Segmentation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Weiler, M.; Geiger, M.; Welling, M.; Boomsma, W.; Cohen, T. 3D steerable CNNs: Learning rotationally equivariant features in volumetric data. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; Volume 31, pp. 10381–10392. [Google Scholar]
- Esteves, C.; Allen-Blanchette, C.; Makadia, A.; Daniilidis, K. Learning SO(3) Equivariant Representations with Spherical CNNs. Int. J. Comput. Vis. 2020, 128, 588–600. [Google Scholar] [CrossRef]
- Kondor, R.; Lin, Z.; Trivedi, S. Clebsch–Gordan Nets: A Fully Fourier Space Spherical Convolutional Neural Network. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; Volume 31, pp. 10138–10147. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3D model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Maron, H.; Galun, M.; Aigerman, N.; Trope, M.; Dym, N.; Yumer, E.; Kim, V.G.; Lipman, Y. Convolutional neural networks on surfaces via seamless toric covers. ACM Trans. Graph. 2017, 36, 71. [Google Scholar] [CrossRef]
- Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Luo, S.; Hu, W. Diffusion probabilistic models for 3D point cloud generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2837–2845. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).