A Lightweight Deep Learning Approach for Detecting External Intrusion Signals from Optical Fiber Sensing System Based on Temporal Efficient Residual Network

Abstract

Deep neural networks have been widely applied to fiber optic sensor systems, where the detection of external intrusion in metro tunnels is a major challenge; thus, how to achieve the optimal balance between resource consumption and accuracy is a critical issue. To address this issue, we propose a lightweight deep learning model, the Temporal Efficient Residual Network (TEResNet), for the detection of anomalous intrusion. In contrast to the majority of two-dimensional convolutional approaches, which require a deep architecture to encompass both low- and high-frequency domains, our methodology employs temporal convolutions and a compact residual network architecture. This allows the model to incorporate lower-level features into the higher-level feature formation in subsequent layers, leveraging informative features from the lower layers, and thus reducing the number of stacked layers for generating high-level features. As a result, the model achieves a superior performance with a relatively small number of layers. Moreover, the two-dimensional feature map is reduced in size to reduce the computational burden without adding parameters. This is crucial for enabling rapid intrusion detection. Experiments were conducted in the construction environment of the Guangzhou Metro, resulting in the creation of a dataset containing 6948 signal segments, which is publicly accessible. The results demonstrate that TEResNet outperforms the existing intrusion detection methods and advanced deep learning networks, achieving an accuracy of 97.12% and an F1 score of 96.15%. With only 48,009 learnable parameters, it provides an efficient and reliable solution for intrusion detection in metro tunnels, aligning with the growing demand for lightweight and robust information processing systems.

1. Introduction

Metro tunnels are an essential part of urban infrastructure, and the monitoring of the structural safety of tunnels is significant for train safety [1,2,3]. Illegal or unauthorized high-energy intrusions, such as blasting operations, drilling activities, and excavation by heavy machinery, may damage the structure of the tunnel walls and lead to tunnel collapses [4,5]. Therefore, the timely detection and identification of these intrusions is particularly important for the prevention of accidents. Compared to traditional electrical sensors, fiber optic sensors have the advantages of electromagnetic immunity, high sensitivity, long distance transmission, and multiplexing [6,7]; they have become one of the most reliable tunnel monitoring technologies in recent years.

Fiber optic vibration sensing can be classified into the following three categories, according to the sensing principle: scattering [8,9], fiber grating [10], and interferometric [11,12]. Among these, Distributed Acoustic Sensing (DAS) technology, which is based on backward Rayleigh scattering, is one of the most mature fiber optic sensing technologies for vibration measurement [13,14]; however, in long-distance quantitative detection, the signal-to-noise ratio and accuracy of the collected information are low due to the weak intensity of the backscattered light, which is prone to false alarms. To overcome the problem of low sensitivity, Li et al. [15] utilized scattering-enhanced optical fibers with ultra-weak grating arrays as distributed sensing units, achieving the timely and accurate identification and localization of illegal intrusions on drilling rigs in simulation experiments. The method still suffers from interference fading and weak signals [16]. Compared to scattering and grating array-sensing technologies, interferometric sensing directly monitors disturbance events along the fiber by detecting changes in the phase of forward- or backward-reflected light signals [17]. It has the advantages of a high signal-to-noise ratio, a high measurement accuracy, easy data processing, and a good real-time performance [18]. In this paper, the designed quasi-distributed optical fiber sensing system based on a Michelson interferometer [19] is employed to collect the vibration signals from the tunnel walls. A large number of sensors are required for the comprehensive and thorough monitoring of metro tunnels, which will generate massive amounts of signal data.

Deep learning models [20,21,22] are capable of extracting high-level features from huge amounts of data, with a superior performance compared to traditional methods [23,24]. Yu et al. [25] applied deep neural networks to a 33km fiber optic sensing system to identify and classify signals of external intrusion events, which is sufficient to quickly identify and locate disruptive events in complex environments with large amounts of monitoring data. Jia et al. [26] proposed a method that combines a back propagation neural network to locate leaks in pipelines, with a root mean square error as low as 1.01%. Xie et al. [8] proposed an unsupervised deep learning method that learns only normal DAS data features from normal events; the method achieves a detection rate of 91.5%. A two-layer convolutional neural network (CNN)-based classifier [27] was developed, where one layer was used to distinguish between third-party activities and environmental disturbances, and the other was used to determine the specific type of third-party event. The classifier achieved an accuracy rate of over 97%. Wu et al. [28] combined a CNN and support vector machine (SVM), detecting that the accuracy of five fiber optic sensor signals can reach more than 98% in oil pipeline monitoring applications. The above methods demonstrate the great potential of CNNs in detection tasks. Nevertheless, these methods usually focus only on the detection accuracy of the network [29,30,31], ignoring the need for computational efficiency and the real-time performance of anomalous intrusion detection systems in metro tunnels.

The large amount of data that need to be processed to provide the comprehensive and thorough monitoring of metro tunnels requires computationally efficient methods. In addition, real-time monitoring is crucial for intrusion detection systems in metro tunnels, as delayed responses can lead to significant safety risks. Real-time anomaly detection helps to prevent accidents, improve maintenance schedules, and optimize operational efficiency. Several lightweight networks have been proposed to monitor marine ecosystems via fiber optic signals [32] or structural damages via guided wave signals [33,34], which have a high computational efficiency and a high accuracy. However, the actual underground tunnel anomaly signals are characterized by complex environmental noise, and the anomaly signals are easily drowned out by the environmental noise (e.g., tunnel-boring machines, fans, manual work, and metro running in the distance); the aforementioned lightweight networks capturing high-level features through deep architecture do not perform well in these scenarios. Therefore, according to the characteristics of tunnel intrusion signals, the objective of this paper is to design a lightweight network based on temporal convolution and a compact residual network architecture, without the need to stack multiple layers in order to generate high-level features. Compared to existing state-of-the-art networks, the accuracy, precision, and recall are expected to be improved to more than 90%; the number of parameters reduced by more than 30%; and the inference time reduced by 50% in order to meet the demand for efficient and accurate tunnel anomaly detection in industrial environments.

Considering the above objectives, this paper proposes a lightweight deep learning model, the Temporal Efficient Residual Network (TEResNet), for the detection of anomalous intrusion signals. The overall system of fiber optic sensor external intrusion detection is shown in Figure 1. Taking into account the sensitivity, stability, and practicality, we adopt the optical fiber acceleration sensor based on a Michelson interferometer to collect the signal of abnormal intrusion in metro tunnels. First, the signals obtained from the optic fiber accelerometers are converted into short-time Fourier transform (STFT) features. The features are then fed into TEResNet for training and detection. Unlike most 2D convolutional methods, which require deep architecture to cover low- and high-frequency domains, our method leverages temporal convolutions in conjunction with a compact residual network architecture. Specifically, the network integrates all low-level features into the formation of high-level features in subsequent layers. In this way, it effectively exploits the informative features present in the lower layers, thus eliminating the need for stacking multiple layers to generate high-level features. An excellent performance is achieved even with a relatively limited number of layers. The experiments were conducted in the construction environment of the Guangzhou Metro, where we built a dataset containing 6948 signal segments, representing various intrusion scenarios. The results demonstrate that TEResNet not only surpasses traditional intrusion detection methods, but also outperforms state-of-the-art deep learning models. With only 48,009 learnable parameters, it achieves a high detection accuracy and robustness, making it an efficient and practical solution for metro tunnel intrusion detection.

Our contributions are threefold, as follows:

• A novel lightweight architecture—TEResNet—is proposed. All low-level features are incorporated into the formation of high-level features in subsequent layers, thus eliminating the need to stack multiple layers in order to generate high-level features.
• A new dataset comprising 6948 signal segments was collected in the construction environment of the Guangzhou Metro, which has been made publicly available to facilitate further research.
• Experiments show that with only 48,009 learnable parameters, TEResNet achieves an accuracy of 97.12% and an F1 score of 96.15%, which is a superior performance compared to existing methods and advanced neural networks.

The remainder of this paper is organized as follows: Section 2 details the data acquisition process and dataset preprocessing methods. Section 3 introduces the principles of the proposed approach, with a particular focus on temporal convolution, along with signal characterization and the network architecture. Section 4 outlines the evaluation metrics, presents the results of ablation studies, and discusses the performance of the model in comparative experiments. Finally, Section 5 concludes the paper and offers insights into potential directions for future research.

2. Dataset

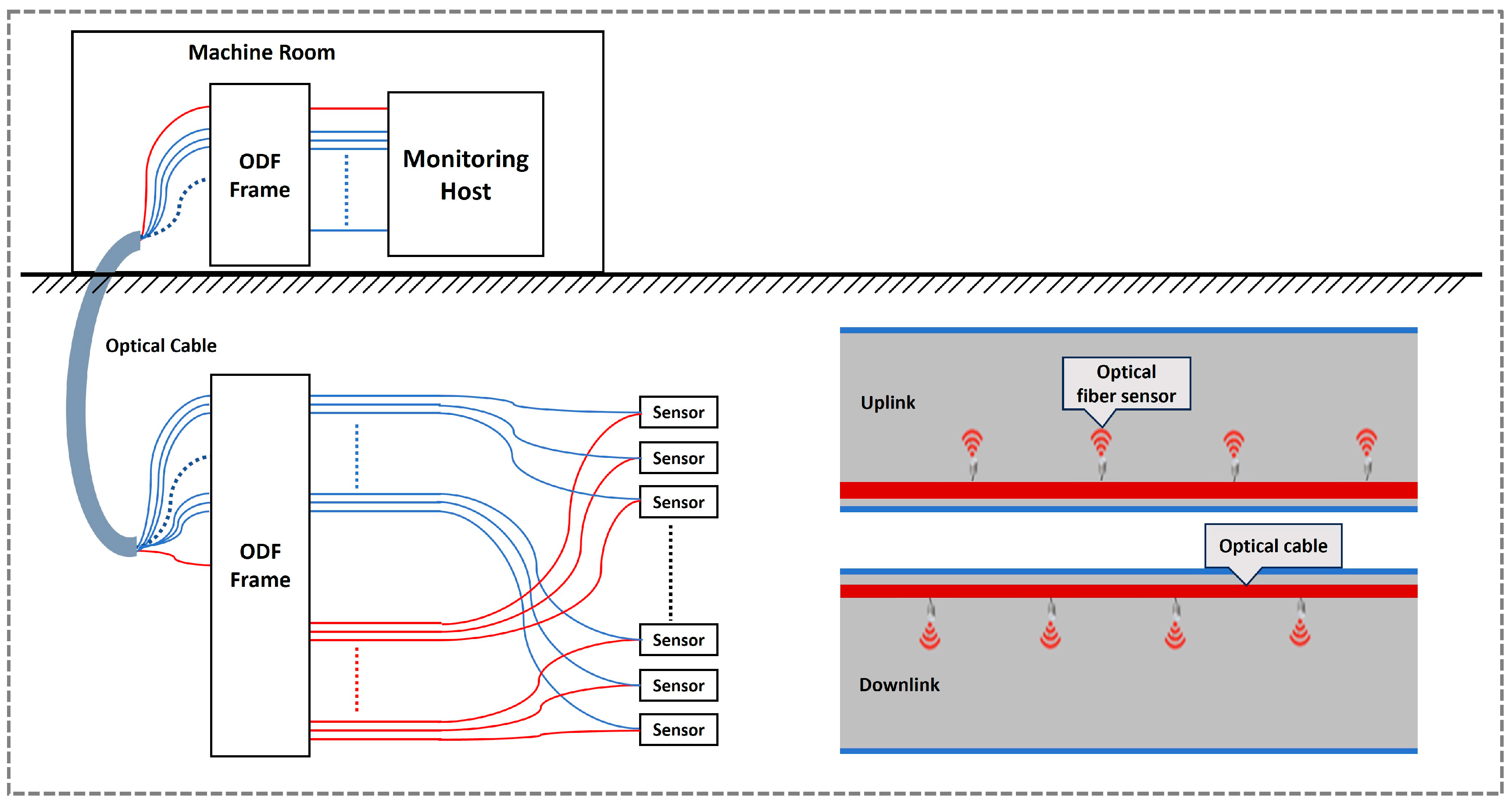
2.1. Data Acquisition and Analysis

The quasi-distributed fiber optic sensing system designed in this paper for abnormal vibration detection in metro tunnels is shown in Figure 2. To detect the vibration signals generated by the construction of mechanical equipment inside or above the tunnel, multiple highly sensitive fiber optic acceleration sensors are installed at different locations in the uplink and downlink of the metro tunnel with equal intervals. The transmission cable is connected to the monitoring host through the optical fiber distribution frame (ODF) and transmits the signal to the system host, which processes and analyzes the abnormal vibration information and provides alarms, thus achieving the all-weather, all-time, real-time detection of abnormal vibration in metro tunnels.

To explore robust external intrusion detection methods in construction environments, we conducted preliminary experiments using percussive tap (PT) to simulate external anomaly intrusion. Figure 3 illustrates the geometry of the metro tunnel, the sensor installation locations, and the percussion test setup. The figure shows two adjacent metro tunnel segments, separated by a 10 m ventilation shaft. Each tunnel segment is 6 m in diameter and 20 m long, and is located 21 m below ground level. The sensor locations are labeled A, B, and C, and the four percussion tap points are labeled PT1 to PT4. We performed several percussive taps at different locations and acquired these abnormal signals with multiple optic fiber acceleration sensors based on a Michelson interferometer.

The sensors are installed in the following three different orientations to collect data: aligned with the axial direction of the pipe, mounted perpendicular to the pipe wall, and positioned tangentially to the pipe wall, as shown in Figure 4. By capturing vibrations in these different directions, the data collection ensures that the training dataset contains multiple vibration modes and directions, which is critical for accurate external intrusion detection in real-world applications. Figure 5 gives an example of a collected intrusion signal; it can be observed that the signal collected at point A can clearly distinguish each percussive tap, whereas the signals at points B and C are almost indistinguishable, probably due to signal attenuation [35] over a long distance. In addition, as the experiment is conducted in a construction environment, there were various sources of noise in the surrounding area, such as the operation of tunnel-boring machines and fans, manual work, metro running in the distance, etc. Therefore, there is an urgent need to develop external intrusion detection models that are robust in complex noise environments.

2.2. Dataset Preprocessing

The experiments are carried out in a station and interval construction zone of the Guangzhou Metro in Guangdong Province, China, where we use a percussion tap to simulate external anomaly intrusion. The fiber optic accelerometers have a sampling rate of 4000 Hz and can receive frequencies in the range of 0.5–2000 Hz, with a resolution of 2 × 10⁻⁵ g. We collected signals from different locations and different ways of mounting the sensors.

During the data processing phase, the raw vibration signals collected by the sensors are first normalized to remove the direct current (DC) offset and normalize the amplitude of the signals, using the following equation:

$$x={\displaystyle \frac{x-mean(x)}{\max (\left|x-mean(x)\right|)}}$$

(1)

where $x$ denotes the time sequence signal. After that, the signal is labeled according to the following rules. As shown in Figure 6, the signal is transformed in the frequency domain to find the region where the energy is concentrated; the number of windows in the region is calculated and converted to the number of sampling point k. The starting position of the signal mutation is found empirically; then, the signal is labeled as 1 for the corresponding k sampling points, and 0 for the part of the signal that is running normally or in the background noise. The continuous signal is then segmented into a fixed length of 512 sample points (with a duration of 0.128 s) with a stride of 50 points, as shown in Figure 7. Finally, we create the dataset according to the following rule: when the window contains complete bursts of spikes (i.e., the point labeled 1 in Figure 6 is completely covered by a window), the example is labeled 1; otherwise, it is labeled 0.

Table 1. The number of samples included in the external intrusion detection dataset for metro tunnels in the construction environment.

	Train	Test
Normal	4650	255
Abnormal	1898	162
Total	6548	417

provides a summary of the metro tunnel external intrusion detection dataset created in this study, where all anomalous intrusions are simulated by manual tapping. The dataset is divided into two categories—normal and abnormal events—with a further split between training and testing sets. In the training set, there are 4650 normal samples and 1898 abnormal samples, resulting in a total of 6548 training samples. The testing set includes 255 normal samples and 162 abnormal samples, leading to a total of 417 test samples. Figure 8 shows some of the signals in the training and test datasets; both the training and test sets contain signals with different noise levels, as well as multiple tapping intensities, demonstrating the diversity and representativeness of the datasets. These signals cover a wide range of possible real-world scenarios, thus ensuring the applicability of the model in real-world environments. The external intrusion detection dataset is available at https://github.com/guoziye97/Metro-Tunnel-Anomaly-Detection-Data (accessed on 20 January 2025).

3. Proposed Lightweight Deep Learning Approach

In this section, the characteristics of external intrusion signals are first analyzed, and STFT features are selected as inputs to the network. Then, the proposed external intrusion detection network is introduced with details of time convolution and dilated convolution, as well as with basic blocks.

3.1. Characteristic Analysis

As mentioned in Section 2, in the time domain, the acquired percussion signal may appear as an impact spike, but it can also become indistinguishable, probably due to signal attenuation over long distances. Additionally, as the experiment was conducted in a construction environment, various noise sources in the surrounding area contributed to interference. These sources included the operation of tunnel-boring machines and fans, manual work activities, and the distant running of metro trains. Figure 9 illustrates an example of the acquired data, including time and frequency domain representations of the intrusion signal. Figure 9a shows a time domain plot of the intrusion signal, where the spike in the waveform may represent an impact from an external source. However, these spikes are difficult to identify due to signal attenuation or noise interference. Figure 9b shows the time–frequency image of this intrusion signal after STFT [36]. In this spectrogram, we can observe the intensity and frequency distribution of the signal over time, and the five knocks are presented as distinguishable high-frequency energy, which is useful for identifying the characteristic frequency pattern associated with the intrusion; thus, we use the STFT feature as an input to the neural network.

3.2. Temporal Efficient Residual Network

It has been mentioned in Section 2.1 that the three sensors are installed at different locations; thus, the same tapping event reaches the three sensors at different times. To detect external anomalous intrusions in time, we use a single-channel signal as the input to the model so that sensors closer to the sound source are the first to respond to anomalous events. In addition, the distance of the sound source from the sensors has a strong correlation with the degree of signal attenuation, whereby the further the distance, the more signal attenuation. However, the distance of the sound source in the real environment is arbitrary, and the model needs to have a high detection capability under different attenuation conditions. Therefore, collecting single-channel signals received from different sensors to build the training set helps to improve the generalization of the model, where sensors at different locations are able to respond to anomalous intrusions.

3.2.1. Overview of the Proposed TEResNet

Conventional methods for processing STFT features typically use small convolutional kernels (e.g., 3 × 3) to extract high-level characteristics by stacking multiple convolutional layers. It is effective for images, but for time-varying frequency signals, it is difficult for shallower networks to capture both low- and high-frequency information features. Time convolution [37] provides a new insight into the analysis of time-varying signals, transforming the time–frequency map into a frame-by-frame time series rather than a traditional visualization image. This sort of processing is more in line with the natural properties of time series data, highlights the dominance of the temporal dimension of the signal, and has been shown to be effective in speech signal processing [38,39]. In addition, Cocke et al. [40] have shown that dilated convolutions are helpful in the processing of time-varying frequency signals; we employ dilated convolution [41] to increase the receptive field of the convolution kernel.

The overall architecture of TEResNet consists of STFT feature inputs, feature reshaping, an initial convolutional layer, three basic ResNet-style [42] blocks, the pooling layer, the fully connected layer, and the sigmoid layer, as shown in Figure 10; we make full use of the important information of the frequency features, which are treated as the core of each time frame. The initial convolutional layer and the basic blocks have convolutional kernel sizes of 3 × 1 and 9 × 1, respectively, and both employ temporal convolution to extract high-level features of the signal. The convolutional layers of the last two basic blocks utilize dilated convolution. The dilated factors are two and four, respectively, as a way to increase the receptive field. Batch normalization (BN) accelerates the training process by normalizing the activations, while the rectified linear unit (ReLU) activation introduces non-linearity, enhancing the model’s capacity to capture complex patterns. Max pooling and average pooling are applied to down-sample the input, reducing its spatial dimensions and the parameters of the model, which helps in extracting essential features from the data.

3.2.2. Temporal Convolution

Figure 11 illustrates the difference between conventional 2D convolution and temporal convolution when dealing with STFT features as inputs. Assuming a stride of 1 and that zero padding is applied to give the input and output the same resolution, given the input $X\in {ℝ}^{w\times h\times c}$ and weights $W\in {ℝ}^{k_w\times k_h\times c\times c^{\prime }}$, the output of the 2D convolution is $Y\in {ℝ}^{w\times h\times c^{\prime }}$. STFT is widely used to convert raw audio into a time–frequency representation $I\in {ℝ}^{t\times f}$, where $t$ denotes the time axis and $f$ denotes the feature axis extracted from the frequency domain, as shown in Figure 11a. Most previous studies have defined the input tensor as $X\in {ℝ}^{w\times h\times c}$, where $w=t$, $h=f$, and $c=1$.

Conventional CNNs often use smaller convolutional kernels to convert low-level features into higher-level features, as shown in Figure 11b. As a result, deeper convolutional layers need to be stacked to capture rich information from both high and low frequencies. Let us assume that by simply stacking n 3 × 3 convolutional layers with a stride of 1, the receptive field of the network grows only to 2n + 1. Researchers have suggested the application of attentional mechanisms, recurrent units, or pooling to alleviate this problem, but these usually introduce a large number of parameters that increase the computational burden.

Temporal convolution provides a new perspective on the analysis of fiber optic sensing signals, redefining the time–frequency diagram as a frame-by-frame time series, rather than a traditional visualized image. This treatment is more attuned to the natural properties of audio and similar time series data, highlighting the dominance of the temporal dimension of the signal, while making full use of the important information of the frequency features.

Based on this, the convolution shown in Figure 11c is performed, which reshapes the input from $X_{2d}$ to $X_{1d}$. We consider $I$ as one-dimensional sequence data, where the features of each time frame are denoted by $f$, resulting in $X_{1d}\in {ℝ}^{t\times 1\times f}$. The convolution kernel covers the entire frequency range, which makes full use of the information in the lower layers without the need to stack multiple layers to form high-level features. By applying temporal convolution, the size of the 2D feature map is reduced, while keeping the same number of parameters. Assuming that the weight of the conventional 2D convolution is $W_{2d}\in {ℝ}^{3\times 3\times 1\times c}$, the weight of the temporal convolution is $W_{1d}\in {ℝ}^{3\times 1\times f\times c^{\prime }}$ and the number of parameters is equal, i.e., $c^{\prime }=3\times c/f$. Assuming that $t=100$, $f=40$, $c=120$, and $c^{\prime }=9$, temporal convolution requires fewer computations $MAC\mathrm{s}=3\times 3\times 1\times f\times t\times c=\mathrm{4,320,000}$ than 2D convolution $MAC\mathrm{s}=3\times 1\times f\times t$$1\times c^{\prime }=\mathrm{108,000}$. In addition, the output feature maps of temporal convolution $Y_{1d}\in {ℝ}^{t\times 1\times c^{\prime }}$ are smaller than the output feature maps of conventional 2D convolution $Y_{2d}\in {ℝ}^{t\times f\times c}$. The reduction in feature map size greatly decreases the computational burden and memory requirements of subsequent slices, which is critical for fast external intrusion identification.

3.2.3. Dilated Convolution

To further capture global information, we introduce dilated convolution as well. Dilated convolution, also known as hollow convolution, expands the receptive field of a convolution kernel by introducing holes (i.e., intervals) between the elements of a standard convolution kernel, thus capturing a larger range of input information, as shown in Figure 12. The core idea of dilated convolution is to control the expansion of the receptive field through a ‘dilated factor’, usually denoted as $d$. For a $k\times k$ convolution kernel, if the dilated factor is $d$ then the distance between adjacent convolution kernel elements is $d-1$, with a receptive field size of $(k+(k-1)(d-1))\times (k+(k-1)(d-1))$. Thus, the larger the dilated factor, the more the receptive field grows, allowing the convolution to capture a greater range of contextual information without increasing the parameters.

3.2.4. Basic Block of ResNet Style

The basic block, designed for feature extraction from optical fiber sensing signals, is adapted from ResNet18 [42]. It comprises two 9 × 1 convolutional layers, followed by batch normalization (BN), ReLU activation, and a residual connection. The residual connection links the input and output (after BN) of the convolutional layers, allowing the network to learn identity mappings. It helps mitigate issues like gradient vanishing and explosion. The residual connection operates as follows:

$$H(x)=identify(x)+F(x)$$

(2)

where $H(x)$ represent the output of the basic block, $x$ denote the input to the convolutional layer, $F(x)$ is the transformed feature obtained after passing through the two convolutional layers, and $identify(x)$ denotes the input identity mapping of $x$, i.e., the input is passed directly to the output without any transformation. The purpose of this design is to preserve the original information of the input signal during feature extraction, thus increasing the sensitivity of the network to subtle features, while avoiding the loss of information caused by the deep network.

4. Results

In this section, the performance of the proposed detection model is verified, and the performance of the method is evaluated by comparing it to existing external intrusion detection methods and advanced deep learning networks.

4.1. Evaluation Indicators

In the experimental validation, four indicators are used to evaluate the performance of the proposed method, including accuracy, recall, precision, and F1 score, with the following meanings, respectively.

Table 2. Prediction results confusion matrix for binary classification.

True	Predicted
	Negative	Positive
Negative	TN (True Negative)	FP (False Positive)
Positive	FN (False Negative)	TP (True Positive)

shows the confusion matrix of the binary classification.

(1)

Accuracy: the proportion of the number of samples correctly categorized out of all samples to the total number of samples, calculated using the following formula:

$$Acc(\%)={\displaystyle \frac{TP+TN}{TP+FN+FP+TN}}\times 100$$

(3)

(2)

Precision: the proportion of samples predicted by the model to be positive that are actually positive, calculated using the following formula:

$$Precision(\%)={\displaystyle \frac{TP}{TP+FN}}\times 100$$

(4)

(3)

Recall: the proportion of the number of samples accurately predicted as positive by the model to the number of all positive samples, calculated using the following formula:

$$Recall(\%)={\displaystyle \frac{TP}{TP+FN}}\times 100$$

(5)

(4)

F1 score: a reconciled mean evaluation metric of precision and recall, calculated using the following formula:

$$F1-score(\%)=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}\times 100$$

(6)

4.2. Experiments and Analysis

4.2.1. Ablation Experiments and Parameter Selection

The experimental environment is configured with Python3.11, PyTorch2.0.1, Intel(R) Core(TM) i9-12900H CPU, NVIDIA GeForce RTX3060 GPU, and 6GB RAM. During training, we used the Adam optimizer [43] for 50 epochs, with the initial learning rate set to 0.0001. The batch size is set to 128 when training the network. The properties of the dataset used for the experiments are described in Section 2. During data preprocessing, the short-time Fourier transform (STFT) is applied with a window size of 128, using a Hamming window and a hop size of 20.

In the proposed TEResNet, the number of channels in the first convolutional layer and the basic block serves as a crucial parameter. It directly impacts detection accuracy while also playing a significant role in determining the degree of the lightweighting of the model. To investigate the effect of this parameter, we conducted four sets of experiments, denoted as parameter 1, 2, 3, and 4, where M, N, P, and Q are used to denote the number of channels in the first convolutional layer and the three basic blocks; the specific settings are shown in

Table 3. Four sets of parameters, corresponding to the number of channels in the first convolutional layer and the three subsequent basic blocks.

	M	N	P	Q
Parameter 1	8	8	8	16
Parameter 2	8	8	16	24
Parameter 3	8	16	24	32
Parameter 4	8	24	32	48

. The loss function curves and model performance for the four sets of parameters are shown in Figure 13. As the number of channels increases, the number of model parameters gradually increases, and the loss function decreases faster. However, parameter 4, with the fastest decreasing loss function, does not lead to the best test accuracy, which may be due to overfitting caused by the larger model parameters. Therefore, we chose the model with parameter 3 for continuous signal testing and comparison experiments.

In order to explore the impact of the dilated convolution, we conducted ablation experiments; the loss and accuracy curves for conditions using and not using the dilated convolution of parameter 3 are given in Figure 14. As can be seen from the figure, the loss of the model using the dilated convolution decreases faster and the test accuracy is higher, verifying that the dilated convolution is able to expand the sensory field and thus improve the model accuracy.

4.2.2. Comparative Experiments

To evaluate the performance of the proposed network, we compare the proposed network to existing external intrusion detection methods and state-of-the-art deep learning networks, with the same training conditions, hyperparameters, and hardware environment as described at the beginning of Section 4.2.1.

CNN: the model processes data by extracting local features through a convolutional layer and reducing the dimensionality through a pooling layer, and performs well in image recognition and signal processing.

LSTM [44]: The long short-term memory (LSTM) network captures long-term dependencies in sequential data using input, forget, and output gates. It can address the vanishing gradient problem and is widely used in natural language processing and time series forecasting.

GRU [45]: Gated Recurrent Units (GRUs) simplify RNNs by combining input and forget gates into a single update gate, reducing parameters and computational complexity. GRUs maintain sequence dependency modeling while improving training efficiency.

CNN-LSTM-AM [46]: the model combines CNN for feature extraction, long short-term memory (LSTM) for temporal dependencies, and an attention mechanism (AM) to dynamically emphasize important features, enhancing the performance in external intrusion detection.

Transformer [47]: this model is known for its self-attention mechanism, which effectively captures global relationships in sequences, making it suitable for time series analysis.

1D ResNet [42]: a one-dimensional adaptation of ResNet that uses residual blocks to address gradient vanishing in deep networks, effectively capturing complex temporal features.

LCANet [33]: the model utilizes group- and depth-wise separable convolutions, channel shuffling, and multi-head self-attention to enhance feature extraction while minimizing parameters, demonstrating high efficiency and reliability in structural health monitoring.

STFT+2DResNet [42]: this applies STFT to convert signals into spectrograms, and then uses 2D ResNet to extract and classify features, combining frequency and temporal information for non-stationary signal analysis.

CLDNN [25]: The model integrates CNN, LSTM, and DNN layers. CNN extracts local features, LSTM captures temporal dependencies, and DNN classifies, enabling comprehensive feature fusion for effective external intrusion detection.

Figure 15 illustrates the confusion matrix of each model on the dataset. Compared to traditional deep learning methods, such as CNN, LSTM, ResNet, and the latest lightweight network, TEResNet demonstrates a superior performance in the detection task of both categories of signals (intrusion and non-intrusion signals). In particular, it shows a high sensitivity in the detection of intrusion signals (category 1).

Table 4. Performance comparison of the proposed method with existing external intrusion detection methods and advanced deep learning networks, where the bolded results represent the best performance.

Methods	Accuracy (%)/Precision (%)/Recall (%)	F1 Score (%)	Parameters	Inference Time (ms/Sample)
CNN	75.54/65.63/77.78	71.19	395,681	0.0544
LSTM	76.50/64.95/85.80	73.94	3,289,601	0.0180
GRU	75.30/63.98/83.33	72.39	2,500,097	0.0095
CNN-LSTM-AM	86.57/100/65.43	79.10	4,316,293	1.1912
Transformer	88.73/89.12/80.86	84.79	530,434	24.30
1DResNet	88.49/100/70.37	82.61	3,844,930	0.0800
LCANet	90.41/100/75.31	85.92	87,105	0.1269
STFT+2DResNet	95.68/100/88.89	94.12	11,168,193	0.3196
CLDNN	96.40/100/90.74	95.15	4,742,081	0.0626
TEResNet (our)	97.12/100/92.59	96.15	48,009	0.0480

and Figure 16 further quantify the performance metrics of each method, including accuracy, recall, precision, F1 score, number of model parameters, and inference speed. The poor performance of using CNN, LSTM, or GRU networks alone indicates that these single structures have difficulty adequately capturing the complex features of fiber vibration signals and networks, with a combination of multiple structures demonstrating a better performance in this task. Among the models with an accuracy higher than 90%, STFT+2DResNet and CLDNN perform more prominently. STFT+2DResNet successfully captures the frequency domain characteristics of the signal via STFT, as well as extracting the features via 2D ResNet. The CLDNN model, on the other hand, combines the CNN, LSTM, and DNN layers, and has a strong adaptive capability for modeling time series signals. However, these two models have relatively more parameters and complex models, which may lead to overfitting, and the inference speed is not fast enough to meet the requirements of lightweight and fast inference in practical applications. In contrast, TEResNet performs well in terms of accuracy and computational efficiency, with an accuracy of 97.12% and an F1 score of 96.15%, which is significantly better than the other models. In terms of inference time, LSTM and GRU are faster but have poor detection performance. Among the models with accuracy greater than 90%, TEResNet has the fastest inference speed of 0.0480 ms/sample, with only 48,009 trainable parameters, which achieves the improvement of accuracy and efficiency. This is due to the fact that it makes full use of the structural advantages of temporal convolution and residual networks, and is able to efficiently extract key features in the temporal signal with fewer layers.

Precision and recall are also crucial metrics in intrusion detection, and the results in Table 4 show that the models with accuracy greater than 90% have 100% precision, which indicates that false positives occur less frequently, and that the system rarely generates false alarms; however, the recall can only reach a maximum of 92.59%, which indicates that there are more false negative cases, and the system misses a portion of the real attacks. Figure 17 shows the time series signals, their spectrograms, and the corresponding output probabilities for correctly and incorrectly classified abnormal samples. The correctly classified samples usually have significant feature patterns, which are manifested as regular and strong fluctuations in the time series signals, a concentrated distribution of energy in the spectrograms, and consistently high predicted probabilities, often reaching values above 0.9. In contrast, the misclassified samples lack clear features, as evidenced by irregular amplitude fluctuations in the time series signals, scattered energy distribution in the spectrograms, and very low predicted probabilities, typically below 0.1. These issues may arise from noise interference or signal attenuation, which are common challenges in anomalous intrusion detection for industrial environments. In addition to that, an important reason for this is that abnormal signals in intrusion detection tasks tend to be a minority class. When the real attack samples are insufficient or unevenly distributed, the model does not learn the minority class features sufficiently and is prone to miss reports. In the future, we will further expand the dataset to increase the number or diversity of intrusion data, so that the model can better identify the various features in the learning phase, thus improving the ability to capture real attacks.

Table 5. Comparison of TEResNet with the latest lightweight network LCANet in terms of accuracy, F1 score, number of parameters, and inference speed.

Methods	Accuracy (%)	F1 Score (%)	Parameters	Inference Time (ms/Sample)
LCANet	90.41	85.92	87,105	0.1269
TEResNet (our)	97.12 (+7.4%)	96.15 (+11.9%)	48,009 (−44.9%)	0.0480 (−62.2%)

compares the performance of TEResNet to the existing lightweight model LCANet. TEResNet achieves an accuracy of 97.12%, which is 7.4% higher than that of LCANet, and the F1 score is 11.9% higher than that of LCANet. Especially for a lightweight model, our model has 44.9% less parameters and 62.2% less inference time than LCANet, showing more significant lightweight and efficiency advantages. LCANet combines the advantages of group- and depth-wise separable convolutions, channel shuffling, and multi-head self-attention; however, LCANet is still essentially a two-dimensional convolution on STFT feature maps, with limited feature extraction capability in the time dimension of the signal. In contrast, TEResNet adopts a new idea of feature processing, redefining the input signal features as a frame-by-frame time series instead of the traditional two-dimensional matrix. This approach is more in line with the natural properties of audio signals and similar time series data, highlighting the dominance of the time dimension of the signal while making full use of the important information of frequency characteristics.

4.2.3. Complete Signal Testing

The above experiments are tested on segmented signal fragments, while real engineering applications require the detection of continuous signals, which are also more complex. To verify the performance of the proposed method in engineering applications, we tested the above-trained model on continuous signals and output the probability values in real time. Figure 18 and Figure 19 show the comparison between the original signal and the external intrusion detection probability generated by the softmax function. Among them, the sensor in Figure 19 is further away from the percussive tap point and is more affected by noise, making it a harder task.

As can be seen from Figure 18, the output probability of each model roughly matches the anomaly in the original signal (the mutated part of the blue signal). Among them, the output probability peaks of the CNN-LSTM-AM model are the most obvious and can better capture the anomalies; the prediction values of the CNN, LSTM, GRU, and Transformer models fluctuate a lot and are weakly robust against noise; the 1D ResNet model produces a large number of probability peaks near the anomalies, but it is also susceptible to the influence of noise, which leads to the false alarms. The STFT+2D ResNet model has a noise with a certain suppression effect and relatively few false alarms, while the CLDNN model has a detection performance similar to that of the 1D ResNet, but is also susceptible to noise. The TEResNet performs well, with its external intrusion detection probability accurately corresponding to real anomalies.

In the more challenging scenario, i.e., Figure 19, the output probabilities of the CNN-LSTM-AM model capture some of the anomalies, but the overall magnitude is small; the CNN, LSTM, GRU, Transformer, and 1D ResNet models show a lot of fluctuations in the normal signal region, leading to many false positives; the STFT+2D ResNet model mitigates the false positive problem to some extent, but it is still not completely eliminated; and the CLDNN model also has more false positives. The proposed model is still able to accurately detect anomalies in this complex scenario, and the output probability curves overlap strongly with the real anomalies, while showing strong robustness to noise interference. Overall, the model significantly outperforms other models in the continuous signal external intrusion detection task with a higher accuracy and robustness.

5. Conclusions

In this paper, we propose a novel network, TEResNet, that enables robust and lightweight external intrusion detection in metro tunnels. To address the challenges of efficiently detecting anomalous signals, TEResNet combines temporal convolutions with a compact residual network architecture. Unlike traditional two-dimensional convolutional methods, which require deep architectures to capture both low- and high-frequency domains, it integrates lower-level features into the generation of higher-level features, thereby reducing the number of layers while still maintaining a superior performance. This design not only enhances robustness, but also significantly reduces the size of the feature map, effectively lowering the computational burden and enabling rapid detection. To evaluate the method, we conducted experiments in the construction environment of the Guangzhou Metro and created a dataset for external intrusion detection. After preprocessing the signals collected by fiber optic sensors, STFT features are extracted as inputs to the neural network. Experimental results validate the performance of TEResNet, achieving an accuracy of 97.12% and an F1 score of 96.15%. With only 48,009 learnable parameters, it demonstrates the effectiveness and reliability of anomalous detection while offering a lightweight and efficient solution. It has practical implications for real-time intrusion detection in structures such as metros, train tracks, and bridges, enabling the monitoring of the operation of such infrastructures with low resource consumption.

Since external intrusions are simulated by tapping, the dataset is limited in diversity, making it difficult to comprehensively assess the performance under real-world conditions. Future work will expand the dataset by considering more intrusion scenarios and environmental conditions to ensure that the system is able to handle situations that have never been seen or simulated before. In addition, practical factors, such as the optimal placement of sensors, integration of the system into complex metro tunnel environments, and regular maintenance schedules, will all have an impact on the performance of the method, and we will add a simulation analysis and field trials to refine these aspects.