Abstract
Spatially selective nerve stimulation is an active area of research, with the capability to reduce side effects and increase the clinical efficacy of nerve stimulation technologies. Several research groups have demonstrated proof-of-concept devices capable of performing spatially selective stimulation with multi-contact cuff electrodes in vivo; however, optimizing the technique is difficult due to the large possibility space granted by a multi-electrode cuff. Our work attempts to elucidate the most valuable stimulation montages (current ratios between stimulating electrodes) provided by a multi-contact cuff. We characterized the performance of five different montage types when stimulating fibers in different “electrode configurations”, with configurations including up to three rings of electrode contacts, 13 different counts of electrodes per ring, and five electrode arc lengths per electrode count (for 195 unique configurations). Selected montages included several methods from prior art, as well as our own. Among montage types, the most spatially selective stimulation was one we refer to as “X-Adjacent” stimulation, in which three adjacent electrodes are active per ring. Optimized X-adjacent montages achieved an average fiber specificity of 71.9% for single-ring electrode configurations when stimulating fibers located at a depth of two-thirds of the nerve radius, and an average fiber specificity of 77.2% for two-ring configurations. These values were the highest among montages tested, and in combination with our other metrics, led these montages to perform best in the majority of cost functions investigated. This success leads us to recommend X-Adjacent montages to researchers exploring spatially selective stimulation.
1. Introduction
Electrical stimulation of peripheral nerves has received significant attention in recent years, in part because of its capability to treat many different ailments [1,2]. Vagus nerve stimulation—the most well-studied of peripheral nerve neuromodulation—is FDA approved for treatment of epilepsy [3] and drug-resistant depression [4] and has been researched for treatment of heart failure [5], rheumatoid arthritis [6], stroke recovery [7], and more [8]. Other peripheral nerve stimulation targets have been used for pain suppression [9], bladder control [10], and digestive diseases [11]—to name only a few examples.
One of the major recurring challenges in peripheral nerve stimulation is the issue of side-effect management. The main side effects of cervical-level vagus nerve stimulation, for instance, include hoarseness, activation of the coughing and swallowing reflex, voice change, throat pain, and dyspnea [12]. While these side effects are considered “well-tolerated” [13], they have the potential to reduce the effectiveness of treatment because the activation of uncomfortable side effects can occur before the activation of physiologically relevant effects [14]. When this occurs in an animal model, researchers may be unaware of the side effects or willing to proceed with the experiment regardless—but in humans, stimulation amplitude is limited by patient comfort levels [12,14,15]. This is a possible contributor to the fact that vagus nerve stimulation achieves antidepressive effects in animal models, but such effects are more difficult to reproduce in humans [4,15].
Spatially selective stimulation is a recent approach to this problem, involving delivering current to only the subset of fibers associated with clinically efficacious effects [16,17]. The most common design for a spatially selective stimulation device is a multi-contact cuff electrode [18,19], as opposed to penetrating electrodes, which have challenges with long-term safety [20,21]. The ring of electrode contacts allows for current steering to different angular positions around the nerve (with more electrode contacts allowing for greater resolution and angular precision) [16,22]. The two most critical questions to ask when performing spatially selective stimulation are, “where is the stimulation target?” and “what montage will best activate the stimulation target?”. This paper is concerned with the latter question.
Spatially selective vagus nerve stimulation has already been demonstrated in vivo; Aristovich et al. [17] performed a stimulation in sheep that achieved separation of cardiac activity from respiratory activity using a two-ring, 28-contact electrode in 2021. More recently, other groups have performed spatially selective stimulation in vivo: a single-ring 8-contact electrode [23] and a 6-contact electrode [24] were both explored in 2023. Each group has a very different electrode design and stimulation montage, but each achieves spatially selective stimulation in their respective applications.
In addition to differing electrode designs, there is still disagreement among the scientific community regarding “optimized” spatially selective stimulation. Of course, there is no singular optimal solution; any selected method will come with trade-offs. Considerations must be made to balance the maximum selectivity of a stimulation montage, the reliability at which the maximum selectivity can be achieved, and the safety of the desired stimulation. Dali et al. [25] performed an analysis of spatially selective stimulation from the starting point of a tripolar (three-ring) cuff with four radial contacts per ring, using simulated annealing to determine the current applied at each electrode. Their work studied three different stimulation heuristics and found that one achieved the highest selectivity, one achieved the best reliability, and one struck a balance between the others. Kent and Grill [22] studied the number of electrodes in flat interface nerve electrode (FINE) cuffs and round cuff designs, concluding that a ten-contact cuff electrode could achieve spatial selectivity with multi-electrode activation calculated by a genetic algorithm. Later, Aristovich et al. [17] performed an optimization for the size of electrodes used to stimulate a given nerve. Contrasting the previous two papers, they concluded that the most cost-effective spatially selective stimulation would be achieved with a bipolar (two-ring) cuff with 14 radial contacts per ring. Interestingly, the cost function of this analysis led to the conclusion that the best stimulation montage involved activation of only a single pair of longitudinally spaced electrodes at a time.
The disagreement among the above conclusions motivates us to compare the stimulation montages seen in previous work, as well as our own. While changing the number of electrode rings and contacts per ring, we explore the merits of using simple stimulation montages (such as activating a single pair of electrodes as in [17]), globally optimized montages (such as the simulated annealing approach used in [25]), and our own stimulation montages.
Our group recently developed a “Stimulation Balancing Focality and Intensity” (SBFI), a montage designed to optimize multi-electrode transcranial direct current stimulation (tDCS) [26]. The mathematics of SBFI (documented in Wang et al. [26]) revolve around a convex problem in which the electric field applied to a target region must approximate a designated target, while power delivered to non-target regions must be minimized. This new innovation has encouraged our group to investigate the success of SBFI-powered stimulation montages when applied to nerves. In this paper, we explore the value of using different stimulation montages and different electrode configurations to maximize spatial selectivity of stimuli on in silico peripheral nerves.
This work investigates the merits of five different stimulation montage types across 195 unique electrode configurations while quantifying four metrics of success. Section 2 introduces these montages, configurations, and metrics. Section 3 shows the resulting data collected from our in-silico experimentation and what it means for each montage’s success. In Section 4, we lay out our recommendations for researchers hoping to perform spatially selective nerve stimulation with cuff electrodes.
2. Materials and Methods
2.1. Finite Element Modelling and Neural Simulation
In order to perform the desired in silico experiments, two computational models were used: a finite element model (FEM) powered by COMSOL v4.3 and an axon model powered by NERON (version 8.2.3). Additional data processing and testing of stimulation montages was performed in MATLAB R2024 and Python 3.9.6.
A cylindrical nerve with a diameter of 2.5 mm was constructed to approximate a human vagus nerve. In order to keep the FEM as generalized as possible, no fascicles were included in the nerve—prior art has shown that this no-fascicle approach maximizes generalizability to unknown nerve geometries [25]. Instead, the nerve included a 100 µm thick epineurium surrounding a homogenous endoneurium. The conductivity of the epineurium was 0.0826 S/m [27], while the conductivity of the endoneurium was 0.0826 S/m in the transverse direction and 0.571 S/m in the longitudinal direction (as in [25,28], to show preference to longitudinal conduction by fibers). The computational nerve was surrounded by a salt bath with conductivity 2 S/m [25,27] and a cuff electrode with a diameter of 2.7 mm. The 100 µm thick cuff substrate was modeled as silicone, with conductivity 10–17 S/m, and included a layer of 10 µm thick stainless steel on top of which the electrode contacts were modeled. The electrode surface material was modeled as PEDOT-PSS and was given a contact impedance of 500 Ohms × mm2 (as recommended by [17,29]). Electrical ground was placed both far upstream and far downstream of the nerve model to allow current to flow in both directions.
A set of electrode configurations were modeled along with the nerve, including configurations using 1, 2, and 3 rings of electrode contacts. Each ring contained electrodes with a 1 mm longitudinal length, and a 1.5 mm longitudinal separation between ring edges or between a ring and the edge of the cuff. In total, the cuff lengths were therefore 4 mm for single-ring configurations, 6.5 mm for two-ring configurations, and 9 mm for three-ring configurations. The number of tetrahedral mesh elements was approximately 500,000 for single-ring designs, 650,000 for two-ring designs, and 800,000 for three-ring designs (“approximately” because 65 configurations were considered for each number of rings, with some variation in the number of mesh elements among designs).
Neurons were not physically built into the FEM. Instead, to predict the activation of neurons in the 3D space, a Lead-Field Matrix (LFM) was computed for each model. Using a quasi-static assumption, the voltage and linear activating function applied to each voxel were found per unit of current applied to each electrode. The current delivered to a node of Ranvier within the 3D space was determined by the activating function applied to the voxel closest to that node, as well as the geometrical properties of the neuron (as in [25]). This method of calculating current applied to each node is computationally very efficient, but we recognize that accuracy could be improved by using a time-dependent study over the quasi-static assumption. Notably, by not building fiber geometry into the FEM, we are ignoring interactions where shallow fibers may shield deeper fibers from applied current. For the purpose of maintaining realistic computational speeds over our many trials, we follow in the footsteps of other computational work that does not consider these effects [17,25,27,28].
To determine whether a fiber would experience an action potential, each fiber was simulated in NEURON, version 8.2.3 [30], facilitated by custom Python scripts with a fixed timestep of 1 µs (0.001 ms). Current was applied to nodes of Ranvier with the method described in [31]: approximating extracellular current via an equivalent intracellular current clamp stimulation. To ensure consistency, a tailored Hodgkin Huxley mechanism was incorporated into each fiber to simulate membrane potential behaviors utilizing ion concentrations similar to those in [31]. Myelinated fiber axons were constructed as alternating node-internode segments using dimensions obtained in [31,32]. Unmyelinated fibers were modeled as uniform unmyelinated axons with dimensions from [33].
A proper understanding of safety constraints requires testing with different fiber types. Therefore, we explored the following 4 different fibers:
- 16 μm fiber diameter, myelinated, from [31], referred to in this work as “Aα fiber”.
- 8.7 μm fiber diameter, myelinated, from [31], referred to in this work as “Aβ fiber”.
- 2 μm fiber diameter, myelinated, from [32], referred to in this work as “Aδ fiber”.
- 0.8 μm fiber diameter, unmyelinated, from [33], referred to in this work as “C fiber”.
Stimulation of these in silico fibers was always performed via a single biphasic pulse with variable amplitude, and pulse width equal to the target fiber’s chronaxie.
2.2. Investigated Electrode Configurations and Stimulation Montages
As mentioned in Section 1, a total of 195 electrode configurations were tested. Each configuration had a different number of electrode rings, a different number of electrodes per ring, and/or a different radial electrode size. Three ring options (1, 2, and 3) and thirteen different electrode contact numbers were tested (4, 5, 6, …, 16). These configurations were chosen because they represent the range of configurations commonly used in previous studies of spatially selective stimulation. Five different radial electrode sizes were examined for each number of contacts. For this investigation, radial electrode sizes are expressed as a fraction of the total nerve circumference, so a radial size of “1/2” would describe an electrode wrapped 180° around the nerve (this is done to facilitate easy scaling of parameters to other nerve sizes). Depending on the number of electrodes used, investigated radial sizes varied from 1/6th to 1/26th of the nerve circumference.
A primary focus of this paper is the 5 different stimulation montages tested. The montage types included “Longitudinal”, “X-Adjacent”, “X-Decay”, “SBFI”, and “Simulated Annealing”. Each is explained below. Modifications were made to each montage to accommodate the presence of one, two, or three rings of electrodes. Figure 1 shows representations of each stimulation montage for each number of rings.
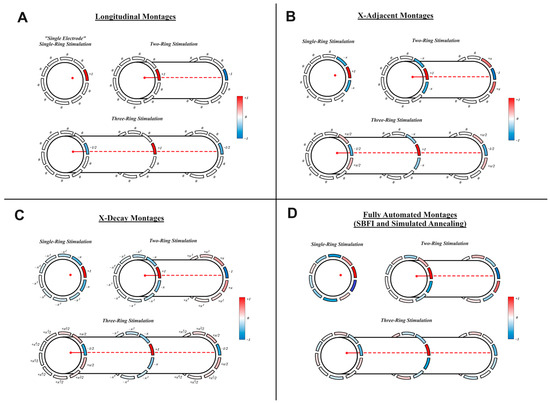
Figure 1.
Stimulation Montages Cartoon depictions of each montage investigated for various electrode configurations. Current ratios are shown for the following: (A) longitudinal stimulation, (B) X-adjacent stimulation, (C) X-decay stimulation, and (D) SBFI and simulated annealing methods (which were determined via optimization with the respective method). In each cartoon, a set of rings with 10 electrodes each is wrapped around a nerve segment. The red point/line denotes the target fiber within the nerve. Red color denotes greater cathodic stimulation, and blue color denotes greater anodic stimulation at an electrode (our convention gives positive values to cathodic current). Note that not all montages are spatially charge-balanced, and therefore biphasic pulses were used to facilitate all stimulations.
- “Longitudinal”: The most straightforward montage, and the easiest to implement, longitudinal stimulation relies on a single pair of longitudinally separated electrodes. One member of the pair receives one arbitrary unit (AU) of cathodic current, and the other receives one AU of anodic current. The two-ring implementation of this montage is recommended by [17] as a potential optimal solution. As shown in Figure 1A, the distribution of current is modified for three rings of electrodes to utilize the additional ring—splitting the anodic current among the available longitudinally located electrodes. Additionally, note that single-ring configurations have no longitudinally spaced electrodes—the single-ring version of this montage will therefore only include stimulation from a single electrode and will be referred to as “Single Electrode” stimulation to prevent confusion for the remainder of this paper. Single-electrode stimulation is not spatially charge-balanced but can be applied safely via biphasic pulse, which is standard practice regardless of montage.
- “X-Adjacent”: X-Adjacent montages are similar to longitudinal montages but also include activation of electrodes adjacent to the primary longitudinal electrodes. As shown in Figure 1B, electrodes adjacent to a primary cathodic source receive “X” anodic current, while electrodes adjacent to a primary anodic source receive “X” cathodic current. The value of X lies between zero and one and is determined via simulated annealing to achieve maximum success in our “Fiber Specificity” metric (described in “Metrics of Success” below). We are testing X-Adjacent montages because prior art has observed increases in spatial specificity when activating electrodes adjacent to primary sources in this way [22,25]. Note that when X is equal to zero, this montage simply becomes a longitudinal stimulation.
- “X-Decay”: X-decay montages are an extrapolation of X-adjacent montages, using all available electrodes. As shown in Figure 1C, each electrode farther away from a ring’s primary electrode will receive an additional power of X in its current calculation. Since X is a value between zero and one, electrodes farther away from the primary electrode receive less current. X-decay “X” values are calculated via simulated annealing in the same way as X-adjacent values. We are testing X-decay montages to observe the benefits and drawbacks of recruiting all possible electrodes, in comparison to the more straightforward X-Adjacent montages.
- “SBFI”: Our unique method is called “Stimulation Balancing Focality and Intensity” (SBFI). It was originally presented in [26] as a montage to accurately perform multi-electrode transcranial direct current stimulation. The method calculates the current to be applied at each electrode by maximizing voltage delivered to a target region while minimizing voltage delivered to non-target regions. As a result, SBFI optimizes a montage that will deliver high three-dimensional spatial specificity without requiring computationally expensive simulations of action potentials. This is accomplished by finding the value of that minimizes the convex expression as follows:where represents the current applied to the electrodes, represents the LFM of the target region, represents the LFM of non-target regions, and represent the number of voxels in the target/nontarget regions, represents the desired stimulation to be delivered to each target voxel, and is an adjustable term balancing focality and intensity (in this case, since the purpose of the technique is to solve for the current ratios between electrodes, we simply use , and a vector of ones for ). The solution that minimizes the above convex expression was found using CVX in MATLAB [34,35]. After is calculated, the current ratios between electrodes were found by scaling such that one electrode receives a stimulation of AU.
The target region defined by was selected differently depending on the number of electrode rings used. For a single ring of electrodes, includes all voxels in a sphere of diameter (where is the radius of the nerve) tangent to the target fiber/voxel while maintaining minimum distance to the edge of the nerve. For two rings of electrodes, includes two target spheres—one under each ring of electrodes. One target is selected to receive positive voltage, and one to receive negative voltage, mimicking the current distribution of previous montages. The targets for three-ring configurations are extrapolated accordingly, with three targets, selected to receive −1/2 AU, +1 AU, and −1/2 AU, respectively.
- 5.
- “Simulated Annealing”: Prior studies, including [22,25], have used global optimization tools to find the optimal current applied to electrodes to achieve spatially selective stimulation. To compare global optimization to our other montages, we include a simulated annealing montage. This montage begins from the initial condition of the longitudinal stimulation, and simulated annealing is applied in order to maximize success at our “Fiber Specificity” metric (described in “Metrics of Success” below). Simulated annealing was performed in MATLAB with a tolerance of 10−6. To reduce the number of variables for multiple-ring configurations, the two-ring simulated annealing montages constrained current values of one ring to be equal and opposite of the other, and the three-ring simulated annealing montages were constrained such that the outer ring electrode currents were equal to −1/2 multiplied by the center ring electrode currents.
2.3. Metrics of Success
Four metrics of success were used to judge each stimulation configuration and montage: 3D specificity, fiber specificity, robustness, and safety. All metrics were averaged for 150 targets located at different angles around the nerve to remove bias related to fiber location (because some stimulation montages are more effective at activating voxels radially aligned with an electrode). The metrics of success are explained as follows:
- 3D Specificity: Following the definition of a “deep target” given by [17], a target voxel at a depth two-thirds of the distance from the nerve’s circumference to its center was selected. Current was applied to electrodes according to a selected stimulation montage, and the number of voxels that received a greater activating function than the target voxel was counted. 3D Error was calculated as the percent of all voxels with a higher activating function than the target, and 3D Specificity was calculated as 100% minus the 3D Error. Since this percentage is based on the size of the cuff, the results for 1-ring, 2-ring, and 3-ring cuffs have different meanings.
- Fiber Specificity: A set of 2000 identical, cylindrical, longitudinally oriented nerve fibers were assumed to be randomly distributed within the computational nerve. Following the definition of a “deep target” given by [17], a target fiber located deep into the nerve (two-thirds from the nerve’s circumference to its center) was selected, and current was applied to electrodes according to a selected stimulation montage such that the target fiber received a threshold stimulus. The percentage of total fibers activated by the stimulation was counted, revealing the fiber error. Fiber specificity was calculated as 100% minus the fiber error. Since this test calculates the fiber specificity at the exact level of current required to activate the target fiber, it measures maximum fiber specificity.
- Robustness: Reusing the 2000 fibers from the Fiber Specificity test, the order in which the fibers were recruited was determined. Then, a Specificity Index () and Robustness Index () were calculated according to the following equations:where represents the ratio between the activated target fibers and total target fibers, and represents the ratio between the activated non-target fibers and total non-target fibers. Note that the total number of target fibers is 1, and the total number of non-target fibers is 1999 for this test. represents how sensitive the stimulation is to a change in amplitude. Borrowing notation from [25], represents the value of when the applied current is twice as large as the current required to achieve . In simple terms, is the percent of total specificity that is maintained when we accidentally apply too much current—twice as much as the optimal amount. For our analysis, can only have values between 0 and 1, because maximum is always at least zero. Since maximum is already encoded in the fiber specificity metric, only robustness was extracted from this test.
- Safety: Reusing the 2000 fibers from the fiber specificity test amplitude of current at each electrode required to achieve maximum specificity was recorded. The maximum charge density applied to each electrode was then found, and the stimulation was marked as unsafe if the maximum applied charge density resulted in a Shannon neural safety parameter exceeding k = 1.85 [36].
Additionally, differently sized nerve fibers will require different amounts of current to activate. For all other metrics, arbitrary current units and fiber sizes have been acceptable to characterize stimulation effectiveness—however, to properly determine safety, the units of current and size of fibers become relevant. Therefore, this metric was calculated four separate times, once for each fiber type discussed above. For simplicity, all 2000 fibers are modeled as the same fiber type in each test.
2.4. Cost Functions
We recognize that cost functions are imperfect tools for finding optimal stimulation protocols because cost functions can easily be manipulated to produce any predetermined result. However, for the purpose of making actionable recommendations to future researchers, we have chosen a set of 5 cost functions with which to judge the results. The first is naïve to the type of fibers being stimulated in the target nerve, and the other four include safety limits imposed by the four different types of fibers considered in our safety analysis (Aα, Aβ, Aδ, and C).
The naïve cost function is simply a multiplication of each metric of success (with the percentage-based ones subtracted from 100% to reward high percentages). The cost function input variables are our metrics of success: “” is 3D specificity, “” is fiber specificity, “” is robustness index, and is the Shannon neural safety parameter associated with the stimulation of each fiber type ( is the parameter value associated with our simulated Aα fiber). The additional variable represents the length of the cuff (4 mm for single-ring configurations, 6.5 mm for two-ring configurations, and 9 mm for three-ring configurations) and is used to standardize units of 3D specificity among configurations with different numbers of rings.
The other cost functions include the naïve calculation within, but also include a penalty in the denominator, which causes the cost function’s output to approach infinity as the Shannon safety parameter approaches the safety constraint . The naïve cost function includes the safety parameter as a penalty but does not apply the safety constraint as a consideration—therefore, a 10% decrease in the safety parameter will always yield a 10% decrease in overall cost. The other cost functions include the expression for each fiber type, and as a result, a 10% decrease in will have a variable impact on the cost, depending on how close the original charge was to the safety limit. When a stimulation montage uses more charge density than the limit, it produces a negative cost, which is disqualified from consideration.
3. Results
3.1. Two- and Three-Ring Stimulation Are Safer and More Spatially Selective than Single-Ring Stimulation
Figure 2 and Figure 3 show the results of all our tests for single-ring (Figure 2) and two-ring montages (Figure 3). Across all montages, nearly every metric saw improved performance when transitioning from one to two rings: average fiber specificity improvement was 6.27%, average robustness improvement was 26.7% (mostly facilitated by the longitudinal montage, which doubled its robustness from one ring to two rings), and the average safety was improved by 24% (most notably, SBFI had a 44.7% reduction in the Shannon value). The percent 3D specificity was also improved, but note that a different number of rings covers a different amount of 3D space. In our case, the single-electrode/longitudinal montage shows an “improvement” from 73.1% 3D specificity to 79.5% 3D specificity, but factoring in the length of the cuff (4 mm for one ring to 6.5 mm for two rings) reveals that the two-ring montage actually increases current spread by 23.8%. A single ring of electrodes might be desirable in applications where limiting stimulation to a single plane is the highest priority, but for any other circumstance, two- and three-ring montages have improved performance.
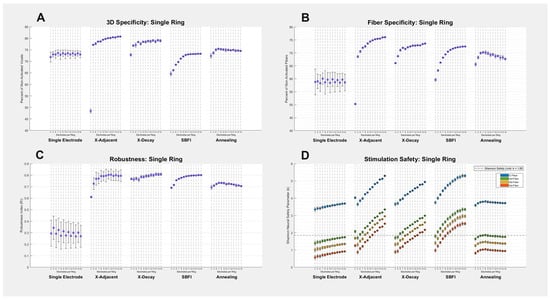
Figure 2.
Single-ring montage results: (A–D) all four metrics of success are shown for each of the five stimulation montages and 13 electrode counts. Each data point on each graph corresponds to a different number of electrodes used in the given montage, and error bars on all graphs represent the standard deviation created by testing multiple electrode sizes. Our study seeks to find the method that maximizes specificity and robustness (y-axes in (A–C)), while minimizing the Shannon safety parameter (Y-axis in (D)). The safety graph’s (D) four different colors represent different fibers observed, and the dashed horizontal line denotes the threshold at which a stimulation exceeds the Shannon neural safety limit k = 1.85. A numerical summary of the data can be found in Appendix A (Table A1).
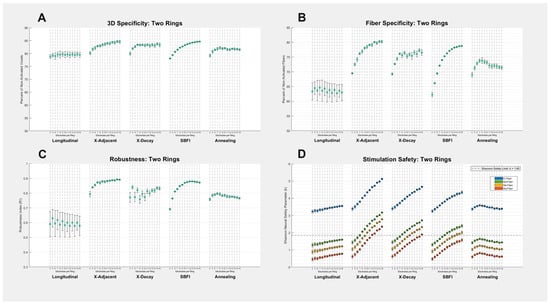
Figure 3.
Two-ring montage results: (A–D) All four metrics of success are shown for each of the five stimulation montages and 13 electrode counts. Each data point on each graph corresponds to a different number of electrodes used in the given montage, and error bars on all graphs represent the standard deviation created by testing multiple electrode sizes. Our study seeks to find the method that maximizes specificity and robustness (Y-axes in (A–C)), while minimizing the Shannon safety parameter (Y-axis in (D)). The safety graph’s (D) four different colors represent different fibers observed, and the dashed horizontal line denotes the threshold at which a stimulation exceeds the Shannon neural safety limit k = 1.85. A numerical summary of the data can be found in Appendix A (Table A2).
Three-ring montages show very similar performance to two-ring montages. Figure A1 (in Appendix A) details results from three-ring montages: the average fiber specificity value is improved by 0.45%, the average robustness is improved by 0.33%, and the average safety is improved by 1.15%, all of which are relatively small improvements. Notably, the 3D specificity values were improved from two- to three-ring montages, and these improvements are large enough to overcome the change in size of the cuff from 6.5 mm to 9 mm in length. Three-ring montages may be superior to two-ring montages at reducing 3D current spread, but future researchers will need to decide whether this improvement is worth the hardware costs associated with including a third ring of electrodes and, therefore, a larger cuff.
3.2. Electrode Size Is Only a Major Concern for Longitudinal Montages
Figure 2 and Figure 3 include error bars on each data point, corresponding to the standard deviation across multiple trials. Each “trial” was made by changing the size of the electrodes (the arc length, not longitudinal length). Therefore, the largest error bars in Figure 2 and Figure 3 correspond to the stimulation methods that are most affected by a change in electrode size. The specificity of longitudinal montages stands out here as most subject to electrode size, which is not surprising given that previous studies have discussed the importance of electrode size in longitudinal stimulation [17]. However, it is noteworthy that other montages are much less influenced by size, and SBFI specificity is almost entirely unaffected by electrode size (with the exception of safety metrics, where size always influences current density). This leads us to predict that as an optimization algorithm converges on an improved multi-electrode stimulation montage, the importance of electrode size becomes less relevant, and the number of electrodes becomes more relevant. In this context, we can think of longitudinal stimulation—in which specificity and robustness are dependent primarily on electrode size—as the opposite of SBFI—in which only the number of electrodes influences specificity and robustness.
3.3. Maximum Specificity and Robustness Was Achieved by the X-Adjacent Montage
The highest specificity and robustness values achieved in this study were given by the X-Adjacent montage. Its average two-ring fiber specificity was 77.2%, and average robustness was 0.87, but these values reached as high as 80% and 0.90, respectively, when the greatest number of electrodes was used. SBFI reached similarly high specificity and robustness values, but only when the number of available electrodes was large. We were not expecting for a montage with access to only three electrodes per ring to out-perform a montage with access to any number of electrodes per ring; however, we noticed that the most successful stimulation protocols used by SBFI and simulated annealing were often very similar to the design of X-adjacent—relying primarily on a single cathodic stimulator shielded by two anodic stimulators. When optimizing for specificity and robustness, this style of stimulation is highly recommended. However, X-adjacent was consistently the least optimized for safety.
3.4. Longitudinal Montages Show Maximum Safety, but Have Low Robustness
In contrast to X-adjacent, the longitudinal montages easily achieved the lowest Shannon safety values, making longitudinal montages optimal when safety constraints are tight. However, the most important weakness of longitudinal stimulation is its low robustness. In applications of peripheral nerve stimulation, it is difficult to know the exact size, shape, and location of a desired stimulation target; therefore, we will seldom know the optimal amount of current to apply at our electrodes. When using a method with low robustness, the application of too much current could inadvertently activate large non-target regions of the nerve, to the detriment of the benefits promised by spatially selective stimulation.
The X-decay montage strikes a balance between the high specificity of X-adjacent and the safety of longitudinal stimulation. In the “Cost Function Performance” section below, X-decay has similar cost function performance to X-adjacent; however, as discussed later, it is much more difficult to implement.
3.5. Simulated Annealing Is Hampered by Local Minima in This Application
In theory, the simulated annealing montage should perform better than the X-adjacent montage in the fiber specificity metric. This is because simulated annealing was optimized for performance in the fiber specificity metric and performs a search over the entire possibility space of electrode amplitude ratios, including those available to X-adjacent. In practice, however, using a function tolerance of 10−6, and one minute of maximum computation time, the method was unable to converge on a more optimal solution and was likely slowed down by many local minima. This is a side effect of using a computationally expensive global optimization tool on a problem with many degrees of freedom (one for each electrode) and an abundance of local minima introduced by the neurons whose activation functions were used to determine stimulation outcomes.
3.6. Cost Function Performance
We explored five different cost functions, according to Section 2.4. Table 1 shows the best performance of each stimulation montage in each cost function (the top montage per cost function is highlighted in green). Additionally, Figure 4 shows how different numbers of electrodes affect the cost function value of each montage.

Table 1.
Optimal cost-function values: minimum cost function achieved for each montage at any available electrode configuration. Investigated montages were sorted by their minimum naïve cost function values, and the top-performing montage for each cost function is highlighted green. Data is marked with “N/A” when no available electrode configurations could satisfy safety constraints for the given stimulation.
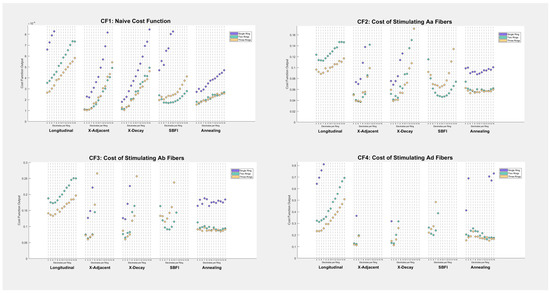
Figure 4.
Cost-function results by electrode number: output cost function values are shown on the Y-axis of each scatter plot. Each point corresponds to a stimulation montage, a number of electrodes per ring, and a number of rings (denoted by color). Some data points appear to be missing on the graphs—this is because their costs are so high that they either lie outside the viewing window or are undefined, in the case that they violate the Shannon neural safety constraint.
Despite including a cost function for unmyelinated C-fibers, there were no results in this study for which stimulation of target C-fibers satisfied the Shannon neural safety limit. This does not mean that spatially selective stimulation of such fibers is impossible; it simply indicates that the tools explored in this investigation are not sufficient to stimulate unmyelinated fibers at our target depth in a nerve of our target size. Researchers who hope to perform spatially selective stimulation on unmyelinated fibers will need to target more shallow nerve regions or perform their investigations on smaller nerves.
As seen in Table 1 and Figure 4, montage selection plays a major role in cost function values, with the best-performing montages scoring up to 6.35 times better than the worst. The best-performing montage in every test was either an X-Adjacent or X-Decay montage. Note that the top four montages in every cost function were the same: two-ring and three-ring X-Adjacent and X-Decay—and the maximum performance of each of these montages was within 5–10% of each other in every case. Longitudinal montages were low-performing, although this can be attributed to the nature of the cost function, which included one term for safety and multiple terms for specificity (longitudinal stimulation was always the safest but least specific).
Before this investigation began, we anticipated SBFI to be the most successful montage; however, it fails to surpass X-Adjacent or X-Decay on our cost functions because its performance is highly dependent on the number of available electrodes. The safety constraints of this analysis are tight enough that rings of fewer electrodes outperform rings of many electrodes (because fewer electrodes allow for larger contacts and less current density). The naive and Aα cost functions shown in Figure 4 suggest that SBFI is the best montage when given a cuff electrode with ten electrodes per ring, but SBFI does not achieve the same success as other montages when the electrode count is small.
4. Discussion
Our results show how delivering current through multiple electrodes increases spatial specificity of nerve stimulation, at the cost of requiring additional current. The two-ring longitudinal montage, for instance, only stimulates using a single pair of electrodes, and at its highest specificity activates approximately one-third of off-target fibers within the nerve before the target. By comparison, the two-ring X-adjacent montage activates only one-fifth of nerve fibers at its best performance. X-adjacent also yielded the highest robustness among our montages, allowing it to maintain high specificity even when the amount of injected current is not optimal. The benefits of using more spatially specific montages come with the drawback of requiring additional current applied at electrode surfaces—an average of 3.49 times as much current density was required for two-ring X-adjacent stimulation than two-ring longitudinal stimulation. Prior art has already shown that two-ring longitudinal stimulation is spatially specific enough to separate cardiac and respiratory function of animal models in vivo [17]; in circumstances that require additional specificity—or circumstances where using additional current is safe—researchers should consider using multi-electrode montages to reduce current spread to non-target fibers.
4.1. Our Recommendations
Montage: We recommend that future researchers use X-Adjacent montages in future spatially selective nerve stimulation. X-Adjacent montages achieved the highest fiber specificity among all methods and showed robustness/3D specificity values that were very close to other top-performing montages. Despite the larger current requirement, X-adjacent was shown to be suitable for stimulation of all myelinated fibers tested, provided that the number of electrodes used per ring was low. As a result, these montages achieved top performance in nearly every cost function explored. They are also reasonably simple montages to implement, as discussed below in the “Computational Time and Modelling Requirements” and “Hardware and Resolution Constraints” sections.
Number of Electrodes: The limiting factor for X-Adjacent stimulation is safety. To maximize safety, we recommend using a small number of electrodes. When safety is not a concern, using as many as 10 or 12 electrodes per ring could be appropriate for this montage; however, when limited by safety constraints our study recommends using five or six electrodes per ring.
Size of Electrodes: Our data shows that radial electrode size is not a critical factor for X-Adjacent stimulation, as long as the value “X” is selected correctly. We therefore recommend that an electrode size be chosen based on the user’s hardware constraints, instead of focusing on optimization.
Number of Electrode Rings: Many single-ring montages/configurations were not represented on the cost function graphs because their cost function values were either too high to be shown or they failed to satisfy safety constraints. Despite yielding high 3D specificity, single-ring configurations have significant safety limitations. We therefore recommend using two rings of electrodes. The addition of a third ring is beneficial to some of our tested montages, but these benefits are small in the face of the additional hardware constraints involved with a third ring.
For a two-ring X-adjacent stimulation with 6 electrodes, we recommend using an X-value of either 0.15 (for stimulation of the smallest myelinated fibers) or 0.2 (for stimulation of larger myelinated fibers). These values of “X” are slight underestimates of our optimized values (shown in Appendix A), which we recommend in the interest of sacrificing a small amount of spatial specificity for safety. Note that as “X” approaches zero, X-adjacent montages become the safer longitudinal montage.
4.2. Influence of Fascicle Geometry
Our models were used to predict how much charge density at electrode surfaces was required to trigger action potentials at target fibers. However, the models we used do not account for all possible nerve geometry—most notably the presence of fascicles. Fascicle perineurium is more resistive than epineurium or endoneurium, and the placement of fascicles, as well as fascicle thickness, alters desired current stimulation on a case-by-case basis. As a result, we can expect real-world stimuli to require more electrical current than what we predict in our study—but by contrast, we also expect the Shannon safety window to be more generous when neurons are located farther from electrodes. Prior art has shown that using a generalized model like ours is still the most useful for finding and testing stimulation montages [25], but we recognize that stimulations optimized in silico are not necessarily well-optimized for individuals.
One advantage of recalculating current ratios before each stimulation event (as in SBFI or simulated annealing) is that additional knowledge of fascicular organization/location improves the calculation. If the location of fascicles is known, a user can set the SBFI target region to any target fascicle(s) while specifically avoiding current delivery to non-target fascicles. And if the types of fibers within the fascicles are known (or estimated), then simulated annealing can be used to attempt activation of individual target fibers while avoiding non-target fibers. The other montages tested in this study are easier to implement but do not benefit from additional information in this way.
4.3. Additional Electrode and Nerve Geometries
We have extensively explored the effects of changing the number of electrodes, the radial size of electrodes, and current ratios applied to electrodes on our various metrics of success. However, there are variables that we have not explored in order to prevent the scope of the possibility space from becoming too vast. The most obvious of these variables include the diameter of the nerve (fixed at 2.5 mm in our analysis), the longitudinal length of electrodes (fixed at 1 mm), and the spacing between electrodes (fixed with 2.5 mm pitch). Previous work [17] has already seen some of the effects of altering some of these parameters, although more investigation is required to properly explore how they will interact with the different stimulation montages used in our study. For future researchers intending to use our stimulation montages on different nerve sizes with different electrode geometries, we have the following suggestions.
We expect that as nerve diameter increases, stimulation safety will decrease. This is expected because the current required to stimulate a fiber at the same relative depth depends on the nerve radius squared—while the surface area increase gained by increasing nerve size is only dependent on the radius. Therefore, we expect that doubling the nerve diameter should double charge density requirements. We also expect the opposite to be true—reducing the nerve radius by half will likely also reduce charge density requirements by half. Therefore, we expect that spatially selective stimulation will be easier to achieve in smaller animal models, where montages optimized for selectivity will be safe enough to implement.
We expect that increasing longitudinal electrode size and electrode spacing will have minimal effects on charge density requirements and fiber specificity—although it will obviously reduce 3D specificity due to greater longitudinal activation. This is because increasing longitudinal electrode size will likely increase the current required to stimulate the target but also increase the surface area of the electrode by the same factor (so density will not change). Additionally, we predict that increasing longitudinal electrode size could decrease robustness. Intuitively, this is because if an electrode is imagined to have infinitesimal arc length, it can be thought of as a line of charge, which delivers variable electric fields to target points depending on its length (a zero-length line is a point-source with electric field proportional to , and an infinite-length line has an electric field proportional to , where denotes distance from the source). We recognize that further investigation is required to confirm or deny these expectations, particularly in the context of variable stimulation montages.
4.4. Computational Time and Modelling Requirements
The computational time of most montages displayed in this work is negligible when translated to practical application. The use of CVX for MATLAB allows SBFI to find a solution to its convex problem in less than one second (for this paper, the computational cost of running SBFI—in addition to loading/storing the data—was approximately 0.6 s per instance of SBFI). In real applications, only one instance of an optimization algorithm will be necessary per new stimulation protocol. Of course, montages without optimization steps (notably longitudinal montages) require zero computational time.
The simulated annealing montages were given a maximum of 1 min to converge on a solution within a predefined tolerance of 1 × 10−6 per electrode configuration. This time was never utilized completely within our study, but times approaching 1 min were normal for large numbers of electrodes in the two-ring and three-ring simulated annealing montages. Using an additional minute to determine a stimulation montage is a downside that the simulated annealing montages do not share with other methods, although it is a small one. The values of X in the X-adjacent and X-decay montages were also chosen by simulated annealing, but the time required to converge on a solution was only 2–10 s per configuration; this was due to the fact that only one variable required optimization.
The most restrictive constraint of SBFI is that it requires a solution to the forward problem and therefore a finite element model of the target nerve. This may not dissuade researchers who are familiar with making FEM models and collecting lead-field data, but unfortunately SBFI is currently not “plug-and-play”, even if a multi-electrode cuff can be obtained (as of this writing, we have not yet made an API for calculating SBFI current ratios on a user-defined nerve). Similarly, other optimization-based methods such as simulated annealing were calculated based on knowledge of fiber action potential thresholds—which means that these montages require even more information than SBFI: both an FEM and a neural fiber model to measure action potential thresholds. Montages with easily defined current ratios have the advantage that they can be implemented without any model building or calculation beyond the safety constraints of the chosen materials.
The X-adjacent and X-decay methods present a potential middle ground for researchers who want to achieve high spatial selectivity without needing to create computational models of fibers and a nerve. Even though our values for “X” were optimized via simulated annealing, choosing non-optimal values for X (or simply the values for X included in Appendix A) may still yield high specificity and robustness with low current requirements. Selecting a value for X below the optimal value will decrease the specificity of the stimulation but has the benefit of improving safety (because as X approaches zero, both the X-adjacent and X-decay montages become longitudinal montages). While we currently cannot predict how nerve diameter and other geometrical changes may influence the optimal value of X, we intend to continue using X-adjacent and X-decay montages as primary stimulation montages of interest in our future work.
4.5. Hardware and Resolution Constraints
An additional challenge with the SBFI, X-decay, and simulated annealing approaches is that these methods optimize current ratios without regard for hardware resolution constraints. We recognize that SBFI might suggest using twenty microamps of current on a particular electrode, even if hardware resolution only allows current to be delivered in increments of fifty microamps. X-decay montages are particularly vulnerable to such hardware constraints—for example, a ten-electrode configuration with an X-value of 0.25 will result in one electrode requiring a current density 256 times smaller than the primary electrode. In a real application, the closest available value of current can be chosen (which may be zero).
Furthermore, there are hardware constraints concerning the number of available channels in a stimulator. Using simulated annealing on a two-ring, ten-electrode configuration requires the use of twenty independent stimulation channels, which for many researchers could prove unrealistic. For reference, stimulation systems are not always built to accommodate one stimulation channel for every stimulating electrode, because not all electrodes need to be active simultaneously. For example, Medtronic recently tested their “SmartStim” implantable neural controller [37] in 2024; the device includes 32 stimulating electrodes but only supports up to eight simultaneous stimulation channels. X-decay and simulated annealing both require a number of stimulation channels equal to the total electrodes, making them inaccessible to researchers who have more electrode contacts than channels. Notably, SBFI is less affected by a restricted number of channels because it is a convex method, and limiting active electrodes is a convex constraint. However, reducing the available electrodes is certain to reduce SBFI’s specificity as well. Longitudinal stimulation has the obvious advantage of only requiring a single pair or trio of electrodes to be active at once, making it the most accessible in this regard.
Once again, X-adjacent montages serve as a viable middle-ground to these logistical concerns. X-adjacent montages are not nearly as vulnerable to resolution constraints as X-decay, SBFI, or simulated annealing. Additionally, X-adjacent stimulation demands three active electrodes per ring regardless of total electrode count, meaning that the recommended two-ring X-adjacent montage requires only six stimulation channels. Depending on available resources, six stimulation channels could be accessible where twenty is not.
4.6. Future Work
In this study, we investigate a large possibility space for spatially selective stimulation—testing various stimulation montages, electrode sizes, numbers of electrode contacts, and numbers of electrode rings. However, our simulations focused on a simplified nerve model with a single endoneurium. Our choice of model gives this work generalizability, but we are eager to test out our stimulation protocols on a more realistic nerve model—one that better reflects the complexity of real nerve fibers, which may exhibit bifurcations, twists, or other non-linear structures, in addition to more fascicles. Future work should explore nerve models based on real nerve histology/geometry, accounting for these anatomical variations to enhance the accuracy of the simulation environment.
Another necessary improvement for future work is the introduction of multiple fiber types within a fascicle. To fully understand our montages’ distribution of current in a general case, we populated our nerve model with 2000 identical fibers. But realistically, a nerve will contain multiple varieties of myelinated and unmyelinated fibers within the same fascicle. An important next step will be investigating how well spatially selective montages can separate the activation of different fiber types.
Inevitably, we intend to translate our findings in this work to in vivo and ex vivo studies. Spatially selective nerve stimulation is currently an active research area, and spatial selectivity of some montages has been shown in live animals; however, to the authors’ knowledge, spatial selectivity of any montages shown in this work has not been quantified in vivo. Applying our most successful stimulation montages to a live animal to quantify spatial selectivity is a clear advancement for our work. If we find that our most successful montages maintain their viability in vivo, it may change the way we perform spatially selective stimulation in the future and improve outcomes for patients treated with peripheral nerve stimulation.
Author Contributions
Conceptualization, J.B. and W.L.; methodology, J.B.; software, J.B. and R.K.; validation, V.S. and R.K.; formal analysis, J.B.; investigation, J.B.; resources, W.L.; data curation, J.B.; writing—original draft preparation, J.B.; writing—review and editing, J.B., V.S., R.K. and W.L.; visualization, J.B. and V.S.; supervision, W.L.; project administration, W.L.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Dr. Patrick Soon-Shiong Endowment Fund and J.M. Maguire Endowed Chair in Engineering.
Data Availability Statement
The authors are willing to share original data and model files associated with this work. Please contact the corresponding author for access to files.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Single-Ring Montage Summary. Shows the average numerical values graphed visually in Figure 2.
Table A1.
Single-Ring Montage Summary. Shows the average numerical values graphed visually in Figure 2.
| Summary: Single-Ring Stimulation Montages | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stimulation Montage | 3D Specificity (%) | Fiber Specificity (%) | RI | Shannon Value k, Aα Fibers (μC/cm2) | Shannon Value k, Aβ Fibers (μC/cm2) | Shannon Value k, Aδ Fibers (μC/cm2) | Shannon Value k, C Fibers (μC/cm2) | |
| Single Electrode | 73.1 ± 0.47 | 59.1 ± 0.60 | 0.295 ± 0.023 | 0.770 ± 0.060 | 1.20 ± 0.060 | 1.59 ± 0.060 | 3.54 ± 0.060 | |
| X-Adjacent | 77.1 ± 8.7 | 71.9 ± 6.9 | 0.772 ± 0.053 | 1.72 ± 0.041 | 2.16 ± 0.041 | 2.54 ± 0.041 | 4.49 ± 0.041 | |
| X-Decay | 77.9 ± 1.7 | 71.7 ± 2.1 | 0.788 ± 0.017 | 1.55 ± 0.040 | 1.98 ± 0.040 | 2.37 ± 0.040 | 4.32 ± 0.040 | |
| SBFI | 71.1 ± 3.0 | 69.3 ± 4.0 | 0.774 ± 0.035 | 1.97 ± 0.082 | 2.40 ± 0.082 | 2.79 ± 0.082 | 4.74 ± 0.082 | |
| Simulated Annealing | 74.6 ± 0.81 | 68.8 ± 1.3 | 0.718 ± 0.012 | 0.968 ± 0.042 | 1.40 ± 0.042 | 1.79 ± 0.042 | 3.74 ± 0.042 | |

Table A2.
Two-Ring Montage Summary. Shows the average numerical values graphed visually in Figure 3.
Table A2.
Two-Ring Montage Summary. Shows the average numerical values graphed visually in Figure 3.
| Summary: Two-Ring Stimulation Montages | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stimulation Montage | 3D Specificity (%) | Fiber Specificity (%) | RI | Shannon Value k, Aα Fibers (μC/cm2) | Shannon Value k, Aβ Fibers (μC/cm2) | Shannon Value k, Aδ Fibers (μC/cm2) | Shannon Value k, C Fibers (μC/cm2) | |
| Longitudinal | 79.5 ± 0.30 | 63.6 ± 0.62 | 0.596 ± 0.016 | 0.629 ± 0.054 | 1.06 ± 0.054 | 1.45 ± 0.054 | 3.40 ± 0.054 | |
| X-Adjacent | 83.3 ± 1.3 | 77.2 ± 3.4 | 0.870 ± 0.028 | 1.51 ± 0.036 | 1.94 ± 0.036 | 2.33 ± 0.036 | 4.28 ± 0.036 | |
| X-Decay | 82.9 ± 0.98 | 75.2 ± 2.1 | 0.803 ± 0.027 | 1.28 ± 0.037 | 1.71 ± 0.037 | 2.10 ± 0.037 | 4.05 ± 0.037 | |
| SBFI | 82.6 ± 2.1 | 74.2 ± 5.3 | 0.840 ± 0.057 | 1.09 ± 0.050 | 1.52 ± 0.050 | 1.91 ± 0.050 | 3.86 ± 0.050 | |
| Simulated Annealing | 81.5 ± 0.78 | 72.2 ± 1.3 | 0.779 ± 0.011 | 0.695 ± 0.037 | 1.13 ± 0.037 | 1.52 ± 0.037 | 3.47 ± 0.037 | |
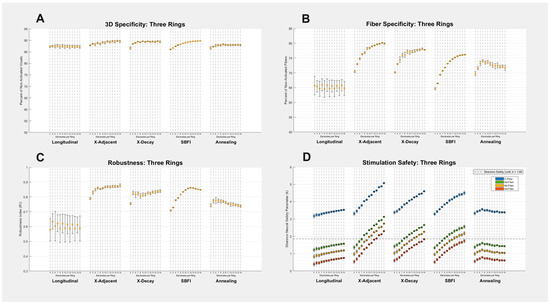
Figure A1.
Three-Ring Montage Results: (A–D) All four metrics of success are shown for each of the five stimulation montages and 13 electrode counts. Each data point on each graph corresponds to a different number of electrodes used in the given montage, and error bars on all graphs represent the standard deviation created by testing multiple electrode sizes. Our study seeks to find the method that maximizes Specificity and Robustness (Y-Axes in (A–C)), while minimizing the Shannon safety parameter (Y-Axis in (D)). The safety graph’s (D) four different colors represent different fibers observed, and the dashed horizontal line denotes the threshold at which a stimulation exceeds the Shannon neural safety limit k = 1.85. A numerical summary of the data can be found in the Appendix A (Table A3).

Table A3.
Three-Ring Montage Summary. Shows the average numerical values graphed visually in Figure A1.
Table A3.
Three-Ring Montage Summary. Shows the average numerical values graphed visually in Figure A1.
| Summary: Three-Ring Stimulation Montages | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stimulation Montage | 3D Specificity (%) | Fiber Specificity (%) | RI | Shannon Value k, Aα Fibers (μC/cm2) | Shannon Value k, Aβ Fibers (μC/cm2) | Shannon Value k, Aδ Fibers (μC/cm2) | Shannon Value k, C Fibers (μC/cm2) | |
| Longitudinal | 87.4 ± 0.16 | 65.2 ± 0.53 | 0.602 ± 0.018 | 0.597 ± 0.052 | 1.03 ± 0.052 | 1.42 ± 0.052 | 3.37 ± 0.052 | |
| X-Adjacent | 89.0 ± 0.61 | 77.4 ± 3.0 | 0.856 ± 0.024 | 1.46 ± 0.037 | 1.89 ± 0.037 | 2.28 ± 0.037 | 4.23 ± 0.037 | |
| X-Decay | 89.1 ± 0.80 | 76.1 ± 2.3 | 0.819 ± 0.022 | 1.23 ± 0.038 | 1.66 ± 0.038 | 2.05 ± 0.038 | 4.00 ± 0.038 | |
| SBFI | 88.6 ± 1.2 | 72.6 ± 3.8 | 0.818 ± 0.052 | 1.21 ± 0.055 | 1.64 ± 0.055 | 2.03 ± 0.055 | 3.98 ± 0.055 | |
| Simulated Annealing | 87.8 ± 0.41 | 72.5 ± 1.1 | 0.757 ± 0.014 | 0.664 ± 0.048 | 1.10 ± 0.048 | 1.49 ± 0.048 | 3.43 ± 0.048 | |

Table A4.
Single-Ring X-Adjacent X-Values: Values optimized via simulated annealing for maximum fiber specificity in single-ring X-Adjacent montage.
Table A4.
Single-Ring X-Adjacent X-Values: Values optimized via simulated annealing for maximum fiber specificity in single-ring X-Adjacent montage.
| Single-Ring X-Adjacent: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.462 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.376 | 0.183 | 0.270 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.389 | 0.149 | 0.224 | 0.285 | 0.344 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.362 | 0.125 | 0.199 | 0.258 | 0.309 | 0.351 | 0.385 | - | - | - | - | - | - | |
| 1/14 | 0.367 | 0.121 | 0.180 | 0.246 | 0.285 | 0.333 | 0.360 | 0.394 | 0.415 | - | - | - | - | |
| 1/16 | - | 0.110 | 0.171 | 0.227 | 0.279 | 0.316 | 0.345 | 0.376 | 0.398 | 0.415 | 0.433 | - | - | |
| 1/18 | - | - | - | 0.218 | 0.267 | 0.304 | 0.330 | 0.359 | 0.385 | 0.396 | 0.414 | 0.432 | 0.445 | |
| 1/20 | - | - | - | - | - | 0.294 | 0.306 | 0.344 | 0.376 | 0.395 | 0.404 | 0.418 | 0.433 | |
| 1/22 | - | - | - | - | - | - | - | 0.330 | 0.365 | 0.384 | 0.400 | 0.411 | 0.419 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.379 | 0.394 | 0.403 | 0.415 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.398 | 0.416 | |

Table A5.
Single-Ring X-Decay X-Values: Values optimized via simulated annealing for maximum fiber specificity in single-ring X-Decay montage.
Table A5.
Single-Ring X-Decay X-Values: Values optimized via simulated annealing for maximum fiber specificity in single-ring X-Decay montage.
| Single-Ring X-Decay: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.237 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.172 | 0.209 | 0.248 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.145 | 0.177 | 0.215 | 0.242 | 0.267 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.120 | 0.160 | 0.197 | 0.227 | 0.248 | 0.265 | 0.277 | - | - | - | - | - | - | |
| 1/14 | 0.106 | 0.156 | 0.188 | 0.212 | 0.233 | 0.252 | 0.265 | 0.276 | 0.285 | - | - | - | - | |
| 1/16 | - | 0.152 | 0.177 | 0.203 | 0.229 | 0.248 | 0.254 | 0.266 | 0.276 | 0.284 | 0.294 | - | - | |
| 1/18 | - | - | - | 0.202 | 0.222 | 0.239 | 0.251 | 0.261 | 0.267 | 0.278 | 0.286 | 0.292 | 0.299 | |
| 1/20 | - | - | - | - | - | 0.232 | 0.246 | 0.253 | 0.259 | 0.274 | 0.281 | 0.286 | 0.293 | |
| 1/22 | - | - | - | - | - | - | - | 0.251 | 0.260 | 0.268 | 0.271 | 0.281 | 0.289 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.265 | 0.271 | 0.278 | 0.283 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.276 | 0.280 | |

Table A6.
Two-Ring X-Adjacent X values: Values optimized via simulated annealing for maximum fiber specificity in two-ring X-Adjacent montage.
Table A6.
Two-Ring X-Adjacent X values: Values optimized via simulated annealing for maximum fiber specificity in two-ring X-Adjacent montage.
| Two-Ring X-Adjacent: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.173 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.134 | 0.205 | 0.281 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.120 | 0.183 | 0.244 | 0.303 | 0.362 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.107 | 0.170 | 0.223 | 0.277 | 0.329 | 0.370 | 0.402 | - | - | - | - | - | - | |
| 1/14 | 0.106 | 0.157 | 0.215 | 0.272 | 0.314 | 0.351 | 0.386 | 0.407 | 0.427 | - | - | - | - | |
| 1/16 | - | 0.153 | 0.209 | 0.258 | 0.303 | 0.343 | 0.371 | 0.394 | 0.414 | 0.429 | 0.443 | - | - | |
| 1/18 | - | - | - | 0.250 | 0.289 | 0.332 | 0.361 | 0.384 | 0.404 | 0.417 | 0.432 | 0.444 | 0.453 | |
| 1/20 | - | - | - | - | - | 0.321 | 0.352 | 0.378 | 0.399 | 0.412 | 0.425 | 0.436 | 0.444 | |
| 1/22 | - | - | - | - | - | - | - | 0.372 | 0.392 | 0.409 | 0.421 | 0.433 | 0.441 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.403 | 0.418 | 0.430 | 0.438 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.427 | 0.435 | |

Table A7.
Two-Ring X-Decay X values: Values optimized via simulated annealing for maximum fiber specificity in two-ring X-Decay montage.
Table A7.
Two-Ring X-Decay X values: Values optimized via simulated annealing for maximum fiber specificity in two-ring X-Decay montage.
| Two-Ring X-Decay: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.176 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.131 | 0.184 | 0.224 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.118 | 0.168 | 0.204 | 0.232 | 0.257 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.106 | 0.157 | 0.193 | 0.218 | 0.241 | 0.260 | 0.274 | - | - | - | - | - | - | |
| 1/14 | 0.103 | 0.149 | 0.185 | 0.210 | 0.230 | 0.248 | 0.263 | 0.274 | 0.285 | - | - | - | - | |
| 1/16 | - | 0.145 | 0.182 | 0.203 | 0.224 | 0.240 | 0.255 | 0.268 | 0.277 | 0.286 | 0.293 | - | - | |
| 1/18 | - | - | - | 0.199 | 0.219 | 0.233 | 0.249 | 0.262 | 0.271 | 0.279 | 0.286 | 0.292 | 0.299 | |
| 1/20 | - | - | - | - | - | 0.231 | 0.244 | 0.257 | 0.266 | 0.274 | 0.280 | 0.286 | 0.292 | |
| 1/22 | - | - | - | - | - | - | - | 0.253 | 0.260 | 0.272 | 0.278 | 0.283 | 0.289 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.269 | 0.274 | 0.281 | 0.286 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.280 | 0.283 | |

Table A8.
Three-Ring X-Adjacent X values: Values optimized via simulated annealing for maximum fiber specificity in three-ring X-Adjacent montage.
Table A8.
Three-Ring X-Adjacent X values: Values optimized via simulated annealing for maximum fiber specificity in three-ring X-Adjacent montage.
| Three-Ring X-Adjacent: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.162 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.124 | 0.204 | 0.287 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.104 | 0.180 | 0.242 | 0.305 | 0.354 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.106 | 0.162 | 0.223 | 0.273 | 0.326 | 0.362 | 0.393 | - | - | - | - | - | - | |
| 1/14 | 0.0935 | 0.164 | 0.206 | 0.258 | 0.309 | 0.340 | 0.368 | 0.392 | 0.417 | - | - | - | - | |
| 1/16 | - | 0.147 | 0.195 | 0.247 | 0.296 | 0.326 | 0.354 | 0.379 | 0.403 | 0.417 | 0.436 | - | - | |
| 1/18 | - | - | - | 0.237 | 0.288 | 0.318 | 0.346 | 0.368 | 0.392 | 0.407 | 0.422 | 0.435 | 0.449 | |
| 1/20 | - | - | - | - | - | 0.313 | 0.339 | 0.361 | 0.381 | 0.398 | 0.412 | 0.426 | 0.438 | |
| 1/22 | - | - | - | - | - | - | - | 0.356 | 0.375 | 0.393 | 0.406 | 0.421 | 0.428 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.387 | 0.403 | 0.418 | 0.423 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.416 | 0.420 | |

Table A9.
Three-Ring X-Decay X values: Values optimized via simulated annealing for maximum fiber specificity in three-ring X-Decay montage.
Table A9.
Three-Ring X-Decay X values: Values optimized via simulated annealing for maximum fiber specificity in three-ring X-Decay montage.
| Three-Ring X-Decay: X Values | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode Arc Length | Number of Electrodes | |||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1/6 | 0.211 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 1/8 | 0.117 | 0.194 | 0.209 | - | - | - | - | - | - | - | - | - | - | |
| 1/10 | 0.102 | 0.177 | 0.190 | 0.226 | 0.245 | - | - | - | - | - | - | - | - | |
| 1/12 | 0.0974 | 0.161 | 0.181 | 0.214 | 0.236 | 0.249 | 0.266 | - | - | - | - | - | - | |
| 1/14 | 0.0909 | 0.161 | 0.170 | 0.199 | 0.229 | 0.235 | 0.252 | 0.266 | 0.277 | - | - | - | - | |
| 1/16 | - | 0.146 | 0.169 | 0.193 | 0.220 | 0.227 | 0.245 | 0.256 | 0.267 | 0.277 | 0.286 | - | - | |
| 1/18 | - | - | - | 0.185 | 0.213 | 0.227 | 0.239 | 0.251 | 0.262 | 0.270 | 0.277 | 0.284 | 0.293 | |
| 1/20 | - | - | - | - | - | 0.226 | 0.236 | 0.246 | 0.257 | 0.264 | 0.271 | 0.278 | 0.286 | |
| 1/22 | - | - | - | - | - | - | - | 0.242 | 0.254 | 0.260 | 0.268 | 0.273 | 0.280 | |
| 1/24 | - | - | - | - | - | - | - | - | - | 0.257 | 0.265 | 0.270 | 0.277 | |
| 1/26 | - | - | - | - | - | - | - | - | - | - | - | 0.269 | 0.274 | |
References
- Olofsson, P.S.; Tracey, K.J. Bioelectronic Medicine: Technology Targeting Molecular Mechanisms for Therapy. J. Intern. Med. 2017, 282, 3–4. [Google Scholar] [CrossRef]
- Johnson, R.; Wilson, C.G. A Review of Vagus Nerve Stimulation as a Therapeutic Intervention. J. Inflamm. Res. 2018, 11, 203–213. [Google Scholar] [CrossRef]
- Panebianco, M.; Zavanone, C.; Dupont, S.; Restivo, D.A.; Pavone, A. Vagus Nerve Stimulation Therapy in Partial Epilepsy: A Review. Acta Neurol. Belg. 2016, 116, 241–248. [Google Scholar] [CrossRef]
- Austelle, C.W.; O’LEary, G.H.; Thompson, S.; Gruber, E.; Kahn, A.; Manett, A.J.; Short, B.; Badran, B.W. A Comprehensive Review of Vagus Nerve Stimulation for Depression. Neuromodul. Technol. Neural Interface 2022, 25, 309–315. [Google Scholar] [CrossRef]
- Sabbah, H.N. Electrical Vagus Nerve Stimulation for the Treatment of Chronic Heart Failure. Clevel. Clin. J. Med. 2011, 78 (Suppl. 1), S24–S29. [Google Scholar] [CrossRef] [PubMed]
- Koopman, F.A.; Chavan, S.S.; Miljko, S.; Grazio, S.; Sokolovic, S.; Schuurman, P.R.; Mehta, A.D.; Levine, Y.A.; Faltys, M.; Zitnik, R.; et al. Vagus Nerve Stimulation Inhibits Cytokine Production and Attenuates Disease Severity in Rheumatoid Arthritis. Proc. Natl. Acad. Sci. USA 2016, 113, 8284–8289. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.; Wang, Z.; Bai, J.; Xiong, J.; Chen, J.; Ni, J. Research Advances in the Application of Vagus Nerve Electrical Stimulation in Ischemic Stroke. Front. Neurosci. 2022, 16, 1043446. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhan, G.; Cai, Z.; Jiao, B.; Zhao, Y.; Li, S.; Luo, A. Vagus Nerve Stimulation in Brain Diseases: Therapeutic Applications and Biological Mechanisms. Neurosci. Biobehav. Rev. 2021, 127, 37–53. [Google Scholar] [CrossRef]
- Xu, J.; Sun, Z.; Wu, J.; Rana, M.; Garza, J.; Zhu, A.C.; Chakravarthy, K.V.; Abd-Elsayed, A.; Rosenquist, E.; Basi, H.; et al. Peripheral Nerve Stimulation in Pain Management: A Systematic Review. Pain Physician 2021, 24, E131–E152. [Google Scholar] [CrossRef]
- Li, L.-F.; Leung, G.K.-K.; Lui, W.-M. Sacral Nerve Stimulation for Neurogenic Bladder. World Neurosurg. 2016, 90, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Bonaz, B.; Sinniger, V.; Pellissier, S. Vagus Nerve Stimulation: A New Promising Therapeutic Tool in Inflammatory Bowel Disease. J. Intern. Med. 2017, 282, 46–63. [Google Scholar] [CrossRef] [PubMed]
- Ben-Menachem, E. Vagus Nerve Stimulation, Side Effects, and Long-Term Safety. J. Clin. Neurophysiol. 2001, 18, 415–418. [Google Scholar] [CrossRef]
- Redgrave, J.; Day, D.; Leung, H.; Laud, P.; Ali, A.; Lindert, R.; Majid, A. Safety and Tolerability of Transcutaneous Vagus Nerve Stimulation in Humans; a Systematic Review. Brain Stimul. 2018, 11, 1225–1238. [Google Scholar] [CrossRef]
- Mertens, A.C.; Raedt, R.; Gadeyne, S.; Carrette, E.; Boon, P.; Vonck, K. Recent Advances in Devices for Vagus Nerve Stimulation. Expert Rev. Med. Devices 2018, 15, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Rush, A.J.; Marangell, L.B.; Sackeim, H.A.; George, M.S.; Brannan, S.K.; Davis, S.M.; Howland, R.; Kling, M.A.; Rittberg, B.R.; Burke, W.J.; et al. Vagus Nerve Stimulation for Treatment-Resistant Depression: A Randomized, Controlled Acute Phase Trial. Biol. Psychiatry 2005, 58, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Tyler, D.J.; Durand, D.M. Functionally Selective Peripheral Nerve Stimulation With a Flat Interface Nerve Electrode. IEEE Trans. Neural Syst. Rehabil. Eng. 2002, 10, 294–303. [Google Scholar] [CrossRef]
- Aristovich, K.; Donega, M.; Fjordbakk, C.; Tarotin, I.; Chapman, C.A.; Viscasillas, J.; Stathopoulou, T.-R.; Crawford, A.; Chew, D.; Perkins, J.; et al. Model-based Geometrical Optimisation and in Vivo Validation of a Spatially Selective Multielectrode Cuff Array for Vagus Nerve Neuromodulation. J. Neurosci. Methods 2021, 352, 109079. [Google Scholar] [CrossRef]
- Wodlinger, B.; Durand, D.M. Selective Recovery of Fascicular Activity in Peripheral Nerves. J. Neural Eng. 2011, 8, 056005. [Google Scholar] [CrossRef]
- Goodall, E.V.; de Breij, J.; Holsheimer, J. Position-selective Activation of Peripheral Nerve Fibers With a Cuff Electrode. IEEE Trans. Biomed. Eng. 1996, 43, 851–856. [Google Scholar] [CrossRef]
- Clark, G.A.; Ledbetter, N.M.; Warren, D.J.; Harrison, R.R. Recording sensory and motor information from peripheral nerves with Utah Slanted Electrode Arrays. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society 2011, Boston, MA, USA, 30 August–3 September 2011. [Google Scholar] [CrossRef]
- Nanivadekar, A.C.; Ayers, C.A.; Gaunt, R.A.; Weber, D.J.; Fisher, L.E. Selectivity of Afferent Microstimulation at the DRG Using Epineural and Penetrating Electrode Arrays. J. Neural Eng. 2019, 17, 016011. [Google Scholar] [CrossRef]
- Kent, A.R.; Grill, W.M. Model-based Analysis and Design of Nerve Cuff Electrodes for Restoring Bladder Function by Selective Stimulation of the Pudendal Nerve. J. Neural Eng. 2013, 10, 036010. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jayaprakash, N.; Song, W.; Toth, V.; Vardhan, A.; Levy, T.; Tomaio, J.; Qanud, K.; Mughrabi, I.; Chang, Y.-C.; Rob, M.; et al. Organ- and function-specific anatomical organization of vagal fibers supports fascicular vagus nerve stimulation. Brain Stimul. 2023, 16, 484–506. [Google Scholar] [CrossRef]
- Blanz, S.L.; Musselman, E.D.; Settell, M.L.; Knudsen, B.E.; Nicolai, E.N.; Trevathan, J.K.; Verner, R.S.; Begnaud, J.; Skubal, A.C.; Suminski, A.J.; et al. Spatially selective stimulation of the pig vagus nerve to modulate target effect versus side effect. J. Neural Eng. 2023, 20, 016051. [Google Scholar] [CrossRef]
- Dali, M.; Rossel, O.; Andreu, D.; Laporte, L.; Hernández, A.; Laforet, J.; Marijon, E.; Hagège, A.; Clerc, M.; Henry, C.; et al. Model Based Optimal Multipolar Stimulation Without a Priori Knowledge of Nerve Structure: Application to Vagus Nerve Stimulation. J. Neural Eng. 2018, 15, 046018. [Google Scholar] [CrossRef]
- Wang, Y.; Brand, J.; Liu, W. Stimulation Montage Achieves Balanced Focality and Intensity. Algorithms 2022, 15, 169. [Google Scholar] [CrossRef]
- Choi, A.-J.; Cavanaugh, J.; Durand, D. Selectivity of Multiple-contact Nerve Cuff Electrodes: A Simulation Analysis. IEEE Trans. Biomed. Eng. 2001, 48, 165–172. [Google Scholar] [CrossRef]
- Calvetti, D.; Wodlinger, B.; Durand, D.M.; Somersalo, E. Hierarchical Beamformer and Cross-talk Reduction in Electroneurography. J. Neural Eng. 2011, 8, 056002. [Google Scholar] [CrossRef] [PubMed]
- Chapman, C.R.; Aristovich, K.; Donega, M.; Fjordbakk, C.T.; Stathopoulou, T.-R.; Viscasillas, J.; Avery, J.; Perkins, J.D.; Holder, D. Electrode Fabrication and Interface Optimization for Imaging of Evoked Peripheral Nervous System Activity With Electrical Impedance Tomography (EIT). J. Neural Eng. 2018, 16, 016001. [Google Scholar] [CrossRef]
- Hines, M.L.; Carnevale, N.T. The NEURON Simulation Environment. Neural Comput. 1997, 9, 1179–1209. [Google Scholar] [CrossRef]
- McIntyre, C.C.; Richardson, A.G.; Grill, W.M. Modeling the Excitability of Mammalian Nerve Fibers: Influence of Afterpotentials on the Recovery Cycle. J. Neurophysiol. 2002, 87, 995–1006. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.D.; McIntyre, C.C. Quantifying the Neural Elements Activated and Inhibited by Globus Pallidus Deep Brain Stimulation. J. Neurophysiol. 2008, 100, 2549–2563. [Google Scholar] [CrossRef] [PubMed]
- Sundt, D.; Gamper, N.; Jaffe, D.B. Spike Propagation Through the Dorsal Root Ganglia in an Unmyelinated Sensory Neuron: A Modeling Study. J. Neurophysiol. 2015, 114, 3140–3153. [Google Scholar] [CrossRef]
- CVX Research, Inc. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0. 2011. Available online: http://cvxr.com/cvx (accessed on 11 May 2025).
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs, Recent Advances in Learning and Control (a tribute to M. Vidyasagar). In Lecture Notes in Control and Information Sciences; Blondel, V., Boyd, S., Kimura, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 95–110. [Google Scholar]
- Shannon, R.V. A model of safe levels for electrical stimulation. IEEE Trans. Biomed. Eng. 1992, 39, 424–426. [Google Scholar] [CrossRef] [PubMed]
- Lambrecht, J.M.; Cady, S.R.; Peterson, E.J.; Dunning, J.L.; Dinsmoor, D.A.; Pape, F.; Graczyk, E.L.; Tyler, D.J. A distributed, high-channel-count, implanted bidirectional system for restoration of somatosensation and myoelectric control. J. Neural Eng. 2024, 21, 036049. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).