TWISS: A Hybrid Multi-Criteria and Wrapper-Based Feature Selection Method for EMG Pattern Recognition in Prosthetic Applications

Abstract

This paper proposes TWISS (TOPSIS + Wrapper Incremental Subset Selection), a novel hybrid feature selection framework designed for electromyographic (EMG) pattern recognition in upper-limb prosthetic control. TWISS integrates the multi-criteria decision-making method TOPSIS with a forward wrapper search strategy, enabling subject-specific feature optimization based on a ranking that combines filter metrics, including Chi-squared, ANOVA, and Mutual Information. Unlike conventional static feature sets, such as the Hudgins configuration (48 features: four per channel, 12 channels) or All Features (192 features: 16 per channel, 12 channels), TWISS dynamically adapts feature subsets to each subject, addressing inter-subject variability and classification robustness challenges in EMG systems. The proposed algorithm was evaluated on the publicly available Ninapro DB7 dataset, comprising both intact and transradial amputee participants, and implemented in an open-source, fully reproducible environment. Two Google Colab tools were developed to support diverse workflows: one for end-to-end feature extraction and selection, and another for selection on precomputed feature sets. Experimental results demonstrated that TWISS achieved a median F1-macro score of 0.6614 with Logistic Regression, outperforming the All Features set (0.6536) and significantly surpassing the Hudgins set (0.5626) while reducing feature dimensionality. TWISS offers a scalable and computationally efficient solution for feature selection in biomedical signal processing and beyond, promoting the development of personalized, low-cost prosthetic control systems and other resource-constrained applications.

1. Introduction

The development of robust and adaptive systems for electromyographic (EMG) pattern recognition has become a key component in enhancing the performance of myoelectric prostheses and human–machine interfaces. EMG-activated prostheses enable individuals with limb loss to regain a significant degree of motor functionality by interpreting residual muscle signals, offering a technologically advanced and non-invasive alternative to traditional control methods. In particular, forearm EMG signals have been widely used in upper-limb prosthetic control due to their superficial accessibility and rich informational content [1,2,3]. Recent studies have also shown that deep learning models can generalize across subjects and conditions, even under scenarios involving electrode shifts or noisy acquisitions [4,5].

In recent years, various approaches have been proposed to enhance the accuracy of EMG pattern recognition, including deep learning models that integrate convolutional and recurrent neural networks. One example is the ConSGruNet architecture, which has reported classification accuracies exceeding 99% in multiclass tasks [6]. However, these strategies often require large training datasets, computationally demanding architectures, and frequent user-specific calibrations, which limit their applicability in low-cost, real-world settings. Increasing the number of EMG channels significantly improves classification accuracy and functional control in users with transradial amputation, underscoring the need for efficient and personalized Feature Selection (FS) methods suitable for real-world clinical environments [7]. Recent studies have proposed lightweight CNN-based and transformer-based models that retain high classification accuracy while lowering computational demands, enabling potential deployment in embedded or wearable systems [8,9,10]. Hybrid systems that combine EMG with functional electrical stimulation have also stabilized prosthetic control [11], but they demand additional infrastructure and still face challenges in efficient personalization.

Despite these advances, EMG systems remain constrained by high inter-user variability (e.g., physiology, electrode placement, fatigue), the non-stationary nature of EMG signals, and the need for FS strategies that balance accuracy, computational cost, and generalization [12,13,14]. These issues are critical in scenarios that require user-specific customization or limited computational resources, such as low-cost prostheses or portable systems. To address these issues, recent work has explored normalization strategies, feature disentanglement, and hybrid handcrafted–deep feature sets that enhance interpretability and cross-subject generalization [15,16]. These developments underscore the growing importance of Feature Selection (FS) in balancing performance, generalization, and computational efficiency in EMG-based systems.

FS is central to overcoming these demands, as it directly affects classifier accuracy, model interpretability, and computational feasibility. Traditionally, FS strategies have been categorized into filter methods, which evaluate features independently of the classifier using statistical or information criteria, and wrapper methods, which assess subsets of features based on model performance [17]. Filter methods are computationally efficient but can overlook interactions among features. In contrast, wrapper methods can achieve higher accuracy at an increased computational cost, especially in high-dimensional applications or those requiring user-specific customization [18,19]. Hybrid FS algorithms with evolutionary search (e.g., PSO, ACO, multi-objective genetic algorithms) have reported improvements in accuracy with reduced redundancy [20,21].

More recently, hybrid approaches have been proposed that combine the advantages of both methods, incorporating statistical techniques alongside heuristic optimization algorithms. For example, some studies have applied heuristics such as the Grey Wolf Optimizer or Simulated Annealing, successfully reducing dimensionality without compromising classification accuracy [22]. Recent work has also explored hybrid methods that combine clustering and metaheuristic search strategies, such as two-stage approaches using K-means and Cuckoo Search, which have demonstrated notable accuracy improvements in resource-constrained environments, including IoT and WSN applications [23]. Similarly, in biomedical contexts, feature selection methods integrating matrix rank theory with genetic algorithms have demonstrated the potential to reduce redundancy and optimize predictive performance without compromising accuracy [24]. Several studies also indicate that combining filter and wrapper strategies enables subject-tailored models, which is important in scenarios with high interindividual variability, such as transradial amputations [7]. Moreover, comprehensive reviews on the use of multi-criteria decision-making (MCDM) techniques in biomedical engineering have shown that, although methods such as TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) and AHP (Analytic Hierarchy Process) are widely adopted across various domains, their application in EMG feature selection remains limited [25].

Despite the widespread use of FS techniques in EMG signal analysis, no prior studies have been found that apply the TOPSIS method in this specific domain. Nevertheless, TOPSIS has been used in other machine learning and FS contexts. For instance, Singh et al. [26] applied a multi-criteria decision-making scheme based on TOPSIS to evaluate and compare different FS techniques on a network traffic dataset, considering multiple performance metrics. Assafo and Langendörfer [27] proposed a TOPSIS-assisted approach to prioritize features for anomaly detection in milling tools under varying operating conditions. Similarly, Chaudhuri and Sahu [28] developed a hybrid FS algorithm in which TOPSIS was used as a preliminary filter to reduce the feature set, which was subsequently optimized using the Binary Jaya wrapper algorithm. These examples indicate the potential of multi-criteria approaches, but direct application to EMG remains open.

To address this gap, this article presents a hybrid FS tool called TWISS (TOPSIS + Wrapper Incremental Subset Selection), which combines the multi-criteria ranking capability of TOPSIS with an incremental wrapper strategy with linear complexity. This tool enables the selection of feature subsets tailored to the user, aiming to support personalized, efficient, and cost-effective solutions. The method was validated using four subjects from the NinaPro DB7 dataset, and its performance was compared to reference approaches such as the Hudgins Feature Set and the full feature set (All Features), using the macro F1-macro score as the evaluation metric.

The main contribution of this work is a generalizable methodological framework and tool for FS that balances accuracy and computational feasibility, supporting accessible, user-adapted prosthetic control systems. By incorporating a multi-criteria method into the selection process, TWISS offers a promising alternative for advancing toward EMG interfaces that are more customized, scalable, and adaptable to users.

2. Materials and Methods

The proposed tool, named TWISS (TOPSIS + Wrapper Incremental Subset Selection), combines a feature selection (FS) scheme based on a multi-criteria decision-making approach, Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), with an incremental wrapper-based search strategy [29]. This design aims to optimize classifier performance while reducing the dimensionality of the feature set, enabling efficient adaptation to different users. 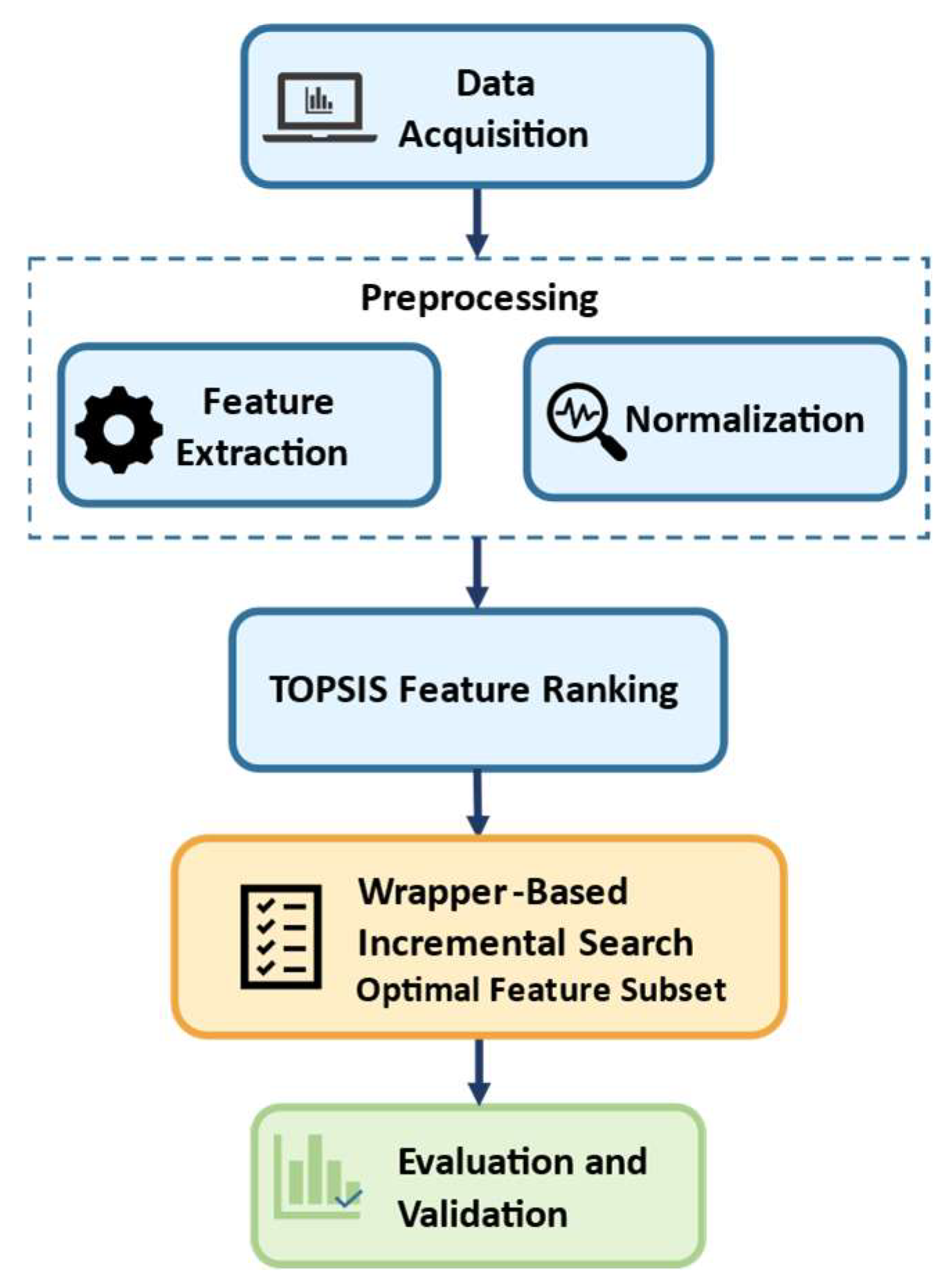Figure 1 illustrates the general methodological workflow of the proposed approach. For readability, acronyms are defined on first use and subsequently used throughout; see Abbreviations at the end of the manuscript.

2.1. Dataset Description

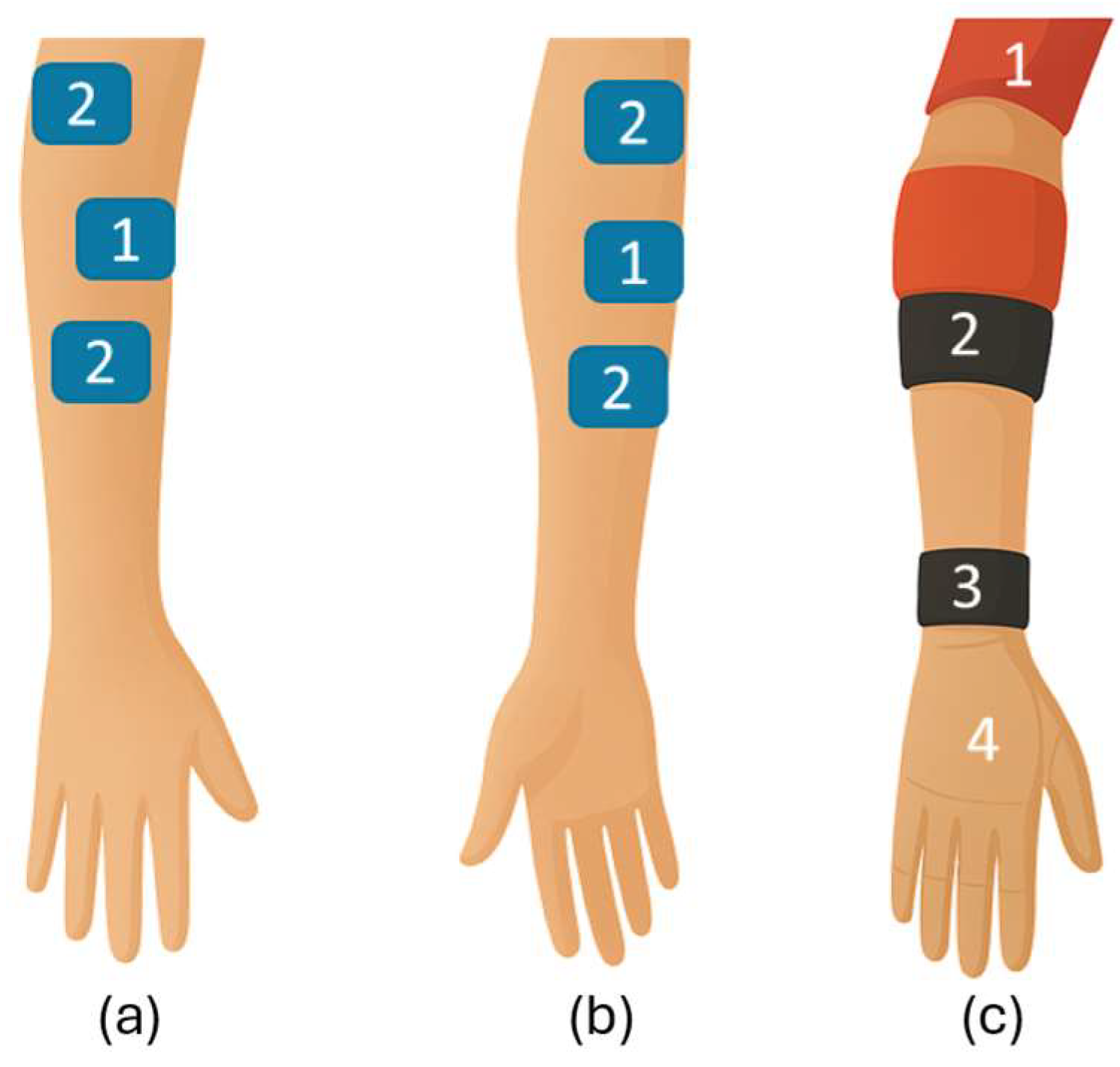
To validate the proposed tool, this study used the publicly available NinaPro DB7 [30], whose experimental protocol and data acquisition methodology are thoroughly described in [31]. This dataset is widely recognized in the literature for its quality and diversity of EMG recordings from both healthy individuals and transradial amputees. It contains surface electromyography (sEMG) signals acquired using 12 wireless Delsys Trigno IM sensors (Delsys Inc., Natick, MA, USA) strategically placed on the forearm, biceps, and triceps muscles, as shown in Figure 2, which was created by the authors, based on the anatomical configuration described in the Ninapro repository. These sensors simultaneously record EMG signals and motion data (accelerometer, gyroscope, and magnetometer), enabling anatomically accurate and high-density sampling. The sampling frequency for EMG channels is 2000 Hz. During the acquisition process, participants performed movements by following visual cues from instructional videos. Two main exercise protocols were executed: (1) basic finger and wrist movements, and (2) functional hand gestures and grasps.

Each movement was performed for 5 s, followed by a 3 s rest period, with 6 repetitions per gesture. The dataset comprises 22 subjects, including 20 healthy individuals and 2 transradial amputees. All movements were executed (or imagined, in the case of amputees) with the right hand. To preserve a subject-specific analysis, each subject’s recordings were processed independently.

Raw data files were downloaded in .mat (MATLAB R2024a) format and integrated into a processing routine developed in Python 3.9.12, using libraries such as NumPy, SciPy, and scikit-learn. Each file includes synchronized variables representing sEMG channels, inertial signals (accelerometer, gyroscope, and magnetometer), movement labels, and repetition identifiers.

2.2. Preprocessing and Feature Extraction

Preprocessing of EMG signals is essential for improving data quality and enabling robust feature extraction. In this study, preprocessing retained only the relevant data streams from NinaPro DB7 (12 sEMG channels from the emg key and labels from the restimulus key) and segmented the signals into 250 ms windows, transforming the input into a structure suitable for feature extraction in tsfresh.

A custom preprocessing strategy designed for this study was then implemented to enhance temporal representation and mitigate class imbalance caused by rest signals. Following Krasoulis et al. [31], who noted that balancing was achieved by discarding a large proportion of rest instances, the issue was addressed by removing portions of the overrepresented Rest segments near state transitions, while keeping Rest as a frequent label for classification. Based on the temporal indices i_x that delimit each rest segment, a new interval [j_x, j_x+1] was calculated using the following expression:

$$j_x=⌊i_x+{\displaystyle \frac{w_x(1-k)}{2}}⌋$$

(1)

$$j_{x+1}=⌈i_x+{\displaystyle \frac{w_x(1+k)}{2}}⌉$$

(2)

where w_x = i_x+1 − i_x represents the length of the rest segment, and k ∈ (0,1) is a contraction factor. The operators ⌊⋅⌋ and ⌈⋅⌉ denote the floor and ceiling functions, respectively (i.e., rounding down and rounding up to the nearest integer). This operation retains only the central portion of the rest interval, where the distinction from active contractions is most evident.

For example, consider a rest segment spans from i_x = 1000 to i_x+1 = 1200. Its length is w_x = 200. Using k = 0.5:

• j_x = ⌊1000 + 200(1 − 0.5)/2⌋ = ⌊1000 + 50⌋ = 1050
• j_x+1 = ⌈1000 + 200(1 + 0.5)/2⌉ = ⌈1000 + 150⌉ = 1150

Thus, the reduced rest interval is [1050, 1150], preserving only the central 100 samples (50% of the original segment).

The percentages of rest data removed for each subject were as follows: 94.48% (S1), 93.50% (S2), 95.61% (S21), and 96.65% (S22). After this reduction, a balanced distribution of samples per class was achieved. The total number of segments analyzed per subject was: Subject 1 = 4010, Subject 2 = 4321, Subject 21 = 3815 and Subject 22 = 3815.

Feature extraction was performed on each 250 ms window using 16 descriptors across 12 channels. The time-domain metrics included mean absolute value (MAV), waveform length (WL), zero crossings (ZC), slope sign changes (SSC), fourth-order autoregressive coefficients (AR(4)), variance (VAR), root mean square (RMS), and Willison amplitude (WAMP). The frequency-domain metrics included mean frequency (MNF), median frequency (MDF), peak frequency (PKF), and mean power (MNP). These features are thoroughly described in [32] and were implemented in Python using the TSFRESH library [33], supplemented with custom functions. The final descriptor set was selected after reviewing fifteen related studies to identify the most frequently used metrics, with some of them absent from the original library, which were specifically programmed and integrated into an extended version of TSFRESH.

2.3. Proposed Method: TWISS

The proposed TWISS tool combines the multi-criteria decision-making technique TOPSIS with an incremental wrapper-based approach, aiming to select feature subsets that maximize classification performance while maintaining low computational cost. This method first ranks features according to their relevance using TOPSIS, and then incrementally incorporates those that contribute to performance improvement based on classifier feedback. The full implementation, configuration files, and public Google Colab tools developed for this study are openly available in the TWISS Public Info repository [34], enabling replication or adaptation to other datasets.

2.3.1. Feature Evaluation Matrix

To assess the individual contribution of each of the 192 extracted attributes, a decision matrix D ∈ ℝ^n×m was constructed, where n = 192 is the number of features and m = 3 represents the evaluation criteria:

• Chi-squared: tests dependence between a non-negative feature and the class label.
• Mutual Information (MI): measures shared information between variables.
• Analysis of variance (ANOVA) F-test: assesses significant differences among group means.

2.3.2. Application of the TOPSIS Method

TOPSIS was applied to rank the features based on their relative closeness to the ideal solution. The procedure included the following steps:

• Normalization of the feature matrix D, using vector normalization:

$$r_{ij}={\displaystyle \frac{d_{ij}}{\sqrt{\sum _{i=1}^n{\left(d_{ij}\right)}^2}}},i=1,\dots ,m;j=1,\dots ,n$$

(3)

• Weighting of the criteria: Equal weights were assigned to the three criteria in this study to avoid introducing subjective bias in the absence of prior evidence favoring any single metric, providing a transparent and reproducible baseline. The tool also supports user-defined weights with automatic normalization for problem-specific prioritization when justified by domain knowledge.
• Identification of the ideal solution A⁺ and anti-ideal solution A⁻:

$$A^{+}=\left\{max\left(r_{ij}\right) for benefit criteria;min\left(r_{ij}\right) for cost criteria\right\}$$

(4)

$$A^{-}=\left\{min\left(r_{ij}\right) for benefit criteria;max\left(r_{ij}\right) for cost criteria\right\}$$

(5)

• Computation of the Euclidean distance to the ideal and anti-ideal solutions.

$$S_i^{\pm }=\sqrt{\sum _{j=1}^m{(r_{ij}-A_j^{\pm })}^2}$$

(6)

• Calculation of the relative closeness index C_i.

$$C_i={\displaystyle \frac{S_i^{-}}{S_i^{+}+S_i^{-}}}$$

(7)

After applying the method, the features were sorted in descending order according to their C_i values, resulting in a multi-criteria ranking.

2.3.3. Wrapper-Based Incremental Selection

Once the features were ranked by their C_i index, an incremental selection procedure was applied. To ensure robustness, a stratified hold-out validation strategy was used: 80% for training and 20% for testing for each subject (S1, S2, S21, and S22). This split preserved the class distribution, ensuring that the test set remained representative of the overall dataset. The main performance metric was the F1_macro, defined as:

$${F1}_{macro}={\displaystyle \frac{1}{K}}\sum _{k=1}^K{\displaystyle \frac{2\times {Precision}_k\times {Recall}_k}{{Precision}_k+{Recall}_k}}$$

(8)

Starting with the highest-ranked feature, one feature was added at a time, and the classifier’s performance was evaluated using stratified 4-fold cross-validation on the training data. Every time a classifier was trained, a grid search strategy was included in the training process to ensure optimization at each step of the cross-validation. The optimal feature subset was defined as the point at which adding new features no longer yielded a significant improvement in the average F1-macro score or when the target maximum number of features was reached, which served as the stopping criterion. This strategy aimed to balance classification performance and computational efficiency.

2.3.4. Real-Time Consideration

TWISS performs feature selection offline during the calibration stage. Once the subject-specific subset is obtained, online operation only requires standard feature extraction and classification over short analysis windows. Therefore, the selection step does not introduce per-window latency at run time.

2.4. Classifier and Experimental Validation

2.4.1. Classifiers

To evaluate the performance of the feature subsets selected by TWISS, two classifiers were compared: Logistic Regression (LR) and Linear Discriminant Analysis (LDA). LR was selected for its simplicity, interpretability, and strong performance on low-dimensional datasets, aligning with the goal of reducing computational complexity. LDA was also considered but showed less favorable results in this setting.

2.4.2. Cross-Validation and Evaluation Metrics

Each score distribution from the 4-fold cross validation was evaluated according to the research questions. The evaluations use the nonparametric Scott–Knott ESD test (NPSK) [35] and Mann–Whitney U tests, along with the Jaccard index. The NPSK test groups medians into statistically distinct, non-overlapping clusters by maximizing significant between-group differences while keeping within-group differences negligible (non-significant), using non-parametric statistics.

This step produces performance rankings of the techniques, presented in graphs and tables. These evaluations are carried out for different study subgroups, meaning possible combinations or breakdowns of one or more of the following categories:

a. Subject under study.

b. Classifier used.

c. Number of features used.

The results obtained with TWISS were compared with two reference approaches:

• Hudgins features set: a classical EMG feature set including MAV, ZC, SSC, and WL (48 features: 4 per channel, 12 channels).
• All Features: the complete set including MAV, WL, ZC, SSC, AR (order 4), VAR, RMS, WAMP, MNF, MDF, PKF, and MNP (192 features: 16 per channel, 12 channels) without dimensionality reduction.

Additionally, TWISS represents a methodological improvement over the authors’ previous developments, which employed artificial neural networks and single-channel sEMG acquisition systems for real-time pattern recognition in transradial prosthetic applications [36]. Although those systems achieved high accuracy using a small set of time-domain features, TWISS introduces a more generalizable and efficient FS strategy, scalable to multichannel recordings and adaptable to different subjects.

2.5. Comparative FS Methods

To assess the performance of the proposed TWISS method, multiple feature selection (FS) algorithms spanning filter, wrapper, and hybrid categories were implemented and compared, establishing baselines for evaluating the effectiveness of the multi-criteria hybrid approach. Three filter methods were considered, Chi-squared (χ²), Mutual Information (MI), and Analysis of Variance (ANOVA), implemented via scikit-learn functions in Python within a custom classification module (selector.py). Each method produces a feature ranking based on its statistical criterion and selects the top n features accordingly. Their inclusion is motivated by widespread use in prior studies, low computational cost, and solid statistical underpinnings [37,38]. In addition, a TOPSIS-based filter was included; by integrating multiple metrics, it operates as a hybrid approach.

On the other hand, wrapper and hybrid strategies were considered. The classic wrapper algorithm selected was Sequential Forward Selection (SFS) with search-space complexity O(n²) for worst case scenario, while the hybrid variants implemented an IWSS strategy. Lastly, the proposed TWISS method was included as a hybrid variant guided by the multi-criteria ranking produced by the TOPSIS-based Filter.

Table 1. Evaluated FS methods and their underlying principles.

Method Type	Method Name	Label Used	Main Principle	Search-Space Complexity
Static	Hudgins set	hudgins	Expert-defined fixed set	NA
Static	All Features set	all	Full feature set	NA
Filter	Chi-Squared Filter	filter_chi2	Statistical dependence (χ2 test)	O (1)
Filter	MI Filter	filter_mutual_information	Information theory (joint entropy)	O (1)
Filter	ANOVA Filter	filter_anova	Mean difference (F-statistic)	O (1)
Filter	TOPSIS Filter	filter_topsis	Hybrid MCDM	O (1)
Wrapper	SFS	forward	Iterative wrapper	O (n2)
Hybrid	IWSS + Chi-Squared Ranking	iwss_chi2	Incremental search guided by χ2 ranking	O (n)
Hybrid	IWSS + Mutual Information Ranking	iwss_mutual_information	Incremental search guided by MI ranking	O (n)
Hybrid	IWSS + ANOVA Ranking	iwss_anova	Incremental search guided by ANOVA ranking	O (n)
Hybrid	TWISS (TOPSIS + Wrapper)	twiss	Multi-criteria (TOPSIS-based) + Incremental search	O (n)

summarizes the evaluated methods, the labels used throughout the article, and the statistical or heuristic principle underlying each one.

Finally, to isolate the contribution of each stage, the comparative analyses are conducted as an ablation under the same evaluation protocol and matched subset sizes. Four configurations are considered: (i) Filter-only (Chi-squared, Mutual Information, or ANOVA ranking) without the incremental wrapper, with search-space complexity O(1); (ii) IWSS (incremental wrapper selection guided by a single criterion, one of Chi-squared, Mutual Information, or ANOVA) with complexity O(n); and (iii) TWISS (TOPSIS-based ranking followed by an incremental wrapper selection) with complexity O(n). Unless otherwise stated, ablation results are reported with the F1-macro score, using LR and LDA classifiers and subset sizes of 48 (and 24 for the reduced setting).

2.6. Integration and Configuration of the TWISS Tool

A total of eleven FS techniques were evaluated, including two static reference approaches (Hudgins and All Features, described previously) and nine dynamic methods (filter, wrapper, and hybrid types), whose foundations are summarized in Table 1. To ensure a fair comparison, common subset sizes of 24 or 48 features were defined for all dynamic techniques, and standardized labels were used throughout the study to facilitate identification. To facilitate the use of the proposed method, an interactive tool was developed in Google Colab. This tool allows users to upload datasets in CSV format, configure algorithm parameters, and execute the complete FS process.

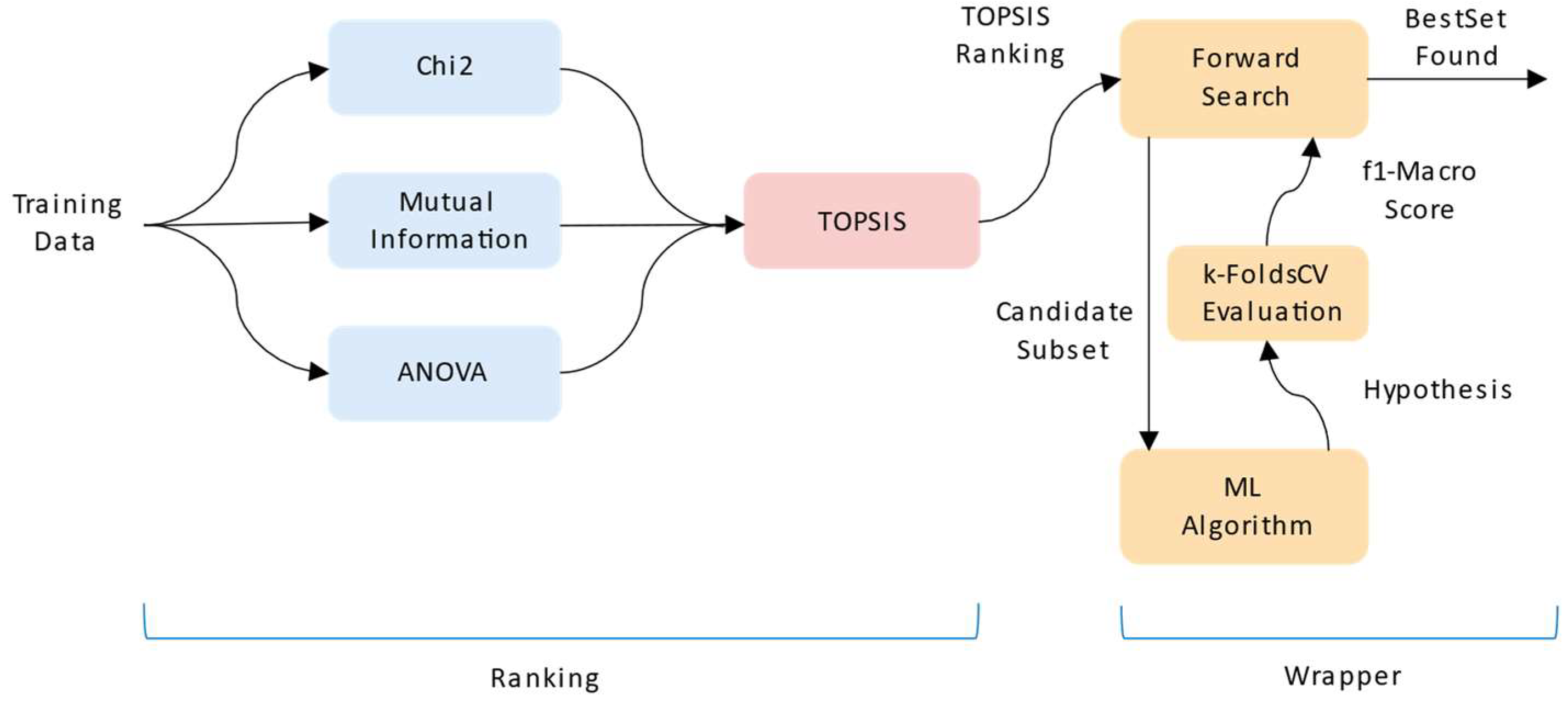
Figure 3 presents a detailed overview of the TWISS workflow. The process begins with the application of three filter-based metrics (Chi-squared, MI, and ANOVA), whose results are combined using TOPSIS to generate a multi-criteria ranking. Based on this ranking, a forward incremental search is performed, evaluating the addition of each feature through 4-fold cross-validation with a selected classifier and a grid search strategy. At each iteration, the F1-macro score is calculated, and the selected feature subset is updated if an improvement is detected. The process continues until a stopping criterion is met, either based on a maximum number of features or stagnation in performance. Algorithm 1 presents TWISS in pseudocode, combining a single TOPSIS-based ranking (Chi-squared, MI, ANOVA) with a ranking-guided forward wrapper evaluated via 4-fold cross-validation; inputs, outputs, and optional controls (ε, maximum features, stopping rule) are specified for reproducibility.

Algorithm 1: Pseudocode of the TWISS method

Inputs: X ∈ ℝ^{n×p}//training features (n samples, p features) y//training labels $ℳ$//set of feature-quality criteria for the filter (e.g., MI, χ2, ANOVA, etc.) 𝓛//base learner used by the wrapper J(·)//performance metric (e.g., AUC, F1). ε ≥ 0//minimal improvement threshold (default ε = 0) max_feats//optional cap on selected features (default max_feats = p) stop_rule//optional stopping rule (e.g., no improvement for m steps)

Outputs: S_included//selected feature subset History//list of (feature, wrapper_score) evaluations

Procedure: 1:  S_included ← ∅ 2:  S_excluded ← {1, 2, …, p} 3:  best_score ← 0//baseline for the first step 4:  History ← ∅ 5:  //One-off filtering: rank features with TOPSIS using criteria in $ℳ$ 6:  scores ← FILTER_TOPSIS(X, y, S_excluded, $ℳ$)//one score per feature in S_excluded 7:  R ← features in S_excluded sorted by scores (desc)//best → worst 8:  for each f in R do 9:      S_cand ← S_included ∪ {f} 10:      s ← WRAPPER_SCORE(X[:, S_cand], y; learner = 𝓛, metric = J)//e.g., CV estimate 11:      History ← History ∪ {(f, s)} 12:      S_excluded ← S_excluded \ {f} 13:    if s > best_score + ε then 14:      S_included ← S_cand 15:      best_score ← s 16:    end if 17:    if |S_included| = max_feats or stop_rule(History, S_included, S_excluded) then 18:      break 19:    end if 20:  end for 21:  return S_included, History

The implemented tool, shown in Figure 4, enables the configuration of multiple parameters: dataset file selection, target column specification, enable/disable individual metrics (Chi-squared, MI, and ANOVA), weight assignment to each metric (from 0.0 to 1.0), classifier selection (LDA or LR), and the maximum number of features to select. Additionally, it allows users to run the entire process using either example data or their own customized datasets. The input must be structured in a tabular format, with each row representing a sample and columns corresponding to features and the target label.

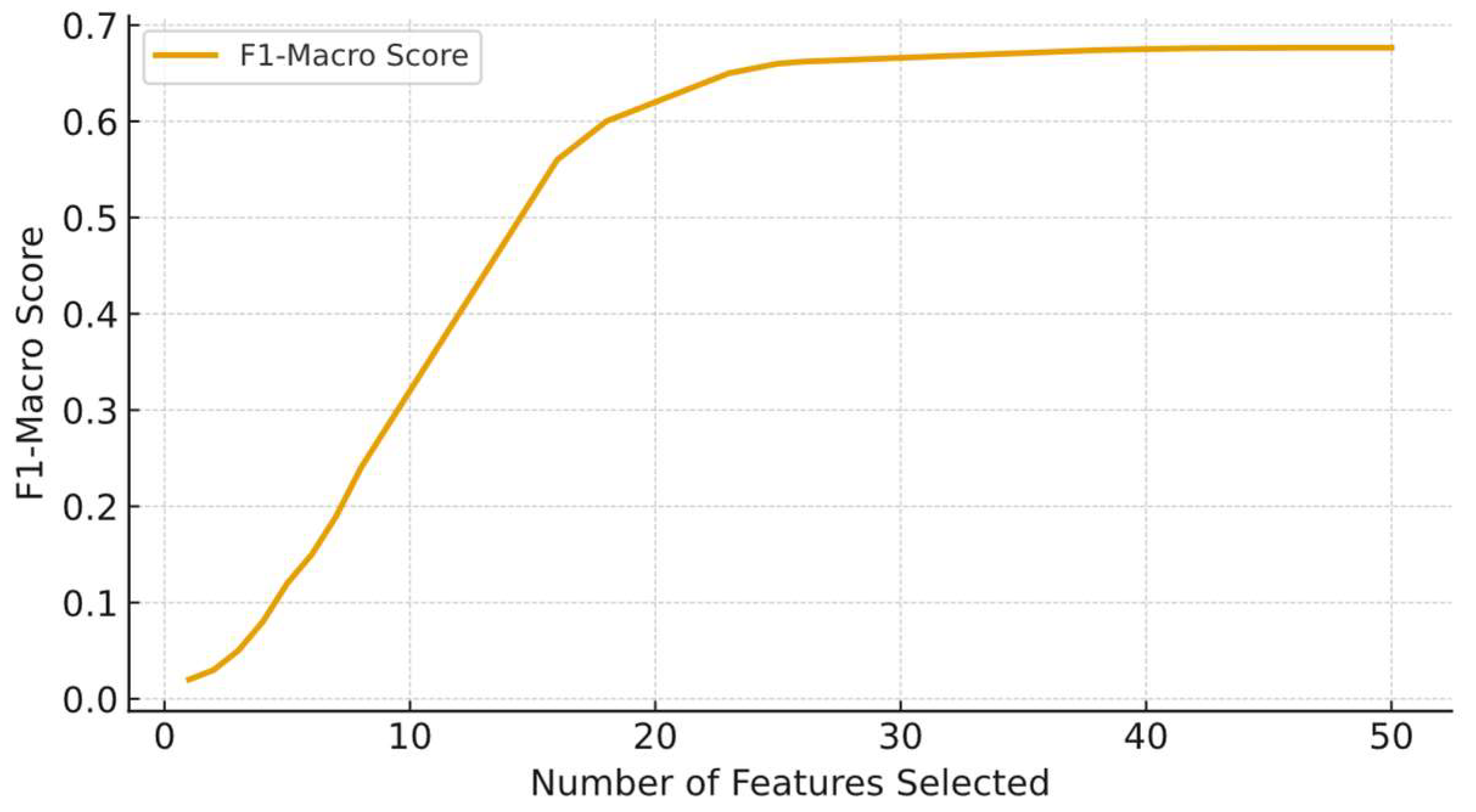
During execution, the tool provides detailed feedback at each iteration. It reports the feature being evaluated, the corresponding F1-macro, the decision to accept or reject it, and the cumulative number of selected features. Upon completion, a summary is presented, including the optimal subset, the final performance score, execution time, and a historical performance graph, as shown in Figure 5. Additionally, a downloadable JSON file is generated containing the selected features ranked by quality.

3. Results and Discussion

3.1. General Performance of FS Techniques

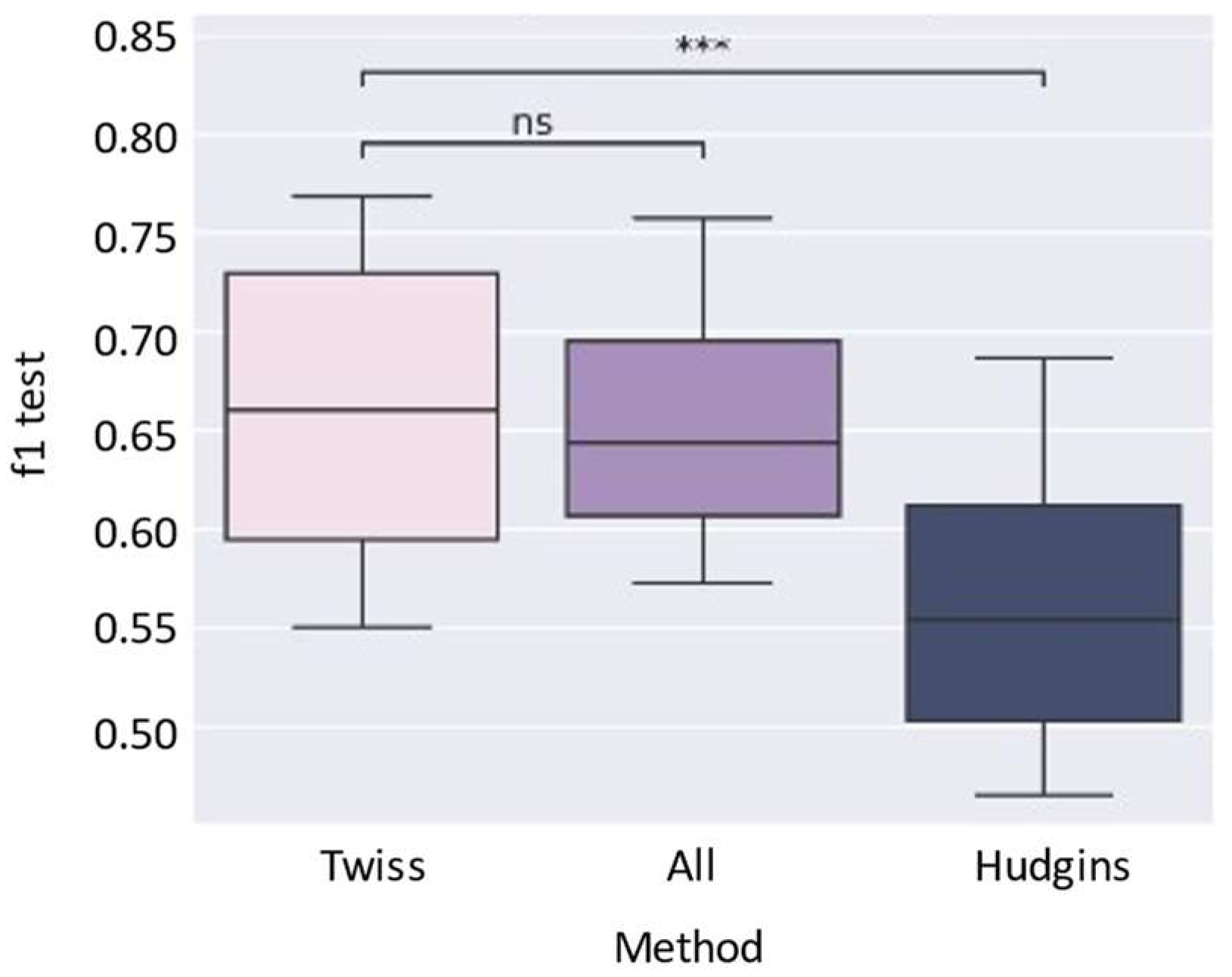
To assess the overall performance of the proposed algorithm, TWISS was compared against two widely used static approaches: Hudgins and All Features. In this initial comparison, the LR classifier was used, and the number of selected features was fixed at 48 for all methods.

Figure 6 provides a summary of the overall performance using boxplots for each technique. The symbols indicate significance levels: ns means p > 5 × 10⁻² (not significant), while * (1 × 10⁻² < p ≤ 5 × 10⁻²), ** (1 × 10⁻³ < p ≤ 1 × 10⁻²), *** (1 × 10⁻⁴ < p ≤ 1 × 10⁻³), and **** (p ≤ 1 × 10⁻⁴) all indicate significant differences. These conventions are used consistently throughout the paper, specifically in Figure 6, Figure 7, Figure 8 and Figure 9.

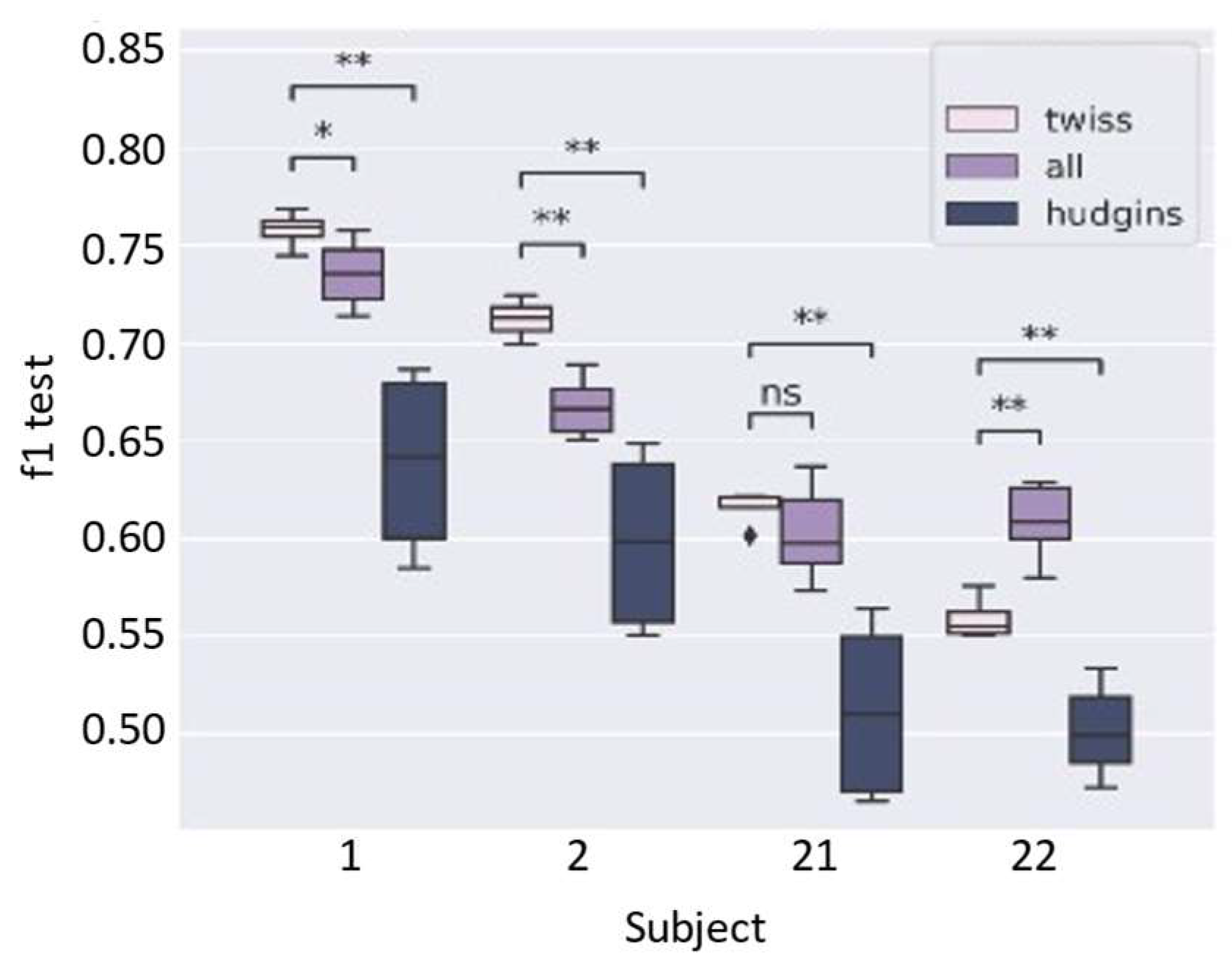
TWISS achieves a higher median F1-macro test score. This trend is confirmed when analyzing the performance per subject (Figure 7), where TWISS outperforms the other techniques in 3 out of the 4 evaluated subjects. These findings are quantitatively summarized in

Table 2. Performance of TWISS (48 features) and static methods (All Features and Hudgins) using the LR classifier per subject. The highest score per subject is highlighted in green.

Subject	Method	F1-Macro Test
		Mean	Std. Dev.
1	All	0.7353	0.0161
	Hudgins	0.6392	0.0454
	TWISS	0.7583	0.0101
2	All	0.6669	0.0138
	Hudgins	0.5979	0.0454
	TWISS	0.7124	0.0106
3	All	0.6036	0.0231
	Hudg0069ns	0.5114	0.0442
	TWISS	0.6160	0.0098
4	All	0.6084	0.0191
	Hudgins	0.5017	0.0217
	TWISS	0.5589	0.0118

, where TWISS shows the best average scores for Subjects 1, 2, and 21. In the case of Subject 22, although the All Features approach yields slightly better performance, TWISS still shows competitive results, outperforming Hudgins in all cases. Notably, TWISS exhibits the lowest variance across subjects, indicating more consistent performance.

Under the same evaluation protocol and matched subset sizes (48 selected features, LR classifier), static baselines (All Features, Hudgins) yield lower global F1-macro than the wrapper-based configuration. In contrast, TWISS leverages the multi-criteria ranking to guide the wrapper and attains the highest global F1-macro while also reducing variance across subjects (Figure 6 and Figure 7 and Table 2). The consolidated results are summarized in

Table 3. Summary at 48 selected features (LR). Global macro F1-macro averaged over Subjects 1, 2, 3, and 4.

Configuration	F1-Macro (LR, 48 Features)
Static set—All Features	0.654
Static set—Hudgins	0.563
TWISS	0.661

, which reports the global macro F1-macro at 48 features (LR) for the three ablation configurations.

The difference between techniques was also statistically validated using the Mann–Whitney U test (two-sided). In Figure 6, the difference between TWISS and Hudgins is shown to be highly significant, whereas no statistically significant differences were found between TWISS and All Features. These findings support that TWISS successfully reduces the total number of features while maintaining or improving performance compared to traditional approaches.

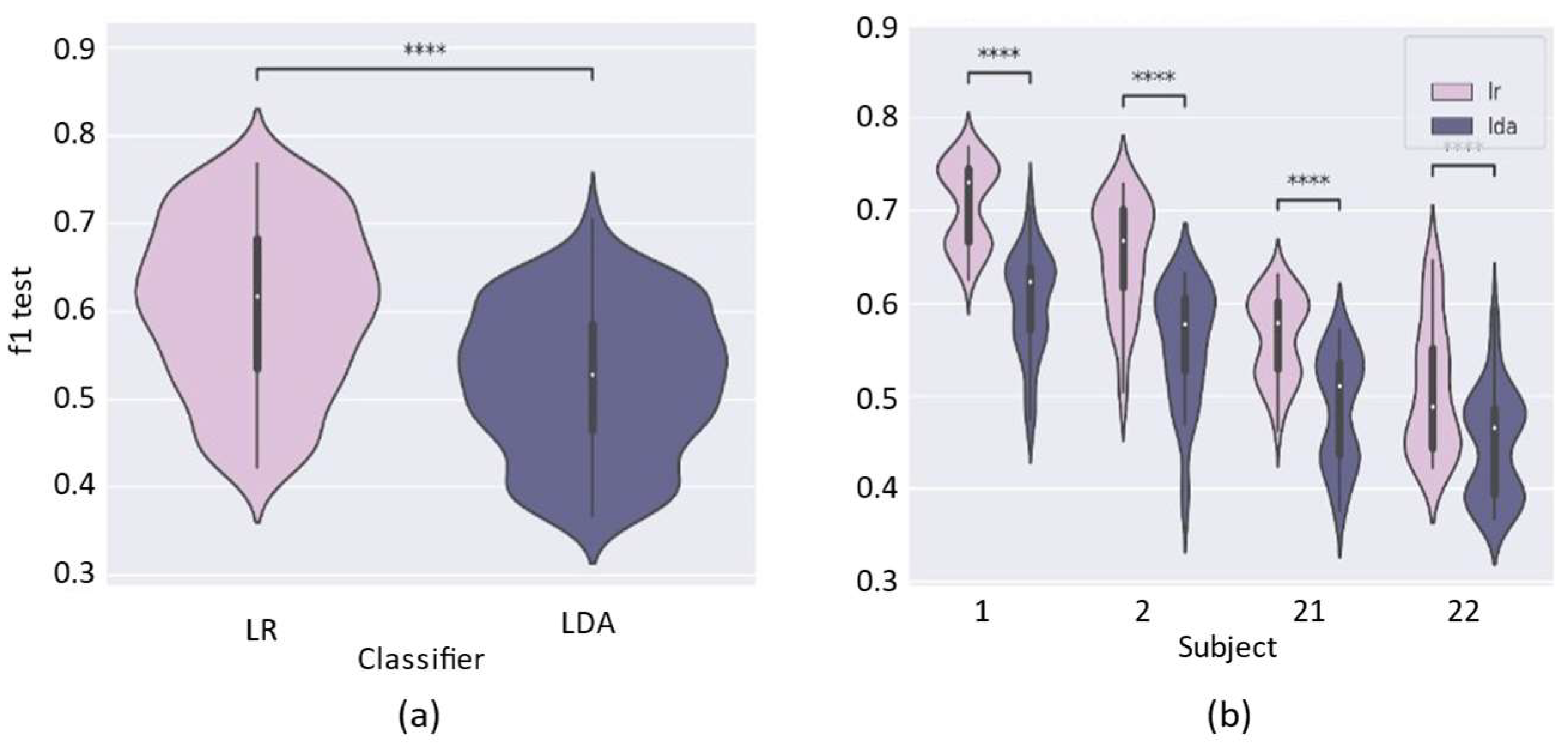
Figure 8a presents the overall performance of TWISS for both classifiers. A consistently better performance is observed when using LR compared to LDA, and this difference is statistically significant under the adopted protocol. As shown in Figure 8b, this trend holds across all subjects, reinforcing the decision to adopt LR as the base classifier for the main experiments.

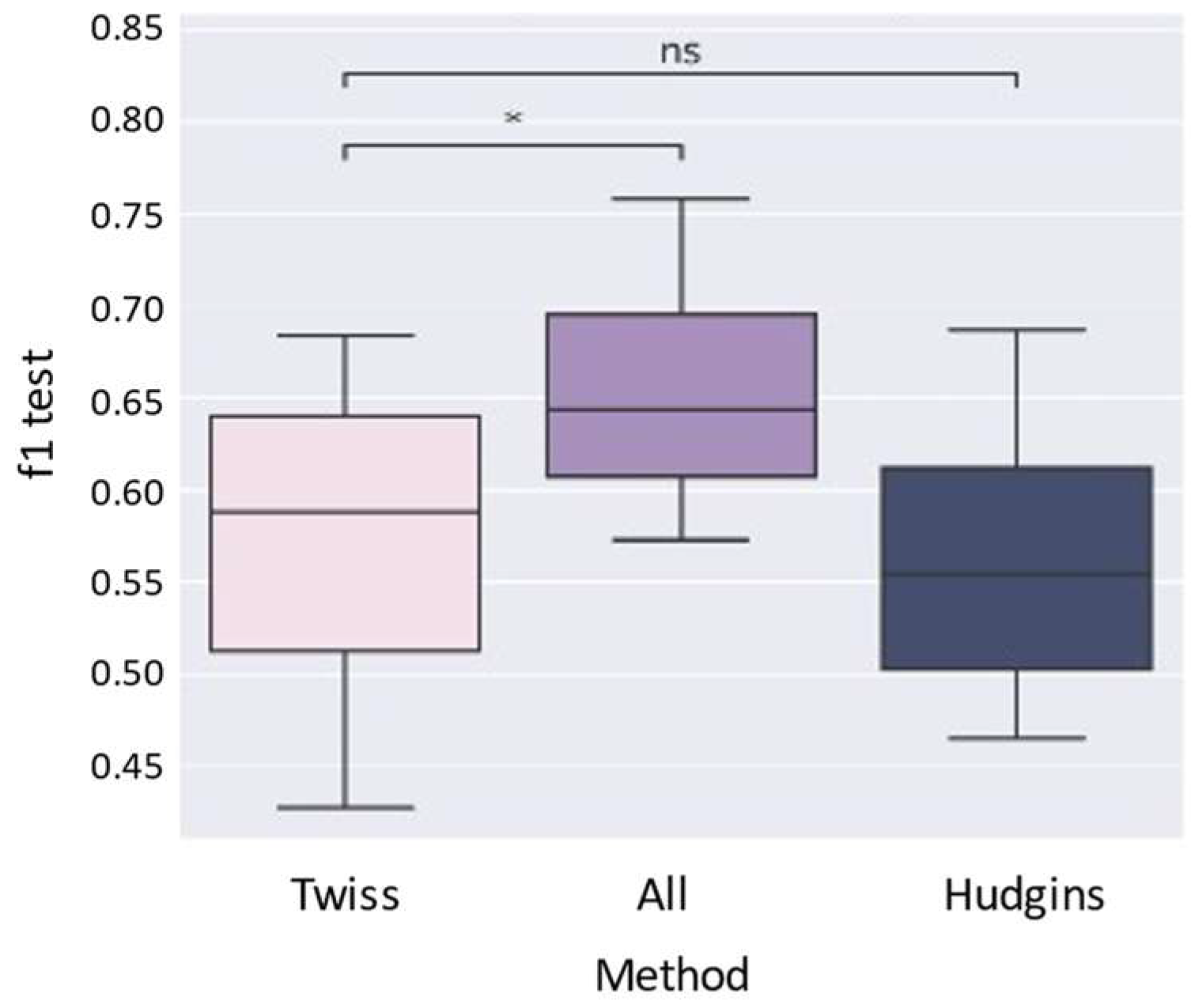
Finally, Figure 9 shows the comparative analysis with 24 selected features. While TWISS still outperforms Hudgins, All Features achieves better global performance in this setting. However, since All Features uses 192 features, TWISS remains preferable in contexts where effective dimensionality reduction is required without sacrificing accuracy.

3.2. Overall Comparison of TWISS Performance Against Other Dynamic FS Techniques

For a broader comparison, the performance of TWISS was evaluated against nine dynamic FS techniques, including filter, wrapper, and hybrid methods, along with the All Features baseline and the Hudgins set. These techniques are described in Table 1. The analysis was conducted using NPSK, a fixed subset size of 48 features and two classifiers: LR and LDA. The results for each classifier are summarized in Figure 10 and Figure 11, respectively.

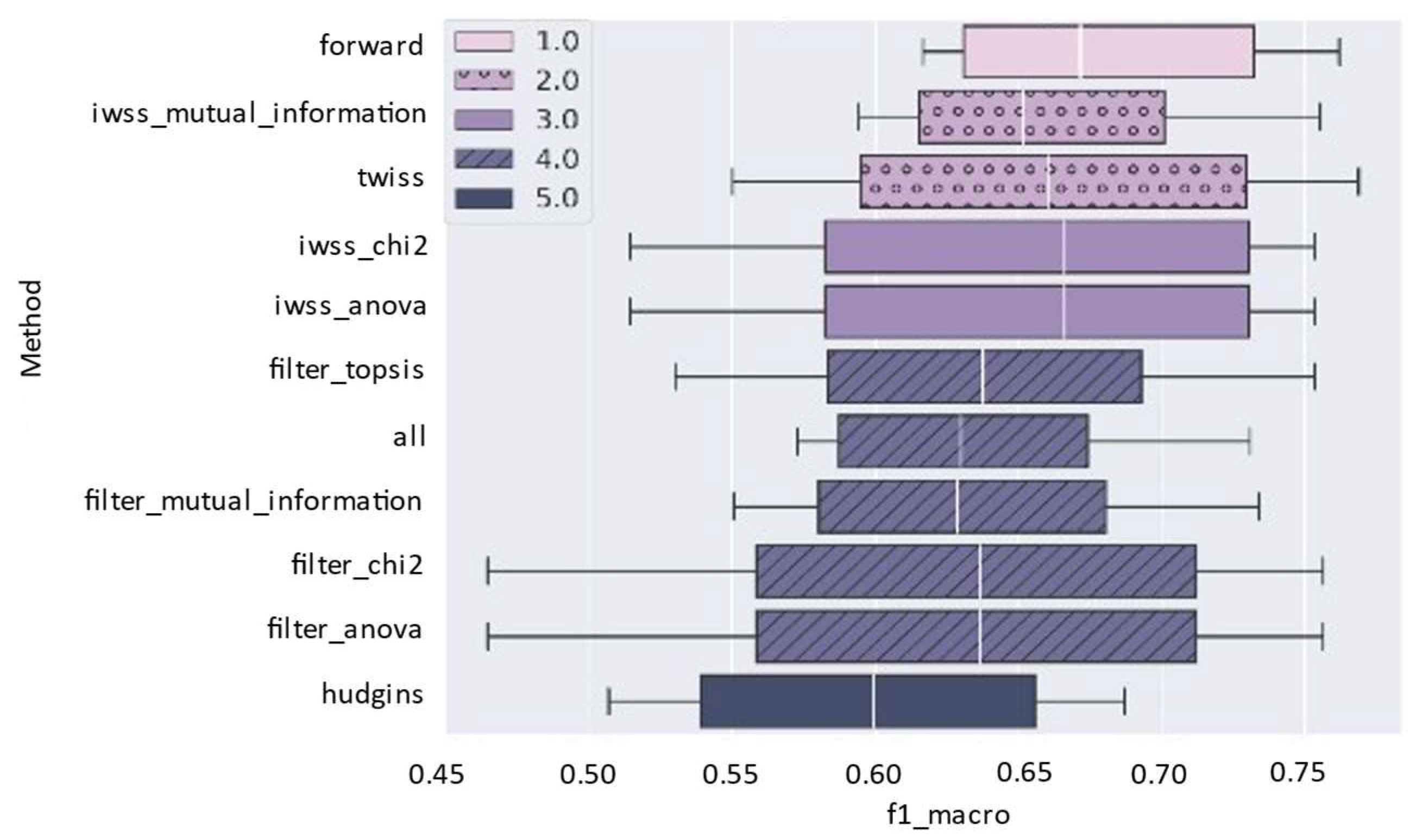
As shown in Figure 10, when using the LR classifier, the SFS method (labeled forward in the plot) achieved the highest average performance, followed by the hybrid approaches IWSS + Mutual Information Ranking and TWISS. In this setting, TWISS consistently ranked among the top-performing methods, with average F1-macro scores around 0.66, outperforming all filter techniques, as well as the full feature set (All Features). This behavior suggests that combining multi-criteria strategies with an incremental wrapper-based approach can enhance the selection of relevant features, offering an effective trade-off between accuracy and dimensionality.

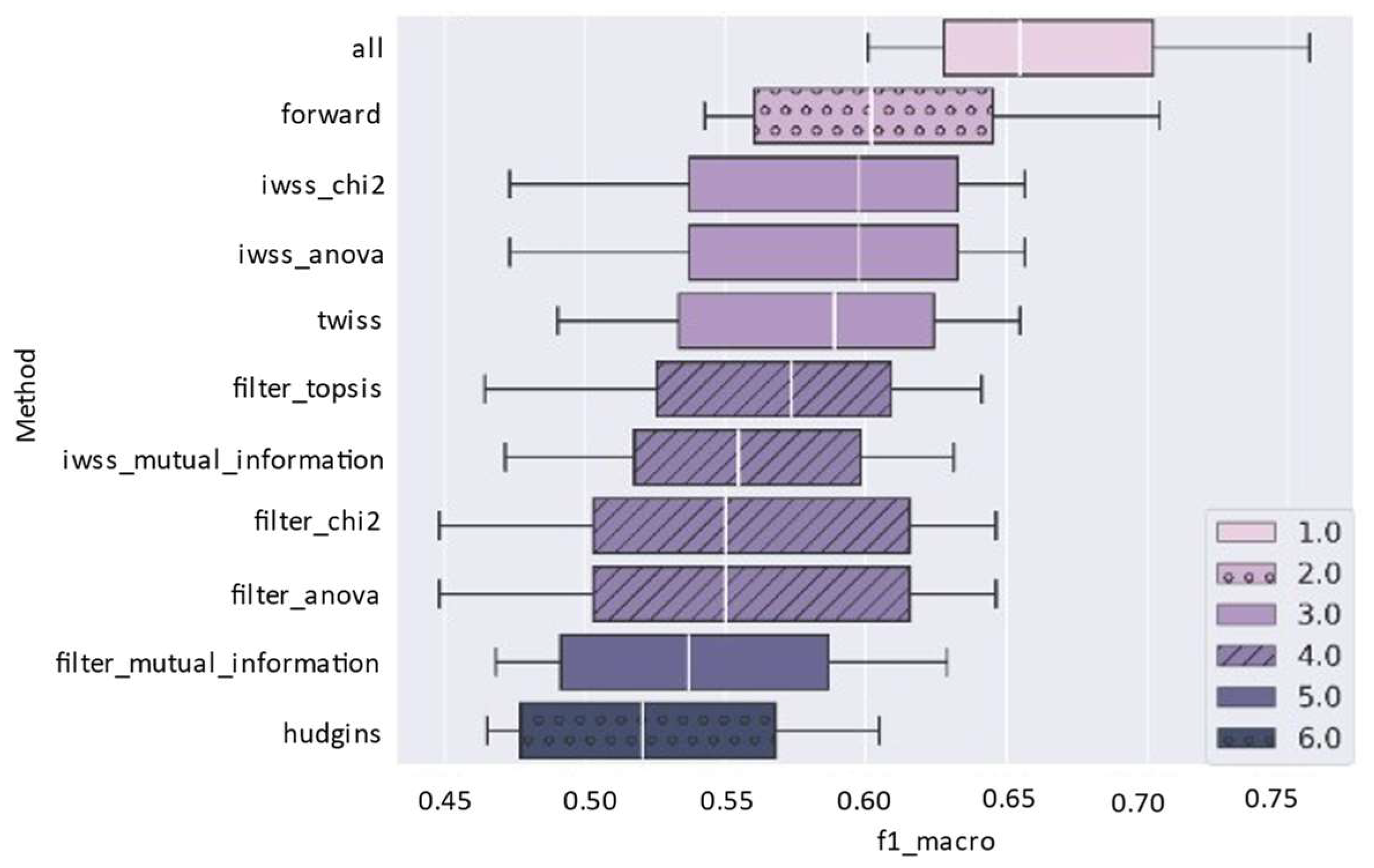
With the LDA classifier (Figure 11), the overall ranking changed slightly: although All Features achieved the highest average performance and SFS ranked second, TWISS remained competitive, ranking third, outperforming most filter-based methods and some hybrid approaches. These results suggest that TWISS maintains its robustness across different classifiers, although its advantage over other techniques may vary depending on the nature of the classifier used. This finding highlights LDA’s robustness: its mechanism of maximizing class separability reduces dependence on FS. However, as Figure 8 suggests, it can be suboptimal because other models may benefit more from FS, ultimately yielding better results. Finally, given its poor performance in Figure 10 and Figure 11, the Hudgins feature set is not recommended. The results indicate that alternative feature selection methods would likely be more effective.

Overall, these results are consistent with the ablation perspective: Filter-only approaches provide the lowest average F1-macro at 48 features, Wrapper-only (SFS) improves over filters but at a high search cost, and TWISS, guided by the multi-criteria ranking, remains among the top performers across classifiers while using substantially fewer evaluations than SFS. This supports the complementary roles of the ranking stage and the incremental wrapper in TWISS.

While performance is important, computational cost is also a key consideration.

Table 4. Paired t-test comparison of execution times (in minutes) between TWISS and other methods (n = 8).

Technique	Mean (min)	Std Dev (min)	p-Value	Failed to Reject Null Hypothesis
filter_anova	0.0002	0.0000	0.0017	Yes
filter_chi2	0.0036	0.0024	0.0019	Yes
filter_mutual_information	0.0559	0.0183	0.0078	Yes
filter_topsis	0.0530	0.0081	0.0071	Yes
forward	19.7018	17.7315	0.0079	Yes
iwss_anova	0.1891	0.1812	0.3406	No
iwss_chi2	0.1923	0.1818	0.3572	No
iwss_mutual_information	0.2988	0.2816	0.9163	No
TWISS	0.2855	0.2088	1.0000	No

shows a comparison of the average execution times (in minutes) and their standard deviations for each technique, based on 8 repetitions. As expected, filter-based methods yielded significantly lower times (e.g., filter_anova with 0.0002 min) compared to hybrid methods such as TWISS (0.2855 min) and SFS was the slowest.

These results support the conclusion that TWISS offers a strong compromise between predictive accuracy and computational efficiency. While some filter-based methods achieve faster execution times, TWISS consistently ranks among the top-performing techniques in terms of classification performance, maintaining practical runtimes suitable for real-world applications.

3.3. Cross-Subject Generalization Analysis

To assess the generalization capability of the features selected by TWISS, a cross-subject analysis was performed by training classifiers with data from one individual and evaluating their performance with data from another.

Table 5. Average F1-macro scores for all cross-subject pairs using an LR classifier trained on data from Subject X with 48 features selected by TWISS from Subject Y with statistical significance determined by paired t-tests.

Features from Subject	Subject 1	Subject 2	Subject 21	Subject 22
Subject 1	0.7583	0.7124 (=)	0.6160 (=)	0.6160 (>)
Subject 2	0.7586 (=)	0.7020	0.6304 (=)	0.6304 (>)
Subject 21	0.7259 (<)	0.6920 (<)	0.6130	0.6130 (>)
Subject 22	0.6770 (<)	0.6172 (<)	0.5962 (=)	0.5962

Symbols denote: (<) significant decrease, (>) significant increase, (=) no significant difference.

presents the average macro F1-macro score obtained for each possible training–testing combination, using a set of 48 features selected by TWISS for each subject. This analysis allows identifying whether the extracted features are representative and transferable across different individuals.

The notation in Table 5 indicates whether the difference between each cross-subject configuration and the baseline condition is statistically significant, based on paired t-tests. Main-diagonal cases indicate training and testing on the same subject. Specifically:

• (<) denotes a statistically significant decrease in performance compared to the original subject’s features.
• (>) denotes a statistically significant increase in performance.
• (=) indicates no statistically significant difference.

The results show that most cross-subject combinations exhibit a significant decrease or equal performance compared to using features from the same subject (diagonal of the table). For instance, feature from Subject 1 with training data from Subject 2 yields an F1-macro score of 0.7124, slightly higher than the same-subject baseline (0.7020), with no statistically significant difference. However, in cases where subjects present greater morphological differences or dissimilar myoelectric patterns, such as when using features from Subject 21 or 22 to train a model for Subject 2, statistically significant drops in performance are observed. Interestingly, features from Subjects 1 and 2 led to significantly higher performance when tested on Subject 22, suggesting the existence of transferable features in some directions.

Table 6. Jaccard index comparing the similarity between the feature sets of size 48 generated for each subject and the static Hudgins set.

Feature Set From	Subject 1	Subject 2	Subject 21	Subject 22	Hudgins
Subject 1	1.0000	0.3913	0.2973	0.2000	0.2308
Subject 2	0.3913	1.0000	0.3151	0.2468	0.2468
Subject 21	0.2973	0.3151	1.0000	0.2152	0.2632
Subject 22	0.2000	0.2468	0.2152	1.0000	0.2152
Hudgins	0.2308	0.2468	0.2632	0.2152	1.0000

complements this analysis by presenting the Jaccard index values computed between the sets of features selected for each subject. This index quantifies the similarity between subsets, enabling an assessment of how consistently TWISS selects common features. The low values obtained between subject pairs (e.g., 0.2000 between Subject 1 and Subject 22) indicate that TWISS tends to select subject-specific feature subsets, likely reflecting the inter-subject variability inherent to EMG signals. Nevertheless, the overlap suggests that certain robust features are consistently selected. Jaccard index values below 0.40 for most subject pairs reaffirm that TWISS adapts its FS to the specific characteristics of each subject.

Together, these results indicate that TWISS effectively identifies informative and subject-specific feature subsets, capturing individual myoelectric patterns with precision. Although variability across subjects leads to differences in performance and feature composition, the method also reveals certain transferable features that hold potential for cross-subject applications. These findings suggest that TWISS provides a solid foundation for personalized classification systems and could be further enhanced through strategies such as inter-subject normalization or adaptive modeling to improve generalizability. These cross-subject findings align with the ablation analysis, in which the wrapper stage refines the multi-criteria ranking into subject-specific subsets while preserving a core of transferable features.

3.4. TWISS Performance with 24 Features

In addition to the analysis conducted with 48 features, the performance of TWISS was evaluated under a reduced subset scenario comprising 24 selected features. This analysis is particularly relevant in contexts where reducing computational complexity is essential without substantially compromising classification performance. As shown in Figure 9, TWISS with 24 features outperformed the static Hudgins set and remained competitive with All Features when using the LR classifier.

Although a slight decrease in average F1-macro score was observed compared to the 48-feature configuration, TWISS maintained a strong performance profile. The statistically significant improvement (p < 0.05) over Hudgins further underscores the benefits of dynamic FS over static approaches.

Overall, these findings confirm that TWISS effectively retains the most informative features even under strict subset size constraints. Its ability to sustain high classification performance while reducing dimensionality supports its suitability for real-world applications where computational resources are limited and operational efficiency is a priority.

4. Conclusions

This study proposed a novel hybrid FS method—TWISS (TOPSIS + Wrapper Incremental Subset Selection)—which incorporates the TOPSIS multi-criteria decision-making technique as a ranking mechanism within the FS process for EMG signals. To the best of our knowledge, this integration has not been previously explored in this domain, representing both a methodological and practical contribution to the field of biomedical signal analysis.

Through a systematic evaluation against nine methods, TWISS demonstrated a consistent balance between classification accuracy and time complexity, thereby enhancing dimensionality reduction efficiency. The method achieved high macro F1-macro scores across two different classifiers (LR and LDA), outperforming traditional filter techniques and proving competitive with other hybrid or SFS approaches. Moreover, TWISS maintained competitive performance even when the number of selected features was reduced to 24, confirming its suitability for resource-constrained applications. The cross-subject generalization analysis revealed the customization of the feature subsets.

However, the lowest performance was generally observed in amputee subjects, which can be explained by the lower quality of their signals, as they must imagine movements that are unnatural for their amputated limb. Therefore, a more in-depth study is needed to enhance signal quality, allowing results to be comparable to those obtained from healthy subjects. Therefore, deeper study is needed to improve signal quality so that results become comparable to those obtained from healthy subjects.

Future work includes validating TWISS with nonlinear classifiers, such as support vector machines (SVMs), random forest (RF), and gradient boosting, as well as incorporating additional filter-based metrics into the multi-criteria framework. Additionally, it will analyze the impact of different weight configurations in the TOPSIS decision scheme, including the use of domain-informed criteria. Further efforts could also evaluate the method’s robustness under real-world operating conditions, such as electrode displacement, motion artifacts, and cross-session or cross-dataset variability. Although TWISS has not been tested in an embedded system, the feature sets used in this study are commonly applied in real-time EMG pattern recognition and have been successfully implemented in interactive control systems. Future work could explore the integration of TWISS into real-time pipelines on embedded platforms to assess its feasibility and performance under strict timing constraints.