Abstract
In this paper a novel adaptive rapidly-exploring random trees algorithm based on cross-entropy optimization (CE-RRT) is proposed. We seek to provide a low-cost, fast, and effective solution for path planning of robots in various complex environments. Firstly, an adaptive sampling strategy is introduced to make the search directional. Then, an adaptive step adjustment strategy is proposed to improve the search efficiency of the algorithm. Finally, the cross-entropy algorithm is introduced to optimize redundant nodes in feasible paths and improve path quality. In order to verify the feasibility and effectiveness of the proposed algorithm, it is used to solve path planning problems in two two-dimensional environments and one three-dimensional environment. The RRT and RRT* algorithms are used as benchmarks to measure the effectiveness of the three optimization strategies. The simulation demonstrates that the proposed CE-RRT algorithm can effectively improve search efficiency and path quality. Particularly (path shortened by 26%, 22.70%, and 49.11%), the CE-RRT algorithm exhibits stronger robustness in three-dimensional environments. In addition, the proposed CE-RRT algorithm can be used to plan a reasonable path for the dual robot based on the dual Sawyer simulation platform.
1. Introduction
The motion planning problem is an important research topic in the field of robots, encompassing mobile robots and manipulators [1]. Motion planning for robots refers to planning a collision-free path within their working environment [2]. In most work scenarios involving robots, including but not limited to robot navigation [3], industrial automation [4], and autonomous vehicles [5], the performance of motion planning algorithms is of great significance. Within the robot workflow, it is crucial for them to efficiently and quickly plan a viable path once they have identified the tasks they need to perform. Therefore, the research on the robot motion planning algorithm has been continuously and extensively concerned.
Robot motion planning algorithms are mainly divided into three categories: graph-based search algorithms, sampling-based algorithms, and intelligent biomimetic path planning algorithms. The commonly used graph-based search algorithms include Dijkstra’s algorithm, the A* algorithm [6], and the D* algorithm [7], etc. These methods build maps containing known environment and obstacle information and then use graph theory to find a feasible path from start to goal in discrete space. They can certainly identify the optimal path if it exists. However, their computational efficiency is low when maps are complex, making them unsuitable for path planning in high-dimensional spaces. Intelligent bionic planning algorithms primarily include neural networks [8], genetic algorithms [9], ant colony optimization [10], and so on. These algorithms can enable robots to achieve some autonomy and intelligence in complex, unknown environments. However, they require lengthy search times and are prone to local extremum, with difficulties in parameter tuning.
Sampling-based path planning algorithms mainly include probabilistic roadmap (PRM) [11,12] and rapidly-exploring random trees (RRT) [13] algorithms, and their variables are based on random sampling rather than discretizing the configuration space [14]. These methods construct a set of trajectories by iteratively adding random samples, and the probability of finding a solution is 100% when the number of iterations approaches infinity. They have higher search efficiency and can be used to solve high-dimensional path planning problems. In addition, they can effectively handle path planning problems with non-holonomic constraints. However, the solutions obtained by these algorithms are not optimal and often worse, requiring further optimization. Moreover, PRM is often inefficient when the geometric shape of the obstacle is not a priori known.
Consequently, the simple and efficient characteristics of the RRT algorithm have made it widely popular and attracted the attention of numerous researchers. A series of improvement measures have been proposed; they can be divided into unidirectional and multi-directional based on the expansion direction of the random tree. In terms of one-way random tree expansion, Kalisiak et al. [15] proposed a new variation of the RRT planner, which demonstrates good performance in both loosely constrained and highly constrained environments. Ichnowski et al. [16] presented a parallel RRT (PRRT) for feasible and optimal motion planning designed for modern multicore CPUs. For the shortage of RRT, Karaman et al. [17] proposed the RRT* algorithm with asymptotic optimality and added random geometry and pruning optimization theory based on the RRT node to ensure the nodes can converge to the current optimal value. In terms of multi-directional random tree expansion, Lavalle et al. [18] proposed bi-directional random tree (bi-RRT) for path planning of high-dimensional manipulators. The RRT-connect [19] introduced the greedy expansion idea based on bi-RRT and sets cyclic expansion in the target random tree to speed up the connection speed of dual random tree nodes. The RRT algorithm has undergone long-term development and has achieved many research results. However, there remains a certain gap between the feasible path and the optimal path, and further research is still needed.
The cross-entropy (CE) algorithm is a new heuristic algorithm for studying stochastic optimization problems in recent years [20]. The core idea of the CE algorithm is to find the predicted distribution that is the same or closest to the true distribution through a certain random process [21]. It is particularly suitable for solving optimization problems with continuous variables, and it has lower computational complexity and stronger robustness compared with other intelligent optimization algorithms [22,23]. Therefore, combining the CE algorithm with the RRT algorithm to fully leverage their advantages is a direction worth exploring.
Motivated by the aforementioned discussion, the purpose of this paper is to propose a CE-RRT algorithm by combining the CE algorithm with the RRT algorithm for more efficient and excellent path planning. The main contribution of the work is summarized as follows:
- (1)
- An adaptive RRT algorithm based on cross-entropy optimization (CE-RRT) is proposed by introducing three improved strategies. Firstly, an adaptive sampling strategy is introduced to make the search directional. Secondly, an adaptive step adjustment strategy is proposed to improve the search efficiency of the algorithm; it can adaptively adjust the growth step based on obstacle information. Thirdly, a path smoothing method is introduced to reduce redundant nodes in the path, and then the CE algorithm is used to optimize the smoothed path and improve its quality.
- (2)
- A two-dimensional maze environment, a two-dimensional cluttered environment, and a three-dimensional environment are used to test the CE-RRT algorithm. The RRT algorithm is used as a benchmark to measure the effectiveness of the three proposed optimization strategies. The simulation results show that adaptive sampling and adaptive step adjustment strategies can effectively increase the search speed of the algorithm, and the CE algorithm can also significantly improve path quality.
The article consists of five sections, including the introduction (Section 1). Section 2 defines the motion planning problem and provides a more detailed introduction to the RRT algorithm and CE algorithm. Section 3 proposes the CE-RRT algorithm, and performance tests are shown in Section 4. Section 5 presents a dual robot welding path planning simulation experiment. Section 6 briefly describes the obtained results and future works.
2. Background
This section defines the motion planning problem and provides a more detailed introduction to the RRT algorithm and CE algorithm. These algorithms form the basis of the proposed CE-RRT algorithm.
2.1. Problem Definition
Define as the configuration space, as the obstacle area, and as the closed area between and , where d is the dimension of the configuration space, or the degree of freedom of the robot. defines a path planning problem, where is the initial state and is the goal region. Once the path point reaches the interior of the goal region , it can be considered as reaching the goal state. The schematic diagram in two-dimensional configuration space is shown in Figure 1. Based on the above explanation, the definitions of collision-free path, feasible path planning, and optimal path planning are as follows:
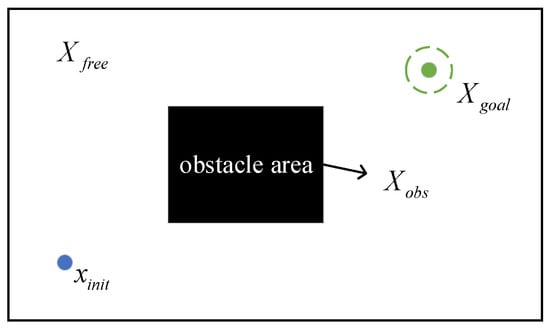
Figure 1.
Path planning in two-dimensional configuration space.
Definition 1.
(Collision-free path): Define a bounded continuous changing function as a path. A path is collision-free, if .
Definition 2.
(Feasible path planning): For a given path planning problem , feasible path planning is to find a feasible path such that is collision-free, , and .
Definition 3.
(Optimal path planning): For a given path planning problem , optimal path planning is to find a feasible path that minimizes the cost such that , where is the cost function of path f.
2.2. RRT Algorithm
The RRT algorithm is a sampling-based path planning algorithm, and its main process is shown in Algorithm 1. The known input information includes environment information , initial state , goal state (region) , growth step , and maximum number of iterations . The feasible path from to is output. Firstly, initialize the random tree and add the initial node to . Then, repeat steps 3~15 until a feasible path is found or the maximum number of iterations is reached. In each iteration of the algorithm, a node is randomly generated from the collision-free area (step 4), and then the node closest to is found on the random tree (step 5). Next, starting from , a new node is generated along the direction from to with a step size (step 6). In step 7, the generated path is performed to collision detection. If no collision occurs, output flag s = 0 and add the new node to the random tree . In steps 11~14, when the new node reaches the goal area , the path planning ends and outputs the feasible path f found, and the loop ends.
On the basis of the above description, the RRT algorithm has the following possible drawbacks. Firstly, the search direction of the algorithm is determined by a random node , it is completely random and lacks a certain direction guidance mechanism, this can easily lead to the waste of computing resources. Secondly, the growth step is fixed, and a too small can significantly reduce computational efficiency, while a too large can easily cause collisions, lacking a mechanism for adaptive adjustment of the step with the environment. In addition, the paths generated by the RRT algorithm often have significant differences from the optimal path, and existing smoothing operations are mostly based on greedy strategies, lacking global optimization capabilities. Therefore, it is necessary to propose a series of improvement strategies to improve these shortcomings.
| Algorithm 1: RRT algorithm |
| Input: The environment information, The initial state of the robot, The goal region of the robot |
| Maximum number of iterations, growth step |
| Output: Feasible path f |
| 1 |
| 2 |
| 3 for to do |
| 4 Randomly generated in |
| 5 |
| 6 |
| 7 |
| 8 if (, no collision) then |
| 9 |
| 10 end if |
| 11 if (arrived ) then |
| 12 |
| 13 break |
| 14 end if |
| 15 end for |
| 16 Return: |
2.3. CE Algorithm
The core idea of the CE algorithm is to find the predicted distribution that is the same or closest to the true distribution through a certain random process, mainly using a normal distribution. The traditional CE algorithm is listed in Algorithm 2 [24]. Firstly, the appropriate initial and are selected for the normal distribution based on the range of variable values (steps 1~2). At the beginning, a larger value can be selected for sigma, allowing the normal distribution to have a larger search range. It indicates that the predicted distribution is very close to the true distribution when converges to a very small value (steps 4~5). Then the main loop started until . In each iteration, N samples are generated based on normal distribution (step 6), and their corresponding fitness values are calculated (step 7). After sorting the fitness values (step 8), samples with lower fitness are selected as elite samples for parameter updating and the next iteration (steps 10~12). When the algorithm reaches the termination criteria, the mean of the approximate optimal solutions is output as the optimization result.
| Algorithm 2: CE optimization algorithm | |
| Input: Initial mean , variance , sample size N, elite sample rate , smoothing coefficient | |
| Output: Mean of generation t | |
| 1 | Randomly generate a rational number |
| 2 | Randomly generate a rational number |
| 3 | , () represents rounding down |
| 4 | , |
| 5 | while do |
| 6 | Generate N samples based on normal distribution |
| 7 | Calculate fitness function values |
| 8 | |
| 9 | Select individuals with smaller fitness |
| 10 | Parameter updating: , |
| 11 | Smoothing operation: , |
| 12 | |
| 13 | end while |
| 14 | Return: |
3. The Proposed CE-RRT Algorithm
This section introduces the proposed CE-RRT algorithm, including the main process and algorithm details.
3.1. Main Procedure of the Proposed CE-RRT Algorithm
The main procedure of the proposed algorithm is described in Algorithm 3; this framework is proposed based on the RRT algorithm. Firstly, initialize the random tree , add the initial node to , and initialize the collision flag s, where s = 0 indicates that the newly generated path is collision-free. Then, repeat steps 4~17 until a feasible path is found or the maximum number of iterations is reached. In step 18, a path smoothing method is used to process the feasible path f and reduce redundant nodes in f. Then use the CE algorithm to optimize the smoothed path and obtain the optimal feasible path . Aiming at the shortcomings of the RRT algorithm, three improvement strategies are proposed in CE-RRT. Firstly, an adaptive sampling strategy is proposed; it adds a sampling direction guidance mechanism to solve the problem of low solving efficiency caused by random sampling (step 5). Secondly, an adaptive step size adjustment strategy is introduced to improve the problems of low solving efficiency or easy collision caused by fixed step (step 7). Thirdly, a path smoothing method is used to smooth feasible paths f and reduce redundant nodes (step 18); then, the CE algorithm is used to optimize the smoothed path and obtain a feasible path with higher quality (step 19). In the next section, the proposed improvement strategies are described in detail.
| Algorithm 3: CE-RRT algorithm | |
| Input: , iterations , initial step , sampling probability , step increments and | |
| Output: The optimal path from to | |
| 1 | |
| 2 | , collision sign, no collision |
| 3 | for to do |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | if (, no collision) then |
| 10 | |
| 11 | end if |
| 12 | if (arrived ) then |
| 13 | |
| 14 | break |
| 15 | end if |
| 16 | end for |
| 17 | |
| 18 | |
| 19 | Return: |
3.2. Details of Improvement Strategies
This section explains the details of the three proposed improvement strategies.
3.2.1. Adaptive Sampling Strategy
In the RRT algorithm, the generation of random point is completely random without any specific directional guidance. This will cause many sampling points to be wasted and reduce the search efficiency of the algorithm. Therefore, a sampling strategy with directional guidance is introduced; it can adaptively adjust the sampling direction based on obstacle information . The details of this sampling strategy are listed in Algorithm 4.
Firstly, the sampling flag r is assigned a value in steps 1~10, when r = 1, sampling with a direction-guided mechanism is performed, and when r = 2, random sampling is performed. In steps 3~7, the direction sampling is selected with probability at the i-th iteration, when the nodes generated by the previous generation do not collide. In steps 8~10, random sampling must be selected when collides. This demonstrates the adaptability of the proposed sampling strategy (steps 3~10). Then, adaptive sampling is performed in steps 11~15, when r = 1, , the random tree grows toward the goal area; when r = 2, a new is randomly selected from . It should be noted that if the random tree keeps growing towards the goal area, it is easy to fall into a local extremum when encountering obstacles. The existence of probability can avoid this problem to a certain extent.
The probability for directional sampling was determined through systematic experimentation. We tested values across the range [0.1, 0.9] in the 2D and 3D environments. The results show that = 0.7 consistently provided the best balance between directed exploration (improving search speed) and maintaining sufficient randomness to avoid local minima and ensure robustness in diverse environments.
| Algorithm 4: | |
| Input: , collision sign s, adaptive sampling probability | |
| Output: Random node | |
| 1 | if (, no collision) then |
| 2 | Generate a random number from [0, 1] |
| 3 | if then |
| 4 | |
| 5 | else |
| 6 | |
| 7 | end if |
| 8 | else |
| 9 | |
| 10 | end if |
| 11 | if then |
| 12 | |
| 13 | else |
| 14 | Randomly generated in |
| 15 | end if |
| 16 | Return: |
3.2.2. Adaptive Step Adjustment Strategy
For a given path planning problem , the growth step of the random tree is fixed when using the RRT algorithm for solving. When the size is small, it is easy to increase the solving time and reduce the solving efficiency; when the size is large, it is easy to cross smaller obstacles, making it difficult to find a feasible path. Therefore, an adaptive step adjustment strategy is introduced to reach the goal region faster. The strategy increases the step when there are fewer obstacles and decreases the step when there are more obstacles. The specific details are listed in Algorithm 5. The basic idea of this strategy is relatively simple. When the node of the previous generation is a valid node without collision, the step size of the current generation is increased to approach the goal area faster (step 2). When the node is an invalid node, that is, it collides with an obstacle, the current step is reduced to facilitate local search near the obstacle and find a feasible path (step 4). In addition, step variation and are determined based on specific problems.
The step size adjustment factors Δε1 (increase factor) and Δε2 (decrease factor) were determined through systematic experimentation across the tested environments. We evaluated and on the 2D and 3D environments. The chosen values ( = 0.2, = 0.1) consistently demonstrated optimal performance by balancing rapid expansion toward the goal when obstacles are sparse ( = 0.2) with fine-grained navigation in cluttered regions to avoid collisions ( = 0.1). This asymmetry ( > ) reflects the empirical observation that accelerating expansion in open spaces yields greater efficiency gains than reducing steps during collisions, while maintaining overall robustness across diverse environments.
| Algorithm 5: | |
| Input: , , step variation , collision sign s | |
| Output: | |
| 1 | if (, no collision) then |
| 2 | |
| 3 | else |
| 4 | |
| 5 | end if |
| 6 | Return: |
3.2.3. Path Optimization Strategy Based on CE Algorithm
The feasible path f obtained based on the RRT algorithm often contains many path points, which is not convenient for direct optimization by using the CE algorithm. Therefore, a path smoothing method is first used to remove redundant path points of path f; then, the CE algorithm is used to optimize the smoothed path and obtain the optimized path .
- (1)
- Path smoothing method
The specific details of the path smoothing method are shown in Algorithm 6. Firstly, initialize the smooth path . Then, loop iterations are performed in steps 2~23 until the termination condition is met. In each iteration, n is the number of nodes on the feasible path f, and steps 4~19 are specific smoothing operations. When there is no collision between two nodes and on path f, the length of the straight path is l1; in steps 9~11, the length of the path f between nodes and is obtained as l2. In steps 12~14, when l1< l2, it means that the straight path is better; the path points between and can be removed, and these nodes are stored in the set dp. All the path points that may be removed are stored in the set dp after the loop operation of steps 4~16. Subsequently, duplicate elements in the set dp are removed (step 17), and the path nodes contained in the set dp are deleted from the path f. In steps 20~22, the smooth path is updated after conditional judgment, and one iteration ends here. Finally, when there are no nodes that can be deleted on the path f, the algorithm stops iterating and outputs the smoothed path .
| Algorithm 6: | |
| Input: , feasible path f | |
| Output: The smoothed path | |
| 1 | |
| 2 | while do |
| 3 | , |
| 4 | for to do |
| 5 | for to do |
| 6 | |
| 7 | if (, no collision) then |
| 8 | |
| 9 | for to do |
| 10 | |
| 11 | end for |
| 12 | if then |
| 13 | |
| 14 | end if |
| 15 | end if |
| 16 | end for |
| 17 | Remove duplicate elements |
| 18 | |
| 19 | end for |
| 20 | if then |
| 21 | |
| 22 | end if |
| 23 | end while |
| 24 | Return: |
- (2)
- Path optimization method based on CE algorithm
The specific process of the path optimization method based on the CE algorithm is shown in Algorithm 7. Taking the two-dimensional path planning problem as an example, the smooth path can be mathematically represented as a matrix of size , where n is the number of path points. Considering the path length L as the optimization objective, an optimization problem is established:
where f is a feasible path and is a path point on f, , L is the length of path f.
In Algorithm 7, firstly, the smooth path is used as the initial value of the optimization path , and the variance parameter of the CE algorithm is initialized to a matrix of size . Only the middle (n − 2) nodes are optimized because the starting and ending points of the path are fixed. Then, the algorithm performs loop iterations in steps 4~29. In steps 5~7, the x and y coordinates of the other n-2 nodes in the path are stored in the sets px and py respectively, except for the starting and ending points. In steps 8~13, each element of the sets px and py is taken as the mean, and each element in the matrix is taken as the variance, and N samples are generated according to the normal distribution and stored in the matrices point_x and point_y respectively, where point_x and point_y are two-dimensional matrices of size . In steps 14~21, N paths are generated based on the elements in the matrices point_x and point_y and stored in the structure path_offspring. It can also be understood that path_offspring is an offspring population containing N individuals. In step 22, in order to retain the excellent characteristics of the population during the evolution process, the best individual of the previous generation is merged with the offspring population path_offspring. In step 23, collision detection is performed on each individual in the population path_offspring, and valid individuals without collision are stored in a new population path_offspring_new. Then, the path length of each individual in the population path_offspring_new is calculated, and individuals with smaller path lengths are selected as elite samples and stored in the archive. The variance parameter is updated according to the elite samples in Archive, and the individual with the smallest path length is selected to update . In step 28, the smoothing operation of the CE algorithm is performed to reduce the probability that the algorithm falls into a local extremum. One iteration ends here, and the optimized path is output after cycles.
In step 26, the variance parameter is updated using elite samples from the Archive. The Archive contains elite paths (each of length n − 2 after removing start/end points). To compute :
- Grouping by position: For each path point position j (j ∈ [1, n − 2]), create a matrix of size , where each row corresponds to the (x, y) coordinates of the j-th path point from each elite path.
- Variance Calculation: The variance matrix obtained iswhere sigma is a function that calculates the variance of a column vector, the size of the matrix is .
| Algorithm 7: Path optimization method based on CE algorithm | |
| Input: Sample size N, elite sample rate , smoothness coefficient , , maximum number of optimizations | |
| Output: The optimized path | |
| 1 | |
| 2 | |
| 3 | Generate a matrix of size with all elements set to 1 |
| 4 | for to do |
| 5 | for to do |
| 6 | , |
| 7 | end for |
| 8 | , |
| 9 | for to do |
| 10 | for to do |
| 11 | , |
| 12 | end for |
| 13 | end for |
| 14 | |
| 15 | for to do |
| 16 | |
| 17 | for to do |
| 18 | |
| 19 | end for |
| 20 | |
| 21 | end for |
| 22 | |
| 23 | Select valid individuals without collision in the population path_offspring |
| 24 | Calculate the path length of each individual in the population path_offspring_new |
| 25 | Select individuals with smaller path lengths as elite samples |
| 26 | Update variance based on individuals in Archive |
| 27 | Select the individual with the shortest path length in Archive |
| 28 | |
| 29 | end for |
| 30 | Return: |
4. Simulation Experiments and Analysis
In this section, a series of simulation experiments are performed to evaluate the performance of the proposed CE-RRT algorithm. The RRT algorithm is used as a benchmark to measure the effectiveness of the three proposed optimization strategies.
4.1. Environments and Evaluation Indicators
Three environments are used in the simulations: the 2-dimensional (2D) maze-like environment in Figure 2a (starting point (15, 5), ending point (45, 45)), the 2D cluttered environment in Figure 2b (starting point (3, 3), ending point (47, 47)), and the 3-dimensional (3D) environment in Figure 2c (starting point (15, 10, 25), ending point (15, 46, 25)). Three environments are the same size, all . Two indicators are used to compare the performance of algorithms: is the length of feasible path f, and is the time to find path f. These algorithms will immediately stop once the feasible solutions are found.
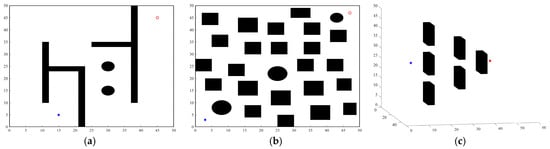
Figure 2.
Three simulation environments: (a) 2D maze environment; (b) 2D cluttered environment; (c) 3D environment.
4.2. Comparison Algorithms and Parameter Settings
The CE-RRT is compared with the existing RRT and RRT* algorithms in three environments. In addition, for the three proposed improvement strategies, the improvement algorithms when each strategy exists separately are also added for comparison to verify their effectiveness. ‘A-RRT’, ‘B-RRT’, and ‘C-RRT’ denote RRT algorithms that separately include adaptive sampling strategy, adaptive step size adjustment strategy, and path optimization strategy based on the CE algorithm, respectively.
The detailed parameter settings of all algorithms are listed in Table 1. The parameters of the CE-RRT algorithm are included in A-RRT, B-RRT, and C-RRT. All algorithms and experiments are implemented in the MATLAB 2021b environment, and the hardware environment is an Intel i9@2.3 GHz CPU and 32G memory, which were sourced in Chengdu, China.

Table 1.
The parameter settings for all algorithms.
4.3. Simulation of Three Environments
4.3.1. 2D Maze Environment
A sparse environment like a maze is one of the most common working environments for autonomous mobile robots, and the RRT algorithm performs well in it. Six algorithms are applied to the 2D maze environment shown in Figure 2a for simulation, and the performance results are shown in Figure 3. In Figure 3, the generated paths of RRT ( = 152.74, = 29.30), A-RRT ( = 150.46, = 15.96), B-RRT ( = 153.88, = 1.08), C-RRT ( = 117.06, = 30.25), CE-RRT ( = 113.02, = 13.01), and RRT* ( = 162.73, = 10.47) are shown.
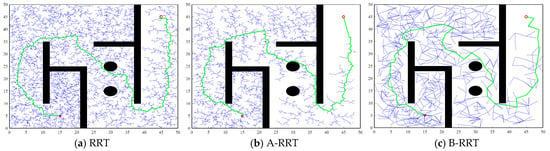
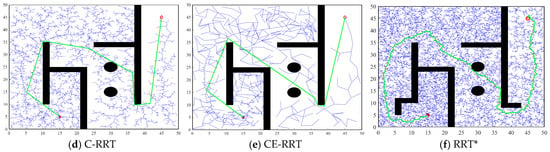
Figure 3.
Simulation results of six algorithms in the 2D maze environment.
The result of the RRT algorithm in Figure 3a is used as a benchmark, and the analysis of the results in Figure 3b–f is as follows. In Figure 3b, the efficiency of A-RRT in finding a feasible path is significantly improved, and the is reduced by 45.53%, from 29.30 s to 15.96 s; this indicates that the adaptive sampling strategy has a good effect. In Figure 3c, the solving efficiency of B-RRT is greatly improved, and the is reduced by 96.31%, from 29.30 s to 1.08 s; this indicates that the proposed adaptive step adjustment strategy is effective. However, due to the large step , it is easy to cause the feasible path f to deviate from the optimal solution. In Figure 3d, the path quality has been greatly improved after the optimization of path f by using the CE algorithm, and the length has been reduced by 23.36%, from 152.74 to 117.06. In Figure 3e, the CE-RRT algorithm reduces path length by 26% and search time by 55.60%. In Figure 3f, compared with RRT*, the path length of CE-RRT is shortened by 30.55%, but the time consumed is also increased by 24.26%. This indicates that CE-RRT has obvious advantages in terms of path quality but needs improvement in time efficiency. However, the RRT* algorithm has a 2% probability of planning failure, indicating that it has poor robustness.
The statistical results of 100 simulations are shown in box plots 4 and 5, and detailed data are listed in Table 2. The ‘Fail’ value is the number of failures. Failure refers to the algorithm not being able to find the approximate optimal path within 20,000 iterations. From Figure 4 and Figure 5, it can be seen that the adaptive sampling and adaptive step adjustment strategies effectively reduce the search time of the RRT algorithm, and the quality of the feasible path is significantly improved after optimization by using the CE algorithm. From Figure 6, it is apparent that the CE-RRT algorithm demonstrates superior optimization of the feasible path length compared to the C-RRT algorithm. This suggests that the addition of the other two strategies contributes positively to reducing . Furthermore, as shown in Table 2, a smaller standard deviation indicates that the CE-RRT algorithm has strong robustness.

Table 2.
Statistical results of 100 simulations in the 2D maze.
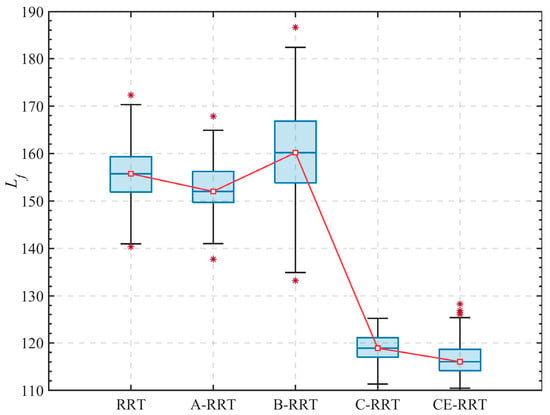
Figure 4.
in the 2D maze.
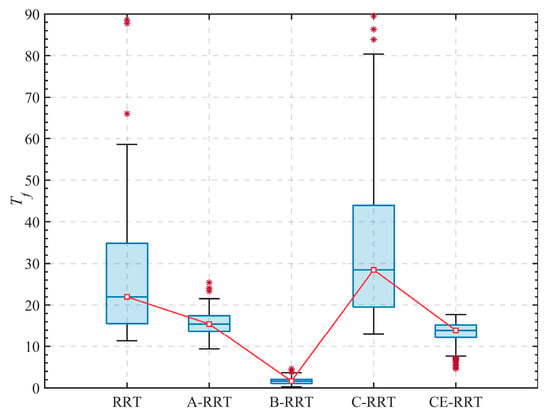
Figure 5.
in the 2D maze.
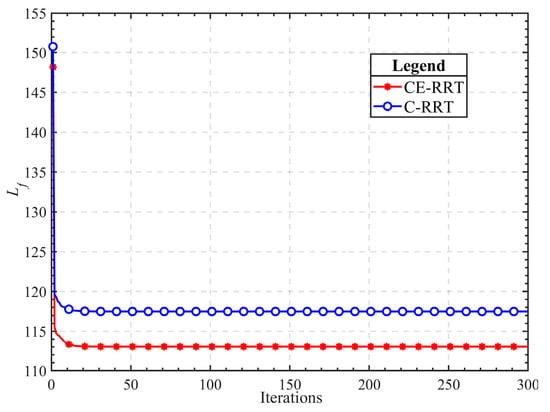
Figure 6.
Optimization results in the 2D maze.
4.3.2. 2D Cluttered Environment
Dense and cluttered environments are also common working environments for mobile robots, and complex environments can better test the effectiveness of path planning algorithms. Five algorithms are applied to the 2D maze environment shown in Figure 2b for simulation, and the performance results are shown in Figure 7. In Figure 7, the generated paths of RRT ( = 82.47, = 4.15), A-RRT ( = 70.86, = 1.23), B-RRT ( = 81.05, = 0.55), C-RRT ( = 68.94, = 33.17), CE-RRT ( = 63.75, = 30.03), and RRT* ( = 85.58, = 6.91) are shown.

Figure 7.
Simulation results of six algorithms in the 2D cluttered environment.
The result of the RRT algorithm in Figure 7a is used as a benchmark, and the analysis of the results in Figure 7b–e is as follows. In Figure 7b,c, there is a significant improvement in the efficiency of the algorithm, with the time reduced by 70.36% and 86.75%, respectively. This indicates that the proposed adaptive sampling and adaptive step adjustment strategies remain effective in the 2D cluttered environment. In Figure 7d,e, the path quality is significantly improved, with path length shortened by 16.41% and 22.70%, respectively, indicating that the optimization of the CE algorithm is positive. In Figure 7f, compared with the RRT* algorithm, the path length of CE-RRT is shortened by 25.51%, but the time consumed increases significantly. However, the time consumption of C-RRT and CE-RRT has also significantly increased.
The statistical results of 100 simulations are shown in box plots 8 and 9, and detailed data are listed in Table 3. Figure 8 and Figure 9 show that the search time of A-RRT and B-RRT is significantly reduced, but the length of feasible paths obtained by B-RRT slightly increases. This is because larger search steps can easily lead to a decrease in search accuracy. In addition, C-RRT and CE-RRT exhibit significant advantages in path length, but they also consume more time. From Figure 10, the CE-RRT algorithm still has better performance, and it has converged after about 20 iterations. Therefore, the number of iterations of the CE algorithm can be reduced to shorten the running time of the entire algorithm.

Table 3.
Statistical results of 100 simulations in the 2D cluttered.
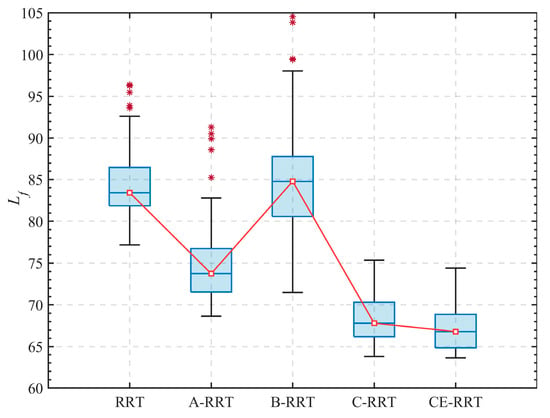
Figure 8.
in the 2D cluttered.
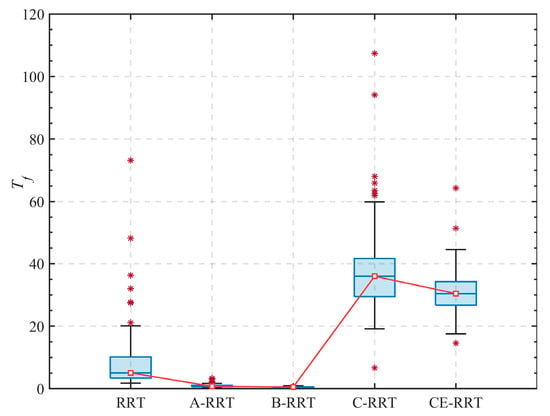
Figure 9.
in the 2D cluttered.
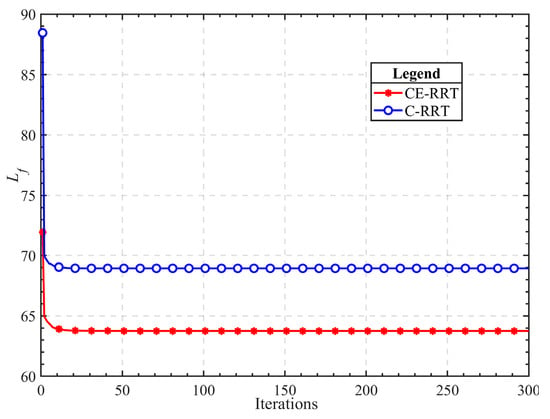
Figure 10.
Optimization results in the 2D cluttered.
4.3.3. 3D Environment
The 3D environment with obstacles is the main working environment for robotic arms. Five algorithms are applied to the 3D environment shown in Figure 2c for simulation, and the performance results are shown in Figure 11. In Figure 11, the generated paths of RRT ( = 77.36, = 32.90), A-RRT ( = 66.88, = 0.46), B-RRT ( = 71.96, = 0.65), C-RRT ( = 45.71, = 34.94), CE-RRT ( = 39.37, = 12.97), and RRT* ( = 65.67, = 45.50) are shown.
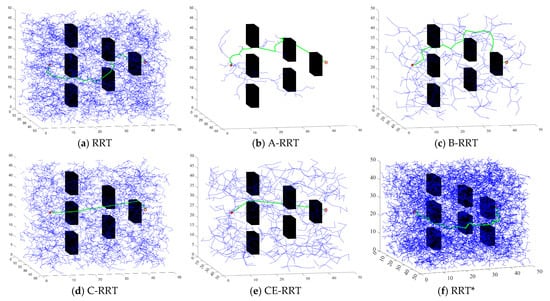
Figure 11.
Simulation results of six algorithms in the 3D environment.
The result of the RRT algorithm in Figure 11a is used as a benchmark, and the analysis of the results in Figure 11b–e is as follows. From Figure 11b,c, it can be seen that the search efficiency of A-RRT and B-RRT is greatly improved, with the time reduced by 98.60% and 98.02%, respectively. This indicates that the proposed adaptive sampling and step adjustment strategies are still very effective in a 3D environment. Similarly, as shown in Figure 11d,e, the quality of feasible paths has also been significantly improved, with lengths shortened by 40.91% and 49.11%, respectively. In Figure 11f, compared with RRT, the path quality obtained by the RRT* algorithm is relatively better; however, due to the addition of the “neighborhood search” and “path reconnection” steps, the time cost has also increased significantly. Moreover, the efficiency of CE-RRT has also been significantly improved.
The statistical results of 100 simulations are shown in Figure 12 and Figure 13, and detailed data are listed in Table 4. Similar to the conclusion in 2D environments, the proposed adaptive sampling and adaptive step size adjustment strategies can still significantly improve the search efficiency of the algorithm in 3D environments. The proposed optimization strategy based on the CE algorithm can greatly reduce path length and improve path quality. As shown in Table 4, the failure rate of the RRT algorithm in a 3D environment is 16%. The failure rates of A-RRT, B-RRT, and CE-RRT are all 0 after introducing the improved strategy, verifying the effectiveness of the improved strategy. This also indicates that the CE-RRT algorithm has stronger robustness. The failure rate of C-RRT is 7%, as the CE algorithm only optimizes feasible paths and does not affect the failure rate of the algorithm. The failure rate of the RRT* algorithm is 17%, and its performance in the 3D environment needs further improvement. It can be seen from Figure 14 that the running time of the entire algorithm can still be shortened by reducing the number of iterations of the CE algorithm.
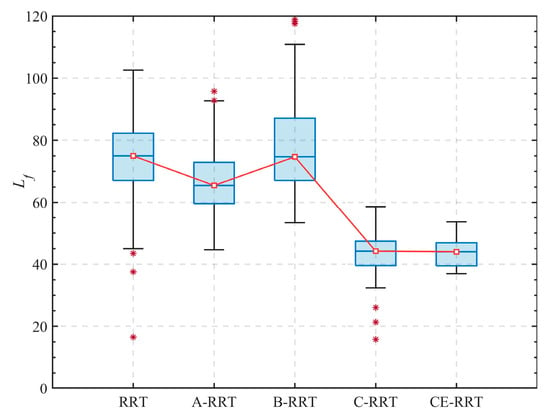
Figure 12.
in the 3D environment.
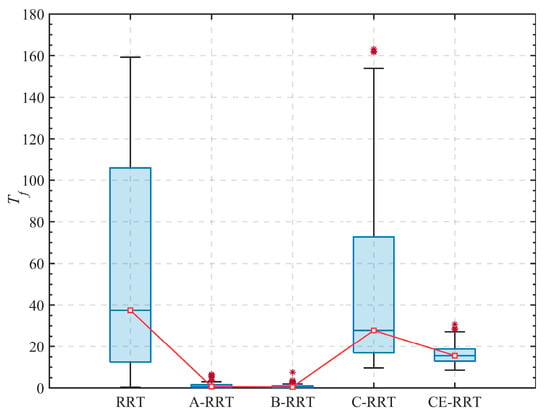
Figure 13.
in the 3D environment.

Table 4.
Statistical results of 100 simulations in the 3D environment.
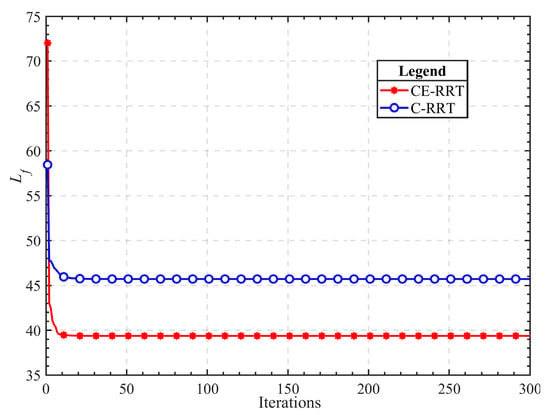
Figure 14.
Optimization results in the 3D environment.
The testing environments employed in this study (2D maze, 2D cluttered, and 3D static environments) were deliberately selected to isolate and rigorously evaluate the core performance contributions of the three proposed strategies within the CE-RRT algorithm: adaptive sampling, adaptive step adjustment, and CE-based path optimization. These controlled settings provide a clear baseline for quantifying improvements in search efficiency (reduced time ) and path quality (reduced length ) over standard RRT and RRT* algorithms. The significant performance gains demonstrated in Section 4.3.1, Section 4.3.2 and Section 4.3.3 validate the effectiveness of these strategies in static obstacle configurations.
However, we acknowledge that these environments represent a foundational level of complexity compared to many real-world robotic applications. Real-world scenarios often involve more intricate obstacle geometries, narrow passages (bottlenecks), and, critically, dynamic elements such as moving obstacles or changing goals. While the current study successfully establishes CE-RRT’s capabilities in static environments—a necessary prerequisite—we recognize that testing in environments featuring bottlenecks and moving obstacles is crucial for a more comprehensive evaluation of the algorithm’s robustness and adaptability. Addressing these more complex and realistic scenarios, including the development of dynamic extensions to CE-RRT, is identified as a key direction for future work (as further discussed in Section 6). The results presented here provide the essential groundwork for such subsequent investigations.
5. Welding Path Planning Simulation
In this section, a simulation experiment is designed based on the dual Sawyer robot simulation platform to verify the effectiveness of the proposed CE-RRT algorithm for the welding task of some long welds on a large, complex component.
5.1. Experimental Platform
As shown in Figure 15, a dual robot collaborative welding simulation platform is built using two Sawyer robotic arms in the Gazebo environment based on the Robot Operating System (ROS) [25], equipped with a 2-m-high and 5-m-long slide rail. Four typical welding seams are shown in Figure 1, Figure 2, Figure 3 and Figure 4. The hardware environment is an Intel i5-10500@3.1GHz CPU with 8G memory, the operating system is Ubuntu 16.04, and the C++ 11 programming language is used.
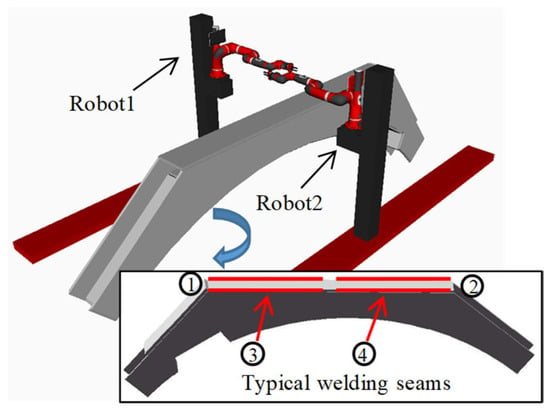
Figure 15.
Dual robot simulation platform.
5.2. Dual Robot Welding Path Planning Experiment
The proposed CE-RRT algorithm is used to plan a feasible path for the two Sawyer robots to complete the welding task based on the experimental platform of the two Sawyer robots in Figure 15 and the selected typical welding seams. The motion planning results of the dual robot based on the CE-RRT algorithm are shown in Figure 16. Figure 16a shows the path planning of the dual robot from the initial state to the welding preparation state, Figure 16b shows the path planning of the primary welding process of the dual robot (the welding seam 2 is assigned to robot 1, and the welding seam 3 is assigned to robot 2), and Figure 16c shows the path planning of the dual robot from the welding preparation state to the initial state. From the results of Figure 16a,c, it can be seen that the workspaces of the two robots partially overlap, but reasonable path planning makes them not collide; this also verifies the effectiveness of the CE-RRT algorithm.
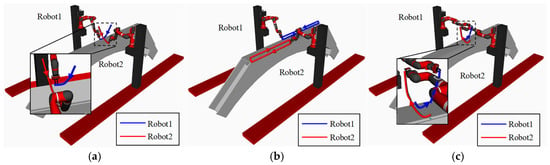
Figure 16.
Path Planning of dual robot welding based on the CE-RRT algorithm: (a) Reaching the welding preparation state; (b) primary welding process; (c) Return to the initial state.
6. Conclusions
In this paper, a novel adaptive RRT algorithm based on CE optimization (CE-RRT) is proposed by introducing three improved strategies. The purpose is to solve robot path planning problems more quickly and stably. A series of experiments are conducted to evaluate the performance of the CE-RRT algorithm in a 2D maze environment, a 2D cluttered environment, and a 3D environment. The RRT algorithm is used as a benchmark to measure the effectiveness of the three proposed optimization strategies. The results demonstrate that adaptive sampling and adaptive step adjustment strategies can effectively increase the search speed of the algorithm, and the CE algorithm can also significantly improve path quality (the path of CE-RRT is shortened by 26%, 22.70%, and 49.11%). Particularly, the statistical results of 100 simulations indicate that the CE-RRT algorithm exhibits stronger stability in 3D environments. In addition, the CE-RRT algorithm is used to plan a reasonable path for the dual robots to perform tasks based on the dual Sawyer robot simulation platform.
While the CE-RRT algorithm demonstrates significant improvements in search efficiency and path quality within the static environments tested in this study, several promising avenues for future research have been identified:
- (1)
- Extension to Dynamic Environments: The most critical next step is to extend CE-RRT to handle dynamic environments with moving obstacles. This requires developing mechanisms for real-time obstacle detection and prediction and integrating dynamic constraints into the adaptive sampling, step adjustment, and path optimization strategies. The robust performance observed in the static 3D environment (Section 4.3.3) provides a strong foundation for tackling this challenge.
- (2)
- Evaluation in More Complex Static Scenarios: Further validation is needed in environments featuring highly intricate geometries, dense obstacle fields, and narrow bottlenecks beyond those tested here.
- (3)
- Parameter Sensitivity Analysis: A systematic investigation into the sensitivity of CE-RRT’s performance to its key parameters across diverse environments is warranted to provide clearer guidelines for practical deployment.
- (4)
- Real-World Implementation: Transitioning the algorithm from simulation to physical robot platforms (beyond the dual-Sawyer simulation) and addressing real-world uncertainties (sensor noise, actuation errors) is essential for demonstrating its practical utility.
Author Contributions
Conceptualization, D.Z. and Q.T.; methodology, D.Z., Q.T. and L.M.; formal analysis, Q.T.; data curation, J.L.; writing—original draft preparation, Q.T.; writing—review and editing, D.Z.; supervision, L.M.; project administration, Y.S.; funding acquisition, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Sichuan Province Science and Technology Support Program (No. 2020ZDZX0015).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
References
- Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.A.; Burgard, W. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006; Volume 2, pp. 3671–3678. [Google Scholar]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Luo, X. An overview of calibration technology of industrial robots. IEEE-CAA J. Autom. Sin. 2021, 8, 23–36. [Google Scholar] [CrossRef]
- Gonzalez, D.; Perez, J.; Milanes, V.; Nashashibi, F. A review of motion planning techniques for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1135–1145. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A. The focussed d* algorithm for real-time replanning. In IJCAI’95: Proceedings of the 14th International Joint Conference on Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; Volume 2, pp. 1652–1659. [Google Scholar]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.-H. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Kavraki, L.; Kolountzakis, M.; Latombe, J.-C. Analysis of probabilistic roadmaps for path planning. IEEE Trans. Robot. 1998, 14, 166–171. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.-C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Research Report 9811. 1998. Available online: https://www.semanticscholar.org/paper/Rapidly-exploring-random-trees-%3A-a-new-tool-for-LaValle/d967d9550f831a8b3f5cb00f8835a4c866da60ad (accessed on 1 September 2025).
- Jeong, I.-B.; Lee, S.-J.; Kim, J.-H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Kalisiak, M.; van de Panne, M. RRT-blossom: RRT with a local flood-fill behavior. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA), Orlando, FL, USA, 15–19 May 2006; pp. 1237–1242. [Google Scholar] [CrossRef]
- Ichnowski, J.; Alterovitz, R. Scalable multicore motion planning using lock-free concurrency. IEEE Trans. Robot. 2014, 30, 1123–1136. [Google Scholar] [CrossRef] [PubMed]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Kuffner, J.; LaValle, S. RRT-connect: An efficient approach to single-query path planning. IEEE Int. Conf. Robot. Auto. 2000, 2, 995–1001. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Optimization of computer simulation models with rare events. Eur. J. Oper. Res. 1997, 99, 89–112. [Google Scholar] [CrossRef]
- Tang, Q.; Ma, L.; Zhao, D.; Lei, J.; Wang, Y. A multi-objective cross-entropy optimization algorithm and its application in high-speed train lateral control. Appl. Soft Comput. 2022, 115, 108151. [Google Scholar] [CrossRef]
- Kovaleva, M.; Bulger, D.; Zeb, B.A.; Esselle, K.P. Cross-entropy method for electromagnetic optimization with constraints and mixed variables. IEEE Trans. Antennas Propag. 2017, 65, 5532–5540. [Google Scholar] [CrossRef]
- Haber, R.E.; del Toro, R.M.; Gajate, A. Optimal fuzzy control system using the cross-entropy method. A case study of a drilling process. Inf. Sci. 2010, 180, 2777–2792. [Google Scholar] [CrossRef]
- Kroese, D.P.; Porotsky, S.; Rubinstein, R.Y. The cross-entropy method for continuous multi-extremal optimization. Methodol. Comput. Appl. Probab. 2006, 8, 383–407. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.P.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source robot operating system. In Proceedings of the ICRA Workshop Open Source Software; Kobe, Japan, 12–17 May 2009, Volume 3, p. 5.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).