Evaluating the Promethee ii Ranking Quality

Abstract

Multicriteria decision aid consists in helping decision makers to compare (rank, choose, sort, etc.) different alternatives which are evaluated on conflicting criteria. One well-known family of multicriteria decision aid methods is Promethee. It is based on pairwise comparisons of the alternatives to produce a complete or a partial ranking. Promethee is widely used in practical applications, and different aspects of its theoretical properties have already been studied in the literature. However, no work has been proposed to assess the quality of the rankings it produces with regard to the pairwise preference matrix it exploits. This work addresses this problem by proposing a new indicator of the quality of the rankings produced by Promethee ii. This indicator is derived from a new property of the net flow score procedure. The indicator is illustrated on both artificial and real datasets.

1. Introduction

Multicriteria decision aid (MCDA) aims to help decision makers in solving problems where alternatives are simultaneously evaluated on multiple conflicting criteria. Usually, three prominent families of methods can be identified: aggregating, outranking, and interactive procedures. The focus of this contribution will be on Promethee (more precisely, Promethee ii), which belongs to the outranking methods (with one of the first mentions of the technique in [1]).

The Promethee procedure is based on two main steps:

• The computation of a valued pairwise preference matrix between all pairs of alternatives;
• The exploitation of this preference matrix to compute a partial or a complete ranking (through the computation of positive, negative, and net flow scores).

Even though this method has a wide range of applications and continues to be used in various fields (as shown in Section 2), there is very little work in the way of evaluating the results of the method. This led to the following research question:

Is there a way to assess the quality of the results provided by the application of the Promethee ii method to a given dataset?

This question is central in the sense that the computation of flow scores is always possible once the preference matrix has been computed. As a consequence, complete or partial rankings can always be built based on these scores, as they result as the output of a constructive procedure. Like in statistics, assessing the quality of a given output is essential.

Let us note that the idea of evaluating the coherence/consistency of an MCDA method is not novel. For instance, in the Analytic Hierarchy Process (AHP), this aspect is evaluated through what is called a consistency index [2].

Thus, in this contribution, we propose a complementary view with a focus on the adequacy between the preference matrix and the ranking obtained by the net flow score procedure. In the same spirit as [2], we provide an indicator to quantify the ranking quality in the context of the Promethee ii method (which will be briefly recalled in Section 3). This will be derived from a new property of the net flow score procedure that will be explained in Section 4. A new quality index will then be developed in Section 5. The proposed approach will then be illustrated on artificial and real datasets in Section 6. Finally, Section 7 concludes this work and explores avenues of further research.

2. Literature Review

Promethee has known extensive interest since its inception, with many research and application papers being published throughout the years. This is attested by the online Promethee bibliographical database, which contained nearly 2400 references as of September 2020 [3] as well as by a literature review published in 2010 [4] which focuses on the application of the method. This trend remains prevalent today, with research on extensions and applications to various fields or problems. Hereunder, we provide some recent examples of applications of the method:

• Food sector: with a recent application where Promethee was used in conjunction with other MCDA methods to prioritize obstacles and opportunities in the implementation of short food supply chains [5];
• Energy sector: where suitable locations for on-shore wind farms are identified with the help of Promethee ii [6];
• Computer science: with a novel method for rules extraction from artificial neural networks by integrating Promethee into a multi-objective genetic algorithm [7].

In addition to these practical applications, multiple software for the use of Promethee were developed. One of the latest is Promethee-Cloud [8]. These software aims to provide a tool to support the decision-making activity in an enterprise.

While popular in practice, few studies were conducted on the inner workings of Promethee ii. One particularly studied aspect of the method is its susceptibility to rank reversal (RR) occurrences. Rank reversals are not proper to Promethee methods but affect most outranking methods. This phenomenon was initially discussed in the context of the AHP method with the very first mention of rank reversal in [9]. Later, this was pointed out for other decision aid methods such as Promethee [10] or ELECTRE [11]. Since then, several studies have investigated under which conditions rank reversal could occur in Promethee i and Promethee ii with the latest threshold on RR occurrence in [12]. Another avenue of research consists of the axiomatic characterization of the net flow procedure. As far as we are aware, the first characterization was made in 1992 in [13]. Then, in 2022, Ref. [14] provided an axiomatic interpretation of the Promethee ii method. These two works are focused on the understanding of the net flow score procedure (once the preference matrix has been computed). Recently, the compensatory aspects of the methods were also studied in [15].

In addition, several works also focus on the stability of Promethee methods and the influence of their internal parameters. The first was in 1995, with [16]. Then, in 2018, Ref. [17] proposed an alternative approach using inverse optimization to define sensitivity intervals for the weights of the criteria. Ref. [18] later proposed another sensitivity analysis of the intra-criterion parameters, and finally, Ref. [19] studied the stability of the ranking according to the evaluations of the alternatives.

Promethee has also had several extensions. For instance, in 2014, Ref. [20] proposed a method combining Stochastic Multicriteria Acceptability Analysis (SMAA) with the Promethee methods. Or more recently, Ref. [21] introduced the best–worst Promethee method, which avoids the rank reversal problem.

3. Promethee

In this section, a short introduction about Promethee methods, and more particularly Promethee ii, is presented. For more details, the interested reader can refer to the description provided in [22].

Let us consider a decision problem composed of a set $A=\{a_1,\cdots ,a_n\}$ defining the n alternatives of the decision problem which have to be evaluated according to a set $F=\{f_1,\cdots ,f_k\}$ of k criteria. Without loss of generality, these criteria are assumed to be maximized.

As already said, Promethee ii works by computing pairwise comparisons and flow scores. The pairwise comparisons are performed as follows. First, the differences between the evaluations of each pair of alternatives on each criterion are computed:

$$d_c(a_i,a_j)=f_c\left(a_i\right)-f_c\left(a_j\right)$$

(1)

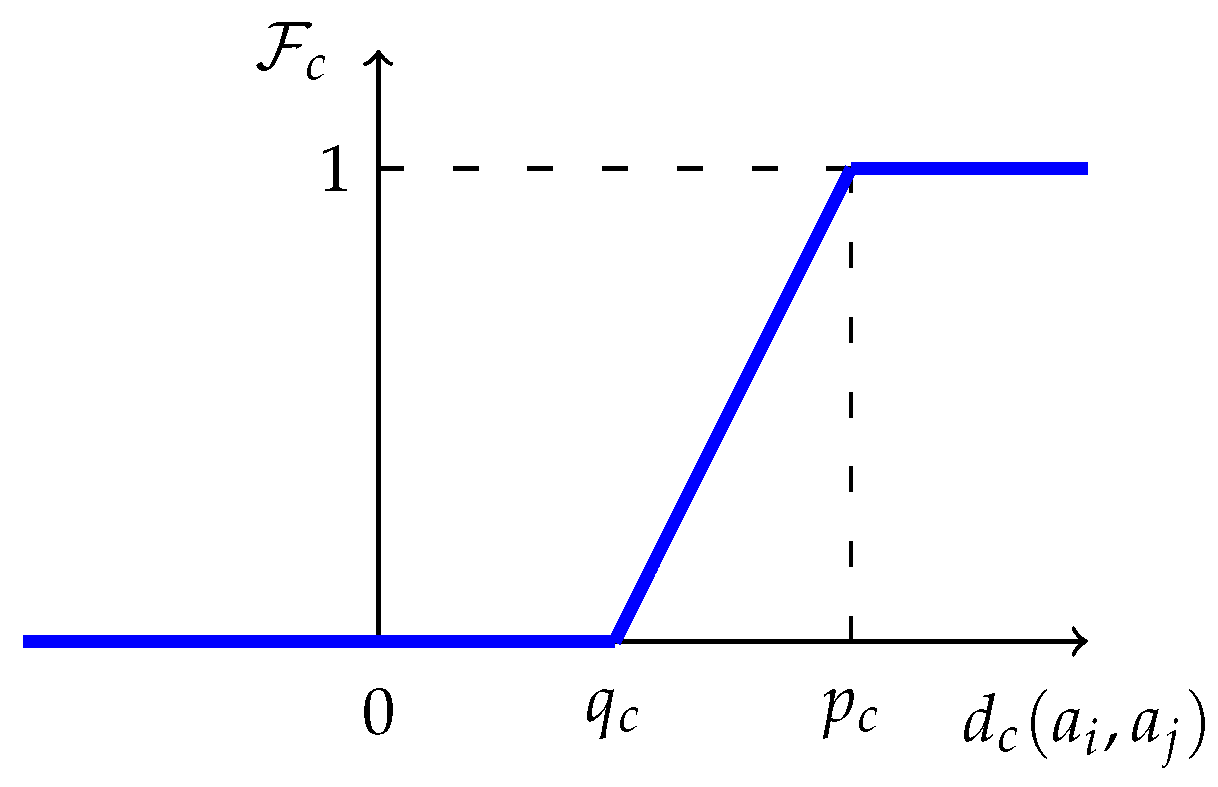
In a second step, these differences are transformed into mono-criterion preference indices ${\pi }_{ij}^c={\mathcal{F}}_c\left(d_c(a_i,a_j)\right)$. ${\mathcal{F}}_c$ is a monotonically increasing preference function in $[0,1]$. The exact forms of $\mathcal{F}$ are left to the decision maker to decide. In [23], however, the authors proposed 6 different types of preference functions that should reasonably satisfy most decision contexts. The so-called linear preference with an indifference threshold function, shown in Figure 1, is an example of a widely used function. In this case, the decision maker has to instantiate the values of two parameters, denoted $q_c$ and $p_c$, which respectively represent an indifference and a strict preference threshold for criterion $f_c$.

The method supposes that the decision maker is able to provide positive and normalized weights denoted ${\omega }_c$ for the different criteria. These weights are then used to compute the pairwise preference index between a pair of alternatives $a_i$ and $a_j$, denoted ${\pi }_{ij}$, as follows:

$${\pi }_{ij}=\sum _{c=1}^k{\omega }_c·{\pi }_{ij}^c$$

(2)

These pairwise preferences (also referred to as pairwise comparisons) can be organized in what is called a preference matrix. For instance, with three alternatives, the obtained preference matrix will be

$$\left(\begin{array}{ccc}0& {\pi }_{12}& {\pi }_{13}\\ {\pi }_{21}& 0& {\pi }_{23}\\ {\pi }_{31}& {\pi }_{32}& 0\end{array}\right)$$

(3)

However, this representation is only an intermediary step in the computation of the Promethee ii ranking. The next step is to compute the negative and positive outranking flows as follows:

$$\begin{array}{c}\hfill {\varphi }_i^{+}={\displaystyle \frac{1}{n-1}}\sum _{a_j\in A,j\ne i}{\pi }_{ij}\\ \hfill {\varphi }_i^{-}={\displaystyle \frac{1}{n-1}}\sum _{a_j\in A,j\ne i}{\pi }_{ji}\end{array}$$

(4)

On the one hand, the positive flow of a given alternative represents its mean advantage over all the other alternatives. This has to be maximised. On the other hand, the negative flow of a given alternative represents its mean weakness to all the other alternatives. This has to be minimised.

The net flow score of $a_i$ is then the positive outranking flow minus the negative outranking flow:

$${\varphi }_i={\varphi }_i^{+}-{\varphi }_i^{-}$$

(5)

The net flow scores are lying in the interval $[-1,1]$ and are interpreted as follows: the higher the better. The complete ranking of the alternatives is deduced from the values of the net flow scores: $a_i⪰a_j⟺\varphi \left(a_i\right)\ge \varphi \left(a_j\right)$ with $a_i⪰a_j$ meaning that $a_i$ has an equal or better ranking than $a_j$.

While the computation of net flow scores to rank the alternatives seems to be reasonable (a balance between the “advantages” of a given alternatives minus its “weaknesses”), additional theoretical justifications are needed to convince practitioners that the method is grounded. As already pointed out, the works [13,24] also follow this direction. In the next section, we provide a complementary argument.

4. A New Interpretation of Promethee ii’s Net Flow Procedure

In this work, a new possible interpretation is presented for the Promethee ii’s outranking procedure. This interpretation is stated as follows:

“Promethee ii ranks the alternatives to maximise the sum of all paths of at most length 2 starting from any alternative and ending on any alternative, worst in the ranking.”

Without loss of generality, we will consider the following ranking of the alternatives: $a_1⪰a_2⪰a_3⪰a_4⪰\dots ⪰a_n$. In this case, the sum of all paths of length two starting from any alternative and ending on any alternative worst in the ranking ($PL2$) can be defined as

$$PL2=\sum _{i=1}^{n-1}\sum _{j=i+1}^n\sum _{k=1}^n\left({\pi }_{ik}+{\pi }_{kj}\right)$$

(6)

Hereunder, we show that the value of this index is maximal only if the order of the alternatives also aligns with the order provided by the values of the net flows. This can be proven by the following decomposition:

$$\begin{array}{cc}\hfill \sum _{i=1}^{n-1}\sum _{j=i+1}^n\sum _{k=1}^n\left({\pi }_{ik}+{\pi }_{kj}\right)& =(n-1)\left[\sum _{i=1}^{n-1}\sum _{j=i+1}^n({\varphi }_i^{+}+{\varphi }_j^{-})\right]\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & =(n-1)\left[\sum _{i=1}^{n-1}\sum _{j=i+1}^n({\varphi }_i+{\varphi }_i^{-}+{\varphi }_j^{-})\right]\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & =(n-1)\left[\sum _{i=1}^{n-1}{\varphi }_i\sum _{j=i+1}^{n}1+\sum _{i=1}^{n-1}{\varphi }_i^{-}\sum _{j=i+1}^{n}1+\sum _{j=1}^n{\varphi }_j^{-}\sum _{i=1}^{j-1}1\right]\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & =(n-1)\left[\sum _{i=1}^{n-1}{\varphi }_i\sum _{j=i+1}^{n}1+\sum _{i=1}^{n-1}{\varphi }_i^{-}\sum _{j=i+1}^{n}1+\sum _{i=1}^n{\varphi }_i^{-}\sum _{j=1}^{i-1}1\right]\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & =(n-1)\left[\sum _{i=1}^{n-1}{\varphi }_i\sum _{j=i+1}^{n}1+(n-1)\sum _{i=1}^n{\varphi }_i^{-}\right]\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & =(n-1)\left[\underset{dep.seq.}{\underbrace{{\displaystyle \sum _{i=1}^n}(n-i){\varphi }_i}}+\underset{indep.seq.}{\underbrace{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\pi }_{ij}}}\right]\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & =(n-1)\left[\underset{dep.seq.}{\underbrace{{\displaystyle \sum _{i=1}^n}(n-i){\varphi }_i}}+C\right]\hfill \end{array}$$

(13)

with C being the sum of all pairwise preferences, independent of the order of the alternatives.

$PL2$ can be therefore be reformulated as

$$PL2=(n-1)\ast [C+(n-1){\varphi }_1+(n-2){\varphi }_2+(n-3){\varphi }_3+(n-4){\varphi }_4+\dots +0]$$

(14)

From Equation (14), it is straightforward to notice that $PL2$ will be maximal if and only if ${\varphi }_1\ge {\varphi }_2\ge {\varphi }_3\ge {\varphi }_4\ge \dots \ge {\varphi }_n$.

In the article by [13], it was shown that there is a set of admissible transformations that can be performed on the pairwise preferences without changing the net flow scores. This means that there are the following different preference matrices:

• Those that lead to the same net flow scores;
• Those that, as a consequence, lead to the same solution of the maximisation problem (same order of the alternatives maximising $PL2$);
• Those that differ regarding the sum of preferences (and therefore also have different optimal values of $PL2$).

A natural question can now be raised: Among all the preference matrices leading to the same net flow scores, which one is the most appropriate? In particular, are there elements of the preference matrix that are not used to compute net flow scores?

5. Defining the Quality of Net Flow Scores

In Section 3, it has been shown that the ranking produced by the net flow scores is, for a fixed set of pairwise preferences, the ranking maximising the $PL2$ indicator. While this constitutes another argument in the consistency of the Promethee ii method, this result cannot be used to characterise whether the net flow scores obtained with Promethee ii effectively represent the preference relation obtained from a specific decision problem. To tackle this problem, a new indicator $\mathcal{I}$ will be defined, which assesses how well a preference matrix is represented by the net flow scores of Promethee ii.

5.1. The Class of Equivalent Problems

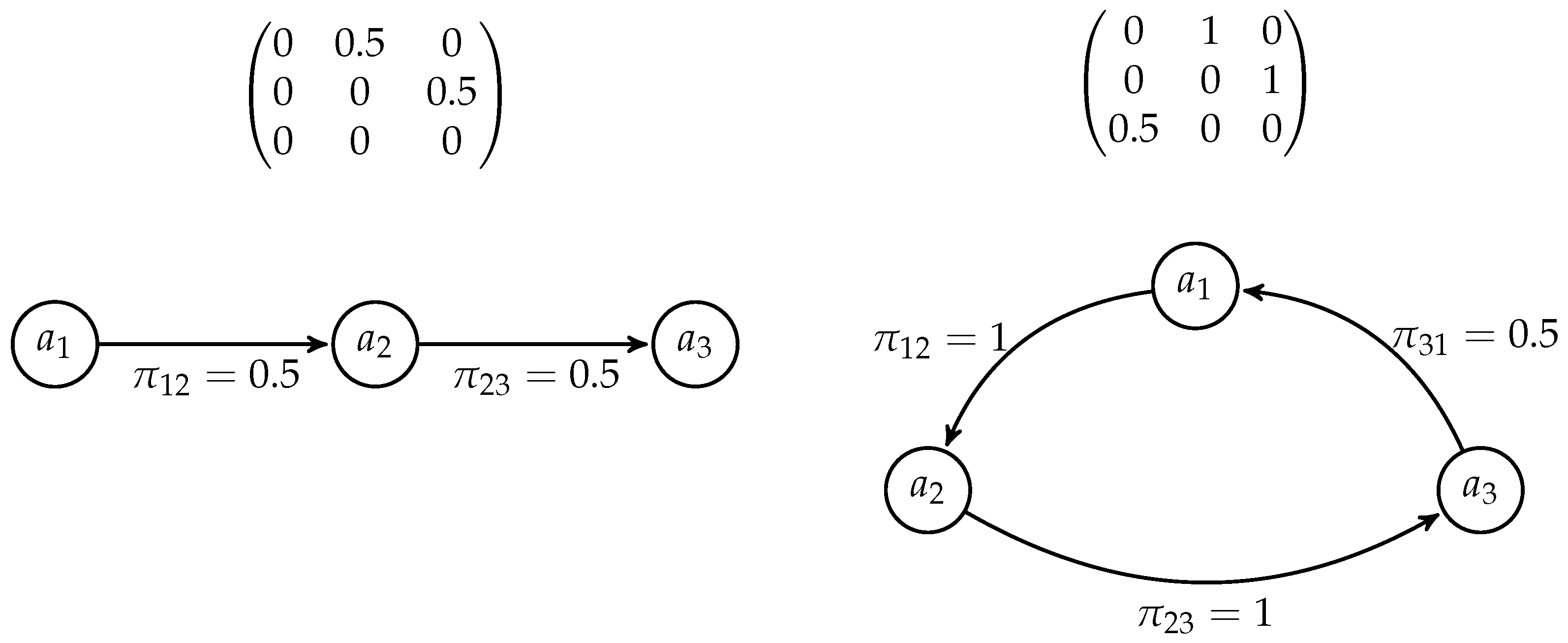
Let us start by showing an extreme case (see Figure 2). Let us consider two different preference matrices obtained by the application of Promethee. Since a pairwise preference of 0 can be seen as the absence of preference, they can both be presented in graph form, where only the pairwise preferences that are higher than 0 result in directed edges:

In both cases, $\varphi \left(a_1\right)=0.25,\varphi \left(a_2\right)=0,\varphi \left(a_3\right)=-0.25$, leading to an identical ranking of the alternatives, which is illustrated in Figure 3.

Since all alternatives have the same net flow scores, ${\sum }_{i=1}^n(n-i){\varphi }_i$ will be equal in both problems. However, since they differ in their sum of pairwise preferences (${\sum }_{i=1}^n{\sum }_{j=1}^n{\pi }_{ij}$), their respective values of $PL2$ will be different. This difference is related to the presence of a cycle in the second preference matrix. This was already observed before in [13]. The author demonstrated that the addition or removal of cycles of a constant value in the preference matrix did not alter the net flow scores. Thus, the addition of cycles can artificially increase the sum of preferences and, by extension, the value of $PL2$.

It is well known that cycles in the preference relation are in contradiction with the transitive property required for a consistent ranking. Furthermore, since cycles of a constant value can always be removed without influencing the net flow scores, the preference values associated with these cycles are not exploited by the Promethee ii procedure. As a consequence, it follows that for a given set of net flow scores, the preference matrix with no cycles can be seen as better represented by the net flow scores than the one with cycles. Thus, the aim of our indicator is to compare the initial preferences matrix to an ideal one that lacks cycles but leads to identical net flow scores.

5.2. Finding a Preference Matrix Without Cycles

Finding all cycles in a graph or matrix is typically solved by a Depth First Search (DFS) algorithm. This problem is an NP-hard problem, and solving it can be exponentially time-consuming with the number of alternatives. This was observed for randomly generated datasets. However, a basic transformation of the initial preference matrix could result in the removal of many cycles without having to look for all of them. This is what is proposed in this section. And, to validate such claims, empirical evidence that the matrix resulting from this transformation yields $\mathcal{I}$ values comparable to those obtained from cycle-free matrices is provided.

We denote by $\breve{\pi }$ the preference relation obtained from $\pi$ by removing all the cycles. The preference relation obtained with the basic transformation is denoted by $\tilde{\pi }$. It is obtained as follows:

$${\tilde{\pi }}_{ij}=max({\pi }_{ij}-{\pi }_{ji},0)\forall i,j$$

(15)

This transformation results in a preference matrix where, if ${\tilde{\pi }}_{ij}>0$, then ${\tilde{\pi }}_{ij}=0$ (for all pairwise preferences). This is the form showcased in Figure 2 of the example in the previous section.

It is important to note that this transformation consists of the removal of cycles between two alternatives i and j. Indeed, if both ${\pi }_{ij}>0$ and ${\pi }_{ji}>0$, it means that there is a preference of i over j but also of j over i. By [13], a cycle in pairwise preferences can always be removed by reducing all pairwise preferences of this cycle by the minimum pairwise preference. In our case, it means

$${\tilde{\pi }}_{ij}={\pi }_{ij}-min({\pi }_{ij},{\pi }_{ji})and{\tilde{\pi }}_{ji}={\pi }_{ji}-min({\pi }_{ij},{\pi }_{ji})$$

(16)

This can be reformulated and generalized to Equation (15). However, this does not necessarily remove all the cycles from the initial preference matrix. As shown in the example (Figure 2), even after applying this transformation, a cycle still exists.

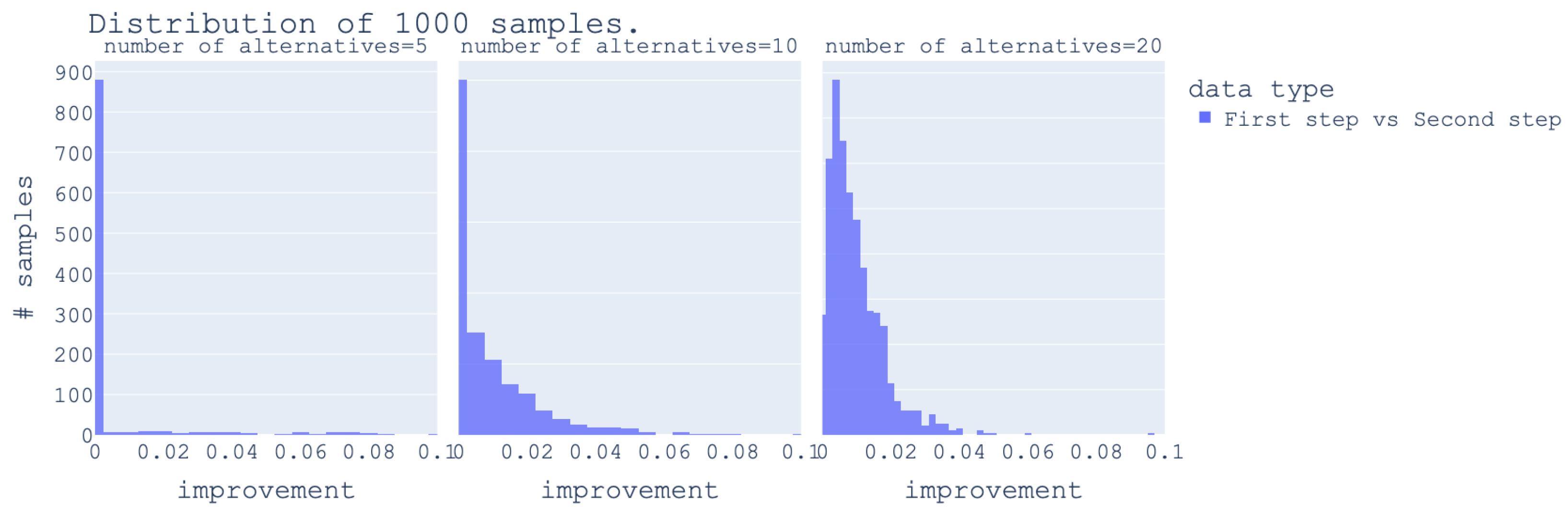
To better understand the number of cycles left after this basic transformation and the impact on the sum of pairwise preferences (${\sum }_{i=1}^n{\sum }_{j=1}^n{\pi }_{ij}$), an empirical comparison between the sum after the first step and the sum after the second step was conducted. However, since finding cycles using DFS on artificial can be exponentially time-consuming, the tests were limited to at most 20 alternatives (as shown in the Figure 4). The data was randomly generated. First, a table of evaluation for n alternatives with k criteria each was generated with an uniform distribution. Then PROMETHEE II was applied with randomly generated weights (also uniformly distributed) and using the linear preference function (see Figure 1). For each criterion, the indifference threshold was fixed as the first quartile of all possible differences between alternatives on the given criterion. Similarly, the preference threshold was the third quartile of all differences. After conducting tests with varying numbers of criteria, the changes in the distribution were minor, so only one test was retained for this article and is displayed in Figure 4.

The improvement axis in the Figure 4 is obtained by the following equation:

$${\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{\tilde{\pi }}_{ij}-{\sum }_{i=1}^n{\sum }_{j=1}^n{\breve{\pi }}_{ij}}{{\sum }_{i=1}^n{\sum }_{j=1}^n{\tilde{\pi }}_{ij}}}$$

(17)

This can be interpreted as the ratio of the sum of pairwise preferences that still need to be removed from $\pi$ to remove all cycles after the basic transformation presented in Equation (15).

Looking at Figure 4, it is quite clear that for a small number of preferences, there is no significant improvement. When adding alternatives, the improvements get a little better, with most being around 1% of the previous step. Considering the small amount of gains when moving from 5 alternatives to 20, and with the fact that finding cycles in a sizable preference matrix becomes highly computationally demanding, the second step was left as a future improvement of the quality index (this improvement could be achieved by taking advantages of Promethee ii properties to avoid doing a DFS for finding cycles).

5.3. Defining the Quality Index

Since only the basic transformation presented in Equation (15) has to be applied, the quality index can be defined in simple terms. Let $\tilde{\mathrm{\Pi }}={\sum }_{i=1}^n{\sum }_{j=i}^n|{\pi }_{ij}-{\pi }_{ji}|$ be the ideal value. When considering a given problem and its associated preference matrix. It is possible to compare $\mathrm{\Pi }={\sum }_{i=1}^n{\sum }_{j=1}^n{\pi }_{ij}$ (where the ${\pi }_{ij}$ are the pairwise preferences of the problem) to $\tilde{\mathrm{\Pi }}$ that is associated to the same net flow scores. Then an indicator $\mathcal{I}$ can be defined as follows:

$$\mathcal{I}={\displaystyle \frac{\mathrm{\Pi }-\tilde{\mathrm{\Pi }}}{\mathrm{\Pi }}}$$

(18)

The indicator is such that $\mathcal{I}\in [0,1]$. It can be interpreted as the percentage of the initial preference matrix that can be removed without modifying the net flow score. If $\mathcal{I}$ is high, a lot of cycles are present in the initial preference matrix. On the contrary, when it is close to 0, all the elements of the matrix are in agreement with the net flow score (i.e., very few cycles are present in the initial preference matrix). As a consequence, it has to be minimized.

6. Results

Using the previously defined index, some tests can be conducted both on simulated data and on five real datasets: Human Development Report [25], Times Higher Education World University Ranking [26], World Happiness Report [27], ASEM Sustainable Connectivity Index [28], and Environmental Performance Index [29].

6.1. Results on Simulated Data

This section studies the evolution of the index with two types of simulated data.

• Random: This data is generated using a uniform distribution, similarly to that described in Section 5.2;
• Artificial: This data is artificially generated such as to maximize the number of cycles in the dataset. It is worth noting that the generation of artificial datasets is deterministic (thus, for a given number of alternatives and criteria, only one artificial dataset exists). The complete mathematical formulation used to generate the artificial data can be found in Appendix A.

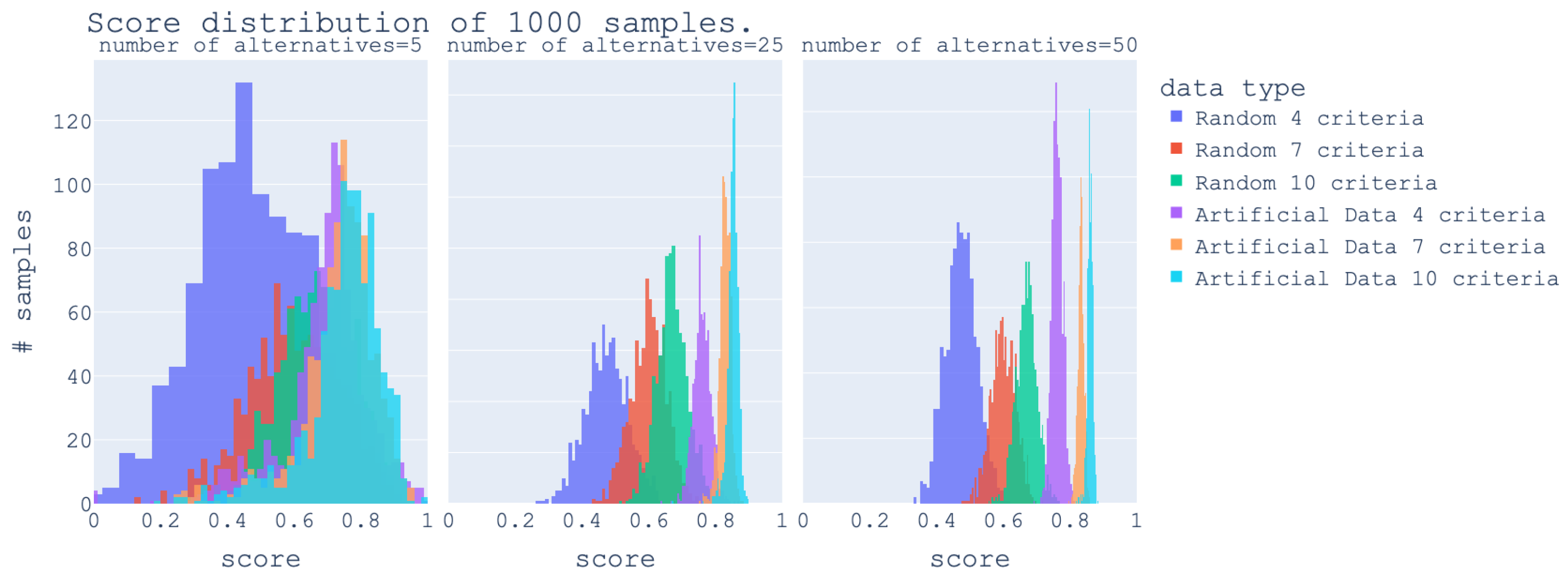
Tests on different numbers of criteria were conducted. The results shown in Figure 5 are fairly similar for a fixed number of criteria, regardless of the number of alternatives. The mode of each distribution is more or less the same value. From 5 alternatives to 25 alternatives, there is a large change in the width of each distribution. As the number of alternatives grows, the probability of having a well-ordered dataset (respectively, datasets with lots of cycles) decreases. This is due to the way the datasets are generated (each data point is uniformly distributed and its generation is independent from others). This is unrealistic when considering the field of MCDA, where there are, most of the time, dependence and conflict between criteria, and alternatives will never be uniformly distributed. For the artificial data, a random sampling on an initial 1000 alternatives was used to reach the 5, 25, and 50 alternatives of each distribution. As the sample is getting closer to the original number of alternatives, the distribution becomes narrower. The main takeaway from the artificial data is the high score it achieves (as it is an extreme case). However, this score is not 1 since a score of 1 would mean the net flow scores are all null (since it is the only way the sum of the pairwise preference can be null), and by the generation conducted, this is not achievable. Moreover, having all net flows score equal to zero is highly unrealistic as well.

In this randomly generated data, as the number of criteria grows, the likelihood of performing well diminishes (in Figure 5, with 3 criteria, some of the random samples can score quite well, while with 10 criteria, the best scores do not go below 0.5). This can be explained by the fact that cycles result from the multicriteria nature of the problem and how the preferences are constructed. Indeed, in the degenerated case consisting of only 1 criterion, no cycle is possible. Therefore, it is not surprising that problems with fewer criteria are less likely to have cycles in their preference relations.

6.2. Results on Real Datasets

As stated previously, the real datasets considered are Human Development Report [25], Times Higher Education World University Ranking [26], World Happiness Report [27], ASEM Sustainable Connectivity Index [28], and Environmental Performance Index [29]. For more information on the specifics of each dataset, Appendix B provides the criteria and number of alternatives (the rest can be found using the references). In addition to the real datasets, an artificial dataset of 10 criteria and 1000 alternatives was added to provide a point of comparison. As stated previously, the artificial dataset is an extreme case that contains one of the greatest amounts of cycles for its size.

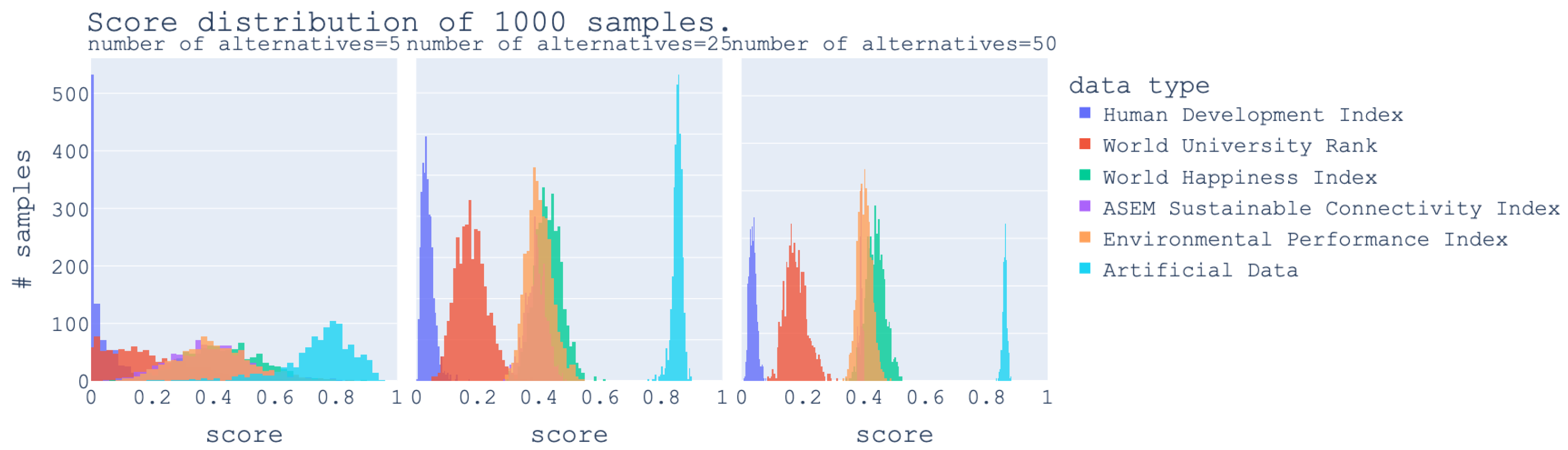
For each dataset, Promethee ii was applied on a randomly selected set of alternatives using the same preference function and thresholds as the random data. As shown in Figure 6, the number of samples and number of alternatives are the same as in the test on random data.

There is still a slight trend in the number of criteria. The lower the number of criteria, the better the ranking tends to perform. This supports the idea that as the number of criteria grows, it becomes harder to avoid conflicts among the alternatives and, thus, harder to reach a good score. In such a case, applying Promethee ii might result in many concessions and can lead to untrustworthy results. However, for certain datasets (e.g., Environmental Performance Index), if most criteria are concordant, the dataset can outperform datasets with a lower number of criteria (Environmental Performance Index with 11 criteria scores better than World Happiness Index with 6 criteria).

Another observation is that even though the World University Rank has the same number of criteria as the randomly generated data with 4 criteria (Figure 5 and Figure 6 both in blue), no matter the sample, they all perform better than the random data. Furthermore, both the World University Ranking and the Human Development Ranking perform very well, with, depending on the sample, a near-perfect score. This shows that both rankings provided by Promethee ii can be trusted. In contrast, the World Happiness Index is much worse. This can be caused by several factors: highly conflicting criteria, contradictions in the pairwise preferences, the presence of a cycle in the pairwise preferences, etc. Nevertheless, this results in less robust rankings. They are prone to changes and contradictions. Thus, in comparison to the other two rankings, applying Promethee ii with the considered weights and preference functions on the World Happiness Index might not be recommended.

The ASEM dataset is the smallest, with only 51 alternatives. Both the Environmental Performance Index dataset and the World Happiness Report dataset are also fairly small with 105 alternatives and 137 alternatives, respectively. The Human Development Report has 190 alternatives. And, for the World University Rank, the number of alternatives is 1394, much larger than the rest. Due to the difference in size, the sampling is limited to at most 50 alternatives. To complete this distribution analysis, for all of those datasets, the final score can be computed and can be found in

Table 1. Value of $\mathcal{I}$ on the complete datasets.

Datasets	$\mathcal{I}$
Human Development Index	0.03
World University Rank	0.18
World Happiness Index	0.46
ASEM Sustainable Connectivity Index	0.39
Environmental Performance Index	0.40
Artificial Data	0.75

.

As shown in Table 1, the ranking of the net flow scores produced on the World Happiness Index dataset is less representative of its respective preference relation. Even though the ASEM index and the Environmental Performance index have more criteria, they do score better. These preliminary results already showcase how much more informed one can be when applying the Promethee ii method. In this case, both the World University Rank and the Human Development Index score very well. It follows that both these datasets can lead to well-defined rankings obtained from preference matrices with very few cycles. In contrast, the last three real datasets are less precise in their resulting rankings. The net flow procedure of Promethee ii will simplify multiple cycles to produce these final ranking, which, therefore, particularly for the World Happiness Index, represent the decision problem less accurately.

6.3. Link with Rank Reversal

As highlighted in [14], rank reversal can be seen as a consequence of a third alternative in opposition to the direct preference between two alternatives. In other words, possible rank reversals result from the non-transitive nature of the pairwise preference matrix.

In this section, we confirm this intuition by comparing the value of the index $\mathcal{I}$ with the latest (and most accurate) threshold on the presence of rank reversal [12]. This is performed by reporting under % RR (in

Table 2. Comparison of the quality of the rankings produced with the netflow procedure and the proportion of pairs of alternatives subject to rank reversals in all datasets.

Datasets	$\mathcal{I}$	% RR
Human Development Index	0.03	0.23
World University Rank	0.18	0.30
World Happiness Index	0.46	0.65
ASEM Sustainable Connectivity Index	0.39	0.53
Environmental Performance Index	0.40	0.49
Artificial Data	0.86	1

) the proportion of alternatives that could potentially have their rank reversed (according to the mentioned threshold).

As predicted, there seems to be a trend linking the rankings’ scores and the proportion of potential rank reversals. However, both values are not entirely proportional. Even though the ASEM Index scores lower than the Environmental Performance Index, its percentage of rank reversal is higher. This is not surprising either since not all cycles are necessarily considered when computing the score and since the threshold is not an exact metric (there are still false positives; see [12]). Both of these aspects will result in imprecision and explain why both scores are not fully correlated.

In addition, Table 2 also shows that the artificial data does indeed correspond to an extreme (most likely unreachable) case, with all its 1000 alternatives subject to rank reversal.

Finally, in this article, the focus is on evaluating the presence of cycles in the preference matrix. The goal is to provide a metric on the whole ranking so that the decision maker can decide whether or not they can trust the results. In contrast, studies on the RR focus on evaluating the respective positions of pairs of alternatives in the ranking. This provides local insights, which are aggregated in Table 2. Indeed, the % RR column hides the relationships between pairs of alternatives by simply counting the number of alternatives that can have their rank reversed but does not provide any indication about the alternatives with which their rank could be reversed.

7. Conclusions

While net flow scores can always be computed given any preference matrix, one expects that some preference matrices better fit the net flow score procedure. In this contribution, one proposes a novel indicator $\mathcal{I}$ (varying between 0 and 1) to evaluate this aspect. It is derived from a new property of the net flow score procedure and is illustrated on both artificial and real datasets.

Several remaining questions deserve future attention. First, the removal of cycles was limited to cycles of length 2. This approximation was justified empirically on datasets limited in size and should be expanded to all datasets. Second, there is a dependence between the index values, the number of criteria and the parameters of Promethee ii. There was a preliminary investigation that could be taken further. Finally, even though the index is a percentage and can be interpreted by a decision maker, no clear threshold, below which one should not trust the resulting ranking, was provided.

In conclusion, this contribution aims to provide an additional way for the decision maker to assess the results of Promethee ii. Given a good value for the indicator, it can provide confidence in the ranking obtained and justify the application of Promethee ii to the dataset.