Star Bicolouring of Bipartite Graphs

Abstract

We give an integer linear program formulation for the star bicolouring of bipartite graphs. We develop a column generation method to solve the linear programming relaxation to obtain a lower bound for the minimum number of colours needed. We determine the star bicolouring using the iterative rounding method. We give computational results on arrowhead matrices, sparse random matrices, complete bipartite graphs, and matrices from the Harwell–Boeing collection. The findings demonstrate that the proposed method effectively establishes lower and upper bounds for the minimum number of colours needed for a star bicolouring of bipartite graphs, particularly for sparse bipartite graphs.

1. Introduction

A proper colouring of a graph G assigns colours to the vertices so that adjacent vertices have different colours. Grunbaum [1] introduced the notion of star colouring as follows: a proper colouring of G where every path on four vertices uses at least three colours is known as star colouring. We are interested in a version of star colouring, called star bicolouring of bipartite graphs, in which the graph to be star coloured is a bipartite graph, and the two partitions (of the bipartite graph) do not share any colour in common.

Star bicolouring of bipartite graphs arises in the context of computing or approximating sparse Jacobian matrices of mappings of the form $f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^n$ efficiently in nonlinear optimisation and nonlinear equations solving [2,3,4,5,6,7,8].

The input for star bicolouring is a bipartite graph $G=(L\cup R,E)$, where L and R are the two sets of vertices corresponding to the bipartition, and $E\subseteq L\times R$ is the set of edges. We will describe in Section 2 the construction of this bipartite graph for approximating sparse Jacobian matrices. The goal is to assign a minimum number of colours to the vertices of the bipartite graph such that (i) the colouring is proper, and vertices connected by an edge have different colours; (ii) every path over four vertices uses at least three different colours; and (iii) the vertices in L and the vertices in R do not share a colour. Note that (iii) implies (ii).

Constraint (ii) is also referred to as the path colouring constraint. Without the path colouring constraint, two colours suffice to star bicolour any bipartite graph. With the path colouring constraint, the number of colours needed is large. Consider the complete bipartite graph $K_{n,n}$. In any colouring that uses at most $n-1$ colours, there are some two vertices on each side in the bipartition that obtain the same colour. The path over these four vertices is not properly coloured. Thus the number of colours needed for star bicolouring is of the order as the number of nodes in the bipartite graph.

Related Work: An acyclic colouring of graph G is a proper colouring in which every cycle uses at least three different colours. Grunbaum [1] demonstrated that every planar graph can be acyclically coloured using at most nine colours. He conjectured that five colours are sufficient for the acyclic colouring of planar graphs, and Borodin [9] later proved this conjecture. Kostochka and Melnikov [10] showed that five colours are necessary for the acyclic colouring of bipartite planar graphs.

Grunbaum also introduced the concept of star colouring, a proper colouring where every path on four vertices uses at least three colours. Notably, any star colouring is also an acyclic colouring. This means that star colourings may require more colours than acyclic colourings. Limited results are available on star colourings of planar graphs. Note that star bicolouring, the problem considered here, has additional constraints: the graph is bipartite, and the colours used in the two partitions are different.

Albertson et al. [11] demonstrated that 10–20 colours are sufficient for star colouring arbitrary planar graphs. Nesetril and Ossona de Mendez [12] showed that any bipartite planar graph can be star coloured with 18 colours. They also showed that every planar graph can be star coloured with 30 colours. Additionally, Fertin et al. [13] gave such an example for grid graphs of a size of at least 4 × 4, whereas Ramamurthi and Sanders [14] provided examples of bipartite planar graphs that require five colours to be star coloured. They also showed that bipartite outerplanar graphs can be star coloured using five colours. It is NP-complete to determine if a planar bipartite graph can be star coloured using three colours [11].

Upper bounds on the star chromatic number in terms of the maximum degree have been studied extensively. Albertson et al. [11] showed an upper bound of $\le k^2-k+2$, where k is the maximum degree sufficient for star colouring. For a maximum degree of at most three, they show that seven colours suffice for star colouring. For graphs with maximum average degrees of at most $26/11,18/7,8/3$, Bu et al. [15] showed that the star chromatic number is at most four, five, and six, respectively. Fertin et al. [13] showed that $k^{3/2}$ colours suffice for star colouring, and they exhibited a graph for which $\Omega (k^3/logn)$ are needed.

Let us denote the minimum number of colours for star bicolouring of a bipartite graph $G=(L,R,E)$ with ${\chi }_s\left(G\right)$. The following general lower [5,16] and upper bounds are known.

$${\displaystyle \frac{\left|E\right|}{max\left\{\right|L|,|R\left|\right\}}}\le {\chi }_s\left(G\right)\le min\left\{\right|L|,|R\left|\right\}+1$$

(1)

The upper bound is evident, as one can always colour one side with a single colour, and the other side uses a different colour for each node. This bound is quite weak. Juedes and Jones [5] gave an approximation algorithm for the star bicolouring problem. The algorithm works by calculating distance-2 independent sets, greedily, of vertices (from either L or R) containing a vertex with the highest degree and then assigning them all to the same colour class. The choice of independent sets from L or R is based on the average maximum degree in $L,R$. This algorithm has an approximation ratio of $O\left(n^{2/3}\right)$ and a time complexity of $O\left(m^2\sqrt{n}\right)$, where n is the number of vertices, and m is the number of edges in the G.

The bipartite graphs that typically arise in the context of the applications, described in the next section, are large but sparse. Several efficient heuristic methods that perform well in practice have been proposed over the years for the star bicolouring problem [3,5,6,8]. Studies have reported successive reductions in the number of colours required for the standardised set of test matrices such as the Harwell–Boeing collection [17]. A lower bound on star colouring number is also a lower bound on the star bicolouring number (for bipartite graphs). The upper bounds computed using heuristic methods are still far from the lower bound in Equation (1). Therefore, it is natural to develop stronger lower bounds for star bicolouring, and this motivates our study.

Contributions: The main contributions of this paper include a novel method to solve the star bicolouring problem and the derivation of new results for various bipartite graphs that arise in the field of numerical optimisation. We provide an exponentially sized integer linear program (ILP) whose optimal solution has value ${\chi }_s\left(G\right)$ and which uses the linear programming (LP) relaxation to compute a lower bound on ${\chi }_s\left(G\right)$. The ILP is exponentially sized; therefore, we give a column generation method to solve the LP. The pricing problem to be solved is modelled as an ILP. We also give computationally efficient heuristic to solve the pricing problem. We use the method of iterative rounding [18] to compute an upper bound on the star bichromatic number. The computational results indicate that our lower bound obtained using the column generation procedure is close to the upper bound computed using the iterative method in practice for sparse bipartite graphs. Our method is general and can easily be adapted to handle colouring constraints on other structures. For instance, acyclic colourings of bipartite graphs can be found using the approach presented here.

To the best of our knowledge, this is the first such formulation and computational study for the star bicolouring problem.

Results:We ran small-sized computational experiments that evaluate linear programming relaxation and an iterative rounding approach to determine the star bicolouring number of bipartite graphs. The details are in Section 6.1. The algorithms were programmed in the GNU Octave and GLPK to solve the linear programming (LP) relaxation using column generation. The focus of the experiments was to assess (i) the effectiveness of column generation in computing lower bounds and to evaluate the effectiveness of the iterative rounding method to compute upper bounds for the star bicolouring number. The experiments used four types of graph families, and our results are summarised next.

Arrowhead Matrices: The diagonal entries were one, and the first row/column entries were set to one. The proposed method effectively computed good lower and upper bounds for the star bicolouring.

Random Sparse Matrices: The column generation procedure effectively determined tight lower bounds, and the iterative rounding method determined very good upper bounds for randomly generated sparse matrices (10 × 10, with an average of three nonzero entries per row).

Complete Bipartite Graphs: $K_{n,n}$ demonstrates the limitations of fractional colouring lower bounds in dense graphs. The iterative rounding method delivered reasonably good upper bounds in for the matrices tested despite the weak lower bound in Observation 1.

Harwell-Boeing Matrices: We tested the approach on three small matrices from the Harwell–Boeing collection: can-24, ibm32, and bcspwr01. The matrices have orders of 25 × 24, 24 × 32, and 24 × 39, respectively. For these matrices, we modified the iterative rounding approach. The running times for the Harwell–Boeing matrices were reasonable. However, the star bicolouring was not optimal.

We analysed the running time of the algorithms, comparing the time needed to solve the master problem versus the time needed to solve the pricing problems for both sparse and dense inputs. The column generation procedure was inefficient when many columns were added. This is because an ILP is solved to generate a column. Therefore, we proposed heuristic methods to improve efficiency, potentially sacrificing optimality for near-optimal solutions. The LP solution was not optimal, but the iterative rounding method still yielded good upper bounds for the star bicolouring number.

Structure: Section 2 discusses related research, with a brief introduction to the sparse Jacobian matrix determination problem. Section 3, Section 4 and Section 5 present the integer linear program for star bicolouring bipartite graphs, the associated pricing subproblem, and the iterative rounding method for star bicolouring. In Section 6, we present and analyse results from numerical experiments. This section also contains a heuristic algorithm for bicolouring. Section 7 concludes the paper.

2. Sparse Jacobian Determination

In this section, we provide a brief introduction to an application area that gives rise to the star bicolouring problem considered in this paper.

Many algorithms in nonlinear optimisation and nonlinear equations require the knowledge of first- or higher-order derivatives of the underlying mathematical mappings. Except for very simple functions, the hand calculation of derivatives is an error-prone and tedious process. Fortunately, there are interesting and effective alternatives such as finite differencing and algorithmic differentiation (AD) [19].

Let F be a once continuously differentiable function $F:{\mathbb{R}}^n\to {\mathbb{R}}^m$ for which the Jacobian $F^{\prime }$ evaluated at $x\in {\mathbb{R}}^n$ is sparse. Assuming that the sparsity pattern of matrix $J\equiv F^{\prime }\left(x\right)$ is available, one can define “seed matrices” $S\in {\{0,1\}}^{n\times p}$ and $W\in {\{0,1\}}^{m\times q}$ based on the given sparsity pattern and compute the products

$$B=JS \mathrm{and} C=W^{T}J$$

using algorithmic differentiation. The compressed matrices B and C are obtained via p forward passes and q reverse passes of the AD, where each “pass” requires work proportional to a small constant multiple of the cost of evaluating the mapping F at the given argument [19]. For sparse problems numbers, p and q are usually much smaller than the matrix dimension n and m, respectively. In a direct method, the nonzero entries of the Jacobian matrix can be recovered from the compressed matrices B and C by requiring that the seed matrices S and W be chosen such that, for each $J_{ij}\ne 0$, there is an index k for which

$$J_{ij}=B_{ik} \mathrm{or} J_{ij}=C_{kj}.$$

The goal is to minimise the work, i.e., to obtain suitable matrices S and W with $(p+q)$ minimised. Curtis, Powell, and Reid in a seminal paper [4] provided the first row compression algorithm (a row compression is a one-sided compression where only the seed matrix S is defined), which was later improved by Coleman and Moré [2], who provided the first graph colouring interpretation of the compression problem. The classical arrowhead matrix example demonstrates that one-sided compression may not yield the full exploitation of sparsity. Hossain and Steihaug [8] and Coleman and Verma [3] independently proposed techniques for combined column and row compression for the sparse Jacobian determination problem. The following bicolouring formulation was provided in [8]. Let $A\in {\{0,1\}}^{m\times n}$ be a matrix with a sparsity pattern identical to the Jacobian J. Define bipartite graph

$$G\left(A\right)=(L,R,E),$$

where L and R are the sets of vertices corresponding to the columns and rows of A, respectively, and E is the set of edges between vertices in $u_i\in L$ and $v_j\in R$ such that $\{u_i,v_j\}\in E$ if and only if $a_{ij}\ne 0$. Mapping $\varphi :L\cup R\to \{1,\dots ,(p+q\left)\right\}$ is a $(p+q)$ bicolouring [8] if the following conditions are satisfied:

1.

$\{u_i,v_j\}\in E$ implies that $\varphi \left(u_i\right)\ne \varphi \left(v_j\right)$.

2.

The set of colours used on vertices in L and R are disjoint, i.e., for indices i and j with $u_i\in L$ and $v_j\in R,$ $\varphi \left(u_i\right)\ne \varphi \left(v_j\right)$.

3.

Every path $u_i-v_j-u_k-v_l$ in $G\left(A\right)$ uses at least three distinct colours.

The minimum bicolouring of $G\left(A\right)$ is a $(p+q)$ bicolouring with the sum $(p+q)$ minimised. Determining the Jacobian matrix J directly from the products $JS$ and $W^{\top }J$ for appropriate seed matrices $S\in {\{0,1\}}^{n\times p}$ and $W{\{0,1\}}^{m\times q}$ with $(p+q)$ minimized has been shown to be equivalent to the minimum bicolouring of the bipartite graph $G\left(A\right)$ [8].

The $(p+q)$ bicolouring problem introduced above is also referred to as star bicolouring in the literature. The bicolouring formulation of [3,5,6] defined a “neutral” colour to indicate that the edges incident on vertices coloured with the neutral colour had already been determined by the “positive” colours. Ref. [8] showed that such neutral or redundant colours in a $(p+q)$ bicolouring can be avoided altogether by computing a complete direct cover [8]. For a comprehensive introduction to the star bicolouring and related colouring problems arising in the sparse Jacobian matrix determination problem, we refer to the SIAM Review paper [6].

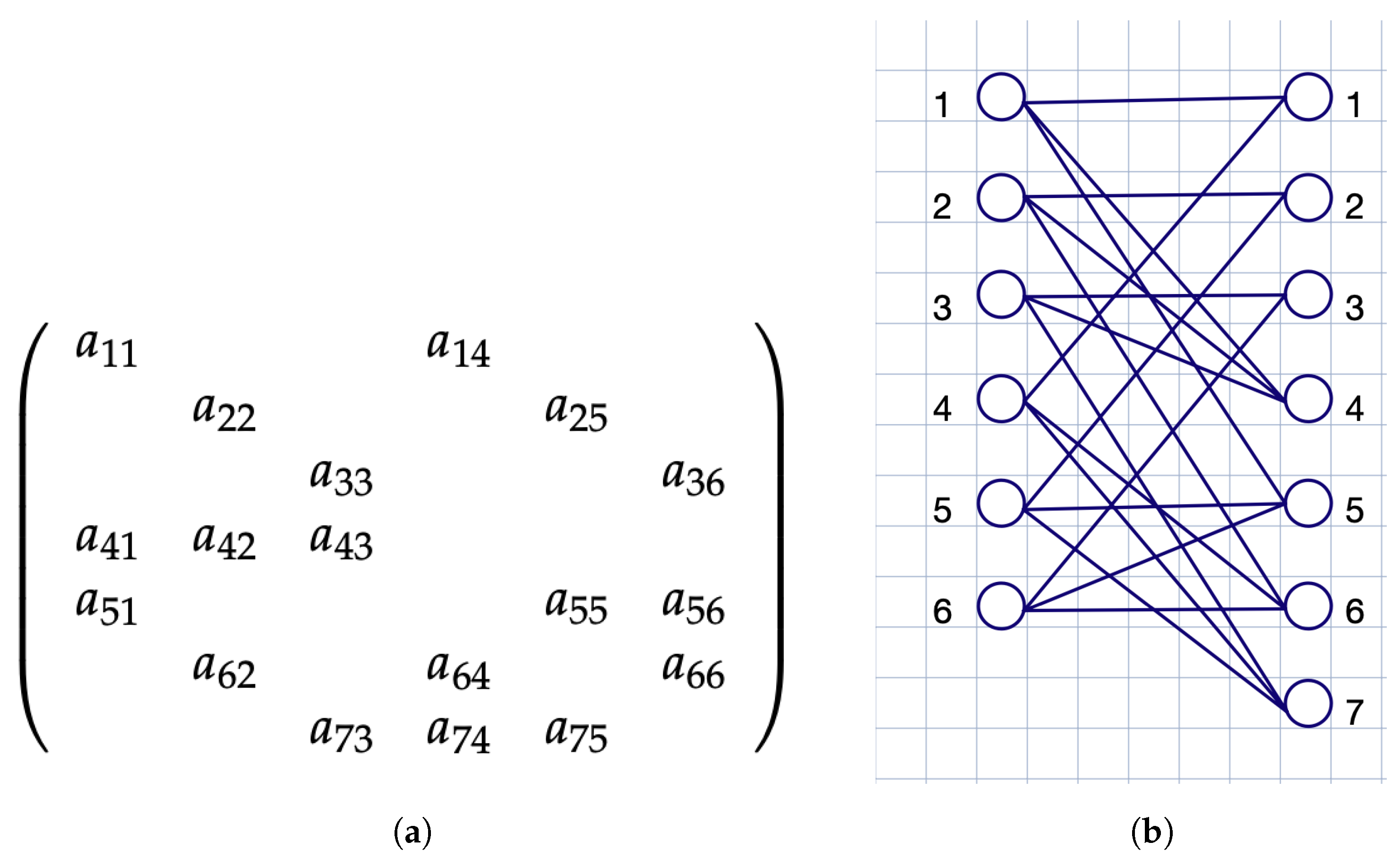
An Illustrative Example

To illustrate the main ideas in our graph colouring formulation of the sparse Jacobian matrix determination, we refer to Figure 1, where the matrix shown in (a) has six columns and seven rows. The corresponding bipartite graph associated with its sparsity pattern shown in (b) has $\left|L\right|=6$ vertices for the columns and $\left|R\right|=7$ vertices for the rows. Consider the following subsets of rows and columns:

$$\begin{array}{cc}\hfill \mathrm{Column} \mathrm{Groups}& \mathrm{Row} \mathrm{Groups}\\ \hfill \left\{1,4\right\},\left\{2,5\right\},\left\{3,6\right\}& \left\{1,2,3\right\},\left\{4,5,6,7\right\}\\ \end{array}$$

where each subset (of rows/columns) is assigned a different colour, say, colour1, colour2, colour3, colour4, colour0, reading left to right, respectively. It can be verified that this is a valid star bicolouring. Furthermore, colour0 is redundant in that all the nonzero unknowns of the Jacobian are determined from the remaining colour groups. We construct the seed matrices S and W,

$$\begin{array}{c}S=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right) \mathrm{and} W^{\top }=\left(\begin{array}{ccccccc}1& 1& 1& 0& 0& 0& 0\end{array}\right)\end{array}$$

from the colouring information, and we compute the respective compressed Jacobian.

$$\begin{array}{cc}B=JS=\left(\begin{array}{ccc}{a}_{11}+a_{14}& 0& 0\\ 0& a_{22}+a_{25}& 0\\ 0& 0& a_{33}+a_{36}\\ a_{41}& a_{42}& a_{43}\\ a_{51}& a_{55}& a_{56}\\ a_{64}& a_{62}& a_{66}\\ a_{74}& a_{75}& a_{73}\end{array}\right),& C=W^{\top }J=\left(\begin{array}{cccccc}{a}_{11}& a_{22}& a_{33}& a_{14}& a_{25}& a_{36}\end{array}\right)\end{array}$$

As commented earlier, we have omitted the colouring information from colour0 in the seed matrix W. It can be directly verified that each nonzero unknown appears unperturbed as an entry in one of the two compressed matrices. Hence, the Jacobian is fully determined from the two compressed matrices with a prior knowledge of the sparsity pattern. The example matrix used here was originally proposed by Stanley Eisenstat and requires at least six Forward AD Passes in a one-sided compression, since the associated column intersection graph is a complete graph on six vertices [8]. Therefore, the bicolouring method saves two AD Passes.

For column compression (of A or $A^{\top }$), a satisfactory lower bound on the number of matrix–vector products (or AD passes) is given by ${max}_i{\rho }_i$, where ${\rho }_i$ denotes the number of nonzero entries in row i. An easily computed lower bound on the number of “positive” colours has been derived in [16] $\lceil {\displaystyle \frac{nnz}{max\{m,n\}}}\rceil$ by using a consistency argument in solving the system of linear equations defined by the products $B=JS \mathrm{and} C=W^{\top }J$. Juedes and Jones derive the same bound using a graph theoretic argument [5]. The primary motivation for the current work is to derive a formal framework for the lower and upper bounds for the star bicolouring problem. Analogous to the work of [7], our ILP formulation of the star bicolouring does not distinguish between colours to keep the integer linear program simple.

3. ILP for Star Bicolouring

We used the set cover formulation for the colouring problem, with additional constraints on paths. For $s\subseteq L,R$, let $x_s$ be a binary variable. If $x_s$ is 1, then all the vertices in s have the same colour. The following is an integer programming formulation for the star colouring problem. Denote as P the set of length-four paths in graph G and as $\mathcal{P}(·)$ the power set.

$$\begin{array}{cc}\hfill min& \sum _{a\in \mathcal{P}\left(L\right)}{x}_a+\sum _{b\in \mathcal{P}\left(R\right)}{x}_b\hfill \\ \hfill & \sum _{a\in \mathcal{P}\left(L\right):v\in a}{x}_a=1\hfill & \hfill \forall v\in L\\ \hfill & \sum _{b\in \mathcal{P}\left(R\right):v\in b}{x}_b=1\hfill & \hfill \forall v\in R\\ \hfill & \sum _{s\cap p\ne \varphi }{x}_s\ge 3\hfill & \hfill \forall p\in P\\ \hfill & x_s\in \{0,1\}\hfill & \hfill \forall s\in \mathcal{P}\left(L\right),\mathcal{P}\left(R\right).\end{array}$$

The first two constraints are the ‘proper’ colouring constraints. They state that each node must be assigned a unique colour, and the two sides of the bipartite graph do not share a colour. The first two equality constraints also ensure that the sets chosen as the solution to the integer program above are a partition of the vertex set. The last constraint ensures that each path has at least three colours. To see this, suppose for the sake of contradiction that some path p is not properly coloured, but the last constraint is satisfied for path p. There are at least three sets $a,b,c$ that have empty intersection with path p. Sets $a,b,c$ do not have a common intersection pairwise. Therefore, at least three nodes in p obtain distinct colours. If we drop the last set of integrality constraints in the ILP above, then the problem is referred to as the fractional star colouring problem. The optimum value to the fractional star colouring instance G, denoted as ${\chi }_{fs}$, is a lower bound on ${\chi }_s\left(G\right)$. We compute ${\chi }_{fs}$ using column generation. The ILP formulation above is exponential in the size of the graph.

We examine the integrality gap of this formulation next. For a bipartite graph G, the ratio $g\left(G\right)={\displaystyle \frac{{\chi }_s\left(G\right)}{{\chi }_{fs}\left(G\right)}}$ is known as the integrality gap for instance G. The integrality gap for star bicolouring is the maximum integrality gap over all the inputs, which are ${max}_{G}g\left(G\right)$. We note that the integraliy gap of the formulation is unbounded. Let $K_{n,n}$ be the complete bipartite graph on $2n$ vertices, where the two partitions are of the same size n.

Observation: 1.

The integrality gap for $K_{n,n}$ is $O\left(n\right)$—more precisely, $g\left(K_{n,n}\right)\ge n/4.$

Note that if a total of $n-1$ colours are used; then, each side in the bipartition has some two vertices of the same colour. This means that there is a path of over four vertices that is two-coloured. Hence, $\chi \left(s\right)\left(G\right)\ge n.$ Next, we give a feasible solution to the LP relaxation with an objective value of four. The size of the power sets $\mathcal{P}\left(L\right)$ and $\mathcal{P}\left(R\right)$ is $2^n$ each. Each vertex $v\in L\left(R\right)$ belongs to $2^{n-1}$ subsets in $\mathcal{P}\left(L\right)\left(\mathcal{P}\right(R\left)\right)$. Consider a fractional solution in which for each $s\in \mathcal{P}\left(L\right)\cup \mathcal{P}\left(R\right)$, $x_s=2/2^n.$ For each vertex $v\in L$ we have,

$$\sum _{s\in \mathcal{P}\left(L\right):v\in s}{x}_s=2^{n-1}\ast 2/2^n=1.$$

The same holds for $v\in R$.

So, the first two constraints are satisfied by this solution. For each path p, there are two vertices in L and two in $R.$ The subsets of $L\left(R\right)$ that intersect path p can be divided into three groups: ones that contain exactly one of the two vertices from the path and ones that contain exactly two vertices in that path. The number of each such subset is $2^{n-2}$. Therefore, the total number of subsets of L intersecting p is $3\ast 2^{n-2}.$ Similar reasoning holds for R. Therefore, ${\sum }_{s:s\cap p\ne \varphi }{x}_s\ge 2/2^n\ast (6\ast 2^{n-2})=3.$ So, the solution $x_s=2/2^n$ is feasible. The value of the objective function is $2\ast 2^n\ast 2/2^n=4.$

4. Column Generation—Pricing Problem

Gilmore and Gomory [20] proposed a column generation technique to solve problems with a large number of variables/columns. The column generation algorithm is effective when the columns corresponding to variables are combinatorial objects such as cycles, tours, paths, and subtrees. The idea is to start with a few columns that give a feasible solution that is not necessarily optimal. The primal with a small number of columns is known as the restricted master problem (RMP). A new column is generated by solving a pricing subproblem instead of searching for possible columns not present in the RMP. The addition of the new column (with a negative reduced cost) improves the value of the solution to the primal problem. The pricing subproblem is an optimisation problem. At times, it is a linear programming problem [21]. The pricing subproblem aims to find a column with a negative reduced cost. This is similar to the pricing step of the simplex method for finding a nonbasic variable with a negative reduced cost. If the minimum reduced cost is non-negative, the algorithm halts; otherwise, the new column is added to the restricted master problem, and the process iterates.

The goal of the pricing problem is to find a new column for the LP that, when added to the current solution, will reduce the objective function value. In this case, the pricing problem is formulated as an integer linear program (ILP). This ILP seeks to find a new set of vertices to colour with a single colour that satisfies the star bicolouring constraints and that has a negative reduced cost.

We compute ${\chi }_{fs}$ by introducing columns with negative reduced costs in the basis one at a time. The column insertion/exchange process is implicit in the simplex method. It was noted by Dantzig and Wolfe that a separate optimization problem (the pricing problem) can be solved to determine the column with a negative reduced cost [21]. Let $r,c$ be the size of the two partitions, and let $p=\left|P\right|$ be the number of paths in the bipartite graph. Then, a column C of incidence matrix is a 0/1 vector of length $r+c+p$. First, $r+c$ components of C correspond to vertices. They identify the subset of vertices s that are assigned the same colour. There are two entries $i,j$ such that $1\le i\le r$ and $r+1\le j\le r+c$ cannot simultaneously be 1. Otherwise, the two sides share a colour. The remaining p entries in the column indicate whether path $P_i$ contains one of the nodes in the set s. Let $\pi$ be the vector of dual values to the LP relaxation above. The pricing problem can now be cast as the following ILP. $P_i$ refers to the $i^{th}$ path below.

$$\begin{array}{cc}\hfill max& \sum _{i=1}^{r+c+p}{\pi }_i{x}_i\hfill \end{array}$$

(2)

$$\begin{array}{cc}{x}_i+x_j\le 1\hfill & \hfill \forall i\in [1\dots r], j\in [r+1\dots r+c]\end{array}$$

(3)

$$\begin{array}{cc}{x}_{r+c+i}\le \sum _{j\in P_i}{x}_j\hfill & \hfill \forall i\in [1\dots p]\end{array}$$

(4)

$$\begin{array}{cc}{x}_j\le x_{r+c+i}\hfill & \hfill \forall j\in P_i\end{array}$$

(5)

$$\begin{array}{cc}{x}_i\in \{0,1\}\hfill & \hfill \forall i\in [1\dots r+c+p]\end{array}$$

(6)

If the optimal solution $x^{\ast }$ to the ILP above has a value strictly larger than 1, then introducing a column, given by the optimal solution to the pricing problem, in the existing basis will lead to an improved solution for the master problem.

5. Iterative Rounding for Star Bicolouring

We used iterative rounding to convert the fractional colouring into an integral colouring. The iterative rounding technique has been used widely to give approximation algorithms for a variety of problems (see [18]). In each iteration, we pick a variable, one with the largest fractional value, and set it to 1, as shown in the pseudo-code below:

1.

Solve the LP relaxation using column generation.

2.

If all the variables are integral, then GOTO END.

3.

Let x be the variable with the largest fractional value. Set $x=1$. This can be done by either addition of a constraint in the basis or by changing the lower bound on x to 1. GOTO Step 1.

4.

END.

The number of iterations that column generation is called in Step 1 is bounded by the number of subsets. In a subsequent section, we will examine another heuristic for choosing the variable to round in Step 3.

6. Computational Results

All computations were carried on an AMD Athlon (TM) II X4 630 2.8 GHz quad-core CPU with 4 GB of memory, running x86-64 GNU/Linux (AMD: Santa Clara, CA, USA). The proof of concept code was written in GNU Octave 3.8.1 and used GLPK 4.52 to solve the LP and the Mixed Integer Linear Program (MILP) subproblems. The code is not the most optimized in the sense that the master problem was solved using a call to glpk after the addition of a column. The code can be further optimized for production systems. In the tables to follow, UB refers to the integral colouring constructed using iterative rounding. LB refers to the the optimal solution ${\chi }_{fs}$ to the master problem. The number of rows (columns) in a matrix is referred to by r(c). The number of nonzeros in a matrix is denoted by ‘nnz’. ‘Paths’ denotes the number of paths over four vertices in the bipartite graph. The bipartite graphs themselves are specified by a matrix M. The rows and columns of M correspond to the vertices, and nonzero entries correspond to edges. The bipartite graphs that we consider need not be planar.

6.1. MILP for the Pricing Problem

In this section, we report the lower and the upper bounds for some families of bipartite graphs. We consider the graphs arising from arrowhead matrices, sparse matrices, and with a constant number of nonzeros in each row. Our goal is to present evidence that the column generation procedure is effective at computing good lower and upper bounds on the star chromatic number for sparse bipartite graphs. We used existing solvers (LP, MILP) available in Octave GLPK, and we did not address efficient implementation of the column generation procedure.

6.1.1. Arrowhead Matrices

Arrowhead matrices are defined as matrices with entries in the main diagonal, the first row, and the first column is 1. The table below shows the results for arrowhead matrices of small orders. The minimum number of colours required for an arrowhead matrix is four.

Order	UB	LB	r	c	nnz	nnz/max(r,c)	Paths
2	3	3	2	2	4	2	1
3	5	3	3	3	7	2.3333	8
4	4	3.3333	4	4	10	2.5	21
5	5	3.3333	5	5	13	2.6	40
6	5	3.4000	6	6	16	2.6666	65
7	5	3.4400	7	7	19	2.7142	96
8	5	3.4667	8	8	22	2.75	133
9	7	3.4762	9	9	25	2.7777	176
10	5	3.5000	10	10	28	2.8	225
11	6	3.5000	11	11	31	2.818	280

6.1.2. Random Sparse Matrices

We considered random matrices of the order $10\times 10$ with three nonzero entries in each row on average. In Octave notation, the matrix is generated as M = 3/10*ones(10,10) > rand(10,10).

Instance	UB	LB	r	c	nnz	nnz/(r+c)	Paths
1	7	3.3667	10	10	29	2.9	145
2	7	3.4227	10	10	33	3.3	165
3	5	3.3333	10	10	21	2.1	56
4	8	3.4000	10	10	29	2.9	145
5	9	3.4167	10	10	27	2.7	132
6	7	3.4127	10	10	27	2.7	131
7	7	3.3333	10	10	27	2.7	128
8	11	3.6333	10	10	42	4.2	442
9	9	3.4635	10	10	34	3.4	264
10	7	3.4167	10	10	34	3.4	213

6.1.3. Complete Bipartite Graphs

Here, we study the complete bipartite graphs. As expected, the fractional colouring lower bound is quite weak for dense graphs. But, the matrices that we are interested in are sparse. The iterative rounding procedure generated a solution worse then the trivial upper bound of $n+1$. The colouring generated contains $n+2$ colours in all the instances considered below. As $K_{n,n}$ requires at least n colours, a colouring number of $n+2$ is ‘quite good’ from an approximation point of view.

Order	UB	LB	r	c	nnz	nnz/max(r,c)	Paths
2	3	3	2	2	4	2	1
3	5	3	3	3	9	3	9
4	6	3.3333	4	4	16	4	36
5	7	3.3333	5	5	25	5	100
6	8	3.5000	6	6	36	6	225
7	9	3.5000	7	7	49	7	441

6.2. Heuristic for the Pricing Problem

Recall that the vertices in L are indexed as $[1\dots r]$, and the vertices in R are indexed as $[r+1\dots n]$, where n is the total number of vertices in the bipartite graph. There are p paths indexed as $[1\dots p]$. The solution to the pricing problem is a vector y such that $\pi y$ is maximum, and y does not contain any two vertices from L and R. The dual values ${\pi }_1,{\pi }_2,\dots ,{\pi }_n$ are unconstrained, they can be positive or negative, as the corresponding primal constraints are held at equality in any feasible solution. The dual values ${\pi }_{n+1},\dots ,{\pi }_{n+p}$ are constrained to be positive. Variables $y_{n+i}$ come out to 1 if any vertex on path i is chosen. Stated otherwise, if path i contains vertices $a,b,c,d$, then $y_{n+i}$ is 1 if any of $y_a,y_b,y_c,y_d$ are 1. Without loss of generality, assume that we are working with set L. Then $y_c,y_d$ are 0. The following bounds on $y_{n+i}$ are immediate for an integral y. Recall that $P_i$ refers to the $i^{th}$ path.

$$1/2(y_a+y_b)\le y_{n+i}\le (y_a+y_b)$$

Our objective ${\sum }_{i=1}^{n+p}{\pi }_i{y}_i$ comes out to

$$\ge \sum _{i=1}^n{\pi }_i{y}_i+\sum _{i=1}^{p}1/2(\sum _{j\in P_i}{y}_j){\pi }_{n+i}$$

Rearranging the terms, we obtain

$$\ge \sum _{i=1}^n{y}_i({\pi }_i+1/2\sum _{j:i\in P_j}{\pi }_{n+j}).$$

(7)

Our heuristic is to find the set in L or R using the expression (7). In each iteration of the pricing problem, we choose all nodes i for which ${\pi }_i+1/2{\sum }_{j:i\in P_j}{\pi }_{n+j}>0$, with the rationale being, if $y_i$ is 1, then the minimum contribution due to each vertex to our objective is positive (${\pi }_i+1/2{\sum }_{j:i\in P_j}{\pi }_{n+j})$.

The pricing heuristic takes $O(n+p)$ time, where n is the number of nodes, and p is the number of paths. The number of paths can be considerably more than the number of vertices. It is possible to reduce the running time of the heuristic to $O\left(n\right)$ by dropping off the computation of the term $1/2{\sum }_{j:i\in P_j}{\pi }_j$. This is equivalent to choosing nodes with positive dual values. However this bound is not effective, and even for Arrowhead matrices of order n, the upper bound computed using iterative rounding is $n+1$.

Next, we present simulation results when the pricing problem is solved heuristically. We report only on the order of the growth of the running times and the integral colouring constructed using the iterative rounding approach. The fractional numbers are not meaningful, as the pricing problem is not solved exactly, though they are close to the optimal LP solution ${\chi }_{fs}$.

6.2.1. Arrowhead Matrices

As noted before, the minimum number of colours required for arrowhead matrices is four. When the pricing problem was being solved exactly, the iterative colouring number was at times larger than five. The iterative colouring number is smaller here.

order	UB	fractional	r	c	nnz	nnz/max(r,c)	#paths	r (A)	c (A)
4	5	5	4	4	10	2.5	21	29	20
5	5	3.6500	5	5	13	2.6	40	50	38
6	5	5	6	6	16	2.6666	65	77	44
7	4	5.1429	7	7	19	2.7142	96	110	47
8	5	3.8923	8	8	22	2.75	133	149	75
9	5	6	9	9	25	2.7777	176	194	89
10	5	4.1494	10	10	28	2.8	225	245	108
11	5	4.7634	11	11	31	2.818	280	302	117
15	5	4.2168	15	15	43	2.8666	560	590	232

The profile data for an arrowhead matrix of order $15\times 15$ are

#	Function Attr	Time (s)	Calls
31	glpk	10.136	162
15	colgen	0.151	5
16	glpk	0.074	162
35	pricing	0.047	152

The glpk values are the calls made to solve the master problem in function colgen. The pricing subproblem was solved in function pricing. The procedure is quite efficient compared to the MILP approach for solving the pricing subproblem.

6.2.2. Sparse Random Matrices

For comparison with earlier data, we considered sparse matrices of order $10\times 10$ with three nonzeros in each row on average. The matrix was generated as earlier: M = 3/10*ones(10,10) > rand(10,10).

id	UB	fractional	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)
1	9	3.9258	10	10	29	2.9	151	171	99
2	9	5.8500	10	10	30	3	168	188	88
3	10	4.7929	10	10	32	3.2	189	209	116
4	7	4.4950	10	10	25	2.5	110	130	94
5	9	3.9993	10	10	29	2.9	131	151	112
6	8	4.4209	10	10	27	2.7	117	137	105
7	12	9	10	10	39	3.9	349	369	102
8	11	3.8893	10	10	30	2	161	181	101
9	8	5.1064	10	10	29	2.9	147	167	95

The profile data for a random matrix of order $20\times 20$, for a total of 11 runs, are

#	Function Attr	Time (s)	Calls
31	glpk	247.862	2985
16	colgen	2.952	99
17	glpk	1.064	2985

On average, a $20\times 20$ random sparse matrix can be coloured in under 25 s.

6.2.3. Dense Matrices

We considered $K_{n,n}$ for the varying order. The iterative colouring number and the matrix characteristics are listed below.

Order	UB	fractional	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)
4	5	5	4	4	16	4	36	44	19
5	7	5.5000	5	5	25	5	100	110	20
6	9	5.4000	6	6	36	6	225	237	40
7	11	7	7	7	49	7	441	455	42
8	9	8	8	8	64	8	784	800	41
9	11	5.5250	9	9	81	9	1296	1314	70

The profile data for $K_{9,9}$ are below.

#	Function Attr	Time (s)	Calls
31	glpk	38.635	56
15	colgen	0.116	3

6.2.4. HB Collection

We also tested our approach on three small-sized matrices from the Harwell–Boeing collection. For matrices with orders larger than $25\times 25$, we set all the variables with maximum fractional value to 1 as opposed to setting a single variable with maximum fractional value to 1 in each iteration. This was done to reduce the number of calls to the column generation procedure colgen. It is to be noted that iterative rounding still satisfied the first n equality constraints in the master problem. No two sets that were rounded up to 1 share a node in any iteration. We did not worry about this intersection when a single variable was rounded to 1 in each iteration.

Matrix	UB	r	c	nnz	nnz/max(r,c)	#paths	r (A)	c (A)	time (s)
can-24	25	24	24	160	6.6666	4038	4086	428	447.829
ibm32	24	32	32	126	3.9375	1364	1428	757	679.309
bcspwr01	24	39	39	131	3.3589	756	834	1170	437.11

The running times are reasonable, but the quality of colouring leaves room for improvement.

6.3. Heuristic for Pricing and Variable Choice

In the textbook description of the iterative rounding algorithm, the variable with the largest fractional value is chosen to be promoted to 1. Other heuristic choices may work well depending on the problem structure. Here, we studied the performance of one such natural heuristic. For each vertex v, let $w\left(v\right)$ be the number of paths of length four that contain v. We chose the variable $x_s$ such that, for the corresponding set S, the total weight ${\sum }_{v\in S}w\left(v\right)$ would be maximum over all fractional $x_s$. The heuristic does not change the order of the running time of the algorithm. In fact, it takes considerably less time to compute the colouring, as the heuristic tries to ensure that a number of constraints are satisfied in each iteration. This reduces the number of iterations in practice.

6.3.1. Arrowhead Matrices

As shown below, the combined heuristics discovered near-optimal colouring for arrowhead matrices. The running time was considerably reduced.

order	UB	fractional	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)	time (s)
4	5	4	4	4	10	2.5	21	29	17	0.052947
5	6	3.9412	5	5	13	2.6	40	50	33	0.068423
6	5	4.5857	6	6	16	2.6666	65	77	47	0.113911
7	5	6.5556	7	7	19	2.7124	96	110	53	0.126811
8	4	4.8162	8	8	22	2.75	133	149	69	0.20742
9	5	4.8889	9	9	25	2.7777	176	194	113	0.862311
10	5	4.5594	10	10	28	2.8	225	245	113	1.07937
11	5	4.8495	11	11	31	2.8181	280	302	117	1.16417
15	5	4.2168	15	15	43	2.8666	560	590	232	17.7683

6.3.2. $K_{n,n}$

The combined heuristic discovered the optimal solution for the complete bipartite graphs listed below. It should be noted that with the textbook rounding scheme, the algorithm did not lead to optimal colouring for $K_{n,n}$ considered below [18].

Order	UB	fractional	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)	time (s)
4	5	5	4	4	16	4	36	44	12	0.026814
5	6	6	5	5	25	5	100	110	14	0.0416431
6	7	7	6	6	36	6	225	237	18	0.0516698
7	8	8	7	7	49	7	441	455	20	0.0581229
8	9	9	8	8	64	8	784	800	24	0.100278
9	10	10	9	9	81	9	1296	1314	26	0.195343
15	16	16	15	15	225	15	11,025	11,055	44	6.91999

6.3.3. Sparse Random Matrices

We considered sparse matrices of the order $20\times 20$ with three nonzeros in each row on average. Each matrix was generated as earlier: M = 3/10*ones(15,15) > rand(15,15). The table below shows that the heuristics were relatively faster and generated better colourings compared to the standard rounding scheme.

id	UB	fractional	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)	time (s)
1	16	18	20	20	63	3.15	624	664	283	22.8783
2	14	20	20	20	66	3.3	472	512	353	31.3333
3	19	20	20	20	74	3.7	759	799	402	40.2153
4	13	18	20	20	51	2.55	276	316	280	6.61416
5	17	11.4029	20	20	61	3.05	426	466	294	16.4601
6	14	20	20	20	61	3.05	386	426	352	19.4864
7	18	18	20	20	70	3.5	686	726	272	12.6688
8	13	20	20	20	62	3.1	443	483	339	14.8033
9	13	20	20	20	59	2.95	364	404	347	21.3914
10	18	20	20	20	59	2.95	473	513	307	21.0117
11	14	18	20	20	59	2.95	372	412	296	15.4549

6.3.4. HB Collection

For the three small matrices from the Harwell–Boeing collection, we saw a reduction in the number of colours required for one matrix and an increase for the other. The running times were more or less the same as previously.

Matrix	UB	r	c	nnz	nnz/max(r,c)	Paths	r (A)	c (A)	time (s)
can-24	25	24	24	160	6.6666	4038	40860	408	495.198
ibm32	19	32	32	126	3.9375	1364	1428	679	486.722
bcspwr01	29	39	39	131	3.3589	756	834	1040	742.322

7. Conclusions

Determining the minimum number of colours required for star bicolouring a bipartite graph is important in numerical optimisation and in solving nonlinear equations. Specifically, minimising the colours in the star bicolouring of a bipartite graph is equivalent to minimising the computational work in determining the Jacobian matrix. We provided an exponentially sized ILP formulation to determine a lower bound on the minimum number of colours needed for star bicolouring. Due to the exponential size of the ILP, a column generation method was employed to solve the LP relaxation. The column with a negative reduced cost was determined by solving an ILP. We used an iterative rounding technique to convert a fractional star bicolouring solution to an integral one. This approach involved repeatedly solving the LP relaxation and rounding fractional variables to integer values until a feasible integral solution was obtained. We evaluated the approach on various types of bipartite graphs: arrowhead matrices, sparse random matrices, complete bipartite graphs, and matrices from the Harwell–Boeing collection. The results suggest that for sparse bipartite graphs, the proposed method effectively determines lower and upper bounds for the minimum number of colours. The computational cost of solving the pricing problem using ILP is high. However, this is not a limiting factor, as the star bicolouring was computed only once under the assumption that the Jacobian did not change. More efficient, potentially combinatorial or heuristic approaches for solving the pricing problem will be explored in future work.