Abstract
The training phase of a deep learning neural network (DLNN) is a computationally demanding process, particularly for models comprising multiple layers of intermediate neurons.This paper presents a novel approach to accelerating DLNN training using the particle swarm optimisation (PSO) algorithm, which exploits the GPGPU architecture and the Apache Spark analytics engine for large-scale data processing tasks. PSO is a bio-inspired stochastic optimisation method whose objective is to iteratively enhance the solution to a (usually complex) problem by approximating a given objective. The expensive fitness evaluation and updating of particle positions can be supported more effectively by parallel processing. Nevertheless, the parallelisation of an efficient PSO is not a simple process due to the complexity of the computations performed on the swarm of particles and the iterative execution of the algorithm until a solution close to the objective with minimal error is achieved. In this study, two forms of parallelisation have been developed for the PSO algorithm, both of which are designed for execution in a distributed execution environment. The synchronous parallel PSO implementation guarantees consistency but may result in idle time due to global synchronisation. In contrast, the asynchronous parallel PSO approach reduces the necessity for global synchronization, thereby enhancing execution time and making it more appropriate for large datasets and distributed environments such as Apache Spark. The two variants of PSO have been implemented with the objective of distributing the computational load supported by the algorithm across the different executor nodes of the Spark cluster to effectively achieve coarse-grained parallelism. The result is a significant performance improvement over current sequential variants of PSO.
1. Introduction
The growing utilisation of applications with intelligence at the edge, in addition to the cloud, requires the optimisation of load balancing, workload placement, and resource provisioning, particularly when resource-intensive tasks must be relocated from the cloud. This is due to the fact that, in a DLNN, comprising numerous intermediate layers of neurons and a substantial quantity of input data, the computational burden is significant and requires evaluating the fitness of a very large number of particles. Recent studies [1,2,3] have demonstrated that the training phase of neural networks can be expedited through the utilisation of different approaches [4,5,6,7,8,9,10].
In our proposal, we utilise the Apache Spark analytics engine, which supports RDDs (resilient distributed datasets) and the use of lambda functions, as well as the functional programming style inherent in the Scala and Java languages, running on a Java JVM. The fundamental assumption that forms the basis of our research is to extend the existing studies on the parallelisation of the particle swarm optimization (PSO) algorithm beyond the scope of the previous research [11,12,13,14,15,16]. The objective is to develop a novel algorithm that facilitates greater autonomy between the constituent processes, enabling them to specialise in the parallel computation of algorithmic functions without the necessity for synchronization points or the aggregation of partial results across such processes. Accordingly, this algorithm will demonstrate superior performance in the handling and processing of massive datasets on distributed systems, exhibiting both scalability and fault tolerance.
PSO is one of a number of algorithms that are categorised as metaheuristics. These are a class of optimisation algorithms that are commonly used to find near-optimal solutions to complex optimisation problems. The utilisation of PSO in an edge computing environment enables the training of DLNNs on edge devices, as opposed to in centralised data centres or cloud environments. Edge devices are typically situated in closer proximity to the data source, including IoT devices, smartphones, and embedded systems, and often possess limited computational resources in comparison to traditional centralised hosts. Nevertheless, the realisation of an effective PSO implementation is not a simple process, due to the complexity of the computations that are conducted on the particle swarm and their own iterative execution until convergence to a solution that is close to the target with minimal error is achieved.
Among the numerous recent publications on the acceleration of particle swarms on graphic processing units, the works of Hangfeng Liu [17] and Chuan-Chi Wang et al. [18] are worthy of particular mention. Despite the fact that these CUDA-based GPU PSO acceleration proposals offer extremely low latency for computation and memory access, as well as high throughput for suitable workloads, they suffer from poor scalability, which is limited by the resources of a single GPU or a small number of GPUs. It is therefore necessary to exercise caution when managing memory and ensuring synchronization. In contrast, distributed implementations of PSO with Apache Spark are horizontally scalable, allowing for the addition of nodes to the cluster and thus making them suitable for processing very large datasets. However, they can exhibit diminishing returns due to networking and synchronisation overheads.
The application of PSO for the purpose of solving forecasting problems has been the subject of several studies. For example, ref. [16] put forth a DLNN model with an efficient feature fusion for the purpose of predicting building power consumption. The researchers integrated temperature data and employed an innovative feature fusion technique to enhance the learning capacity of the model. The study conducted comprehensive ablation studies to assess the performance of the proposed model. In [12], a hybrid PSO and NN algorithm was proposed for building energy prediction and two modifications were introduced to enhance its performance. The proposed model was compared with simple ANN and SVN, and the effectiveness of the approach was demonstrated. In a previous study [14] PSO was employed in combination with an Adaptive Neuro–Fuzzy Inference System (ANFIS) to ascertain the industrial energy demand in Turkey. The PSO algorithm was employed for the purpose of optimising the parameters of the ANFIS model. A common approach to modifying PSO is to adjust its control parameters, as discussed in [13]. An alternative approach is to combine PSO with other metaheuristic algorithms, including Genetic Algorithms (GAs) [19] and differential evolution (DE) [20]. Furthermore, parallelisation and multi-swarm techniques have been employed to enhance the performance of PSO, which has been deployed for energy consumption forecasting in a range of domains. To illustrate, Ref. [15] put forth a multi-swarm PSO algorithm for static workflow scheduling in cloud fog environments. Their approach demonstrated superior performance in terms of execution time and stability compared to classical PSO [21] and other existing approaches. The deployment of particle swarm optimization (PSO) in a distributed optimization framework such as Apache Spark is mainly justified by its simplicity and its rapid convergence to optimal or near-optimal solutions. This makes it a cost-effective choice for large-scale optimization problems. Furthermore, the communication overhead of PSO is minimal in comparison to other EAs, which may require more complex interactions between individuals, for example, crossover operations in genetic algorithms.
The asynchronous execution of fitness calculations and velocity updates can markedly enhance the efficiency of PSO parallelisation by minimising the time spent on synchronization points. This approach serves to mitigate the latency introduced by the utilisation of instructions analogous to those employed by CUDA’s _syncthreads(), whilst simultaneously capitalising upon the GPU’s capacity to manage concurrent tasks in an efficient manner. Asynchronous versions of the parallel PSO are proposed in [2] and, more recently, in [4]. These versions create full independence between particles moving to their next position with the information available to them at the time of evaluation, without the need to synchronise all particles to obtain the best global values before iteration. This motivates the parallelization of the PSO algorithm according to two different parallelisation schemes, which are discussed in detail in Section 3. The initial parallelization scheme, designated DSPSO, adheres to a synchronous approach. This entails that the best global position found by the particles is globally updated prior the commencement of the subsequent iteration of the algorithm. The DSPSO method was observed to be more efficient in the context of medium-sized datasets, comprising less than (<40,000 data). The second implementation, designated DAPSO, represents an asynchronous parallel variant of the PSO algorithm. In comparison to DSPSO, it exhibited a reduction in execution time for extensive datasets (exceeding >170,000 data points) and demonstrated enhanced scalability and elasticity in response to increases in dataset size. Both variants, DSPSO and DAPSO, have been implemented for a distributed execution environment. This allows the particle fitness computation and particle position update to be distributed across the different execution nodes of a standalone Spark cluster, effectively achieving coarse-grained parallelism. This approach has resulted in significant performance gains over the current sequential variants of PSO.
Furthermore, a library has been developed in Scala that implements the parallelisation of the learning process of multilayer feed-forward neural networks using both variants of the PSO algorithm. This enables the distributed training of a neural network using Spark. As part of the case study, the neural networks were programmed to solve two distinct problems: a regression problem and a classification problem. This allows us to verify that the implemented networks work correctly. While the time cost of developing optimisation strategies is a common challenge faced by researchers, the use of a GPU parallel strategy has the potential to help mitigate this problem. The objective of this study is to exploit the strengths of the PSO algorithm by implementing and utilising two variants of the PSO, distributed synchronously and asynchronously. This approach is expected to enhance the training of the DLNN, enabling more efficient prediction of energy consumption and improved accuracy in solving complex classification problems.
Conversely, we evaluate the efficiency of the implemented DSPSO and DAPSO variants in comparison to their sequential counterparts, as a direct comparison with alternative learning algorithms is not reasonable.
The main contributions of this work are as follows:
- A novel distributed particle swarm optimisation (PSO) algorithm was proposed to enhance the scalability and fault tolerance of its implementation in distributed systems.
- The algorithm has been implemented on Apache Spark, which enables the algorithm to efficiently handle and process large datasets in a distributed environment.
- Two variants of Parallel PSO were proposed. DSPSO is more efficient for medium-sized datasets, while DAPSO is faster and more scalable than DSPSO for large datasets.
- A new library in Scala has been developed with the objective of facilitating distributed training of neural networks using Spark. This library implements the parallelisation of the learning process for ANN, thereby enabling distributed training of ANNs on a distributed processing environment such as Apache Spark..
- A performance comparison of DSPSO and DAPSO against their sequential counterparts was conducted, and their potential for application to edge computing was explored. This was done in order to enable DLNN training on edge devices with limited computational resources.
- This paper illustrates the benefits of utilising GPU parallel strategies to reduce the time cost of developing optimisation strategies. While this paper primarily focuses on distributed implementations using Apache Spark, the findings are also applicable to other GPU parallelisation techniques.
By addressing these issues, this paper makes a contribution to the optimisation of load balancing, workload placement, and resource provisioning for resource-intensive tasks in distributed and edge computing environments.
The rest of the paper is organized as follows: Section 2 provides an overview of PSO algorithms, their common control structure, and the sources of complexity associated with their parallelization on distributed computing platforms. Section 3 presents the two parallelisations of the PSO proposed in this work, along with pseudocodes for both variants. It also provides general details about the algorithms, taking into account the conditions imposed by many-core GPU architectures. These algorithms are used for training the DLNN and obtaining the measurements and plots shown in the results section, which test the algorithms’ efficiency and scalability. Section 4 presents the results of the experiments and offers a discussion of the two case studies proposed for the evaluation of a Spark-based implementation of both PSO variants. The final section provides a summary of the conclusions and outlines future work.
2. Particle Swarm Optimization
Particle swarm optimization (PSO) is a bio-inspired stochastic optimization algorithm. The PSO algorithm was invented by Eberhart and Kennedy in 1995 [21], with the objective of iteratively improving a randomly generated solution with respect to a given objective. The algorithm focuses on a population of entities called particles. A particle is represented as a point in an N-dimensional Cartesian coordinate system (Figure 1). Particles are abstractions of entities that are at a position and move with a velocity. Initially, these particles are randomly assigned a position and velocity. Furthermore, each particle is also responsible for tracking its personal best position and global best position . Consequently, at each time point t, the positions and velocities of each particle are updated as follows:
In this context, the terms and are non-negative constants, referred to as learning factors, while the variables and represent two random numbers with uniform distribution within the interval . Additionally, it is important to consider the inertia constant, denoted by the variable , which enables the balancing of local and global search. This variable is constrained to the interval . Furthermore, the maximum velocity, denoted by , is constrained to the values of .
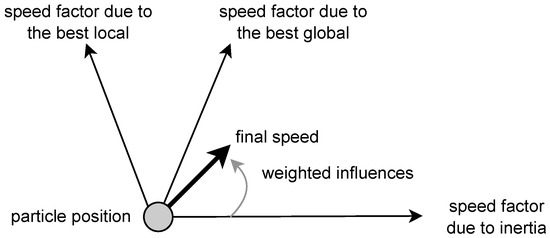
Figure 1.
Graphical representation of a PSO algorithm’s particle with its attributes.
In addition, each particle keeps a record of the personal best position and global best position achieved by other particles up to that time and detected by the current particle. The best position is identified through the utilisation of the fitness function, which represents the objective to be optimized. Consequently, the term “best” in this context denotes the minimum or maximum value identified during the evaluation of the particle position in conjunction with the fitness function defined within the algorithm. The fitness function is a type of objective function employed to ascertain the proximity of a given solution to achieving the objective initially established in the algorithm.
PSO employs an iterative process whereby all particles are evaluated for their fitness in relation to the local and global best positions. The way in which the best position and the fitness attained by the other particles are ascertained hinges on the presence of shared memory between them. In such instances, the determination is conducted by accessing a global variable. In distributed systems, the absence of shared memory necessitates the implementation of a message passing protocol to ensure, to a first approximation, the coherence of the global best position value for all particles.
The proposed solution for the implementation of the distributed parallel PSO algorithm entails the design and implementation of two variants of the distributed PSO, which we have called distributed synchronous (DSPSO) and distributed asynchronous (DAPSO).
2.1. Complexity of the PSO and Approaches for Its Parallelization in a Cluster
The classical PSO algorithm works on the basis of iterations, during which the particles are evaluated in terms of their fitness and their personal and global best positions. At the end of each iteration, the velocities and positions of all particles must be updated, which presents a challenge for the asynchronous parallel implementation of such an update.
The use of PSO to address prediction and classification problems has the following advantages and disadvantages:
- As a metaheuristic algorithm, no specific knowledge of the problem to be solved is required.
- As an evolutionary algorithm, it is readily adaptable to parallel computing structures.
- The ability to work with multiple solutions allows for a higher tolerance for local maxima or minima.
- The primary disadvantage of the PSO algorithm is that it requires a significant amount of time to reach an optimal solution for complex problems, particularly those with a large number of particles or dimensions. This is due to the necessity of conducting numerous evaluations of the fitness function, which can be a considerable drawback in terms of computational efficiency.
The parallelisation of the PSO algorithm for the training of neural networks represents a pioneering strategy with multiple applications and significant benefits in the domain of machine learning and artificial intelligence. The benefits of parallelising the PSO algorithm, as outlined in reference [22], include enhanced efficiency, faster solution exploration, enhanced scalability, increased accuracy and a reduction in development time.
The first variant considered here is the distributed synchronous PSO (DSPSO), which uses the most common form of iteration. First, the fitness of each particle is evaluated using the particle’s position as input. Subsequently, the best personal position of each particle is determined to identify the best global position among all particles. Finally, the position and velocity of each particle are updated based on the best global position.
The second variant, which was subjected to comprehensive study and subsequently implemented in its entirety, is the so-called distributed asynchronous PSO (DAPSO). It differs from the previous variant in that it updates the position and velocity of particles as soon as their fitness is evaluated. Consequently, the position and velocity of each particle may not be necessarily consistent across all the nodes in the cluster during the computation of this variant of the PSO. The distributed nature of this computation will result in a faster execution time than that of DSPSO, without affecting the validity of the final result. This is due to the communication that will be established between the processes responsible for updating the position and velocity of each particle, which will ensure that the global position and velocity detected by each particle in the algorithm will be consistent, as it will adhere to a unique value.
2.2. Background Information Based on Recent Research on the Parallelization of the PSO
The parallelisation of the PSO algorithm for training neural networks represents an efficient and scalable approach with several practical applications and notable advantages. These include the ability to process a DLNN with many layers of intermediate neurons in a much shorter time frame than with traditional implementations that do not take advantage of the massive parallelism currently provided by multicomputers or, in our study, by general graphics processing units (GPGPU). This renders it an invaluable instrument in the domain of machine learning and optimisation, particularly in comparison with other methodological approaches to solving the same problem, as illustrated in Table 1.

Table 1.
Selected approaches for improvement in PSO algorithm implementation to date.
There are currently many implementations of PSO using the CUDA/GPU environment. One of them, called PSO-GPU [1], presents a generic and customisable implementation of a PSO algorithm on top of the CUDA architecture. This implementation exploits the thousands of threads running on the GPU to reduce execution time and increase performance through parallel processing.
FastPSO [17] implements the PSO algorithm using CUDA with a Structure of Arrays (SoA) layout. This approach is designed to achieve optimal performance by leveraging shared memory and tensor cores. The utilisation of shared memory markedly enhances the performance of the PSO algorithm on GPUs by minimising the latency associated with global memory accesses. However, shared memory is inherently constrained in capacity. To address this challenge, the provided implementation segments the arrays into tiles of smaller size than the original arrays. Each tile is loaded into shared memory, and tile-wise instructions are executed at high speeds. The results are stored back into global memory. To further improve performance, tensor cores are used for matrix operations. This approach ensures efficient parallel processing and optimises the GPU’s capabilities to accelerate the PSO algorithm.
The CuPSO [18] algorithm employs a shared queue for all thread blocks and per-block data structures to store the intermediate results, allowing each block of the GPU grid to independently track and store the best solutions found by the threads within that block. This design leverages both shared memory for collaboration and per-block storage for independent evaluation, thereby facilitating efficient parallel optimisation. One strategy currently employed to enhance the performance of PSO algorithm implementations is to adjust their control parameters, thus, achieving enhanced efficiency without compromising precision in determining the objective, as described in [13].
In the article [2], an asynchronous parallel PSO algorithm is presented that significantly improves parallel efficiency. The majority of parallel PSO algorithms have been implemented synchronously, where the fitness functions, positions, and velocities of all particles are evaluated in one iteration before the next iteration starts. These latter approaches usually result in a modest increase in the speed of parallel computation over the sequential variant in cases where a heterogeneous parallel environment is used and/or where the execution time depends on the element of the algorithm being computed. Therefore, the work presented in [2] was the first work to investigate the potential of an an asynchronous parallel implementation of the PSO algorithm and, at the time of its publication, it demonstrated a notable enhancement of PSO implementations. This approach had analogous objectives to those of our study, which concentrated on accelerating the asynchronous PSO algorithm in comparison to the synchronous one. In [20], a hybrid mechanism combining Spark-based particle swarm optimization (PSO) and differential evolution (DE) algorithms (SparkPSODE) is proposed. SparkPSODE is a parallel algorithm that employs RDD and island models. The island model is used to divide the global population into several subpopulations, which are used to reduce the computational time corresponding to the RDD partitions. The efficiency of SparkPSODE is demonstrated through its application to a set of global large-scale optimization benchmark problems. The experimental results, which are presented in comparison with other algorithms, reveal that SparkPSODE achieves superior performance in terms of speedup, scalability and robustness.
There is currently work using Spark to parallelize the genetic algorithm and tackle the problem with very good results. For instance, in reference [3], the GPU is employed to parallelise an evolutionary training algorithm. Additionally, one potential avenue for addressing the challenge of climate change and its ramifications is to examine the energy consumption patterns of buildings. The study of energy consumption can facilitate the acquisition of pertinent information, which may be employed to inform more efficacious decision-making processes and, consequently, to reduce costs and pollution. However, ANN training models based on evolutionary methods generally have a high computational cost in terms of time. This work exploits the high-performance computing capabilities of GPUs to parallelise the PSO evolutionary algorithm for the purpose of training the ANN.
Another area of intense research is the parallel implementation of PSO for very large datasets. Conventional methodologies are inadequate for meeting the demands of big data environments for prediction. Consequently, a hybrid distributed computing framework has been developed in Apache Spark [23] for wind speed prediction using a distributed computing strategy. The framework is capable of dividing the speed data into RDD groups and operating them in parallel.
The primary issue with these solutions is that they are constrained to the parallelisation of the algorithm’s repetitive processes, based on a population size of the dataset.This is essential for accurately computing the population fitness function, but it does not extend to further advances in terms of parallel structuring of the algorithm’s subtasks, which is one of the main objectives of our study.
3. PSO Parallelization Based on Apache Spark and RDD Applied to Training Neural Networks
In order to conduct this study, it is necessary to implement an effective parallelisation of the PSO algorithm according to the conditions imposed by many-core GPGPU architectures.This will be followed by the training of a neural network and the subsequent acquisition of the measurements required for the following section. The mean square error (MSE) is employed for continuous variables to compute fitness, which will be utilised to address regression problems. In contrast, the measures of binary cross-entropy and precision are applied to categorical variables in classification. The two variants of the distributed PSO implemented in this study were employed to train neural networks to solve two distinct problems: (a) a regression problem aimed at predicting the consumption of the institution’s buildings in kilowatt hours and (b) a classification problem based on the utilisation of a Kaggle dataset to ascertain whether a set of people are smokers or not, using a binary objective.
3.1. Distributed Synchronous PSO
The distributed synchronous PSO adopts the master/worker paradigm, wherein the master maintains the state of the entire swarm and sends particles to each worker node for evaluation, as illustrated in the workflows depicted in Figure 2. Furthermore, the master is responsible for managing the synchronization required to control specific iterations of DSPSO. Addtionally, it updates global data relevant to the algorithm through variables of the type Broadcast, which are a type of read-only shared variables, e.g., from the Scala programming language, that are cached and available on all nodes in a Spark cluster to be accessed or used by tasks.
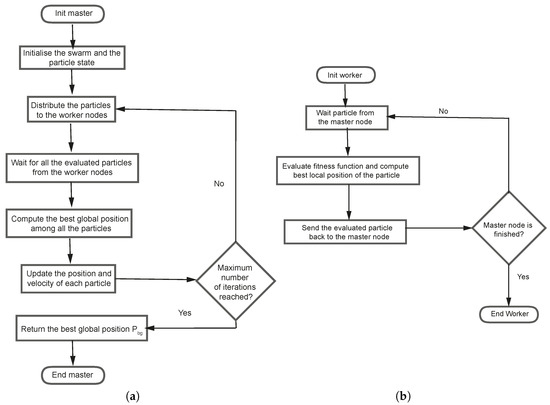
Figure 2.
(a) Master node flowchart in DSPSO. (b) Flowchart of a worker node.
Each Worker node should perform the following steps:
- Wait for a particle to be received from the master node;
- Compute the fitness function f and update the personal best position ;
- Return the evaluated particle to the master node;
- Return to step 1 if the master node has not finished yet.
The Master node process includes the following steps:
- Initialize particle parameters, positions, and velocities;
- Assign the current iteration and initialize the state of the swarm and the received particles;
- Start the current iteration by distributing all particles to the free executors;
- Wait for the results of all evaluated particles (with the calculated fitness function) and the personal best position for this iteration, which is what means the for … sync pseudo-sentence;
- Compute the global best position for each incoming particle until there are no more particles left;
- Updating the velocity vector and the position vector of each particle based on the personal best position and the global best position found by all particles;
- Go back to step 3 if the last iteration has not been reached;
- Return the global best position .
The tasks performed by the master and worker nodes in this variant are given by Algorithm 1 expressed in pseudocode.
| Algorithm 1 DSPSO pseudocode. |
|
The function fitnessEval (f) is executed on the worker nodes and is responsible for receiving a particle, calculating the fitness of the current particle position using the variable broadVar of the aforementioned Scala Broadcast type, and then updating the personal best position of the particle. It finally returns this value. The pseudocode employs the closure anonymous function type, which encompasses the execution environment.
3.2. Distributed Asynchronous PSO
The distinction between DAPSO and DSPSO lies in their differing approaches to synchronization. Unlike DSPSO, DAPSO does not employ iterations that link all particles together. In DAPSO, each particle is evaluated and moves independently of the other particles. This serves to further increase its degree of independence.
This section will present the implemented DAPSO variant, which is distributed and asynchronous and uses Spark RDDs to parallelise the updating of particle positions and velocities. Spark is employed with its low granularity transformations, with the result that the swarm is divided into several subswarms, which are then evaluated in parallel. The particles are updated according to the current state of the entire swarm. This entails modifying both the position and the velocity of each particle as soon as the fitness function is evaluated. In this process, the best global position thus far is taken into account. This results in the complete independence between the particles, which move to their subsequent position with the information available to them at the time of each particle’s evaluation.
The DAPSO distributed algorithm follows the master-worker paradigm, whereby a master node is responsible for coordinating the remaining worker nodes, which are tasked with performing the computations sent by the master. This is illustrated in the workflows presented in Figure 3.
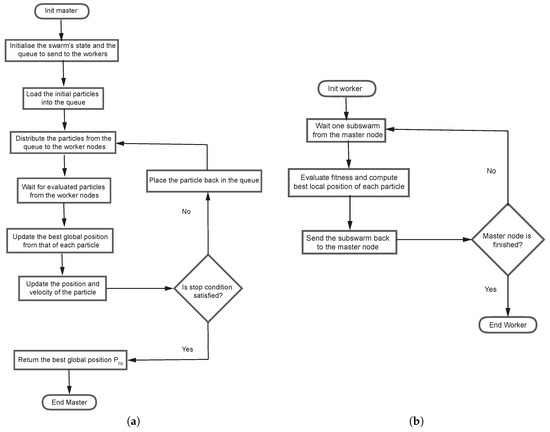
Figure 3.
(a) Master node flowchart with subswarms of size 1. (b) Flowchart of a worker node.
Each particle in the swarm is capable of autonomous movement and evaluation of the fitness function.
The Master node process consists of the following steps:
- Initializing the particle parameters, positions, and velocities;
- Initializing the state of the swarm, as well as that of a particle queue to send to the worker nodes;
- Loading the initial particles into the queue;
- Distributing the particles from the queue to the workers;
- Waiting for the results of all evaluated particles (with the calculated fitness function) of the subswarm and the personal best position for this iteration;
- Updating the velocity vector and position vector of each particle based on the personal best position and the global best position found by all the particles;
- Placing the particles back in the queue and returning to step 4 if the stop condition is not satisfied;
- Returning the best global position .
The process of worker nodes is similar to the synchronous variant, but it now processes particle subswarms.
In order to enhance efficiency, the DAPSO algorithm employs an abstraction called SuperRDD, which comprises a set of interdependent particles operating within the cluster as a unified subswarm. In the context of Spark, a SuperRDD is constituted by the aggregation of multiple individual RDD particles, which are subsequently evaluated.
In contrast with the previous DSPSO algorithm, whereby each particle was sent to the cluster independently, the particles are now grouped into subswarms of variable size, i.e. between one and the total number of particles, denoted by variable S. As the size of the subswarm increases, the asynchrony of the algorithm is reduced, as a greater number of particles become dependent on each other. Nevertheless, this modification enhances the efficiency of the algorithm by removing some of the computational overhead associated with communication between nodes. In this way, and as the number of particles in the RDD increases, fewer Spark jobs need to be scheduled, reducing the communication overhead. However, this results in the particles having to wait for the rest of the RDD to be evaluated by the node.
As for the implementation in Scala and Spark, two fundamental concepts are essential for optimal functionality: an accumulator that receives the evaluated particle data (or SuperRDDs) from the worker nodes and a mechanism for distributing these particles to the worker nodes. The best global position update is performed by the variable broadVar, as in the DSPSO algorithm. The accumulator implementation (see Appendix A) consists of a communication channel with the capacity to store lists of numbers. In what follows, this will be referred to as the accumulator channel. Upon evaluating the particles, the worker nodes send a list containing the particle position, its velocity, and processed fitness value to the aforementioned channel. The master node then reads these elements to update the particle values.
In the pseudocode of the entire DAPSO Algorithm 2, represents the channel to fetch particles in one batch from the worker nodes, and is the fitness update channel to transmit the updated values of these particles.
| Algorithm 2 DAPSO pseudocode. |
|
3.3. Apache Spark Implementation
This work was not programmed directly in CUDA; rather, it employed an open source data processing framework with a processor cluster architecture that enables massively parallel and distributed computations. This is the main feature of the analytics engine, known as Apache Spark [24], which has been designed for efficient processing and analysis of large amounts of data. It is capable of achieving scalability and quality of service when implementing machine learning models. Spark is implemented in the Scala programming language, which was the rationale behind its selection as the primary programming language in this study.
Spark is the most widely used tool for performing scalable computational tasks and data science based on RDDs resilient distributed datasets, as described by Matei Zaharia in reference [25]. RDDs are fault-tolerant parallel structures that allow intermediate results to be persisted in memory and manipulated by a set of operators. They are particularly useful for applications where intermediate computations are reused across multiple computations, such as most iterative machine learning algorithms, including logistic regression, K-means and others. Formally, an RDD is a partitioned collection of read-only records that can be created from deterministic operations on data in stable storage or from other RDDs. In order to distinguish these operations from others, we will refer to them as “transformations”. Examples of these transformations are mapping, filtering, and joining.
There are three important features associated with an RDD: dependencies, partitions (with associated locality information), and transformations (comprising computational functions). Firstly, a list of dependencies is needed, which informs Spark how to construct an RDD from its inputs. In the event that results require replication, Spark can rebuild an RDD from these dependencies and replicate operations on it. This feature endows RDDs with elasticity. Secondly, the partitioning feature enables Spark to distribute the computational parallelisation process across the available cluster executors. Thirdly, transformations are applied to data frames in the following manner: Partition Iterator[T]. Partitioning is a process that involves the division of an initial set of data into smaller, manageable units, which are then processed individually. This is achieved through the use of an iterator, which is a data structure that allows for the sequential traversal of a collection of elements. All three are fundamental to the simple RDD programming model, which forms the foundation for all top-level application programming functionality. This model is based on a functional programming paradigm.
The main goal of RDDs is to define a programmatic interface that can provide fault tolerance in an efficient way. Conversely, distributed shared memory architectures provide an interface based on fine-grained updates of mutable states, such as cells in a table. The only way to ensuring fault tolerance in the latter is to replicate data to other machines or to log updates on nodes.However, this is an inefficient process, particularly in comparison to the approach employed by Spark RDDs.
In the main loop of a neural network implemented for solving prediction problems, three distinct components can be identified: the computation of the fitness function, the updating of local and global data values, and finally, the output of results that can change over time and have time constraints. To achieve the required efficiency of the ANN training implementation, Spark RDDs were employed for both DSPSO and DAPSO implementations. This information can be used to compute the particle’s fitness and update its personal best position. These computations are performed in parallel for each particle in the RDD using Spark. Rather than setting these data along with each task on the cluster executors, Spark distributes the broadcast variables to the machines using efficient broadcast algorithms. This approach is taken in order to achieve lower communication costs in massively parallel applications.
In the Spark environment, data are fragmented into partitions, which represent the elementary unit of data that can be processed autonomously. RDDs are divided into these partitions and distributed across the cluster. The number of partitions is generally adjustable and contingent upon factors such as data volume and the availability of resources within the system. Each RDD is associated with partitions that enable Spark to distribute the parallelisation of computation across executors in the Spark cluster. In certain instances, such as when reading from HDFS, Spark employs locality information to direct work to executors in proximity to the data. This approach reduces the volume of data transmitted over the network (Figure 4), achieving greater efficiency than the map/reduce distributed computing model and Hadoop.
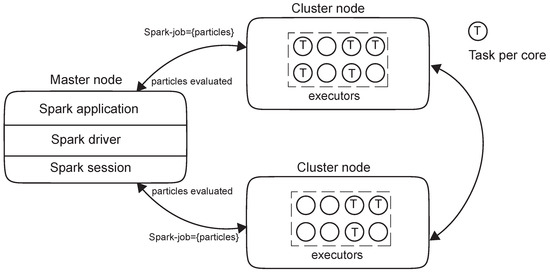
Figure 4.
Spark components communicating through the Spark driver.
4. Case Study and Applications
In order to evaluate a Spark-based implementation that can run on both CPUs and GPUs, it is proposed that two cases be considered. This would allow the full advantage to be taken of the performance capabilities that the DSPSO and DAPSO variants of the PSO algorithm implementation can offer. The following is a summary of the advantages that can be realised through the implementation of a PSO distributed approach:
- Efficiency improvement: The process of parallelisation makes use of the computing power of multiple resources, including graphics processing units (CPUs or GPUs) or central processing units (CPUs), thereby accelerating the training process.
- Faster scanning: The parallelisation of the PSO algorithm permits the evaluation of multiple solutions to be evaluated simultaneously, thereby speeding up the search for optimal solutions in a large parameter space.
- Scalability: The algorithm is capable of handling problems of varying size and complexity, from small tasks to large challenges with massive datasets.
- Increased accuracy: By enabling faster and more efficient training, parallelisation of the PSO algorithm can improve the quality of the neural network models that are designed, resulting in better performance in prediction and classification tasks.
- Reduction in development time: The parallelisation of processes results in a reduction in the time required for the development of machine learning models, due to the acceleration of the training process.
The prediction of energy consumption (EC) across a range of buildings represents a formidable challenge. This explains why companies and governments around the world are directing their attention to this field of study. One of the most crucial areas to address this issue is the prediction of energy consumption (EC) at the local level. This may be exemplified by buildings associated with an organisation or institution. This enables the foresight of prospective occurrences, thereby facilitating the formulation of more judicious resolutions pertaining to energy conservation. In this context, the analysis of energy consumption data recorded by sensors at an individual level, in specific areas or buildings, has the potential to reduce energy costs and mitigate the environmental impact derived from energy production.
In addition to its application to regression problems, the PSO algorithm can also be used to train neural networks focused on solving classification problems. In order to further illustrate this point, we propose here a second case study, for which we have taken a dataset from the Kaggle platform corresponding to the Binary Prediction of Smoker Status using Bio-Signals [26] challenge.
4.1. A Regression Problem: Prediction of the Electrical Consumption of Institution Buildings
In order to achieve the performance required for the application to make meaningful predictions about energy consumption, we propose two Spark-based model implementations for useful EC predictions over a given time horizon.These include, for example, hourly power consumption during a month, as the one presented here, which can be run on both CPUs and GPUs to leverage the full potential of the implementation in terms of performance.
Several studies have provided solutions to the problem of predicting EC in buildings using EAs and ANN. Nevertheless, the principal disadvantage of these techniques is that they exhibit an unreliable response time. To date, a number of approaches have been proposed in a effort to address this challenge, as evidenced by the work presented in [27]. Consequently, there is a significant scope for further research in this field. The paper by [1] presents a number of GPU-based EA implementations, exploring the impact of different data structures, configurations, data sizes, and complexities on the problem solving process.
The two variants DSPSO and DAPSO, implemented in Scala/Spark in this study were employed to address a 24-h EC prediction problem in buildings, which represents one of the fundamental objectives of this research. To evaluate their performance, we used the PSO algorithm as a baseline and the Spark tool to train a perceptron-type neural network to predict the EC of a set of buildings (Figure 5 and Figure 6) at the University of Granada (UGr), Spain. The performance of both implementations of the algorithm was evaluated by measuring the execution time required to run each of them. To this end, an abstraction was employed for each benchmark, whereby a monotonic clock was used for all measurements. This approach ensured that the time was always recorded in a forward direction and was not affected by hardware issues, such as time skew.
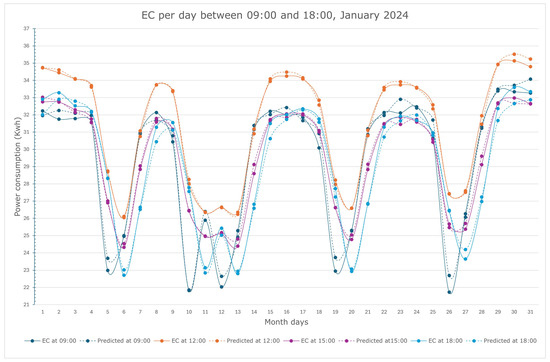
Figure 5.
Prediction with DSPSO implementation of the hourly power consumed during the month of January 2024 by a group of UGr buildings.
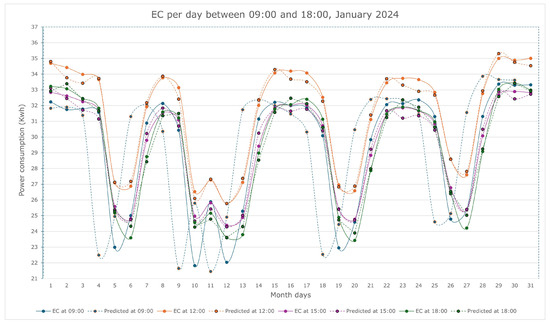
Figure 6.
Prediction with DAPSO implementation of the hourly power consumed during the month of January 2024 by a group of UGr buildings.
4.2. Performance Evaluation of a Regression Problem Implementation
A pre-fed neural network with a single hidden and output layer was created, the parameters of which are given in Table 2. The network was trained using the DSPSO and DAPSO variants and the original sequential PSO algorithm, after which the weights of the final network were extracted into a file of weight vectors of dimension 5224. The mean number of predictions made per hour was 7296, with the mean run times (based on five runs for each measurement) presented in Table 3.

Table 2.
Parameters of the trained neural network for the EC prediction.

Table 3.
Execution times for EC power predictions with 175104 samples.
To assess the performance of the two variants of the PSO algorithm, the parameters given in Table 2 were employed. The input of the neural network is derived from the attributes in the rows of the dataset provided by the institution.These include the day, hour, and minute of the measurement, as well as the scheduled and wasted power for that day, with a 10-minute resolution. The realized implementation of the DSPSO algorithm was evaluated with a synchronous individual update of particle velocity/position, while the DAPSO algorithm with an asynchronous distributed update of the same parameters. In addition, to assess the performance of each algorithm, only one of the initial two constant parameters outlined in Table 4 was increased at a time, while the other was maintained at its original value in each trial.

Table 4.
Parameter configuration for the EC prediction of a set of buildings for the DSPSO and DAPSO variants.
In this way, we were able to analyse how each algorithm responds to an increase in the complexity of a single parameter, namely the number of particles, the number of iterations and the conditions under which they are applied.
Figure 7a demonstrates that, for a limited number of particles (100, 200), the distributed algorithms (DSPSO and DAPSO) exhibit a marginal improvement in performance compared to the traditional sequential PSO algorithm.This is attributed to the overhead introduced by Spark, which affects the overall measured performance. Nevertheless, when the number of particles is increased to 500 and 1000, the distributed algorithms DAPSO and DSPSO are markedly faster, achieving, on average, four and two times the speedup of the traditional PSO, respectively. Figure 7b illustrates a comparable trend to that observed in the preceding graph, as the number of iterations is increased. The execution time of DAPSO is observed to be similar to that of DSPSO for (500, 1000) iterations. This is due to the fact that the number of Spark jobs generated is primarily dependent on the number of iterations. Consequently, for a high number of iterations, the number of jobs generated is comparable for both algorithms. This differs from the observation in Figure 7a, in which the number of iterations was held constant and the number of particles increased. It can thus be concluded that both algorithms perform well regardless of the number of iterations or particles.
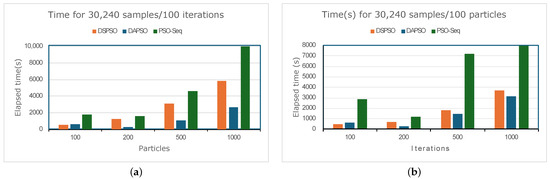
Figure 7.
Performance evaluation with change in the number of (a) particles and (b) iterations.
The performance of the distributed PSO algorithms is enhanced by using multiple executors for the parallel evaluation of particle fitness on a Spark cluster. It is evident that this performance is more visible in complex optimization problems, where the overhead incurred by Spark is negligible compared with that of traditional PSO implementations. Figure 8 illustrate the outcomes in relation to the error (MSE) observed in the assessments of both the DSPSO and the DAPSO implementations. The network was trained on 80% of the data, designated as the training set, while the remaining 20% were reserved for evaluating the error rate, designated as the test set. Figure 8a illustrates that the error values obtained by both algorithms with 100 particles are significantly higher when using 12,000 samples. This is attributable to the excessive creation of tasks when there are insufficient samples, which results in a less representative search space. Consequently, the particles may encounter difficulties in converging towards an optimal solution.
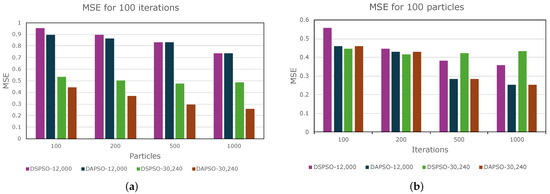
Figure 8.
Mean square error obtained with (a) 100 particles and (b) 100 iterations.
Conversely, it is evident that the error variability rises in conjunction with the number of iterations in the scan Figure 8b when using 12,000 samples This is a consequence of the modifications made to the best position and fitness value computed by the particles. Nevertheless, as the number of particles increases, the errors converge to the same values as the asynchronous algorithm (DAPSO) for 12,000 samples. These findings indicate that the reliability of both implemented variants mainly depends on the quality of the training dataset. The DAPSO variant is generally more accurate, even with fewer samples. The graphs in Figure 8 demonstrate that, for more than 30,240 samples DAPSO produces the lowest error for higher values of the number of particles and iterations.
In order to gain a deeper understanding of the underlying mechanisms and to assess the performance of the algorithms in a more comprehensive manner, it is essential to consider the convergence curves for the regression problem solved by both DSPSO and DAPSO variants. These curves provide valuable insights that extend beyond the mere measurement of raw performance in terms of execution time. DSPSO (Figure 9a) shows a steady enhancement in accuracy and reaches a plateau at around five iterations, indicating convergence towards a good solution. DAPSO (Figure 9b) may exhibit a rapid initial convergence, although this may be subject to fluctuations due to asynchronous updates. Eventually, it appears to stabilise at a similar point as DSPSO.
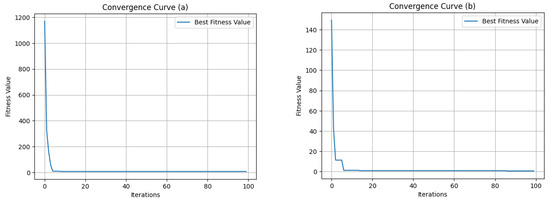
Figure 9.
Convergence curves for each implemented variant: (a) DSPSO and (b) DAPSO.
4.3. A Classification Problem: Binary Prediction of Smoker Status Using Bio-Signals
In a manner analogous to the preceding case study, which was based on the solution of a regression problem, we will demonstrate the correct functioning of the library of neural networks created in Scala for the PSO algorithm and the DSPSO and DAPSO variants. The implemented classes build three neural networks that solve a classification problem using the Smokers dataset from Kaggle and construct three classifiers with the parameter values in Table 5. The first network is trained with PSO, the second with DSPSO, and the third with DAPSO and four SuperRDDs. This allow us to observe that the implemented networks function correctly and compare the efficiency of DAPSO and DSPSO with that of their sequential version.

Table 5.
Parameters of the trained neural networks for Smokers classification.
Accordingly, a dataset was selected from the Kaggle platform, corresponding to a competition where the objective is to predict the binary variable “smoking” using a set of biological characteristics, including the presence of caries, the levels of haemoglobin or triglycerides. The metrics to be used were accuracy, precision, recall, and F1-score.
4.3.1. Statistical Study of Covariates
A statistical study of the covariates on the dataset was conducted using Python libraries, specifically the function from the scipy library [28] to perform the chi-squared test (Table 6) and the statsmodels library [29] to calculate the odds ratio and the relative risk. As the majority of the characteristics in the dataset are continuous, they were converted to categorical variables, with four categories created for each continuous variable, as follows:

Table 6.
Chi-squared tests for each variable.
- Low: Individuals whose scores fall between the 0th and 25th percentiles.
- Medium low: Individuals falling between the 25th percentile and 50th percentiles are classified within this category.
- Medium high: Those falling between the 50th and 75th percentiles are classified here.
- High: Those falling between the 75th and 100th percentiles are classified here.
In this case, a standard confidence level of 95% will be employed, which corresponds to a significance level of . Since the p-value is very close to 0 and much smaller than , the null hypothesis that the variables are independent in all cases will be rejected.
4.3.2. Odds Ratio Calculation
The odds ratio (OR) is a statistical measure employed to quantify the strength of the association between two events. It enables the comparison of the odds of the event occurring in one group with the odds of the event occurring in the other group. The OR is calculated using the following equation:
The odds ratio should be interpreted according to three ranges of values: OR = 1, indicating the absence of association between exposure and outcome; OR , which indicates a positive association between exposure and outcome; and OR , which indicates a negative association between exposure and outcome.
The principal findings of Table 7, which presents odds ratio values, are as follows: (1) Individuals with elevated sugar and relaxation indices are more prone to smoking than those with low indices. (2) There is a correlation between smoking and higher body weight. (3) There is a notable elevation in triglycerides (a type of blood fat) and haemoglobin, accompanied by a considerable reduction in HDL. (4) Furthermore a decrease in LDL and an increase in serum creatinine, a waste product present in the blood, is observed, albeit to a lesser extent. (5) Additionally, a significant increase in alanine aminotransferase (ALT) is evident, which is an enzyme predominantly located in the liver. An excess of ALT in the bloodstream may indicate damage to liver cells.

Table 7.
Odds ratio for categorical variables.
4.3.3. Relative Risk Calculation
Risk ratio (RR) is a statistical measure used to assess the relationship between the probability of a particular outcome in a group exposed to an event compared with a group not exposed. It is given by the following equation:
The results of the RR calculation are to be interpreted in a manner analogous to that employed for the OR calculation. In the event that the RR is equal to 1, it can be concluded that there is no association between exposure and outcome. A value of RR greater than 1 indicates a positive association, suggesting that exposure is associated with an increased risk of the outcome. A value of RR less than 1 indicates a negative association between exposure and outcome.
The principal findings in Table 8 with regard to the RR values, are corroborated by those in Table 7 and can be summarised as follows: (1) As with the previous analysis, there is an association between smoking and higher body weight. (2) Furthermore, there is an increase in blood glucose levels, although less pronounced than that observed in the odds ratio calculation. (3) As in the previous table, there is a significant increase in triglycerides and haemoglobin and a large decrease in HDL. (4) There is also an increase in serum creatinine. (5) There is also a significant increase in alanine aminotransferase (ALT) and a large increase in guanosine triphosphate (GTP).

Table 8.
Relative risk for categorical variables.
4.4. Evaluation of Classification Accuracy Based on Neural Networks Trained with the PSO
We carried out a validation process. We compared all the accuracy assessment points with the ground truth values. The calculated parameters are the next ones.
- -
- Precision: Precision is the probability value that a detected class element is valid. It is given by the following equation:
- -
- Recall: Recall is the probability value that a detected class element is detected in the ground truth. It is given by the following equation:
- -
- F1-score: This is a metric usually calculated to evaluate the performance of a binary classification model. It is given by the following equation:
The orange line in the “receiver operating characteristic” (ROC) curve (Figure 10a) represents the performance of the binary classifier, while the blue dashed line represents the performance of a random classifier.
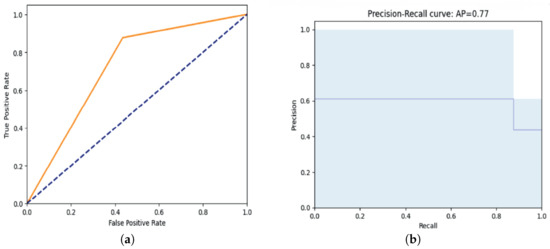
Figure 10.
Classification performance using the DAPSOshown by (a) ROC curve and (b) PR curve.
The points on the blue line in the “precision-recall” (PR) curve (Figure 10b) indicate the precision values corresponding to different recall values.This allows the changes in the precision of the classification to be observed as the recall increases. The light blue shaded area under the PR curve, also designated as Average Precision (AP), provides a unified numerical representation of the precision-recall performance. The average AP of 77% indicates that the model correctly identifies a similar percentage of positive cases in the ground truth across all recall levels.
4.5. Assessment of Implementation Performance
The recall figures obtained in Table 9 demonstrate that the model correctly identifies 74% and 77% of all positive cases, respectively, for an equal number of 100 iterations and 100 particles in the ground truth, utilising the DSPSO and PSO algorithms. The F1-score calculated for 100 particles and 100 iterations corroborates that both measures of precision and recall are consistent with the results obtained through the application of either of the two implemented variants of PSO. This demonstrates a balance between the two measures and that the results have also been obtained with performance.

Table 9.
Accuracy assessment of smoking status using bio-signals with 10 and 100 particles.
Consequently, the model appears to be robust and thus quite acceptable, as evidenced by the summary of one selected run in Table 10. Similar performance was observed for the DSPSO and DAPSO variants, along with the near 0.77 accuracy discussed above, indicating that both algorithms demonstrate good predictive performance.

Table 10.
Performance of DSPSO and DAPSO on a Spark cluster with information on the number of executors and the number of blocks.
Table 10 contains information extracted from the Apache Spark Web UI (Web UI), which is a web-based graphical interface that provides detailed information about the status and performance of running Spark applications. In particular, it shows information about the executors within the cluster, including resource utilisation, particularly the memory blocks used by the entire computation, and the activity of Spark jobs or tasks. In the context of the distributed PSO algorithms implemented in this study, each job comprises a set of particles whose fitness function is evaluated by the executor nodes. Thus, the concurrent execution of multiple jobs on the Spark cluster has been achieved, with each job representing the parallel execution of multiple tasks. In the case of the DAPSO implementation, the master node collects the results of the execution of each task from the cluster in an asynchronous manner, updates the global variables, and returns the particle to the task. This process allows for the reuse of tasks and the pursuit of improved load balancing between them. Consequently, the DAPSO approach results in a notable reduction in the number of tasks required to evaluate the fitness of each particle in the cluster. As can be observed in Table 10, a maximum of five simultaneously active tasks are required. It can be stated that DAPSO is a Spark-jobs “recycler” to a greater extent than DSPSO. Consequently, the memory usage is only 135 KiB, in comparison to the 25MiB required by DSPSO to perform the same task. It can therefore be concluded that the DAPSO variant is more suitable for execution on resource-constrained nodes in an edge architecture.
The hardware and software platforms used for the experiments are listed in Table 11.

Table 11.
The hardware and software platforms for the experiments.
5. Conclusions
The two distributed implementations of the PSO algorithm presented serve to demonstrate the feasibility of their use in training deep neural networks in a distributed environment. The asynchronous DAPSO implementation demonstrates superior performance and accuracy compared to the synchronous DSPSO implementation. It achieves this by performing the tasks of fitness evaluation and particle updating in a fully parallel and independent manner by the workers of an Apache Spark cluster, resulting in highly satisfactory results in terms of performance and scalability. It has been observed that, in cases where the number of samples is limited, the problem size may not be sufficient for DAPSO to achieve optimal performance. However, the MSE obtained with both variants is similar for a significant amount of data, and DAPSO is demonstrably superior in terms of performance to the synchronous DSPSO implementation. This is evidenced by the improvement in processing times observed in both the regression problem with 175,104 samples and the classification problem presented here. In the latter case, due to the considerable size of the dataset, comprising 127,405 samples in the training set and 68 features used for classification, a significant improvement in execution times is achieved.
In terms of implementation on an Apache Spark cluster, the DAPSO variant demonstrates superior performance compared to the DSPSO variant. While the programs developed with Spark can be executed on diverse distributed platforms, this work exclusively presents results from execution on a departmental GPU cluster. As future work, we intend to adapt the presented algorithms for deployment on alternative platforms, such as Kubernetes or Databricks.
Author Contributions
In this study, all authors contributed equally to the research and writing process, with responsibilities shared collaboratively across all stages of the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science and Innovation (Ministerio de Ciencia e Innovación) grant PID2020-112495RB-C21 (funded by MCIN/AEI /10.13039/501100011033).
Data Availability Statement
The code with the implementation of the trained neural network has been used to predict the energy consumption of a set of buildings in the University of Granada (Spain). The Scala/Spark code and the dataset used in this study are available at https://github.com/mcapeltu/PSO_Spark_Scala.git (accessed on 10 August 2024).
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | artificial neural network |
| DAPSO | distributed asynchronous PSO |
| DLNN | deep learning neural network |
| DSPSO | distributed synchronous PSO |
| EA | evolutionary algorithm |
| EC | energy consumption |
| GPGPU | general-purpose computing on graphics processing unit |
| MSE | mean squared error |
| NN | neural network |
| PSO | particle swarm optimization |
| RDD | resilient distributed dataset |
Appendix A. Accumulator Type Representation for the DAPSO Algorithm
| Code 1. Batch queue implementation. |
|
This code represents the “accumulator” component of a distributed parallel Particle Swarm Optimization (PSO) algorithm. The BatchPSO class manages batches of particle data, and the main loop processes these batches, applying the PSO algorithm and updating the best global positions and fitness.
| Code 2. Channel declaration. |
|
| Code 3. Obtaining accumulator particles and updating values. |
|
| Code 4. Distribution of particles to the worker nodes. |
|
References
- Souza, D.L.; Monteiro, G.D.; Martins, T.C.; Dmitriev, V.A.; Teixeira, O.N. PSO-GPU: Accelerating Particle Swarm Optimization in CUDA-Based Graphics Processing Units. In Proceedings of the GECCO11, Dublin, Ireland, 12–16 July 2011. [Google Scholar]
- Gerhard Venter, J.S.S. A Parallel Particle Swarm Optimization Algorithm Accelerated by Asynchronous Evaluations. In Proceedings of the 6th World Congresses of Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazil, 30 May–3 June 2005. [Google Scholar]
- Iruela, J.; Ruiz, L.; Pegalajar, M.; Capel, M. A parallel solution with GPU technology to predict energy consumption in spatially distributed buildings using evolutionary optimization and artificial neural networks. Energy Convers. Manag. 2020, 207, 112535. [Google Scholar] [CrossRef]
- Busetti, R.; El Ioini, N.; Barzegar, H.R.; Pahl, C. A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing. In Proceedings of the 13th International Conference on Cloud Computing and Services Science–CLOSER, Prague, Czech Republic, 26–28 April 2023; SciTePress–Digital Library: Setúbal, Portugal, 2023; Volume 1, pp. 194–203. [Google Scholar]
- Iruela, J.R.S.; Ruiz, L.G.B.; Capel, M.I.; Pegalajar, M.C. A TensorFlow Approach to Data Analysis for Time Series Forecasting in the Energy-Efficiency Realm. Energies 2021, 14, 4038. [Google Scholar] [CrossRef]
- Ruiz, L.; Capel, M.; Pegalajar, M. Parallel memetic algorithm for training recurrent neural networks for the energy efficiency problem. Appl. Soft Comput. 2019, 76, 356–368. [Google Scholar] [CrossRef]
- Ruiz, L.; Rueda, R.; Cuéllar, M.; Pegalajar, M. Energy consumption forecasting based on Elman neural networks with evolutive optimization. Expert Syst. Appl. 2018, 92, 380–389. [Google Scholar] [CrossRef]
- Ruiz, L.G.B.; Cuéllar, M.P.; Calvo-Flores, M.D.; Jiménez, M.D.C.P. An Application of Non-Linear Autoregressive Neural Networks to Predict Energy Consumption in Public Buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Pegalajar, M.; Ruiz, L.; Cuéllar, M.; Rueda, R. Analysis and enhanced prediction of the Spanish Electricity Network through Big Data and Machine Learning techniques. Int. J. Approx. Reason. 2021, 133, 48–59. [Google Scholar] [CrossRef]
- Criado-Ramón, D.; Ruiz, L.; Pegalajar, M. Electric demand forecasting with neural networks and symbolic time series representations. Appl. Soft Comput. 2022, 122, 108871. [Google Scholar] [CrossRef]
- Sahoo, B.M.; Amgoth, T.; Pandey, H.M. Particle swarm optimization based energy efficient clustering and sink mobility in heterogeneous wireless sensor network. Ad Hoc Netw. 2020, 106, 102237. [Google Scholar] [CrossRef]
- Malik, S.; Kim, D. Prediction-Learning Algorithm for Efficient Energy Consumption in Smart Buildings Based on Particle Regeneration and Velocity Boost in Particle Swarm Optimization Neural Networks. Energies 2018, 11, 1289. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Guleryuz, D. Determination of industrial energy demand in Turkey using MLR, ANFIS and PSO-ANFIS. J. Artif. Intell. Syst. 2021, 3, 16–34. [Google Scholar] [CrossRef]
- Subramoney, D.; Nyirenda, C.N. Multi-Swarm PSO Algorithm for Static Workflow Scheduling in Cloud-Fog Environments. IEEE Access 2022, 10, 117199–117214. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Zhang, F.; Chen, F.; Xin, Y. Building Load Forecasting Using Deep Neural Network with Efficient Feature Fusion. J. Mod. Power Syst. Clean Energy 2021, 9, 160–169. [Google Scholar] [CrossRef]
- Liu, H.; Wen, Z.; Cai, W. FastPSO: Towards Efficient Swarm Intelligence Algorithm on GPUs. In Proceedings of the 50th International Conference on Parallel Processing–ICPP 21, Lemont, IL, USA, 9–12 August 2021. [Google Scholar] [CrossRef]
- Wang, C.C.; Ho, C.Y.; Tu, C.H.; Hung, S.H. cuPSO: GPU parallelization for particle swarm optimization algorithms. In Proceedings of the SAC 22: 37th ACM/SIGAPP Symposium on Applied Computing, New York, NY, USA, 25–29 April 2022; pp. 1183–1189. [Google Scholar] [CrossRef]
- Qi, R.-X.; Wang, Z.-J.; Li, S.-Y. A Parallel Genetic Algorithm Based on Spark for Pairwise Test Suite Generationk. J. Comput. Sci. Technol. 2015. [Google Scholar] [CrossRef]
- Fan, D.; Lee, J. A Hybrid Mechanism of Particle Swarm Optimization and Differential Evolution Algorithms based on Spark. Trans. Internet Inf. Syst. 2019, 13, 5972–5989. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Waintraub, M.; Schirru, R.; Pereira, C.M. Multiprocessor modeling of parallel Particle Swarm Optimization applied to nuclear engineering problems. Prog. Nucl. Energy 2009, 51, 680–688. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, H.; Long, Z. A distributed computing framework for wind speed big data forecasting on Apache Spark. Sustain. Energy Technol. Assess. 2020, 37, 100582. [Google Scholar] [CrossRef]
- Apache Spark Foundation. Apache Spark™-Unified Engine for Large-Scale Data Analytics. 2018. Available online: https://spark.apache.org (accessed on 3 July 2024).
- Zaharia, M.; Chowdhury, M.; Das, T.; Dave, A.; Ma, J.; McCauly, M.; Franklin, M.J.; Shenker, S.; Stoica, I. Resilient Distributed Datasets: A Fault-Tolerant Abstraction for In-Memory Cluster Computing. In Proceedings of the 9th USENIX Symposium on Networked Systems Design and Implementation (NSDI 12), San Jose, CA, USA, 25–27 April 2012; pp. 15–28. [Google Scholar]
- Kaggle Community for Data Science and Machine Learning. Binary Prediction of Smoker Status using Bio-Signals Playground Series—Season 3, Episode 24. 2023. Available online: https://www.kaggle.com/competitions/playground-series-s3e24 (accessed on 10 January 2024).
- Oh, K.S.; Jung, K. GPU implementation of neural networks. Pattern Recognit. 2004, 37, 1311–1314. [Google Scholar] [CrossRef]
- Oliphant, T.; Jones, E.; Peterson, P. NumFOCUS SciPy 1.11.2, Open Source Scientific Library for Python, August 2024. Available online: https://scipy.org/ (accessed on 10 January 2024).
- Statsmodels 0.14.0, Open Source Statistical Models Library for Python, August 2024. Available online: https://www.statsmodels.org/ (accessed on 10 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).