Exploring Clique Transversal Variants on Distance-Hereditary Graphs: Computational Insights and Algorithmic Approaches

Abstract

The clique transversal problem is a critical concept in graph theory, focused on identifying a minimum subset of vertices that intersects all maximal cliques in a graph. This problem and its variations—such as the k-fold clique, $\left\{k\right\}$-clique, minus clique, and signed clique transversal problems—have received significant interest due to their theoretical importance and practical applications. This paper examines the k-fold clique, $\left\{k\right\}$-clique, minus clique, and signed clique transversal problems on distance-hereditary graphs. Known for their distinctive structural properties, distance hereditary graphs provide an ideal framework for studying these problem variants. By exploring these issues in the context of distance-hereditary graphs, this research enhances the understanding of the computational challenges and the potential for developing efficient algorithms to address these problems.

1. Introduction

Distance-hereditary graphs were first introduced and studied in the 1970s as part of the broader exploration of special graph classes characterized by specific structural properties. A graph is defined as distance-hereditary if the distance between every pair of vertices in any connected induced subgraph is the same as in the original graph. This preservation of distances under induced subgraphs has led to distance-hereditary graphs being considered an important and intriguing class within graph theory.

The concept was formally defined by Howorka in 1977 [1], who provided the initial characterization and properties of distance-hereditary graphs. This work laid the groundwork for further research into the structural and algorithmic aspects of these graphs. The 1980s and 1990s saw significant advancements in the study of distance-hereditary graphs, with researchers exploring various algorithmic applications and characterizations. For instance, Bandelt and Mulder [2] demonstrated that distance-hereditary graphs could be recognized efficiently, leading to a surge in interest in their algorithmic properties. The recognition algorithm for distance-hereditary graphs, which operates in linear time, was a notable milestone, highlighting the practical feasibility of working with these graphs in computational contexts.

The study of distance-hereditary graphs continues to be a dynamic and evolving field. One of the critical aspects of distance-hereditary graphs is the relationship with interval functions [3]. The interval function $I_G(u,v)$ in a connected graph captures the set of vertices lying on some shortest $u,v$-path, and, in distance-hereditary graphs, every induced path is indeed the shortest. This property has allowed for a novel characterization of these graphs using first-order betweenness axioms and enriching the theoretical framework surrounding them.

In addition to these foundational aspects, Cicerone et al. introduced and explored mutual-visibility in distance-hereditary graphs [4]. Mutual-visibility within a graph pertains to the visibility of vertices along the shortest paths, and it has been shown that the mutual-visibility number can be computed in linear time for distance-hereditary graphs, providing efficient algorithms for specific graph classes.

Further expanding on the properties of distance-hereditary graphs, Dragan et al.  [5] investigated the eccentricity function, demonstrating that it is almost unimodal within these graphs. This research offers a complete characterization of the centers of distance-hereditary graphs and proposes a linear-time algorithm for computing eccentricities, contributing to the efficient processing of these graphs.

The complexity of graph problems within distance-hereditary graphs has also been a subject of intense study. For instance, Ducoffe and Popa addressed the fine-grained complexity of the maximum matching problem in graphs of bounded split-width, including distance-hereditary graphs [6]. Their work answers an open question and introduces new tools for the b-matching problem and dynamic programming.

In graph isomorphism, Gavrilyuk et al. showed that the Weisfeiler-Leman algorithm effectively tests isomorphism for distance-hereditary graphs, reducing the dimension required for this class from the previously known upper bound [7]. This result enhances our ability to differentiate between graphs in this class efficiently.

Paired-domination, another key problem in graph theory, has been examined in the context of distance-hereditary graphs [8]. The work provides an $O\left(n^2\right)$-time algorithm for determining minimum paired-dominating sets.

Moreover, the recognition of distance-hereditary graphs has been explored through distributed interactive proofs [9]. The protocols for recognizing these graphs, with proof sizes as small as $O(logn)$ bits, underscore the feasibility of decentralized algorithms in graph theory.

Finally, the enumeration of distance-hereditary graphs has been advanced by Yamazaki et al. [10], who developed algorithms that are not only theoretically sound but also practical to implement. These algorithms have led to the creation of catalogs for graph classes up to 15 vertices, demonstrating the practical utility of these methods.

The clique transversal problem is a fundamental concept in graph theory, involving the identification of a minimum subset of vertices that intersects all maximal cliques in a graph. This problem, along with its variations—such as the k-fold clique, $\left\{k\right\}$-clique, minus clique, and signed clique transversal problems—has attracted significant attention due to its practical applications [11,12,13,14] and theoretical significance [15,16,17,18]. The k-fold clique, $\left\{k\right\}$-clique, minus clique, and signed clique transversal problems remain unexplored challenges for distance-hereditary graphs. This paper aims to investigate the four clique transversal problems on distance-hereditary graphs. By focusing on these specific problems, this study aims to deepen the understanding of the computational challenges associated with them and to explore the potential for developing efficient algorithms to solve them. The insights gained from this research are expected to contribute significantly to the broader field of graph theory and to provide practical tools for applications in various domains where graph-based modeling is essential.

To solve the four clique transversal problems, this paper identifies their common characteristics and introduces the $(p,d,\ell ,b)$-clique transversal problem. It demonstrates that the k-fold clique, k-clique, minus clique, and signed clique transversal problems are all special cases of the $(p,d,\ell ,b)$-clique transversal problem. This formulation provides a unified approach to solving these four problems. We then present a dynamic programming algorithm specifically designed to solve the $(p,d,\ell ,b)$-clique transversal problem.

Dynamic programming is a versatile and powerful technique for solving complex problems by breaking them down into smaller subproblems, solving all the smaller subproblems, and storing their results, and then combining their solutions to solve the original problem. It is particularly effective for optimization problems, where the goal is to find the best solution among many possible options. The key idea behind dynamic programming is to store the results of subproblems and reuse them when needed, thereby avoiding redundant calculations and significantly improving efficiency.

The development of a dynamic programming algorithm typically involves the following steps:

• Characterize the structure of an optimal solution: Identify how the optimal solution to the problem can be composed of the solutions to its subproblems. This step involves understanding the relationship between the original problem and its subproblems and how to combine the subproblem solutions to form the optimal solution for the entire problem;
• Define the recursive formula: Once the structure of the optimal solution is understood, the next step is to define the recursive relationship (or recurrence relation) that expresses the solution to the original problem in terms of the solutions to its subproblems. This formula is central to the dynamic programming approach, as it dictates how the subproblem solutions are combined;
• Compute the value of an optimal solution in a bottom-up fashion using the recursive formula;
• Analyze the time complexity: The time complexity is generally proportional to the number of subproblems multiplied by the time required to solve each subproblem.

For a fundamental understanding of dynamic programming algorithms and their examples, readers are encouraged to consult Introduction to Algorithms [19]. In this paper, our dynamic programming algorithm is capable of solving the $(p,d,\ell ,b)$-clique transversal problem in $O\left(n{\left(\omega \left(G\right)\right)}^4\right)$ time for a distance-hereditary graph G, where $\omega \left(G\right)$ is the cardinality of a maximum clique in the graph G (when the context is clear, we also use $\omega$ interchangeably).

We develop this dynamic programming algorithm by employing binary ordered decomposition trees—specifically, $PTF$-trees—of distance-hereditary graphs. The idea is to leverage the tree decomposition, a structural characterization of distance-hereditary graphs, to represent the graph as a tree structure where dynamic programming can be efficiently applied to the nodes. Tree decompositions, which capture the hierarchical nature of distance-hereditary graphs, facilitate breaking down the problem into smaller, more manageable subproblems that can be solved iteratively.

For specific examples of dynamic programming algorithms applied to distance-hereditary graphs, readers can refer to research papers [8,20,21,22,23], which address various optimization problems using similar decomposition-based approaches.

To guide the reader through the contributions of this paper, the rest of the paper is organized as follows:

-

In Section 2, we provide the necessary background and preliminary definitions required for understanding the subsequent sections. This includes the recursive definition of distance-hereditary graphs and detailed explanations of the four clique transversal problems. The recursive definition introduces the construction of a binary ordered decomposition tree, known as a PTF-tree, which is central to the development of our algorithm;

-

Section 3 introduces the $(p,d,\ell ,b)$-clique transversal problem, details the problem’s constraints and parameters, and explains how it generalizes the four specific clique transversal problems;

-

In Section 4, we identify how the optimal solution to the $(p,d,\ell ,b)$-clique transversal problem can be composed of the solutions to its subproblems and define the recursive formulas using the recursive definition of distance-hereditary graphs;

-

Section 5 presents our dynamic programming algorithm for solving the $(p,d,\ell ,b)$-clique transversal problem. We guide the reader through the design of the algorithm, illustrating how the value of an optimal solution is computed in a bottom-up manner using the recursive formulas. Additionally, we provide a detailed analysis of the algorithm’s time complexity.

2. Preliminaries

This section covers a few fundamental concepts. For a more in-depth exploration, we recommend referring to standard textbooks or monographs, such as the books of Cormen et al. [19] and Diestel [24].

A graph $G=(V,E)$ consists of a set of vertices V and a set of edges E. When the vertices and edges of a graph G are not explicitly specified, they are denoted by $V\left(G\right)$ and $E\left(G\right)$, respectively. Typically, a graph is assumed to have n vertices and m edges.

Two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ are disjoint if $V_1\cap V_2=\varnothing$ and $E_1\cap E_2=\varnothing$. The union of $G_1$ and $G_2$ is defined as $G_1\cup G_2=(V_1\cup V_2,E_1\cup E_2)$. For a nonempty subset S of the vertices in a graph G, a subgraph of G induced by S, denoted by $G\left[S\right]$, is the graph with vertex set S and edge set $\left\{\right(u,v)\in E(G)\mid u,v\in S\}$. The number of elements in a set S is called the cardinality (or size) of S, denoted by $\left|S\right|$.

A subset of the vertices in a graph is a clique if it consists of only one vertex or if every two distinct vertices in the subset are adjacent. A clique in a graph is maximal if it cannot be contained in any larger maximal clique in the graph. A maximum clique is a maximal clique with the largest possible cardinality. The clique number of a graph G, denoted by $\omega \left(G\right)$, is the cardinality of a maximum clique in G.

A clique transversal set of G is a subset S of the vertices such that $|S\cap C|\ge 1$ for every maximal clique $C\in C\left(G\right)$. The clique transversal problem is to find a clique transversal set of G with minimum cardinality. The minimum cardinality of a clique transversal set of G is denoted by ${\tau }_C\left(G\right)$.

2.1. Clique Transversal Functions

Given a subset Y of real numbers, let $f:X\to Y$ be a function mapping elements from the domain X to the codomain Y. We define $f\left(X^{\prime }\right)$ as ${\sum }_{x\in X^{\prime }}f\left(x\right)$ for any subset $X^{\prime }\subseteq X$. The weight of f is defined as $f\left(X\right)$.

Definition 1

(See [13]). Consider a graph G and a fixed positive integer k. A function $f:V\left(G\right)\to \{0,1\}$ is a k-fold clique transversal function of G is $f\left(C\right)\ge k$ for every $C\in C\left(G\right)$. The minimum weight of a k-fold clique transversal function of G is defined as ${\tau }_C^k\left(G\right)$. The k-fold clique transversal problem is to find a k-fold clique transversal function of G with minimum weight.

Definition 2

(See [13]). Consider a graph G and a fixed positive integer k. A function $f:V\left(G\right)\to \{0,1,\dots ,k\}$ is a $\left\{k\right\}$-clique transversal function of G if $f\left(C\right)\ge k$ for every $C\in C\left(G\right)$. The minimum weight of a $\left\{k\right\}$-clique transversal function of G is defined as ${\tau }_C^{\left\{k\right\}}\left(G\right)$. The $\left\{k\right\}$-clique transversal problem is to find a $\left\{k\right\}$-clique transversal function of G with minimum weight.

Definition 3

(See [13]). A function $f:V\to \{-1,1\}$ is a signed clique transversal function of a graph $G=(V,E)$ if $f\left(C\right)\ge 1$ for every $C\in C\left(G\right)$. The minimum weight of a signed clique transversal function of G is defined as ${\tau }_C^s\left(G\right)$. The signed clique transversal problem is to find a signed clique transversal function of G with minimum weight.

Definition 4

(See [13]). A function $f:V\to \{-1,0,1\}$ is a minus clique transversal function of a graph $G=(V,E)$ if $f\left(C\right)\ge 1$ for every $C\in C\left(G\right)$. The minimum weight of a minus clique transversal function of G is defined as ${\tau }_C^{-}\left(G\right)$. The minus clique transversal problem is to find a minus clique transversal function of G with minimum weight.

2.2. Distance-Hereditary Graphs

The distance between two vertices in a graph is the length of the shortest path connecting them. This length is measured by the number of edges in the path. If no path exists between the two vertices, the distance is considered to be infinite. This concept is fundamental in graph theory and is used to determine how “close” or “far apart” vertices are within a graph. The diameter is a related concept, measuring the greatest distance between any two vertices.

A graph is distance-hereditary if the distance between any two vertices in a connected induced subgraph is the same as in the original graph. Thus, any induced subgraph of a distance-hereditary graph is also distance-hereditary. Theorem 1 gives the recursive definition of distance-hereditary graphs.

Theorem 1 ([20,21])

Distance-hereditary graphs can be defined recursively as follows:

1. 

A graph G consisting of a single vertex v is distance-hereditary, and the twin set $TS\left(G\right)=\left\{v\right\}$. Such a graph is called a primitive distance-hereditary graph;

2. 

Let $G_1$ and $G_2$ be two disjoint distance-hereditary graphs with the twin sets $TS\left(G_1\right)$ and $TS\left(G_2\right)$, respectively. A graph G with $\left|V\right(G\left)\right|\ge 2$, obtained from $G_1$ and $G_2$ through one of the following three operations, is also a distance-hereditary graph:

(a) 

False twin operation: The graph G is formed by the union of $G_1$ and $G_2$, with $TS\left(G\right)=TS\left(G_1\right)\cup TS\left(G_2\right)$, and denoted by $G=G_1⨀G_2$;

(b) 

True twin operation: The graph G is formed by connecting every vertex of $TS\left(G_1\right)$ to all vertices of $TS\left(G_2\right)$, with $TS\left(G\right)=TS\left(G_1\right)\cup TS\left(G_2\right)$, and denoted by $G=G_1⨂G_2$;

(c) 

Pendant vertex operation: The graph G is formed by connecting every vertex of $TS\left(G_1\right)$ to all vertices of $TS\left(G_2\right)$, with $TS\left(G\right)=TS\left(G_1\right)$, and denoted by $G=G_1⨁G_2$.

By Theorem 1, a distance-hereditary graph G has a twin set $TS\left(G\right)$, which is a subset of $V\left(G\right)$ and defined recursively. This theorem also describes the construction of a binary ordered decomposition tree, known as a $PTF$-tree, which consists of $2n-1$ nodes and can be built in linear time. In a $PTF$-tree, each leaf represents a single-vertex graph, and each internal node labeled by ⨁, ⨂, or ⨀ corresponds to an operation from the theorem. Figure 1 illustrates a distance-hereditary graph and its $PTF$-tree.

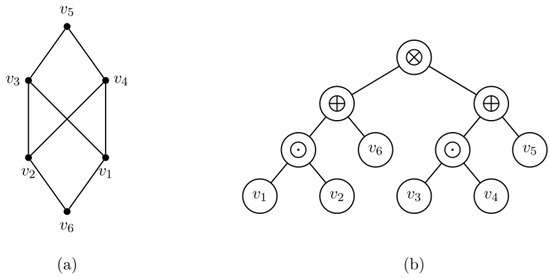
Figure 1. (a) A distance-hereditary graph G. (b) A $PTF$-tree of G.

Definition 5.

  Let $C\left(G\right)$ denote the set of all maximal cliques in a distance-hereditary graph G. Consequently, $C\left(G\right[TS\left(G\right)\left]\right)$ represents the set of all maximal cliques in the subgraph $G\left[TS\right(G\left)\right]$. We define $C_T\left(G\right)$ as the set of maximal cliques in G that are also maximal cliques in $G\left[TS\right(G\left)\right]$. Conversely, $C_{\overline{T}}\left(G\right)$ is defined as the set of maximal cliques in G that are not maximal cliques in $G\left[TS\right(G\left)\right]$. Thus, the set of all maximal cliques in G can be expressed as $C\left(G\right)=C_T\left(G\right)\cup C_{\overline{T}}\left(G\right)$.

Definition 6.

Let $G_1$ and $G_2$ be disjoint distance-hereditary graphs. Suppose that G is either $G=G_1⨁G_2$ or $G=G_1⨂G_2$. We define $C_X\left(G\right)$ as the set $\{C_1\cup C_2\mid C_1\in C\left(G_1\left[TS\left(G_1\right)\right]\right)$, and $C_2\in C\left(G_2\left[TS\left(G_2\right)\right]\right)\}$.

Lemma 1 ([22]).

Suppose that G is a primitive distance-hereditary graph with the vertex v. Then, $C\left(G\right)=C\left(G\left[TS\left(G\right)\right)\right])=C_T\left(G\right)$ and $C_{\overline{T}}\left(G\right)=\varnothing$.

Lemma 2 ([22]).

Let $G_1$ and $G_2$ be disjoint distance-hereditary graphs. If $G=G_1⨀G_2$, then

1. 

$C\left(G\left[TS\left(G\right)\right]\right)=C\left(G_1\left[TS\left(G_1\right)\right]\right)\cup C\left(G_2\left[TS\left(G_2\right)\right]\right)$;

2. 

$C\left(G\right)=C\left(G_1\right)\cup C\left(G_2\right)$,;

3. 

$C_T\left(G\right)=C_T\left(G_1\right)\cup C_T\left(G_2\right)$; and

4. 

$C_{\overline{T}}\left(G\right)=C_{\overline{T}}\left(G_1\right)\cup C_{\overline{T}}\left(G_2\right)$.

Lemma 3 ([22]).

Let $G_1$ and $G_2$ be disjoint distance-hereditary graphs. If $G=G_1⨂G_2$, then

1. 

$C\left(G\left[TS\left(G\right)\right]\right)=C_X\left(G\right)$;

2. 

$C\left(G\right)=C_{\overline{T}}\left(G_1\right)\cup C_{\overline{T}}\left(G_2\right)\cup C_X\left(G\right)$;

3. 

$C_T\left(G\right)=C\left(G\left[TS\left(G\right)\right]\right)$; and

4. 

$C_{\overline{T}}\left(G\right)=C_{\overline{T}}\left(G_1\right)\cup C_{\overline{T}}\left(G_2\right)$.

Lemma 4 ([22]). 

Let $G_1$ and $G_2$ be disjoint distance-hereditary graphs. If $G=G_1⨁G_2$, then

1. 

$C\left(G\left[TS\left(G\right)\right]\right)=C\left(G_1\left[TS\left(G_1\right)\right]\right)$;

2. 

$C\left(G\right)=C_{\overline{T}}\left(G_1\right)\cup C_{\overline{T}}\left(G_2\right)\cup C_X\left(G\right)$;

3. 

$C_T\left(G\right)=\varnothing$; and

4. 

$C_{\overline{T}}\left(G\right)=C\left(G\right)$.

3. The $(p,d,\ell ,b)$-Clique Transversal Problem

Let G be a graph and $b\in \mathbb{Z}$. Suppose that $p\in \{0,-1\}$ and $d,\ell \in {\mathbb{Z}}^{+}$ are fixed. A function $f:V\left(G\right)\to \{p,p+d,\dots ,p+(\ell -1)·d\}$ is a $(p,d,\ell ,b)$-clique transversal function of G if $f\left(C\right)\ge b$ for every $C\in C\left(G\right)$. The minimum weight of a $(p,d,\ell ,b)$-clique transversal function of G is defined as ${\tau }_C(p,d,\ell ,b)\left(G\right)$. The $(p,d,\ell ,b)$-clique transversal problem is to find a $(p,d,\ell ,b)$-clique transversal function of G with minimum weight.

Remark 1.

  Suppose that G is a graph and b is an integer. Let $p\in \{0,-1\}$ and $d,\ell \in {\mathbb{Z}}^{+}$ be fixed. If $b>p+(\ell -1)·d)·\omega (G)$, then G has no $(p,d,\ell ,b)$-clique transversal function. If $b<p·\omega \left(G\right)$, then ${\tau }_C(p,d,\ell ,b)\left(G\right)=p·\left|V\left(G\right)\right)|$.

Lemma 5.

  Let G be a graph. Then,

1. 

${\tau }_C^k\left(G\right)={\tau }_C(0,1,2,k)\left(G\right)$;

2. 

${\tau }_C^{\left\{k\right\}}\left(G\right)={\tau }_C(0,1,k+1,k)\left(G\right)$;

3. 

${\tau }_C^s\left(G\right)={\tau }_C(-1,2,2,1)\left(G\right)$; and

4. 

${\tau }_C^{-}\left(G\right)={\tau }_C(-1,1,3,1)\left(G\right)$.

Proof. 

The statements can be easily verified according to their definitions.    □

Lemma 5 demonstrates that the k-fold clique, $\left\{k\right\}$-clique, minus clique, and signed clique transversal problems are particular cases of the $(p,d,\ell ,b)$-clique transversal problem. The formulation provides a unified approach to solving these four clique transversal problems. Additionally, following Remark 1, we focus the problem on a distance-hereditary graph G for b within the range $p·\omega \left(G\right)\le b\le (p+(\ell -1)·d)·\omega \left(G\right)$.

4. Identifying Subproblem Solutions and Defining the Recursive Formulas

This section explores the methodology for addressing the $(p,d,\ell ,b)$-clique transversal problem by decomposing it into smaller, more manageable subproblems using the recursive definition of distance-hereditary graphs. This section demonstrates how the optimal solution can be systematically constructed by combining the solutions to these subproblems. It also introduces the recursive formulas that forms the foundation of this approach, guiding the reader through the step-by-step process of building the complete solution.

Definition 7.

Suppose that $G=(V,E)$ is a distance-hereditary graph and $p\in \{0,-1\}$. Let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$.

(1) 

A function $f:V\left(G\right)\to \{p,p+d,\dots ,p+(\ell -1)·d\}$ is a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of G if the following conditions are all satisfied:

(i) 

$C_T\left(G\right)=\varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$;

(ii) 

$f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G\right)$;

(iii) 

$f\left(C\right)\ge y$ for every $C\in C\left(G\right[TS\left(G\right)\left]\right)$.

The minimum weight of a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of G is defined as ${\tau }_{p,0}^{d,\ell }(x,y)\left(G\right)$. If a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of G does not exist, then ${\tau }_{p,0}^{d,\ell }(x,y)\left(G\right)=\infty$;

(2) 

A function $f:V\left(G\right)\to \{p,p+d,\dots ,p+(\ell -1)·d\}$ is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of G if the following conditions are all satisfied:

(i) 

$C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)=\varnothing$;

(ii) 

$f\left(C\right)\ge x$ for every $C\in C_T\left(G\right)$;

(iii) 

$f\left(C\right)\ge y$ for every $C\in C\left(G\right[TS\left(G\right)\left]\right)$.

The minimum weight of a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of G is defined as ${\tau }_{p,1}^{d,\ell }(x,y)\left(G\right)$. If a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of G does not exist, then ${\tau }_{p,1}^{d,\ell }(x,y)\left(G\right)=\infty$;

(3) 

A function $f:V\left(G\right)\to \{p,p+d,\dots ,p+(\ell -1)·d\}$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal function of G if the following conditions are all satisfied:

(i) 

$C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$;

(ii) 

$f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G\right)$;

(iii) 

$f\left(C\right)\ge y$ for every $C\in C_T\left(G\right)$;

(iv) 

$f\left(C\right)\ge z$ for every $C\in C\left(G\right[TS\left(G\right)\left]\right)$.

We use ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G\right)$ to denote the minimum weight of a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal function of G. If a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal function of G does not exist, then ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G\right)=\infty$.

Theorem 2.

Suppose that G is a distance-hereditary graph and $b,y,z\in \mathbb{Z}$. Let $p\in \{0,-1\}$ and $d,\ell \in {\mathbb{Z}}^{+}$ be fixed. Then, ${\tau }_C(p,d,\ell ,b)\left(G\right)$ can be computed as follows:

(1) 

If $C_T\left(G\right)=\varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$, then

$${\tau }_C(p,d,\ell ,b)\left(G\right)=\underset{\begin{array}{c}p·\omega \left(G\right)\le y\le (p+(\ell -1)·d)·\omega \left(G\right)\end{array}}{min}\left\{{\tau }_{p,0}^{d,\ell }(b,y)\left(G\right)\right\};$$

(2) 

If $C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)=\varnothing$, then

$${\tau }_C(p,d,\ell ,b)\left(G\right)=\underset{\begin{array}{c}p·\omega \left(G\right)\le y\le (p+(\ell -1)·d)·\omega \left(G\right)\end{array}}{min}\left\{{\tau }_{p,1}^{d,\ell }(b,y)\left(G\right)\right\};$$

(3) 

If $C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$, then

$${\tau }_C(p,d,\ell ,b)\left(G\right)=\underset{\begin{array}{c}p·\omega \left(G\right)\le z\le (p+(\ell -1)·d)·\omega \left(G\right)\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(b,b,z)\left(G\right)\right\}.$$

Proof. 

By Definition 5, $C\left(G\right)=C_T\left(G\right)\cup C_{\overline{T}}\left(G\right)$. If $C_T\left(G\right)=\varnothing$ and $C_{\overline{T}}\left(G\right)=\varnothing$, then G has no vertices. Therefore, only three cases need to be considered:

(1)

$C_T\left(G\right)=\varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$;

(2)

$C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)=\varnothing$;

(3)

$C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$.

In the following, we only prove the correctness of the statement for Case 3; Statements (1) and (2) can be proved similarly.

In this case, $C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$. By Definition 7, a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(b,b,z)$-clique transversal function of G is a $(p,d,\ell ,b)$-clique transversal function of G. Thus,

$${\tau }_C(p,d,\ell ,b)\left(G\right)\le \underset{p·\omega \left(G\right)\le z\le (p+(\ell -1)·d)·\omega \left(G\right).}{min}\left\{{\tau }_{p,2}^{d,\ell }(b,b,z)\left(G\right)\right\}.$$

Conversely, let $C\in C\left(G\right[TS\left(G\right)\left]\right)$ and f be a $(p,d,\ell ,b)$-clique transversal function of G. Clearly, $\left|C\right|\le \omega \left(G\right)$ and $p·\omega \left(G\right)\le f\left(C\right)\le (p+(\ell -1)·d)·\omega \left(G\right)$. Let $f\left(C\right)=z$. The function f is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(b,b,z)$-clique transversal function of G. Hence,

$$\underset{p·\omega \left(G\right)\le z\le (p+(\ell -1)·d)·\omega \left(G\right).}{min}\left\{{\tau }_{p,2}^{d,\ell }(b,b,z)\left(G\right)\right\}\le {\tau }_C(p,d,\ell ,b)\left(G\right).$$

Based on the above discussion, Statement (3) therefore holds.    □

Lemma 6.

Suppose that G is a distance-hereditary graph and $G_{\alpha }$ is a subgraph of G consisting of only one vertex v. Let $p\in \{0,-1\}$, and let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ can be computed as follows:

(1) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(2) 

${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$;

(3) 

Let $i=\lceil (max\{x,y\}-p)/d\rceil ·d+p$. Then,

$${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\left\{\begin{array}{c}pifmax\{x,y\}\le p,\hfill \\ iifp<max\{x,y\}\le p+(\ell -1)·d,\hfill \\ \infty ifp+(\ell -1)·d<max\{x,y\}.\hfill \end{array}\right.$$

Proof. 

The graph $G_{\alpha }$ consists of only one vertex v. By Theorem 1, we have $TS\left(G_{\alpha }\right)=\left\{v\right\}$. Then, $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$, and $C\left(G_{\alpha }\right)=C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=\left\{\left\{v\right\}\right\}$. By Definition 7, we obtain ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$ and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$. Statements (1) and (2) therefore hold.

We now consider Statement (3). Let f be a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function f of $G_{\alpha }$. Clearly, $f\left(v\right)\in \{p,p+d,\dots ,p+(\ell -1)·d\}$. By Definition 7, $f\left(C\right)\ge x$ for every $C\in C_T\left(G_{\alpha }\right)$, and $f\left(C\right)\ge y$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Note that $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=\left\{\left\{v\right\}\right\}$. Therefore, $f\left(v\right)\ge max\{x,y\}$. We consider the following cases.

Case 1: $max\{x,y\}\le p$. Obviously, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=f\left(v\right)=p$.

Case 2: $p<max\{x,y\}\le p+(\ell -1)·d$. Let

$i=\lceil (max\{x,y\}-p)/d\rceil ·d+p$. Then,

$$\begin{array}{cc}\hfill i& =\lceil (max\{x,y\}-p)/d\rceil ·d+p\hfill \\ & \ge \left((max\{x,y\}-p)/d\right)·d+p\hfill \\ & =(max\{x,y\}-p)+p\hfill \\ & =max\{x,y\}.\hfill \end{array}$$

Assume that there exists an integer $j<i$ such that $j\in \{p,p+d,\dots ,p+(\ell -1)·d\}$ and $j\ge max\{x,y\}$. However, this leads to a contradiction as follows:

$$\begin{array}{cc}\hfill j& \le i-d\hfill \\ & =\lceil (max\{x,y\}-p)/d\rceil ·d+p-d\hfill \\ & <\left((max\{x,y\}-p)/d+1\right)·d+p-d\hfill \\ & =(max\{x,y\}-p+d)+p-d\hfill \\ & =max\{x,y\}.\hfill \end{array}$$

Hence, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=i=\lceil (max\{x,y\}-p)/d\rceil ·d+p$.

Case 3: $p+(\ell -1)·d<max\{x,y\}$. Then, $f\left(v\right)>p+(\ell -1)·d$. This contradicts the requirement that $f\left(v\right)\in \{p,p+d,\dots ,p+(\ell -1)·d\}$. Consequently, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$.    □

Lemma 7.

Suppose that G is a distance-hereditary graph and $G_{\alpha }=G_{{\alpha }_1}⨀G_{{\alpha }_2}$ is an induced subgraph of G formed from two disjoint distance-hereditary graphs $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$. Let $p\in \{0,-1\}$, and let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ can be computed as follows:

(1) 

Assume that $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$;

(1.1) 

${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(1.2) 

${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$;

(1.3) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_2}\right).$

(2) 

Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$;

(2.1) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(2.2) 

${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$;

(2.3) 

Let $w=max\{x,y\}$. Then, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_2}\right)$.

(3) 

Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$;

(3.1) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(3.2) 

${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(3.3) 

Let $i\in \{1,2\}$. ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ can be computed as follows:

(3.3.1) 

If $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_2}\right);$$

(3.3.2) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\underset{i\in \{1,2\}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_i}\right)+{\tau }_{p,0}^{d,\ell }(x,z)\left(G_{{\alpha }_{3-i}}\right)\right\};$$

(3.3.3) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)=\varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\underset{i\in \{1,2\}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_i}\right)+{\tau }_{p,1}^{d,\ell }(y,z)\left(G_{{\alpha }_{3-i}}\right)\right\};$$

(3.3.4) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)=\varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\underset{i\in \{1,2\}}{min}\left\{{\tau }_{p,1}^{d,\ell }(y,z)\left(G_{{\alpha }_i}\right)+{\tau }_{p,0}^{d,\ell }(x,z)\left(G_{{\alpha }_{3-i}}\right)\right\}.$$

Proof. 

By definition, an induced subgraph of a distance-hereditary graph is also distance-hereditary. The graph $G_{\alpha }$ is distance-hereditary and $C\left(G_{\alpha }\right)=C_T\left(G_{\alpha }\right)\cup C_{\overline{T}}\left(G_{\alpha }\right)$. If $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$, then $G_{\alpha }$ has no vertices. Therefore, only three cases need to be considered based on their emptiness:

• $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$;
• $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$;
• $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$.

(1) Assume that $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$. By Definition 7, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$ and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$. Statements (1.1) and (1.2) therefore hold.

Now, let us consider Statement (1.3). Since $G_{\alpha }=G_{{\alpha }_1}⨀G_{{\alpha }_2}$, by Theorem 1, we have $G_{\alpha }=G_{{\alpha }_1}\cup G_{{\alpha }_2}$ and $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)\cup TS\left(G_{{\alpha }_2}\right)$. Following Lemma 2, we know that

• $C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)\cup C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$; and
• $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$.

Let $f_1$ and $f_2$ be ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. For every maximal clique $C\in C_{\overline{T}}\left(G_{\alpha }\right)$, either $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Therefore, either $f\left(C\right)=f_1\left(C\right)\ge x$ or $f\left(C\right)=f_2\left(C\right)\ge x$. Similarly, either $f\left(C\right)=f_1\left(C\right)\ge y$ or $f\left(C\right)=f_2\left(C\right)\ge y$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Hence,

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)\le {\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$.

For every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ (respectively, $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, $C\in C_{\overline{T}}\left(G_{\alpha }\right)$ (respectively, $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$). Therefore, $f_1\left(C\right)=f\left(C\right)\ge x$ (respectively, $f_1\left(C\right)\ge y$) for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ (respectively, $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$). Similarly, $f_2\left(C\right)=f\left(C\right)\ge x$ (respectively, $f_2\left(C\right)\ge y$) for every $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$ (respectively, $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$). Thus, the functions $f_1$ and $f_2$ are ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. Consequently,

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right).$$

The above discussion shows that ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,y)\left(G_{{\alpha }_2}\right)$. Statement (1.3) therefore holds.

(2) Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$. Following Definition 7, we can conclude that Statements (2.1) and (2.2) are true. We now consider Statement (2.3). Following Lemma 2, we know that

• $C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)\cup C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$; and
• $C_T\left(G_{\alpha }\right)=C_T{G}_{{\alpha }_1})\cup C_T\left(G_{{\alpha }_2}\right)$.

Recall that $G_{\alpha }=G_{{\alpha }_1}\cup G_{{\alpha }_2}$ and $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)\cup TS\left(G_{{\alpha }_2}\right)$. Since $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$, we have $C\left(G_{\alpha }\right)=C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Therefore, $C_T\left(G_{{\alpha }_1}\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_T\left(G_{{\alpha }_2}\right)=C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$.

Let $f_1$ and $f_2$ be ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. By Definition 7, $f_1\left(C\right)\ge x$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$, and $f\left(C_1\right)\ge y$ for every $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Note that $C_T\left(G_{{\alpha }_1}\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Therefore, $f_1\left(C\right)\ge max\{x,y\}$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Similarly, $f_2\left(C\right)\ge max\{x,y\}$ for every $C\in C_T\left(G_{{\alpha }_2}\right)$ and $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Let $w=max\{x,y\}$. Thus, $f_1$ and $f_2$ are ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively.

Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. For every maximal clique $C\in C_T\left(G_{\alpha }\right)$, either $C\in C_T\left(G_{{\alpha }_1}\right)$ or $C\in C_T\left(G_{{\alpha }_2}\right)$. Hence, either $f\left(C\right)=f_1\left(C\right)\ge w$ or $f\left(C\right)=f_2\left(C\right)\ge w$. Similarly, either $f\left(C\right)=f_1\left(C\right)\ge w$ or $f\left(C\right)=f_2\left(C\right)\ge w$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$. Consequently,

$${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)\le {\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$, and let $w=max\{x,y\}$. By Definition 7, $f\left(C\right)\ge x$ for every $C\in C_T\left(G_{\alpha }\right)$, and $f\left(C\right)\ge y$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Note that $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Therefore, $f\left(C\right)\ge max\{x,y\}$ for every $C\in C_T\left(G_{\alpha }\right)$ and $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$.

Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. Recall that

• $C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)\cup C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$; and
• $C_T\left(G_{\alpha }\right)=C_T{G}_{{\alpha }_1})\cup C_T\left(G_{{\alpha }_2}\right)$.

Thus, $f_1\left(C\right)=f\left(C\right)\ge w$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Similarly, $f_2\left(C\right)=f\left(C\right)\ge w$ for every $C\in C_T\left(G_{{\alpha }_2}\right)$ and $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. The functions $f_1$ and $f_2$ are ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. Consequently,

$${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right).$$

The above discussion shows that ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w,w)\left(G_{{\alpha }_2}\right)$. Statement (2.3) therefore holds.

(3) Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$. By Definition 7, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$ and ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$. Statements (3.1) and (3.2) therefore hold. Next, we consider the remaining statements.

Note that $C_T\left(G_{\alpha }\right)=C_T\left(G_{{\alpha }_1}\right)\cup C_T\left(G_{{\alpha }_2}\right)$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Let $i=\{1,2\}$. Given $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$, we consider four cases:

Case 1: $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$; $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$;

Case 2: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$; $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$;

Case 3: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$; $C_T\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)=\varnothing$;

Case 4: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)=\varnothing$; $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$.

In the following, we prove the statement for Case 1. The statements for the other cases can be proven similarly.

Let $f_1$ and $f_2$ be ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. For every maximal clique $C\in C_{\overline{T}}\left(G_{\alpha }\right)$, either $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Therefore, either $f\left(C\right)=f_1\left(C\right)\ge x$ or $f\left(C\right)=f_2\left(C\right)\ge x$. Similarly, either $f\left(C\right)=f_1\left(C\right)\ge y$ or $f\left(C\right)=f_2\left(C\right)\ge y$ for every maximal clique $C\in C_T\left(G_{\alpha }\right)$. For each clique $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$, either $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ or $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$, and, thus, either $f\left(C\right)=f_1\left(C\right)\ge z$ or $f\left(C\right)=f_1\left(C\right)\ge z$. The function f is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal function of $G_{\alpha }$. Hence,

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)\le {\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. Consider the function $f_1$. It is straightforward that $C\in C_{\overline{T}}\left(G_{\alpha }\right)$ (respectively, $C\in C_T\left(G_{\alpha }\right)$ and $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$) for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ (respectively, $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Therefore, $f_1\left(C\right)=f\left(C\right)\ge x$ (respectively, $f_1\left(C\right)=f\left(C\right)\ge y$ and $f_1\left(C\right)=f\left(C\right)\ge z$) for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ (respectively, $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$). Similarly, $f_2\left(C\right)=f\left(C\right)\ge x$ (respectively, $f_2\left(C\right)=f\left(C\right)\ge y$ and $f_2\left(C\right)=f\left(C\right)\ge z$) for every $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$ (respectively, $C\in C_T\left(G_{{\alpha }_2}\right)$ and $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$). Thus, the functions $f_1$ and $f_2$ are ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,y,z)$-clique transversal functions of $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$, respectively. We have

$${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right).$$

The above discussion shows that ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{{\alpha }_2}\right)$. Statement (3.3.1) therefore holds.    □

Lemma 8.

Suppose that G is a distance-hereditary graph and $G_{\alpha }=G_{{\alpha }_1}⨂G_{{\alpha }_2}$ is an induced subgraph of G formed from two disjoint distance-hereditary graphs $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$. Let $p\in \{0,-1\}$, and let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ can be computed as follows:

(1) 

Assume that $C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)=\varnothing$;

(1.1) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(1.2) 

${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$;

(1.3) 

Let $w=max\{x,y\}$, $w_{min}=p·\omega \left(G\right)$, and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)$ and

$${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{w}_1,w_2\in \mathbb{Z}\\ w_1+w_2=w\\ w_{min}\le w_1,w_2\le w_{max}\end{array}}{min}\left\{\begin{array}{c}{\tau }_{p,1}^{d,\ell }(w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w_2,w_2)\left(G_{{\alpha }_2}\right)\hfill \end{array}\right\}.$$

(2) 

Assume that $C_T\left(G\right)\ne \varnothing$ and $C_{\overline{T}}\left(G\right)\ne \varnothing$;

(2.1) 

${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(2.2) 

${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(2.3) 

Let $i\in \{1,2\}$. Let $w=max\{x,y\}$, $w_{min}=p·\omega \left(G\right)$, and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)$. ${\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)$ can be computed as follows:

(2.3.1) 

If $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,w,w)=\underset{\begin{array}{c}{w}_1,w_2\in \mathbb{Z}\\ w_1+w_2=w,\\ w_{min}\le w_1,w_2\le w_{max}\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,w_2,w_2)\left(G_{{\alpha }_2}\right)\right\};$$

(2.3.2) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,w,w)=\underset{\begin{array}{c}i\in \{1,2\}\\ w_1,w_2\in \mathbb{Z}\\ w_1+w_2=w,\\ w_{min}\le w_1,w_2\le w_{max}\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_i}\right)+{\tau }_{p,0}^{d,\ell }(x,w_2)\left(G_{{\alpha }_{3-i}}\right)\right\};$$

(2.3.3) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)=\varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,w,w)=\underset{\begin{array}{c}i\in \{1,2\}\\ w_1,w_2\in \mathbb{Z}\\ w_1+w_2=w,\\ w_{min}\le w_1,w_2\le w_{max}\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_i}\right)+{\tau }_{p,1}^{d,\ell }(w_2,w_2)\left(G_{{\alpha }_{3-i}}\right)\right\};$$

(2.3.4) 

If $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)=\varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$, then

$${\tau }_{p,2}^{d,\ell }(x,w,w)=\underset{\begin{array}{c}i\in \{1,2\}\\ w_1,w_2\in \mathbb{Z}\\ w_1+w_2=w,\\ w_{min}\le w_1,w_2\le w_{max}\end{array}}{min}\left\{{\tau }_{p,1}^{d,\ell }(w_1,w_1)\left(G_{{\alpha }_i}\right)+{\tau }_{p,0}^{d,\ell }(x,w_2)\left(G_{{\alpha }_{3-i}}\right)\right\}.$$

Proof. 

By Theorem 1, $G_{\alpha }$ is a distance-hereditary graph formed by connecting every vertex of $TS\left(G_{{\alpha }_1}\right)$ to all vertices of $TS\left(G_{{\alpha }_2}\right)$, and $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)\cup TS\left(G_{{\alpha }_2}\right)$. The union of a maximal clique of $G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]$ and a maximal clique of $G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]$ is a maximal clique in $G_{\alpha }$. Furthermore, $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=C_X\left(G_{\alpha }\right)$ by Lemma 3. Therefore, $C_T\left(G_{\alpha }\right)\ne \varnothing$. There are two cases to consider:

• $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$;
• $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$.

(1) Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$. By Definition 7, Statements (1.1) and (1.2) are true.

Let f be a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$, and let $w=max\{x,y\}$. By Definition 7, $f\left(C\right)\ge x$ for every $C\in C_T\left(G_{\alpha }\right)$, and $f\left(C\right)\ge y$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Note that $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. Therefore, $f\left(C\right)\ge max\{x,y\}$ for every $C\in C_T\left(G_{\alpha }\right)$ and $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$. We have

$${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)\le {\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$. By Definition 7, we obtain that $f\left(C\right)\ge w\ge x$ for every $C\in C_T\left(G_{\alpha }\right)$, and $f\left(C\right)\ge w\ge y$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Thus,

$${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)\le {\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right).$$

Following the discussion above, we know that ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)$. Next, let us consider the equation for ${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)$.

Let $w_{min}=p·\omega \left(G\right)$, and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$. Let $w_1$ and $w_2$ be integers such that $w_{min}\le w_1,w_2\le w_{max}$, and $w_1+w_2=w$. Let $f_1$ be ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w_1,w_1)$-clique transversal function of $G_{{\alpha }_1}$ and $f_2$ be ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w_2,w_2)$-clique transversal function of $G_{{\alpha }_2}$. By Definition 7, $f_1\left(C\right)\ge w_1$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Similarly, $f_2\left(C\right)\ge w_2$ for every $C\in C_T\left(G_{{\alpha }_2}\right)$ and $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$.

Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. A maximal clique $C\in C_T\left(G_{\alpha }\right)$ is the union of a clique $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and a clique $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Hence, $f\left(C\right)=f_1\left(C_1\right)+f_2\left(C_2\right)\ge w_1+w_2=w$. Note that $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. We obtain $f\left(C\right)=f_1\left(C_1\right)+f_2\left(C_2\right)\ge w_1+w_2=w$ for every $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. The function f is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$. Consequently,

$${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)\le {\tau }_{p,1}^{d,\ell }(w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w_2,w_2)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w,w)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. Recall that $C_T\left(G_{\alpha }\right)=C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)=C_X\left(G_{\alpha }\right)$. We know that $C_T\left(G_{{\alpha }_1}\right)=C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_T\left(G_{{\alpha }_2}\right)=C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Furthermore, a maximal clique $C\in C_T\left(G_{\alpha }\right)$ is the union of a maximal clique $C_1$ of $G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]$ and a maximal clique $C_2$ of $G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]$. Thus, $f_1\left(C_1\right)+f_2\left(C_2\right)=f\left(C_1\right)+f\left(C_2\right)=f\left(C\right)\ge w$.

Let ${\widehat{C}}_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and ${\widehat{C}}_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$ such that $f\left({\widehat{C}}_1\right)$ and $f\left({\widehat{C}}_2\right)$ are the smallest values in $\{f\left(C_1\right)\mid C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)\}$ and $\{f\left(C_2\right)\mid C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)\}$, respectively. Then, the clique $\widehat{C}={\widehat{C}}_1\cup {\widehat{C}}_2$ is a maximal clique in $G_{\alpha }$.

Let $f\left({\widehat{C}}_1\right)=x_1$ and $f\left(C_2\right)=x_2$. Then, $f_1\left({\widehat{C}}_1\right)+f_2\left({\widehat{C}}_2\right)=f\left({\widehat{C}}_1\right)+f\left({\widehat{C}}_2\right)=f\left(\widehat{C}\right)=x_1+x_2\ge w$. Since $|{\widehat{C}}_1|$ and $|{\widehat{C}}_2|$ are no more than $\omega \left(G\right)$, $w_{min}\le x_1,x_2\le w_{max}$. If $x_1+x_2>w$, then there exist two integers $w_1$ and $w_2$ such that

(i)

$w_{min}\le w_1,w_2\le w_{max}$;

(ii)

$w_1+w_2=w$;

(iii)

$w_1\le x_1$, and $w_2\le x_2$.

If $x_1+x_2=w$, let $w_1=x_1$ and $w_2=x_2$. Therefore, there exist two integer $w_1$ and $w_2$ such that $w_1+w_2=w$, $f_1\left(C_1\right)\ge w_1$ for every $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, and $f_2\left(C_2\right)\ge w_2$ for every $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Obviously, $w_{min}\le w_1,w_2\le w_{max}$. The function $f_1$ is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w_1,w_1)$-clique transversal function of $G_{{\alpha }_1}$, and $f_2$ is a ${\mathsf{\Gamma }}_{p,1}^{d,\ell }(w_2,w_2)$-clique transversal function of $G_{{\alpha }_2}$. Consequently,

$${\tau }_{p,1}^{d,\ell }(w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w_2,w_2)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right).$$

Hence, ${\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(w_2,w_2)\left(G_{{\alpha }_2}\right)$. Statement (1.3) therefore holds.

(2) Assume that $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$. By Definition 7, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$ and ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$. Statements (2.1) and (2.2) therefore hold.

Let $w=max\{x,y\}$. Using arguments similar to those for proving ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,1}^{d,\ell }(w,w)\left(G_{\alpha }\right)$ when $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=\varnothing$, we can prove ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)$. We now consider the equation for ${\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)$.

Note that $C_T\left(G_{\alpha }\right)=C_T\left(G_{{\alpha }_1}\right)\cup C_T\left(G_{{\alpha }_2}\right)$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Let $i=\{1,2\}$. Given $C_T\left(G_{\alpha }\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)\ne \varnothing$, we consider the following:

Case 1: $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$;

Case 2: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$;

Case 3: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)\ne \varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)=\varnothing$;

Case 4: $C_T\left(G_{{\alpha }_i}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_i}\right)=\varnothing$, and $C_T\left(G_{{\alpha }_{3-i}}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_{3-i}}\right)\ne \varnothing$.

In the following, we prove the statement for Case 1. The statements for the other cases can be proven similarly.

Let $w_{min}=p·\omega \left(G\right)$ and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$. Let $w_1$ and $w_2$ be integers such that $w_{min}\le w_1,w_2\le w_{max}$ and $w_1+w_2=w$. Let $f_1$ be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w_1,w_1)$-clique transversal function of $G_{{\alpha }_1}$ and $f_2$ be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w_2,w_2)$-clique transversal function of $G_{{\alpha }_2}$. By Definition 7, $f_1\left(C\right)\ge w_1$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ and $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Similarly, $f_2\left(C\right)\ge w_2$ for every $C\in C_T\left(G_{{\alpha }_2}\right)$ and $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$.

Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. By Lemma 3, $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. For every maximal clique $C\in C_{\overline{T}}\left(G_{\alpha }\right)$, either $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Therefore, $f\left(C\right)=f_1\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f\left(C\right)=f_2\left(C\right)\ge x$ for $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$ .

For each maximal clique $C\in C_T\left(G_{\alpha }\right)$, C is also a maximal clique of $G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]$ and it is the union of a clique $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and a clique $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Thus, $f\left(C\right)=f\left(C_1\right)+f\left(C_2\right)=f_1\left(C_1\right)+f_2\left(C_2\right)\ge w_1+w_2=w$. The function f is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w,w)$-clique transversal function of $G_{\alpha }$. Hence,

$${\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)\le {\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,w_2,w_2)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w,w)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$.

By Lemma 3, $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. For each maximal clique $C\in C_{\overline{T}}\left(G_{\alpha }\right)$, either $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Therefore, $f_1\left(C\right)=f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f_2\left(C\right)=f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$.

By Lemma 3, $C_T\left(G_{\alpha }\right)=C_X\left(G_{\alpha }\right)$. For each maximal clique $C\in C_T\left(G_{\alpha }\right)$, C is the union of a clique $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and a clique $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Then, $f_1\left(C_1\right)+f_2\left(C_2\right)=f\left(C_1\right)+f\left(C_2\right)=f\left(C\right)\ge w$. By applying arguments similar to those used in proving Statement (1.3), there exist two integers $w_1$ and $w_2$ such that $w_1+w_2=w$, $f_1\left(C_1\right)\ge w_1$ for every $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, and $f_2\left(C_2\right)\ge w_2$ for every $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Clearly, $w_{min}\le w_1,w_2\le w_{max}$. By definition, $C_T\left(G_{{\alpha }_1}\right)\subseteq C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_T\left(G_{{\alpha }_2}\right)\subseteq C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Then, $f_1\left(\widehat{C}\right)\ge w_1$ for every $\widehat{C}\in C_T\left(G_{{\alpha }_1}\right)$, and $f_2\left(\widehat{C}\right)\ge w_2$ for every $\widehat{C}\in C\left(G_{{\alpha }_2}\right)$. Thus, $f_1$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w_1,w_1)$-clique transversal function of $G_{{\alpha }_1}$, and $f_2$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,w_2,w_2)$-clique transversal function of $G_{{\alpha }_2}$. Hence,

$${\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,w_2,w_2)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right).$$

We have ${\tau }_{p,2}^{d,\ell }(x,w,w)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,w_1,w_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,w_2,w_2)\left(G_{{\alpha }_2}\right)$. Statement (2.3.1) therefore holds.    □

Lemma 9.

Suppose that G is a distance-hereditary graph and $G_{\alpha }=G_{{\alpha }_1}⨁G_{{\alpha }_2}$ is an induced subgraph of G formed from two disjoint distance-hereditary graphs $G_{{\alpha }_1}$ and $G_{{\alpha }_2}$. Let $p\in \{0,-1\}$, and let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$. Then, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ can be computed as follows:

(1) 

${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\infty$;

(2) 

${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)=\infty$;

(3) 

Let $w_{min}=p·\omega \left(G\right)$, and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$. ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$ can be computed as follows:

(3.1) 

Assume that $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$;

(3.1.1) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.1.2) 

If $C_T\left(G_{{\alpha }_2}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.1.3) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)=\varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(x_2,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.2) 

Assume that $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)=\varnothing$;

(3.2.1) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,1}^{d,\ell }(x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.2.2) 

If $C_T\left(G_{{\alpha }_2}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,1}^{d,\ell }(x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.2.3) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)=\varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,1}^{d,\ell }(x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(x_2,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.3) 

Assume that $C_T\left(G_{{\alpha }_1}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$;

(3.3.1) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,0}^{d,\ell }(x,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.3.2) 

If $C_T\left(G_{{\alpha }_2}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,0}^{d,\ell }(x,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right)\right\};$$

(3.3.3) 

If $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)=\varnothing$, then

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)=\underset{\begin{array}{c}{x}_1,x_2\in \mathbb{Z}\\ x_1+x_2=x\\ y\le x_1\le w_{max}\\ w_{min}\le x_2\le x-y\end{array}}{min}\left\{{\tau }_{p,0}^{d,\ell }(x,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,1}^{d,\ell }(x_2,x_2)\left(G_{{\alpha }_2}\right)\right\}.$$

Proof. 

The graph $G_{\alpha }$ is obtained by connecting every vertex of $TS\left(G_{{\alpha }_1}\right)$ to all vertices of $TS\left(G_{{\alpha }_2}\right)$, and $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)$. By Lemma 4, we have $C_T\left(G_{\alpha }\right)=\varnothing$ and $C\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)\cup C_X\left(G_{\alpha }\right)$. By Definition 7, Statements (1) and (2) are true.

We now consider the following three cases for computing the equation for ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$. Let $i=\{1,2\}$. If $C_T\left(G_{{\alpha }_1}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)=\varnothing$, then $G_{{\alpha }_1}$ has no vertices. Therefore, only three cases need to be considered based on their emptiness:

Case 1: $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$;

Case 2: $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)=\varnothing$;

Case 3: $C_T\left(G_{{\alpha }_1}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$.

Each case above has three subcases. Below, we prove the statements for Case 1 and its subcases. The statements for the other cases and their subcases can be proven similarly.

Case 1: $C_T\left(G_{{\alpha }_1}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_1}\right)\ne \varnothing$. Let $w_{min}=p·\omega \left(G\right)$ and $w_{max}=(p+(\ell -1)·d)·\omega \left(G\right)$.

Case 1.1: $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$. Let $x_1$ and $x_2$ be integers such that $x_1+x_2=x$, $y\le x_1\le w_{max}$, and $w_{min}\le x_2\le x-y$.

Let $f_1$ be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_1,x_1)$-clique transversal function of $G_{{\alpha }_1}$ and $f_2$ be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_2,x_2)$-clique transversal function of $G_{{\alpha }_2}$. By Definition 7, $f_1\left(C\right)\ge x_1$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ or every $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Similarly, $f_2\left(C\right)\ge x_2$ for every $C\in C_T\left(G_{{\alpha }_2}\right)$ or every $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Furthermore, $f_1\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ and $f_2\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$.

Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. By Lemma 4, $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)\cup C_X\left(G_{\alpha }\right)$.

Let $C\in C_{\overline{T}}\left(G_{\alpha }\right)$. If $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$, then $f\left(C\right)=f_1\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f\left(C\right)=f_2\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. If $C\in C_X\left(G_{\alpha }\right)$, then there exist two cliques $C_1$ and $C_2$ such that $C=C_1\cup C_2$, $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, and $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Therefore, $f\left(C\right)=f\left(C_1\right)+f\left(C_2\right)=f_1\left(C_1\right)+f_2\left(C_2\right)\ge x_1+x_2=x$. We obtain $f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{\alpha }\right)$. Let $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. In this case, $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)$. Thus, $f\left(C\right)=f_1\left(C_1\right)\ge x_1\ge y$. The function f is a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Consequently,

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)\le {\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$.

By Lemma 4, $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)\cup C_X\left(G_{\alpha }\right)$. Let $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Then, $C\in C_{\overline{T}}$. Therefore, $f_1\left(C\right)=f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f_2\left(C\right)=f\left(C\right)\ge x$ for every $C_{\overline{T}}\left(G_{{\alpha }_2}\right)$.

Let $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. The clique $C=C_1\cup C_2$ is a maximal clique in $C_{\overline{T}}\left(G_{\alpha }\right)$. We have

$$f_1\left(C_1\right)+f_2\left(C_2\right)=f\left(C_1\right)+f\left(C_2\right)=f\left(C\right)\ge x.$$

In this case, $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)$. Then, $C_1\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$ and $f_1\left(C_1\right)=f\left(C_1\right)\ge y$. It is not difficult to see that $f_1\left(C_1\right)\in \{y,y+1,\dots ,w_{max}\}$ and $f_2\left(C_2\right)\in \{x-y,x-y-1,\dots ,w_{min}\}$. Consequently, there exist two integers $x_1$ and $x_2$ such that

(i)

$y\le x_1\le w_{max}$;

(ii)

$w_{min}\le x_2\le x-y$;

(iii)

$x_1+x_2=x$;

(iv)

$f_1\left(C_1\right)\ge x_1$ for every $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$; and

(v)

$f_2\left(C_2\right)\ge x_2$ for every $C_2\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$.

Note that $C_T\left(G_{{\alpha }_1}\right)\subseteq C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_T\left(G_{{\alpha }_2}\right)\subseteq C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Thus, $f_1\left(C_1\right)\ge x_1$ for every $C_1\in C_T\left(G_{{\alpha }_1}\right)$, and $f_2\left(C_2\right)\ge x_2$ for every $C_2\in C_T\left(G_{{\alpha }_2}\right)$. The function $f_1$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_1,x_1)$-clique transversal function of $G_{{\alpha }_1}$, and $f_2$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_2,x_2)$-clique transversal function of $G_{{\alpha }_2}$. We obtain

$${\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right).$$

Consequently, ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,2}^{d,\ell }(x,x_2,x_2)\left(G_{{\alpha }_2}\right)$. Statement (3.1.1) therefore holds.

Case 1.2: $C_T\left(G_{{\alpha }_2}\right)=\varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)\ne \varnothing$. Let $x_1$ and $x_2$ be integers such that $x_1+x_2=x$, $y\le x_1\le w_{max}$, and $w_{min}\le x_2\le x-y$.

Let $f_1$ be a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_1,x_1)$-clique transversal function of $G_{{\alpha }_1}$ and $f_2$ be a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,x_2)$-clique transversal function of $G_{{\alpha }_2}$. By Definition 7, $f_1\left(C\right)\ge x_1$ for every $C\in C_T\left(G_{{\alpha }_1}\right)$ or every $C\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, and $f_2\left(C\right)\ge x_2$ for every $C\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Furthermore, $f_1\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ and $f_2\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$.

Let f be a function of $G_{\alpha }$ such that $f\left(v\right)=f_1\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and $f\left(v\right)=f_2\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$. By Lemma 4, $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)\cup C_X\left(G_{\alpha }\right)$.

Let $C\in C_{\overline{T}}\left(G_{\alpha }\right)$. If $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$ or $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$, then $f\left(C\right)=f_1\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f\left(C\right)=f_2\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. If $C\in C_X\left(G_{\alpha }\right)$, then there exist two cliques $C_1$ and $C_2$ such that $C=C_1\cup C_2$, $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$, and $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. Therefore, $f\left(C\right)=f\left(C_1\right)+f\left(C_2\right)=f_1\left(C_1\right)+f_2\left(C_2\right)\ge x_1+x_2=x$. We obtain $f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{\alpha }\right)$. Let $C\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$. In this case, $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)$. Thus, $f\left(C\right)=f_1\left(C_1\right)\ge x_1\ge y$. The function f is a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Consequently,

$${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)\le {\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right).$$

Conversely, let f be a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,y)$-clique transversal function of $G_{\alpha }$. Let $f_1$ be a function of $G_{{\alpha }_1}$ such that $f_1\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_1}\right)$, and let $f_2$ be a function of $G_{{\alpha }_2}$ such that $f_2\left(v\right)=f\left(v\right)$ for every $v\in V\left(G_{{\alpha }_2}\right)$.

By Lemma 4, $C_T\left(G_{\alpha }\right)=\varnothing$ and $C_{\overline{T}}\left(G_{\alpha }\right)=C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)\cup C_X\left(G_{\alpha }\right)$. Let $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)\cup C_{\overline{T}}\left(G_{{\alpha }_2}\right)$. Then, $C\in C_{\overline{T}}$. Therefore, $f_1\left(C\right)=f\left(C\right)\ge x$ for every $C\in C_{\overline{T}}\left(G_{{\alpha }_1}\right)$, and $f_2\left(C\right)=f\left(C\right)\ge x$ for every $C_{\overline{T}}\left(G_{{\alpha }_2}\right)$.

Let $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$ and $C_2\in C\left(G_{{\alpha }_2}\left[TS\left(G_{{\alpha }_2}\right)\right]\right)$. The clique $C=C_1\cup C_2$ is a maximal clique in $C_{\overline{T}}\left(G_{\alpha }\right)$. We have

$$f_1\left(C_1\right)+f_2\left(C_2\right)=f\left(C_1\right)+f\left(C_2\right)=f\left(C\right)\ge x.$$

In this case, $TS\left(G_{\alpha }\right)=TS\left(G_{{\alpha }_1}\right)$. Then, $C_1\in C\left(G_{\alpha }\left[TS\left(G_{\alpha }\right)\right]\right)$ and $f_1\left(C_1\right)=f\left(C_1\right)\ge y$. It is not difficult to see that $f_1\left(C_1\right)\in \{y,y+1,\dots ,w_{max}\}$ and $f_2\left(C_2\right)\in \{x-y,x-y-1,\dots ,w_{min}\}$. Consequently, there exist two integers $x_1$ and $x_2$ such that

(i)

$y\le x_1\le w_{max}$;

(ii)

$w_{min}\le x_2\le x-y$;

(iii)

$x_1+x_2=x$;

(iv)

$f_1\left(C_1\right)\ge x_1$ for every $C_1\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$; and

(v)

$f_2\left(C_2\right)\ge x_2$ for every $C_2\in C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$.

Note that $C_T\left(G_{{\alpha }_1}\right)\subseteq C\left(G_{{\alpha }_1}\left[TS\left(G_{{\alpha }_1}\right)\right]\right)$. Thus, $f_1\left(C_1\right)\ge x_1$ for every $C_1\in C_T\left(G_{{\alpha }_1}\right)$. The function $f_1$ is a ${\mathsf{\Gamma }}_{p,2}^{d,\ell }(x,x_1,x_1)$-clique transversal function of $G_{{\alpha }_1}$, and $f_2$ is a ${\mathsf{\Gamma }}_{p,0}^{d,\ell }(x,x_2)$-clique transversal function of $G_{{\alpha }_2}$. Hence,

$${\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right)\le {\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right).$$

We obtain ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)={\tau }_{p,2}^{d,\ell }(x,x_1,x_1)\left(G_{{\alpha }_1}\right)+{\tau }_{p,0}^{d,\ell }(x,x_2)\left(G_{{\alpha }_2}\right)$. Statement (3.1.2) therefore holds.

Case 1.3: $C_T\left(G_{{\alpha }_2}\right)\ne \varnothing$ and $C_{\overline{T}}\left(G_{{\alpha }_2}\right)=\varnothing$. Following the arguments similar to those for proving Case 1.2, we can prove that Statement (3.1.3) is true.    □

5. The Algorithm

By Lemmas 1–9 and Theorem 2, we introduce Algorithm 1 to compute ${\tau }_C(p,d,\ell ,b)\left(G\right)$ for a distance-hereditary graph G using dynamic programming. The algorithm uses an input $PTF$-tree T of G rooted at r to break down the graph into smaller subproblems represented by nodes and traverses the tree in post order, ensuring that all children of a node are processed before the node itself. At each node, the algorithm solves the subproblem using results from its children, applying dynamic programming principles, and combines solutions from the child nodes to solve the parent node’s problem, storing results to avoid redundant calculations. The root node contains the solution to the original problem after all nodes are processed.

For each node $\alpha$ of T, let $T_{\alpha }$ be the subtree of T rooted at node $\alpha$. The algorithm uses $G_{\alpha }$ to represent the subgraph of G induced by the leaves of $T_{\alpha }$. Thus, $\alpha$ represents a vertex or a subgraph $G_{\alpha }$ formed by operations on its children. If $\alpha$ is not a leaf, ${\alpha }_1$ and ${\alpha }_2$ are its left and right child nodes, respectively.

For each visited node $\alpha$, we compute ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ for $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$ based on Lemmas 1–9 and Theorem 2. We assume that the root of T is node r, so $G=G_r$. Note that there are $2n-1$ nodes in a $PTF$-tree. See Algorithm 1 for further details.

Algorithm 1:

Theorem 3.

Suppose that G is a distance-hereditary graph with the clique number ω. Let $p\in \{0,-1\}$, and let $d,\ell ,x,y,z$ be integers such that $d,\ell \in {\mathbb{Z}}^{+}$ are fixed, and $p·\omega \left(G\right)\le x,y,z\le (p+(\ell -1)·d)·\omega \left(G\right)$. Algorithm 1 computes ${\tau }_C(p,d,\ell ,b)\left(G\right)$ in $O\left(n{\omega }^4\right)$ time.

Proof. 

The correctness of Algorithm 1 can be verified by Lemmas 1–9 and Theorem 2. To analyze the running time, we proceed as follows:

• Initialization:
  • Sorting the nodes of the $PTF$-tree T in post-order takes $O\left(n\right)$ time;
  • Computing the clique number $\omega$ for a distance-hereditary graph also takes $O\left(n\right)$ time [23]. Therefore, computing $w_{min}$ and $w_{max}$ takes $O\left(n\right)$ time if the clique number is not given as an input;
• Main Loop:
  • The algorithm processes $2n-1$ nodes of the tree;
  • For each node, it iterates over all combinations of $x,y,z$ within the range $\{w_{min},w_{m+1},\dots ,w_{m+1}\}$, where $w_{min}=p·\omega$ and $w_{max}=(p+(\ell -1)·d)·\omega$;
  • The total number of combinations is $O\left({\omega }^3\right)$;
• Inner Loop Computation:
  • For each node combination of $x,y,z$, the algorithm computes ${\tau }_{p,0}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, ${\tau }_{p,1}^{d,\ell }(x,y)\left(G_{\alpha }\right)$, and ${\tau }_{p,2}^{d,\ell }(x,y,z)\left(G_{\alpha }\right)$ by the specified lemmas. Each computation is $O\left(\omega \right)$;
• Complexity Per Node:
  • The computations for each node result in the time complexity of $O\left({\omega }^4\right)$;
• Total Complexity:
  • The final two steps are to compute ${\tau }_C(p,d,\ell ,b)\left(G_r\right)$ by Lemmas 1–4 and Theorem 2, and output the result. They take $O\left(\omega \right)$ time;
  • Since there are $2n-1$ nodes in the tree, the total running time is $O\left(n{\omega }^4\right)$.

□

6. Conclusions

This study presents a significant advancement in understanding and applying clique transversal problems within distance-hereditary graphs by introducing the $(p,d,\ell ,b)$-clique problem. The framework proposed herein offers a unified approach to addressing various clique-related problems, enhancing both the theoretical foundations and practical implementations in this domain. One of the key contributions is the development of a dynamic programming algorithm with the complexity of $O\left(n{\omega }^4\right)$, which is efficient for distance-hereditary graphs. This algorithm not only streamlines the process of solving these complex problems but also sets the stage for its potential application to other graph classes. The efficiency and practicality of the algorithm make it a valuable tool for researchers and practitioners working with large-scale graphs where clique problems are prevalent. Moreover, this work has broader implications in graph theory, offering new insights into the structure and behavior of distance-hereditary graphs. By providing a comprehensive framework and a powerful algorithmic tool, this paper opens up new avenues for research and application in related fields, such as network analysis, bioinformatics, and social network modeling. Future research could build upon these findings by extending the proposed methods to other graph classes. Further optimization of the dynamic programming algorithm could enhance its performance, making it applicable to even larger and more complex graph structures. Such advancements would not only broaden the scope of this work but also significantly contribute to the overall body of knowledge in algorithmic graph theory.