Abstract
Decision making plays a pivotal role in shaping outcomes across various disciplines, such as medicine, economics, and business. This paper provides practitioners with guidance on implementing a decision tree designed to optimise treatment assignment policies through an interpretable and non-parametric algorithm. Building upon the method proposed by Zhou, Athey, and Wager (2023), our policy tree introduces three key innovations: a different approach to policy score calculation, the incorporation of constraints, and enhanced handling of categorical and continuous variables. These innovations enable the evaluation of a broader class of policy rules, all of which can be easily obtained using a single module. We showcase the effectiveness of our policy tree in managing multiple, discrete treatments using datasets from diverse fields. Additionally, the policy tree is implemented in the open-source Python package mcf (modified causal forest), facilitating its application in both randomised and observational research settings.
Keywords:
causal machine learning; conditional average treatment effects; multiple treatments; offline policy learning; decision trees JEL Classification:
C21; C87; C14; C69
1. Introduction
Policymakers are keen to gain insights into policy impacts, aiming to facilitate future applications. Therefore, current econometrics research is dedicated to developing methods that accurately estimate policy effects, specifically focusing on understanding relevant heterogeneity across sub-populations. Such methods for analysing conditional average treatment effects include, for instance, forest-based algorithms, double machine learning, or meta-learners [1,2,3]. However, it is important to distinguish between estimating heterogeneity and providing guidance on the design of treatment assignment mechanisms. The latter pertains to the policy learning research area, which effectively uses information from randomised or observational studies to assign individuals to future treatments.
The seminal work of [4] pioneered the literature on policy learning, which was then further developed by [5,6,7,8,9], among others. Specifically, ref. [5] introduces a policy learner that attains convergence rates in settings with a binary treatment and known propensity scores. Ref. [7] proposes a policy learner that achieves the same convergence rate even without known propensity scores, making it well suited for observational studies. Finally, ref. [9] proposes the cross-fitted augmented inverse propensity weighted learning (CAIPWL) policy learner, which achieves optimal convergence rates in multi-action settings with unknown propensity scores.
This work presents the mcf policy tree as implemented in the mcf package. The policy learner is based on the algorithm proposed by [9] but introduces three key modifications: policy scores calculation, implementation of constraints, and different handling of categorical and continuous variables.
The first modification is in policy score calculation. The mcf computes consistent and asymptotically normally distributed policy scores to estimate individualised average treatment effects (IATEs) [10]. These scores differ from the doubly robust scores used in the original algorithm, as the mcf algorithm minimises estimation errors of the conditional mean responses and their covariance while also considering propensity score heterogeneity to reduce selection bias. Unlike doubly robust scores, the IATEs depend only on features, not outcomes or treatments. The second modification concerns the implementation of constraints. Constraints are incorporated as treatment-specific cost values, subtracted from the policy scores. This also applies to constraints indirectly related to costs, such as treatment share limitations, ensuring comprehensive decision-making considerations. The third modification is the handling of categorical and continuous variables. Traditional methods often use one-hot encoding for categorical features, leading to extreme leaves with many values in shallow trees. The mcf policy tree, however, allows several categories on both sides of a split, thus avoiding such issues (see Chapter 9.2.4 in [11] for a detailed explanation of this approach). For continuous and unordered features with many values, users can specify an approximation parameter to determine potential splitting points, providing finer granularity compared to the single global approximation parameter A in [9]. For instance, considering a four-level tree, the number of splitting points is A/8 at the 4th level (the top of the tree), A/4 at the 3rd level, A/2 at the 2nd level, and A at the 1st level (the bottom of the tree).
To the best of our knowledge, the mcf policy tree algorithm is the first method to integrate all these features into a single optimal policy module. Consequently, our work introduces a more holistic and modern policy learner, demonstrating its versatility across various fields. By doing so, we aim to facilitate its application for practitioners, providing them with a comprehensive and advanced tool for policy analysis.
2. Framework
The mcf package is a forest-based causal machine learning algorithm that produces consistent and asymptotically normal treatment effect estimates for various levels of granularity in randomised control trials and in observational studies. In observational studies, identifying causal effects requires several key assumptions: ignorability, overlap, the stable unit treatment value assumption, and exogeneity of features (see [12] for detailed explanations of these assumptions). When the assumptions are satisfied, causal effects can be identified at different aggregation levels. These include average potential outcomes (APO), the average treatment effect (ATE), conditional average treatment effects like individualised average treatment effects (IATEs), and grouped aggregates of these effects.
The IATEs represent the average effects for the most granular sub-groups, characterised by specific realisations of the available exogenous features. Evaluating the IATEs enables the detection of potential heterogeneous effects across sub-groups of the population. Observing such heterogeneity indicates that certain individuals may benefit more or less from a particular treatment, highlighting the need to refine treatment assignment mechanisms and subsequently inform policy recommendations. Such refinement can be achieved through policy learning by defining the objective of an optimal assignment rule.
Following the framework of [9] for optimal allocations with multiple treatments, let denote a policy rule mapping individuals to programmes based on their characteristics . Each policy rule is part of a candidate set denoted by , where the objective is to maximise the policy value function . This function represents the average population outcome when employing policy rule for programme assignment, aiming to find the rule that maximises the average outcome across the population.
To find the optimal policy rule within the policy tree class , we introduce the OptimalPolicy() class of the mcf package. This class explores the space of decision trees to maximise a value function using individual policy scores such as potential outcomes or IATEs. The algorithm conducts exhaustive and recursive searches across pre-specified variables and values, assigning all observations in a terminal leaf node to a single treatment. This approach ensures that policy decisions are based on maximising the identified causal effects within relevant sub-groups, thereby enhancing the precision and effectiveness of policy recommendations.
Algorithm 1 illustrates, in a simplified way, how the tree-search algorithm works. To introduce it, we can assume the following notation: For i observations, represents the features, specifically, is the number of ordered features and is the number of unordered features; is the treatments space; is the vector (or matrix) of policy scores for each observation i; is the potential outcome for each observation for each treatment j; and the associated sum is the reward . Finally, L is an integer indicating the depth of the tree plus one. The module optpolicy_pt_eff_functions.py (accessed on 10 July 2024) gives more details on the algorithm.
| Algorithm 1 Policy Tree |
|
Besides the policy tree, the OptimalPolicy() class provides a best-score method to create an assignment rule. This method simply assigns units to the treatment with the highest estimated potential outcome. Although computationally cheap, this best-score method lacks clear interpretability for the allocation rules, which may make it difficult for policymakers to adopt it. To address the issue of interpretability, one could analyse individuals’ characteristics retrospectively. For example, the evaluate() method of the OptimalPolicy() class shows the distribution of features for each treatment. This information helps to understand the relationship between characteristics and assigned treatments.
3. Empirical Studies
The mcf package offers empirical researchers dual valuable functionalities: the possibility of conducting heterogeneity analyses, as shown in [13], and refining the decision-making process by optimising treatment allocation rules. This section studies three real-world applications from different scientific fields based on distinct research settings. In these empirical tasks, we first perform an effect heterogeneity evaluation, calling the ModifiedCausalForest() class of the mcf algorithm. We then use the potential outcomes estimated by the mcf to optimise the treatment allocations generated by the policy trees using the mcf’s OptimialPolicy() class. The samples from all three studies are split using the same approach. Specifically, 40% of the data are allocated for training the mcf, and another 40% for estimating the effects and training the policy learning algorithm. Finally, the remaining 20% of the data are reserved for predicting out-of-sample policy rules and welfare. This allocation helps to estimate the treatment effect effectively and to mitigate the risk of overfitting, particularly for deeper trees.
3.1. Study 1: Oregon Health Insurance Experiment
In 2008, Oregon initiated a lottery with limited spots to provide low-income individuals access to its Medicaid program. This lottery offers an opportunity to examine the impact of expanding access to public health insurance within a randomised controlled setting. Researchers analysed various outcomes over the two years following the experiment, including healthcare utilisation, financial strain, health status, labour market outcomes, and political participation. Extensive studies have been conducted by [14,15,16,17,18,19,20,21], among others. Overall, findings suggest that access to Medicaid leads to an increase in healthcare utilisation and a decrease in financial strain and depression, albeit without statistically significant improvements in physical health or labour market outcomes. This analysis follows [14] and specifically focuses on the impact of being selected in the lottery on primary care visits during the first year post-selection. We rely on survey data collected within the experimental setting, given that the hospital records are not publicly available. The end-line survey, conducted after 12 months, was completed by 23,777 individuals. The outcome is measured by a binary variable indicating if primary care has been utilised during the year. Among the several outcomes available (e.g., emergency room usage or drug prescription), we choose primary care utilisation because of its importance from a policy perspective. Indeed, primary care visits may lead to preventive care for more serious diseases and, consequently, prevention of more expensive medical care.
After dropping observations with missing values, the size of our dataset is 23,527 observations, with 50% of the individuals having Medicaid health insurance. As in [14], our intention-to-treat specification incorporates additional features, such as socio-demographic factors, which are valuable for exploring heterogeneity and informing policy, even though they are not essential for identifying causal effects. On the contrary, although assignment to the lottery is random, all family members of randomly selected individuals can apply for Medicaid. Therefore, the probability of receiving treatment depends on the number of family members, which we include as a control variable. Table A1 and Table A4 in Appendix A describe the 11 variables used for data analysis.
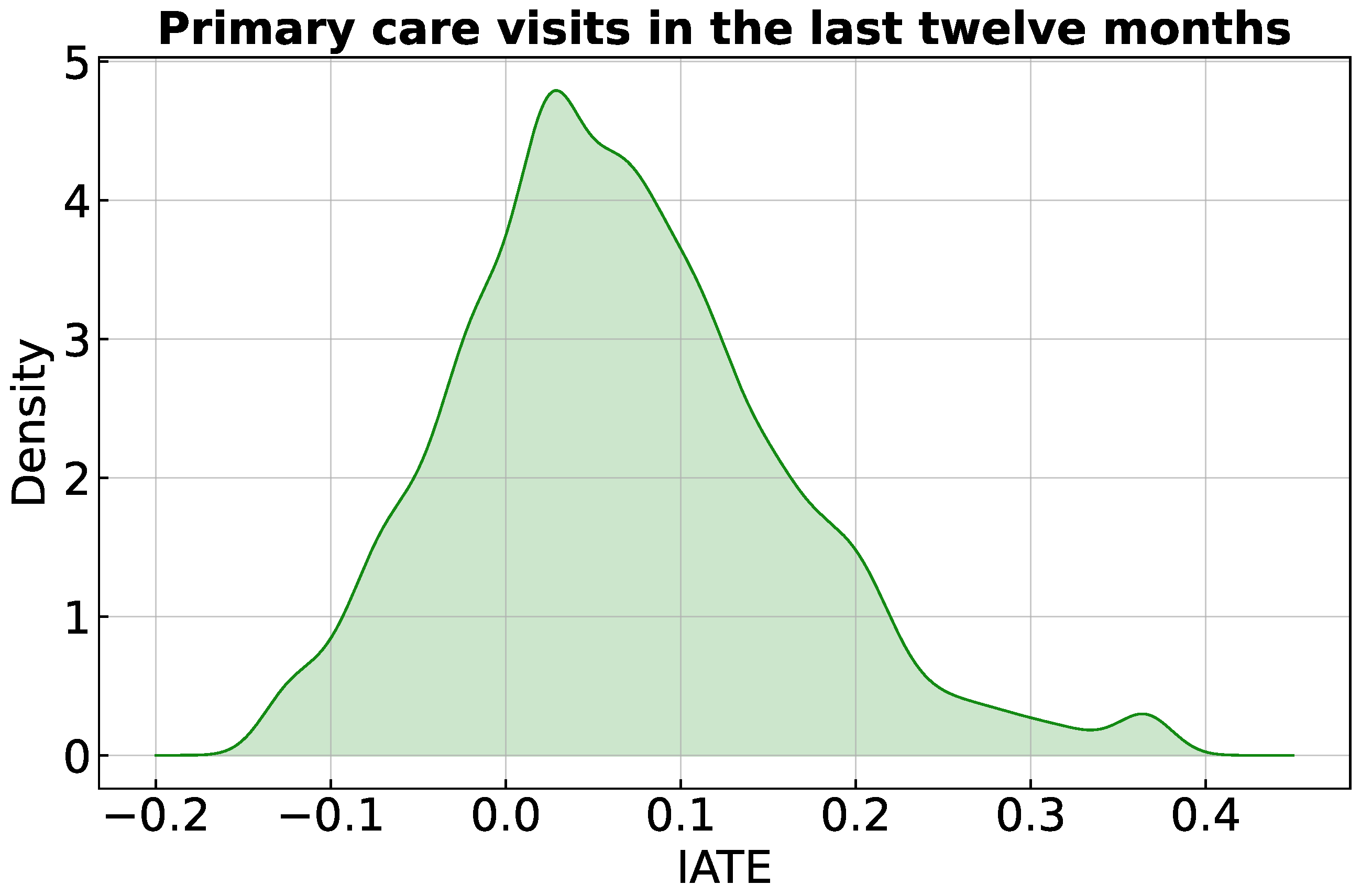
We evaluate the distribution of the IATEs to detect potential effect heterogeneity. Figure 1 displays a density plot of the IATEs, ranging from −0.13 to 0.37, with a mean value of 0.07 and an average standard error of 0.1. The variation in the effects justifies our following analysis for decision making, aiming at expanding the number of primary care visits by optimising the treatment allocation process.
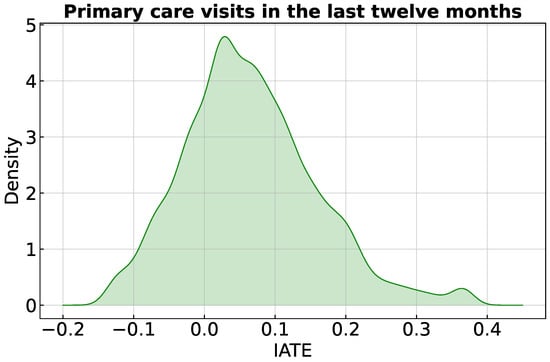
Figure 1.
Distribution of IATE. Mean (average standard error) of the IATEs: 0.07 (0.1).
Table 1 provides details on welfare, measured as utilisation of primary care visits and allocation shares of individuals for various policies. We compare the results of the policy trees with our two baseline policies, namely the observed and random treatment allocations. In this study, we examine both unconstrained and constrained policy trees. Given the lack of specific cost information for Medicaid insurance, we assume that only approximately half of the population (as in the empirical data) can be covered by this health insurance. The algorithm enforces constraints by finding a cost value to subtract from the policy score. It adjusts the treatment costs to ensure that the allocation of observations to treatments does not exceed the maximum treatment shares. We build our constrained policy trees by specifying either the depth of a first optimal tree (constrained optimal policy tree) or, optionally, specifying, in addition, the depth of a second optimal policy tree (constrained sequentially optimal policy tree). In the latter case, the second tree is built within the strata obtained from the leaves of the first tree. The final policy tree will not be optimal. However, its performance in terms of welfare is comparable to that of an optimal tree with the same depth, with the advantage of reduced computational time. For example, in this application, the runtime for a constrained optimal policy tree of depth-4 is 3 min and 3 s, whereas a constrained sequentially optimal policy tree takes only 30 s. Additional details on the runtime comparison of the policy trees can be found in Appendix A.3.1 of Appendix A. Note that the policytree package of [22] also provides sequentially optimal policy trees, which are referred to as hybrid policy trees by the authors.

Table 1.
Treatment allocations: Oregon health insurance experiment.
In Table 1, all the policy trees show an increase in welfare with respect to the baseline policies. The unconstrained policy trees achieve the highest welfare, increasing the probability of primary care visits from 51.70% to 54.97%. They allocate almost all individuals to the treatment, which can be interpreted as access to Medicaid insurance for nearly everyone. Compared to the unconstrained policy trees, those with the capacity constraint always report a small decrease in the probability of primary care visits, allocating a significantly lower proportion of individuals to the treatment. Constrained optimal policy trees and constrained sequentially optimal policy trees, with a last sequentially optimal sub-tree of the same depth, show comparable and stable results in terms of welfare achieved. From a computational point of view, such findings may be relevant for large datasets, since policy trees with sequentially optimal layers reduce computation time while performing similarly well.
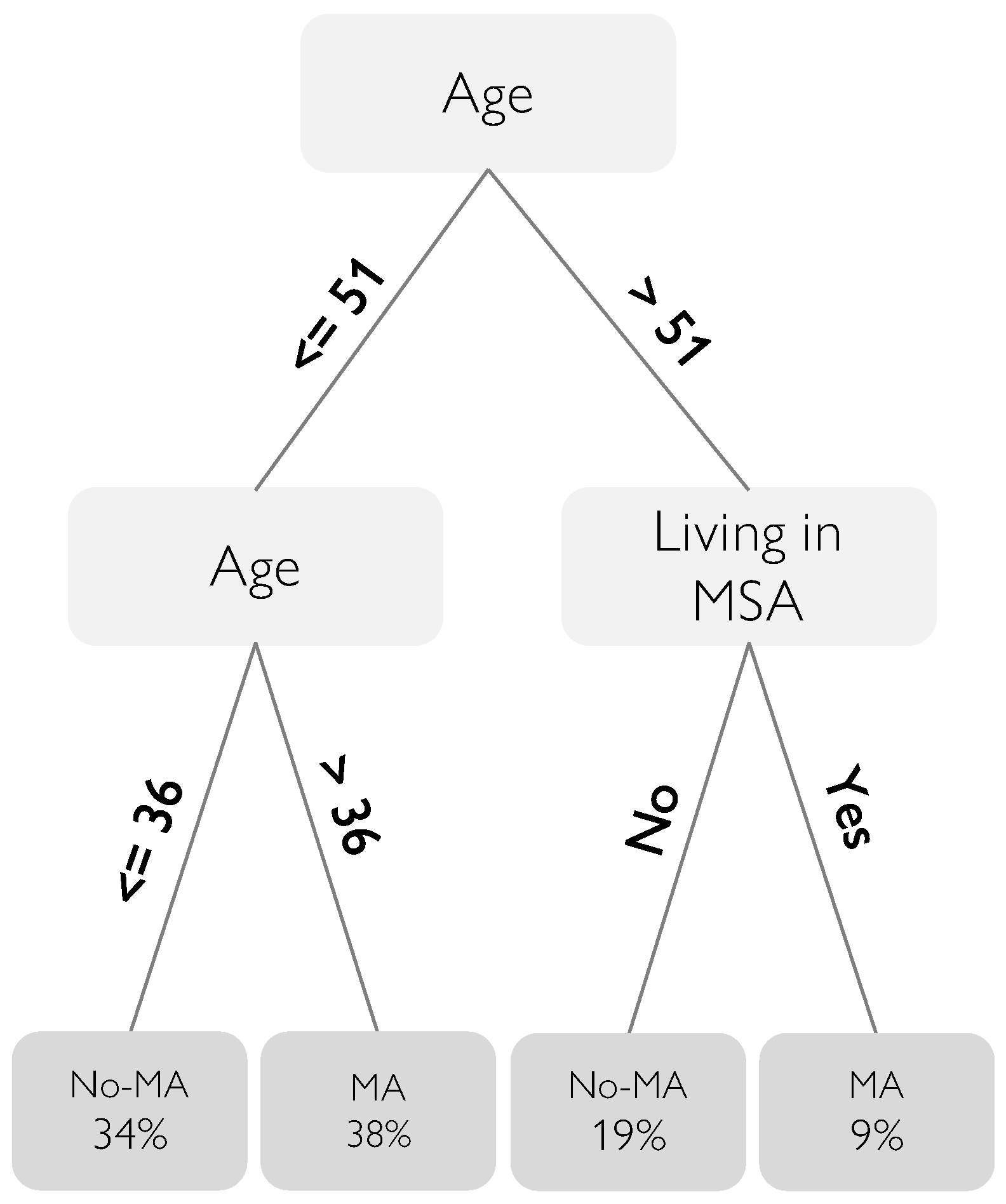
Figure 2 presents the allocation rules of a constrained optimal policy tree with a depth of 2. Notably, even at this relatively shallow depth, the policy tree demonstrates improvements in welfare compared to the observed allocations and the simplest allocation rules. Individuals with age between 37 and 51 years old (38% of the sample) are assigned to Medicaid. Additionally, individuals older than 51 living in metropolitan areas, constituting 9% of our sample, are also allocated to the program. Conversely, individuals younger than 36 and older than 51 who do not live in metropolitan areas are excluded from the program. For reference, note that the age ranges from 20 to 63.
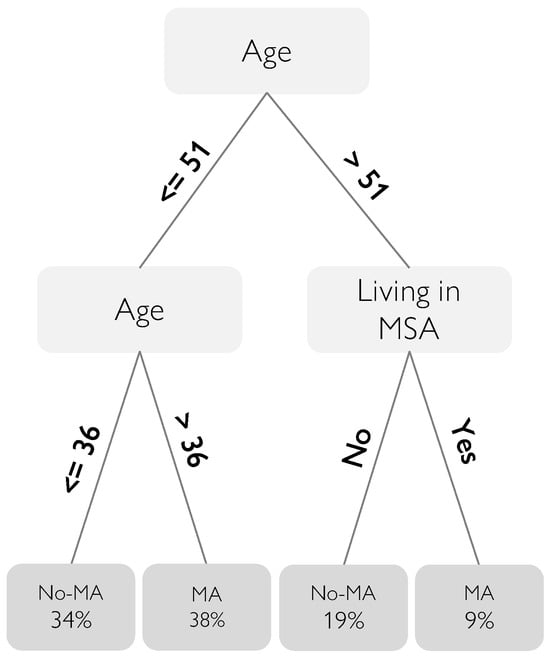
Figure 2.
Allocation rule for a constrained optimal policy tree of depth-2. Note: The policy tree shows the shares of individuals allocated to each treatment. The splitting variables of the tree are age and an indicator variable for living in a metropolitan area (MSA). The final leaves of the trees indicate the treatments and corresponding shares of allocated individuals. The treatment used in the analysis is the indicator for being assigned to the lottery, which consequently gives access to Medicaid. For representation reasons, the tree reports the following: No-MA, no access to Medicaid (not extracted for the lottery); MA, access to Medicaid (extracted for the lottery).
3.2. Study 2: Right Heart Catheterisation
In a seminal study, ref. [23] investigated the impact of right heart catheterisation (RHC) on various outcomes, including subsequent survival, healthcare costs, intensity of care, and length of hospital stay. Their findings revealed a positive association between RHC and mortality, as well as increased costs and prolonged length of stay. This conclusion was corroborated by subsequent research utilising different estimation methods, such as those employed by [24,25,26,27]. In accordance with previous research, we also use the dataset originally collected from the SUPPORT prospective cohort study (Study to Understand Prognoses and Preferences for Outcomes and Risks of Treatments), as in [23]. This dataset includes 5735 observations on ill and hospitalised individuals between 1989 and 1994 in five medical centres in the US. Of these individuals, 38% received the surgery. Ref. [13] utilises the same information to provide new results on effect heterogeneity by exploring the functionalities of the mcf package.
In this empirical application, we focus on finding an optimal allocation of RHC to patients to increase their probability of survival six months after the medical surgery. Previous work has exploited expert opinion to identify eight features as relevant confounding factors [25]. These features include an index of activities of daily living two weeks before admission, age, the acute physiology and chronic health evaluation score (APACHE III), the Glasgow coma score, mean blood pressure, the probability of surviving two months (based on model estimations), an indicator for do not resuscitate status on the first day, and information on nine primary disease categories. Recognising the significance of these factors, we employ them as features in the policy tree to obtain assignment rules for decision making. Age and mean blood pressure are continuous variables, and we allow the tree algorithm to automatically determine the optimal split points based on the default number of evaluation points in the mcf package.
Our analysis starts by estimating the policy scores and IATEs. Additionally to the high-priority factors, we include potential confounding features (e.g., information on having cancer, possessing health insurance, etc.) to achieve identification through a selection-on-observable approach. Table A2 and Table A5 of Appendix A comprehensively describe all 55 confounders.
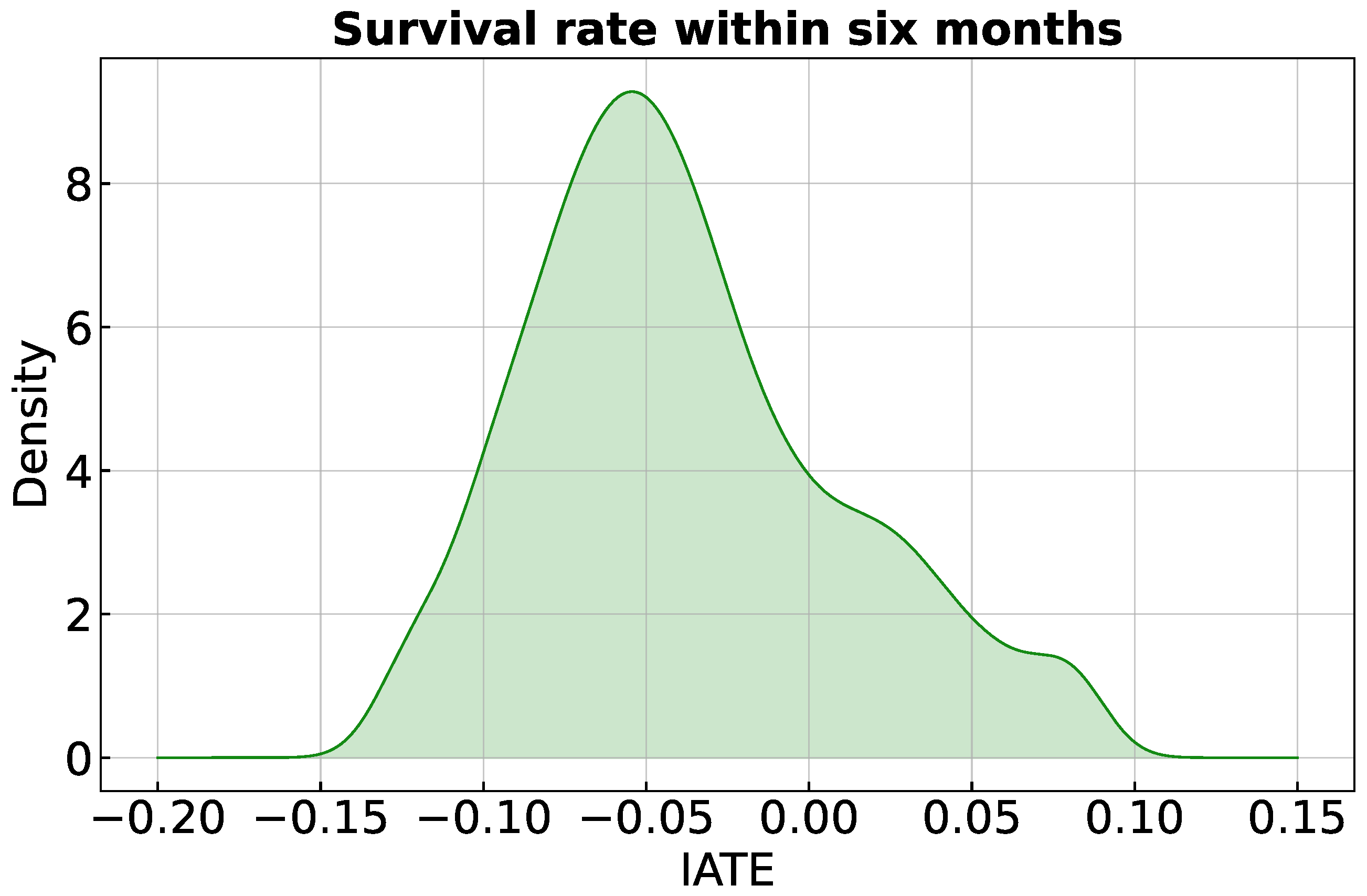
Figure 3 displays the density function of the IATEs, the most granular treatment effects. While slightly right-skewed, the distribution shows positive and negative treatment effects, ranging from −0.12 to 0.08, and an average standard error of 0.06. This result underscores the (rather moderate) heterogeneous response to the surgery, indicating that while some individuals benefit from the intervention, others do not. Such heterogeneity emphasises the importance of conducting a treatment allocation analysis to investigate potential improvements in the allocations of individuals.
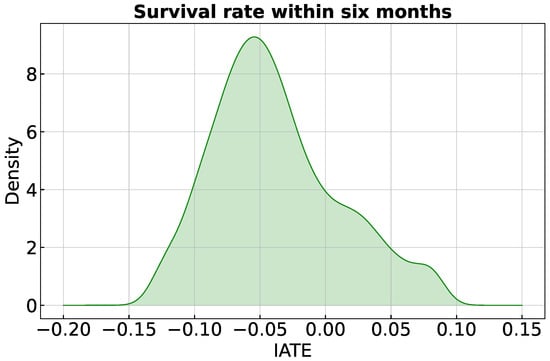
Figure 3.
Distribution of IATE. Mean (average standard error) of the IATEs: −0.04 (0.06).
Table 2 shows that simple allocation schemes may improve the overall survival rate while decreasing the number of surgeries at the same time. Again, the first two rows of Table 2 present results using the empirically observed and random assignment of individuals to treatments, which are used as baseline comparison policies. The remaining rows show the results of policy trees aiming to optimise the treatment allocation and increase the survival rate. Given the relatively small sample size, this study focuses on optimal trees with depths of two and three, alongside policy trees with depths of 3 and 4, including a final sequentially optimal sub-tree (+1).

Table 2.
Treatment allocations: right heart catheterisation.
Table 2 first reveals that the observed treatment allocation outperforms a random treatment assignment in terms of the survival rate (68.23% vs. 67.88%). Considering the performance of the policy trees, the findings suggest treatment allocations that could further increase the average survival rate within six months after the intervention up to 69.99%, while significantly diminishing the number of individuals receiving surgery by more than 50%. The maximum welfare gain, among the policy trees estimated, is already achieved with a policy tree of depth two. Deeper trees do not lead to a relevant increase in the survival rate. However, they reduce the share of individuals undergoing an operation. For example, compared to the depth-2 tree, the depth-3+1 tree indicates a reduction in survival rate by only 0.02 percentage points (69.99% vs. 69.97%) but decreases the share of patients having surgery by nearly three percentage points (19.21% vs. 16.22%).
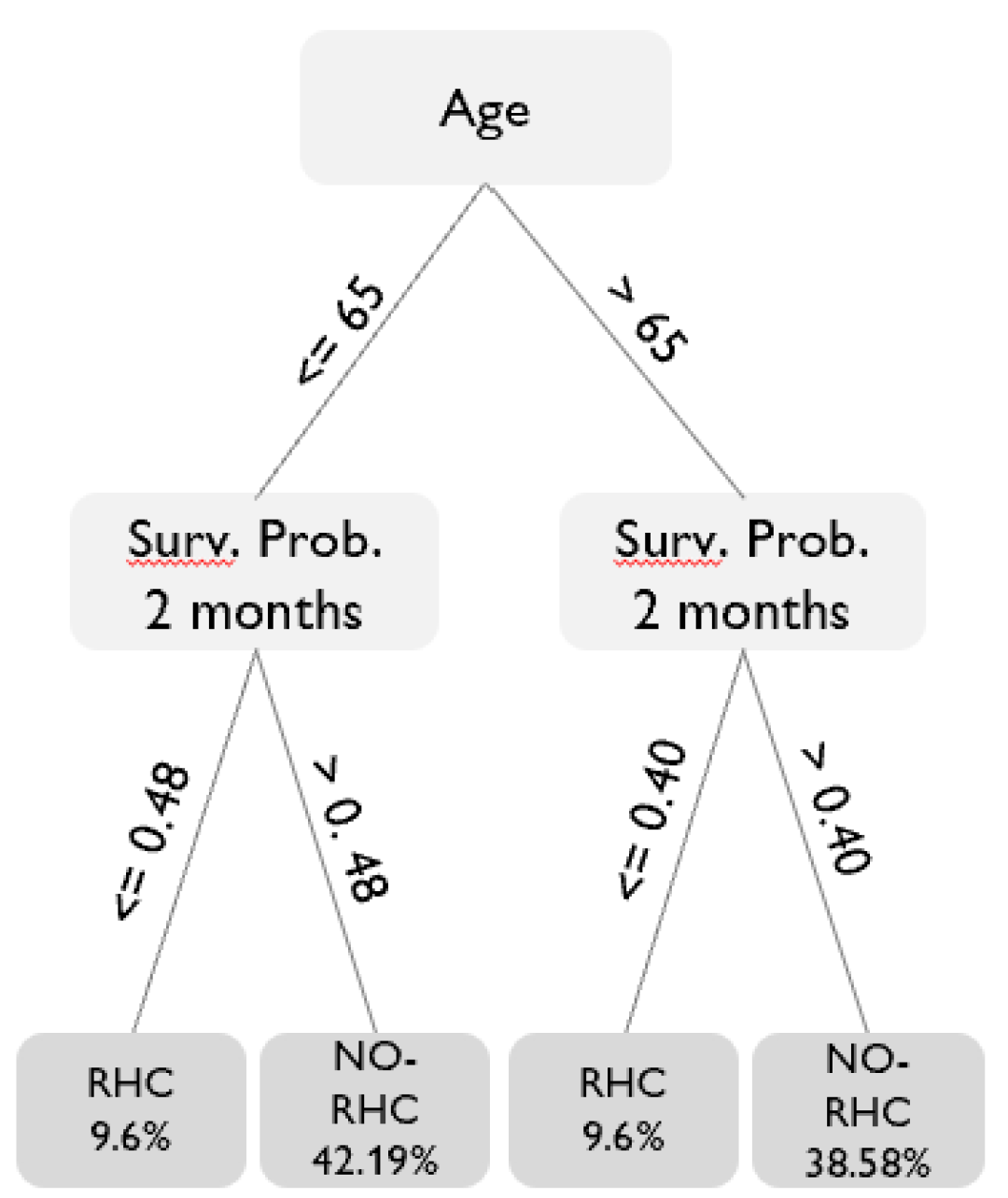
Since the maximum welfare gain is already attained with a depth-2 tree, Figure 4 displays the decision rules established by this tree, which is also the most straightforward to interpret. The policy tree performs the first split on age, while the second splitting variable is the estimated probability of surviving within two months, measured before the surgery. The decision tree allocates individuals with an age below 65 years and a survival probability below 48%, as well as those with an age above 65 years and a survival probability below 40%, to surgery. Note that tables representing all policy tree rules used are available in Appendix A.
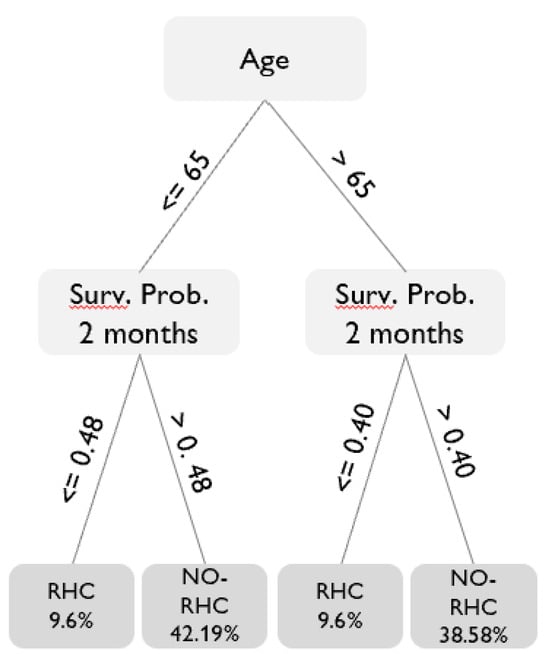
Figure 4.
Allocation rule for an optimal policy tree of depth-2. Note: The policy tree shows the shares of individuals allocated to treatment. The split variables are age and the probability of surviving within two months. The variable is measured before the decision of surgery. The final leaves of the trees indicate the treatments and corresponding shares of individuals allocated.
3.3. Study 3: Interest Rates and Loan Returns
In 2003, ref. [28] conducted a randomised controlled trial to examine the impact of personalised pricing by a microfinance lender in South Africa. They randomised interest rates to study the effect on the decision to borrow (extensive margin) and, among other outcomes, on the lender’s revenues (intensive margin). Considering the intensive margin, the overall findings suggest that lower interest rates only marginally decrease profits.
This study is particularly relevant because microfinance initiatives may serve broader purposes beyond profit maximisation. They can play a crucial role in promoting financial inclusion among specific population subgroups. Moreover, any initial losses incurred by the lender could be offset by a wider uptake of microfinance services.
Therefore, this study employs the same data and the intention-to-treat strategy of [28] to investigate the impact of receiving a mail invitation with different interest rates on the lender’s returns. Ref. [29] also leverages this dataset to propose policy allocations aimed at maximising the lender’s revenue while considering fairness implications. This paper does not explicitly take a stance on fairness. Consequently, we include variables commonly regarded as sensitive in the literature.
The dataset includes 48,852 individuals who received an invitation letter to apply for a loan at the offered interest rate. Differently from the study of [28], our specification incorporates socio-demographic information (see Table A3 and Table A6 in Appendix A for the complete variable list and descriptive statistics) collected from the bank operator before the randomisation. While not crucial for treatment effects identification, these variables are important for exploring heterogeneity and conducting policy learning analysis. In addition, we discretise the treatment variable in three different interest rate groups: low, medium, and high rates, based on the client’s risk profile. The cut-offs are indicated in [28] and are based on the risk category of clients pre-approved by the lender. The discretisation into three groups enhances the interpretability of results from a policy perspective, particularly when employing policy trees.
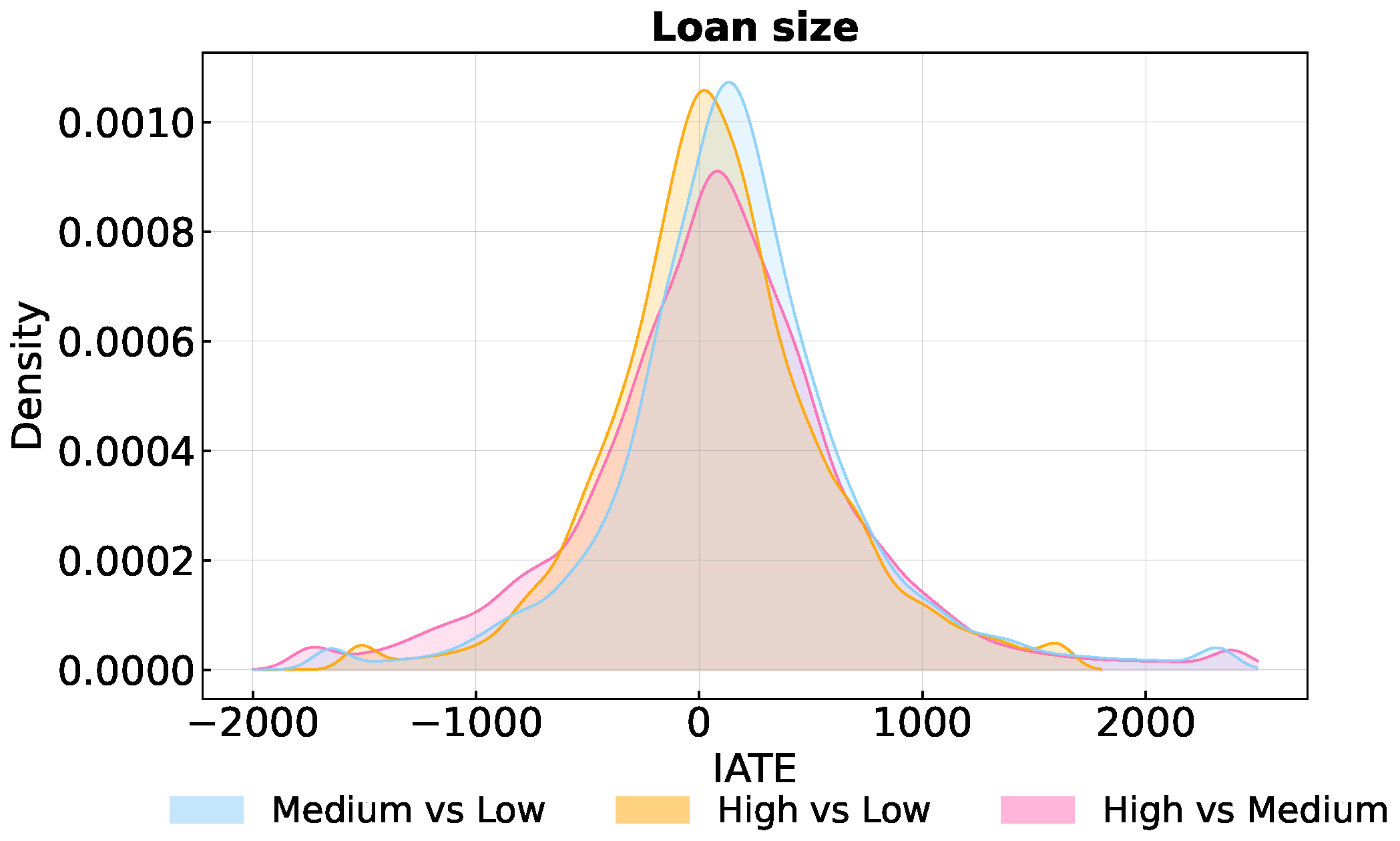
As for the other applications, our heterogeneity analysis is based on the distribution of the IATEs. Specifically, we compare the medium- and high-interest rate treatment groups with respect to the low-rate group and the high-interest rate group with the medium-rate group. As illustrated in Figure 5, all distributions show positive and negative treatment effects. Examining the medium- and high-interest rate groups compared to the low-rate group, the effects range from ZAR -1520 (ZAR -1656) to ZAR 1610 (ZAR 2327), with an average effect of ZAR 78 (ZAR 163) and an average standard error of ZAR 506 (ZAR 487). When comparing the high-rate group to the medium-rate group, the effects range from ZAR -1748 to ZAR 2393, with an average effect of ZAR 81 and a standard error of ZAR 547.
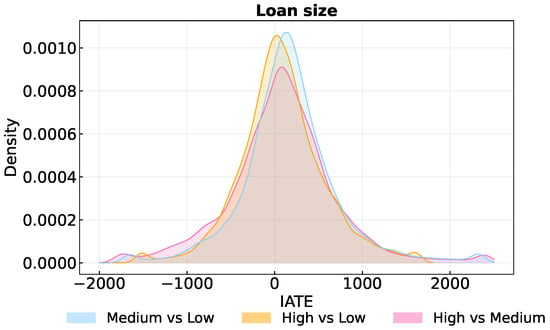
Figure 5.
Distribution of IATE. Note: Means of the IATEs for the high- (medium-) vs. low-interest rate groups: ZAR 78 (ZAR 163). Average standard errors of the IATEs for the high- (medium-) vs. low-interest rate groups: ZAR 506 (ZAR 487). For the high- vs. medium-interest rate group, the mean is ZAR 81 with an average standard error of ZAR 547.
These findings indicate the existence of effect heterogeneity, which could be used to potentially enhance the allocation mechanism.
As for the previous studies, we use policy trees of different depths and compare the welfare produced by the different allocations with the welfare from random and observed allocations. Due to this application’s relatively larger sample size, we also demonstrate the performance of both shallow and deeper trees. Additionally, we explore various combinations of trees: optimal, optimal with one final sequentially optimal tree (+1), and optimal with two final sequentially optimal trees (+2).
Table 3 indicates that the observed and random allocations lead to the same welfare since the observed allocations are based on a stratified random assignment. The table also shows that the policy trees increase welfare compared to the baseline policies, irrespective of the tree depth. Even implementing a policy tree of depth two demonstrates an increase in overall welfare by 31%, and deeper trees continue to yield improvements, although at a decreasing rate. The allocation pattern of the optimal policy trees shows that deeper trees tend to shift individuals away from the high-rate to a lower-risk group while increasing the average returns at the same time. The welfare estimated with the mixed trees (one or two sequentially optimal final trees) is slightly lower than those obtained by the fully optimal tree. For example, the optimal policy tree of depth four generates a welfare of ZAR 701, higher than the ZAR 686 (ZAR 685) yielded by the depth-3+1 (depth 2+2) mixed policy tree.

Table 3.
Treatment allocations: interest rates and loan returns.
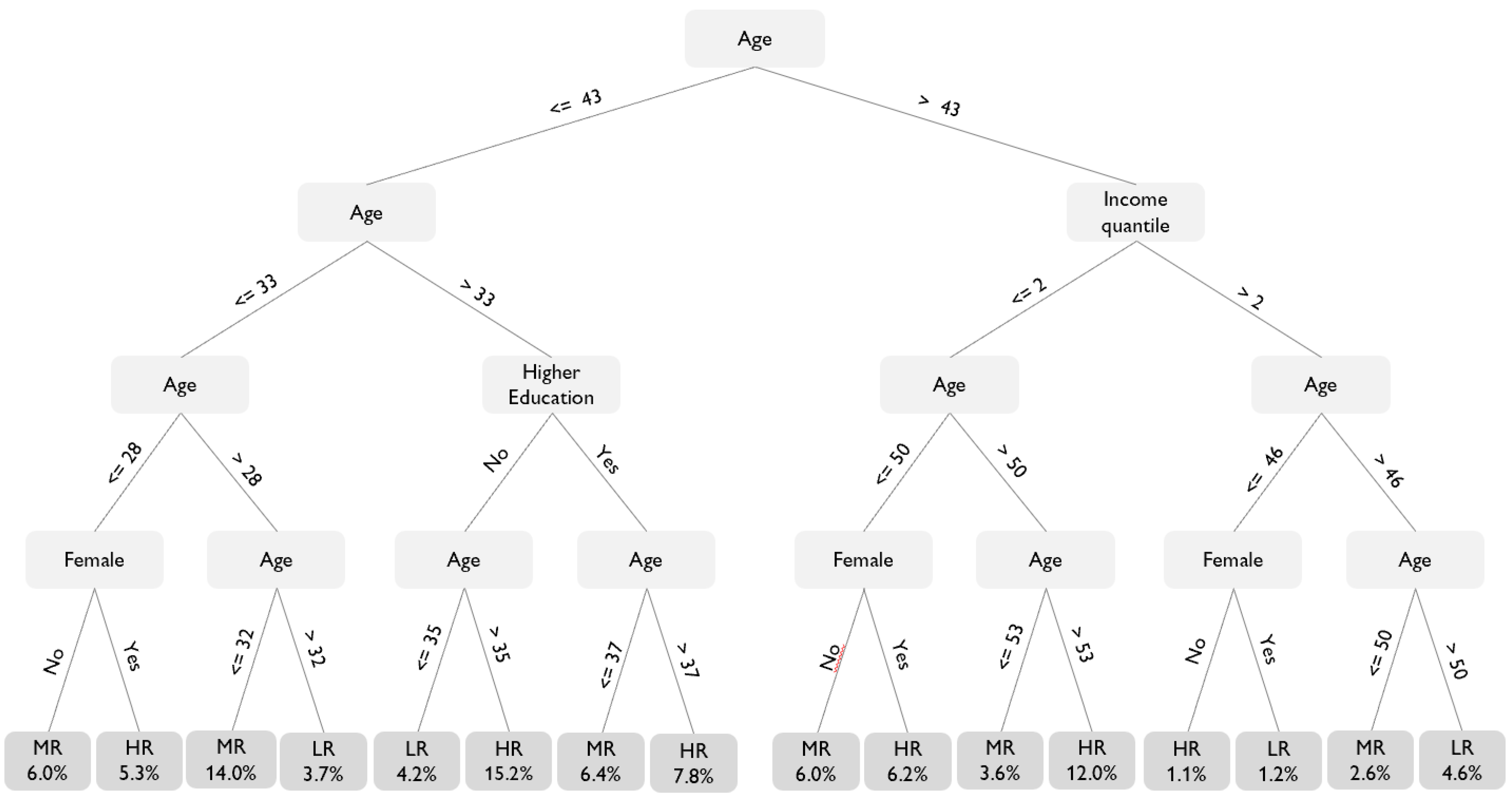
Figure 6 shows the allocation rule for an optimal policy tree of depth 4, which combines both a large welfare improvement and policy rules that are relatively easy to interpret. As indicated in Table 3, the policy tree assigns roughly half of the sample to the high-rate treatment. Among this subgroup, the highest share (16% of the overall sample) falls between the ages of 35 and 43 and lacks higher education. Low-income individuals older than 53 also constitute a significant portion of the high-risk cohort (12% of the whole sample). The highest share of individuals assigned to the medium interest rate (14% of the sample) range from 28 to 32 years of age. The largest subgroup assigned to the low-rate group consists of high-income individuals older than 50 years (4.6% of the sample).
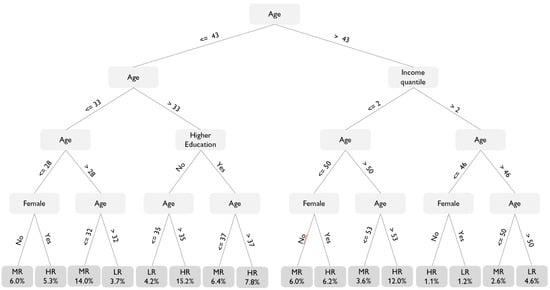
Figure 6.
Allocation rule for an optimal policy tree of depth-4. Note: The policy tree shows the shares of individuals allocated to each treatment. The splitting variables of the tree are gender, age, income quantile, and an indicator for achieved higher education. The final leaves of the trees indicate the treatments and corresponding shares of allocated individuals. LR: low rate, MR: medium rate, HR: high rate.
For detailed information on the treatment allocation rules for the other policy trees, we direct the reader to Appendix A.4.3.
4. Technical Considerations and Conclusions
An optimal tree of arbitrary depth is computationally challenging due to its NP-hard nature. However, specifying a particular depth allows for polynomial-time resolution, making the depth of the tree a critical complexity parameter [22]. Typically, estimating optimal trees beyond a depth of 4 (16 leaves) becomes challenging with moderate-sized training data. To improve computational performance, one option is to reduce the depth, sacrificing some efficiency for computational speed (and improved interpretability). Another option is to use sequentially optimal trees. This means building a shallow initial tree, followed by a second shallow tree built from the sub-final leaves of the first one. Building the trees in sequence is much faster than constructing a single, deeper tree of the same overall depth. Alternatively, the minimum leaf size is crucial for performance optimisation. Setting leaf sizes too small can be impractical and increase computation times. Additionally, users can enhance speed by reducing the size of the training data at the cost of amplifying sampling noise. Another approach to enhancing speed is to limit the number of values considered during splitting. For continuous variables, the mcf algorithm evaluates by default only 100 equally spaced values, while it assesses 100 random combinations for categorical variables. Although this approximation improves computational efficiency, it may lead to some loss in accuracy, particularly as the data in the leaf nodes diminishes.
Furthermore, like predictive trees, policy trees can also exhibit instability regarding policy rules or welfare estimation. However, how to conduct inference about the stability of policy trees remains an open question in the literature. Ref. [7] proposes a form of cross-validation to evaluate the accuracy of policy learning procedures, and they assess improvements over a random baseline. Similarly, ref. [9] proposes an alternative form of cross-validation and tests whether optimal policy rules perform significantly better than sending all units to the same treatment. While the assessment of policy tree stability is not currently tackled in the present paper, future research efforts may concentrate on developing methods to evaluate this aspect effectively.
To conclude, this paper contributes to the literature in various ways. First, we demonstrate the functionalities of the mcf policy tree algorithm across diverse fields, including medicine, epidemiology, and business, within both randomised and observational research settings. Second, we provide new empirical results on causal effect heterogeneity and policy learning using well-known data in these scientific fields. We derive our findings using the mcf method to initially compute policy scores based solely on features. Subsequently, these scores are utilised to determine optimal assignment rules, taking into account constraints. Our approach avoids one-hot encoding for categorical features and allows for specifying an approximation parameter dependent on tree depth for features with numerous values. Third, all replication materials, including data and programming codes, can be downloaded from our Github repository (accessed on 10 July 2024). We use the open-source Python package mcf (version 0.5.1). It provides the classes ModifiedCausalForest() for estimation and OptimalPolicy() for decision making.
The OptimalPolicy() class presents a notable advantage by providing a practical implementation of policy trees within multi-action settings, facilitating the creation of explainable assignment rules. Moreover, it offers best-scores and random allocation methods, which can be utilised for comparative welfare estimation.
Author Contributions
H.B. and F.M. mostly contributed to the conceptualisation, data curation, formal analysis, visualisation, and writing (original draft, review, and editing) of this manuscript. M.L. developed most of the algorithm’s code. All authors have read and agreed to the published version of the manuscript.
Funding
Michael Lechner and Federica Mascolo gratefully acknowledge financial support from the Swiss National Science Foundation (SNSF) (grant number SNSF 407740_187301).
Data Availability Statement
All data are available on GitHub.
Acknowledgments
We thank GPT-3.5 and Grammarly for editorial help.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Codebooks

Table A1.
Codebook for the Oregon health insurance study (Section 3.1).
Table A1.
Codebook for the Oregon health insurance study (Section 3.1).
| Variable | Description |
|---|---|
| doc_any_12m | any primary care visits |
| treatment | indicator equal to 1 if extracted for the lottery |
| age | in years, calculated as difference between 2008 and birth year |
| numhh_list | number of people in household on lottery list |
| draw | survey mailing wave |
| birthyear_list | birth year: lottery list data |
| have_phone_list | gave a phone number on lottery sign up: lottery list data |
| pobox_list | gave a PO Box as an address: lottery list data |
| english_list | individual requested english-language materials: lottery list data |
| female_list | indicator for female: lottery list data |
| zip_msa | zip code from lottery list is a metropolitan statistical area |

Table A2.
Codebook for the right heart catheterisation study (Section 3.2).
Table A2.
Codebook for the right heart catheterisation study (Section 3.2).
| Variable | Description |
|---|---|
| adld3pc | index of activities of daily living 2 weeks prior to admission |
| age | age in years |
| alb1 | albumin level in grams per deciliter |
| amihx | indicator for definite myocardial infarction |
| aps1 | acute physiology and chronic health evaluation score (APACHE III) |
| bili1 | bilirubin level in milligrams per deciliter |
| ca | cancer; 3 categories: metastatic cancer (Metastatic), no cancer (No), cancer (Yes) |
| card | indicator for cardiovascular diagnosis |
| cardiohx | indicator for acute myocardial infarction, peripheral vascular disease, severe, and very severe cardiovascular symptoms (NYHA-classes III and IV) |
| cat1 | primary disease; 9 categories: acute respiratory failure (0), congestive heart failure (1), chronic obstructive pulmonary disease (2), cirrhosis (3), colon cancer metastatic to the liver (4), non-traumatic coma (5), non-small-cell cancer of the lung, stage III or IV (6), multiorgan system failure with malignancy (7), indicator for multiorgan system failure with sepsis (8) |
| cat2 | secondary disease; 3 categories: missings or others (0), multiorgan system failure with malignancy (1), multiorgan system failure with sepsis (2) |
| cat2_miss | indicator for missings in cat2 |
| chfhx | indicator for congestive heart failure |
| chrpulhx | indicator for chronic, severe, or very severe pulmonary disease |
| crea1 | creatinine level in milligrams per deciliter |
| das2d3pc | Duke activity status index (DASI) two weeks before admission |
| dementhx | indicator for dementia, stroke or cerebral infarct, Parkinson’s disease |
| dnr1 | indicator for do not resuscitate status on the first day |
| dth30 | outcome indicator for mortality within 6 months |
| edu | education in years |
| gastr | indicator for gastrointestinal diagnosis |
| gibledhx | indicator for upper gastrointestinal bleeding |
| hema | indicator for hematologic diagnosis |
| hema1 | hematocrit levels in percent |
| hrt1 | heart rate in beats per minute |
| immunhx | indicator for immunosuppression, organ transplant, HIV positivity, diabetes mellitus with or without end organ damage, connective tissue disease |
| income | income in US dollars; 4 categories: below 11 k (0), 11–25 k (1), 25–50 k (2), above 50 k (3) |
| liverhx | indicator for cirrhosis, hepatic failure |
| malighx | indicator for solid tumor, metastatic disease, chronic leukemia/myeloma, acute leukemia, lymphoma |
| meanbp1 | mean blood pressure in millimeters of mercury |
| meta | indicator for metabolic diagnosis |
| neuro | indicator for neurological diagnosis |
| ninsclas | medical insurance; 6 categories: Medicaid (0), Medicare (1), Medicare and Medicaid (2), no medical insurance (3), private medical insurance (4), private medical insurance and Medicaid (5) |
| ortho | indicator for orthopedic diagnosis |
| paco21 | partial pressure of arterial carbon dioxide in millimeters of mercury |
| pafi1 | ratio between partial pressure of arterial oxygen in millimeters of mercury and fraction of inspired oxygen |
| ph1 | potential of hydrogen (pH) at logarithmic scale |
| pot1 | blood potassium level in millimoles per liter |
| psychhx | indicator for psychiatric history, active psychosis or severe depression |
| race | race; 3 categories: African American (0), other race (1), Caucasian (2) |
| renal | indicator for renal diagnosis |
| renalhx | indicator for chronic renal disease, chronic hemodialysis, or peritoneal dialysis |
| resp | indicator for respiratory diagnosis |
| resp1 | respiratory rate |
| scoma1 | Glasgow coma score |
| seps | indicator for sepsis diagnosis |
| sex | indicator for gender (1 = male) |
| sod1 | sodium level in milliequivalents per liter |
| surv2md1 | probability of surviving two months (based on support model estimations) |
| swang1 | treatment indicator for right heart catheterisation |
| temp1 | body temperature in degrees Celsius |
| transhx | indicator for transfer exceeding 24 h from another hospital |
| trauma | indicator for trauma diagnosis |
| urin1 | urine output per day in milliliters |
| urin1_miss | indicator for missings in urin1 |
| wblc1 | white blood cells in thousands per cubic millimeter |
| wtkilo1 | weight in kilograms |

Table A3.
Codebook for the interest rates and loan returns study (Section 3.3).
Table A3.
Codebook for the interest rates and loan returns study (Section 3.3).
| Variable | Description |
|---|---|
| adj_loan | loan size (loansize variable) multiplied by the interest rate (final4 variable) applied to calculate returns. |
| offer_risk | treatment, based on the original offered interest rate (offer4); offer_risk is equal to 1 for the offers with a value less than or equal to 7.75, indicating an associated low risk; offers with values greater than 7.75 but less than or equal to 9.75 are categorised as 2, associated to moderate risk; offers with a value greater than 9.75 are categorised as 3, associated to high risk. |
| age | age in years |
| dependants | number of individuals who rely on the primary household for economic support and care |
| qnt_income | quintiles of gross income |
| wave | number indicating in which wave the offer letter has been sent |
| risk_num | number from 1 to 3 indicating the client’s risk category |
| female | indicator for gender, equal to 1 if female |
| married | indicator for civil status, equal to 1 if married |
| edhi | indicator for higher education, equal to 1 if this level is achieved |
| rural | indicator for living in rural area |
Appendix A.2. Data
This section shows descriptive tables for each study, including mean and standardised difference (in parentheses) of conditioning variables. The standardised difference is calculated as , where and indicate the sample mean of variable among individuals in the programme j and the control group, respectively.

Table A4.
Descriptive statistics for the Oregon health experiment.
Table A4.
Descriptive statistics for the Oregon health experiment.
| Variable | No Medicaid | Medicaid | |
|---|---|---|---|
| Mean | Mean | Std. Diff. | |
| age | 42.31 | 42.20 | (0.90) |
| numhh_list | 1.25 | 1.35 | (20.22) |
| draw | 3.91 | 4.33 | (16.75) |
| birthyear_list | 1966 | 1966 | (0.90) |
| have_phone_list | 0.89 | 0.90 | (2.52) |
| pobox_list | 0.13 | 0.13 | (0.04) |
| english_list | 0.92 | 0.91 | (3.53) |
| female_list | 0.60 | 0.58 | (2.94) |
| zip_msa | 0.75 | 0.75 | (1.01) |
| doc_any_12m | 0.49 | 0.51 | (3.85) |
| N. observations | 11,844 | 11,683 | |
Note: The table shows the means and standardised differences (in parentheses) of the conditioning variables for each treatment state.

Table A5.
Descriptive statistics for the right hearth catheterisation study.
Table A5.
Descriptive statistics for the right hearth catheterisation study.
| Variable | No RHC | RHC | |
|---|---|---|---|
| Mean | Mean | Std. Diff. | |
| adld3pc | 1.63 | 1.47 | (11.36) |
| age | 61.76 | 60.75 | (6.14) |
| alb1 | 3.16 | 2.96 | (27.85) |
| amihx | 0.03 | 0.04 | (7.43) |
| aps1 | 50.93 | 60.74 | (50.14) |
| bili1 | 1.93 | 2.64 | (16.25) |
| card | 0.28 | 0.42 | (29.49) |
| cardiohx | 0.16 | 0.20 | (11.56) |
| cat2_miss | 0.81 | 0.77 | (9.93) |
| chfhx | 0.17 | 0.19 | (6.95) |
| chrpulhx | 0.22 | 0.14 | (19.23) |
| crea1 | 1.92 | 2.47 | (27.78) |
| das2d3pc | 20.37 | 20.70 | (6.26) |
| dementhx | 0.12 | 0.07 | (16.31) |
| edu | 11.57 | 11.86 | (9.14) |
| gastr | 0.15 | 0.19 | (12.09) |
| gibledhx | 0.04 | 0.02 | (7.04) |
| hema | 0.07 | 0.05 | (6.17) |
| hema1 | 32.70 | 30.51 | (26.93) |
| hrt1 | 112.87 | 118.93 | (14.69) |
| immunhx | 0.26 | 0.29 | (8.04) |
| income | 0.70 | 0.83 | (13.52) |
| liverhx | 0.07 | 0.06 | (4.89) |
| malighx | 0.25 | 0.20 | (10.14) |
| meanbp1 | 84.87 | 68.20 | (45.51) |
| meta | 0.05 | 0.04 | (2.81) |
| neuro | 0.16 | 0.05 | (35.30) |
| ortho | 0.00 | 0.00 | (2.70) |
| paco21 | 39.78 | 36.71 | (25.57) |
| pafi1 | 240.18 | 192.39 | (43.40) |
| ph1 | 7.39 | 7.38 | (11.98) |
| pot1 | 4.08 | 4.05 | (2.71) |
| psychhx | 0.08 | 0.05 | (14.32) |
| renal | 0.04 | 0.07 | (11.63) |
| renalhx | 0.04 | 0.05 | (3.16) |
| resp | 0.42 | 0.29 | (26.95) |
| resp1 | 28.91 | 26.59 | (16.69) |
| scoma1 | 22.25 | 18.97 | (10.98) |
| seps | 0.15 | 0.24 | (23.38) |
| sex | 0.54 | 0.59 | (9.31) |
| sod1 | 137.04 | 136.33 | (9.22) |
| surv2md1 | 0.61 | 0.57 | (19.85) |
| temp1 | 37.63 | 37.59 | (2.14) |
| transhx | 0.09 | 0.15 | (16.98) |
| trauma | 0.01 | 0.02 | (10.40) |
| urin1 | 993.38 | 1102.33 | (7.12) |
| urin1_miss | 0.55 | 0.49 | (10.69) |
| wblc1 | 15.24 | 16.19 | (8.24) |
| wtkilo1 | 64.93 | 72.21 | (25.83) |
| dnr1 | 0.14 | 0.07 | (22.76) |
| ca | 1.11 | 1.10 | (2.03) |
| cat1 | 2.65 | 3.52 | (25.79) |
| cat2 | 0.28 | 0.41 | (18.49) |
| ninsclas | 2.70 | 2.99 | (16.25) |
| race | 1.61 | 1.63 | (2.37) |
| dth30 | 0.69 | 0.62 | (15.56) |
| N. observations | 3551 | 2184 | |
Note: The table shows the means and standardised differences (in parentheses) of the conditioning variables for each treatment state.

Table A6.
Descriptive statistics for the interest rates and loan returns study.
Table A6.
Descriptive statistics for the interest rates and loan returns study.
| Variable | Low Rate | Medium Rate | High Rate | |||
|---|---|---|---|---|---|---|
| Mean | Mean | Std. Diff. | Mean | Std. Diff. | Std. Diff. | |
| (vs. Low) | (vs. Low) | (vs. Medium) | ||||
| age | 41.63 | 41.07 | (5.00) | 41.16 | (4.23) | (0.76) |
| dependants | 1.73 | 1.55 | (10.02) | 1.44 | (16.61) | (6.66) |
| qnt_income | 1.53 | 1.47 | (5.41) | 1.47 | (5.18) | (0.24) |
| wave | 2.58 | 2.62 | (7.05) | 2.60 | (4.31) | (2.73) |
| risk_num | 2.41 | 2.84 | (65.55) | 3.00 | (96.93) | (60.70) |
| female | 0.48 | 0.48 | (0.70) | 0.48 | (0.04) | (0.74) |
| married | 0.45 | 0.44 | (1.88) | 0.44 | (1.07) | (0.80) |
| edhi | 0.39 | 0.39 | (0.06) | 0.39 | (1.21) | (1.15) |
| rural | 0.18 | 0.17 | (1.05) | 0.17 | (1.89) | (0.84) |
| adj_loan | 795.33 | 639.65 | (4.59) | 463.75 | (10.23) | (5.98) |
| N. observations | 22,011 | 14,107 | 12,734 | |||
Note: The table shows the means and standardised differences (in parentheses) of the conditioning variables for each treatment state.
Appendix A.3. Policy Trees Runtime Comparison
This section shows the running times of the policy trees presented in the three studies. The running times are given in minutes, seconds, and fractions of a second for the training and evaluation samples. This work uses the mcf package version 0.5.1. and an HP Z8 G4 server with 2 processors Intel Xeon 6242R 3.1 GHz 20Cores 205 W, 1 TB (16 × 64 GB) RAM DDR4 2933 ECC REG 2CPU, GPU NVIDIA RTX A5000 24 GB 4DP GFX.
Appendix A.3.1. Policy Trees Running Time: Oregon Health Insurance Experiment
| Task and Sample | Running Time | ||
| Unconstrained tree depth | 2 | 3 | |
| Policy tree training data: | 0:02.116 | 0:08.093 | |
| Evaluation of training data: | 0:00.172 | 0:00.125 | |
| Policy tree allocation data: | 0:00.534 | 0:00.424 | |
| Evaluation of test data | 0:00.109 | 0:00.093 | |
| Constrained tree depth | 2 | 3 | 4 |
| Policy tree training data: | 0:02.686 | 0:10.297 | 3:03.169 |
| Evaluation of training data: | 0:00.156 | 0:00.140 | 0:00.141 |
| Policy tree allocation data: | 0:00.486 | 0:00.486 | 0:00.534 |
| Evaluation of test data: | 0:00.158 | 0:00.079 | 0:00.110 |
| Constrained sequential trees depth | 2+1 | 3+1 | |
| Policy tree training data: | 0:03.093 | 0:29.504 | |
| Evaluation of training data: | 0:00.141 | 0:00.267 | |
| Policy tree allocation data: | 0:00.580 | 0:01.098 | |
| Evaluation of test data: | 0:00.141 | 0:00.320 | |
Appendix A.3.2. Policy Trees Running Time: Right Heart Catheterisation Study
| Task and Sample | Running Time | |||
| Tree depth | 2 | 3 | 2+1 | 3+1 |
| Policy tree training: | 0:08.327 | 13:23.021 | 0:28.872 | 11:18.153 |
| Evaluation of training: | 0:00.126 | 0:00.137 | 0:00.152 | 0:00.177 |
| Policy tree allocation: | 0:00.258 | 0:00.287 | 0:00.508 | 0:00.388 |
| Evaluation of allocation: | 0:00.079 | 0:00.125 | 0:00.139 | 0:00.168 |
Appendix A.3.3. Policy Trees Running Time: Interest Rates and Loan Returns Study
| Task and Sample | Running Time | ||
| Unconstrained tree depth | 2 | 3 | 4 |
| Policy tree training data: | 0:08.334 | 0:29.838 | 10:22.988 |
| Evaluation of training data: | 0:00.172 | 0:00.221 | 0:00.173 |
| Policy tree allocation data: | 0:00.571 | 0:00.528 | 0:00.543 |
| Evaluation of test data: | 0:00.140 | 0:00.115 | 0:00.165 |
| Unconstrained sequential trees depth | 2+1 | 3+1 | 4+1 |
| Policy tree training data: | 0:7.667 | 0:25.610 | 5:53.018 |
| Evaluation of training data: | 0:0.236 | 0:0.189 | 0:0.220 |
| Policy tree allocation data: | 0:1.670 | 0:1.733 | 0:1.472 |
| Evaluation of test data: | 0:0.157 | 0:0.157 | 0:0.110 |
| Unconstrained sequential trees depth | 2+2 | 3+2 | 4+2 |
| Policy tree training data: | 0:09.591 | 0:25.590 | 3:45.807 |
| Evaluation of training data: | 0:00.252 | 0:00.284 | 0:00.236 |
| Policy tree allocation data: | 0:01.887 | 0:02.141 | 0:02.010 |
| Evaluation of test data: | 0:00.157 | 0:00.173 | 0:00.173 |
Appendix A.4. Policy Trees Rules
This section shows policy rules for individuals allocated to treatment only. All tables indicate the splitting variables and related values produced by our policy trees. The codebooks in Appendix A.1 provide the corresponding variable descriptions.
Appendix A.4.1. Policy Rules: Oregon Health Insurance Experiment

Table A7.
Unconstrained optimal policy tree of depth-2.
Table A7.
Unconstrained optimal policy tree of depth-2.
| Splitting variables and values |
| female_list = 0, numhh_list = 1 |
| female_list = 0, numhh_list > 1 |
| female_list = 0, age ≤ 47 |
| female_list = 0, age > 47 |
Note: Policy rule for individuals assigned to Medicaid.

Table A8.
Unconstrained optimal policy tree of depth-3.
Table A8.
Unconstrained optimal policy tree of depth-3.
| Splitting variables and values |
| age ≤ 50, age ≤ 31, age ≤ 26 |
| age ≤ 50, age ≤ 31, age > 26 |
| age ≤ 50, age > 31, age ≤ 38 |
| age ≤ 50, age > 31, age > 38 |
| age > 50, numhh_list = 1, age ≤ 60 |
| age > 50, numhh_list = 1, age > 60 |
| age > 50, numhh_list > 1, age ≤ 59 |
| age > 50, numhh_list > 1, age > 59 |
Note: Policy rule for individuals assigned to Medicaid.

Table A9.
Constrained optimal policy tree of depth-2.
Table A9.
Constrained optimal policy tree of depth-2.
| Splitting variables and values |
| age ≤ 51, age > 36 |
| age > 51, numhh_zip_msa = 0 |
Note: Policy rule for individuals assigned to Medicaid.

Table A10.
Constrained optimal policy tree of depth-3.
Table A10.
Constrained optimal policy tree of depth-3.
| Splitting variables and values |
| numhh_list = 1, age ≤ 51, age > 37 |
| numhh_list = 1, age > 51, zip_msa = 0 |
| numhh_list > 1, female_list = 0, age > 25 |
| numhh_list > 1, female_list = 1, zip_msa = 0 |
Note: Policy rule for individuals assigned to Medicaid.

Table A11.
Constrained sequentially optimal policy trees of depth-2+1.
Table A11.
Constrained sequentially optimal policy trees of depth-2+1.
| Splitting variables and values |
| age ≤ 50, age > 39, age ≤ 40 |
| age ≤ 50, age > 39, age > 40 |
| age > 50, numhh_zip_msa = 0, age ≤ 53 |
| age > 50, numhh_zip_msa = 0, age > 53 |
| age > 50, zip_msa = 1 numhh_list > 1 |
Note: Policy rule for individuals assigned to Medicaid.

Table A12.
Constrained optimal policy tree of depth-4.
Table A12.
Constrained optimal policy tree of depth-4.
| Splitting variables and values |
| numhh_list = 1, zip_msa = 0, female_list = 0, age > 28 |
| numhh_list = 1, zip_msa = 0, female_list > 0.500, age > 35 |
| numhh_list = 1, zip_msa = 1, age > 39, age ≤ 51 |
| numhh_list > 1, female_list = 0, zip_msa < 0, age ≤ 36 |
| numhh_list > 1, female_list = 0 zip_msa = 0, age > 36 |
| numhh_list > 1, female_list = 0, zip_msa = 1, age > 28 |
| numhh_list > 1, female_list = 1, english_list = 0, age ≤ 42 |
| numhh_list > 1, female_list = 1, english_list = 1, zip_msa = 0 |
Note: Policy rule for individuals assigned to Medicaid.

Table A13.
Constrained sequentially optimal policy tree of depth-3+1.
Table A13.
Constrained sequentially optimal policy tree of depth-3+1.
| Splitting variables and values |
| numhh_list > 1, female_list = 0, age > 27 |
| numhh_list = 1, age ≤ 51, age > 37, age < 39 |
| numhh_list = 1, age ≤ 51, age > 37, age > 39 |
| numhh_list = 1, age > 51, zip_msa = 0, age ≤ 53 |
| numhh_list = 1, age > 51, zip_msa = 0, age > 53 |
| numhh_list > 1, female_list = 1, zip_msa = 0, age ≤ 53 |
| numhh_list > 1, female_list = 1, zip_msa = 0, age > 53 |
| numhh_list > 1, female_list = 1, zip_msa = 1, english_list = 0 |
Note: Policy rule for individuals assigned to Medicaid.
Appendix A.4.2. Policy Rules: Right Heart Catheterisation Study

Table A14.
Unconstrained optimal policy tree of depth-2.
Table A14.
Unconstrained optimal policy tree of depth-2.
| Splitting variables and values |
| age ≤ 65, surv2md1 ≤ 0.480 |
| age > 65, surv2md1 ≤ 0.402 |
Note: Policy rule for individuals assigned to RHC.

Table A15.
Unconstrained optimal policy tree of depth-3.
Table A15.
Unconstrained optimal policy tree of depth-3.
| Splitting variables and values |
| cat1 in: 0 1 2 6 8, age ≤ 70, surv2md1 ≤ 0.450 |
| cat1 in: 0 1 2 6 8, age > 70, surv2md1 ≤ 0.402 |
| cat1 not in: 0 1 2 6 8, cat1 in: 3 5, aps1 > 64 |
| cat1 not in: 0 1 2 6 8, cat1 not in: 3 5, surv2md1 ≤ 0.467 |
Note: Policy rule for individuals assigned to RHC.

Table A16.
Unconstrained sequentially optimal policy trees of depth-2+1.
Table A16.
Unconstrained sequentially optimal policy trees of depth-2+1.
| Splitting variables and values |
| age ≤ 65, surv2md1 ≤ 0.480, aps1 ≤ 80 |
| age ≤ 65, surv2md1 ≤ 0.480, aps1 > 80 |
| age > 65, surv2md1 ≤ 0.402, aps1 > 50 |
Note: Policy rule for individuals assigned to RHC.

Table A17.
Unconstrained sequentially optimal policy trees of depth-3+1.
Table A17.
Unconstrained sequentially optimal policy trees of depth-3+1.
| Splitting variables and values |
| cat1 in: 0 2 8, age ≤ 69, surv2md1 ≤ 0.450, cat1 = 0 |
| cat1 in: 0 2 8, age ≤ 69, surv2md1 ≤ 0.450, cat1 not in: 0 |
| cat1 in: 0 2 8, age > 69, surv2md1 ≤ 0.402, aps1 > 61 |
| cat1 not in: 0 2 8, cat1 in: 3 5, aps1 > 64, aps1 ≤ 77 |
| cat1 not in: 0 2 8, cat1 in: 3 5, aps1 > 64, aps1 > 77 |
| cat1 not in: 0 2 8, cat1 not in: 3 5, surv2md1 ≤ 0.467, surv2md1 ≤ 0.384 |
| cat1 not in: 0 2 8, cat1 not in: 3 5, surv2md1 ≤ 0.467, surv2md1 > 0.384 |
Note: Policy rule for individuals assigned to RHC.
Appendix A.4.3. Policy Rules: Interes Rates and Loan Returns Study

Table A18.
Unconstrained optimal policy tree of depth-2.
Table A18.
Unconstrained optimal policy tree of depth-2.
| Splitting variables and values | Treatment allocation |
| age ≤ 50, age > 36 | HR |
| age > 50, qnt_income ≤ 2 | HR |
| age ≤ 50, age ≤ 36 | MR |
| age > 50, qnt_income > 2 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A19.
Unconstrained optimal policy tree of depth-3.
Table A19.
Unconstrained optimal policy tree of depth-3.
| Splitting variables and values | Treatment allocation |
| age > 46, qnt_income > 2, age > 50 | LR |
| age ≤ 46, age ≤ 28, female = 0 | MR |
| age ≤ 46, age ≤ 28, female = 1 | HR |
| age ≤ 46, age > 28, age ≤ 36 | MR |
| age > 46, qnt_income ≤ 2, age ≤ 53 | MR |
| age ≤ 46, age > 28, age > 36 | HR |
| age > 46, qnt_income ≤ 2, age > 53 | HR |
| age > 46, qnt_income > 2, age ≤ 50 | HR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A20.
Unconstrained optimal policy tree of depth-4.
Table A20.
Unconstrained optimal policy tree of depth-4.
| Splitting variables and values | Treatment allocation |
| age > 43, qnt_income > 2, age > 46, age > 50 | LR |
| age ≤ 43, age ≤ 33, age > 28, age > 32 | LR |
| age ≤ 43, age > 33, edhi = 0, age ≤ 35 | LR |
| age > 43, qnt_income > 2, age ≤ 46, female = 1 | LR |
| age ≤ 43, age ≤ 33, age ≤ 28 female = 1 | MR |
| age ≤ 43, age ≤ 33, age > 28, age ≤ 32 | MR |
| age ≤ 43, age > 33, edhi =1, age ≤ 37 | MR |
| age > 43, qnt_income ≤ 2, age ≤ 50, female = 0 | MR |
| age > 43, qnt_income ≤ 2, age > 50, age ≤ 53 | MR |
| age ≤ 43, age ≤ 33, age ≤ 28, female = 0 | HR |
| age ≤ 43, age > 33, edhi = 0, age > 35 | HR |
| age ≤ 43, age > 33, edhi = 1, age > 37 | HR |
| age > 43, qnt_income ≤ 2, age ≤ 50, female = 1 | HR |
| age > 43, qnt_income ≤ 2, age > 50, age > 53 | HR |
| age > 43, qnt_income > 2, age ≤ 46, female = 0 | HR |
| age > 43, qnt_income > 2, age > 46, age ≤ 50 | HR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A21.
Unconstrained sequentially optimal policy trees of depth-2+1.
Table A21.
Unconstrained sequentially optimal policy trees of depth-2+1.
| Splitting variables and values | Treatment allocation |
| age ≤ 50, age ≤ 36, age > 32 | LR |
| age > 50, qnt_income > 2, age ≤ 57 | LR |
| age > 50, qnt_income > 2, age > 57 | LR |
| age ≤ 50, age ≤ 36, age ≤ 32 | MR |
| age > 50, qnt_income ≤ 2, age ≤ 53 | MR |
| age ≤ 50, age > 36, age ≤ 38 | HR |
| age ≤ 50, age > 36, age > 38 | HR |
| age > 50, qnt_income ≤ 2, age > 53 | HR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A22.
Unconstrained sequentially optimal policy trees of depth-3+1.
Table A22.
Unconstrained sequentially optimal policy trees of depth-3+1.
| Splitting variables and values | Treatment allocation |
| age ≤ 46, age ≤ 28, female = 0, age ≤ 27 | MR |
| age ≤ 46, age ≤ 28, female = 0, age > 27 | HR |
| age ≤ 46, age ≤ 28, female = 1, age ≤ 25 | HR |
| age ≤ 46, age ≤ 28, female = 1, age > 25 | HR |
| age ≤ 46, age > 28, age ≤ 36, age ≤ 32 | MR |
| age ≤ 46, age > 28, age ≤ 36, age > 32 | LR |
| age ≤ 46, age > 28, age > 36, age ≤ 37 | HR |
| age ≤ 46, age > 28, age > 36, age > 37 | HR |
| age > 46, qnt_income ≤ 2, age ≤ 53, qnt_income = 0 | HR |
| age > 46, qnt_income ≤ 2, age ≤ 53, qnt_income > 0 | MR |
| age > 46, qnt_income ≤ 2, age > 53, rural = 0 | HR |
| age > 46, qnt_income ≤ 2, age > 53, rural = 1 | HR |
| age > 46, qnt_income > 2, age ≤ 50, female = 0 | LR |
| age > 46, qnt_income > 2, age ≤ 50, female = 1 | HR |
| age > 46, qnt_income > 2, age > 50, age ≤ 58 | LR |
| age > 46, qnt_income > 2, age > 50, age > 58 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A23.
Unconstrained sequentially optimal policy trees of depth-4+1.
Table A23.
Unconstrained sequentially optimal policy trees of depth-4+1.
| Splitting variables and values | Treatment allocation |
| age > 44, female = 0, qnt_income > 2, age ≤ 50 | HR |
| age > 44, female = 0, qnt_income > 2, age > 50 | LR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age ≤ 27 | MR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age > 27 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 1, age ≤ 25 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 1, age > 25 | HR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, rural = 0 | MR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, rural = 1 | MR |
| age ≤ 44, age ≤ 33, age > 28, age > 32, female = 0 | LR |
| age ≤ 44, age ≤ 33, age > 28, age > 32, female = 1 | LR |
| age ≤ 44, age > 33, edhi = 0, age ≤ 35, qnt_income = 0 | HR |
| age ≤ 44, age > 33, edhi = 0, age ≤ 35, qnt_income > 0 | LR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income ≤ 2 | HR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income > 2 | HR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37, qnt_income = 0 | MR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37, qnt_income > 0 | MR |
| age ≤ 44, age > 33, edhi = 1, age > 37, rural = 0 | HR |
| age ≤ 44, age > 33, edhi = 1, age > 37, rural = 1 | HR |
| age > 44, female = 0, qnt_income ≤ 2, age ≤ 53, qnt_income = 0 | HR |
| age > 44, female = 0, qnt_income ≤ 2, age ≤ 53, qnt_income > 0 | MR |
| age > 44, female = 0, qnt_income ≤ 2, age > 53, age ≤ 55 | HR |
| age > 44, female = 0, qnt_income ≤ 2, age > 53, age > 55 | HR |
| age > 44, female = 1, age ≤ 53, age ≤ 50, age ≤ 47 | HR |
| age > 44, female = 1, age ≤ 53, age ≤ 50, age > 47 | HR |
| age > 44, female = 1, age ≤ 53, age > 50, edhi = 0 | HR |
| age > 44, female = 1, age ≤ 53, age > 50, edhi = 1 | MR |
| age > 44, female = 1, age > 53, edhi = 0, age ≤ 65 | HR |
| age > 44, female = 1, age > 53, edhi = 0, age > 65 | MR |
| age > 44, female = 1, age > 53, edhi = 1, age ≤ 58 | LR |
| age > 44, female = 1, age > 53, edhi = 1, age > 58 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A24.
Unconstrained sequentially optimal policy trees of depth-2+2.
Table A24.
Unconstrained sequentially optimal policy trees of depth-2+2.
| Splitting variables and values | Treatment allocation |
| age ≤ 48, age ≤ 36, age ≤ 28, female = 0 | MR |
| age ≤ 48, age ≤ 36, age ≤ 28, female > 0 | HR |
| age ≤ 48, age ≤ 36, age > 28, age ≤ 32 | MR |
| age ≤ 48, age ≤ 36, age > 28, age > 32 | LR |
| age ≤ 48, age > 36, female = 0, age ≤ 46 | HR |
| age ≤ 48, age > 36, female = 0, age > 46 | MR |
| age ≤ 48, age > 36, female > 0, age ≤ 37 | MR |
| age ≤ 48, age > 36, female > 0, age > 37 | HR |
| age > 48, qnt_income ≤ 2, qnt_income = 0, age ≤ 52 | HR |
| age > 48, qnt_income ≤ 2, qnt_income = 0, age > 52 | HR |
| age > 48, qnt_income ≤ 2, qnt_income > 0, age ≤ 53 | MR |
| age > 48, qnt_income ≤ 2, qnt_income> 0, age > 53 | HR |
| age > 48, qnt_income > 2, age ≤ 51 | LR |
| age > 48, qnt_income > 2, age > 51 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A25.
Unconstrained sequentially optimal policy trees of depth-3+2.
Table A25.
Unconstrained sequentially optimal policy trees of depth-3+2.
| Splitting variables and values | Treatment allocation |
| age ≤ 44, age ≤ 28, female = 0, age ≤ 26, qnt_income ≤ 1 | MR |
| age ≤ 44, age ≤ 28, female = 0, age ≤ 26, qnt_income > 1 | MR |
| age ≤ 44, age ≤ 28, female = 0, age > 26, qnt_income ≤ 1 | HR |
| age ≤ 44, age ≤ 28, female = 0, age > 26, qnt_income > 1 | MR |
| age ≤ 44, age ≤ 28, female = 1, qnt_income ≤ 1, qnt_income = 0 | HR |
| age ≤ 44, age ≤ 28, female = 1, qnt_income ≤ 1, qnt_income > 0 | HR |
| age ≤ 44, age ≤ 28, female = 1, qnt_income > 1, qnt_income ≤ 2.5 | HR |
| age ≤ 44, age ≤ 28, female > 1, qnt_income > 1, qnt_income > 2.5 | HR |
| age ≤ 44, age > 28, age ≤ 36, age ≤ 33, age ≤ 32 | MR |
| age ≤ 44, age > 28, age ≤ 36, age ≤ 33, age > 32 | LR |
| age ≤ 44, age > 28, age ≤ 36, age > 33, edhi = 0 | LR |
| age ≤ 44, age > 28, age ≤ 36, age > 33, edhi = 1 | MR |
| age ≤ 44, age > 28, age > 36, female = 0, qnt_income ≤ 1 | HR |
| age ≤ 44, age > 28, age > 36, female = 0, qnt_income > 1 | HR |
| age ≤ 44, age > 28, age > 36, female = 1, qnt_income ≤ 2 | HR |
| age ≤ 44, age > 28, age > 36, female = 1, qnt_income > 2. | MR |
| age > 44, qnt_income ≤ 2, female = 0, age ≤ 55, qnt_income = 0 | HR |
| age > 44, qnt_income ≤ 2, female = 0, age ≤ 55, qnt_income > 0 | MR |
| age > 44, qnt_income ≤ 2, female = 0, age > 55, age ≤ 61 | HR |
| age > 44, qnt_income ≤ 2, female = 0, age > 55, age > 61 | HR |
| age > 44, qnt_income ≤ 2, female = 1, age ≤ 50, age ≤ 46 | HR |
| age > 44, qnt_income ≤ 2, female = 1, age ≤ 50, age > 46 | HR |
| age > 44, qnt_income ≤ 2, female = 1, age > 50, age ≤ 53 | MR |
| age > 44, qnt_income ≤ 2, female = 1, age > 50, age > 53 | HR |
| age > 44, qnt_income > 2, age ≤ 50, age ≤ 47 | HR |
| age > 44, qnt_income > 2, age ≤ 50 age > 47 | HR |
| age > 44, qnt_income > 2, age > 50, age ≤ 59 | LR |
| age > 44, qnt_income > 2, age > 50, age > 59 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.

Table A26.
Unconstrained sequentially optimal policy trees of depth-4+2.
Table A26.
Unconstrained sequentially optimal policy trees of depth-4+2.
| Splitting variables and values | Treatment allocation |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age ≤ 26, qnt_income ≤ 1 | MR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age ≤ 26, qnt_income > 1 | MR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age > 26, qnt_income ≤ 1 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 0, age > 26, qnt_income > 1 | MR |
| age ≤ 44, age ≤ 33, age ≤ 28, female > 1, qnt_income ≤ 1, qnt_income = 0 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 1, qnt_income ≤ 1, qnt_income > 0 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 1, qnt_income > 1, qnt_income ≤ 2.5 | HR |
| age ≤ 44, age ≤ 33, age ≤ 28, female = 1, qnt_income > 1, qnt_income > 2.5 | HR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, edhi = 0, age ≤ 30 | MR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, edhi = 0, age > 30 | HR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, edhi = 1, qnt_income = 0 | HR |
| age ≤ 44, age ≤ 33, age > 28, age ≤ 32, edhi = 1, qnt_income > 0 | MR |
| age ≤ 44, age ≤ 33, age > 28, age > 32, female = 0 | LR |
| age ≤ 44, age ≤ 33, age > 28, age > 32, female > 0 | LR |
| age ≤ 44, age > 33, edhi = 0, age ≤ 35, qnt_income = 0 | HR |
| age ≤ 44, age > 33, edhi = 0, age ≤ 35, qnt_income > 0 | LR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income ≤ 2, age ≤ 36 | LR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income ≤ 2, age > 36 | HR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income > 2, age ≤ 39 | HR |
| age ≤ 44, age > 33, edhi = 0, age > 35, qnt_income > 2, age > 39 | HR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37, qnt_income ≤ 2, qnt_income ≤ 1 | MR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37, qnt_income ≤ 2, qnt_income > 1 | LR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37, qnt_income > 2, female = 0 | MR |
| age ≤ 44, age > 33, edhi = 1, age ≤ 37 qnt_income > 2, female = 1 | MR |
| age ≤ 44, age > 33, edhi = 1, age > 37, qnt_income ≤ 2, qnt_income ≤ 1 | HR |
| age ≤ 44 age > 33, edhi = 1, age > 37, qnt_income ≤ 2, qnt_income 1 | HR |
| age ≤ 44, age > 33, edhi = 1, age > 37, qnt_income > 2, female = 0 | HR |
| age ≤ 44, age > 33, edhi = 1, age > 37, qnt_income > 2, female = 1 | MR |
| age > 44, qnt_income ≤ 1, age ≤ 52, female = 0, qnt_income = 0 | HR |
| age > 44, qnt_income ≤ 1 age ≤ 52, female = 0, qnt_income > 0 | MR |
| age > 44, qnt_income ≤ 1, age ≤ 52, female = 1, age ≤ 47, qnt_income = 0 | HR |
| age > 44, qnt_income ≤ 1, age ≤ 52, female = 1, age ≤ 47, qnt_income > 0 | MR |
| age > 44, qnt_income ≤ 1, age ≤ 52, female = 1, age > 47, qnt_income = 0 | MR |
| age > 44, qnt_income ≤ 1 age ≤ 52, female= 1, age > 47, qnt_income > 0 | MR |
| age > 44, qnt_income ≤ 1, age > 52, age ≤ 60, qnt_income = 0, age ≤ 56 | HR |
| age > 44, qnt_income ≤ 1, age > 52, age ≤ 60, qnt_income = 0, age > 56 | HR |
| age > 44, qnt_income ≤ 1, age > 52, age ≤ 60, qnt_income > 0, age ≤ 55 | MR |
| age > 44, qnt_income ≤ 1, age > 52, age ≤ 60, qnt_income > 0, age > 55 | HR |
| age , qnt_income , age , age , age , age | HR |
| age , qnt_income , age , age , age , age | HR |
| age , qnt_income , age , age , age , age | HR |
| age , qnt_income , age , age , age , age | HR |
| age , qnt_income , qnt_income , female = 0, age , age | MR |
| age , qnt_income , qnt_income , female = 0, age , age | MR |
| age , qnt_income , qnt_income , female = 0, age , age | LR |
| age , qnt_income , qnt_income , female = 0, age , age | HR |
| age , qnt_income , qnt_income , female = 1, age , age | HR |
| age , qnt_income , qnt_income , female = 1, age , age | MR |
| age , qnt_income , qnt_income , female = 1, age , age | HR |
| age , qnt_income , qnt_income , female = 1, age , age | HR |
| age , qnt_income , qnt_income , age , age , female = 0 | HR |
| age , qnt_income , qnt_income , age , age , female = 1 | LR |
| age , qnt_income , qnt_income , age , age , female = 0 | LR |
| age , qnt_income , qnt_income , age , age , female | HR |
| age , qnt_income , qnt_income , age , age , female = 0 | LR |
| age , qnt_income , qnt_income , age , age , female = 1 | LR |
| age , qnt_income , qnt_income , age , age , female = 0 | LR |
| age , qnt_income , qnt_income , age , age , female = 1 | LR |
Note: Policy rule for individuals assigned to HR: high rate, MR: medium rate, and LR: low rate.
References
- Athey, S.; Imbens, G.W. The state of applied econometrics: Causality and policy evaluation. J. Econ. Perspect. 2017, 31, 3–32. [Google Scholar] [CrossRef]
- Baiardi, A.; Naghi, A.A. The value added of machine learning to causal inference: Evidence from revisited studies. Econom. J. 2024, 27, utae004. [Google Scholar] [CrossRef]
- Künzel, S.R.; Sekhon, J.S.; Bickel, P.J.; Yu, B. Metalearners for estimating heterogeneous treatment effects using machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 4156–4165. [Google Scholar] [CrossRef] [PubMed]
- Manski, C.F. Statistical treatment rules for heterogeneous populations. Econometrica 2004, 72, 1221–1246. [Google Scholar] [CrossRef]
- Kitagawa, T.; Tetenov, A. Who should be treated? empirical welfare maximization methods for treatment choice. Econometrica 2018, 86, 591–616. [Google Scholar] [CrossRef]
- Mbakop, E.; Tabord-Meehan, M. Model selection for treatment choice: Penalized welfare maximization. Econometrica 2021, 89, 825–848. [Google Scholar] [CrossRef]
- Athey, S.; Wager, S. Policy learning with observational data. Econometrica 2021, 89, 133–161. [Google Scholar] [CrossRef]
- Kitagawa, T.; Tetenov, A. Equality-minded treatment choice. J. Bus. Econ. Stat. 2021, 39, 561–574. [Google Scholar] [CrossRef]
- Zhou, Z.; Athey, S.; Wager, S. Offline multi-action policy learning: Generalization and optimization. Oper. Res. 2023, 71, 148–183. [Google Scholar] [CrossRef]
- Lechner, M.; Mareckova, J. Comprehensive Causal Machine Learning. arXiv 2024, arXiv:2405.10198. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Imbens, G.W.; Wooldridge, J.M. Recent Developments in the Econometrics of Program Evaluation. J. Econ. Lit. 2009, 47, 5–86. [Google Scholar] [CrossRef]
- Bodory, H.; Busshoff, H.; Lechner, M. High resolution treatment effects estimation: Uncovering effect heterogeneities with the modified causal forest. Entropy 2022, 24, 1039. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, A.; Taubman, S.; Wright, B.; Bernstein, M.; Gruber, J.; Newhouse, J.P.; Allen, H.; Baicker, K.; the Oregon Health Study Group. The Oregon health insurance experiment: Evidence from the first year. Q. J. Econ. 2012, 127, 1057–1106. [Google Scholar] [CrossRef] [PubMed]
- Baicker, K.; Taubman, S.L.; Allen, H.L.; Bernstein, M.; Gruber, J.H.; Newhouse, J.P.; Schneider, E.C.; Wright, B.J.; Zaslavsky, A.M.; Finkelstein, A.N. The Oregon experiment—effects of Medicaid on clinical outcomes. N. Engl. J. Med. 2013, 368, 1713–1722. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, A.N.; Taubman, S.L.; Allen, H.L.; Wright, B.J.; Baicker, K. Effect of Medicaid coverage on ED use—Further evidence from Oregon’s experiment. N. Engl. J. Med. 2016, 375, 1505–1507. [Google Scholar] [CrossRef] [PubMed]
- Baicker, K.; Allen, H.L.; Wright, B.J.; Finkelstein, A.N. The effect of Medicaid on medication use among poor adults: Evidence from Oregon. Health Aff. 2017, 36, 2110–2114. [Google Scholar] [CrossRef]
- Carcillo, S.; Grubb, D. From Inactivity to Work. 2006. Available online: https://www.oecd-ilibrary.org/social-issues-migration-health/from-inactivity-to-work_687686456188 (accessed on 10 July 2024).
- Baicker, K.; Finkelstein, A. The Impact of Medicaid Expansion on Voter Participation: Evidence from the Oregon Health Insurance Experiment; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2018. [Google Scholar]
- Finkelstein, A.; Hendren, N.; Luttmer, E.F. The value of medicaid: Interpreting results from the oregon health insurance experiment. J. Political Econ. 2019, 127, 2836–2874. [Google Scholar] [CrossRef] [PubMed]
- Baicker, K.; Finkelstein, A.; Song, J.; Taubman, S. The impact of health insurance expansions on other social safety net programs. Am. Econ. Rev. 2014, 104, 322–328. [Google Scholar] [CrossRef]
- Sverdrup, E.; Kanodia, A.; Zhou, Z.; Athey, S.; Wager, S. Policytree: Policy Learning via Doubly Robust Empirical Welfare Maximization over Trees. J. Open Source Softw. 2023, 5, 2232. [Google Scholar] [CrossRef]
- Connors, A.F.; Speroff, T.; Dawson, N.V.; Thomas, C.; Harrell, F.E.; Wagner, D.; Desbiens, N.; Goldman, L.; Wu, A.W.; Califf, R.M.; et al. The effectiveness of right heart catheterization in the initial care of critically III patients. JAMA 1996, 276, 889–897. [Google Scholar] [CrossRef]
- Knaus, W.A.; Harrell, F.E.; Lynn, J.; Goldman, L.; Phillips, R.S.; Connors, A.F.; Dawson, N.V.; Fulkerson, W.J.; Califf, R.M.; Desbiens, N.; et al. The SUPPORT prognostic model: Objective estimates of survival for seriously ill hospitalized adults. Ann. Intern. Med. 1995, 122, 191–203. [Google Scholar] [CrossRef] [PubMed]
- Ramsahai, R.R.; Grieve, R.; Sekhon, J.S. Extending iterative matching methods: An approach to improving covariate balance that allows prioritisation. Health Serv. Outcomes Res. Methodol. 2011, 11, 95–114. [Google Scholar] [CrossRef]
- Keele, L.; Small, D.S. Pre-analysis Plan for a Comparison of Matching and Black Box-based Covariate Adjustment. Obs. Stud. 2018, 4, 97–110. [Google Scholar] [CrossRef]
- Keele, L.; Small, D.S. Comparing covariate prioritization via matching to machine learning methods for causal inference using five empirical applications. Am. Stat. 2021, 75, 355–363. [Google Scholar] [CrossRef]
- Karlan, D.S.; Zinman, J. Credit elasticities in less-developed economies: Implications for microfinance. Am. Econ. Rev. 2008, 98, 1040–1068. [Google Scholar] [CrossRef]
- Kallus, N.; Zhou, A. Fairness, welfare, and equity in personalized pricing. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, Toronto, ON, Canada, 3–10 March 2021; pp. 296–314. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).