A Novel Hybrid Crow Search Arithmetic Optimization Algorithm for Solving Weighted Combined Economic Emission Dispatch with Load-Shifting Practice
Abstract
1. Introduction
1.1. The Literature Review
1.2. Research Gap and Objective of the Paper
1.3. Methodology and Contributions
- A unique hybrid CSAOA is suggested as the optimization technique for this study. Prior to using it to address the DEED issue, the suggested methodology is additionally tested on six multi-dimensional and varied modal benchmark functions.
- The test system leverages a combination of conventional generating plants and combined heat and power (CHP) plants. This allows for the evaluation of various dispatch strategies, including dynamic economic dispatch, emission dispatch, and weighted economic emission dispatch, contributing to the optimization of power generation based on cost, emissions, or a balance of both.
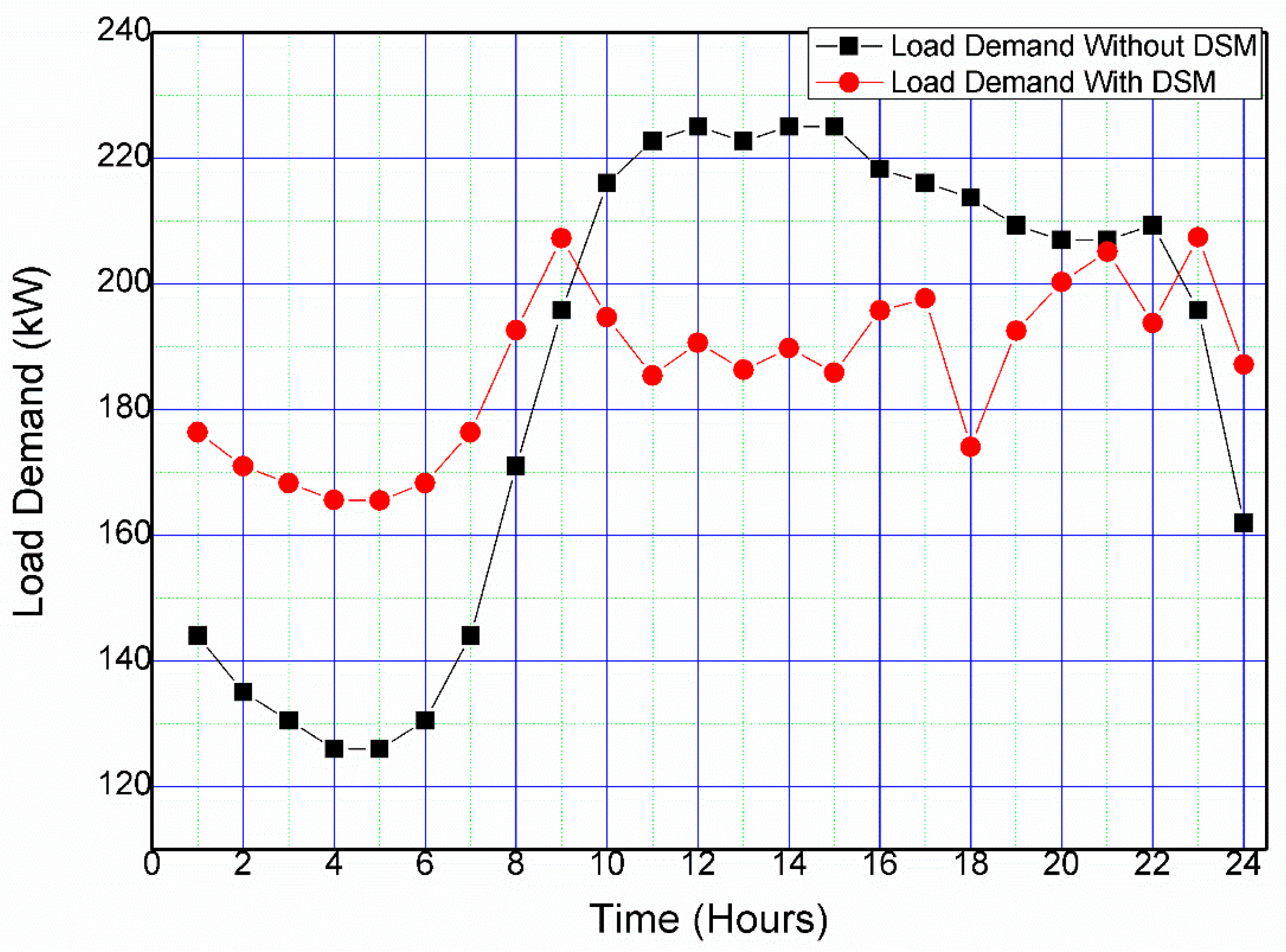
- A load-shifting policy called demand side management (DSM) is also considered and all the above-mentioned studies are also conducted in the presence of DSM to highlight its benefits.
2. Objective Function Formulation
2.1. Cost Function for DG Units
2.2. Emission Dispatch for DG Units
2.3. PPF-Based Combined Economic Emission Dispatch
2.4. FP-Based Combined Economic Emission Dispatch
2.5. The Proposed Environment-Constrained Economic Dispatch (ECED)
- Setting μ = 0.5, or providing equal weight to both goal functions, is known to provide the fastest and most effective steps towards obtaining the best compromised solution.
- The choice with the largest quality compromise will have a smallest CPI-EPI difference, where the CPI is cost performance index and EPI is emission performance index. The formulae for CPI and EPI are denoted by Formulas (7) and (8).
- The generating cost of the higher quality compromise will be closer to ECDmin, while the pollution output will be lower than EMDmin.
2.6. Equality and Inequality Constraints
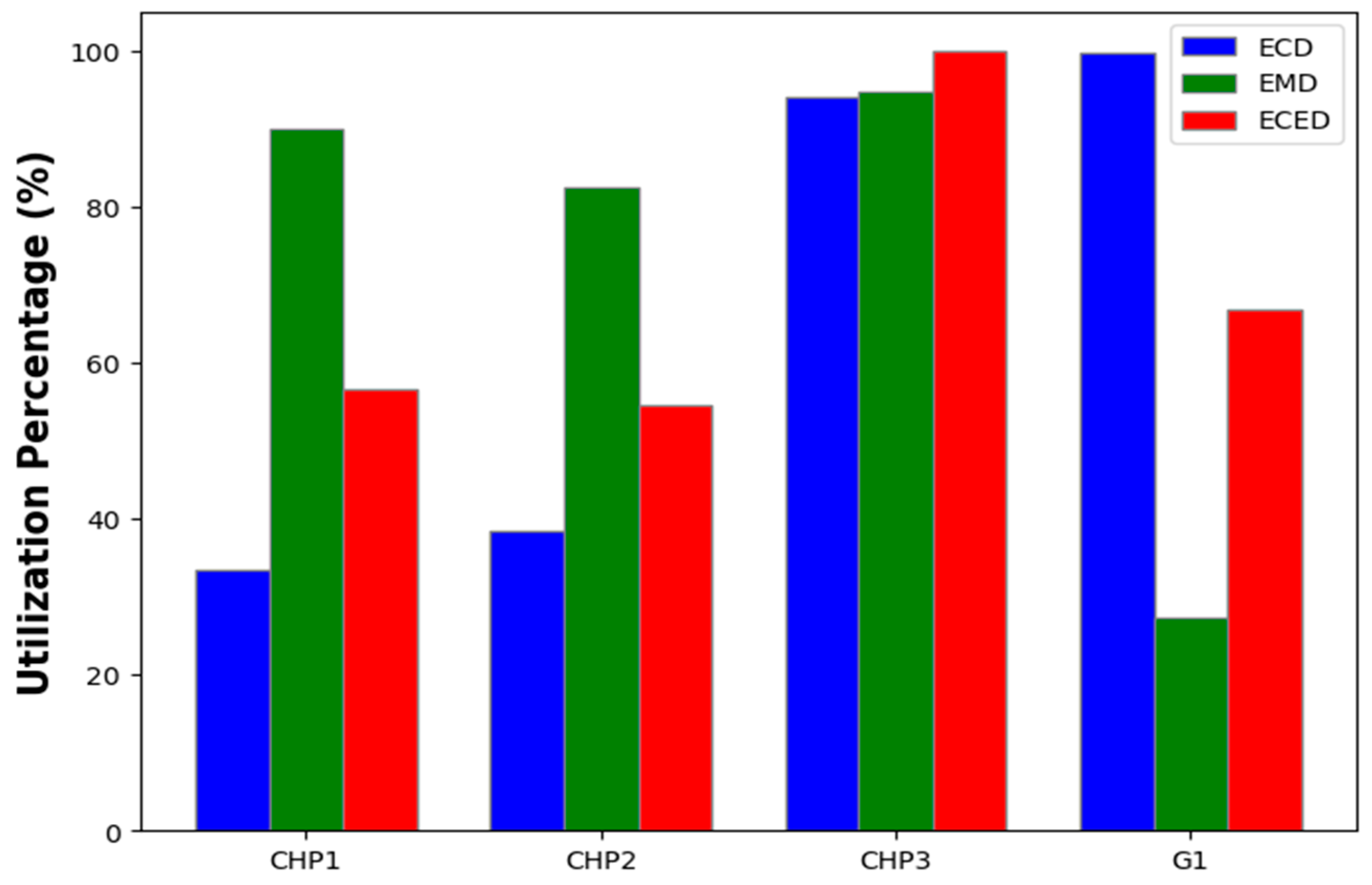
2.7. Utilization Percentage
2.8. Demand Side Management
3. Optimization Techniques
3.1. Crow Search Algorithm
3.2. Arithmetic Optimization Algorithm (AOA)
3.3. Hybrid CSAOA
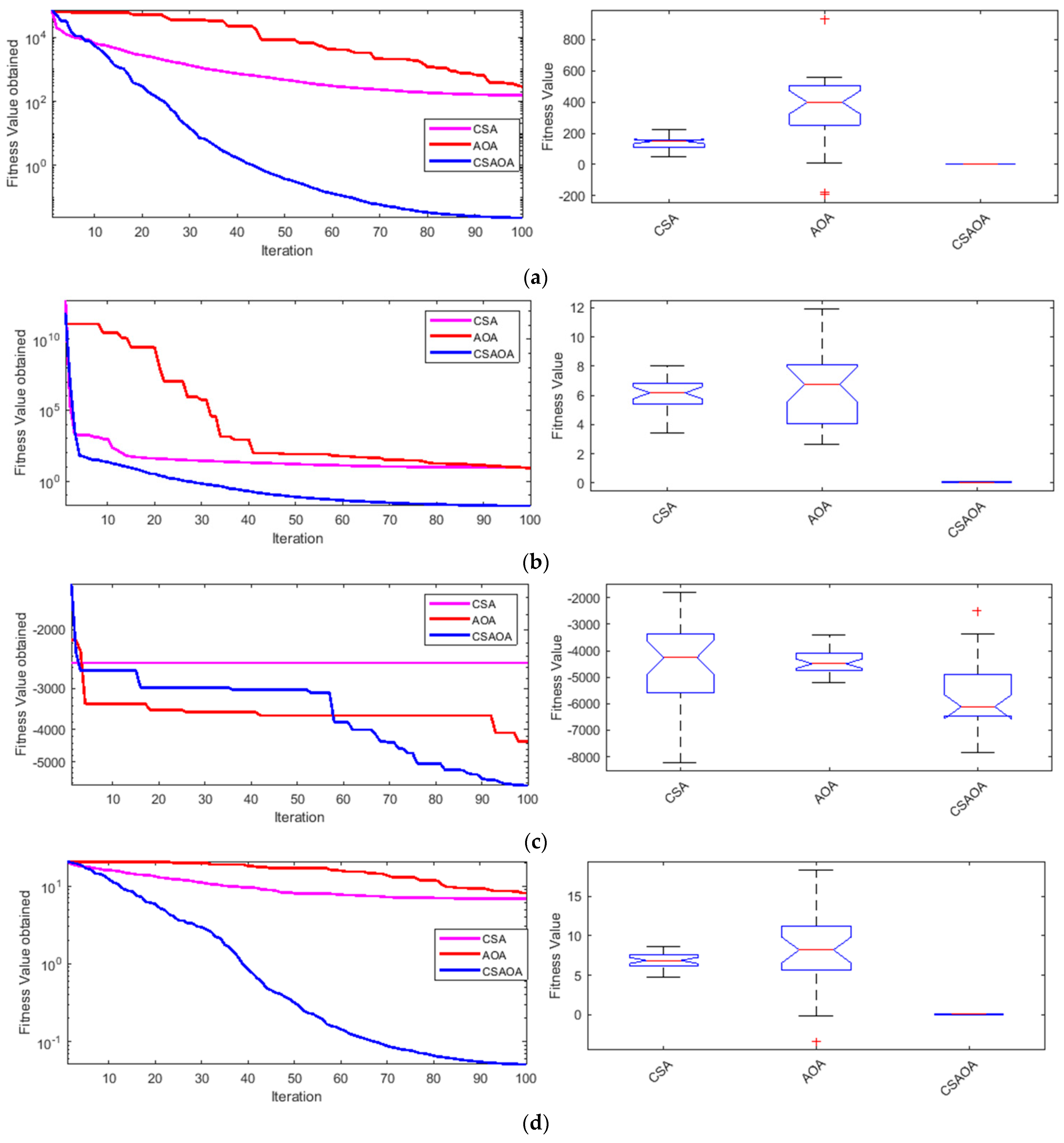
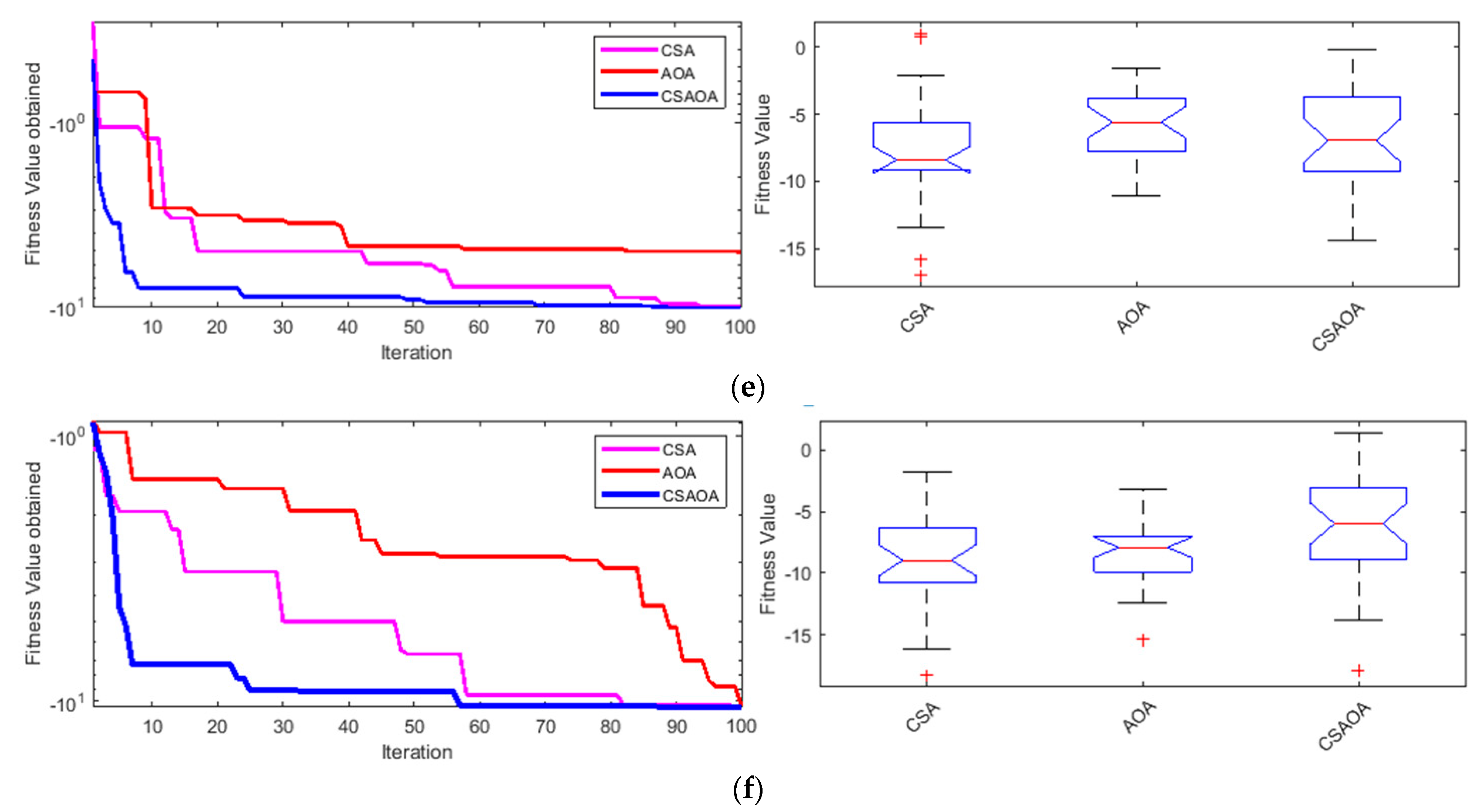
3.4. Realization on Benchmark Functions
4. Case Study and Proof of Concept
4.1. Test System 1
- The minimum generation cost is found to be USD 296,744 using CSAOA, which is further reduced to USD 293,098 when DSM integrated load demand is accounted for.
- The minimum emission is 54 tons and 31 tons without and with DSM, respectively.
- When ECED is assessed to find a trade-off solution between least cost and pollutants (using µ = 0.5), the solution set is found to be (USD 32,4067, 134 tons) which is further improved to (USD 322,365.5, 133 tons) when DSM incorporated load demand model is considered.
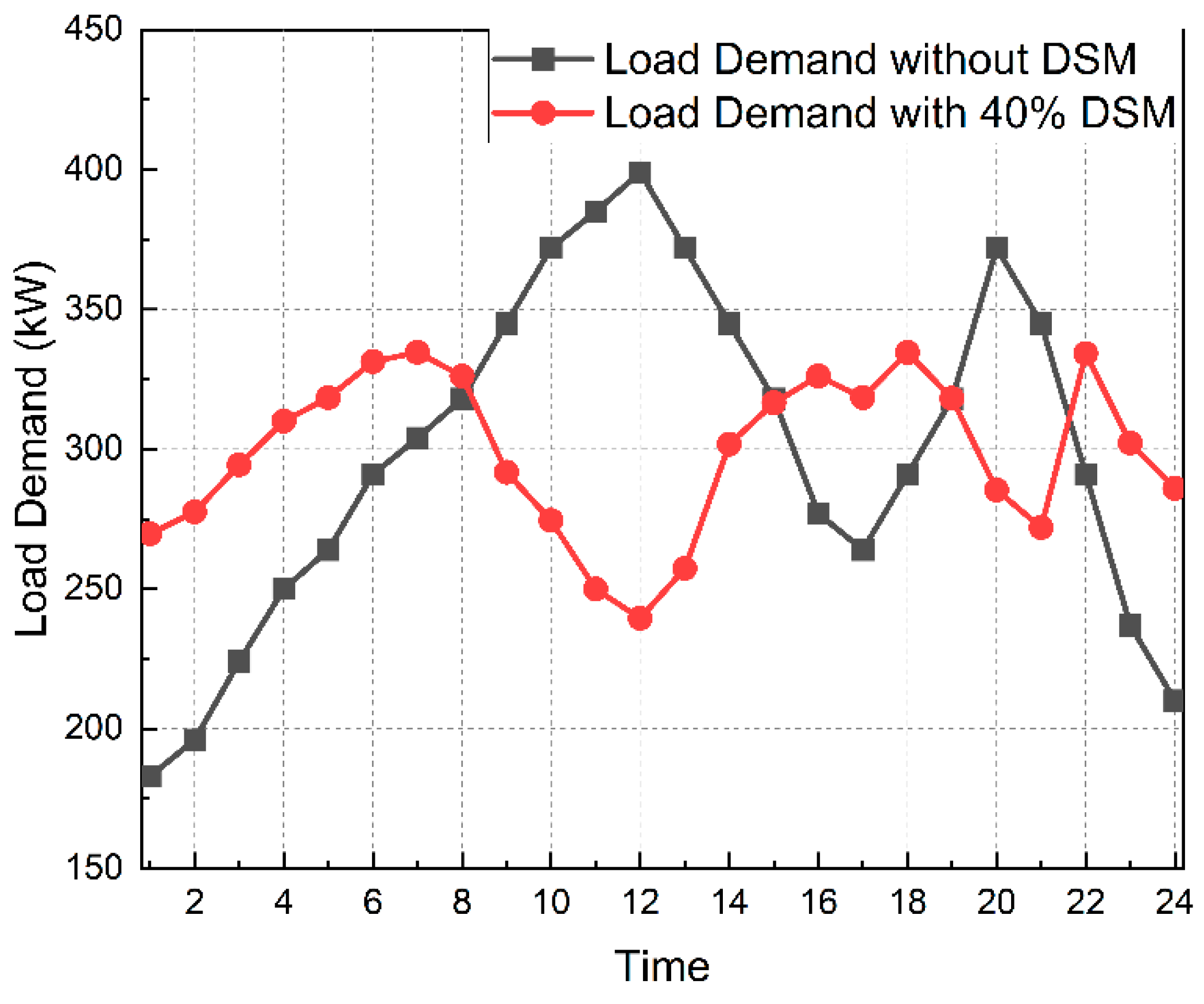
4.2. Test System 2
- (a)
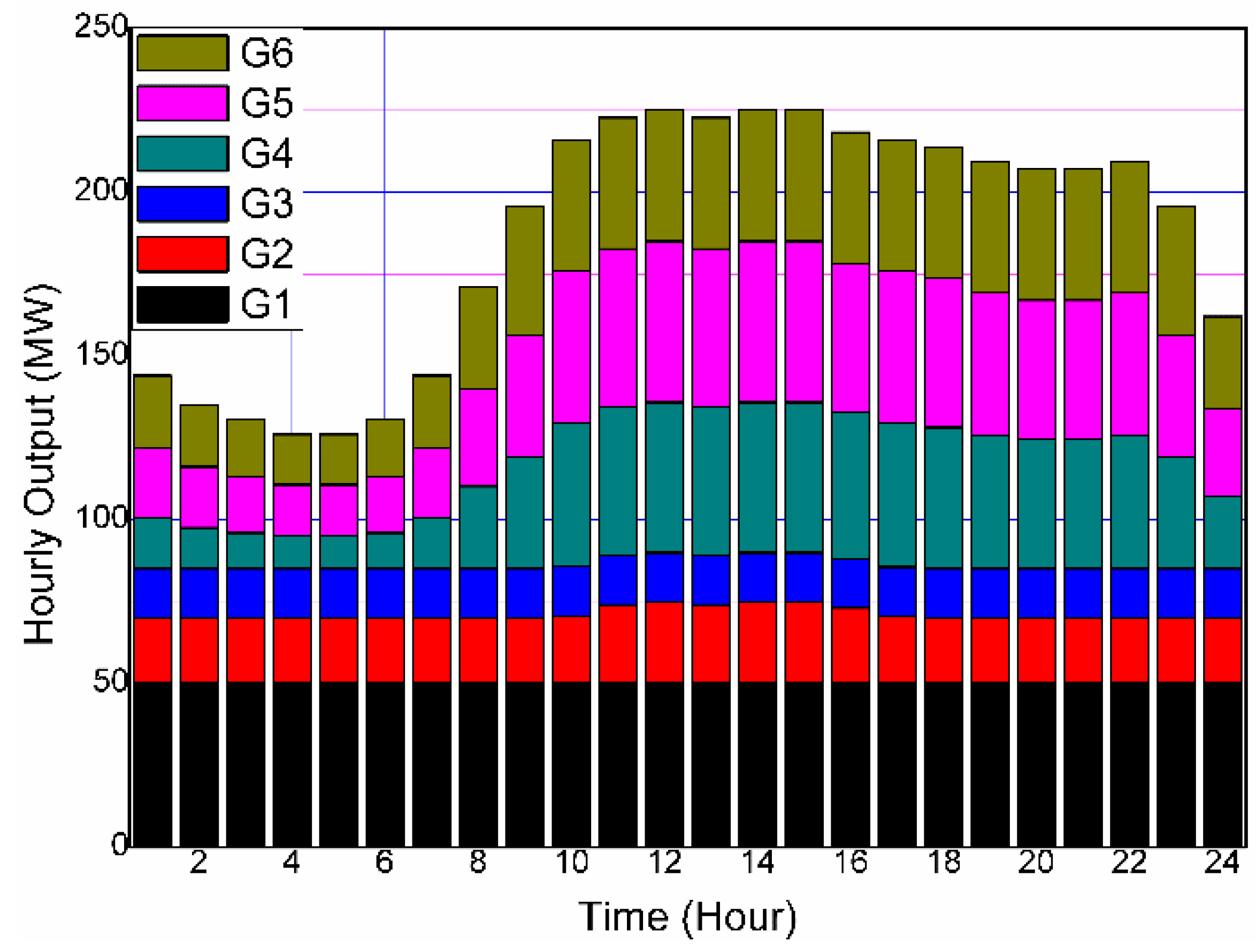
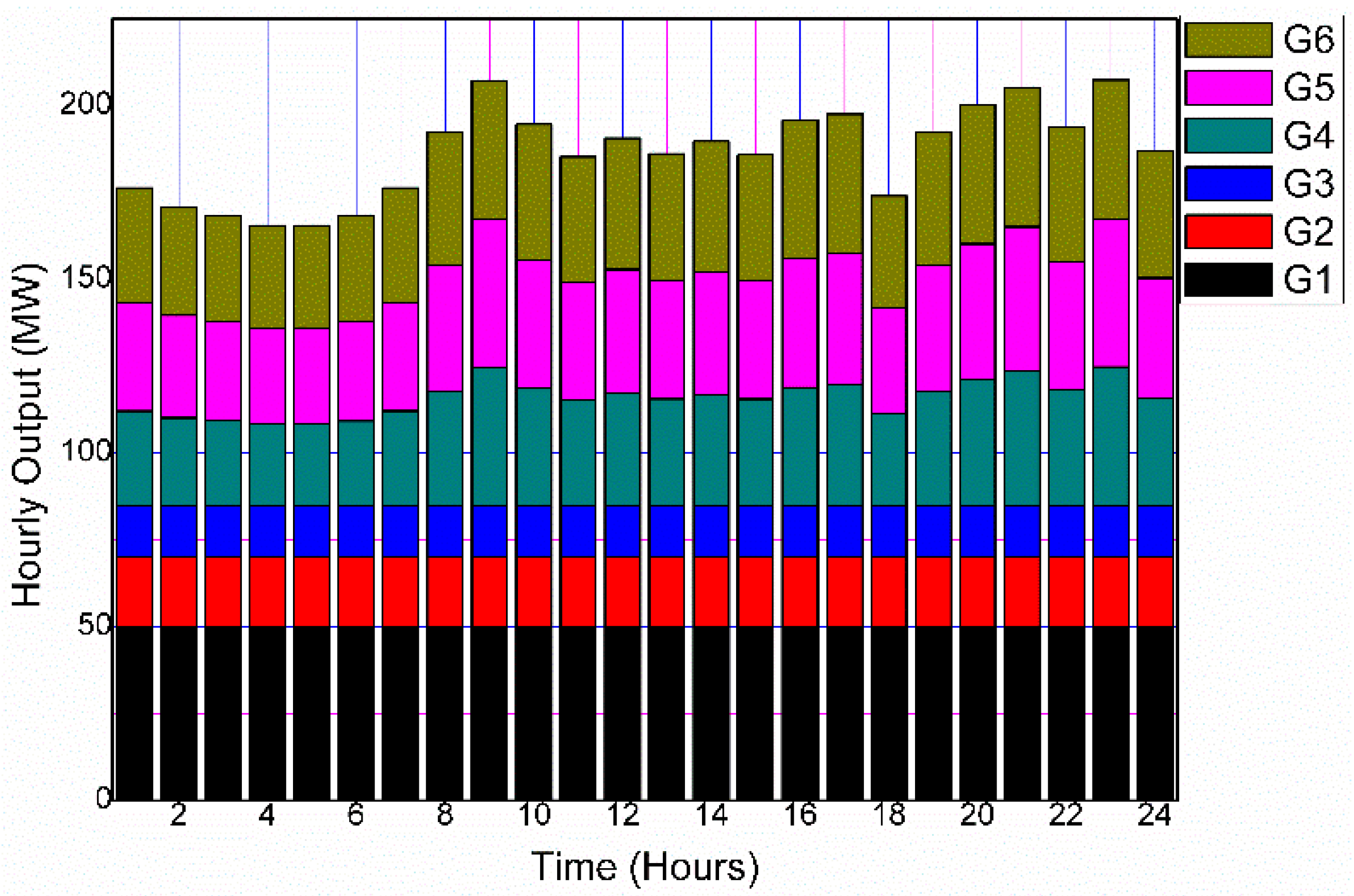
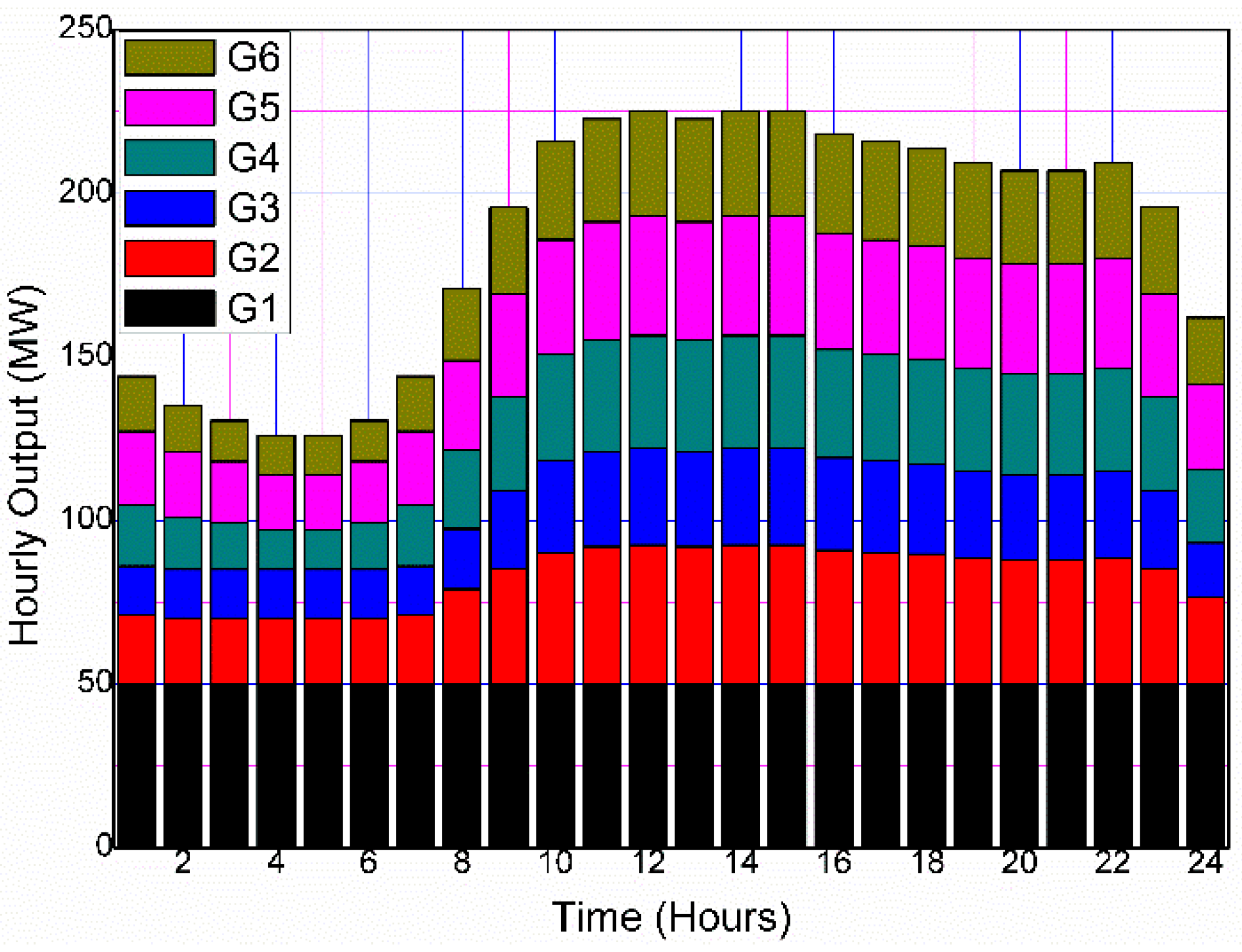
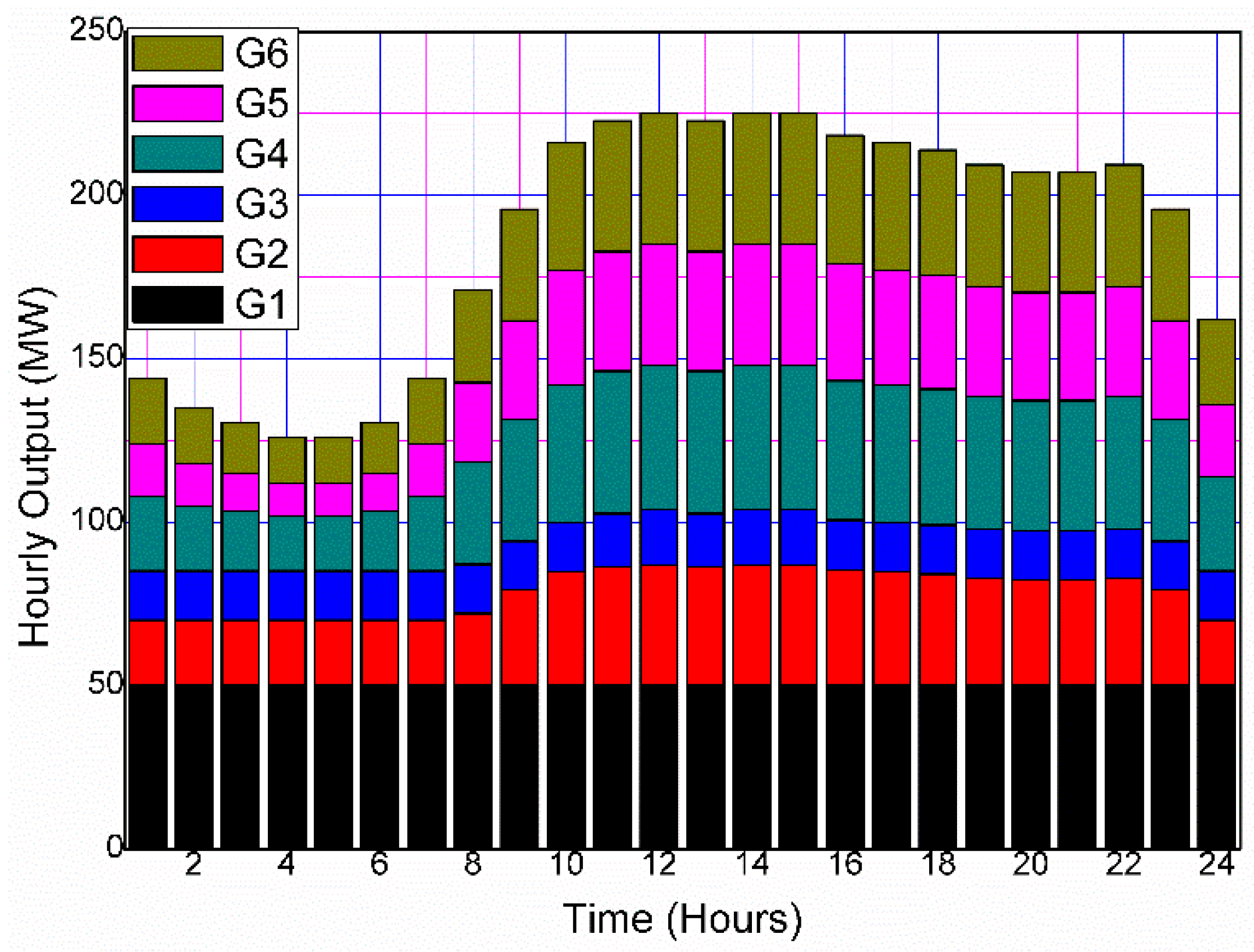
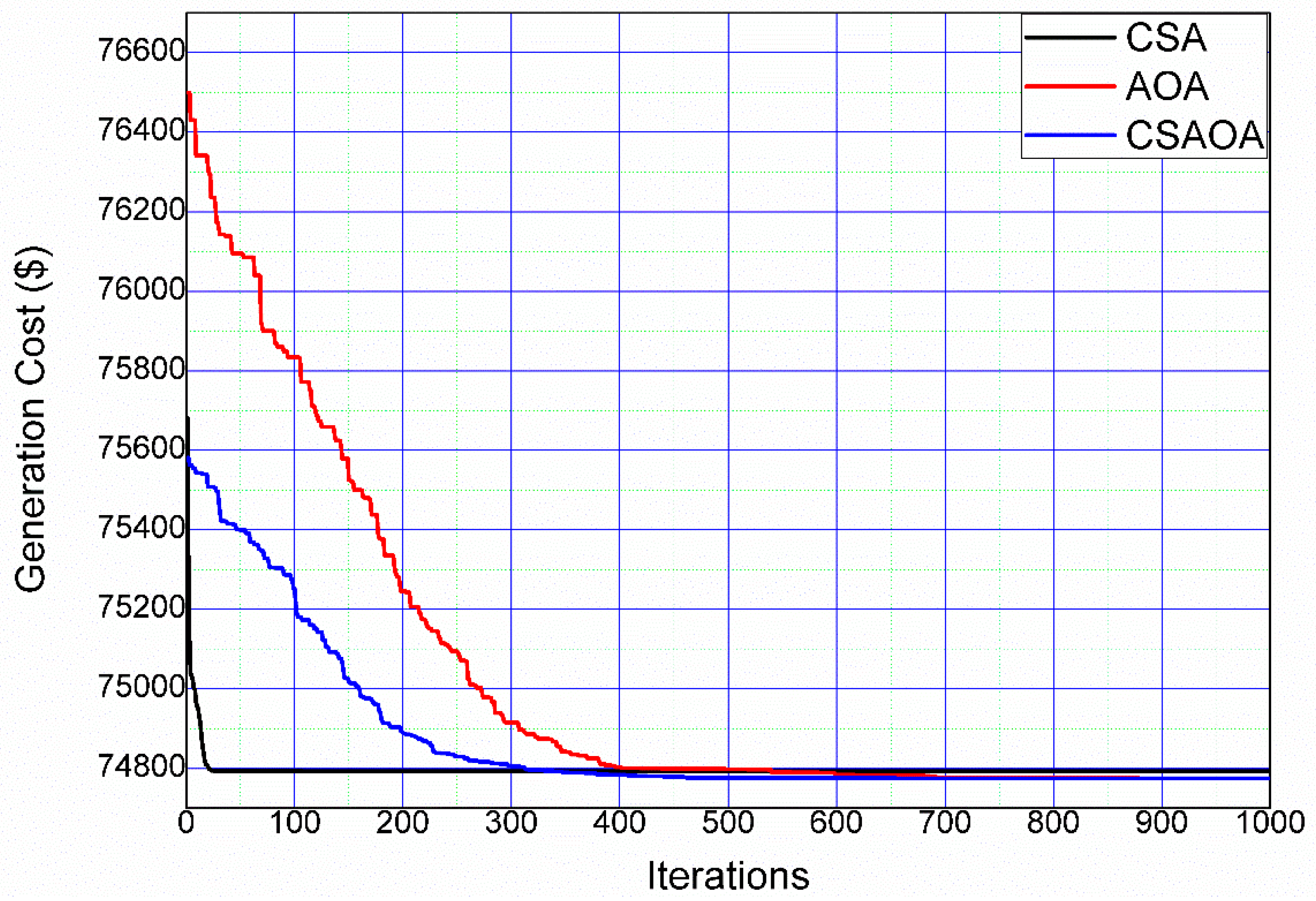
- Cost (ECD) minimization performed on test system 2. The minimum generation cost of the system is found to be USD 76,085 without DSM, which further reduces to USD 74,774 with DSM, respectively. Figure 7 and Figure 8 illustrate, respectively, the hourly production of distributed energy resources (DERs) in the graphical representation, when the cost of generating is USD 76,085 and USD 74,774. On comparing Figure 6, Figure 7 and Figure 8, the hourly load pattern can be easily traced, meaning that the total load demands every hour are fulfilled by the DERs.
- (b)
- Emission (EMD) minimization is performed on test system 2. The minimum emissions of the plant could be reduced to 236 tons ultimately when DSM is implemented, and the load demand is restructured.
- (c)
- CEED is performed as per the PPF method and FP method. With the PPF method, the cost and emission combination is USD 314,678, 256 tons and, with the FP method, the cost and emission combination is found to be USD 90,775, 249 tons. These values produce much more improved outcomes when the load demand is reorganized utilizing the DSM approach. It can be clearly seen that the FP method of CEED is a better option for obtaining a minimum cost and emission combination compared with PPF-based CEED.
- (d)
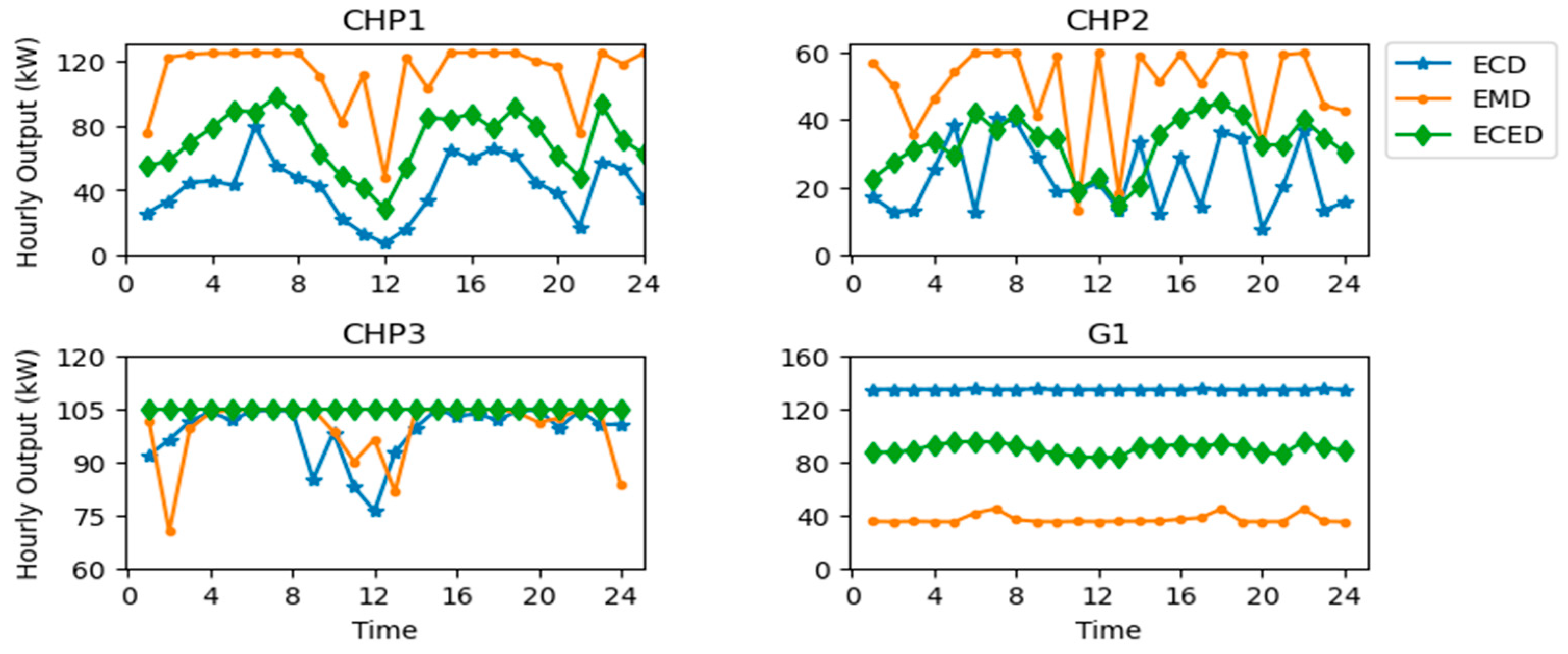
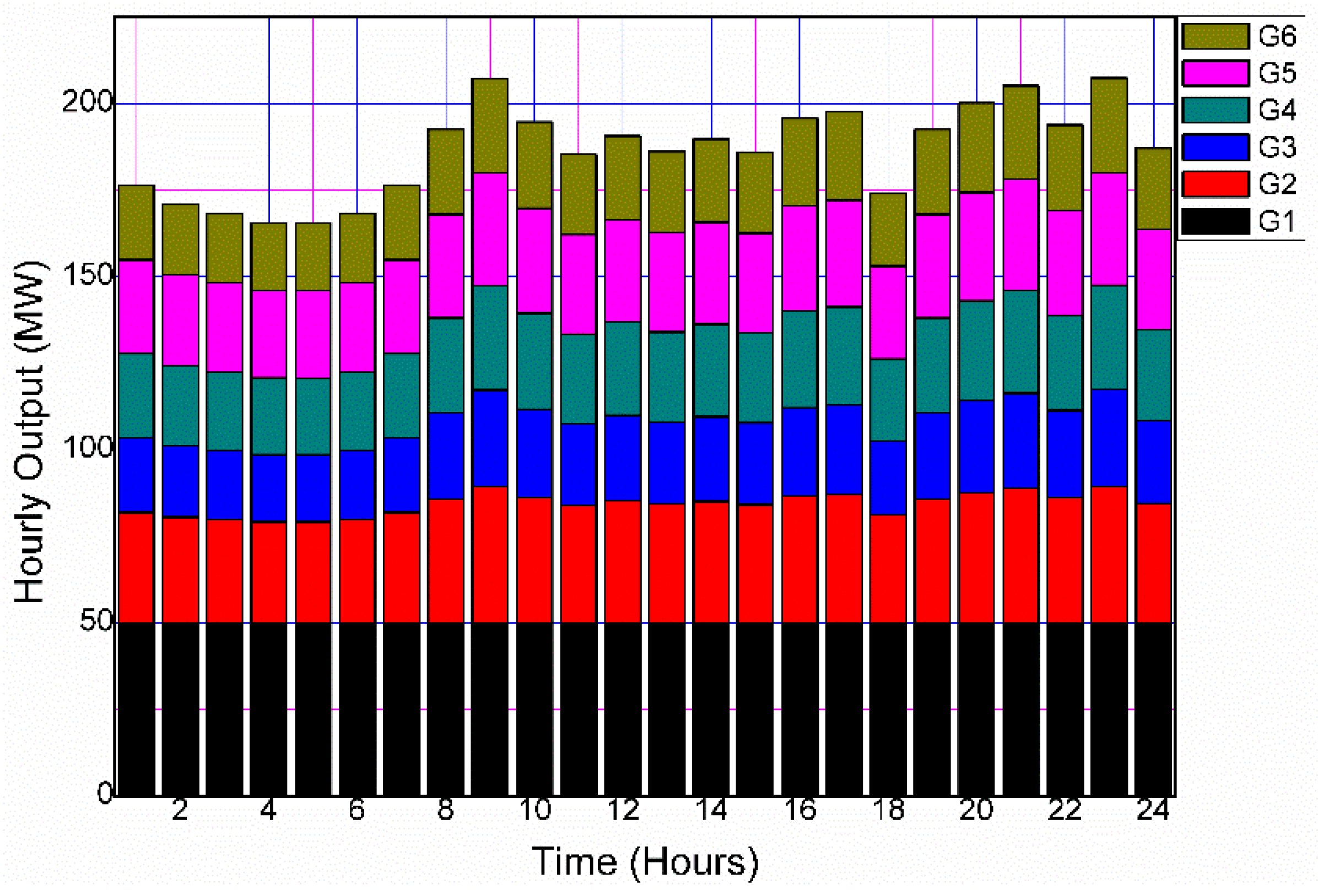
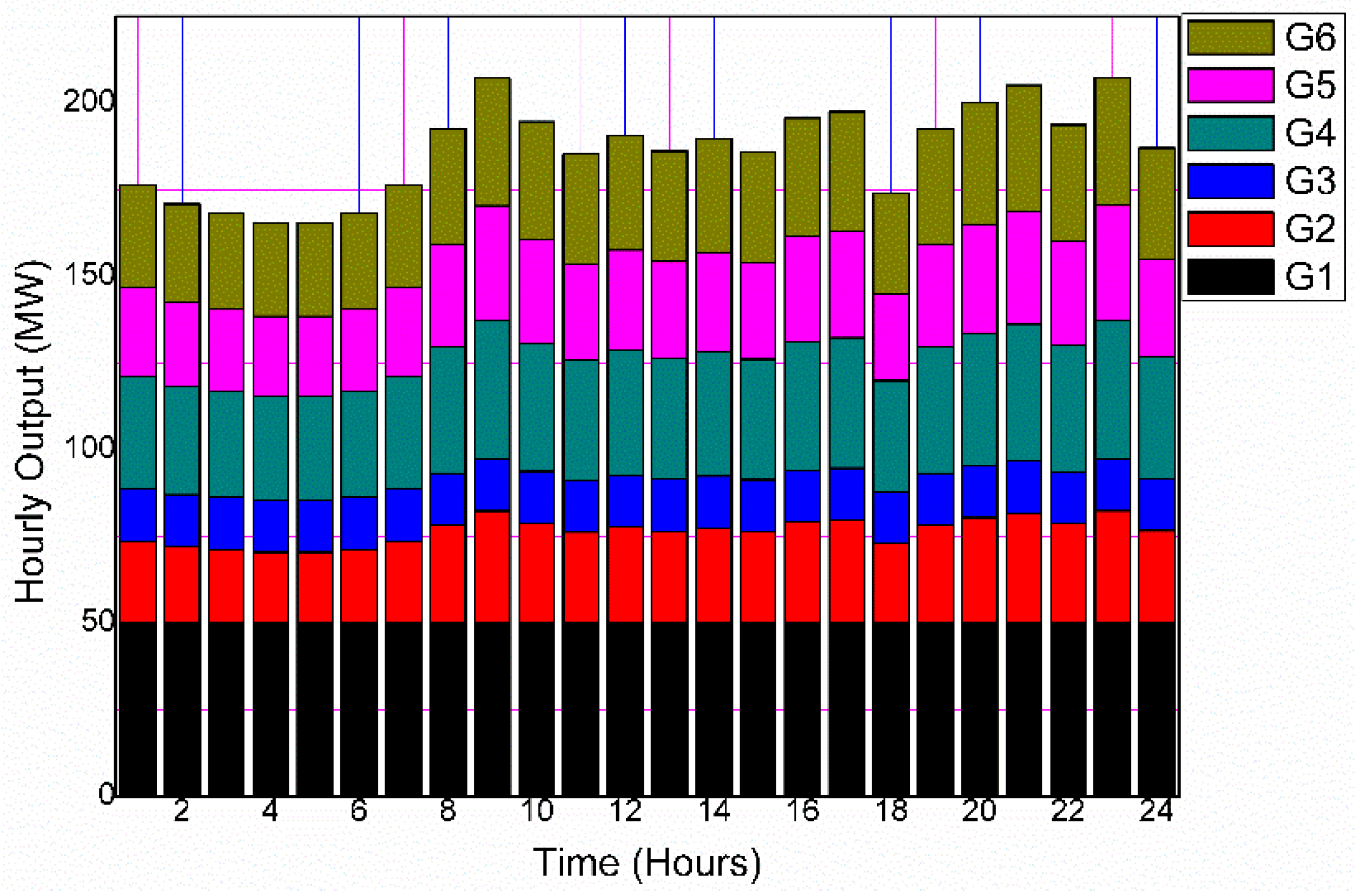
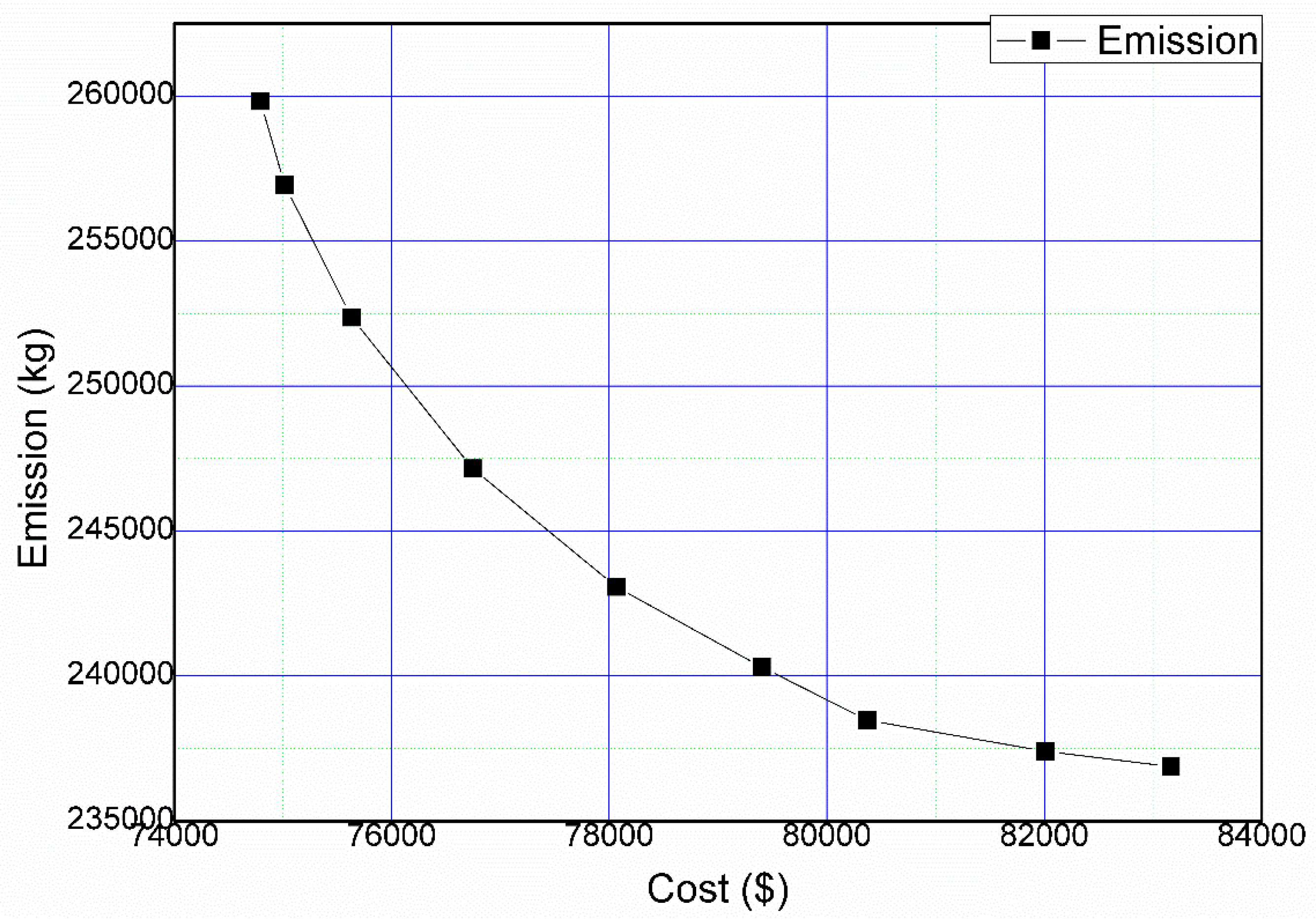
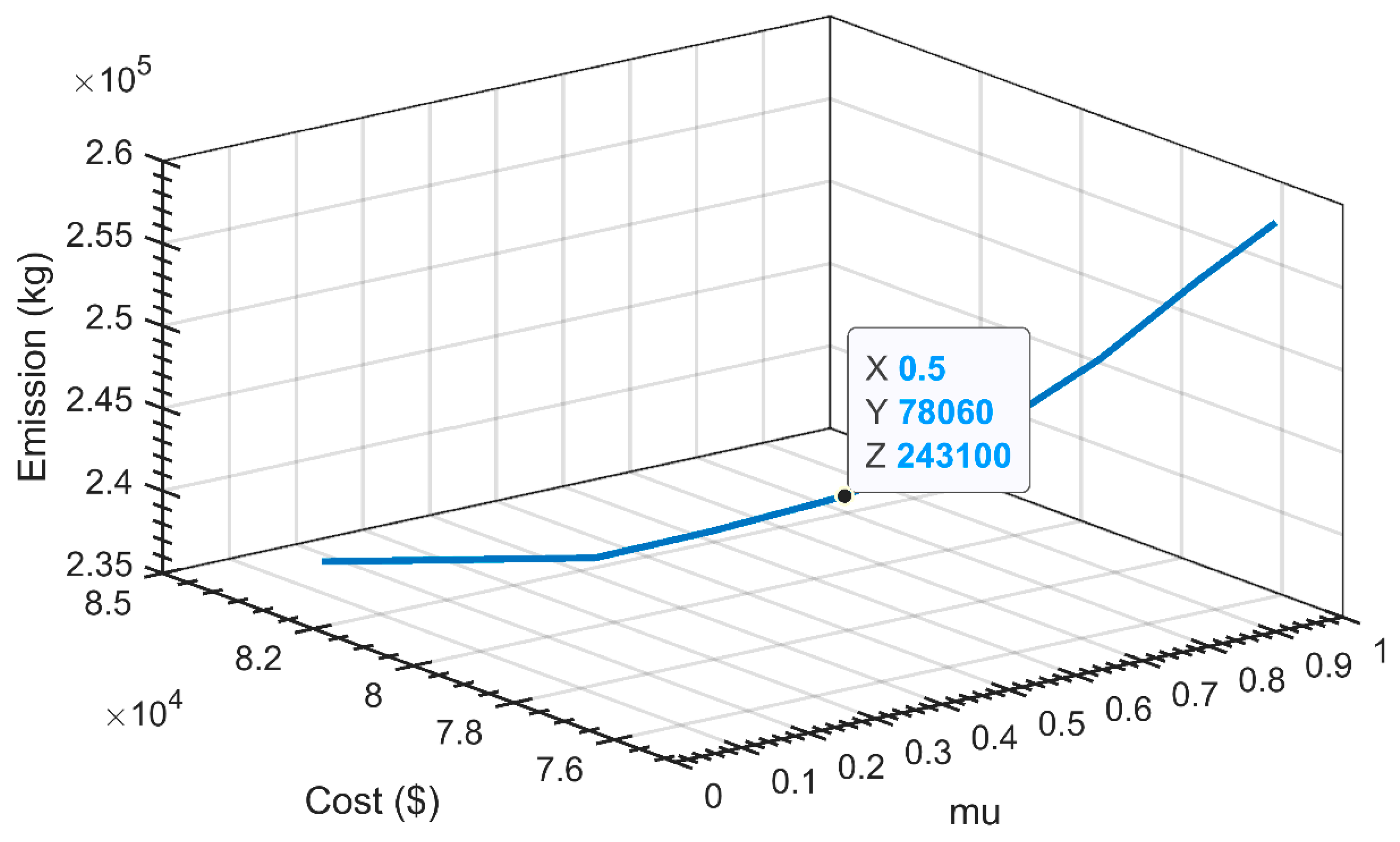
- Weighted combined economic emissions dispatch with equal weightage to both cost and emissions function is found to be the best measure of CEED, with a minimum value of USD 78,304 and 246 tons for cost and emissions, respectively. These values, as mentioned above, reduce further for the DSM-based load demand model to USD 78,064 and 243 tons. The hourly output of DERs is shown in Figure 9 and Figure 10, where the weighted ECED is used as the fitness function. Both the cost and emission functions are given equal weights. Similarly, Figure 11 and Figure 12 display the hourly output of DERs when PPF-based CEED is considered as the fitness function.
- (e)
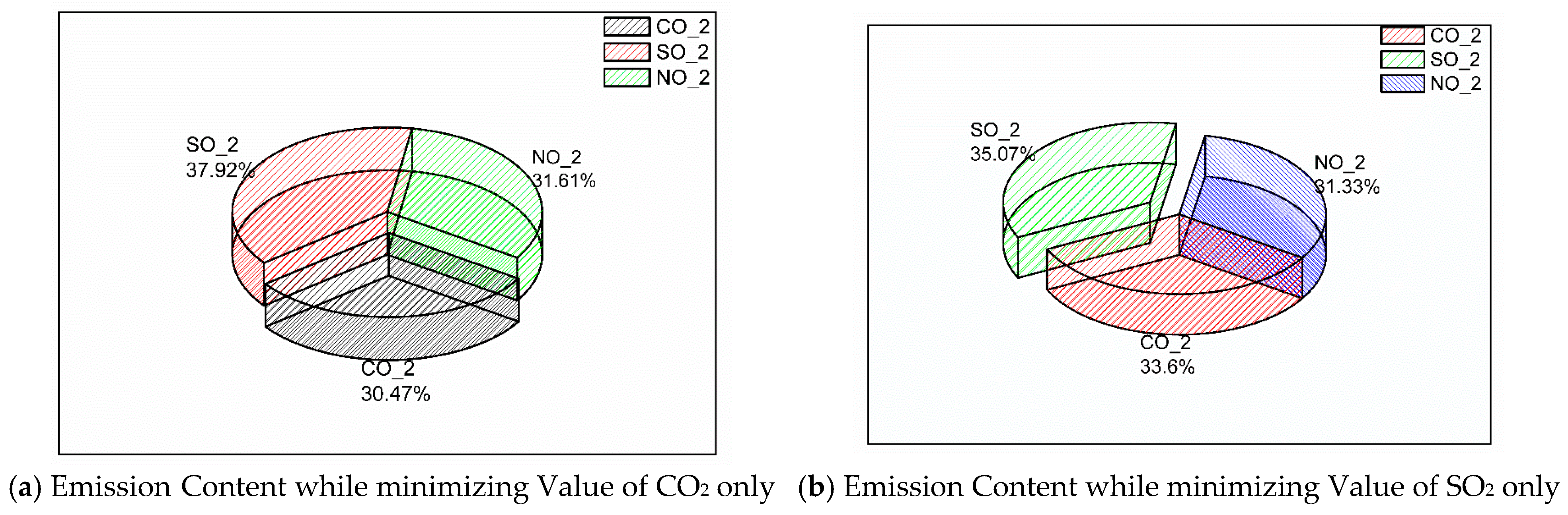
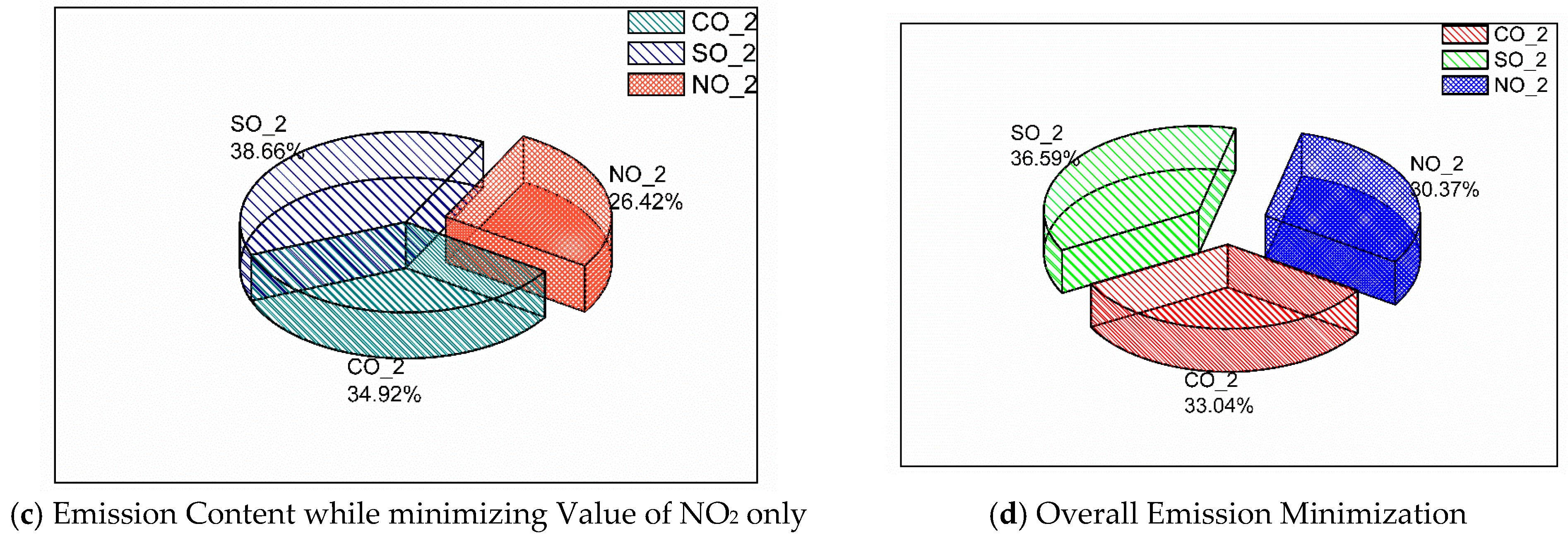
- Thereafter, the minimization of CO2, SO2, and NOx are individually considered as EMD fitness functions and are minimized one at a time. When CO2 is individually minimized to 75 tons, the values of SO2 and NOx are 93 tons and 77 tons, which add to an amount of 246 tons of total emission value. Similarly, SO2 and NOx are minimized individually, and all the results are mentioned in Table 14. The values of CO2, SO2, and NOx when the total emission is minimized is also shown in Table 14. Figure 13a–d are the pie-chart representations of Table 14, which highlights the shares of individual emission components as a part of the total emission. The average share of SO2, CO2, and NOx are 37%, 33%, and 30%, respectively.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a, b, c, d | Cost coefficients |
| j | Index of generator |
| Emission coefficients | |
| Pj | Power of the generator |
| n | Index for number of generators |
| CO2, NOX, SO2 | Emissive pollutant components |
| ppf | Price penalty factor |
| Maximum values of power of the jth generator | |
| Form of price penalty factor during maximum cost and maximum pollution | |
| FP | Fractional programming |
| µ | Constant lies between 0 to 1 |
| Minimum cost | |
| Maximum cost | |
| Minimum emission | |
| Maximum emission | |
| CPI | Cost performance index |
| EPI | Emission performance Index |
| Dt | Load demand |
| Index for time | |
| UP | Utilization percentage |
| Hourly output | |
| Grid cost | |
| Elastic load | |
| Inelastic load | |
| iter/max_iter | Iteration/maximum iteration |
| fl | Flight length |
| Random | |
| AP | Awareness probability |
| m | Memory |
| UL | Upper limit |
| LL | Lower limit |
| MOA | Mathematics optimizer accelerator |
| MOP | Mathematics optimizer probability |
| Piter | Present iteration |
| x | Solution set |
| z, λ | Tuning parameter |
| M_iter | Maximum iteration |
| Small integer number | |
| Fmean | Mean value |
| Fworst | Worst value |
| Bench mark function | |
| N | Total number of distinct runs |
| PV | Photo voltaic |
| WT | Wind turbine |
References
- Ramesh, B.; Mohan, V.C.J.; Reddy, V.V. Application of BAT algorithm for combined economic load and emission dispatch. J. Electr. Eng. 2013, 13, 6. [Google Scholar]
- Karakonstantis, I.; Vlachos, A. Ant colony optimization for continuous domains applied to emission and economic dispatch problems. J. Inf. Optim. Sci. 2015, 36, 23–42. [Google Scholar] [CrossRef]
- Roy, P.K.; Bhui, S. Multi-objective quasi-oppositional teaching learning based optimization for economic emission load dispatch problem. Int. J. Electr. Power Energy Syst. 2013, 53, 937–948. [Google Scholar] [CrossRef]
- Chandrasekaran, K.; Simon, S.P. Wind-thermal integrated power system scheduling problem using Cuckoo search algorithm. Int. J. Oper. Res. Inf. Syst. (IJORIS) 2014, 5, 81–109. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Ali, E.; Elazim, S.A. Flower pollination algorithm to solve combined economic and emission dispatch problems. Eng. Sci. Technol. Int. J. 2016, 19, 980–990. [Google Scholar] [CrossRef]
- Apostolopoulos, T.; Vlachos, A. Application of the firefly algorithm for solving the economic emissions load dispatch problem. Int. J. Comb. 2011, 2011, 523806. [Google Scholar] [CrossRef]
- Hota, P.; Barisal, A.; Chakrabarti, R. Economic emission load dispatch through fuzzy based bacterial foraging algorithm. Int. J. Electr. Power Energy Syst. 2010, 32, 794–803. [Google Scholar] [CrossRef]
- Song, Y.; Wang, G.; Wang, P.; Johns, A. Environmental/economic dispatch using fuzzy logic controlled genetic algorithms. IEE Proc.-Gener. Transm. Distrib. 1997, 144, 377–382. [Google Scholar] [CrossRef]
- El Ela, A.A.; Abido, M.; Spea, S. Differential evolution algorithm for emission constrained economic power dispatch problem. Electr. Power Syst. Res. 2010, 80, 1286–1292. [Google Scholar] [CrossRef]
- Kumar, A.; Dhanushkodi, K.; Kumar, J.; Paul, C. Particle swarm optimization solution to emission and economic dispatch problem. In Proceedings of the TENCON 2003, Conference on Convergent Technologies for Asia-Pacific Region, Bangalore, India, 5–17 October 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 435–439. [Google Scholar]
- Srivastava, A.; Das, D.K. A bottlenose dolphin optimizer: An application to solve dynamic emission economic dispatch problem in the microgrid. Knowl.-Based Syst. 2022, 243, 108455. [Google Scholar] [CrossRef]
- Lin, C.; Liang, H.; Pang, A. A fast data-driven optimization method of multi-area combined economic emission dispatch. Appl. Energy 2023, 337, 120884. [Google Scholar] [CrossRef]
- Li, L.-L.; Lou, J.-L.; Tseng, M.-L.; Lim, M.K.; Tan, R.R. A hybrid dynamic economic environmental dispatch model for balancing operating costs and pollutant emissions in renewable energy: A novel improved mayfly algorithm. Expert Syst. Appl. 2022, 203, 117411. [Google Scholar] [CrossRef]
- Yu, X.; Duan, Y.; Luo, W. A knee-guided algorithm to solve multi-objective economic emission dispatch problem. Energy 2022, 259, 124876. [Google Scholar] [CrossRef]
- Sutar, M.; Jadhav, H. A modified artificial bee colony algorithm based on a non-dominated sorting genetic approach for combined economic-emission load dispatch problem. Appl. Soft Comput. 2023, 144, 110433. [Google Scholar] [CrossRef]
- Hassan, M.H.; Yousri, D.; Kamel, S.; Rahmann, C. A modified Marine predators algorithm for solving single-and multi-objective combined economic emission dispatch problems. Comput. Ind. Eng. 2022, 164, 107906. [Google Scholar] [CrossRef]
- Wu, P.; Zou, D.; Yu, N.; Zhang, G.; Kong, L. An improved NSGA-III for the dynamic economic emission dispatch considering reliability. Energy Rep. 2022, 8, 14304–14317. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hu, J. An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar] [CrossRef]
- Li, D.; Yang, C.; Zou, D. A nondominated sorting genetic algorithm III with three crossover strategies for the combined heat and power dynamic economic emission dispatch with or without prohibited operating zones. Eng. Appl. Artif. Intell. 2023, 123, 106443. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Xuan, K.; Ouyang, H. A NSGA-II variant for the dynamic economic emission dispatch considering plug-in electric vehicles. Comput. Ind. Eng. 2022, 173, 108717. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Multi-objective dynamic economic and emission dispatch with demand side management. Int. J. Electr. Power Energy Syst. 2018, 97, 334–343. [Google Scholar] [CrossRef]
- Mohapatra, P. Combined economic emission dispatch in hybrid power systems using competitive swarm optimization. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 8955–8971. [Google Scholar] [CrossRef]
- Xiong, G.; Shuai, M.; Hu, X. Combined heat and power economic emission dispatch using improved bare-bone multi-objective particle swarm optimization. Energy 2022, 244, 123108. [Google Scholar] [CrossRef]
- Shin, H.; Kim, W. Comparison of the centralized and decentralized environmentally constrained economic dispatch methods of coal-fired generators: A case study for South Korea. Energy 2023, 275, 127364. [Google Scholar] [CrossRef]
- Zhou, X.; Ma, Z.; Zou, S.; Zhang, J. Consensus-based distributed economic dispatch for Multi Micro Energy Grid systems under coupled carbon emissions. Appl. Energy 2022, 324, 119641. [Google Scholar] [CrossRef]
- Bhamidi, L.; Sivasubramani, S. Optimal planning and operational strategy of a residential microgrid with demand side management. IEEE Syst. J. 2019, 14, 2624–2632. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Dynamic economic and emission dispatch with renewable energy integration under uncertainties and demand-side management. Electr. Eng. 2022, 104, 2237–2248. [Google Scholar] [CrossRef]
- Nourianfar, H.; Abdi, H. Economic emission dispatch considering electric vehicles and wind power using enhanced multi-objective exchange market algorithm. J. Clean. Prod. 2023, 415, 137805. [Google Scholar] [CrossRef]
- Lv, D.; Xiong, G.; Fu, X. Economic emission dispatch of power systems considering solar uncertainty with extended multi-objective differential evolution. Expert Syst. Appl. 2023, 227, 120298. [Google Scholar] [CrossRef]
- Yang, D.; Xu, Y.; Liu, X.; Jiang, C.; Nie, F.; Ran, Z. Economic-emission dispatch problem in integrated electricity and heat system considering multi-energy demand response and carbon capture Technologies. Energy 2022, 253, 124153. [Google Scholar] [CrossRef]
- Carrillo-Galvez, A.; Flores-Bazán, F.; Parra, E.L. Effect of models uncertainties on the emission constrained economic dispatch. A prediction interval-based approach. Appl. Energy 2022, 317, 119070. [Google Scholar]
- Wu, M.; Xu, J.; Li, Y.; Zeng, L.; Shi, Z.; Liu, Y.; Wen, M.; Li, C. Low carbon economic dispatch of integrated energy systems considering life cycle assessment and risk cost. Int. J. Electr. Power Energy Syst. 2023, 153, 109287. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Malik, S.H.; Alvi, U.-E.; Hong, K.-S. Multi-area economic emission dispatch for large-scale multi-fueled power plants contemplating inter-connected grid tie-lines power flow limitations. Energy 2022, 261, 125178. [Google Scholar] [CrossRef]
- Basu, M. Multi-county combined heat and power dynamic economic emission dispatch incorporating electric vehicle parking lot. Energy 2023, 275, 127523. [Google Scholar] [CrossRef]
- Tang, X.; Li, Z.; Xu, X.; Zeng, Z.; Jiang, T.; Fang, W.; Meng, A. Multi-objective economic emission dispatch based on an extended crisscross search optimization algorithm. Energy 2022, 244, 122715. [Google Scholar] [CrossRef]
- Lai, W.; Zheng, X.; Song, Q.; Hu, F.; Tao, Q.; Chen, H. Multi-objective membrane search algorithm: A new solution for economic emission dispatch. Appl. Energy 2022, 326, 119969. [Google Scholar] [CrossRef]
- Sundaram, A. Multiobjective multi verse optimization algorithm to solve dynamic economic emission dispatch problem with transmission loss prediction by an artificial neural network. Appl. Soft Comput. 2022, 124, 109021. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Q.; Liu, M.; Yang, N.; Gao, R.; Sobhani, B. Optimal dispatch of dynamic power and heat considering load management, water pump system, and renewable resources by grasshopper optimization algorithm. J. Energy Storage 2023, 57, 106166. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Prashanth, G.R.; Joshi, S.S.; Narayanan, K.; Malik, H.; Márquez, F.P.G. Optimal fuzzy based economic emission dispatch of combined heat and power units using dynamically controlled Whale Optimization Algorithm. Appl. Energy 2022, 315, 119033. [Google Scholar] [CrossRef]
- Hao, W.-K.; Wang, J.-S.; Li, X.-D.; Song, H.-M.; Bao, Y.-Y. Probability distribution arithmetic optimization algorithm based on variable order penalty functions to solve combined economic emission dispatch problem. Appl. Energy 2022, 316, 119061. [Google Scholar] [CrossRef]
- Wang, H.; Fang, Y.; Zhang, X.; Dong, Z.; Yu, X. Robust dispatching of integrated energy system considering economic operation domain and low carbon emission. Energy Rep. 2022, 8, 252–264. [Google Scholar] [CrossRef]
- Sharifian, Y.; Abdi, H. Solving multi-zone combined heat and power economic emission dispatch problem considering wind uncertainty by applying grasshopper optimization algorithm. Sustain. Energy Technol. Assess 2022, 53, 102512. [Google Scholar] [CrossRef]
- Chaurasia, R.; Gairola, S.; Pal, Y. Technical, economic, and environmental performance comparison analysis of a hybrid renewable energy system based on power dispatch strategies. Sustain. Energy Technol. Assess 2022, 53, 102787. [Google Scholar] [CrossRef]
- Vigya; Raj, S.; Shiva, C.K.; Vedik, B.; Mahapatra, S.; Mukherjee, V. A novel chaotic chimp sine cosine algorithm Part-I: For solving optimization problem. Chaos Solitons Fractals 2023, 173, 113672. [Google Scholar] [CrossRef]
- Raj, S.; Mahapatra, S.; Babu, R.; Verma, S. Hybrid intelligence strategy for techno-economic reactive power dispatch approach to ensure system security. Chaos Solitons Fractals 2023, 170, 113363. [Google Scholar] [CrossRef]
- Mahapatra, S.; Raj, S. A novel meta-heuristic approach for optimal RPP using series compensated FACTS controller. Intell. Syst. Appl. 2023, 18, 200220. [Google Scholar]
- Raj, S.; Bhattacharyya, B. Weak bus determination and real power loss minimization using Grey wolf optimization. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Raj, S.; Bhattacharyya, B. Optimal placement of TCSC and SVC for reactive power planning using Whale optimization algorithm. Swarm Evol. Comput. 2018, 40, 131–143. [Google Scholar] [CrossRef]
- Dehedkar, S.N.; Raj, S. Determination of optimal location and Implementation of Solar Photovoltaic system using ETAP. In Proceedings of the 2022 IEEE 2nd International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur, India, 15–17 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Dey, B.; Raj, S.; Babu, R.; Chhualsingh, T. An approach to attain a balanced trade-off solution for dynamic economic emission dispatch problem on a microgrid system. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 1300–1311. [Google Scholar] [CrossRef]
- Rajasomashekar, S.; Aravindhababu, P. Biogeography based optimization technique for best compromise solution of economic emission dispatch. Swarm Evol. Comput. 2012, 7, 47–57. [Google Scholar] [CrossRef]
- Basak, S.; Bhattacharyya, B. Optimal scheduling in demand-side management based grid-connected microgrid system by hybrid optimization approach considering diverse wind profiles. ISA Trans. 2023, 139, 357–375. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Dey, B.; Misra, S.; Chhualsingh, T.; Sahoo, A.K.; Singh, A.R. A hybrid metaheuristic approach to solve grid centric cleaner economic energy management of microgrid systems. J. Clean. Prod. 2024, 448, 141311. [Google Scholar] [CrossRef]


| Objective | Optimization Models Used | System Description | Incorporation of RES | Year | Reference |
|---|---|---|---|---|---|
| Dynamic economic load dispatch | Bottlenose dolphin optimizer (BDO) | Twenty-nine functions including seven uni-modal functions | PV, WT | 2022 | [11] |
| Minimize operation cost and pollution | Improved mayfly optimization algorithm | Thermal power plant along with PV, WT, and BESS | PV, WT | 2022 | [13] |
| Minimize operation cost and pollution | Knee-guided algorithm (KGA) | 6, 10, and 11 generating units | NA | 2022 | [14] |
| Decreasing the emission of greenhouse gases and the fuel cost | Marine predators algorithm (MMPA) | 3, 5, 6, and 26 generating units | NA | 2022 | [16] |
| Fuel cost, pollutant emission, and system reliability | NSGA-III (I-NSGA-III) | 5, 10, and 30 units | NA | 2022 | [17] |
| Minimize the total generation cost in a dynamic economic dispatch problem | Distributed management algorithm for DEDP | 6 generating units | NA | 2023 | [18] |
| Multi-objective dynamic economic and emission dispatch | Multi-objective particle swarm optimization (MOPSO) | 6 generating units with DSM implementation | NA | 2018 | [21] |
| Reduction of carbon emissions, in addition to low cost and high efficiency | Competitive swarm optimization (CSO) algorithm | Thermal–solar (TS), thermal–wind (TW), and thermal–wind–solar (TWS) | PV, WT | 2022 | [22] |
| Environmental economic dispatch problem | Distributed augmented Lagrangian (ADAL) method | 4 multi-micro-energy grid systems | Battery | 2022 | [25] |
| Minimization of MG total annual cost and total annual emission | Multi-objective optimization | Residential MG consisting of 1000 smart homes with different DSM participation levels | PV, WT, BESS | 2019 | [26] |
| Generation side operational benefits and reduction in environmental pollution level | (NSGA-II) and Monte Carlo simulation (MCS) | DSM-based six thermal generating units, one solar-powered generator, and one wind-powered generator | 6 MT, along with 1 PV and WT | PV, WT | [27] |
| Reducing carbon emissions and improving wind power consumption | Multi-objective optimization | IEEE-30 bus power system and a 6 bus district heating system | WT | 2022 | [30] |
| Energy sustainability and climatic benefits | Crow search optimization algorithm (CSA) | Six benchmark test systems with multi-dimensional constraints | PV, WT | 2022 | [33] |
| Reduction in cost of economic operation and the pollutant emission | Crisscross search optimization (CSO) algorithm | IEEE-30 bus system, 40 generators system, and hydrothermal generation system | NA | 2022 | [35] |
| Reduce the overall generation cost of the system. | CSAJAYA | DSM-implemented two microgrid distribution systems | WT | 2023 | [50] |
| Function | Dim | Range | fmin | |
|---|---|---|---|---|
| 30 | [−100, 100] | 0 | Unimodal Benchmark Functions | |
| 30 | [−10, 10] | 0 | ||
| 30 | [−500, 500] | −418.9829 × 5 | Multimodal Benchmark Functions | |
| 30 | [−32, 32] | 0 | ||
| 30 | [0, 10] | −10.1532 | Fixed Dimension Multimodal Benchmark Functions | |
| 30 | [0, 10] | −10.5363 |
| Function | Unimodal benchmark functions | F1 | F2 | ||||
| Algorithm | CSA | AOA | CSAOA | CSA | AOA | CSAOA | |
| Best | 82.18 | 117.14 | 0.0096 | 4.19 | 3.58 | 0.01 | |
| Worst | 332.1716 | 1061.23 | 0.14 | 9.00 | 14.25 | 0.07 | |
| Mean | 150.3337 | 409.08 | 0.03 | 6.02 | 6.60 | 0.04 | |
| SD | 48.6507 | 246.52 | 0.02 | 1.13 | 2.50 | 0.01 | |
| Function | Multimodal benchmark functions | F3 | F4 | ||||
| Algorithm | CSA | AOA | CSAOA | CSA | AOA | CSAOA | |
| Best | −7320.13 | −5886.74 | −7915.45 | 5.42 | 4.17 | 0.01 | |
| Worst | −1967.51 | −3502.98 | −2871.64 | 9.53 | 20.55 | 0.12 | |
| Mean | −4414.72 | −4454.94 | −5513.72 | 6.76 | 8.88 | 0.04 | |
| SD | 1691.85 | 536.98 | 1076.63 | 0.81 | 5.46 | 0.01 | |
| Function | Fixed-dimension multimodal benchmark functions | F5 | F6 | ||||
| Algorithm | CSA | AOA | CSAOA | CSA | AOA | CSAOA | |
| Best | −10.14 | −9.81 | −10.15 | −10.53 | −10.40 | −10.53 | |
| Worst | −2.62 | −2.37 | −2.68 | −2.41 | −2.32 | −2.42 | |
| Mean | −7.29 | −6.03 | −6.41 | −8.52 | −8.04 | −6.23 | |
| SD | 3.55 | 2.95 | 3.79 | 3.36 | 2.57 | 3.83 | |
| Power-Only Generators i | 1 | CHP-Based Generators | 1 | 2 | 3 |
|---|---|---|---|---|---|
| a (USD/MW3) | 2.55 × 102 | a (USD/MW3) | 1.25 × 103 | 2.65 × 103 | 1.57 × 103 |
| b (USD/MW2) | 7.70 × 100 | b (USD/MW2) | 3.60 × 101 | 3.45 × 101 | 2.00 × 101 |
| c (USD/MW) | 1.72 × 10−3 | c(USD/MW) | 4.35 × 10−2 | 1.04 × 10−1 | 7.20 × 10−2 |
| d (USD) | 1.15 × 10−4 | d (USD) | 6.00 × 10−1 | 2.20 × 100 | 2.30 × 100 |
| α (tons/MW2) | 4.09 × 10−4 | α (tons/MW2) | 2.70 × 10−2 | 2.50 × 10−2 | 2.00 × 10−2 |
| β (tons/MW2) | −0.0005554 | β (tons/MW2) | 1.10 × 10−2 | 5.10 × 10−2 | 4.00 × 10−2 |
| γ (tons) | 6.49 × 10−4 | γ (tons) | 1.65 × 10−3 | 2.20 × 10−3 | 1.10 × 10−3 |
| Pj,max (MW) | 1.35 × 102 | ||||
| Pj,min (MW) | 3.50 × 101 |
| Without DSM | With DSM | |
|---|---|---|
| Total Demand (kW) | 7171 | 7171 |
| Mean Demand (kW) | 298.7 | 298.7 |
| Peak Demand (kW) | 399 | 334.62 |
| Reduction in Peak (%) | - | 16.14% |
| Load Factor | 0.7489 | 0.8929 |
| Without DSM | With DSM | |||
|---|---|---|---|---|
| Fitness Function | Cost (Thousands of USD) | Emission (tons) | Cost (Thousands of USD) | Emission (tons) |
| ECD | 296.744 | 286 | 293.098 | 287 |
| EMD | 359.919 | 54 | 367.956 | 31 |
| ECED (µ = 0.5) | 324.066 | 134 | 322.365 | 133 |
| Best | Worst | Mean | Hits | STD | Time (s) | |
|---|---|---|---|---|---|---|
| CSA [S] | 0.37458 | 0.39503 | 0.380715 | 21 | 0.009532 | 8.0068 |
| AOA [S] | 0.37299 | 0.38851 | 0.378163 | 20 | 0.007441 | 7.8993 |
| CSAOA [P] | 0.37282 | 0.37662 | 0.373707 | 23 | 0.001635 | 7.0934 |
| Unit | ai | bi | ci | di | Pi,min | Pi,max |
|---|---|---|---|---|---|---|
| USD/MW | USD/MW | USD/MW | USD/MW | (MW) | (MW) | |
| P1 | 1.00 × 10−1 | 9.20 × 10−2 | 1.45 × 10−1 | −1.36 × 10−1 | 5.00 × 10−1 | 2.00 × 100 |
| P2 | 4.00 × 10−1 | 2.50 × 10−2 | 2.20 × 10−1 | −3.50 × 10−3 | 2.00 × 10−1 | 8.00 × 10−1 |
| P3 | 6.00 × 10−1 | 7.50 × 10−2 | 2.30 × 10−1 | −8.10 × 10−2 | 1.50 × 10−1 | 5.00 × 10−1 |
| P4 | 2.00 × 10−1 | 1.00 × 10−1 | 1.35 × 10−1 | −1.45 × 10−2 | 1.00 × 10−1 | 5.00 × 10−1 |
| P5 | 1.30 × 10−1 | 1.20 × 10−1 | 1.15 × 10−1 | −9.80 × 10−3 | 1.00 × 10−1 | 5.00 × 10−1 |
| P6 | 4.00 × 10−1 | 8.40 × 10−2 | 1.25 × 10−1 | −7.56 × 10−2 | 1.20 × 10−1 | 4.00 × 10−1 |
| Unit | Emission Coefficients of SO2 | Penalty Factor of SO2 | |||
|---|---|---|---|---|---|
| αSO2 | βSO2 | γSO2 | δSO2 | hs | |
| tons/kW | tons/kW | tons/kW | tons/kW | tons/kW | |
| 1 | 5.0000 × 10−4 | 1.5000 × 10−1 | 1.7000 × 101 | −9.0000 × 101 | 1.0852 × 100 |
| 2 | 1.4000 × 10−3 | 5.5000 × 10−2 | 1.2000 × 101 | −3.0500 × 101 | 1.0616 × 100 |
| 3 | 1.0000 × 10−3 | 3.5000 × 10−2 | 1.0000 × 101 | −8.0000 × 101 | 2.1051 × 100 |
| 4 | 2.0000 × 10−3 | 7.0000 × 10−2 | 2.3500 × 101 | −3.4500 × 101 | 5.9760 × 10−1 |
| 5 | 1.3000 × 10−3 | 1.2000 × 10−1 | 2.1500 × 101 | −1.9750 × 101 | 6.7720 × 10−1 |
| 6 | 2.1000 × 10−3 | 8.0000 × 10−2 | 2.2500 × 101 | −2.5600 × 101 | 6.1920 × 10−1 |
| Unit | Emission Coefficients of NOx | Penalty Factor of NOx | |||
|---|---|---|---|---|---|
| αNOX | βNOX | γNOX | δNOX | hn | |
| tons/kW | tons/kW | tons/kW | tons/kW | tons/kW | |
| 1 | 1.2000 × 10−3 | 5.2000 × 10−2 | 1.8500 × 101 | −2.6000 × 101 | 9.4070 × 10−1 |
| 2 | 4.0000 × 10−4 | 4.5000 × 10−2 | 1.2000 × 101 | −3.5000 × 101 | 1.4962 × 100 |
| 3 | 1.6000 × 10−3 | 5.0000 × 10−2 | 1.3000 × 101 | −1.5000 × 101 | 1.3870 × 100 |
| 4 | 1.2000 × 10−3 | 7.0000 × 10−2 | 1.7500 × 101 | −7.4000 × 101 | 8.3080 × 10−1 |
| 5 | 3.0000 × 10−4 | 4.0000 × 10−2 | 8.5000 × 100 | −8.9000 × 101 | 2.1705 × 100 |
| 6 | 1.4000 × 10−3 | 2.4000 × 10−2 | 1.5500 × 101 | −7.5000 × 101 | 1.0930 × 100 |
| Unit | Emission Coefficients of CO2 | Penalty Factor of CO2 | |||
|---|---|---|---|---|---|
| αCO2 | βCO2 | γCO2 | δCO2 | hc | |
| tons/kW | tons/kW | tons/kW | tons/kW | tons/kW | |
| 1 | 1.5000 × 10−3 | 9.2000 × 10−2 | 1.4000 × 101 | − 16.00 | 7.8230 × 10−1 |
| 2 | 1.4000 × 10−3 | 2.5000 × 10−2 | 1.2500 × 101 | − 93.50 | 1.1895 × 100 |
| 3 | 1.6000 × 10−3 | 5.5000 × 10−2 | 1.3500 × 101 | − 85.00 | 1.4356 × 100 |
| 4 | 1.2000 × 10−3 | 1.0000 × 10−2 | 1.3500 × 101 | − 24.50 | 1.1333 × 100 |
| 5 | 2.3000 × 10−3 | 4.0000 × 10−2 | 2.1000 × 101 | − 59.00 | 7.4560 × 10−1 |
| 6 | 1.4000 × 10−3 | 8.0000 × 10−2 | 2.2000 × 101 | − 70.00 | 7.1580 × 10−1 |
| Without DSM | With 40% DSM | |
|---|---|---|
| Peak Load Demand (MW) | 225 | 207.385 |
| Ave. Load Demand (MW) | 186.56 | 186.56 |
| Total Load Demand (MW) | 4477.5 | 4477.4990 |
| Load Factor | 0.8291 | 0.8996 |
| Reduction in Peak (%) | Reference | 7.829% |
| Cost and Emission Profiles | Without DSM | With DSM | |
|---|---|---|---|
| ECD | Cost minimization (thousands of USD) | 76.085 | 74.774 |
| EMD | Emission minimization (tons) | 240 | 236 |
| CEED (PPF) | Cost (thousands of USD) | 314.678 | 310.264 |
| Emission (tons) | 256 | 254 | |
| CEED (FP) | Cost (thousands of USD) | 90.775 | 92.192 |
| Emission (tons) | 249 | 244 | |
| ECED (µ = 0.5) | Cost (thousands of USD) | 78.304 | 78.064 |
| Emission (tons) | 246 | 243 |
| CO2 Minimum | SO2 Minimum | NOx Minimum | Minimum Emission | |
|---|---|---|---|---|
| CO2 | 75 | 80 | 88 | 78 |
| SO2 | 93 | 84 | 97 | 86 |
| NOx | 77 | 75 | 66 | 71 |
| Overall | 246 | 240 | 252 | 236 |
| Minimum Attained Cost (USD) | Maximum Attained Cost (USD) | Average Attained Cost (USD) | Standard Deviations | Hits to Minimum Cost | Execution Time (s) | |
|---|---|---|---|---|---|---|
| CSA | 74,792 | 74,829 | 74,806.80 | 18.4361 | 18 | 5.06 |
| AOA | 74,775 | 74,822 | 74,789.10 | 21.9063 | 21 | 4.05 |
| CSAOA | 74,774 | 74,782 | 74,775.60 | 3.2547 | 24 | 3.20 |
| Scenario | fl | z | Cost with DSM (USD) | Execution Time (s) |
|---|---|---|---|---|
| 1 | 1.5 | 1 | 74,774.7027 | 4.8003 |
| 2 | 2 | 5 | 74,774.6995 | 4.8003 |
| 3 | 2.5 | 9 | 74,774.6984 | 4.8003 |
| 4 | 1.5 | 1 | 74,774.7054 | 3.2005 |
| 5 | 2 | 5 | 74,774.6986 | 3.2005 |
| 6 | 2.5 | 9 | 74,774.6987 | 3.2005 |
| 7 | 1.5 | 1 | 74,774.7075 | 9.6006 |
| 8 | 2 | 5 | 74,774.9023 | 9.6006 |
| 9 | 2.5 | 9 | 74,774.6983 | 9.6006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, B.; Sharma, G.; Bokoro, P.N. A Novel Hybrid Crow Search Arithmetic Optimization Algorithm for Solving Weighted Combined Economic Emission Dispatch with Load-Shifting Practice. Algorithms 2024, 17, 313. https://doi.org/10.3390/a17070313
Dey B, Sharma G, Bokoro PN. A Novel Hybrid Crow Search Arithmetic Optimization Algorithm for Solving Weighted Combined Economic Emission Dispatch with Load-Shifting Practice. Algorithms. 2024; 17(7):313. https://doi.org/10.3390/a17070313
Chicago/Turabian StyleDey, Bishwajit, Gulshan Sharma, and Pitshou N. Bokoro. 2024. "A Novel Hybrid Crow Search Arithmetic Optimization Algorithm for Solving Weighted Combined Economic Emission Dispatch with Load-Shifting Practice" Algorithms 17, no. 7: 313. https://doi.org/10.3390/a17070313
APA StyleDey, B., Sharma, G., & Bokoro, P. N. (2024). A Novel Hybrid Crow Search Arithmetic Optimization Algorithm for Solving Weighted Combined Economic Emission Dispatch with Load-Shifting Practice. Algorithms, 17(7), 313. https://doi.org/10.3390/a17070313









