Abstract
A metaheuristic algorithm named the Crystal Structure Algorithm (CrSA), which is inspired by the symmetric arrangement of atoms, molecules, or ions in crystalline minerals, has been used for the accurate modeling of Mono Passivated Emitter and Rear Cell (PERC) WSMD-545 and CS7L-590 MS solar photovoltaic (PV) modules. The suggested algorithm is a concise and parameter-free approach that does not need the identification of any intrinsic parameter during the optimization stage. It is based on crystal structure generation by combining the basis and lattice point. The proposed algorithm is adopted to minimize the sum of the squares of the errors at the maximum power point, as well as the short circuit and open circuit points. Several runs are carried out to examine the V-I characteristics of the PV panels under consideration and the nature of the derived parameters. The parameters generated by the proposed technique offer the lowest error over several executions, indicating that it should be implemented in the present scenario. To validate the performance of the proposed approach, convergence curves of Mono PERC WSMD-545 and CS7L-590 MS PV modules obtained using the CrSA are compared with the convergence curves obtained using the recent optimization algorithms (OAs) in the literature. It has been observed that the proposed approach exhibited the fastest rate of convergence on each of the PV panels.
1. Introduction
Owing to the urgent need to protect the environment from pollution, scientists have been working hard to build a wide variety of accurate models that are intended to provide efficient Renewable Energy (RE) substitutes for traditional energy obtained from fossil fuels [1,2]. One of the main issues in environmental difficulties is the emergence of environmental pollution due to the use of traditional energy sources. As a potential remedy for this issue, using alternative RE sources has attracted much attention lately. Nuclear power, wind, solar, tidal, wave, and other RE sources are commercially feasible. The sources indicated above offer a wide range of practical applications in areas including agriculture, hot water distribution, wireless sensors, and photovoltaic (PV) systems. In contrast to the consequences of fossil fuels, solar power has gained substantial attention recently from institutions, governments, and academics for its long-lasting benefits in producing electricity via photovoltaic energy while avoiding environmental harm [1,2,3]. PV technology is of great significance in technology and scientific research since it provides a comprehensive future vision. The significance of its contribution to RE, energy independence, climate change mitigation, and economic prosperity cannot be exaggerated. Through the inclusion of PV in scientific research, researchers and statisticians may actively contribute to the development of solar cell technology, therefore facilitating further advancements in the sector and promoting a future that relies on sustainable and environmentally friendly energy sources. In order to fully harness the potential of solar energy, reduce prices, and establish a sustainable and resilient energy future, it is imperative to maintain ongoing scientific research and innovation in PV technology.
PV systems efficiently convert solar energy into electrical power, which is essential for the global growth of RE [4,5]. However, the effective energy delivery of PV systems is hampered by external factors, such as dust deposition in the vast networks of the PV grid. Airborne particles, erratic weather patterns, and temperature fluctuations all negatively impact solar cell performance and reduce their overall efficiency. One way to potentially address these issues is to find precise PV models that maximize the efficiency of solar cell energy output. In order to use a PV system efficiently, it is first necessary to know the system’s current–voltage (I-V) characteristics, in both theory and practice. This requires accurate mathematical modeling of the system. The most common versions of solar photovoltaic systems may be described as follows: a current source paralleled with a diode and two resistors, one of which is linked in series and the other in shunt [6].
To create a Single-Diode Model (SDiM) for PV parallel circuits, as seen in Figure 1, one must combine a single diode with two resistors. The addition of more diodes to the PV models increases the number of unknown factors, which raises the complexity of the model itself. Within a PV-comparable circuit, the SDiM includes five unknown features associated with PV behavior. In contrast, the Double-Diode Model (DDiM), which is created by pairing two diodes as seen in Figure 2, has seven unknown parameters. Subsequent models also adhere to a similar pattern. Numerous factors, such as saturation current, series/parallel resistance, shunt-resistant current, and shunt resistor, are included in diode models. It is necessary to compute and extract these unknown parameters from the information provided by the I–V curve. Since inaccurate predictions of these factors might result in significant differences in the manufacturing process, careful consideration of these components is necessary for solar cell process models to be effective. As a result, estimating these properties is an important task that improves PV system optimization. Photovoltaic systems often rely on implicit, nonlinear, multi-variable, and multi-modal equations in their mathematical models [7].
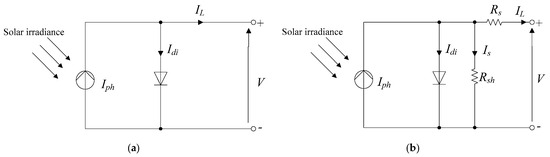
Figure 1.
SDiM of (a) ideal solar PV cell, (b) practical solar PV cell.
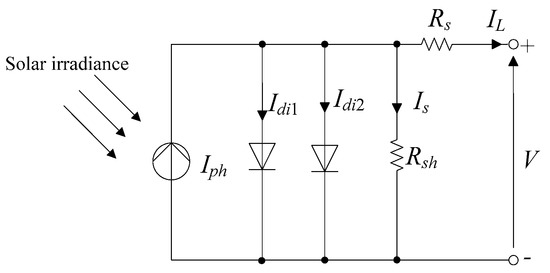
Figure 2.
DDiM of solar PV cell.
As per the researchers’ findings, solving PV models remains a difficult problem. They have proposed many methods to solve this, with the goals of timeliness, precision, and reliability, for extracting, evaluating, and simulating PV parameters [4,5,8]. Over the past few decades, there have been numerous efforts to understand, optimize, and estimate the photovoltaic parameters derived from various mathematical models of PV systems. The complexity of non-linearities in PV models has been addressed and evaluated using various techniques published in academic works with the goals of efficiency and accuracy. It has been discovered that simplifying equations negatively affects the precision and usefulness of the outcomes. Recent research [4] found that, in comparison to the I-V characteristic technique, this strategy’s capacity to reliably extract parameters was limited. In order to determine the characteristics of the PV system, the technique that uses I-V characteristic curves seeks to lessen the differences between the current data produced by simulations and the current data acquired through tests. By applying this process, the parameters can be determined and resolved in a variety of ways.
Numerous scholars have created a range of models of PV systems in the existing literature, such as the SDiM and DDiM. Furthermore, the efficiency of the photovoltaic model relies on undisclosed internal traits. It is difficult to maintain and assess all the unknown factors because of deterioration, aging, and erratic operating states. It is impossible to design, estimate, simulate, and optimize PV modules without first determining the relevant electrical parameters. Consequently, research is being conducted to determine how well swarm optimization techniques work for measuring PV system characteristics. Analytical methods [9] produce specific approximations or oversimplified assumptions while disregarding accuracy compromises. However, to compute the current and voltage corresponding to the maximum power output, this analytical model has been streamlined by disregarding the effects of parallel and series resistances. The Lagrange multiplier method was proposed in [10] for the SDiM/DDiM to optimize the power outputs of PV solar cells. The essential details were taken from the datasheet provided by the manufacturer and reduced in [11], where the power first derivative was used to produce a boundary need for a zero-voltage state. In addition, the I-V curve’s four random locations and their slopes are shown in [12] in order to precisely extract the SDiM parameters without analytical approximations or simplifications. Nevertheless, such an analytical method is constrained to standard testing situations. This fails when they change and contain many calculations [13].
Conversely, numerical methods have been introduced, such as deterministic and metaheuristic algorithms. The deterministic approach may produce local optima if the beginning values are inaccurate, and the real model may struggle to meet the constraints of the objective function equation [14]. On the other hand, the PV model parameters can be found efficiently and straightforwardly using metaheuristic methods. Consequently, metaheuristic techniques have been studied to address parameter extraction. For electric solar PV systems, the gorilla troops optimizer [GTO] [15], dandelion OA [DOA] [16], and artificial hummingbird optimizer [AHBO] [17] have been developed. Gradient-based optimization using a rank-based strategy and logistic map has been expanded to SM55 and KC200GT using the SDiM and DDiM [18]. Differential Evolution (DE) has been used in numerous studies [19,20] to address the challenge of identifying parameters in the PV model. In [21], a DE was combined with a Teaching–Learning-Based Optimizer (TLBO) while accounting for the learners’ ranking likelihood. For the SDiM and DDiM, a similar DE with a reversible learning process, multi-population tactics, and mutation method has been shown in [22]. An enhanced TLBO was developed in [23] using several instructional strategies and executed in a comparative manner on both the SDiM and DDiM. Both the RTC France solar cell and the Photowatt-PWM201 PV cell had their parameters estimated through two straightforward, direct methods: Rao-2 and Rao-3 [24]. The backtracking search technique was used as part of an elite strategy in [25] and was applied to both the SDiM and DDiM. The Nelder–Mead simplex (horizontal and vertical) crossovers were combined with Harris Hawks optimization in [26] and used on KC200GT, SM55, and ST40, encompassing the DDiM and SDiM. The Imperialist competitive algorithm was used in [27] to estimate the ideal PV parameters. Considering different electrical models based on the number of diode branches, the JAYA method for PV parameter extraction has been modified by incorporating a chaotic map, as detailed in [28]. This revised method is coupled with a learning approach grounded in an elite opponent process [29]. An orthogonal learning strategy-based grey Wolf method has been demonstrated in [30] to identify the unknowns in various solar PV models. A novel two-step method for deriving the SDiM parameters of PV modules from experimental data on power-voltage characteristics was presented in [31]. In the literature [32,33,34,35,36], we can observe more hybrid solar parameter extraction algorithms. The characteristics of the InGaP/InGaAs/Ge TJS PV panel were extracted using the moth search [37], water cycle [38], and heap optimizer [39] approaches, taking into account the Triple-Junction (TJS) PV panel. The performances of a TJSC-based PV module under various temperature and irradiation conditions were evaluated and verified in [37,38,39] and compared to several alternative optimizing techniques. Various metaheuristic and analytical approaches used for solar parameter extraction are listed in Table 1.

Table 1.
An overview of the metaheuristic and analytical approaches used in the literature.
Several strategies have been suggested to address the problem of acquiring the parameters of the PV model. Nevertheless, precisely and dependably establishing the values of these factors continues to be a substantial difficulty. The “No-Free-Lunch” principle hypothesis [7,40,41] states that no algorithm can solve optimization problems optimally. This hypothesis provides a possible explanation for the question at hand. This phenomenon occurs because even while an approach may show remarkable effectiveness in solving a specific problem, there is no guarantee that it will achieve comparable levels of success in addressing other challenges. Hence, it is crucial to persist in carrying out studies in order to ascertain a potent meta-heuristic strategy. Many artistic works are influenced by the concept of “No-Free-Lunch,” which also allows for the modification of current algorithms to solve new issues.
Inspired by the principles behind crystal structure development from adding the basis to the lattice points, Talatahari et al. [42] proposed a novel metaheuristic optimization approach named CrSA. The algorithm’s unique quality lies in its parameter-free design, enabling the adjustment of exploration and exploitation stages within the primary loop. Moreover, its position updating process for candidate solutions is segmented into four distinct phases, achieving exceptional results by effectively catering to both local and global search requirements across the entirety of the search space.
In this work, we use the CrSA to accurately model Mono PERC solar PV modules. The proposed algorithm is a succinct and parameter-free method that does not require the determination of any inherent parameters during the optimization phase. It operates by merging the basis and lattice point to generate a crystal structure. The proposed algorithm is adopted to minimize the sum of the squares of the errors at the maximum power point, as well as at the short circuit and open circuit points. Several runs are carried out to examine the V-I characteristics of the PV panels under consideration and the nature of the derived parameters. The parameters generated by the proposed technique offer the lowest error over several executions, indicating that it should be implemented in the present scenario.
The main aims of this study are:
- This study aims to introduce a new nature-inspired intelligence OA named CrSA, which will be used to estimate the parameters of Mono PERC solar PV modules.
- The mathematical modeling of the SDiM and DDiM of the Mono PERC solar PV modules has been analyzed.
- The error between practical values and simulation results has been examined for high accuracy at short circuit, open circuit, and maximum power points for the PV modules under consideration.
- The proposed method has been compared with the recent OAs in the literature by using convergence analysis.
The structure of the paper is as follows: Section 2 provides an overview of the suggested CrSA. Section 3 presents the mathematical modeling of the SDiM and DDiM. In Section 4, the objective function formulation and the application of the CrSA for solar PV module parameter extraction are detailed. Section 5 offers an analysis and discussion of the simulation outcomes. Section 6 concludes with final remarks.
2. Crystal Structure Algorithm
This study offers a unique CrSA approach that improves the derivation of PV parameter values for several PV models. The CrSA is a new metaheuristic optimization method drawn from the principles governing the formation of crystal structures. Inspired by the principle of symmetric arrangement of constituents in crystalline minerals, the CrSA was developed by Siamak Talatahari et al. [42].
The following are the key features of the CrSA:
- 1
- No internal parameters are required: The CrSA does not require any internal parameters to be tuned in its optimization process.
- 2
- Position updating process: In its position updating process, the candidate solutions are updated in four main phases, ensuring that very efficient searches of local and global areas of the search space are conducted.
The CrSA has been designed to solve complicated optimization problems in an efficient and accurate manner. Its competitive performance shows applicability in a wide range of domains.
Mathematical Modelling of the CrSA
The mathematical model of the CrSA is described, incorporating the fundamental principles of crystals with appropriate adjustments. In this approach, every potential solution of the optimization method is regarded as an individual crystal within the space. For the purpose of iteration, a specific quantity of crystals is chosen randomly for initialization.
Here, n represents the quantity of crystals and d represents the problem’s dimension. The beginning placements of these crystals are randomly assigned throughout the search space as follows:
The beginning position of the crystals is determined by the value of . The lowest and highest allowable values for the jth decision variable of the ith candidate solution are represented as and , respectively. represents a random number ranging from 0 to 1.
According to the definition of “basis” in crystallography, all of the crystals at the corners are regarded as the major crystals (), which are chosen at random by taking into account the crystals that were first generated. It should be mentioned that the current is subtracted from each step’s random selection procedure. The best-configured crystal is represented by , and the mean values of crystals chosen at random are represented by .
Candidate solution positions in the search space are adjusted by employing fundamental lattice principles. This updating process consists of four distinct types:
- “Cubicle” with :
- “Cubicle” with :
- “Cubicle” with :
- “Cubicle” with and :
In the given set of four equations, represents the new position, represents the old position, and , , , and are random numerical values.
This method incorporates exploration and exploitation, two essential components of metaheuristics. This is achieved through Equations (3) to (4), where simultaneous local and global searches are undertaken. To address the issue of solution variables that do not satisfy the boundary constraints, a mathematical flag is introduced. This flag triggers a modification of the boundary for the variables that fall beyond the specified range. The termination criterion is determined by the maximum number of iterations at which the optimization process is halted after a predetermined number of iterations. The algorithm’s pseudo-code is shown in Table 2.

Table 2.
Pseudo code of the CrSA.
3. Mathematical Modeling of PV Models
The first step in PV modeling is determining the model’s parameters, which may be achieved by analyzing experimental data. Following model development, the model may be used to examine how the temperature, irradiance, and load affect the PV system’s efficiency. The models can also be used to maximize the PV systems’ efficiency. This is figuring out how to best align and arrange solar cells to produce the most energy possible.
PV cells, also referred to as solar cells, are electronic devices specifically engineered to transform solar radiation into electrical energy. These devices are constructed using semiconductor components, such as silicon. These materials have the capacity to absorb photons released by sunshine, therefore releasing electrons and enabling the movement of electric current. Solar panels are frequently joined in series and parallel combinations to increase their voltage and electrical output. Solar panels have a wide range of uses, including generating energy for household and business reasons, providing power in remote locations, and enabling the operation of portable electronic equipment such as calculators and mobile phones. Solar cells are continuously improving in terms of efficiency and cost-effectiveness, making them a more appealing choice for capturing clean and sustainable energy. Equivalent circuit models are used to depict every aspect of the I-V spectrum of a cell or component. These models consist of a set of sequential functions that are calculated based on established operating restrictions.
A mathematical model may accurately depict the output properties of the PV model. This will demonstrate the biological processes that occur within the cell of the module. The SDiM and DDiM models are widely utilized. The characteristics of the PV cell are retrieved by assuming that the cells have equivalent characteristics and operate under similar circumstances. This criterion is used to formulate the objective functions for the model’s description.
3.1. Single-Diode Model
The SDiM is recognized as a fundamental circuit type that is regularly utilized and built upon physical principles. The SDiM is commonly used because of its ease of integration and thoroughness in characterizing the intrinsic characteristics of stationary solar cells.
Figure 1a illustrates the single-diode model used to represent a solar cell. The photon current () generated in the solar cell as a result of solar irradiance is transferred to the load after being extracted. The current flowing through a diode is known as (). In addition, the circuit model can be adjusted according to the modifications illustrated in Figure 1b. These modifications take into account the combined resistance of contacts, metal grids, and p and n layers, represented by the series resistance (), as well as the leakage current of the p-n junction, which is accounted for by the shunt resistance ().
Through the application of Kirchhoff’s current law (KCL), the relationship between the output current (), , diode current (), and shunt-resistor current () can be expressed as
The mathematical equations for and are expressed as
Through the utilization of Equations (8) and (9), Equation (7) undergoes modification as
where denotes the saturation current, signifies the diode quality factor, represents the output voltage, τ represents the temperature of the p-n junction (in kelvin), represents the electron charge, denotes the number of solar cells in series, and stands for the Boltzmann constant.
Equation (10) indicates that the parameters , , and need to be recovered from the SDiM.
Under open circuit (OC) circumstances (), Equation (8) is changed to
Equation (10) is changed under short circuit (SC) circumstances () to
Through utilizing Equations (9) and (10), the expression for is obtained as
At the maximum power point (MPP) (), Equation (8) is written as
3.2. Double-Diode Model
One limitation of the SDiM is its inability to consider the impact of ongoing recombination losses in the reduction region. In addressing this issue, the researchers introduced the DDiM, known for its ability to calculate recombination current losses in the depletion zone by incorporating an extra diode. The DDiM is thought to provide superior accuracy in comparison to the SDiM. The photoproduced current source in the DDiM is realized by employing a diode pair. The D1 diode generates the propagation current in the p-n junction, whereas the D2 diode handles the effects of recombination in the junction area related to space freightage.
To enhance the precision of the I-V characteristics of the PV panel, it is advisable to utilize the DDiM instead of the SDiM. The DDiM takes into account the impact of recombination current loss in the depletion area resulting from the recombination carriers. The solar PV module-equivalent circuit, represented as a DDiM, is illustrated in Figure 2.
The output current () can be expressed using KCL as
where and represent diode currents, which can be expressed in terms of saturation currents and , as well as diode quality factors and , as shown:
By employing Equations (9), (16), and (17), Equation (15) is altered as
Equation (18) indicates that the following seven parameters need to be derived from the DDiM: , , , and .
Under OC circumstances (), Equation (16) is changed as
Equation (18) is changed under SC circumstances () as
At the MPP ( ), Equation (18) is written as
4. Application of the CrSA for Parameter Extraction of the Solar Module
The proposed CrSA can be used to evaluate various parameters in both the SDiM and DDiM of solar PV modules.
4.1. Formulation of the Objective Function
The main goal of the extraction phase in determining coefficients for different PV models using OAs is to assess the efficacy of each parameter and determine the most ideal value for each parameter in the given context. This issue is under investigation. This strategy aims to reduce the discrepancy between estimated and measured current data by minimizing the error to the greatest extent possible. It is necessary to design and optimize the objective function to assess the suggested coefficients. The goal function is formulated to minimize the disparity between the estimated and measured current values to the greatest feasible degree. The existing literature focuses solely on achieving accuracy at the MPP. However, this study’s objective function is designed to ensure accuracy at three different operating points: the OC, SC, and MPP.
In order to create an accurate model, the minimizing of errors in these places is taken into consideration. For the SDiM, the errors at the OC (), SC (), and MPP () can be measured using Equations (11), (12), and (14). For the DDiM, this can be achieved using Equations (19)–(21). To extract the parameters of a solar PV module and obtain the optimal parameters, the objective function is formulated as net error , which is the sum of the squares of , , and . The steps to determine errors for a model with a single diode are as follows: (31)–(33).
For the SDiM:
Error at the OC point
Error at the SC point
Error at the MPP
Therefore, the objective function that has to be minimized for the SDiM is as follows
For the DDiM:
Error at the OC point
Error at the SC point
Error at the MPP
Therefore, the objective function that has to be minimized for the DDiM is as follows
4.2. Procedure for Estimating PV Module Parameters
The steps below outline how to use the proposed algorithm to compute the parameters of a solar PV module:
- Set the initial values for the variables of the solar PV module and the algorithm according to the information provided in Table 1, Table 2 and Table 3.
 Table 3. Datasheet parameters of the Mono PERC solar cell.
Table 3. Datasheet parameters of the Mono PERC solar cell. - Validate the upper limit of the iteration count before proceeding to the subsequent phases. If the condition is not met, proceed to Step 7.
- Consider the SDiM and DDiM for the solar PV module under discussion using Equations (7)–(21).
- Utilize Equations (3)–(6) to execute the proposed CrSA for the study work being examined.
- Minimize the overall error, as defined by Equations (25) and (29), for Steps 3 and 4 in each iteration.
- Increment the iteration count and go to Step 2.
- Conduct a comprehensive analysis of different solar PV modules and identify the optimal values for the corresponding circuit parameters.
5. Simulation Results
The suggested technique for extracting parameters from solar PV modules has been evaluated using the Mono PERC solar PV module. Table 3 lists the datasheet for the solar PV panel that was chosen and Table 4 lists the SDiM and DDiM parameter constraints. The primary goal of the study is to identify the five and seven parameters of the SDiM and DDiM of the PV panel provided. After using the suggested procedure across 500 iterations for 20 cycles of testing, the findings are detailed below.

Table 4.
Limits of SDiM and DSiM parameters.
5.1. Results for the SDiM of Mono PERC Solar PV Modules
The parameter estimation process utilizes Mono PERC WSMD-545 and CS7L-590 MS solar PV modules. Table 5 presents the optimal parameters of the SDiM of the Mono PERC WSMD-545 solar PV module obtained from 20 runs, while Figure 3 illustrates the outcomes of the simulation. Among the five parameters in the SDiM, , , and are optimized using the CrSA method, while and are obtained from the derived analytical equations.

Table 5.
The optimal estimated parameters for the SDiM of the Mono PERC WSMD-545 solar PV module using the CrSA and the analytical technique.
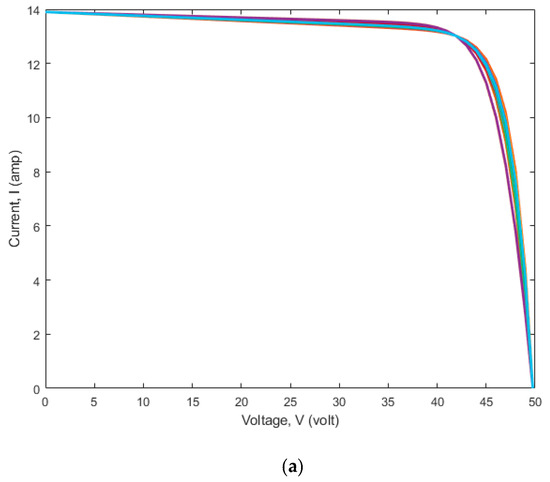
Figure 3.
(a) V-I characteristics of the SDiM of the Mono PERC WSMD-545 solar PV panel; (b) optimal solution set for parameter extraction of the SDiM of the Mono PERC WSMD-545 solar PV panel.
Table 6 presents the optimal parameters of the SDiM of the Mono PERC CS7L-590 MS solar PV module obtained from 20 runs, while Figure 4 illustrates the outcomes of the simulation. Among the five parameters in the SDiM, , , and are optimized using the CrSA method, while and are obtained from the derived analytical equations.

Table 6.
The optimal estimated parameters for the SDiM of the Mono PERC CS7L-590 MS solar PV module using the CrSA and the analytical technique.
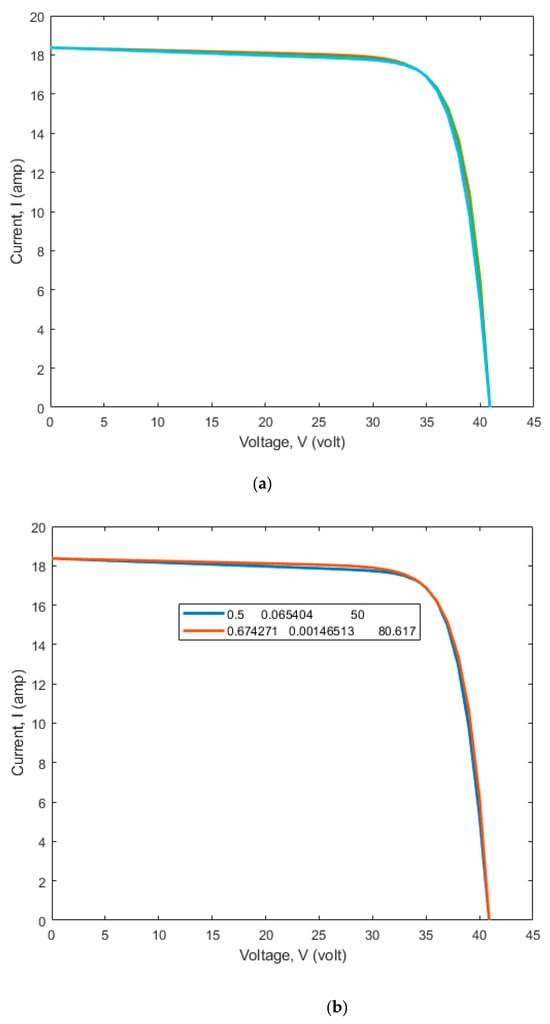
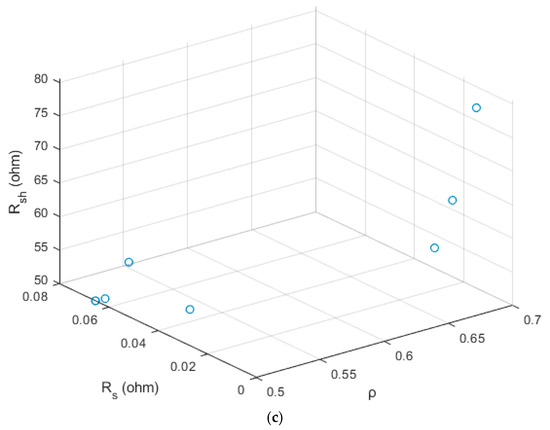
Figure 4.
(a) V-I characteristics of the SDiM of the Mono PERC CS7L-590 MS solar PV panel; (b) V-I characteristics with maximum and of the SDiM of the Mono PERC CS7L-590 MS solar PV panel; (c) optimal solution set for parameter extraction of the SDiM of the Mono PERC CS7L-590 MS solar PV panel.
Figure 3 and Figure 4 demonstrate that the 20 V-I characteristics intersect at three specific points, which is the main consideration for developing the objective function. The error at three places is nearly 10−14; however, in most investigations, the error is only considered at the MPP. Consequently, all 20 trials yield practically indistinguishable V-I characteristics when considering different possible parameter extractions. Among the five parameters in the SDiM, , , and are optimized using the CrSA method, while the and are obtained from the derived analytical equations. The V-I curves acquired in each run are optimum due to the optimized parameters within the defined search space bounds. This is because the provided approach is metaheuristic. The values of and determine the slope of the curve at the OC and SC locations. The data clearly indicate that the two curves with the greatest values of and satisfy the key criteria by intersecting at all three critical feature points.
5.2. Results for the DDiM of Mono PERC Solar PV Modules
Among the seven parameters in the DDiM, , , , , and are optimized using the CrSA method, while and are obtained from the derived analytical equations. Table 7 presents the optimal parameters of the DDiM of the Mono PERC WSMD-545 obtained from 20 runs, while Figure 5 illustrates the outcomes of the simulation.

Table 7.
The optimal estimated parameters for the DDiM of the Mono PERC solar PV module using the CrSA and the analytical technique.
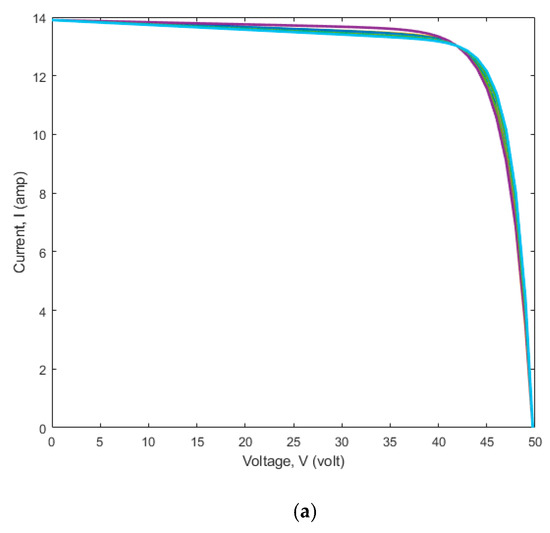
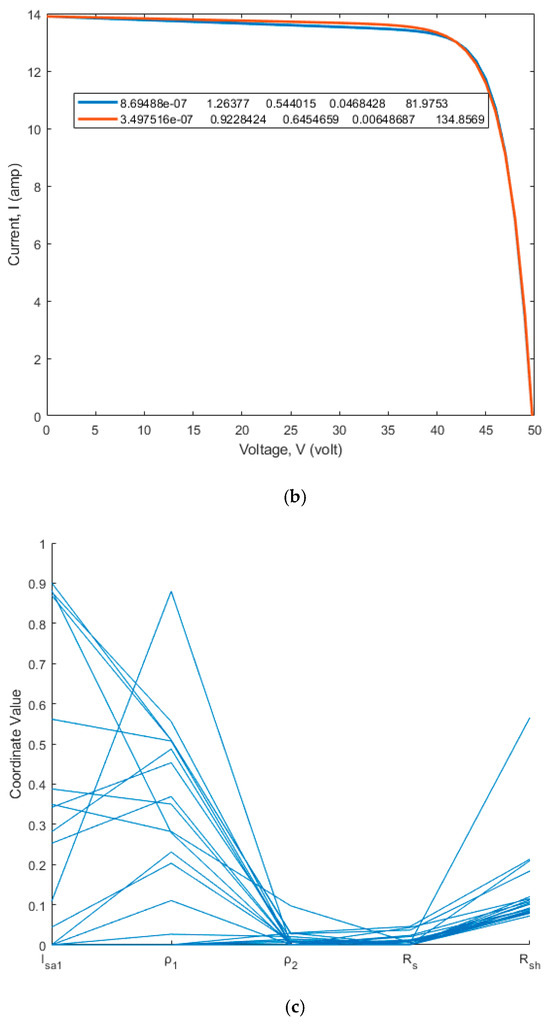
Figure 5.
(a) V-I characteristics of the DDiM of the Mono PERC WSMD-545 solar PV panel; (b) V-I characteristics with maximum and of the DDiM of the Mono PERC WSMD-545 solar PV panel; (c) optimal solution set for parameter extraction of the DDiM of the Mono PERC WSMD-545 solar PV panel.
Table 8 presents the optimal parameters of the DDiM of the Mono PERC CS7L-590 MS obtained from 20 runs, while Figure 6 illustrates the outcomes of the simulation.

Table 8.
The optimal estimated parameters for the DDiM of the Mono PERC CS7L-590 MS solar PV module using the CrSA and the analytical technique.
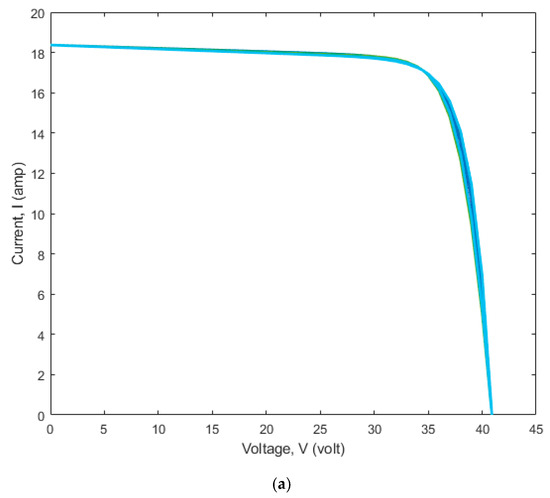
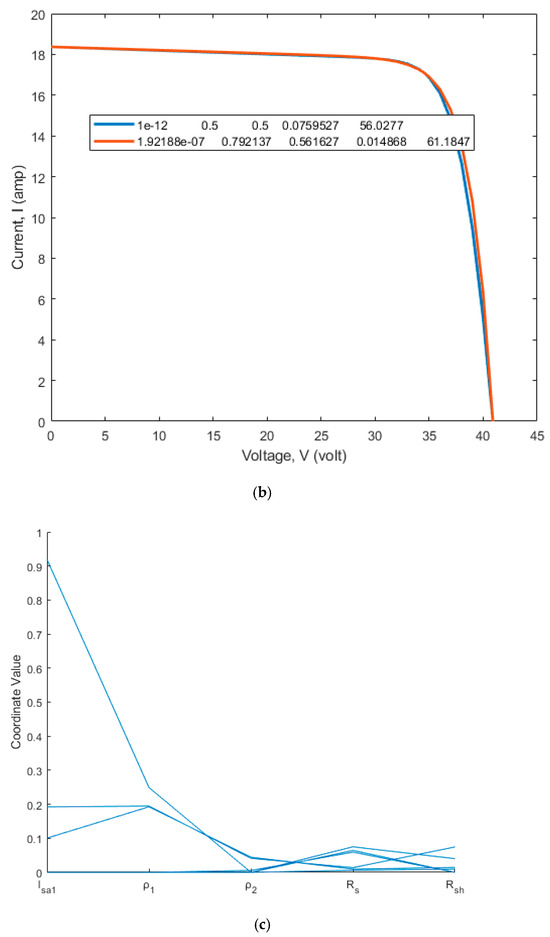
Figure 6.
(a) V-I characteristics of the DDiM of the Mono PERC CS7L-590 MS solar PV panel; (b) V-I characteristics with maximum and of the DDiM of the Mono PERC CS7L-590 MS solar PV panel; (c) optimal solution set for parameter extraction of the DDiM of the Mono PERC CS7L-590 MS solar PV panel.
The 20 V-I characteristics flow through three locations in Figure 5 and Figure 6, which is the primary factor considered in the objective function. The error at the three places is nearly 10−14. Out of seven parameters in the DDiM, five parameters, , , , , and , are optimized using the CrSA method, and the remaining two parameters, and , are obtained from the derived analytical equations. The V-I curves acquired in each run are optimum due to the optimized parameters within the defined search space bounds. This is because the provided approach is metaheuristic.
From the simulation results of the SDiM and DDiM of Mono PERC WSMD-545 and CS7L-590 MS solar PV panels, it is evident that the parameters estimated using the suggested CrSA method guarantee the precision of the V-I characteristics and that the three points obtained align with the datasheet.
5.3. Convergence Analysis
Figure 7 displays the convergence trends of the SDiM and DDiM of Mono PERC WSMD-545 and CS7L-590 MS solar PV panels, respectively, using CrSA, SABA [6], GTO [15], DOA [16], and AHBO [17]. These curves are utilized for evaluating the computational capability of the CrSA. According to the convergence rate study, the CrSA outperforms the SABA, GTO, DOA, and AHBO algorithms in terms of accuracy.
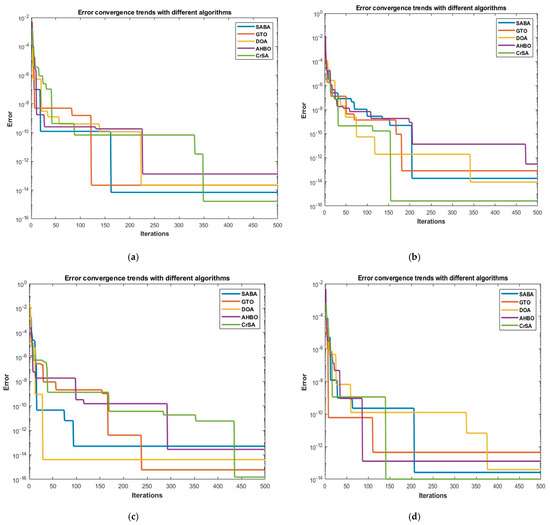
Figure 7.
Error convergence trends with SABA [6], GTO [15], DOA [16], AHBO [17], and CrSA algorithms of (a) SDiM WSMD−545, (b) DDiM WSMD−545, (c) SDiM CS7L−590 MS, and (d) DDiM CS7L−590 MS Mono PERC solar PV modules.
5.4. Discussion
This work utilizes the CrSA method to enhance the efficiency of parameter extraction in PV models, as well as perform a comparative analysis with alternative strategies. Based on the simulation findings, we can summarize the following:
- (a)
- In over 20 trials, the CrSA consistently produces highly accurate results when using the provided error function as the objective function.
- (b)
- The simulation results indicate that the estimated parameters yield V-I curves that accurately pass through all three crucial points, with an error of approximately 10−14.
- (c)
- The proposed method has been compared with the recent OAs in the literature by using convergence analysis. It has been observed that the proposed approach exhibited the fastest rate of convergence on each of the PV panels.
- (d)
- The results indicate that the proposed algorithm demonstrated satisfactory performance characteristics and its practical application is highly recommended.
6. Conclusions
An algorithm inspired by the symmetric arrangement of atoms, molecules, or ions in crystalline minerals called CrSA has been proposed in this work for parameter extraction of the SDiM and DDiM of Mono PERC WSMD-545 and CS7L-590 MS solar PV panels. Both the SDiM and DDiM models use an analytical method to determine two parameters, whereas the CrSA is used to derive the other parameters. The efficacy of the proposed method is evaluated by minimizing the objective function. Further, comparative analysis has been conducted with the existing OAs in the literature by using convergence analysis. It has been observed that the CrSA exhibited the fastest rate of convergence on each of the PV panels. As a result, we finally conclude that the CrSA has shown to be an effective parameter estimation technique. The applicability of the proposed approach may be extended to the parameter estimation of triple-diode PV panels in the future by using state-of-the-art learning techniques to improve its performance.
Author Contributions
Conceptualization, methodology, software, T.C. and R.D.; formal analysis, investigation, R.I.V. and Ł.K.; writing—review and editing, T.C., K.S. and R.D.; funding acquisition, Ł.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mahajan, M.; Kumar, S.; Pant, B.; Khan, R. Improving Accuracy of Air Pollution Prediction by Two Step Outlier Detection. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–7. [Google Scholar]
- Bošnjaković, M.; Santa, R.; Crnac, Z.; Bošnjaković, T. Environmental Impact of PV Power Systems. Sustainability 2023, 15, 11888. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Sheng, H.; Li, C.; Wang, H.; Yan, Z.; Xiong, Y.; Cao, Z.; Kuang, Q. Parameters Extraction of Photovoltaic Models Using an Improved Moth-Flame Optimization. Energies 2019, 12, 3527. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Gu, Q. A comprehensive survey on meta-heuristic algorithms for parameter extraction of photovoltaic models. Renew. Sustain. Energy Rev. 2021, 141, 110828. [Google Scholar] [CrossRef]
- Moustafa, G. Parameter Identification of Solar Photovoltaic Systems Using an Augmented Subtraction-Average-Based Optimizer. Eng 2023, 4, 1818–1836. [Google Scholar] [CrossRef]
- Ghetas, M.; Elshourbagy, M. Parameters extraction of photovoltaic models using enhanced generalized normal distribution optimization with neighborhood search. Neural Comput. Applic 2024. [Google Scholar] [CrossRef]
- Sallam, K.M.; Hossain, M.A.; Chakrabortty, R.K.; Ryan, M.J. An improved gaining-sharing knowledge algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2021, 237, 114030. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, S.; Yeh, W.; Chen, Z.; Wu, L. Parameters extraction of solar cell models using a modifed simplifed swarm optimization algorithm. Sol. Energy 2017, 144, 594–603. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Al-Dahidi, S.; Mussetta, M.; Amechnoue, K. Analytical optimization of photovoltaic output with Lagrange Multiplier Method. Optik 2019, 199, 163379. [Google Scholar] [CrossRef]
- Ezzahra Ait Salah, F.; Maouhoub, N.; Tifidat, K.; Nam, Y.; Abouhawwash, M. An efficient analytical approach for forecasting the peak power of PV panels working in outdoor conditions based on explicit model. Energy Convers. Manag. 2023, 20, 100423. [Google Scholar]
- Toledo, F.J.; Blanes, J.M. Analytical and quasi-explicit four arbitrary point method for extraction of solar cell single-diode model parameters. Renew. Energy 2016, 92, 346–356. [Google Scholar] [CrossRef]
- Gnetchejo, P.J.; Ndjakomo Essiane, S.; Dadjé, A.; Ele, P. A combination of Newton-Raphson method and heuristics algorithms for parameter estimation in photovoltaic modules. Heliyon 2021, 7, e06673. [Google Scholar] [CrossRef] [PubMed]
- Romero, B.; del Pozo, G.; Arredondo, B. Exact analytical solution of a two diode circuit model for organic solar cells showing S-shape using Lambert W-functions. Sol. Energy 2012, 86, 3026–3029. [Google Scholar] [CrossRef]
- Ginidi, A.; Ghoneim, S.M.; Elsayed, A.; El-Sehiemy, R.; Shaheen, A.; El-Fergany, A. Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 2021, 13, 9459. [Google Scholar] [CrossRef]
- Vais, R.I.; Sahay, K.; Chiranjeevi, T.; Devarapalli, R.; Knypiński, Ł. Parameter Extraction of Solar Photovoltaic Modules Using a Novel Bio-Inspired Swarm Intelligence Optimisation Algorithm. Sustainability 2023, 15, 8407. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; El-Fergany, A. Electrical parameters extraction of PV modules using artificial hummingbird optimizer. Sci. Rep. 2023, 13, 9240. [Google Scholar] [CrossRef] [PubMed]
- Ahmadianfar, I.; Gong, W.; Heidari, A.A.; Golilarz, N.A.; Samadi-Koucheksaraee, A.; Chen, H. Gradient-based optimization with ranking mechanisms for parameter identifcation of photovoltaic systems. Energy Rep. 2021, 7, 3979–3997. [Google Scholar] [CrossRef]
- Song, Y.; Wu, D.; Mohamed, A.W.; Zhou, X.; Zhang, B.; Deng, W. Enhanced Success History Adaptive DE for Parameter Optimization of Photovoltaic Models. Complexity 2021, 20212, 6660115. [Google Scholar] [CrossRef]
- Yuan, S.; Ji, Y.; Chen, Y.; Liu, X.; Zhang, W. An Improved Differential Evolution for Parameter Identification of Photovoltaic Models. Sustainability 2023, 15, 13916. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wang, L.; Yan, X.; Hu, C. A hybrid adaptive teaching–learning-based optimization and diferential evolution for parameter identifcation of photovoltaic models. Energy Convers. Manag. 2020, 225, 113474. [Google Scholar] [CrossRef]
- Song, Y.; Wu, D.; Deng, W.; Gao, X.-Z.; Li, T.; Zhang, B.; Li, Y. MPPCEDE: Multi-population parallel co-evolutionary diferential evolution for parameter optimization. Energy Convers. Manag. 2021, 228, 113661. [Google Scholar] [CrossRef]
- Izci, D.; Ekinci, S.; Hussien, A.G. Efficient parameter extraction of photovoltaic models with a novel enhanced prairie dog optimization algorithm. Sci. Rep. 2024, 114, 7945. [Google Scholar] [CrossRef] [PubMed]
- Premkumar, M.; Babu, T.S.; Umashankar, S.; Sowmya, R. A new metaphor-less algorithms for the photovoltaic cell parameter estimation. Optik 2020, 208, 164559. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Cheng, Z.; Wang, H. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Y.; Cai, Z.; Asghar Heidari, A.; Chen, H.; Zhang, Y. Super-evolutionary mechanism and Nelder-Mead simplex enhanced salp swarm algorithm for photovoltaic model parameter estimation. IET Renew. Power Gener. 2023, 1–29. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Parameter estimation of photovoltaic system using imperialist competitive algorithm. Renew. Energy 2017, 111, 307–320. [Google Scholar] [CrossRef]
- Jian, X.; Cao, Y. A Chaotic Second Order Oscillation JAYA Algorithm for Parameter Extraction of Photovoltaic Models. Photonics 2022, 9, 131. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C. A novel Elite Opposition-based Jaya algorithm for parameter estimation of photovoltaic cell models. Optik 2018, 155, 351–356. [Google Scholar] [CrossRef]
- Xavier, F.J.; Pradeep, A.; Premkumar, M.; Kumar, C. Orthogonal learning-based Gray Wolf Optimizer for identifying the uncertain parameters of various photovoltaic models. Optik 2021, 247, 167973. [Google Scholar] [CrossRef]
- Reddy, S.S.; Yammani, C. A novel two step method to extract the parameters of the single diode model of Photovoltaic module using experimental Power-Voltage data. Optik 2021, 248, 167977. [Google Scholar] [CrossRef]
- Devarapalli, R.; Rao, B.V.; Al-Durra, A. Optimal parameter assessment of Solar Photovoltaic module equivalent circuit using a novel enhanced hybrid GWO-SCA algorithm. Energy Rep. 2022, 8, 12282–12301. [Google Scholar] [CrossRef]
- Abd El-Mageed, A.A.; Al-Hamadi, A.; Bakheet, S.; Abd El-Rahiem, A.H. Hybrid Sparrow Search-Exponential Distribution Optimization with Differential Evolution for Parameter Prediction of Solar Photovoltaic Models. Algorithms 2024, 17, 26. [Google Scholar] [CrossRef]
- Vandrasi, R.K.; Kumar, B.S.; Devarapalli, R. Solar photovoltaic module parameter extraction using a novel hybrid chimp-sine cosine algorithm,” Energy Sources A: Recover. Util. Environ. Eff. 2022, 1–20. [Google Scholar] [CrossRef]
- Gatla, V.R.; Injeti, S.K.; Kotte, S.; Polamarasetty, P.K.; Nuvvula, R.S.S.; Vardhan, A.S.S.; Singh, M.; Khan, B. An Effective Approach for Extracting the Parameters of Solar PV Models Using the Chaotic War Strategy Optimization Algorithm With Modified Newton Raphson Method. IEEE J. Electron Devices Soc. 2023. [Google Scholar] [CrossRef]
- Naraharisetti, J.N.L.; Devarapalli, R.; Bathina, V. Parameter extraction of solar photovoltaic module by using a novel hybrid marine predators–success history based adaptive differential evolution algorithm,” Energy Sources A: Recover. Utili. Environ. Eff. 2020, 1–23. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Sayed, E.T.; Olabi, A.G.; Rezk, H. Optimal parameter identifcation of triple-junction photovoltaic panel based on enhanced moth search algorithm. Energy 2019, 188, 116025. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. A novel optimal parameters identifcation of triple-junction solar cell based on a recently meta-heuristic water cycle algorithm. Sol. Energy 2017, 157, 778–791. [Google Scholar] [CrossRef]
- Houssein, E.H.; Nassef, A.M.; Fathy, A.; Mahdy, M.A.; Rezk, H. Modifed search and rescue optimization algorithm for identifying the optimal parameters of high efciency triple-junction solar cell/module. Int. J. Energy Res. 2022, 46, 13961–13985. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Abd El-Mageed, A.A.; Gad, A.G.; Sallam, K.M.; Munasinghe, K.; Abohany, A.A. Improved binary adaptive wind driven optimization algorithm-based dimensionality reduction for supervised classification. Comput. Ind. Eng. 2022, 167, 107904. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M.; Tolouei, M.; Talatahari, B.; Sareh, P. Crystal Structure Algorithm (CryStAl): A Metaheuristic Optimization Method. IEEE Access 2021, 9, 71244–71261. [Google Scholar] [CrossRef]
- ARKA_SERIES_WSMD_515_545. Available online: https://cdn.enfsolar.com/z/pp/g9bqbs274a/ARKA-SERIES-WSMD-515-545-WEL-E-PD-515-545-144-MP-HC-06-17-11.pdf (accessed on 25 April 2024).
- Canadian_Solar_CS7L_MS_575_605. Available online: https://static.csisolar.com/wp-content/uploads/sites/2/2020/10/02101505/Canadian_Solar-Datasheet-CS7L-MS-575-605-V1.6C1_AU.pdf (accessed on 10 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).