Abstract
We study an online distribution problem in which a producer has to send a load from an origin to a destination. At each time period before the deadline, they ask for transportation price quotes and have to decide to either accept or not accept the minimum offered price. If this price is not accepted, they have to pay a penalty cost, which may be the cost to ask for new quotes, the penalty cost for a late delivery, or the inventory cost to store the load for a certain duration. The aim is to minimize the sum of the transportation and the penalty costs. This problem has interesting real-world applications, given that transportation quotes can be obtained from professional websites nowadays. We show that the classical online algorithm used to solve the well-known Secretary problem is not able to provide, on average, effective solutions to our problem, given the trade-off between the transportation and the penalty costs. Therefore, we design two classes of online algorithms. The first class is based on a given time of acceptance, while the second is based on a given threshold price. We formally prove the competitive ratio of each algorithm, i.e., the worst-case performance of the online algorithm with respect to the optimal solution of the offline problem, in which all transportation prices are known at the beginning, rather than being revealed over time. The computational results show the algorithms’ performance on average and in the worst-case scenario when the transportation prices are generated on the basis of given probability distributions.
1. Introduction
Online problems are optimization problems in which the instance is revealed in an online manner and the solution is produced online. We study an online distribution problem where transportation prices are revealed over time. The producer has to accept one of these prices in order to send a load to a customer. The decision is taken on the basis of the transportation prices revealed so far. Only the range in which the transportation prices will fall is known, and the unit penalty cost must be paid whenever the offered price is not accepted. The latter cost may be the cost of obtaining a new quote, the penalty for a late delivery, the inventory cost the company has to pay to store the load for a certain time, or a combination of these costs. This penalty cost is constant from one period to the next.
This problem has interesting real-world applications. In the last few years, transportation quotes have been easily obtainable from professional websites. For example, please refer to Shiply (www.shiply.com) or to Freightquote (www.freightquote.com). After providing the data concerning the load (origin, destination, type of products, weight and volume), transportation prices are obtained from transportation companies. At the end of the first time period, a decision must be made: to accept or to reject the minimum offered price without any information on the prices that will be observed in the future. These steps are repeated until a price is accepted. Note that the prices provided by the transportation companies over time do not follow any trend because they mainly depend on the availability of other requests from close enough origins and destinations.
For this problem, we design online algorithms, i.e., algorithms that make irrevocable decisions without full knowledge of the problem instance. The decision makers have full knowledge of the past, but no (or just partial) knowledge of the future. To evaluate their performance, Sleator et al. [1] suggested that these algorithms be compared with optimal offline algorithms. Moreover, Karlin et al. [2] introduced the concept of a competitive ratio. An online algorithm ALG is c-competitive (with ) if, given any problem instance I, the cost of the solution given by the online algorithm ALG is no more than c times the cost of an optimal offline algorithm that knows the entire sequence of transportation prices in advance:
The smallest c such that is called the competitive ratio of ALG. For the sake of simplicity, in the following, we will omit the reference to I. The availability of the competitive ratio provides a guarantee for the worst-case performance of the online algorithm with respect to the optimal solution of the offline problem, where all information is already available at the beginning, before the first decision is made. The competitive ratio is also interesting from a managerial point of view, because the producer knows that, by using the online algorithm, the total cost they will pay over the time horizon will be at most c times the cost of the offline problem. If several online algorithms are available, the one with the smallest competitive ratio should be used to achieve the best possible worst-case performance guarantee.
We refer to Borodin and El-Yaniv [3] and to Hentenryck and Bent [4] for a comprehensive description of online algorithms and competitive analyses, to Albers [5] for a survey on online algorithms, and to Jaillet and Wagner [6] for a survey of online vehicle routing problems. Recent contributions have been presented by Chen et al. [7] for an online machine minimization problem; Ma et al. [8] for online knapsack problems; Berǵe et al. [9] for the online k-Canadian traveller problem; Li et al. [10,11], Yu and Jacobson [12], Shamsaei et al. [13], and Jiang et al. [14] for online scheduling problems; Akbari et al. [15] for a post-disaster road restoration problem; Zhang et al. [16] for the management of online orders in modern crowdsourced truck logistics platforms; Shiri et al. [17] for ambulance routing in disaster response with partial or no information on victim conditions; Fujii et al. [18] for the Secretary problem with predictions; Arnosti et al. [19] for static threshold policies in the prophet Secretary problem; Salem et al. [20] for Secretary problems with biased evaluations using partial ordinal information; Shiri et al. [21] for the ambulance routing problem on a road network; and Chen et al. [22] for a review of online integrated production and distribution scheduling. Finally, for an extensive overview of the most recent contributions on online algorithms, we refer the work by to Höhne et al. [23,24,25] and Amouzandeh et al. [26]. In particular, the last survey covers papers published in 2023 concerning online algorithms for server problems, matching problems, packing problems, scheduling problems, allocations and auction problems, and other miscellaneous problems.
The distribution problem we study is related to the well-known Secretary problem, the prophet inequality problem (see Ferguson [27] and Correa et al. [28]), and the one-way trading problem (see El-Yaniv et al. [29]). However, to the best of our knowledge, our problem is new. In fact, in the Secretary problem, the number of secretaries who will be interviewed is known in advance, while in our problem, only the maximum number of quotes is known. Moreover, no penalty cost is charged in the Secretary problem. In addition, in the Secretary problem, the objective is slightly different; namely, in the Secretary problem, we seek to maximize the probability of selecting the best option, while in our problem, we minimize the total cost. Finally, the Secretary problem has a simple solution: reject the first k offers and, after that, accept the next better one. Instead, we will computationally show that this solution is significantly worse than those of the online algorithms we propose for the distribution problem. Our problem is also different from the one-way trading problem, as we pay the penalty cost.
The paper is organized as follows. In Section 2, the problem is formally described. In Section 3 and Section 4, the competitive ratio of algorithms with a given time of acceptance and of algorithms with a threshold price, respectively, is provided. In Section 5 and Section 6, a numerical comparison of these competitive ratios and computational results, obtained when transportation prices are randomly generated from given probability distributions, is provided.
2. Problem Description
We consider the problem in which a producer has to ship a load to a customer. The shipment can be performed in any of the discrete time periods , where H is the deadline to send this load. In each time period t, each transportation company in a given set offers a price to send this load. Each offered price is not lower than a minimum value p and not greater than a maximum value P, where P is the default price, e.g., the cost the producer has to pay to send the load by using their own vehicles or the transportation price to pay to a carrier with predefined tariffs. The producer has to decide either to accept the minimum price offered at time period t, say , or to reject it. In the former case, the shipment is performed at price , while in the latter case, a penalty cost h is charged to obtain new quotes, due to a late delivery, to store the load for one time period, or due to a combination of the above. The problem is to determine the price the producer has to accept in order to minimize the sum of transportation and penalty costs.
3. Online Algorithms with a Given Time of Acceptance
In this section, we provide the competitive ratio of online algorithms in which the minimum price offered at a given time period j is accepted. Each of these algorithms can be formally described as follows.
Algorithm : At time period j, accept .
If we denote the total cost obtained by applying the algorithm by and the optimal cost of the offline problem by , then the following theorem holds.
Theorem 1.
.
Proof of Theorem 1.
Since the producer accepts price at time period j, the total cost obtained by applying algorithm is The optimal offline cost is not lower than p. Therefore, □
We now show that this algorithm cannot have a better competitive ratio. Consider first the following instance: , , for . The total cost generated by the algorithm is , while the optimal offline cost is (obtained by accepting the price offered at time 0); therefore, in this instance, Consider now the following instance: , , for and . Since the total cost generated by the algorithm is and the optimal cost is (obtained by accepting the price offered at time 1), then in this instance, for
Since the worst-case ratio of the algorithms is increasing in j, the following theorem holds.
Theorem 2.
In the worst case, the best algorithm with a given time of acceptance is , with a competitive ratio .
This result is very interesting also from a managerial point of view. If is used, the maximum percent cost increase with respect to the optimal solution of the offline problem is given by . For example, if , this means that the online algorithm will give a percent cost increase of at most 100% with respect to the cost of the optimal solution of the offline problem.
We now show that there exists a class of instances in which the algorithm gives an optimal solution to the online problem. In particular, when the penalty cost h is greater than or equal to the difference between the default price P and the minimum price p, it is always optimal to select the first offered price.
Theorem 3.
is optimal in the class of instances with .
Proof of Theorem 3.
The total cost generated by any algorithm ALG either is the cost of accepting at time 0, that is, , or is not lower than the cost of accepting the minimum price p at time 1, that is, . Since in the latter case, as and , then gives an optimal solution. □
We now analyze the worst-case performance of online algorithms in which the minimum price offered from 0 to a given time period j is accepted at time period j. Although these algorithms are not fairly comparable to the previous ones, since the price offered in a period does not expire at the end of the period, the results can serve, in most cases, as an aspirational benchmark. Each of these algorithms can formally be described as follows.
Algorithm : At time period j, accept the minimum price offered from time period 0 to time period j.
If we denote the total cost obtained by applying the algorithm by , then the following theorem holds.
Theorem 4.
.
Proof of Theorem 4.
Since the producer accepts the minimum price offered from 0 to j at time period j, the total cost obtained by applying algorithm is where . Let us distinguish the following two cases.
Case 1: ,
In this case, the optimal offline cost is not lower than . Therefore, since is a decreasing function in and .
Case 2: for some
In this case, the optimal offline cost is not lower than the minimum between and . Therefore, □
We now show that this algorithm cannot have a better competitive ratio. Consider the following instance for Case 1: , . The total cost generated by algorithm is , while the optimal offline cost is (obtained by accepting the price offered at time 0). Therefore, in this instance, Consider now the following two instances for Case 2: for , where , and , . The total cost generated by algorithm is , while the optimal offline cost is (obtained by accepting the price offered at time 0, since ). Therefore, in this instance, for The second instance is the following: , , , , and . The total cost generated by algorithm is , while the optimal offline cost is (obtained by accepting the price offered at time , as ); therefore, in this instance, for
Since the competitive ratio of algorithm is , while it is for , the two algorithms have the same worst-case performance for , while the following theorem holds for .
Theorem 5.
In the worst case, dominates when .
4. Online Algorithms with a Given Threshold Price
In this section, we analyze the class of algorithms in which the first price less than or equal to a given threshold () is accepted. This type of online algorithm is very useful from a practical point of view, given that it is simple to use. Moreover, we will now prove that it has a better worst-case performance with respect to the algorithms with a given time of acceptance. We first consider the case in which, at time period H, the price is accepted if every prior price has been rejected (algorithm ); then, we consider the case in which the minimum price offered from 0 to H is accepted at time period H if every prior price has been rejected (algorithms ).
Each of the algorithms can be formally described as follows.
Algorithm :
Accept the first price that is no greater than . At time period H, accept if every prior price has been rejected.
If we denote the total cost obtained by applying the algorithm by , then the following theorem holds.
Theorem 6.
.
Proof of Theorem 6.
Consider first the case in which there exists a time period s between 0 and such that . The cost generated by algorithm is . The optimal offline cost is no lower than the minimum between and , as is greater than for and it is greater or equal than p starting from time period s. Therefore,
Consider now the case in which the producer accepts . The cost generated by the algorithm is no greater than , while the optimal cost is no lower than , as was greater than for each . Therefore, in this case, Hence, □
We now show that this algorithm cannot have a better competitive ratio. Consider first the following instance: for all , , for all and h such that , i.e., , and . The cost generated by algorithm is , while the optimal offline cost is . Therefore, in this instance, for Consider now the following instance: , where , for all and . The cost generated by algorithm is , while the optimal offline cost is obtained by accepting at time 0, that is, . Therefore, in this instance, for
Let us now compute the optimal threshold in the worst case.
Theorem 7.
In the worst case, if , then the optimal threshold is .
Proof of Theorem 7.
Consider the competitive ratio . Since the first component is increasing in and the second is decreasing in , the threshold that minimizes the competitive ratio satisfies . Therefore, since is non-negative, then . □
Note that if or if , then is the optimal threshold, implying that is accepted at time 0. In fact, in the second case, the competitive ratio is a decreasing function in in the interval , while in the first case, the competitive ratio is an increasing function in . However, setting implies accepting price at time period H in the worst case. This is dominated by accepting at time period 0.
Theorem 8.
If , then . Otherwise, .
Consider now the case in which the minimum price offered from 0 to H is accepted at time period H if every prior price has been rejected (algorithm ). Although these algorithms are not fairly comparable to the previous one, since the price offered in a period does not expire at the end of the period, the result can serve, in most cases, as an aspirational benchmark. Each of these algorithms can be described as follows.
Algorithm :
Accept the first price that is no greater than . At time period H, accept the minimum price offered from 0 to H if every prior price has been rejected.
Let us denote the total cost generated by applying Algorithm by .
Theorem 9.
.
Proof of Theorem 9.
Consider first the case in which there exists a time period s between 0 and such that . The cost generated by algorithm is . The optimal offline cost is no lower than the minimum between and . Therefore,
Consider now the case in which at time period H the producer accepts the minimum price offered between 0 and H. The cost generated by algorithm is , while the optimal offline cost is no lower than , as was greater than for each . Therefore, in this case, since and are decreasing functions in . Therefore, □
We now show that this algorithm cannot have a better competitive ratio. Consider first the following instance: for all , , for all and h such that , i.e., . The cost generated by algorithm is , while the optimal offline cost is . Therefore, in this instance, for Consider now the following instance: , where , for all and . The cost generated by algorithm is , while the optimal offline cost is obtained by accepting at time 0, that is, . Therefore, in this instance, for
Since the competitive ratio of algorithm is , while it is for , the following theorem holds.
Theorem 10.
In the worst case, dominates .
Let us now compute the optimal threshold in the worst case.
Theorem 11.
In the worst case, if , then the optimal threshold is .
Proof of Theorem 11.
Consider the competitive ratio . Since the first component is increasing in and the second is decreasing in , the threshold that minimizes the competitive ratio satisfies . Therefore, since is non-negative, then . □
Note that . If , then is the optimal threshold, implying that is accepted at time 0. In fact, in this case, the competitive ratio is a decreasing function in in the interval .
Theorem 12.
If , then . Otherwise, .
5. Comparison of the Competitive Ratios
In this section, we provide a numerical comparison of the competitive ratios when , , and . The results are shown in Table 1. We just consider , and because all other algorithms are dominated in the worst case. In particular, we do not show the performance ratios of , as it has the same worst-case performance of , as stated in Section 3. Instead, we show the performance ratios of in a separate column, as it provides an aspirational benchmark for the performance of , as stated in Section 4.

Table 1.
Comparison of the competitive ratios.
Note that all competitive ratios are not decreasing in h and that is dominated by , which is dominated, not surprisingly, by , in the worst case. This means that should be used in practice. Moreover, if it is possible to select the minimum price offered from 0 to H at time period H, instead of just the price offered at time period H, is able to provide better competitive ratios when the penalty cost is small enough.
6. Computational Results
In this section, we first show the performance of the online algorithms when the transportation prices are obtained from a professional website. Then, we show the results we obtained in a systematic computational experiment in which the transportation prices are randomly generated in the interval on the basis of given probability distributions. Our competitive algorithms are compared with the algorithm used to optimally solve the Secretary problem: reject the first k offers and, after that, accept the next better one. This algorithm is called . For the sake of convenience, we provide a glossary of the algorithms that have been implemented in this article in Table 2.

Table 2.
Glossary of algorithms.
6.1. A Real-World Instance
We first show the performance of the online algorithms with transportation prices obtained from a professional website to check what happens under real market conditions. We consider a load of 20 pallets, with a weight of 1000 pounds each, sent from New York to Los Angeles. The minimum price p is set to USD 3000, while the default price P is set to USD 6000. The deadline H is set to 8 days. For this load, we obtained the prices shown in Figure 1. Given these prices, we analyze the performance of the online algorithms when the penalty cost h is set equal to USD 0.01, 0.1, 1, 10, 100 to cover different practical situations. In the Secretary problem algorithms, k is set equal to 1 and 3.
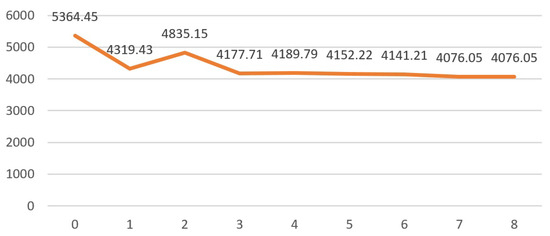
Figure 1.
Offered transportation prices.
The results reported in Table 3 show that is significantly dominated by . In fact, the average cost increase for is 29.07%, while for , it is only 1.77%. Moreover, is able to outperform in all cases, with the only exception of the case with , due to the high penalty cost. On average, the cost increase is 2.12%. The Secretary problem algorithms and perform worse than , as their cost increase is 4.43% and 2.03%, respectively. Finally, as expected, dominates, on average, .

Table 3.
Performance of the online algorithms on the real-world data.
6.2. Randomly Generated Instances
We now show the results obtained when the transportation prices are randomly generated in the interval on the basis of the following probability distributions: uniform, exponential with , normal with mean 150 and standard deviation 5, normal with mean 150 and standard deviation 15, triangular with mode 150, and beta with . We consider the discretized and truncated version of these distributions in the support . These probability distributions have been selected to capture different market conditions with low and high volatilities.
We generate 100, 500, and 1000 scenarios to check the convergence of the expected costs of the online algorithms. Since convergence is computationally guaranteed with 1000 scenarios, we only show the results obtained with 1000 scenarios. The values of the parameters p, P, H, and h are defined as in Section 5. Note that H is equal to 5 and 15 time periods and the penalty cost h ranges from 0.01 to 100 to cover very different scenarios in terms of penalty costs and deadlines. This allows us to check the versatility and adaptability of the algorithms. In the Secretary problem algorithms, k is set equal to 1 and 2 when and is equal to when . For the sake of brevity, we do not show the results obtained for when , as the resulting cost tends to increase with k due to the penalty cost.
The computational results are shown in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. Each table is organized as follows: the first column gives the unit penalty cost h. Then, for each probability distribution, five columns show, for each value of the penalty cost, the average results obtained by the corresponding online algorithms , , , and , where when and when , over 1000 scenarios. Table 4, Table 5 and Table 6 show the average cost, the average ratio of the cost with respect to the cost of the offline problem, and the maximum ratio of the cost with respect to the cost of the offline problem, respectively, when . Table 7, Table 8 and Table 9 show the average cost, the average ratio, and the maximum ratio, respectively, when .

Table 4.
Average costs when .

Table 5.
Average ratios when .

Table 6.
Maximum ratios when .

Table 7.
Average costs when .

Table 8.
Average ratios when .

Table 9.
Maximum ratios when .
The computational results show that, for both and , the average ratios are significantly lower than the corresponding maximum ratios. Moreover, the maximum ratios tend to be very close to the competitive ratios shown in Table 1. is significantly dominated by , which is dominated by when the maximum ratios are computed, and tends to be dominated on average. The performance of the latter algorithm is very good. For each probability distribution, the average and maximum ratios decrease, even if not monotonically, with h and they are equal to 1, as expected, for (see Theorem 3). The ratios are very different with different probability distributions. In particular, the uniform distribution gives the largest ratios, while the normal distribution with a mean of 150 and a standard deviation of 5 gives the smallest ratios.
We do not show in detail the performance of the algorithms and for . As expected, the computational results show that the average and the maximum ratios increase with j and that dominates (as an example, see Table 10 for the case with and Uniform distribution).

Table 10.
Average and maximum ratios for and when and a uniform distribution is assumed.
Finally, the results show that, for any probability distribution, the algorithm used to optimally solve the Secretary problem is significantly worse than the algorithms we propose to solve the distribution problem, both for and . Moreover, the average and maximum ratios of the algorithm tend to increase when k increases due to the penalty cost. These results highlight the need for designing specific algorithms for the online distribution problem. Finally, we note that the Secretary problem algorithms become more competitive when the penalty cost is low.
7. Conclusions
We studied an online distribution problem in which a producer has to decide either to accept or not accept the transportation price currently offered to send a load to a customer. The aim is to minimize the sum of transportation costs and penalty costs, which are incurred whenever the current price is not accepted. This problem can be viewed as a new variant of the Secretary problem. We demonstrated computationally that the algorithm used to optimally solve the Secretary problem is not effective for this problem due to the different objective functions. Therefore, we designed two specific classes of online algorithms to solve it: algorithms with a given time of acceptance and algorithms with a given threshold price. For each algorithm, we proved its competitive ratio. We showed that the competitive ratios of the algorithms in the second class dominate the ones of the algorithms in the first class. The computational results, for which the transportation prices were either obtained from a professional website or randomly generated from given probability distributions, allowed us to computationally demonstrate the same type of dominance. The probability distributions we used were able to generate scenarios with different levels of volatility in the transportation prices. Moreover, note that our algorithms require short computational times and, therefore, they are scalable to any deadline we may have in real-world online distribution settings. However, in future work, we might experiment with more sophisticated algorithms, including hybrid algorithms that combine the features of some of the algorithms proposed in this paper. We might also modify the algorithm based on the Secretary problem to take into account the size of the penalty, as well as the deadline. In addition, a user-friendly software package could be developed to implement the algorithms we have proposed, making them accessible to professionals who may benefit from their application.
Author Contributions
Conceptualization, A.B., L.B. and B.L.G.; Methodology, A.B., L.B. and B.L.G.; Software, A.B., L.B. and B.L.G.; Formal analysis, A.B., L.B. and B.L.G.; Data curation, A.B., L.B. and B.L.G.; Writing—original draft, A.B., L.B. and B.L.G.; Writing—review & editing, A.B., L.B. and B.L.G.; Supervision, A.B., L.B. and B.L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors wish to thank the editor and the two anonymous referees for their valuable comments that allowed us to improve the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sleator, D.D.; Tarjan, R.E. Amortized efficiency of list update and paging rules. Commun. ACM 1985, 28, 202–208. [Google Scholar] [CrossRef]
- Karlin, A.R.; Manasse, M.S.; Rudolph, L.; Sleator, D.D. Competitive snoopy caching. Algorithmica 1988, 3, 79–119. [Google Scholar] [CrossRef]
- Borodin, A.; El-Yaniv, R. Online Computation and Competitive Analysis; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hentenryck, P.V.; Bent, R. Online Stochastic Combinatorial Optimization; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Albers, S. Online algorithms: A survey. Math. Program. 2003, 97, 3–26. [Google Scholar] [CrossRef]
- Jaillet, P.; Wagner, M.R. Online vehicle routing problems: A survey. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Berlin/Heidelberg, Germany, 2008; pp. 221–237. [Google Scholar]
- Chen, L.; Megow, N.; Schewior, K. An O(log m)-Competitive Algorithm for Online Machine Minimization. SIAM J. Comput. 2018, 47, 2057–2077. [Google Scholar] [CrossRef]
- Ma, W.; Simchi-Levi, D.; Zhao, J. A Competitive Analysis of Online Knapsack Problems with Unit Density. arXiv 2019, arXiv:1907.08735. [Google Scholar] [CrossRef]
- Bergé, P.; Desmarchelier, J.; Guo, W.; Lefebvre, A.; Rimmel, A.; Tomasik, J. Multiple Canadians on the road: Minimizing the distance competitive ratio. J. Comb. Optim. 2019, 38, 1086–1100. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Feng, Q. Online batch scheduling with kind release times and incompatible families to minimize makespan. Optim. Lett. 2018, 12, 301–310. [Google Scholar] [CrossRef]
- Li, K.; Zhang, H.J.; Cheng, B.Y.; Pardalos, P.M. Uniform parallel machine scheduling problems with fixed machine cost. Optim. Lett. 2018, 12, 73–86. [Google Scholar] [CrossRef]
- Yu, G.; Jacobson, S.H. Online c-benevolent job scheduling on multiple machines. Optim. Lett. 2018, 12, 251–263. [Google Scholar] [CrossRef]
- Shamsaei, F.; Telha, C.; Van Vyve, M. On the on-line maintenance scheduling problem. Optim. Lett. 2018, 12, 387–397. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, P.; Cheng, T.; Ji, M. Optimal online algorithms for MapReduce scheduling on two uniform machines. Optim. Lett. 2019, 13, 1663–1676. [Google Scholar] [CrossRef]
- Akbari, V.; Shiri, D.; Salman, F.S. An online optimization approach to post-disaster road restoration. Transp. Res. Part Methodol. 2021, 150, 1–25. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, K.; Xu, Y.; Xu, Y.; Tong, W. Online crowdsourced truck delivery using historical information. Eur. J. Oper. Res. 2022, 301, 486–501. [Google Scholar] [CrossRef]
- Shiri, D.; Akbari, V.; Tozan, H. Online optimisation for ambulance routing in disaster response with partial or no information on victim conditions. Comput. Oper. Res. 2023, 159, 106314. [Google Scholar] [CrossRef]
- Fujii, K.; Yoshida, Y. The Secretary Problem with Predictions. Math. Oper. Res. 2023, 49, 653–1302. [Google Scholar] [CrossRef]
- Arnosti, N.; Ma, W. Tight guarantees for static threshold policies in the prophet secretary problem. Oper. Res. 2023, 71, 1777–1788. [Google Scholar] [CrossRef]
- Salem, J.; Gupta, S. Secretary problems with biased evaluations using partial ordinal information. Manag. Sci. 2023. [Google Scholar] [CrossRef]
- Shiri, D.; Akbari, V.; Salman, F.S. Online algorithms for ambulance routing in disaster response with time-varying victim conditions. OR Spectr. 2024, 1–35. [Google Scholar] [CrossRef]
- Chen, Z.L. Online Integrated Production and Distribution Scheduling: Review and Extensions. INFORMS J. Comput. 2024. [Google Scholar] [CrossRef]
- Höhne, F.; Schmitt, S.; van Stee, R. SIGACT News Online Algorithms Column 35: 2019 in review. ACM SIGACT News 2019, 50, 77–92. [Google Scholar] [CrossRef]
- Höhne, F.; Schmitt, S.; van Stee, R. SIGACT News Online Algorithms Column 36: 2020 in review. ACM SIGACT News 2021, 51, 89–107. [Google Scholar] [CrossRef]
- Hohne, F.; Schmitt, S.; van Stee, R. SIGACT news online algorithms column 38: 2021 in review. ACM SIGACT News 2022, 52, 80–96. [Google Scholar] [CrossRef]
- Amouzandeh, A.; Schmitt, S.; van Stee, R. SIGACT News Online Algorithms Column 41: 2023 in review. ACM SIGACT News 2024, 54, 108–125. [Google Scholar] [CrossRef]
- Ferguson, T.S. Who solved the secretary problem? Stat. Sci. 1989, 4, 282–289. [Google Scholar] [CrossRef]
- Correa, J.; Foncea, P.; Hoeksma, R.; Oosterwijk, T.; Vredeveld, T. Recent developments in prophet inequalities. ACM SIGecom Exch. 2019, 17, 61–70. [Google Scholar] [CrossRef]
- El-Yaniv, R.; Fiat, A.; Karp, R.M.; Turpin, G. Optimal search and one-way trading online algorithms. Algorithmica 2001, 30, 101–139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).