Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor
Abstract
1. Introduction
2. Mathematical Modelling
DC Motor Modelling
3. Optimization Algorithms
3.1. Steiglitz–McBride Algorithm as a Parametric Estimator
3.1.1. Pre-Filtering
3.1.2. Estimation
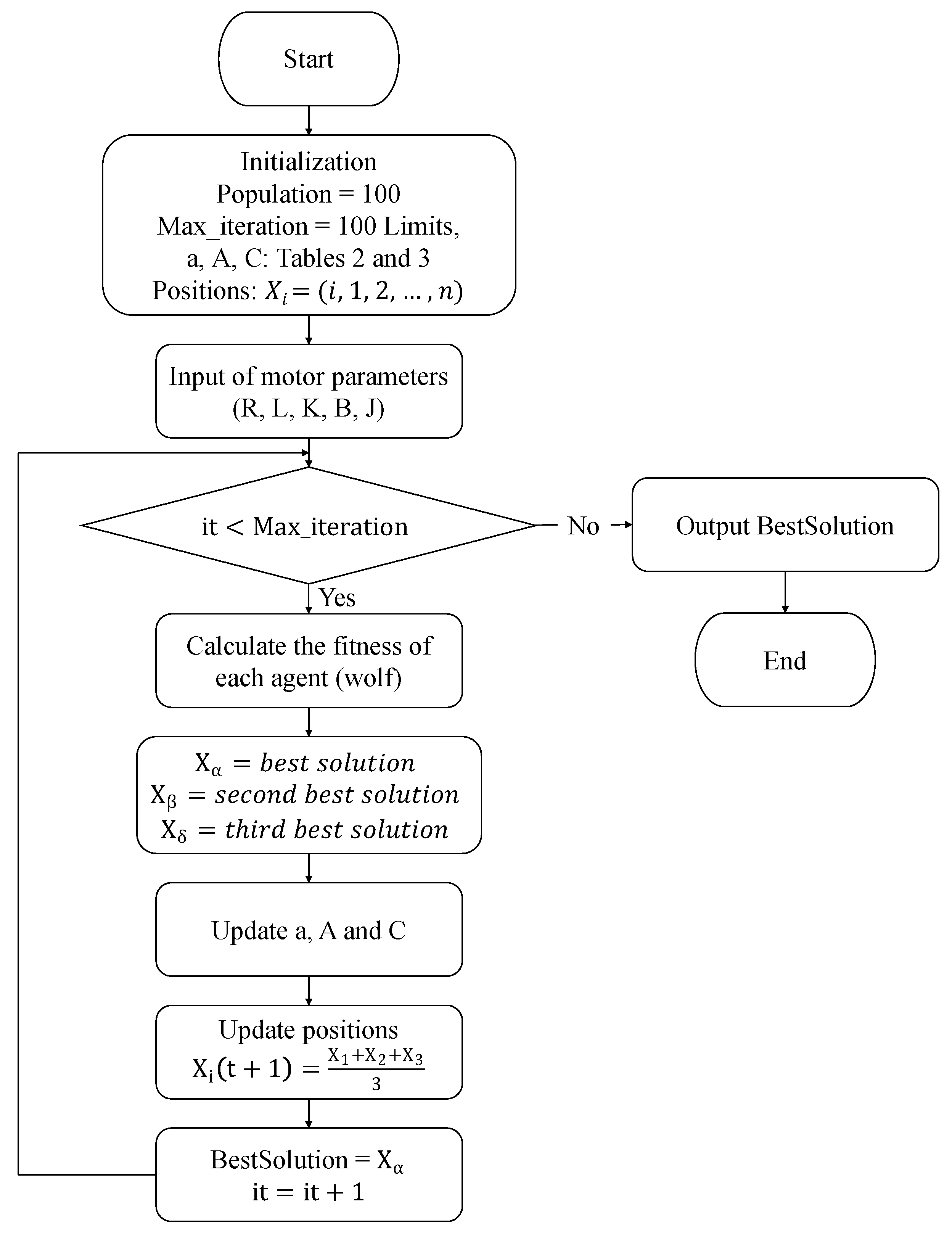
3.2. Grey Wolf Optimizer (GWO)
3.2.1. Encircling Prey
3.2.2. Hunting
3.2.3. Attacking Prey
3.2.4. Search for Prey (Exploration)
| Parameter | Value | Description |
|---|---|---|
| Search agents | 100 | Number of random solutions proposed of each metaheuristic algorithm. |
| Upper limits | R ≤ 1, L ≤ 0.1, K ≤ 0.1, B ≤ 0.001, J ≤ 0.001 | Upper search limit for each DC motor parameter |
| Lower limits | R ≥ 0.1, L ≥ 0.001, K ≥ 0.005, B ≥ 0.00001, J ≥ 0.00001 | Lower search limit for each DC motor parameter |
| Iterations | 100 | Repetitions of each metaheuristic algorithm. |
| Fitness function | Function used to evaluate the performance of each random solution () |
| Algorithm | Specific Parameters | Description |
|---|---|---|
| Genetic Algorithm | Mutation: 20% | An operator that allows the random alteration of a gene to maintain search diversity. |
| Selection: Roulette wheel () | Population with N individuals, for each chromosome i with corresponding fitness value , probability of selection | |
| Type: Crossover | A random point is selected to combine the chromosomes. | |
| Biological pressure: 30% | The percentage of individuals that reproduce | |
| Grey Wolf Optimizer | a, A and C | Intrinsic parameters calculated by original method proposed (see original method in [34]). |
| Jaya | - | Jaya doesnt contain any specific parameter. |
3.3. Jaya Algorithm
3.4. Genetic Algorithm (GA)
3.5. Implementation of Metaheuristic Algorithms
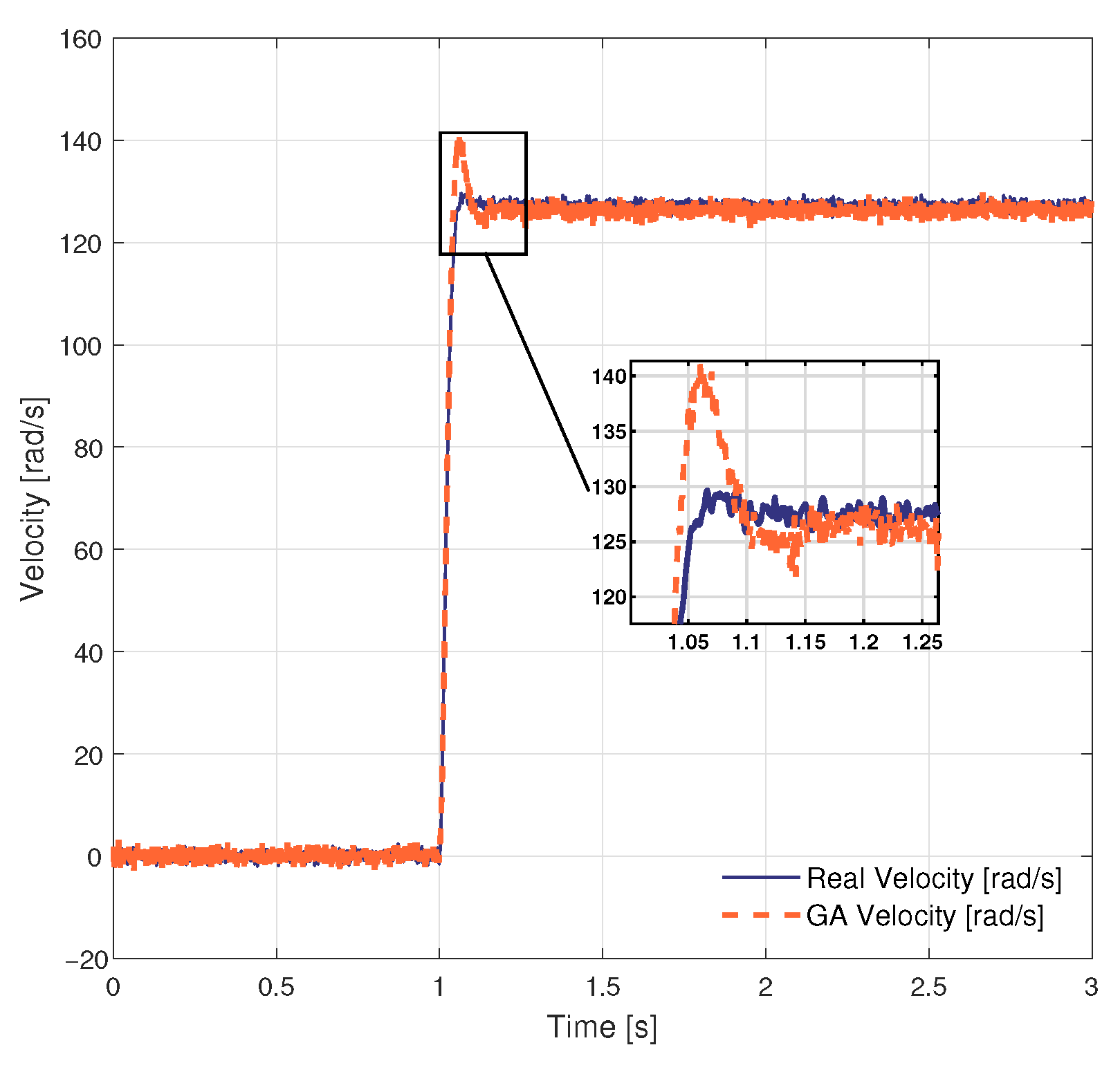
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fazdi, M.F.; Hsueh, P.-W. Parameters Identification of a Permanent Magnet DC Motor: A Review. Electronics 2023, 12, 2559. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Aguilar-Mejia, O.; Favela-Contreras, A.; Lopez-Garcia, I. An online algebraic estimation approach of parameters and variable mechanical torque in shunt DC motors. Int. Trans. Electr. Energy Syst. 2018, 28, e2474. [Google Scholar] [CrossRef]
- Karnavas, Y.L. Application of recent nature-inspired meta-heuristic optimization techniques to small permanent magnet DC motor parameters identification problem. J. Eng. 2020, 2020, 877–888. [Google Scholar]
- Tran, C.D.; Kuchar, M.; Sobek, M.; Sotola, V.; Dinh, B.H. Sensor Fault Diagnosis Method Based on Rotor Slip Applied to Induction Motor Drive. Sensors 2022, 22, 8636. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, C.; Verma, V. Speed and Current Sensor Fault Detection and Isolation Technique for Induction Motor Drive Using Axes Transformation. IEEE Trans. Ind. Electron. 2015, 62, 1943–1954. [Google Scholar] [CrossRef]
- Merrassi, W.E.; Abounada, A.; Ramzi, M. Advanced speed sensorless control strategy for induction machine based on neuro-MRAS observer. Mater. Today Proc. 2021, 45, 7615–7621. [Google Scholar] [CrossRef]
- Nag, T.; Santra, S.B.; Chatterjee, A.; Chatterjee, D.; Ganguli, A.K. Fuzzy logic-based loss minimisation scheme for brushless DC motor drive system. IET Power Electron. 2016, 9, 1581–1589. [Google Scholar] [CrossRef]
- Vikhe, P.S.; Punjabi, N.; Kadu, C.B. DC motor speed control using PID controller in lab view. Int. J. Innov. Sci. Mod. Eng. (IJISME) 2015, 38–41. [Google Scholar]
- Song, T.J.; Oh, K.S. Adaptive Velocity Control Algorithm for DC Motors based on Parameter Estimation of Error Dynamics Under Uncertainty and Load Variation. Trans. Korean Soc. Mech. Eng. A 2020, 44, 83–91. [Google Scholar] [CrossRef]
- Majdoubi, R.; Masmoudi, L.; Bakhti, M.; Elharif, A.; Jabri, B. Parameters estimation of BLDC motor based on physical approach and weighted recursive least square algorithm. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 133–145. [Google Scholar] [CrossRef]
- Knypiński, L.; Reddy, A.V.; Venkateswararao, B.; Devarapalli, R. Optimal design of brushless DC motor for electromobility propulsion applications using Taguchi method. J. Electr. Eng. 2023, 74, 116–121. [Google Scholar] [CrossRef]
- Urra, E.; Cubillos, C.; Cabrera-Paniagua, D.; Mellado, R. hMod: A software framework for assembling highly detailed heuristics algorithms. Softw.-Pract. Exp. 2019, 49, 971–994. [Google Scholar] [CrossRef]
- Zandavi, S.M.; Chung, V.Y.Y.; Anaissi, A. Stochastic dual simplex algorithm: A novel heuristic optimization algorithm. IEEE Trans. Cybern. 2021, 51, 2725–2734. [Google Scholar] [CrossRef]
- Li, Y.; Cherednichenko, A.; Jiang, Z.; Shi, W.; Wu, J. A Novel Generalized Group-Sparse Mixture Adaptive Filtering Algorithm. Symmetry 2019, 11, 697. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey 590 of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, J.; Yan, G. A Dolphin Partner Optimization. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009; Zhou, S.M., Wang, W., Eds.; IEEE Comp Soc. World Res Inst: Xiamen, China, 2009; Volume I, pp. 124–128. [Google Scholar]
- Shuang, B.; Chen, J.; Li, Z. Study Hybrid PS-ACO Algorithm. Appl. Intell. 2011, 34, 64–73. [Google Scholar] [CrossRef]
- Wu, E.; Huang, Y.; Li, D. An Adaptive Particle Swarm Optimization Algorithm for Reactive Power Optimization in Power System. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation (WCICA), Jinan, China, 7–9 July 2010; IEEE: Jinan, China, 2010; pp. 3132–3137. [Google Scholar]
- Shi, J.; Mi, Q.; Cao, W.; Zhou, L. Optimizing BLDC motor drive performance using particle swarm algorithm-tuned fuzzy logic controller. SN Appl. Sci. 2022, 4, 293. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; García-Cerezo, A.; García-Martínez, J.R. Fuzzy logic controller for UAV with gains optimized via genetic algorithm. Heliyon 2014, 10, e26363. [Google Scholar] [CrossRef]
- Serradilla, F.; Canas, N.; Naranjo, J.E. Optimization of the energy consumption of electric motors through metaheuristics and PID controllers. Electronics 2020, 9, 1842. [Google Scholar] [CrossRef]
- Wu, Z.; Du, C. Parameter Identification PMSM Based Improved Cuckoo Algorithm. Neural Process. Lett. 2019, 50, 2701–2715. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ibrahim, M.F.; Ramli, R. Optimal parameter estimation for a DC motor using genetic algorithm. Int. J. Power Electron. Drive Syst. (IJPEDS) 2020, 11, 1047–1054. [Google Scholar] [CrossRef]
- Al-Azzawi, D.S. Evaluation of Genetic Algorithm Optimization in Machine Learning. J. Inf. Sci. Eng. 2020, 36, 231–241. [Google Scholar]
- Cheng, Y.; Lyu, X.; Mao, S. Optimization design of brushless DC motor based on improved Jaya algorithm. Sci. Rep. 2024, 14, 5427. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Li, M.-X.; Liu, W. Application of Improved Genetic Algorithm in Function Optimization. J. Inf. Sci. Eng. 2019, 35, 1299–1309. [Google Scholar]
- Ahamed, S.R.; Parumasivam, P.; Lipu, M.S.H.; Hannan, M.A.; Ker, P.J. A comparative evaluation of PID-based optimisation controller algorithms for DC motor. Int. J. Autom. Control 2020, 14, 634–655. [Google Scholar] [CrossRef]
- Achanta, R.K.; Pamula, V.K. DC Motor Speed Control using PID Controller Tuned by Jaya Optimization Algorithm. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; IEEE: Thandalam, India, 2017; pp. 983–987. [Google Scholar]
- Niu, X.; Feng, G.; Jia, S.; Zhang, Y. Control of brushless DC motor based on fuzzy rules optimized by genetic algorithm used in hybrid vehicle. J. Comput. Methods Sci. Eng. 2021, 21, 951–968. [Google Scholar] [CrossRef]
- Rodriguez-Abreo, O.; Hernandez-Paredes, J.M.; Rangel, A.F.; Fuentes-Silva, C.; Velasquez, F.A.C. Parameter Identification of Motors by Cuckoo Search Using Steady-State Relations. IEEE Access 2021, 9, 72017–72024. [Google Scholar] [CrossRef]
- Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. II. The brushless DC motor drive. IEEE Trans. Ind. Appl. 1989, 25, 274–279. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Montoya-Santiyanes, L.A.; Álvarez-Alvarado, J.M. Non-Linear Regression Models with Vibration Amplitude Optimization Algorithms in a Microturbine. Sensors 2022, 22, 130. [Google Scholar] [CrossRef]
- Rezoug, A.; Iqbal, J.; Tadjine, M. Extended grey wolf optimization–based adaptive fast nonsingular terminal sliding mode control of a robotic manipulator. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2022, 236, 1738–1754. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Agarwal, J.; Parmar, G.; Gupta, R.; Sikander, A. Analysis of grey wolf optimizer based fractional order PID controller in speed control of DC motor. Microsyst.-Technol.-Micro-Nanosyst.-Inf. Storage Process. Syst. 2018, 24, 4997–5006. [Google Scholar] [CrossRef]
- Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Zitar, R.A.; Al-Betar, M.A.; Awadallah, M.A.; Doush, I.A.; Assaleh, K. An Intensive and Comprehensive Overview of JAYA Algorithm, its Versions and Applications. Arch. Comput. Methods Eng. 2022, 29, 763–792. [Google Scholar] [CrossRef] [PubMed]
- Godem Ali, M.I.; Karol, K.; Viliam, F. CAD of Cascade Controllers for DC Drives Using Genetic Algorithm Methods. Procedia Eng. 2014, 96, 182–189. [Google Scholar] [CrossRef][Green Version]
- Kamal, C.; Thyagarajan, T.; Kalpana, D.; Pragadheeshwaran, T. Multiobjective design optimization and analysis of magnetic flux distribution for slotless permanent magnet brushless DC motor using evolutionary algorithms. J. Magn. Magn. Mater. 2019, 476, 524–537. [Google Scholar] [CrossRef]
- Rahideh, A.; Korakianitis, T.; Ruiz, P.; Keeble, T.; Rothman, M.T. Optimal brushless DC motor design using genetic algorithms. J. Magn. Magn. Mater. 2010, 322, 3680–3687. [Google Scholar] [CrossRef]
- Lankarany, M.; Rezazade, A. Parameter Estimation Optimization Based on Genetic Algorithm Applied to DC Motor. In Proceedings of the 2007 International Conference on Electrical Engineering, Lahore, Pakistan, 11–12 April 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Thomas, N.; Poongodi, D.P. Position Control of DC Motor Using Genetic Algorithm Based PID Controller. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009; Volume 2. [Google Scholar]
- Baizid, K.; Yousnadj, A.; Meddahi, A.; Chellali, R.; Iqbal, J. Time scheduling and optimization of industrial robotized tasks based on genetic algorithms. Robot.-Comput.-Integr. Manuf. 2015, 34, 0736–5845. [Google Scholar] [CrossRef]
- Soni, Y.K.; Bhatt, R. BF-PSO optimized PID controller design using ISE, IAE, IATE and MSE error criteria. Int. J. Adv. Res. Comput. Eng. Technol. (IJARCET) 2013, 2, 2333–2336. [Google Scholar]
- Mousakazemi, H.; Mohammad, S. Comparison of the error-integral performance indexes in a GA-tuned PID controlling system of a PWR-type nuclear reactor point-kinetics model. Prog. Nucl. Energy 2021, 132, 103604. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Fuentes-Silva, C.; Hernández-Alvarado, R.; Falcón, M.D.C.P.T. Self-Tuning Neural Network PID with Dynamic Response Control. IEEE Access 2021, 9, 65206–65215. [Google Scholar] [CrossRef]
- Afifi, M.; Rezk, H.; Ibrahim, M.; El-Nemr, M. Multi-Objective Optimization of Switched Reluctance Machine Design Using Jaya Algorithm (MO-Jaya). Mathematics 2021, 9, 1107. [Google Scholar] [CrossRef]
- Dutta, P.; Nayak, S.K. Grey Wolf Optimizer Based PID Controller for Speed Control of BLDC Motor. J. Electr. Eng. Technol. 2021, 16, 955–961. [Google Scholar] [CrossRef]
- Jimenez-Gonzalez, J.; Gonzalez-Montanez, F.; Jimenez-Mondragon, V.M.; Liceaga-Castro, U.; Escarela-Perez, R.; Olivares-Galvan, J.C. Parameter Identification of BLDC Motor Using Electromechanical Tests and Recursive Least-Squares Algorithm: Experimental Validation. Actuators 2021, 10, 143. [Google Scholar] [CrossRef]
















| R | L | K | B | J |
|---|---|---|---|---|
| 0.921042 | 0.0077590 H | 0.073472 | 0.000678 | 0.000136 |
| Fitness Value in Fifty Runs | |||
|---|---|---|---|
| Algorithm | Best | Worse | Average |
| GWO | 0.029 | 0.062 | 0.042 |
| Jaya | 0.35 | 1.92 | 0.99 |
| GA | 0.044 | 1.06 | 0.058 |
| Steiglitz–McBride | GWO | ||||
|---|---|---|---|---|---|
| Parameter | Nominal Value | Value | MSE | Value | MSE |
| R () | 0.921042 | 0.914735 | 00.68% | 0.923696 | 0.42% |
| L (H) | 0.007759 | 0.008893 | 14.49% | 0.007752 | 0.96% |
| K | 0.073472 | 0.073547 | 00.10% | 0.073466 | 0.08% |
| B | 0.000678 | 0.000680 | 00.28% | 0.000677 | 0.16% |
| J | 0.000136 | 0.000135 | 01.03% | 0.000136 | 0.55% |
| Jaya | GA | ||||
|---|---|---|---|---|---|
| Parameter | Nominal Value | Value | MSE | Value | MSE |
| R () | 0.921042 | 0.996974 | 08.24% | 0.817929 | 13.44% |
| L (H) | 0.007759 | 0.008941 | 15.04% | 0.011908 | 89.00% |
| K | 0.073472 | 0.000676 | 01.28% | 0.076071 | 05.75% |
| B | 0.000678 | 0.291812 | 01.61% | 0.000661 | 17.07% |
| J | 0.000136 | 0.000128 | 08.75% | 0.000135 | 17.67% |
| Algorithms | Average Time (min) |
|---|---|
| Steiglitz–McBride | 0.102 |
| GWO | 49.53 |
| Jaya | 51.16 |
| GA | 60.23 |
| Algorithms | ||||
|---|---|---|---|---|
| Parameters | Steiglitz–McBride | GWO | Jaya | GA |
| R | 0.0023 | 0.0040 | 0.0086 | 0.1340 |
| L | 0.0114 | |||
| K | 0.6940 | 0.0044 | ||
| B | ||||
| J | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munciño, D.M.; Damian-Ramírez, E.A.; Cruz-Fernández, M.; Montoya-Santiyanes, L.A.; Rodríguez-Reséndiz, J. Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor. Algorithms 2024, 17, 209. https://doi.org/10.3390/a17050209
Munciño DM, Damian-Ramírez EA, Cruz-Fernández M, Montoya-Santiyanes LA, Rodríguez-Reséndiz J. Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor. Algorithms. 2024; 17(5):209. https://doi.org/10.3390/a17050209
Chicago/Turabian StyleMunciño, David M., Emily A. Damian-Ramírez, Mayra Cruz-Fernández, Luis A. Montoya-Santiyanes, and Juvenal Rodríguez-Reséndiz. 2024. "Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor" Algorithms 17, no. 5: 209. https://doi.org/10.3390/a17050209
APA StyleMunciño, D. M., Damian-Ramírez, E. A., Cruz-Fernández, M., Montoya-Santiyanes, L. A., & Rodríguez-Reséndiz, J. (2024). Metaheuristic and Heuristic Algorithms-Based Identification Parameters of a Direct Current Motor. Algorithms, 17(5), 209. https://doi.org/10.3390/a17050209









