Particle Swarm Optimization-Based Model Abstraction and Explanation Generation for a Recurrent Neural Network
Abstract
1. Introduction
1.1. Related Works
1.1.1. Explanation of RNNs Based on Model Abstraction
1.1.2. Formal Verification or Analysis of RNNs Based on Model Abstraction
1.2. Contributions
- Constructing abstract state traces with k-means clustering and building a tree structure;
- Designing a PSO algorithm to search and learn the abstraction model PFA and find PFA with better complexity and similarity performance when the level of abstraction is constant;
- Using the abstract model PFA to automatically generate an explanation of the importance of input features in classification tasks;
- Exploring the practicality of our framework to adversarial text detection in RNN text classification.
1.3. Structure of This Paper
2. Preliminary
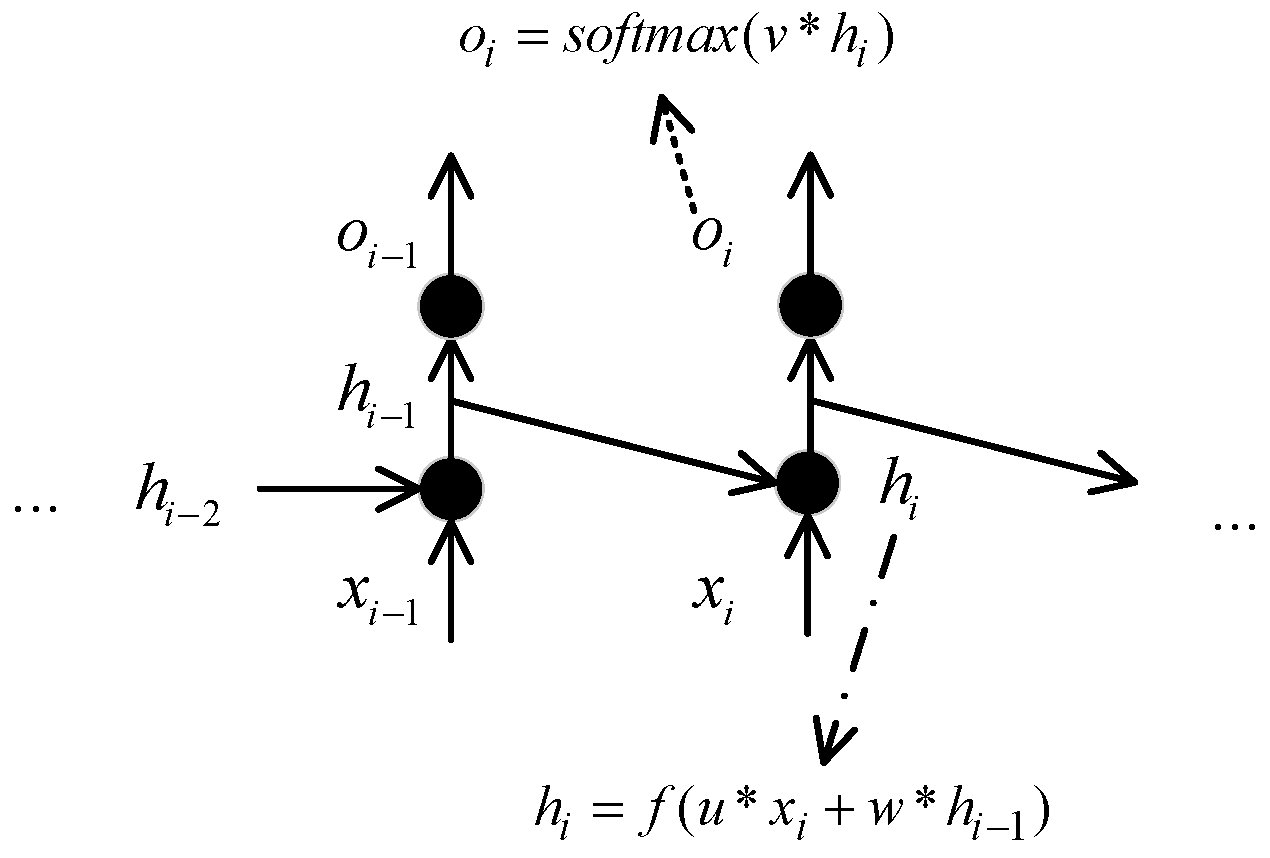
2.1. RNNs
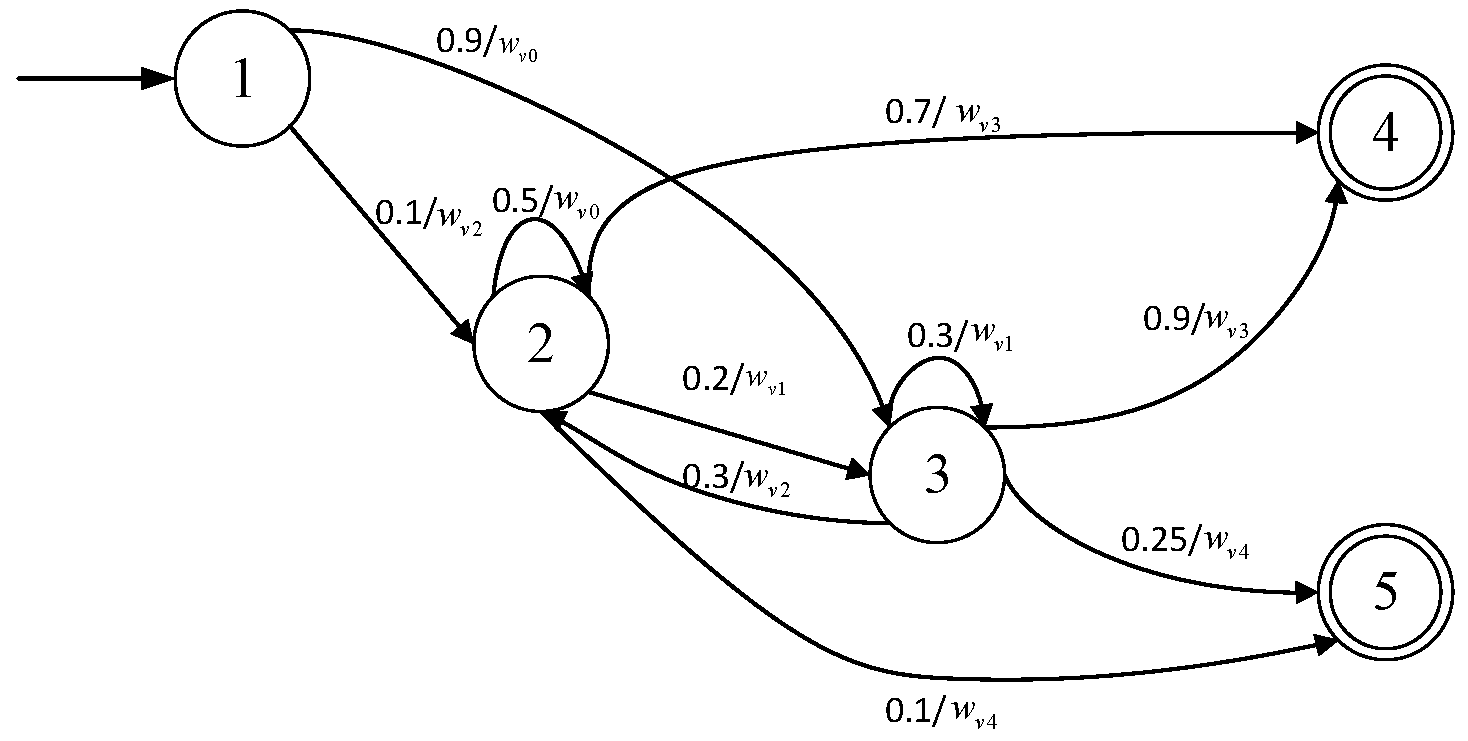
2.2. PFA
- Alphabet: The numerical value at the right of the separator symbol “/” on the arrowed line between each pair of states in the graph is a set: ;
- State set: Q = ;
- Acceptance set: is the set {} in the graph, in which the set of acceptance state labels is {P, N}. They are nodes with double-edged circles.
- Transition probability: A numerical value is at the left side of the separator “/” between states of the PFA, and represents the corresponding probability of transition between states.
3. Model Abstracting and Explaining Framework
- Stage I will be introduced in Section 3.1. Section 3.1.1 corresponds to Step (1)–Step (3). Meanwhile, Section 3.1.2 corresponds to Steps (4)–(9).
- Stage II will be introduced in Section 3.2.
3.1. Learning Abstraction Model for RNNs
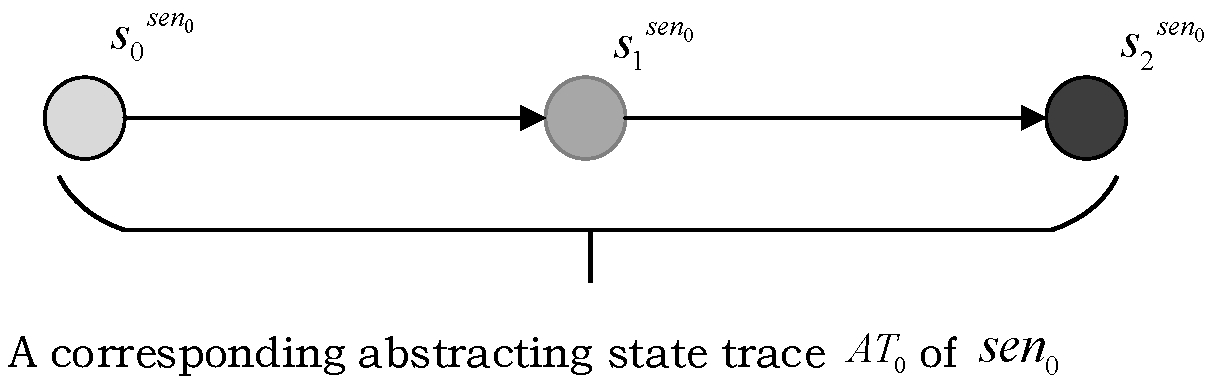
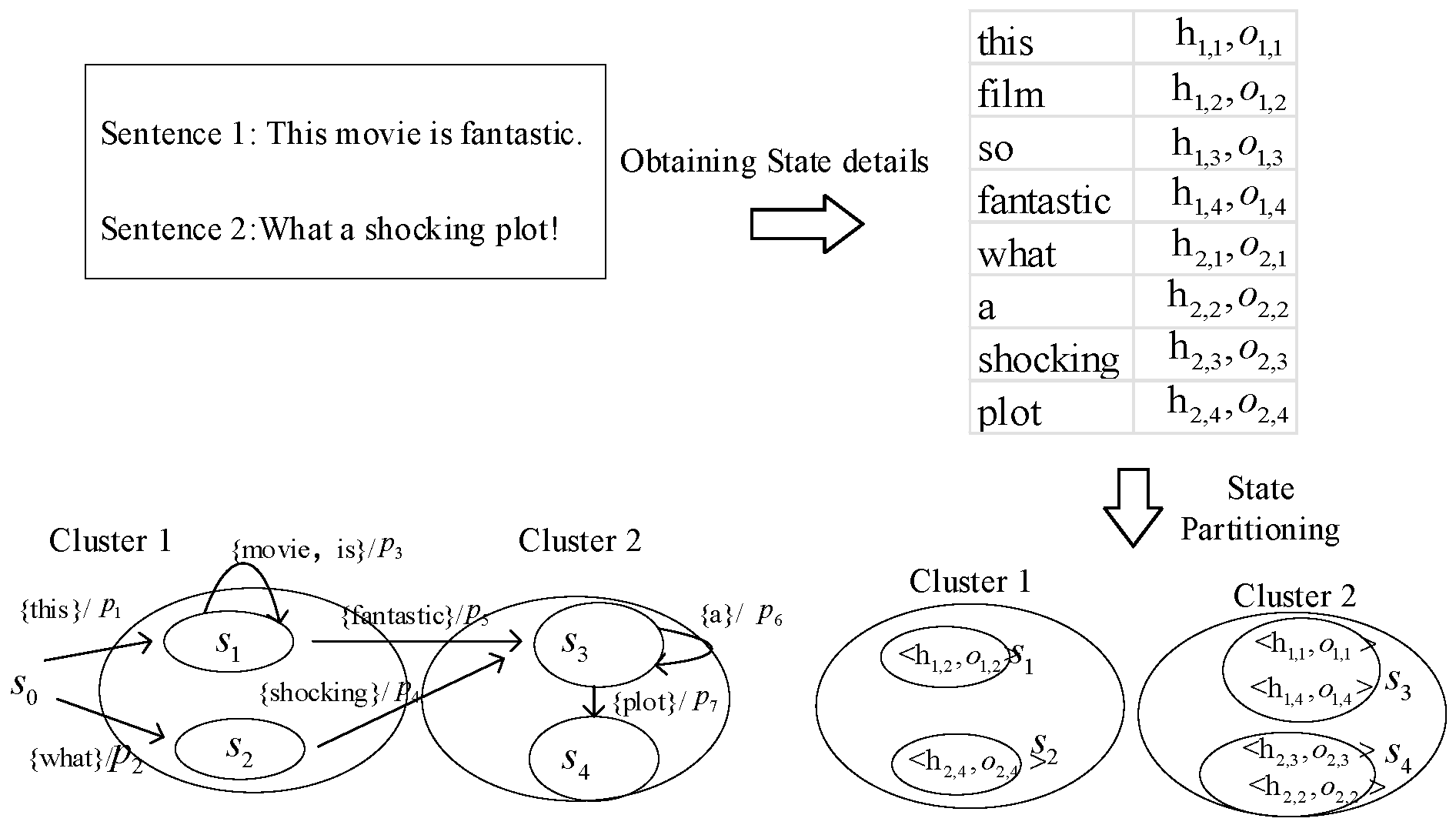
3.1.1. Obtaining the Abstract Traces
3.1.2. Learning PFA
| Algorithm 1. Learning PFA from FPT based on PSO. |
| Inputs: Outputs: 1 ; 2 be the set of nodes in the final PFA; 3 4 PFA’ ← FPT //candidates PFA from FPT by varying the BIC arguments. 5 6 } 7 Calculate the fitness of PD-PSO. //using Equation (1) 8 Update Ptx using Equations (2) and (3) 9 Get the best Ptx that minimizes the fit as much as possible. 10 End while 11 Return Ptx, fit |
3.2. Generating Explanation
| Algorithm 2. Explanation-Generating Algorithm. |
| Input: PFA , text dataset . Output: high-related explanation words Itp, explanation scores Sco.
|
4. Experimental Results
4.1. Experimental Setup
4.2. Results
4.2.1. Effectiveness
4.2.2. Usefulness
- (1)
- Explanation Generating
- (2)
- Adversarial Text Detection
5. Discussion
6. Conclusions and Future Works
6.1. Conclusions
- Learning PFA to integrate the information into the abstraction model;
- Adding PSO module to optimize the state merging algorithm;
- Abstracting RNN models to simplify the research of explainability;
6.2. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yüksel, N.; Börklü, H.R.; Sezer, H.K.; Canyurt, O.E. Review of artificial intelligence applications in engineering design perspective. Eng. Appl. Artif. Intell. 2023, 118, 105697. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, L.; Yu, S.G.; Shi, E.Z.; Qiang, N.; Gao, H.; Zhao, J.Y.; Zhao, S.J. An Explainable and Generalizable Recurrent Neural Network Approach for Differentiating Human Brain States on EEG Dataset. Ieee Trans. Neural Netw. Learn. Syst. 2022. Article ASAP. [Google Scholar] [CrossRef]
- Chang, G.; Gao, H.; Yao, Z.; Xiong, H. TextGuise: Adaptive adversarial example attacks on text classification model. Neurocomputing 2023, 529, 190–203. [Google Scholar] [CrossRef]
- Kapil, P.; Ekbal, A. A deep neural network based multi-task learning approach to hate speech detection. Knowl.-Based Syst. 2020, 210, 106458. [Google Scholar] [CrossRef]
- Peng, X.; Xian, H.; Lu, Q.; Lu, X. Semantics aware adversarial malware examples generation for black-box attacks. Appl. Soft Comput. 2021, 109, 107506. [Google Scholar] [CrossRef]
- Du, M.; Liu, N.; Yang, F.; Ji, S.; Hu, X. On Attribution of Recurrent Neural Network Predictions via Additive Decomposition. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 383–393. [Google Scholar]
- Li, X.Z.; Lin, F.F.; Wang, H.; Zhang, X.; Ma, H.; Wen, C.Y.; Blaabjerg, F. Temporal Modeling for Power Converters with Physics-in-Architecture Recurrent Neural Network. Ieee Trans. Ind. Electron. 2024. Article ASAP. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhang, W.E.; Yue, L. Death comes but why: A multi-task memory-fused prediction for accurate and explainable illness severity in ICUs. World Wide Web-Internet Web Inf. Syst. 2023, 26, 4025–4045. [Google Scholar] [CrossRef]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Yang, C.; Zhou, W.X.; Wang, Z.Y.; Jiang, B.; Li, D.S.; Shen, H.W. Accurate and Explainable Recommendation via Hierarchical Attention Network Oriented towards Crowd Intelligence. Knowl.-Based Syst. 2021, 213, 106687. [Google Scholar] [CrossRef]
- Hong, D.; Segre, A.M.; Wang, T. AdaAX: Explaining Recurrent Neural Networks by Learning Automata with Adaptive States. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington DC, USA, 14–18 August 2022; pp. 574–584. [Google Scholar]
- Yang, M.; Moon, J.; Yang, S.; Oh, H.; Lee, S.; Kim, Y.; Jeong, J. Design and Implementation of an Explainable Bidirectional LSTM Model Based on Transition System Approach for Cooperative AI-Workers. Appl. Sci. 2022, 12, 6390. [Google Scholar] [CrossRef]
- Khmelnitsky, I.; Neider, D.; Roy, R.; Xie, X.; Barbot, B.; Bollig, B.; Finkel, A.; Haddad, S.; Leucker, M.; Ye, L. Analysis of recurrent neural networks via property-directed verification of surrogate models. Int. J. Softw. Tools Technol. Transf. 2023, 25, 341–354. [Google Scholar] [CrossRef]
- Guillaumier, K.; Abela, J. Learning DFAs by Evolving Short Sequences of Merges. In Proceedings of the ICGI 2021—15th International Conference on Grammatical Inference, Virtual/New York City, NY, USA, 23 August 2021; pp. 217–236. [Google Scholar]
- Angluin, D. Learning regular sets from queries and counterexamples. Inf. Comput. 1987, 75, 87–106. [Google Scholar] [CrossRef]
- Vaandrager, F. Model learning. Commun. ACM 2017, 60, 86–95. [Google Scholar] [CrossRef]
- Hou, B.J.; Zhou, Z.H. Learning With Interpretable Structure From Gated RNN. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2267–2279. [Google Scholar] [CrossRef]
- Fan, M.; Si, Z.; Xie, X.; Liu, Y.; Liu, T. Text Backdoor Detection Using an Interpretable RNN Abstract Model. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4117–4132. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, X.; Zhang, Y.; Sun, M. Weighted automata extraction and explanation of recurrent neural networks for natural language tasks. J. Log. Algebr. Methods Program. 2024, 136, 100907. [Google Scholar] [CrossRef]
- Yellin, D.M.; Weiss, G. Synthesizing Context-free Grammars from Recurrent Neural Networks. In Proceedings of the Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2021, Luxembourg City, Luxembourg, 27 March–1 April 2021; Springer: Cham, Switzerland, 2021; pp. 351–369. [Google Scholar]
- Weiss, G.; Goldberg, Y.; Yahav, E. Extracting Automata from Recurrent Neural Networks Using Queries and Counterexamples. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Proceedings of Machine Learning Research; pp. 5247–5256.
- Barbot, B.; Bollig, B.; Finkel, A.; Haddad, S.; Khmelnitsky, I.; Leucker, M.; Neider, D.; Roy, R.; Ye, L. Extracting Context-Free Grammars from Recurrent Neural Networks using Tree-Automata Learning and A* Search. In Proceedings of the ICGI 2021—15th International Conference on Grammatical Inference, Virtual/New York City, NY, USA, 23 August 2021; pp. 113–129. [Google Scholar]
- Wang, J.; Sun, J.; Yuan, Q.; Pang, J. Learning probabilistic models for model checking: An evolutionary approach and an empirical study. Int. J. Softw. Tools Technol. Transf. 2018, 20, 689–704. [Google Scholar] [CrossRef]
- Weiss, G.; Goldberg, Y.; Yahav, E. Learning deterministic weighted automata with queries and counterexamples. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Weiss, G., Goldberg, Y., Yahav, E., Eds.; Curran Associates Inc.: New York City, NY, USA, 2019; pp. 8560–8571. [Google Scholar]
- Dong, G.; Wang, J.; Sun, J.; Zhang, Y.; Wang, X.; Dai, T.; Dong, J.S.; Wang, X. Towards interpreting recurrent neural networks through probabilistic abstraction. In Proceedings of the 35th IEEE/ACM International Conference on Automated Software Engineering, Virtual Event, 21–25 December 2021; pp. 499–510. [Google Scholar]
- Mao, H.; Chen, Y.; Jaeger, M.; Nielsen, T.D.; Larsen, K.G.; Nielsen, B. Learning Probabilistic Automata for Model Checking. In Proceedings of the 2011 Eighth International Conference on Quantitative Evaluation of SysTems, Aachen, Germany, 5–8 September 2011; pp. 111–120. [Google Scholar]
- Bhattacharya, C.; Ray, A. Thresholdless Classification of chaotic dynamics and combustion instability via probabilistic finite state automata. Mech. Syst. Signal Process. 2022, 164, 108213. [Google Scholar] [CrossRef]
- Ishimoto, Y.; Kondo, M.; Ubayashi, N.; Kamei, Y. PAFL: Probabilistic Automaton-Based Fault Localization for Recurrent Neural Networks. Inf. Softw. Technol. 2023, 155, 107117. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, K.; Ororbia, A.G., II; Xing, X.; Liu, X.; Giles, C.L. An Empirical Evaluation of Rule Extraction from Recurrent Neural Networks. Neural Comput. 2018, 30, 2568–2591. [Google Scholar] [CrossRef]
- Carr, S.; Jansen, N.; Topcu, U. Task-Aware Verifiable RNN-Based Policies for Partially Observable Markov Decision Processes. J. Artif. Intell. Res. 2021, 72, 819–847. [Google Scholar] [CrossRef]
- Wang, C.; Lawrence, C.; Niepert, M. State-Regularized Recurrent Neural Networks to Extract Automata and Explain Predictions. Ieee Trans. Pattern Anal. Mach. Intell. 2023, 45, 7739–7750. [Google Scholar] [CrossRef]
- Du, X.; Xie, X.; Li, Y.; Ma, L.; Liu, Y.; Zhao, J. DeepStellar: Model-based quantitative analysis of stateful deep learning systems. In Proceedings of the 2019 27th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Tallinn, Estonia, 26–30 August 2019; pp. 477–487. [Google Scholar]
- Maes, P. Concepts and experiments in computational reflection. In Proceedings of the Conference Proceedings on Object-Oriented Programming Systems, Languages and Applications, Orlando, FL, USA, 4–8 October 1987; pp. 147–155. [Google Scholar]
- Vouros, G. Explainable Deep Reinforcement Learning: State of the Art and Challenges. ACM Comput. Surv. 2023, 55, 92. [Google Scholar] [CrossRef]
- Kwiatkowska, M.; Norman, G.; Parker, D. PRISM 4.0: Verification of Probabilistic Real-Time Systems. In Proceedings of the International Conference on Computer Aided Verification, CAV 2011, Snowbird, UT, USA, 14–20 July 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 585–591. [Google Scholar]
- Chen, C.; Dai, J. Mitigating backdoor attacks in LSTM-based text classification systems by Backdoor Keyword Identification. Neurocomputing 2021, 452, 253–262. [Google Scholar] [CrossRef]
- Wang, B.; Yao, Y.; Shan, S.; Li, H.; Viswanath, B.; Zheng, H.; Zhao, B.Y. Neural Cleanse: Identifying and Mitigating Backdoor Attacks in Neural Networks. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 707–723. [Google Scholar]
- Li, J.; Ji, S.; Du, T.; Li, B.; Wang, T. TextBugger: Generating Adversarial Text Against Real-World Applications. arXiv 2018, arXiv:1812.05271. [Google Scholar]


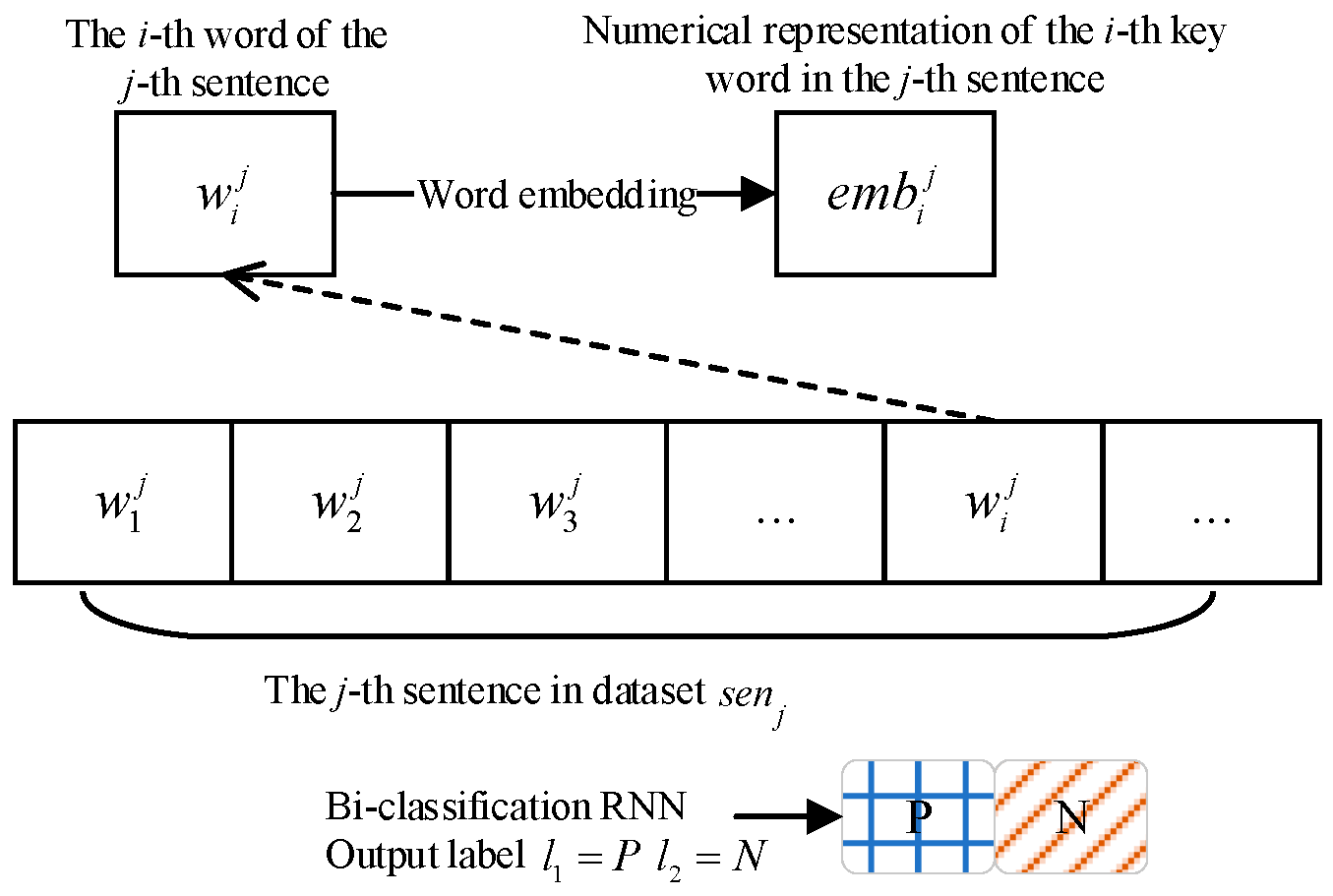






| Grammar | Description |
|---|---|
| Tomita_1 | 1* |
| Tomita_2 | (10)* |
| Tomita_3 | Compliments of ((0|1)* 0)*1(11)*(0(0|1)*1)*0(00)*(1(0|1)*)* |
| Abstracting Technique | IMDB-Re | DLRV-Re | Tomita-Re |
|---|---|---|---|
| BSL1 | 0.43 | 0.39 | 0.62 |
| BSL2 | 0.46 | 0.36 | 0.65 |
| PSO4RNN | 0.67 | 0.47 | 0.83 |
| Time Consumption | BSL1 | BSL2 | PSO4RNN |
|---|---|---|---|
| Tomita-LSTM | 0.23 h | 0.12 h | 0.11 h |
| IMDB-LSTM | 0.34 h | 0.17 h | 0.13 h |
| DLRV-LSTM | 0.37 h | 0.23 h | 0.21 h |
| Technique Type | State Numbers |
|---|---|
| BSL1 on GRU text sentiment analysis | 37 |
| BSL1 on LSTM text sentiment analysis | 43 |
| BSL2 on GRU text sentiment analysis | 25 |
| BSL2 on LSTM text sentiment analysis | 31 |
| PSO4RNN on GRU text sentiment analysis | 22 |
| PSO4RNN on LSTM text sentiment analysis | 28 |
| Dataset | Adversarial Sample Detection Accuracy MSE |
|---|---|
| Tomita | 93% |
| IMDB | 92% |
| DLRV | 89% |
| Characteristics | BSL1 | BSL2 | PSO4RNN |
|---|---|---|---|
| RNN structure explanation | yes | yes | yes |
| Feature importance explanation | no | no | yes |
| Probabilistic information | not considered | yes | yes |
| BIC parameter searching method | none | trial and error | heuristic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, H.; Ma, Y. Particle Swarm Optimization-Based Model Abstraction and Explanation Generation for a Recurrent Neural Network. Algorithms 2024, 17, 210. https://doi.org/10.3390/a17050210
Liu Y, Wang H, Ma Y. Particle Swarm Optimization-Based Model Abstraction and Explanation Generation for a Recurrent Neural Network. Algorithms. 2024; 17(5):210. https://doi.org/10.3390/a17050210
Chicago/Turabian StyleLiu, Yang, Huadong Wang, and Yan Ma. 2024. "Particle Swarm Optimization-Based Model Abstraction and Explanation Generation for a Recurrent Neural Network" Algorithms 17, no. 5: 210. https://doi.org/10.3390/a17050210
APA StyleLiu, Y., Wang, H., & Ma, Y. (2024). Particle Swarm Optimization-Based Model Abstraction and Explanation Generation for a Recurrent Neural Network. Algorithms, 17(5), 210. https://doi.org/10.3390/a17050210







