Point-Sim: A Lightweight Network for 3D Point Cloud Classification

Abstract

Analyzing point clouds with neural networks is a current research hotspot. In order to analyze the 3D geometric features of point clouds, most neural networks improve the network performance by adding local geometric operators and trainable parameters. However, deep learning usually requires a large amount of computational resources for training and inference, which poses challenges to hardware devices and energy consumption. Therefore, some researches have started to try to use a nonparametric approach to extract features. Point-NN combines nonparametric modules to build a nonparametric network for 3D point cloud analysis, and the nonparametric components include operations such as trigonometric embedding, farthest point sampling (FPS), k-nearest neighbor (k-NN), and pooling. However, Point-NN has some blindness in feature embedding using the trigonometric function during feature extraction. To eliminate this blindness as much as possible, we utilize a nonparametric energy function-based attention mechanism (ResSimAM). The embedded features are enhanced by calculating the energy of the features by the energy function, and then the ResSimAM is used to enhance the weights of the embedded features by the energy to enhance the features without adding any parameters to the original network; Point-NN needs to compute the similarity between each feature at the naive feature similarity matching stage; however, the magnitude difference of the features in vector space during the feature extraction stage may affect the final matching result. We use the Squash operation to squeeze the features. This nonlinear operation can make the features squeeze to a certain range without changing the original direction in the vector space, thus eliminating the effect of feature magnitude, and we can ultimately better complete the naive feature matching in the vector space. We inserted these modules into the network and build a nonparametric network, Point-Sim, which performs well in 3D classification tasks. Based on this, we extend the lightweight neural network Point-SimP by adding some trainable parameters for the point cloud classification task, which requires only 0.8 M parameters for high performance analysis. Experimental results demonstrate the effectiveness of our proposed algorithm in the point cloud shape classification task. The corresponding results on ModelNet40 and ScanObjectNN are 83.9% and 66.3% for 0 M parameters—without any training—and 93.3% and 86.6% for 0.8 M parameters. The Point-SimP reaches a test speed of 962 samples per second on the ModelNet40 dataset. The experimental results show that our proposed method effectively improves the performance on point cloud classification networks.

1. Introduction

In recent years, significant advancements have been witnessed in the field of 3D computer vision, which has become a subject of extensive research. Various formats, including meshes, volumetric meshes, depth images, and point clouds, can be utilized to represent 3D data [1]. Point clouds offer an unorganized sparse depiction of a 3D point set while preserving the original geometric information of an object in 3D space. Their representation is characterized by its simplicity, flexibility, and retention of most information without the need for discretization. The rapid development of 3D sensor technology, including various 3D scanners and LiDARs, has facilitated the acquisition of point cloud data [2]. Owing to its abundant geometric, shape, and scale information, 3D point clouds are crucial for scene understanding and find application in diverse fields such as autonomous driving, robotics, 3D reconstruction, and remote sensing, such as through RN4 and RN5.

However, the disorder and irregularity inherent in 3D point cloud data present challenges for deep learning-based point cloud feature extraction methods, which play a vital role in various point cloud processing tasks. Numerous approaches have been proposed to transform point clouds into regular structures, such as projecting into multiview images [3,4] and voxelization [5,6]. Although these methods have shown superior results in point cloud classification and segmentation tasks compared to traditional manual feature extraction techniques, they compromise the intrinsic geometric relationships of 3D data during processing. Moreover, the computational complexity of voxelization, being proportional to the cube of the volume, limits its application in more complex scenes.

To address these challenges, researchers have started considering the direct processing of raw point cloud data to reduce computational complexity and to fully leverage the characteristics of 3D point cloud data. PointNet [7] directly processes raw data by extracting point cloud features through MLP (MultiLayer Perceptron) and max pooling, thereby ensuring permutation invariance of the point cloud. Although the processing method is simple, it yields significant results and has become an important theoretical and ideological foundation in 3D point cloud processing. PointNet++ [8] extends PointNet by considering both global and local features. It obtains key point sets through farthest point sampling (FPS) and constructs a local graph using k-nearest neighbors (k-NN). Subsequently, MLP and max pooling are employed to aggregate the local features.

Since PointNet++, the main trend in deep learning-based point cloud processing methods has been to add advanced local operators and extend the trainable parameters, and while the performance gain rises by the amount of parameters added, so does the cost of computing resources, and deep learning training is often time-consuming. Many previous works have approached deep learning from a lightweight perspective in order to efficiently address the training and inference time issues of deep learning. For example, MobileNet [9] uses depthwise separable convolution to build a lightweight network, which improves the overall network accuracy and speed; UL-DLA [10] proposes an ultralightweight deep learning architecture. It forms a Hybrid Feature Space (HFS), which is used for tumor detection using a Support Vector Machine (SVM), thereby culminating in high prediction accuracy and optimum false negatives. Point-NN [11] proposes a new approach to nonparametric point cloud analysis that employs simple trigonometric functions to reveal local spatial patterns and a nonparametric encoder for networks to extract the training set features, which are cached as a point feature repository. Finally, the point cloud classification is accomplished using naive feature matching. However, its simple use of trigonometric functions in the process of feature embedding is blind and may lead to the neglect of key features. And because of its feature magnitude change in vector space during feature extraction, this will affect the stability of the model and have an impact in the final naive feature matching stage.

Inspired by the above work, we propose a nonparametric network model for point cloud classification task, which is composed of nonparametric modules, and uses the nonparametric attention block ResSimAM(Residual Simple Attention Module) to derive the attention weights, as well as the features during the feature extraction process, in order to enhance the weights of features with higher energy. In the feature extraction stage, a nonlinear feature transformation is achieved by using the Squash operation to squeeze the input features to a certain range without changing the direction in the vector space. The Squash operation helps to preserve the directional information of the feature vectors while eliminating the effect of magnitude, thereby allowing the network to better learn the structure and patterns in the data and better preserving the relationships between the feature vectors, which helps reduce numerical instability due to vector length variations for subsequent naive similarity matching.

The key contributions of our contributions can be summarized as follows:

• Aiming at the problem that there is some blindness in Point-NN when using trigonometric functions to encode features for mapping features into high dimensional space, we calculate the energy of each feature by utilizing an energy function and then add weights for each feature according to its energy, which improves the model’s ability to extract features without adding any trainable parameters to the original model.
• In order to alleviate the influence of feature magnitude in the final naive feature matching, we use the Squash operation in the stage of feature extraction so that the features are squeezed to a certain range without changing the direction in the vector space, thereby eliminating the instability brought by the feature magnitude. This enables the network to better learn the structure and patterns in the data and improve the model classification ability.
• We extend a lightweight parametric model by adding a small number of MLP layers to the nonparametric model feature extraction stage and applying the MLP to the final global features to obtain the final classification results, and we validate the performance of the model in the absence of other state-of-the-art operators.

The remainder of the paper is structured as follows. Section 2 gives related work. Section 3 describes the nonparameter network Point-Sim and the lightweight network Point-SimP methods in detail. We evaluate our methods in Section 4. Section 5 concludes the paper.

2. Related Work

To effectively handle 3D data, scholars have conducted diverse and significant endeavors aimed at addressing the challenges posed by the inherent sparsity and irregularity of point clouds. Such endeavors can be categorized into multiview-based, voxel-based, and point-based methodologies. Initially, we review the learning methodologies grounded in multiview representation and voxelization. Subsequently, we scrutinize point-based learning methodologies, which encompass graph-based and attention-based strategies.

2.1. Multiview-Based Methods

The Multiview Convolutional Neural Network (MVCNN) [4] projects point clouds or 3D shapes onto 2D images, thereby subsequently employing Convolutional Neural Networks (CNNs) for processing the projected 2D images. This methodology integrates feature information from multiple viewpoints into a compact 3D shape descriptor via convolutional and pooling layers. These aggregated features are then fed into a fully connected layer for classification. Zhou [12] proposed the Multiview PointNet (MVPointNet), where the views are acquired through a Transformation Network (T-Net) [7] to generate transformation matrices that determine multiple views captured at identical rotational angles, thereby ensuring the network’s robustness against geometric transformations.

Despite the efficacy of projecting point clouds into multiple views for point cloud segmentation and classification tasks compared to conventional manual feature extraction methods, notable limitations persist. Firstly, predetermined viewpoints are required when projecting 3D point clouds into multiple 2D views. View variations result in differential contributions to the final shape descriptor; similar views yield akin contributions, whereas significantly distinct views offer advantages for shape recognition. Secondly, 2D projections are confined to modeling the surface attributes of objects, which are unable to capture the 3D internal structure adequately. This partial representation disrupts intrinsic geometric relationships within 3D data, thus failing to exploit contextual information comprehensively within 3D space and incurring information loss, which is particularly unsuitable for large-scale scenes. Furthermore, feature extraction via multiview approaches often necessitates pretraining and fine-tuning, thereby consequently escalating workload demands.

2.2. Voxel-Based Methods

The VoxNet framework, as introduced by [5], initially employs an occupancy grid algorithm to represent the original point cloud as multiple 3D grids. Each grid corresponds to a voxel, and subsequent 3D convolutions are applied for feature extraction. Le proposed a hybrid network named PointGrid in the work of [13], which integrates both point and grid representations for efficient point cloud processing. This approach involves sampling a constant number of points in each embedded volumetric grid cell, thus allowing the network to utilize 3D convolutions to extract geometric details.

In contrast, voxel-based methods follow a two-step process. Firstly, the original point cloud undergoes voxelization, thereby converting the unordered point cloud into an ordered structure. Subsequently, 3D convolution is applied for further processing. This approach is more direct and simpler, thus drawing inspiration directly from 2D convolutional neural networks. However, it comes with a significant computational cost, and due to the uniformity of each voxel postvoxelization, there is a loss of information regarding fine structures.

2.3. Point-Based Methods

2.3.1. Graph-Based Methods

Point cloud data, which are characterized by an irregular and a disordered distributions of points, inherently lack explicit interconnections among individual points. Nevertheless, these non-Euclidean geometric relationships can be effectively modeled through graph structures. PointNet [7] stands out as the pioneering network specifically designed for the direct processing of point clouds. Despite the groundbreaking achievements of the PointNet network in tasks such as point cloud classification or segmentation, it remains afflicted by the limitation of its inadequate capture of local neighborhood information. To address this limitation and extract more nuanced local features, Qi [8] extended PointNet by introducing the PointNet++ network framework. The fundamental concept involves the construction of a local hierarchical module within the network. Each layer within this module comprises a sampling layer, a grouping layer, and a feature extraction layer. By selecting the local neighborhood center of mass through the FPS layer—forming a local neighborhood subset via the k-NN layer—and deriving local neighborhood feature vectors through the PointNet layer, the framework adeptly captures local features across a multilevel hierarchical structure. Nonetheless, PointNet++ faces challenges due to its isolation of individual point sample features within the local neighborhood and the adoption of a greedy max pooling strategy for feature aggregation, thereby risking information loss and presenting certain constraints. In response to these issues, Wang [14] proposed Softpoolnet, which introduces the concept of soft pooling by substituting max pooling with a soft pooling mode. Unlike the exclusive retention of maximal features in max operation, soft pooling retains more features by preserving the first N maximal features during pooling. Meanwhile, Zhao [15] introduced 3D point cloud capsule networks, and they created an autoencoder tailored for processing sparse 3D point clouds while preserving spatial alignment and consolidating the outcomes of multiple maximal pool feature mappings into an informative latent representation through unsupervised dynamic routing.

Nevertheless, it fails to adequately handle neighborhood points information, thus resulting in inadequate interactions between points. In order to enhance direct information exchange and foster better communication, DGCNN [16] employs the k-NN algorithm to construct local graphs, thus grouping points in semantic space and facilitating global feature extraction through continuous feature updates of edges and points. Notably, this approach enables the capture of geometric features of the local neighborhood while maintaining permutation invariance. Furthermore, DeepGCN [17] leverages deep Convolutional Neural Network (CNN) principles emphasizing deep residual connections, extended convolution, and dense connections, thereby enabling reliable training in deep models. GACNet [18], on the other hand, enhances segmentation results in edge areas by constructing a graph structure for each point based on its neighboring points and integrating an attention mechanism to compute edge weights between the central point and its neighbors.

Wang [19] proposed a method for training deformed convolution kernels in local feature extraction, wherein an anchor point is initially selected, followed by the selection of neighboring points through k-NN. Subsequently, a set of displacement vectors is constructed to represent features in this region, thereby facilitating continuous updates of these displacement vectors to extract local point cloud features. Finally, multiple sets of learned displacement vectors are weighted and summed to construct the convolutional kernel for feature extraction, which is then applied to perform feature extraction on the image. Notably, Point-NN [11] introduced a nonparametric network for 3D point cloud analysis comprising purely nonparametric components such as FPS, k-NN, trigonometric functions, and pooling operations. Remarkably, it demonstrates exceptional performance across various 3D tasks without any parameters or training, even outperforming existing fully trained models.

2.3.2. Attention-Based Methods

SENet [20] introduces an efficient and lightweight gating mechanism that explicitly constructs correlations between channels. This consideration stems from the acknowledgment that pixels carry varying degrees of importance across different channels. These importance weights are then leveraged to amplify useful features while suppressing less relevant ones. CBAM [21] derives attention mappings separately along two dimensions, channel and spatial, within the feature mapping. Subsequently, these attention mappings are applied to the input for adaptive feature refinement of the feature map. With the demonstrated success of self-attention and transformer mechanisms in natural language understanding [22], there has been a proliferation of efforts in computer vision to substitute convolutional layers with self-attention layers. However, despite its accomplishments, self-attention incurs computational costs that scale quadratically with the size of the input image. PAT [23] employs a self-attention-like mechanism to capture correlation information between points and extract the most salient global features via Gumbel downsampling. Transformer [24] devises a point transformer layer and builds a residual point transformer block around it, thus enabling information exchange between local feature vectors and the generation of new feature vectors for all points. PCT [25] encodes input coordinates into the feature space to generate features and conducts feature learning through the offset attention mechanism. PoinTr [26] processes the point cloud into a series of point proxies, which represent features of local areas within the point cloud. These proxy points encapsulate neighborhood information, which is then inputted into a transformer for further processing. Subsequently, an encoder–decoder architecture is employed to accomplish the point cloud completion task.

3. Methods

In this section, we will present the details of the nonparametric network Point-Sim and the lightweight neural network Point-SimP. We will show the overall structure of the proposed method, which consists of multiple reference-free components and incorporates the operations of the nonparametric attention mechanism and the feature Squash in the process of feature extraction.

3.1. Overall Structure

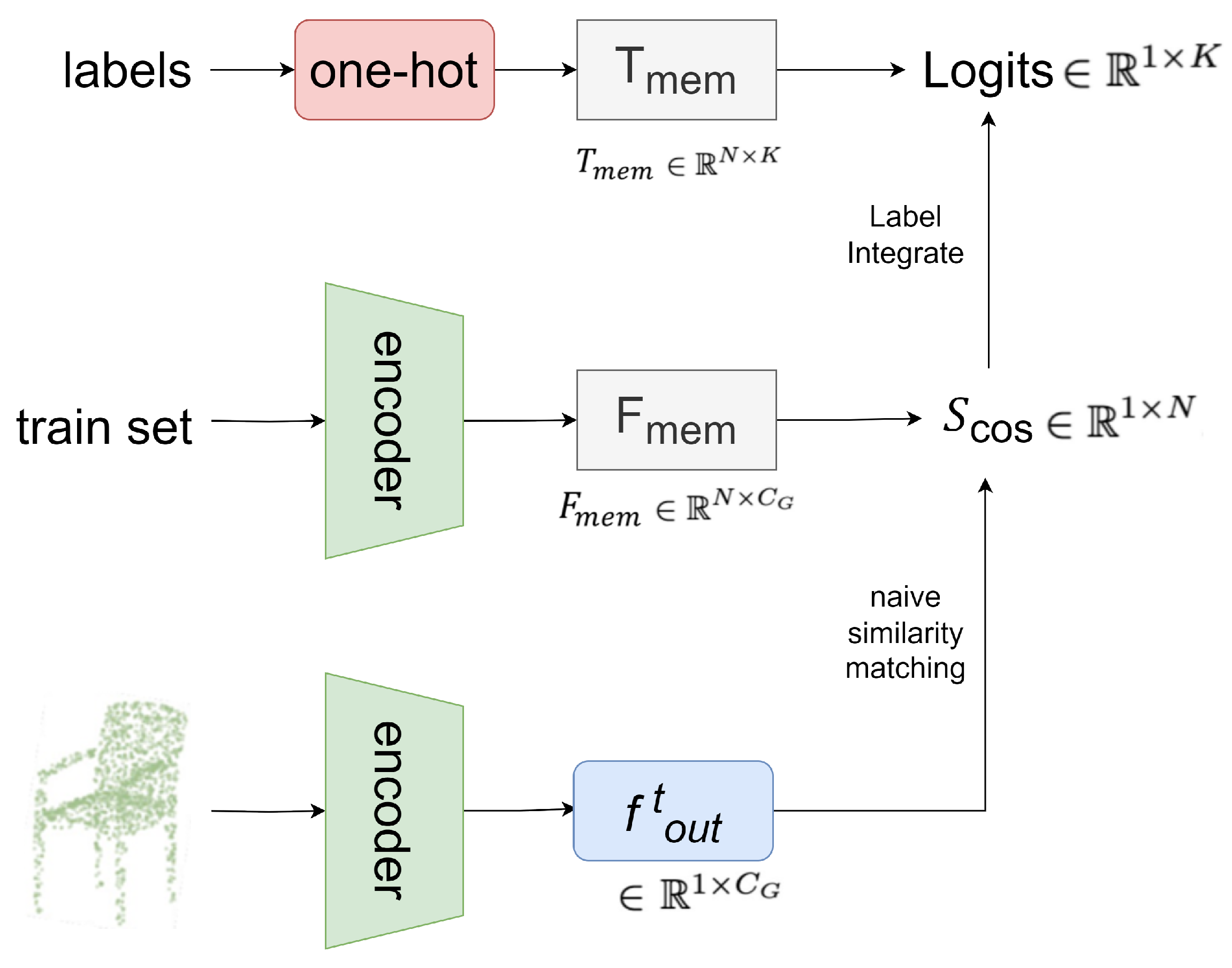
The nonparametric modeling of point cloud classification method known as Point-Sim is shown in Figure 1. In the classification model, nonparametric feature embedding is first performed using trigonometric functions(the Trigo block). Subsequently, in the hierarchical feature extraction stage, the centroids are selected using FPS, and from these centroids, the point clouds are grouped using k-NN. We apply trigonometric functions to map the local geometric coordinate. In order to better match the feature naive similarity, the geometric and local features are added and fed into the Squash block, the features are squeezed to make them smoother, and then the smoothed features are fed into the ResSimAM block so that the model can pay better attention to the features with higher energy; this improves the classification ability of the encoder, and then finally the global features are obtained by using the pooling operation.

The nonparametric point cloud classification model has been extended by integrating neural network layers at various stages within Point-Sim. The constructed Point-SimP network, outlined in Figure 2, introduces a lightweight framework. To enhance the model, the raw embedding layer within the nonparametric network was substituted with an MLP. Furthermore, MLP layers were incorporated post the Feature Expansion and Geometry Extraction phases during feature extraction and applied to the ultimate global feature to obtain the classification outcomes.

3.2. Basic Components

Our approach begins from the local structure, thereby extracting features layer by layer. We select a certain number of key points within the point clouds, utilizing k-NN to select the nearest neighboring points to generate local regions, and update the features of this local region. By repeating multiple stages, we gradually expand the sensory field and obtain the global geometric information of the point clouds. In each stage, we represent the input point clouds of the previous stage as ${\{p_i,f_i\}}_{i=1}^M$, where $p_i\in {\mathbb{R}}^{1\times 3}$ represents the coordinates of point i, and $f_i\in {\mathbb{R}}^{1\times C}$ represents the features of point i. To begin, the point set is downsampled using FPS to choose a subset of points from the original set. In this case, we select $\frac{M}{2}$ local centroids from the M points, where M is an even number.

$${\{p_c,f_c\}}_{c=1}^{\frac{M}{2}}=FPS\left({\{p_i,f_i\}}_{i=1}^M\right)$$

(1)

Afterward, by employing the k-NN algorithm, groups of localized 3D regions are established by selecting the k-nearest neighbors from the original M points for each centroid c (Figure 3).

$${\mathcal{N}}_c=k-NN(p_c,{\left\{p_i\right\}}_{i=1}^M)$$

(2)

where $N_c\in {\mathbb{R}}^{k\times 1}$ represents the k-nearest neighbors.

After obtaining the local information, we perform feature expansion (Figure 4) to obtain the features $f_l\in {\mathbb{R}}^{C\times K}$ of the local points. These are obtained by repeating the centroid point k times and concatenating it with the local features.

$$f_l=Concat\left(Repeat\left(f_c\right),{\left\{f_n\right\}}_{n=1}^k\right)$$

(3)

where $f_c\in {\mathbb{R}}^{C\times 1}$ represents the features of the center point, $f_n\in {\mathbb{R}}^{C\times 1}$ denotes the features of the remaining local points, and $C=2\times D$.

Furthermore, the operator $\Phi (·)$ is utilized to extract the geometry features ${\mathcal{N}}_{\mathcal{C}}$ of each local neighborhood, which comprises trigonometric functions, Squash, and ResSimAM.

$$\Phi (·)=ResSimam\left(Sqush(\mathrm{Trigonometric}(·)+f_l)\right)$$

(4)

Local features $f_l$ are processed using $\Phi (·)$, thus resulting in the enhanced local features $f_j\in {\mathbb{R}}^{C\times K}$.

$$f_j=\Phi \left(f_l\right)$$

(5)

MaxPooling and MeanPooling are performed to aggregate the data, thus producing $f_g\in {\mathbb{R}}^{C\times 1}$, which signifies the global features of the chosen key points.

$$f_g=MaxP\left({\left\{f_j\right\}}_{j\in {\mathcal{N}}_c}\right)+MeanP\left({\left\{f_j\right\}}_{j\in {\mathcal{N}}_c}\right)$$

(6)

Following this, after the above feature extraction stage, max pool aggregation is used to obtain the final high-dimensional global feature $f_{out}\in {\mathbb{R}}^{1\times C_G}$:

$$f_{out}=MaxP\left(f_g\right)$$

(7)

Finally, the resulting feature $f_{out}$ is cached in the memory bank $F_{mem}$, and we construct a corresponding label memory bank $T_{mem}$ as follows:

$$F_{mem}=\mathrm{Concat}\left({\left\{f_{out}\right\}}_{n=1}^N\right)$$

(8)

$$T_{mem}=\mathrm{Concat}\left({\left\{tabl{e}_i\right\}}_{n=1}^N\right)$$

(9)

where $tabl{e}_i$ is the ground truth as one-hot encoding, and n represents the serial number of each point cloud object in training set n from 1 to N.

3.3. Trigonometric Functions Embedding

Referring to positional encoding in the transformer [22], for a point in the input point cloud, we use trigonometric functions to embed it into a C-dimensional vector:

$$\mathrm{Trigonometric}\left(p_i\right)=\mathrm{Concat}(f_i^x,f_i^y,f_i^z)\in {\mathbb{R}}^{1\times C_i}$$

(10)

where $f_i^x,f_i^y,f_i^z\in {\mathbb{R}}^{1\times \frac{C_i}{3}}$ denote the embeddings of three axes, and $C_i$ represents the initialized feature dimension. Taking $f_i^x$ as an example, for channel index $m\in [0,\frac{C_i}{6}]$, we have the following:

$$\begin{array}{c}{f}_i^x\left[2m\right]=sin\left(\alpha x_i/{\beta }^{\frac{6m}{C_i}}\right),\\ f_i^x[2m+1]=cos\left(\alpha x_i/{\beta }^{\frac{6m}{C_i}}\right)\end{array}$$

(11)

where $\alpha$ and $\beta$ respectively control the magnitude and wavelength. Due to the inherent properties of trigonometric functions, the transformed vectors can effectively encode the relative positional information between different points and capture fine-grained structural changes in the three-dimensional shape.

3.4. Nonparametric Attention Module (Squash and ResSimAM)

SimAM [27] devises an energy function to discern the importance of neurons based on neuroscience principles, with most operations selected according to this energy function to avoid excessive structural adjustments. SimAM has been verified to have good performance in 2D parametric models. Due to its nonparametric character, we are considering incorporating this attention mechanism into our 3D point cloud network.

To successfully implement attention, we need to estimate the importance of individual features. In visual neuroscience, neurons that exhibit unique firing patterns from surrounding neurons are often considered to have the highest information content. Additionally, an active neuron may also inhibit the activity of surrounding neurons, which is a phenomenon known as spatial suppression [28]. In other words, neurons that exhibit significant spatial suppression effects during visual processing should be assigned higher priority. As with SimAM, we use the following equation to obtain the minimum energy for each position:

$$e_t^{\ast }=\frac{4({\widehat{\sigma }}^2+\lambda )}{{(t-\widehat{\mu })}^2+2{\widehat{\sigma }}^2+2\lambda }$$

(12)

where $\widehat{\mu }=\frac{1}{M}{\sum }_{i=1}^M{x}_i$, ${\widehat{\sigma }}^2=\frac{1}{M}{\sum }_{i=1}^M{(x_i-\widehat{\mu })}^2$, and M denote the feature dimensions.

The above equation indicates that the lower the energy $e_t^{\ast }$, the greater the difference between the neuron and its surrounding neurons, which is also more important in visual processing. The importance of neurons is represented by $1/e_t^{\ast }$. To enhance the features, we construct a residual network. Firstly, we apply the Squash operation to smooth the features, and then we add the ResSimAM attention operation to the squashed features:

$$\begin{array}{c}\begin{array}{c}\hfill X=Squash(f_i+f_c)\end{array}\\ \begin{array}{c}\hfill \tilde{X}=sigmoid\left(\frac{1}{E}\right)\odot X+X\end{array}\end{array}$$

(13)

where E groups all $e_t^{\ast }$ across all dimensions, and a sigmoid is added to restrict too large values in E.

Algorithm 1 denotes the pseudocode for the implementation of ResSimAM using PyTorch, where $X=Squash\left(f\right)$ as $X=\frac{{\parallel f\parallel }^2}{1+{\parallel f\parallel }^2}\frac{f}{\parallel f\parallel }$, and $\parallel f\parallel$ denotes the module of f.

Algorithm 1: A PyTorch-like implementation of our ResSimAM

Input: $f_i$, $f_c$, $\lambda$    Output: X 1 def forward (${\mathit{f}}_{\mathit{i}}$, ${\mathit{f}}_{\mathit{c}}$, $\mathit{\lambda }$): 2      $\mathrm{X}=\mathrm{Squash}({\mathrm{f}}_{\mathrm{i}}+{\mathrm{f}}_{\mathrm{c}})$; 3      $\mathrm{n}=\mathrm{X}.\mathrm{shape}\left[2\right]-1$; 4      $\mathrm{d}=(\mathrm{X}-\mathrm{X}.\mathrm{mean}(\dim =\left[2\right]\left)\right).\mathrm{pow}\left(2\right)$; 5      $\mathrm{v}=\mathrm{d}.\mathrm{sum}(\dim =[2\left]\right)/\mathrm{n}$; 6      $\mathrm{E}\_\mathrm{inv}=d/\left(4\ast (\mathrm{v}+\mathrm{lambda})\right)+0.5$; 7      return X* $\mathbf{sigmoid}(\mathbf{E}\_\mathbf{inv})+\mathbf{X}$;

The Squash operation enables a nonlinear feature transformation by squeezing the input features to a certain range without changing the direction in the vector space. This squeezing helps to preserve the directional information of the feature vectors while eliminating the effect of magnitude, thereby allowing the network to better learn the structure and patterns in the data and be able to better preserve the relationships between the feature vectors. The feature squeezing operation makes each feature vector have a unit length, which helps with better similarity computation between the vectors, and by normalizing the vectors to a unit length, the magnitude difference between the vectors can be reduced, which helps in reducing the numerical instability due to the change in the length of the vectors for the subsequent similarity matching of the features and improves the generalization ability of the network.

It is worth mentioning that Algorithm 1 does not introduce any additional parameter and can therefore work well in a nonparametric network. The energy function involved in the algorithm only requires computing the mean and variance of features, which are then brought into the energy function for calculation. This allows for the computation of weights to be completed in linear time.

3.5. Naive Feature Similarity Matching

In the naive feature similarity matching stage (Figure 5), for a test point cloud, we similarly utilize a nonparametric encoder to extract its global feature $f_{out}^t\in {\mathbb{R}}^{1\times C_G}$.

Firstly, we calculate the cosine similarity between the test feature $f_{out}^t$ and $F_{mem}$:

$$S_{cos}=\frac{f_{out}^t{F}_{mem}}{\parallel f_{out}^t\parallel \parallel F_{mem}\parallel }\in {\mathbb{R}}^{1\times N}$$

(14)

The above equation represents the semantic relevance between the test point cloud and N training samples. By weighting with Scos, we integrate the one-hot labels from the label memory $T_{mem}$ as:

$$\mathrm{logits}=\phi \left(S_{cos}{T}_{mem}\right)\in {\mathbb{R}}^{1\times K}$$

(15)

where $\phi \left(x\right)=exp(-\gamma (1-x\left)\right)$ serves as an activation function from Tip-adapter [29].

In $S_{cos}$, the higher the score of a similar feature memory pair, the greater its contribution to the final classification logits and vice versa. Through this similarity-based label integration, the point memory bank can adaptively differentiate different point cloud instances without any training.

4. Experiments

To validate the effectiveness, we evaluated the efficacy and versatility of the proposed methods for the shape classification task on the ModelNet40 dataset and ScanObjectNN dataset.

4.1. Shape Classification Task on ModelNet40 Dataset

Dataset: We evaluated our method on the ModelNet40 dataset for the classification task. This dataset comprises a total of 12,311 CAD mesh models, with 9843 models assigned for training and 2468 models for testing. The dataset covers 40 different classes.

In order to optimize memory usage and improve computational speed, we followed the experimental configuration of PointNet [7]. We uniformly selected 1024 points from the mesh surface using only the 3D coordinates as input data. We used the overall accuracy (OA) and the number of parameters for evaluation.

For the parametric network, we applied data augmentation; the data were augmented by adding jitter, point random dropout, and random scale scaling to each coordinate point of the object, where the mean value of jitter is 0, and its standard deviation is 0.1. The random scale scaling was between 0.66 and 1.5, and the probability of each point dropping out ranged from 0 to 0.875. The data were augmented with a weight decay of 0.0001 using an initial learning rate of 0.003 for the Adam optimizer with an initial learning rate of 0.001, and a weight decay of 0.0001 was used. In addition, training was performed using crossentropy loss. The batch size set for training was 32, and the maximum epoch was set to 300.

Experimental Results: The classification results on ModelNet40 are shown in

Table 1. Classification results on ModelNet40.

Method	Overall Accuracy (%)	Parameters	Train Time	Test Speed
PointNet	89.2	3.5 M	-	-
PointNet++	90.7	1.7 M	3.4 h	521
GBNet	93.8	8.4 M	-	189
DGCNN	92.9	1.8 M	2.4 h	617
PointMLP	94.1	12.6 M	14.4 h	189
Point-NN	81.80	0 M	0	275
Point-Sim	83.9	0 M	0	231
Point-SimP	93.3	0.8 M	3.1 h	962

. We compared our results with some recent methods on a RTX 3090 GPU. This comparison signifies that our proposed model generally outperformed several other models. We compared our results with respect to overall accuracy (OA), the number of parameters (Params), training time, and test speed (samples/second) with some recent methods. The proposed nonparametric method achieved an OA of 83.9% with 0 M parameters and without any training time, and the proposed parametric method achieved an OA of 93.3% with 0.8 M parameters, while our light parametric model test speed reached 926 samples per second. And because of the Squash module, our model was able to converge in a relatively short time of 3.1 h. Based on these comparisons with our method and related works, we have reached the conclusion that the network has advantages in terms of training speed and accuracy, as well as device requirements.

Our results are visualized on the ModelNet40 dataset, and the results are shown in Figure 6. For the nonparameterized model Point-Sim, the model OA was improved compared to Point-NN with similar inference speed. For the parameterized model Point-SimP, it was able to greatly improve the inference speed while maintaining the accuracy and had an advantage in the network training time.

We generated a 40 × 40 confusion matrix for our classification results, and the results are shown in Figure 7, in which there are 40 categories, with the horizontal axis representing the predicted labels and the vertical axis representing the ground truth labels (including airplane, bathtub, bed, bench, etc.). By visualizing the confusion matrix, we can see that most of the categories were classified well; for example, all the classifications on label 1 (airplane) and label 19 (keyboard) are correct, but the accuracies on label 16 (flower pot) and label 32 (stairs) still need to be improved. Figure 8 shows some representative results on ModelNet40.

4.2. Shape Classification Task on ScanObjectNN Dataset

Dataset: Although ModelNet40 is a widely adopted benchmark for point cloud analysis, its synthetic nature and the fast-paced advancements in this field may not fully address the requirements of current research. Thus, we have also undertaken experiments utilizing the ScanObjectNN [30] benchmark.

The ScanObjectNN dataset consists of 15,000 objects, with 2902 unique instances found in the real world. These objects belong to 15 different classes. However, analyzing this dataset using point cloud analysis methods can be challenging due to factors such as background interference, noise, and occlusion. Our loss function, optimizer, learning rate evolution scheduler, and data augmentation scheme maintained the same settings as the ModelNet40 classification task. We used the overall accuracy (OA) and the number of parameters for evaluation.

Experimental Results: The classification results obtained from ScanObjectNN are shown in

Table 2. Classification results on ModelNet40.

Method	Overall Accuracy (%)	Parameters
PointNet	68.2	3.5 M
PointNet++	77.9	1.7 M
GBNet	80.5	8.4 M
DGCNN	78.1	1.8 M
PointMLP	85.2	12.6 M
Point-NN	64.9	0 M
Point-Sim	66.3	0 M
Point-SimP	86.6	0.8 M

. We assessed the accuracy of all methods by reporting the performance on the official split of PB-T50-RS. The model achieved an OA of 66.3% with 0 M parameters and 86.6% with 0.8 M parameters, thereby demonstrating the versatility of our proposed method and the robustness of our model under background interference, noise, and occlusion.

4.3. Ablation Study

To showcase the efficacy of our approach, we conducted an ablation study on the classification task in ModelNet40. Furthermore, we performed separate ablation experiments on the ResSimAM and the Squash to assess the impact of removing each component.

In our settings (

Table 3. Settings of ResSimAM and Squash. where ✔ means that the module is included, and - means that the module is not included.

Method	Res-SimAM	Squash
W/O R&S	-	-
W/O S	✔	-
W/O R	-	✔
Point-Sim	✔	✔

), W/O R means no ResSimAM interaction, and W/O S means no Squash. The corresponding results are shown in

Table 4. ResSimAM and Squash ablation results.

Method	Overall Accuracy (%)
W/O R&S	81.8
W/O S	82.4
W/O R	83.2
Point-Sim	83.9

.

We utilized ResSimAM, which resulted in an improvement of the overall accuracy by 0.6%. We employed Squash to squeeze the features, thus leading to a 1.4% improvement in the overall accuracy. And we employed both operations—leading to a 2.1% improvement—and obtained a state-of-the-art result of 83.9% in no-parametric point cloud classification. It has been proven that using ResSimAM can better focus on higher energy features during the feature extraction stage, which can enhance features useful for subsequent processing, while the Squash module enables the input features to be squeezed to a certain range without changing the direction in the vector space, which realizes a nonlinear feature transformation and reduces the numerical instability due to the change of vector length. With ResSimAM, we can indeed better capture features with higher energy for feature enhancement, but it is possible that features with higher energy are not the most appropriate choice in the subsequent processing, so this approach brings some enhancement to the model’s classification ability but with some limitations. For the Squash operation, although squeezing the features facilitates the network to capture the relationship between the features and better perform the naive similarity matching, squeezing the features also brings some loss of feature information. These aspects still need to be improved.

5. Conclusions

This study introduces an innovative approach aimed at improving the efficiency of existing point cloud classification methods. The methods for deep learning-based point cloud processing have become increasingly intricate and often requiring long training times and high costs. We propose a new network model: a nonparametic point cloud classification network. We utilized trigonometric functions for embedding and apply Squash to smooth the features for subsequent processing. Then, we enhanced the features using the nonparametic attention mechanism ResSimAM, thereby leading to significant improvements in the purely nonparametric network for 3D point cloud analysis. Based on this, we also extended a lightweight parametric network, which allows for efficient inference with a small number of parameters. For the nonparametric model, our model achieved 83.9% accuracy on the ModelNet40 dataset without any training, which greatly saves time in training the model for the point cloud classification task. For the lightweight parametric model, we achieved 93.3% accuracy using only 0.8 M parameters, the training time was only 3.1 h, and the inference speed reached 962 samples per second, which will greatly reduce the pressure on hardware devices and keep the inference speed relatively high. Various tasks like autonomous vehicles, virtual reality, and aerospace fields demand real-time data handling, and our lightweight models could work efficiently in these tasks.

Although our method has achieved promising results, there is still room for improvement. For nonparametric network models, the feature extraction ability of our network on diverse datasets still needs to be tested and improved. For the lightweight parametric model, although the Squash operation was used to accelerate the convergence of the network, it brings some impact on the feature extraction ability of the network. In future research, we will focus on enhancing the generality and robustness of the proposed network. Future work needs to consider the computational efficiency of the network and the feature extraction capability of the model, as well as propose more effective and concise lightweight methods. This can be achieved by designing new nonparametric modules and combining them with a small number of neural networks, as well as adopting more efficient computational methods. In future work, we will explore nonparametric models with a wider range of application scenarios.