Abstract
With the rising popularity of the Advanced Driver Assistance System (ADAS), there is an increasing demand for more human-like car-following performance. In this paper, we consider the role of heterogeneity in car-following behavior within car-following modeling. We incorporate car-following heterogeneity factors into the model features. We employ the eXtreme Gradient Boosting (XGBoost) method to build the car-following model. The results show that our model achieves optimal performance with a mean squared error of 0.002181, surpassing the model that disregards heterogeneity factors. Furthermore, utilizing model importance analysis, we determined that the cumulative importance score of heterogeneity factors in the model is 0.7262. The results demonstrate the significant impact of heterogeneity factors on car-following behavior prediction and highlight the importance of incorporating heterogeneity factors into car-following models.
1. Introduction
With the rapid development of the Advanced Driver Assistance System (ADAS), Adaptive Cruise Control (ACC) has been widely adopted. As a result, the demand for more human-like car-following performance in ACC is growing significantly.
The car-following model has been developed for over 70 years and describes the longitudinal interactions between the following vehicle and the heading vehicle [1]. These models have been actively applied to intelligent transportation systems and autonomous driving [2,3]. Since the earliest car-following model was built by Pipes [4] in 1953, a vast number of car-following models have been developed. According to the modeling methods, car-following models were divided into theory-driven models and data-driven models [1].
The theory-driven car-following models use mathematical formulas to express the driver’s car-following behavior. According to different theories, these models can be divided into stimulus–response models [5], desired measures models [6], safety distance or collision avoidance models [7], etc. The advantages of theory-driven car-following models include the following: (1) clear expression of model formulas, with each parameter having a defined physical meaning; and (2) low-latency mathematical calculations are easily computed for the system. However, there are some limitations. Theory-driven car-following models may not effectively capture the intuitive decision-making process of human drivers [1]. They also have strong limitations on input variables. The requirement that each variable must be quantifiable as a clear physical quantity makes it difficult to consider multiple influencing factors, such as human factors and traffic factors, which are difficult to quantify and incorporate into the model. Some researchers have attempted to consider these factors in their models, such as Saifuzzaman [8] and Treiber [9]. However, this often results in complex model parameters that are difficult to calibrate and reduce the model’s usability.
In recent years, with the widespread use of machine learning theory and the availability of large-scale trajectory data, data-driven car-following models have made significant progress. Data-driven car-following models utilize machine learning tools to mine phenomena and underlying patterns within large amounts of car-following behavior data and then predict car-following behaviors. The feasibility of data-driven car-following models was initially verified in 1998 when Kehtarnavaz [10] presented a car-following model based on a feedforward neural network. Subsequently, various machine learning car-following models have been proposed, such as those based on ensemble learning methods [11] and artificial neural networks [12,13]. In the past several years, with the penetration of deep learning models into various fields [14], some data-driven car-following models based on deep learning theory have emerged. For instance, Wang [15] proposed a data-driven car-following model based on the gated recurrent unit (GRU) network. This model takes the velocity, velocity differences, and position differences that were observed over a period of time as inputs and predicts the driver’s car-following behavior at the next moment. The result showed that the model achieved high accuracy on the Next-Generation Simulation Program (NGSIM) dataset. Guo [16] applied the long short-term memory (LSTM) model to car-following behavior modeling. By extracting statistical variables from the trajectory data within a special time window (2 s in this literature), the results showed that the model achieved better performance than the traditional Gipps model. The core idea in these papers is that by considering long-term sequence data in deep learning models, factors such as drivers’ experiences and preferences can be automatically embedded into the model to achieve high-level prediction accuracy. Undoubtedly, the strong imitation ability of deep learning car-following models for human car-following behavior is one of their advantages. However, there are also certain limitations to consider. (1) High latency. Choosing to input long-term sequence trajectory data means that a more complex model structure is required to process it. Wang [15] used 3 hidden layers with a total of 50 neurons (30-10-10 neuron structure) to process them, and Guo [16] used seven hidden layers, which takes a longer processing time. (2) These models lack interpretability because they have no explicit model expression. These limitations may be unacceptable for vehicle driving systems that require real-time processing and explainable decision-making. Furthermore, the memory effect is only one aspect that affects car-following behavior.
Importantly, the heterogeneity of car-following behavior should also be taken into account in car-following modeling [17]. Heterogeneity stems from differences among the agent’s traffic flow, which are the heterogeneity of drivers and vehicle characteristics [17]. Heterogeneity refers to differences in behavior and characteristics between drivers and vehicles. Ossen [17,18,19] used trajectory data to confirm that heterogeneity in car-following behavior does exist. The heterogeneity of car-following behavior can be caused by car-following combinations, driving styles, and traffic flow. Four types of car-following combinations are divided into (1) Car–Car; (2) Car–Truck; (3) Truck–Truck; and (4) Truck–Car. The car-following behavior of truck drivers will be more robust than that of car drivers. It has been observed [19] that the speed of truck drivers is more consistent compared to that of passenger car drivers. This can be attributed to the larger weight of trucks, which makes them less agile. Additionally, it is plausible that truck drivers adopt a more assertive driving style, as they may be able to anticipate future traffic conditions better due to their heightened visibility and greater driving skills. Zheng [20] found that when the heading vehicle is large, the time headway (THW), time to collision (TTC), and safety margin (SM) of the following vehicle are significantly increased. That means the drivers have a lower level of risk acceptance. According to Zhang [21], drivers are inclined to adjust their driving behaviors in response to varying traffic conditions. Jiao [22] proposed the concept of proximity resistance and demonstrated that in congested traffic flow, a higher tolerance for approach resistance leads to lower following distances being maintained. Traffic flow has a larger impact on the proximity resistance of truck drivers than that of car drivers.
Table 1 summarizes the heterogeneity factors:

Table 1.
Heterogeneity factors on car-following behavior.
As we can see, heterogeneous factors will affect the car-following behavior of human drivers. By using a large amount of trajectory data, Ossen et al. [17,19,20,21,24]. confirmed the impact of different factors on car-following behavior, such as vehicle type, preceding vehicle type, and traffic flow. Research shows these factors can have a significant impact on drivers’ behavioral habits or decision-making. For example, the behavior of truck drivers in car-following scenarios tends to exhibit more robust patterns compared to that of passenger car drivers. The drivers tend to adjust their driving behaviors in response to varying traffic conditions. Ossen confirmed that how to comprehensively consider these factors is an important research topic in areas such as traffic modeling and autonomous driving. These factors have an important impact on the car-following performance of human drivers, so it is very beneficial to consider these factors when building an autonomous driving system that is closer to human behavior.
In this research area, some researchers have made contributions. Ahmed’s model [25] takes into account different traffic flows. Its equation is as follows:
where represents the traffic flow by calculating the traffic density of following vehicle within its view (a visibility distance of 100 m was used) at time , , is the velocity of the following vehicle at time , is the spacing from the heading vehicle. Where is the sensitivity lag parameter and are the constant parameters.
Wang [26] proposed the model, which considered driving habits and is shown in Equation (2):
where represents the influence of the driving habit and is the desired distance of the driver. Other variables are similar to Equation (1). However, the model lacked validation using real-world data. As aforementioned, data-driven models possess a powerful capability to replicate human behavior. They encode human preferences implicitly within the model. For example, Wu [27] combined numerous deep neural network structures, such as GRU and CNN, to learn the behavior of human drivers. Human factors such as drivers’ preferences, memory effects, prediction, and attention mechanisms could be automatically addressed by the machine learning model. Wang [15] and Guo [16] also support this point. Aghabayk [28] applied the local linear model tree (LOLIMOT) model to build a car-following model and incorporated the vehicle type into the model. The model proposed by Aghabayk explicitly considers the different scenarios when the preceding vehicle is a truck or a passenger car, while implicitly taking into account the human driver’s preferences and habits. The main statements of these models (including their type, equation, heterogeneity factors embedded, strength, and weakness) are also summarized in Table 2.

Table 2.
Summary of the car-following models considered heterogeneity factors.
As shown in Table 2, these studies have taken into account heterogeneity factors in modeling the following behavior, but there are still research gaps in human-likeness and model methods.
- Current car-following models are too limited in consideration of human-likeness. In theory-driven models, only a few factors are typically included due to the increased complexity that arises from incorporating additional parameters. Furthermore, quantifying certain factors into physically meaningful parameters can be challenging. In data-driven models, the current focus of research primarily revolves around using deep learning models to directly emulate human behavior, often overlooking the consideration of heterogeneity factors. As mentioned before, research on behavioral heterogeneity factors has been extensively analyzed to determine whether they have an impact on car-following behavior. However, these factors are not fully considered in the construction of car-following models in the field of autonomous driving.
Thus, in order to achieve a more human-like effect, we add these factors to the car-following model so that the model can learn this knowledge through machine learning and make human-like responses.
- 2.
- Current car-following models mainly use theory-driven models and deep learning models; the choice of models can be expanded. Incorporating heterogeneity factors into theory-driven models often leads to more parameters, making model calibration challenging. Deep learning models have good performance, but they have complex structures, resource-intensive requirements, and low interpretability. Ensemble learning models provide a promising avenue for further exploration. It can imitate human behavior through machine learning, and it can also embed other heterogeneous factors artificially. Crucially, the ensemble learning model has strong learning ability and is lightweight, which are two of the key factors applied in actual autonomous driving systems.
Therefore, in order to increase the practicality of data-driven car-following models in actual autonomous driving systems, we explore more ensemble learning decision-tree models for car-following modeling.
In summary, to bridge the research gaps in these two aspects, the purpose of our research is to try to embed behavioral heterogeneity factors into the car-following model to achieve more human-like car-following performance. At the same time, we apply the ensemble learning method to expand the breadth of practical application of the car-following model in autonomous driving.
In this paper, we first incorporate heterogeneity factors into the car-following model. Secondly, we use an interpretable machine learning model to build a car-following model based on the HighD (Highway Driving Dataset for Autonomous Driving) dataset. Finally, we conduct a comparison between car-following models that consider heterogeneity and those that do not and quantify the impact of heterogeneity factors on car-following behavior.
Our contributions are highlighted as follows:
- (1)
- Incorporating the heterogeneity factors of car-following behavior into the car-following model to achieve more human-like car-following performance.
- (2)
- Apply decision tree-based ensemble learning algorithms for the data-driven car-following model, which can partially overcome the issues of deep learning models’ lack of interpretability and high latency.
- (3)
- This paper quantifies the impact of heterogeneity factors on car-following behavior. That helps researchers better understand the effect of heterogeneity in car-following modeling.
The remainder of this paper is organized as follows: In Section 2, we introduce the decision tree-based ensemble learning method that will be used in this paper. Then, three different encoding methods are introduced for the heterogeneity factor. Section 3 analyzes the heterogeneity of car-following behavior in the HighD dataset and applies the proposed model to predict the car-following behavior of drivers. We conclude this paper with a discussion in Section 4.
2. Materials and Methodology
2.1. Data and Variables
2.1.1. Data Description
To validate our research, we sought out the widely recognized HighD dataset, which is an open-source dataset widely used in the field. The dataset has been extensively utilized for various studies, including car-following [29,30], lane-changing [31], and trajectory prediction [32]. One of the key advantages of the HighD dataset is its high-quality data and diverse range of scenarios. The HighD dataset comprises post-processed trajectories of 110,000 cars and trucks extracted from drone video recordings captured during the years 2017 and 2018 on German highways. The recordings were conducted at six different locations (refer to Figure 1) along a road segment of approximately 420 m (refer to Figure 2). Each vehicle in the dataset has a median visibility duration of 13.6 s.
Figure 1.
The recording locations in the HighD dataset.
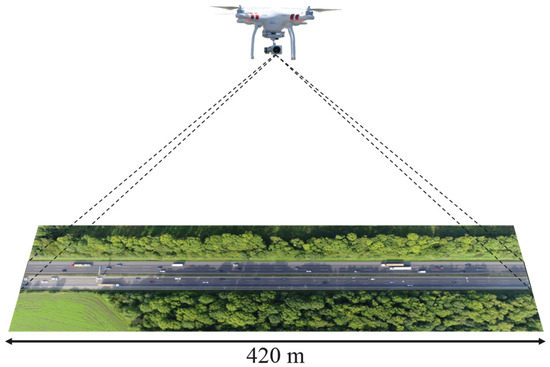
Figure 2.
The recording setup of the HighD dataset.
The dataset provides valuable insights through two primary data files per recording. The first file contains statistical information on the driving behavior and attributes of all vehicles present during the recording period. This includes vehicle identifiers (which remain consistent within the data file), vehicle dimensions, types, and lane positions, as well as maximum acceleration and inter-vehicle distances during operation. Please refer to Table 3 for key indicators. The second data file contains detailed motion information for each vehicle, including speed, acceleration, distance to the preceding vehicle, and preceding vehicle identifiers, recorded at each frame. This information enables a comprehensive understanding of the real-time driving states of vehicles. Please refer to Table 3 for a detailed breakdown.

Table 3.
Key features of the HighD dataset.
In summary, the HighD dataset offers a comprehensive and reliable resource for studying highly automated driving systems. The HighD dataset’s rich features and diverse scenarios make it a valuable asset for our research.
2.1.2. Data Pre-Processing
The aim of this paper is to enhance the human-likeness of the car-following model by incorporating the behavioral heterogeneity factors mentioned earlier. To reduce the influence of other interference factors, such as the external environment and differences in locations, it is better to choose one recording to analyze. In this paper, the 46-th track recording of location 1 has been selected as it exhibits the highest proportion of trucks and the total number of vehicles within the recordings.
Subsequently, in order to extract car-following state data for our experiments, we performed data preprocessing. This involved a two-step approach:
Firstly, we identified vehicles that were actively engaged in car-following. This was achieved by systematically examining the vehicle IDs in the HighD dataset files to identify cases where a vehicle had a preceding vehicle and the car-following duration was at least 15 frames. This filtering criterion was employed to exclude instances where the vehicle was potentially involved in lane-changing maneuvers or exiting the recording area.
Secondly, trajectory data were further refined to ensure that drivers were in a steady car-following state. To achieve this, we applied the following filtering constraints:
- Exclude distance headways larger than 150 m to guarantee the influence of the heading vehicle.
- Exclude the situation of the dangerous car following the scenario where the relative distance is less than 50 m and the relative speed is greater than 3 m/s.
By employing these stringent filtering criteria, we obtained a refined subset of data that accurately captured steady car-following states. This subset serves as the foundation for our experiments and enables us to conduct a comprehensive analysis of car-following behaviors.
In total, the dataset includes 1103 trajectories (207,417 samples extracted), as shown in Table 4.

Table 4.
Overview of the dataset.
In our experiment, 80% of the data were used for training; the rest were used for tests.
2.1.3. Input and Output Variables
This paper includes two types of input variables, one of which is trajectory variables. These variables have been demonstrated to play a significant role in modeling car-following behavior [33]. That is listed in the following Table 5.

Table 5.
Input variables based on trajectory data.
Another type of input variable is heterogeneity. Past researchers have stated that traffic flow and car-following combinations will affect car-following behavior [19,24,34,35,36]. In this paper, different traffic flows are represented by the mean velocity of the lane. Using 80 km/h and 100 km/h as the threshold, the traffic flow is divided into three situations: high flow, medium flow, and low flow. There are four types of car-following combinations: Car–Car, Car–Truck, Truck–Car, and Truck–Truck. When using categorical variables as input features in predictive models, it is necessary to encode them into numerical values. The appropriate encoding method will be an important consideration in the development of the model. This is discussed in Section 2.2.
The output variable is the longitudinal velocity after Ts. The model expression is as follows:
where denotes the categorical variable of traffic flow, denotes the categorical variable of car-following combination, and denotes the implicit function.
2.2. Methodology
In this section, we describe the methodology employed in our study. Firstly, we provide an overview of the experimental workflow, outlining the steps undertaken in our study. Then, we begin by introducing the principles of ensemble learning models, followed by detailed explanations of the two models used in this study: random forest (RF) and XGBoost (XGB). Subsequently, we discussed the encoding methods employed for handling categorical variables. Through this comprehensive methodology, we aim to elucidate the approach taken to develop and evaluate our car-following model.
2.2.1. The Design of the Experimental Process
The Design of the Experimental Process is as follows:
Step 1. Car-Following Dataset Creation: The car-following dataset is created by collecting data and applying filtering techniques to ensure data quality. Steady-state car-following data are selected to capture stable behavior patterns. Additionally, input and output features are carefully chosen to represent relevant aspects of car-following behavior. Please refer to Section 2.1 for more details.
Step 2. Model Selection: the appropriate model is chosen based on the specific requirements of the research.
Step 3. Encoding Method Selection: For heterogeneity variable embedding, we will compare three different encoding methods to select the best one.
Step 4. Model Training and Fine-Tuning: After determining the optimal encoding method, we will train the final model and tune the parameters using grid research.
Step 5. Model Evaluation: This step involves evaluating the trained model to assess its effectiveness in capturing and predicting car-following behavior accurately. For details about model metrics, please refer to Section 2.2.6.
Step 6. Ablation Experiment: An ablation experiment is performed to analyze the impact of removing heterogeneity variables from the model, providing insights into the individual contributions of heterogeneity variables to the overall model performance.
The flow chart of the experiment is shown in Figure 3.
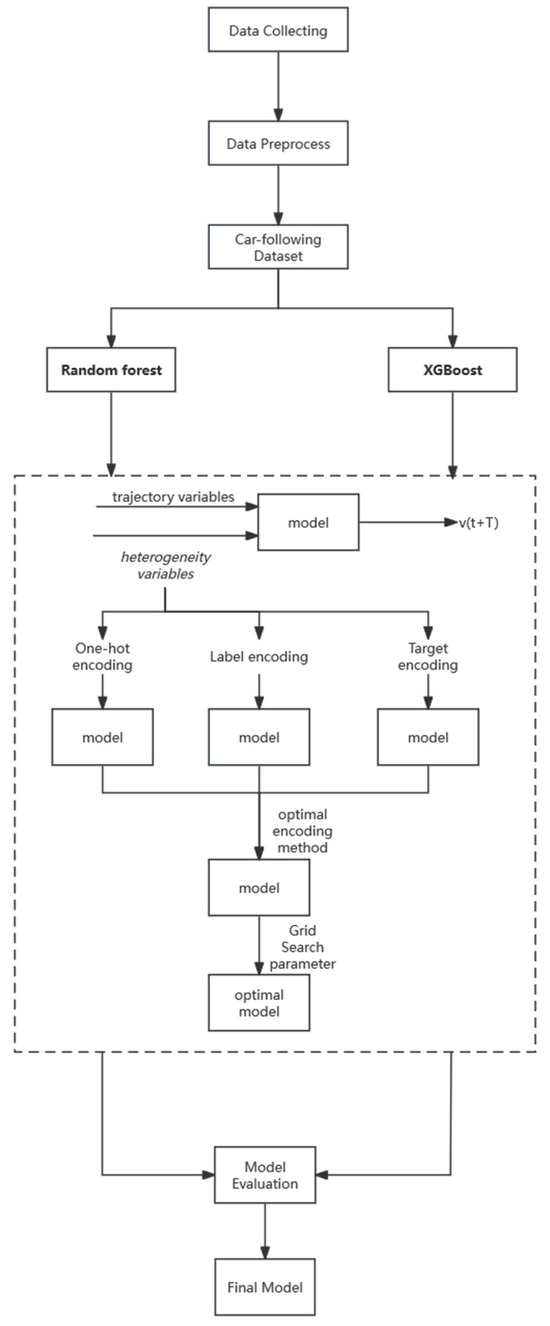
Figure 3.
The flow chart of the experiment.
2.2.2. Ensemble Learning
We chose the eXtreme Gradient Boosting (XGBoost) algorithm and the random forest (RF) algorithm as the experimental models in this paper to determine the final model. They are all types of ensemble learning and tree-based models.
The ensemble learning method gives them excellent performance in capturing complicated patterns within data. Moreover, the special structure of the tree-based model allows them to explain the model’s decision-making clearly, thus enhancing its interpretability. As mentioned in Section 1, current data-driven car-following models based on deep learning suffer from a lack of interpretability and efficiency, which makes it difficult to apply them in real-world scenarios. The theory-driven car-following models are limited in flexibility and accuracy, and their mathematical formula is too abstract to explain the human decision-making process. Therefore, we applied XGBoost and RF models that can strike a balance between interpretability, accuracy, and latency to address this issue.
Ensemble learning is one of many machine learning methods. The core idea is to integrate the results of all basic learners. A major question needs to be answered in ensemble methods: How to combine basic learners to yield the final model? Accordingly, two types of ensemble methods are identified: the Bagging method and the Boosting method. The RF model and the XGBoost model are representatives of them, respectively.
2.2.3. Random Forest Method
Random Forest is a bagging model that trains multiple decision trees in parallel. The final output is determined by aggregating the predictions of individual trees, typically using majority voting [37]. In contrast, the XGBoost algorithm creates an ensemble of decision trees sequentially. Each subsequent tree is trained to correct the errors made by the previous ones, all of which work to improve each other and determine the final output [38]. The following is a further introduction to them.
Random forest (RF) was developed by Breiman and Cutler in 2001 [37]. RF has been actively applied in many areas due to its excellent performance [39]. “Random” means the randomness of sampling from the training dataset and the randomness of selecting features for the basic regression tree. RF model training can be highly parallelized, which is advantageous for the speed of large-sample training in the area of big data. The main process in the RF model is as follows:
For the input dataset , the RF model uses the Bagging sampling method to obtain subsample sets, which each have samples. With the subsample set , features were selected randomly from all features for training the basic learner. Finally, average the results of each basic learner as the prediction result .
Three key parameters affect RF model performance: the number of maximum features selected , the number of regression trees, and the maximum tree depth of each regression tree . The larger is, the better the performance of base learners is, but the independence between base learners will be reduced. Generally, increasing the number of regression trees can improve the accuracy of the model, but at the cost of increased computational complexity and training time. The depth of each tree in a random forest affects its ability to generalize and avoid overfitting. The probability of overfitting increases with larger values of . These parameters will be optimized in this paper by the grid search method [40].
2.2.4. XGBoost Method
XGBoost was developed by Chen and Guestrin [38]. It represented an advanced and scalable implementation of gradient-boosting machines. The fundamental concept is that each new model is designed to fit the prediction residual of the previous model. The predicted result is obtained by aggregating the results of each model, as shown in the following equation:
where = 1, 2, …, . is the number of samples and is the -th regression tree function.
The objective function is composed of a loss function and a regularization item , as shown in Equation (5):
As mentioned above, in time , the objective function can be expressed as in Equation (6):
It seems complicated except for the case of the loss function; XGBoost takes the Taylor expansion to approximate this, as shown in Equation (7):
where the and are as follows:
The prediction result in time can be expressed as:
where is the structure of the tree and is the leaf weight of the tree.
Regularization item represents the complexity of the model to avoid model overfitting, as shown in Equation (10):
where are several leaf nodes, is the sum of the leaf node scores in trees, and are adjusted parameters.
Thus, the objective function can be expressed as follows:
where represents the set of leaf samples in the -th tree.
Then, we define the objective function that can be simplified as follows:
Multiple parameters in XGBoost can be fine-tuned to improve the performance of the model. In this paper, we selected three key parameters in XGBoost for optimization: learning rate, the maximum tree depth of each regression tree, and the number of regression trees. The learning rate is an important parameter in XGBoost that controls the contribution of each weak learner to the final prediction. Specifically, the learning rate determines the scaling factor applied to the prediction of each weak learner, with smaller values leading to a more conservative model that may require more weak learners to achieve high accuracy and larger values leading to a more aggressive model that may be prone to overfitting and instability. The rest of the two parameters are similar to those in the RF model.
2.2.5. Encoding Methods
Common encoding methods include label encoding, one-hot encoding, and target encoding (also known as mean encoding) [41]. Label encoding maps each category to a unique integer, thereby converting categorical variables to numerical variables. This method is simple and easy to implement, but it assumes an inherent order or ranking between categories, which may not always exist. One-hot encoding creates a binary vector for each category, with a value of 1 for the category and 0 for all others. This approach can handle nominal variables with no inherent order but can lead to the curse of dimensionality and may not work well with high-cardinality variables. Target encoding replaces each category with the mean of the target variable for that category, effectively encoding the relationship between the categorical variable and the target. While it can capture non-linear relationships and reduce dimensionality, it is vulnerable to overfitting and may introduce bias if the target variable is correlated with the categorical variable. Therefore, we will use these three encoding methods in the experimental stage to compare the model effects to obtain the most suitable encoding method.
2.2.6. Evaluation Metrics
In this study, we utilize several model evaluation metrics to assess our approach. The metrics employed include Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and R-squared (). These metrics provide comprehensive insights into the performance of the model. The model formulas are listed below:
The MSE is as follows:
The RMSE is as follows:
The MAE is as follows:
The is as follows:
3. Application of the Proposed Methodology
3.1. Heterogeneity in Car-Following Behavior Analysis
In this section, we try to understand the heterogeneity of drivers’ car-following behavior through the distribution of some variables with different car-following combinations and different traffic flows.
As shown in Figure 4, the left picture shows the overall distribution, and the right shows the distribution under different car-following combinations. It can be found that the speed of the Car–Truck, Truck–Truck, and Truck–Car combinations is concentrated around 25 m/s, while the speed of the Car–Car combination is more widely distributed. From the perspective of distribution, the second peak of the overall distribution is mainly caused by Car–Car combinations, and other types of car-following combinations are mainly concentrated on the first peak.
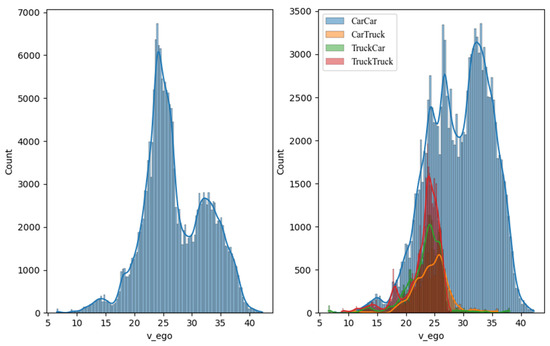
Figure 4.
The distribution of the following vehicle velocity.
The distribution of the time headway is shown in Figure 5. It can be found that the tail of the overall distribution is mainly occupied by the other three combinations. The THW of the Car–Car combination is mainly distributed between 1–3 s. THW is an indicator used to measure the driver’s perception of risk, which represents how long it will take for the following vehicle to reach the heading vehicle at the current speed. It illustrated that the other three types have a stronger sense of risk and tend to maintain lower speeds and higher THW to guarantee safety.
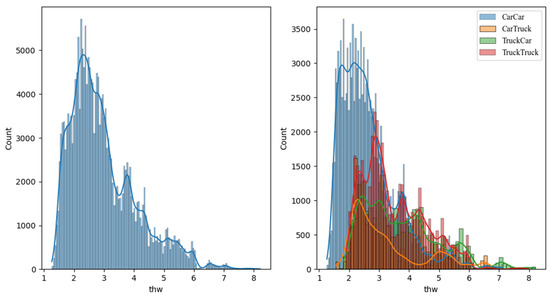
Figure 5.
The distribution of the following vehicle’s time headway.
With different traffic flows, the distribution of the following vehicle velocity is shown in Figure 6. The mixture distribution of velocity almost divided the three normal distributions with different traffic flows.
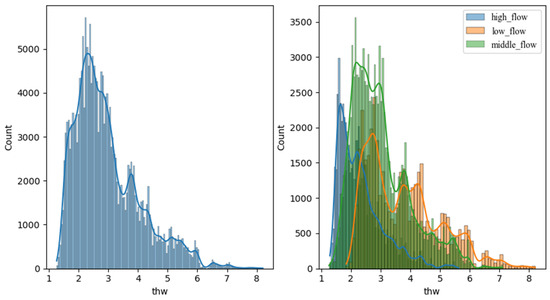
Figure 6.
The distribution of the following vehicle’s velocity.
It is not difficult to find that, after distinguishing car-following combinations and traffic flows, the heterogeneity of car-following behavior has been preliminarily explained. The driver’s behavioral decision (referring to the velocity of ego vehicles in the car-following scenario) is affected by the type of heading vehicles and ego vehicles, as well as the traffic density of the road where they are driving.
In Section 3.3 and Section 3.4, we will encode these heterogeneity factors into car-following models to obtain better car-following prediction performance and further quantify their impact on car-following behavior through the model results.
3.2. Suitable Encoder for Heterogeneity Variables
As shown in Table 6, it can be found that the one-hot method achieves the best results on our models. Therefore, the one-hot method is used for subsequent encoding.

Table 6.
RF results for different encoder methods and XGBoost results for different encoder methods.
3.3. The Model Experiments Result
We use the grid search method for parameter optimization. The parameter setting range is as Table 7.

Table 7.
The parameter setting range in the RF model and XGBoost model.
The obtained optimal parameter combinations are shown in Table 8.

Table 8.
The optimal parameter combinations.
The results obtained with the optimal parameters on the test dataset are presented in Table 9 below. In addition, we have incorporated two widely used machine learning models, namely support vector regression (SVR) [42] and linear regression (LR) [43], to further compare and evaluate the performance of our proposed model in this study.

Table 9.
The model result comparison.
The XGBoost model outperforms other models in all metrics, making it the final model selected for our study. Furthermore, the performance of the XGBoost model (MSE = 0.002) surpasses that of the IDM model (MSE = 0.009) and S3 model (MSE = 0.006) based on the HighD dataset [33]. These findings highlight the effectiveness of the XGBoost model in predicting car-following behavior and demonstrate its superiority over other models reported in the literature. More details are shown in Table 9.
Then, we utilized feature importance results in the XGBoost model to further understand the impact of heterogeneity factors on car-following behavior. In the XGBoost model, the cover type feature importance measures the number of times a feature is used as a split point in a tree model multiplied by the average coverage value (cover) of that feature across all split points. The coverage value indicates the number of samples covered by the feature when it is selected as a split point. The importance of the cover-type features reflects the contribution of a feature to the model, that is, the degree of influence of the feature on the sample points. The larger the coverage value, the more times the feature is selected as a split point in the tree model and the more sample points it covers in each split, indicating a greater contribution of the feature to the model. Figure 7 displays the important feature results for our model.
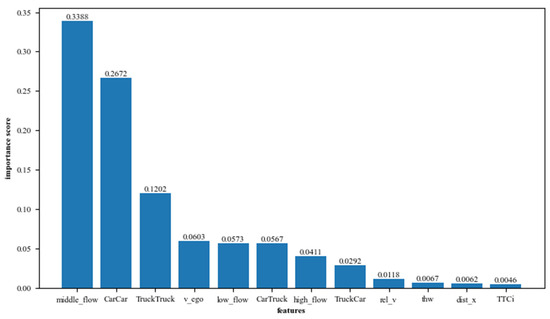
Figure 7.
Features of importance results.
Features are sorted in descending order according to their importance scores, and the top three features are all related to heterogeneity factors (middle-flow: 0.3388; Car–Car: 0.2672; and Truck–Truck: 0.1202). This suggests that different traffic flows and car-following combinations play a significant role in decision tree node splitting. Through this approach, we were able to quantify the impact of heterogeneity factors on car-following behavior.
3.4. The Ablation Experiments Result
Many researchers have conducted extensive studies through ablation experiments to demonstrate the importance of features. For instance, Wang [44] conducted ablation experiments in their study, gradually eliminating different features and observing their impact on the results, thus validating the critical role of specific features in the model. Therefore, we chose ablation experiments to further investigate the importance of heterogeneity factors in the car-following model. We eliminate heterogeneity input features, i.e., traffic flows and car-following combinations (this model is called the comparison model) and observe their impact on the model performance. The obtained results show that the MSE of the comparison model increases by 57.39% compared to the best XGBoost model in this paper. The detailed results are outlined in Table 10.

Table 10.
The ablation experiments result.
Table 9 compares the results of the model with the test dataset. In order to better demonstrate the performance of the model in this paper in different car-following scenarios, we randomly selected some vehicles and compared the results of the models under different traffic flows and different car-following combinations. See Figure 8, Figure 9, Figure 10 and Figure 11.
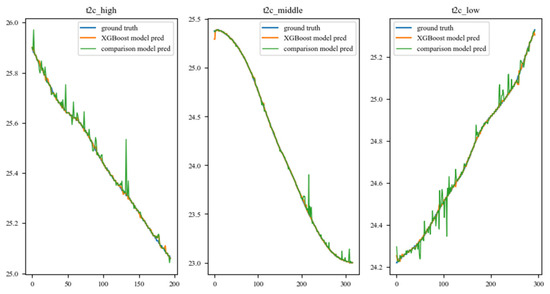
Figure 8.
Prediction trajectory of the Truck–Car combination under different traffic flows. The traffic flow from left to right is high, middle, and low.
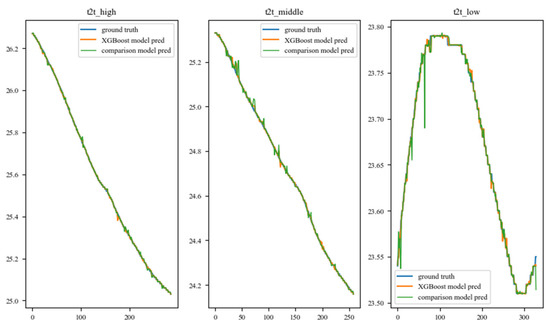
Figure 9.
Prediction trajectory of the Truck–Truck combination under different traffic flows.
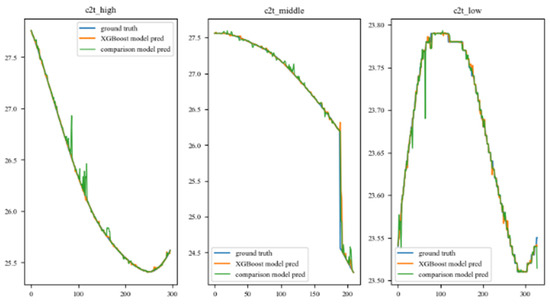
Figure 10.
Prediction trajectory of the Car–Truck combination under different traffic flows.
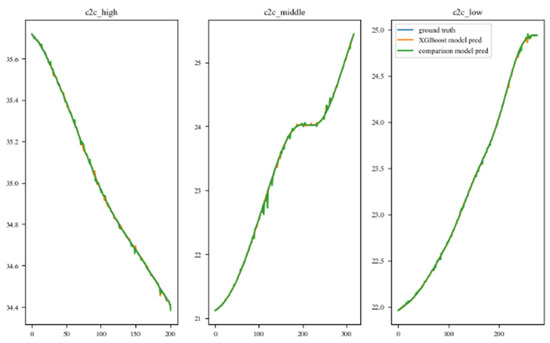
Figure 11.
Prediction trajectory of the Car–Car combination under different traffic flows.
The comparison of these trajectories illustrates that the proposed model in this paper performs better than the comparison model. The proposed model provides more precise and smoother predictions of drivers’ car-following behavior. In contrast, the comparison model only achieved a certain level of effectiveness in the Car–Car scenario, while the proposed model achieved good prediction results under different conditions.
4. Conclusions and Discussion
In summary, this paper demonstrates the superiority of incorporating heterogeneity factors for the car-following model. Firstly, the findings reveal distinct car-following behaviors under different combinations of vehicles and traffic flows. The drivers in the Car–Truck, Truck–Car, and Truck–Truck combinations exhibit a higher level of risk perception, characterized by longer time headway (THW) and lower speeds. These results align with previous research on heterogeneity analysis. Secondly, experiments were conducted to identify the optimal encoding method for incorporating heterogeneity factors, with one-hot encoding found to be the most suitable approach. In the end, the proposed model (MSE = 0.002181, R2 = 0.999927), incorporating heterogeneity factors, outperformed the model that did not consider these factors (MSE = 0.003530, R2 = 0.999881) as well as a theory-driven car-following model (MSE = 0.006). The influence of heterogeneity factors on car-following behavior was quantified through feature importance scores, with middle-flow, Car–Car, and Truck–Truck factors ranking highest. This study provides valuable insights into the intersection of heterogeneity and car-following modeling. It is also a meaningful attempt at the model chosen in this paper. Currently, data-driven models based on deep learning are mainstream, but they are lacking in latency and interpretability. Traditional theory-driven models cannot easily incorporate other variables, like machine learning models. This paper chooses the ensemble learning method based on the decision tree. The experimental results prove that the model in this paper can achieve high accuracy and has a certain degree of interpretability, and there is no doubt that the delay is lower than the deep learning model. This paper provides a basis for the application of the ensemble learning method based on a decision-tree model in car-following model research.
Moving forward, there are several avenues for future research. Due to limitations in the dataset, this study focused solely on car-following models in highway scenarios. However, urban scenarios require consideration of additional factors, such as vehicle-to-vehicle interaction and environmental information. Thus, future research could explore the development of car-following models that incorporate heterogeneity factors, specifically in urban scenes. This would contribute to a more comprehensive understanding of car-following behavior and its implications in diverse driving environments.
Author Contributions
Conceptualization, K.Z., X.Y. and J.W.; methodology, X.Y.; software, K.Z., M.L. and Y.Z.; validation, K.Z.; formal analysis, K.Z. and X.Y.; investigation, X.Y.; resources, K.Z. and X.Y.; data curation, K.Z., M.L. and Y.Z.; writing—original draft preparation, K.Z., M.L. and Y.Z.; writing—review and editing, X.Y. and J.W.; supervision, X.Y. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [10.1109/ITSC.2018.8569552].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, L.; Zhang, C.; Qiu, X.; Li, S.; Wang, H. Research progress on car-following models. J. Traffic Transp. Eng. 2019, 19, 125–138. [Google Scholar] [CrossRef]
- An, S.-H.; Lee, B.-H.; Shin, D.-R. A Survey of Intelligent Transportation Systems. In Proceedings of the 2011 3rd International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011; pp. 332–337. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P.; Bovy, P.H.L. State-of-the-art of vehicular traffic flow modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2001, 215, 283–303. [Google Scholar] [CrossRef]
- Pipes, L.A. An Operational Analysis of Traffic Dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic Dynamics: Studies in Car Following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef] [PubMed]
- Newell, G.F. Nonlinear Effects in the Dynamics of Car Following. Oper. Res. 1961, 9, 209–229. [Google Scholar] [CrossRef]
- Saifuzzaman, M.; Zheng, Z.; Haque, M.; Washington, S. Revisiting the Task–Capability Interface model for incorporating human factors into car-following models. Transp. Res. Part B Methodol. 2015, 82, 1–19. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A. The Intelligent Driver Model with Stochasticity—New Insights into Traffic Flow Oscillations. Transp. Res. Procedia 2017, 23, 174–187. [Google Scholar] [CrossRef]
- Kehtarnavaz, N.; Groswold, N.; Miller, K.; Lascoe, P. A transportable neural-network approach to autonomous vehicle following. IEEE Trans. Veh. Technol. 1998, 47, 694–702. [Google Scholar] [CrossRef]
- Dabiri, S.; Abbas, M. Evaluation of the Gradient Boosting of Regression Trees Method on Estimating Car-Following Behavior. Transp. Res. Rec. 2018, 2672, 136–146. [Google Scholar] [CrossRef]
- Ma, X. A Neural-Fuzzy Framework for Modeling Car-following Behavior. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 2, pp. 1178–1183. [Google Scholar] [CrossRef]
- Khodayari, A.; Ghaffari, A.; Kazemi, R.; Braunstingl, R. A Modified Car-Following Model Based on a Neural Network Model of the Human Driver Effects. IEEE Trans. Syst. Man Cybern. A 2012, 42, 1440–1449. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J.; Quan, P.; Wang, J.; Meng, X.; Li, Q. Prediction of influent wastewater quality based on wavelet transform and residual LSTM. Appl. Soft Comput. 2023, 148, 110858. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, R.; Li, L.; Lin, Y.; Zheng, X.; Wang, F.-Y. Capturing Car-Following Behaviors by Deep Learning. IEEE Trans. Intell. Transp. Syst. 2018, 19, 910–920. [Google Scholar] [CrossRef]
- Fan, P.; Guo, J.; Zhao, H.; Wijnands, J.S.; Wang, Y. Car-Following Modeling Incorporating Driving Memory Based on Autoencoder and Long Short-Term Memory Neural Networks. Sustainability 2019, 11, 6755. [Google Scholar] [CrossRef]
- Ossen, S.; Hoogendoorn, S.P. Multi-anticipation and heterogeneity in car-following empirics and a first exploration of their implications. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 1615–1620. [Google Scholar] [CrossRef]
- Ossen, S.; Hoogendoorn, S.P.; Gorte, B.G.H. Interdriver Differences in Car-Following. Transp. Res. Rec. 2006, 1965, 121–129. [Google Scholar] [CrossRef]
- Ossen, S.; Hoogendoorn, S.P. Heterogeneity in car-following behavior: Theory and empirics. Transp. Res. Part C Emerg. Technol. 2011, 19, 182–195. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, C.; He, Z.; He, T.; Liu, S. Empirical validation of vehicle type-dependent car-following heterogeneity from micro- and macro-viewpoints. Transp. B Transp. Dyn. 2019, 7, 765–787. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, P.; Li, M.; Liu, H.; Yin, B. A New Car-Following Model considering Driving Characteristics and Preceding Vehicle’s Acceleration. J. Adv. Transp. 2017, 2017, 2437539. [Google Scholar] [CrossRef]
- Jiao, Y.; Calvert, S.C.; van Cranenburgh, S.; van Lint, H. Probabilistic Representation for Driver Space and Its Inference From Urban Trajectory Data. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Wang, Q. Analysis on the Heterogeneity of Proximity Resistance in Car Following. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2023. CIE5050-09 Additional Graduation Work. [Google Scholar]
- Xie, D.-F.; Zhu, T.-L.; Li, Q. Capturing driving behavior Heterogeneity based on trajectory data. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050023. [Google Scholar] [CrossRef]
- Ahmed, K.I. Modeling Drivers’ Acceleration and Lane Changing Behavior. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Wang, W.; Zhang, W.; Guo, H.; Bubb, H.; Ikeuchi, K. A safety-based approaching behavioural model with various driving characteristics. Transp. Res. Part C Emerg. Technol. 2011, 19, 1202–1214. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Chen, X.; Ran, B. Memory, attention and prediction: A deep learning architecture for car-following. Transp. B Transp. Dyn. 2019, 7, 1553–1571. [Google Scholar] [CrossRef]
- Aghabayk, K.; Sarvi, M.; Forouzideh, N.; Young, W. New Car-Following Model considering Impacts of Multiple Lead Vehicle Types. Transp. Res. Rec. 2013, 2390, 131–137. [Google Scholar] [CrossRef]
- ElSamadisy, O.; Shi, T.; Smirnov, I.; Abdulhai, B. Safe, Efficient, and Comfortable Reinforcement-Learning-Based Car-Following for AVs with an Analytic Safety Guarantee and Dynamic Target Speed. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 643–661. [Google Scholar] [CrossRef]
- Liang, Y.; Dong, H.; Li, D.; Song, Z. Adaptive eco-cruising control for connected electric vehicles considering a dynamic preceding vehicle. eTransportation 2024, 19, 100299. [Google Scholar] [CrossRef]
- Li, Y.; Liu, F.; Xing, L.; Yuan, C.; Wu, D. A Deep Learning Framework to Explore Influences of Data Noises on Lane-Changing Intention Prediction. IEEE Trans. Intell. Transp. Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Lin, S.; Wang, Y.; Zhao, X. Intention-convolution and hybrid-attention network for vehicle trajectory prediction. Expert Syst. Appl. 2024, 236, 121412. [Google Scholar] [CrossRef]
- Xu, Z.; Wei, L.; Liu, Z.; Liu, Z.; Qin, K. Contrastive of car-following model based on multinational empirical data. J. Chang. Univ. Nat. Sci. Ed. 2023, 1–12, 1 February 2024. [Google Scholar]
- Sun, Z.; Yao, X.; Qin, Z.; Zhang, P.; Yang, Z. Modeling Car-Following Heterogeneities by Considering Leader–Follower Compositions and Driving Style Differences. Transp. Res. Rec. 2021, 2675, 851–864. [Google Scholar] [CrossRef]
- Aghabayk, K.; Sarvi, M.; Young, W. Attribute selection for modelling driver’s car-following behaviour in heterogeneous congested traffic conditions. Transp. A Transp. Sci. 2014, 10, 457–468. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Liu, Y.; Wu, B. An empirical study on heterogeneous traffic car-following safety indicators considering vehicle types. Transp. A Transp. Sci. 2023, 19, 2015475. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Parmar, A.; Katariya, R.; Patel, V. A Review on Random Forest: An Ensemble Classifier. In International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI) 2018; Hemanth, J., Fernando, X., Lafata, P., Baig, Z., Eds.; Lecture Notes on Data Engineering and Communications Technologies; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Volume 26, pp. 758–763. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Rodríguez, P.; Bautista, M.A.; Gonzàlez, J.; Escalera, S. Beyond one-hot encoding: Lower dimensional target embedding. Image Vis. Comput. 2018, 75, 21–31. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Chapter 7—Support vector regression. In Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 123–140. [Google Scholar] [CrossRef]
- Wright, R.E. Logistic regression. In Reading and Understanding Multivariate Statistics; American Psychological Association: Washington, DC, USA, 1995; pp. 217–244. [Google Scholar]
- Wang, Q.; Zhang, W.; Li, J.; Ma, Z. Complements or confounders? A study of effects of target and non-target features on online fraudulent reviewer detection. J. Bus. Res. 2023, 167, 114200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).