An FPT Algorithm for Directed Co-Graph Edge Deletion
Abstract
1. Introduction
2. Our Main Contributions and Technique Highlights
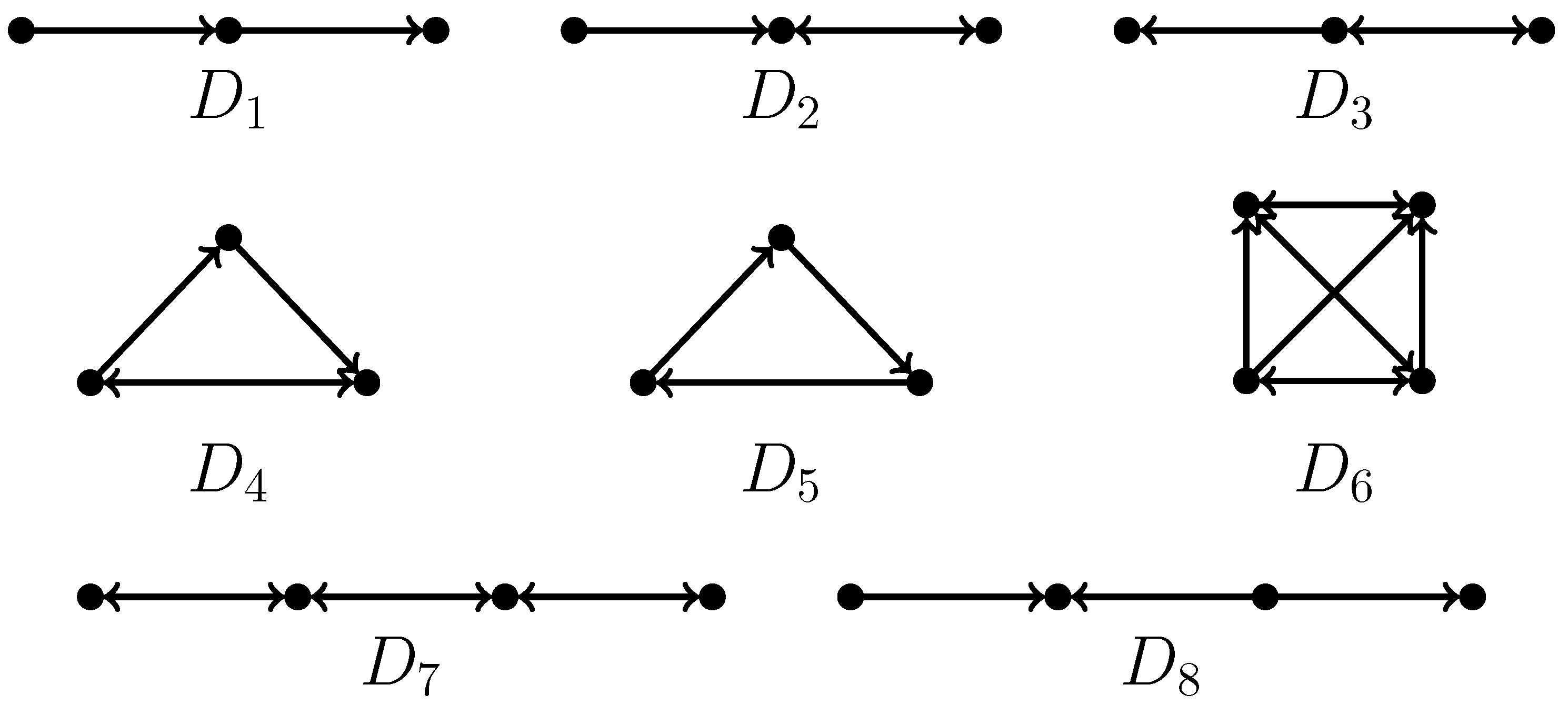
3. Preliminaries
4. Our Results
- (1)
- Deletion of the edgeAfter deleting , vertices a, d, and b form an induced . The deletion of or will induce new forbidden structures, which will trigger the deletion of further edges. In particular, we have the following branching cases, as shown in Figure 3.
- (2)
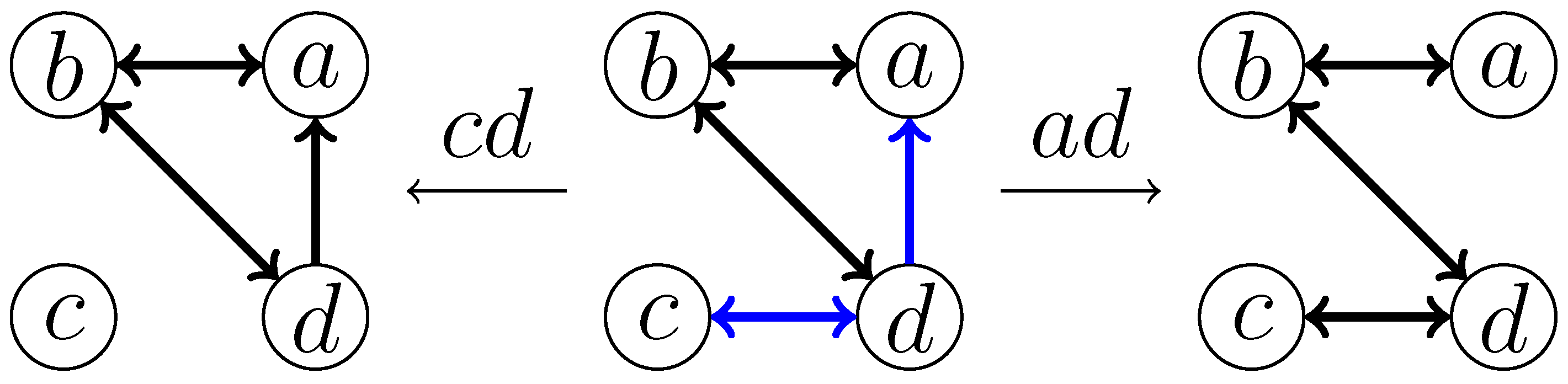
- Deletion of the edgeAfter deleting , induces a and induces a . The deletion of is covered in Case (1). Thus, we need only to consider the deletion of edge to destroy the . It follows that the branching cases and cover all potential solutions where the edge is deleted, as shown in Figure 4 (in the first branching case, we obtain an induced , meaning that further edges need to be deleted. However, as this does not improve the worst-case branching factor, and the induced s are handled by branching rules introduced later, to simplify the presentation, we do not discuss this improvement).
- (3)
- Deletion of the edgeAfter deleting , vertices a, c, and d form an induced , and since the deletion of is covered in Cases (1) and (2), we consider the deletion of . Observe now that b, c, and d form an induced . If we delete , then a, b, and c form an induced , implying that at least one of and needs to be deleted, which is covered in Cases (1) and (2). Therefore, we do not need to consider the case where is deleted. In other words, in this case, we need only the branching case .
- (4)
- Deletion of the edgeThe deletion of triggers the deletion of at least one of and , both of which are covered by previous cases.
- (5)
- Deletion of the edgeAfter deleting , an induced formed by a, b, and d and an induced formed by b, c, and d occur. To destroy the , at least one of and needs to be deleted, both of which are covered by previous cases.
- (6)
- Deletion of the edgeAfter deleting the edge , the vertices b, c, and d form an induced , inviting the further deletion of at least one of and , both of which are covered by previous cases.
- Case
- 1: v has exactly one neighbor in H.We have two subcases to consider, as shown in Figure 5.In both subcases, there are indeed two induced s; hence, deleting only one edge is insufficient. Specifically, for Case 1.1, we apply the following branching rule:For Case 1.2, we apply the following branching rule:Both branching rules have the same branching vector of and a corresponding maximum branching factor of .
- Case
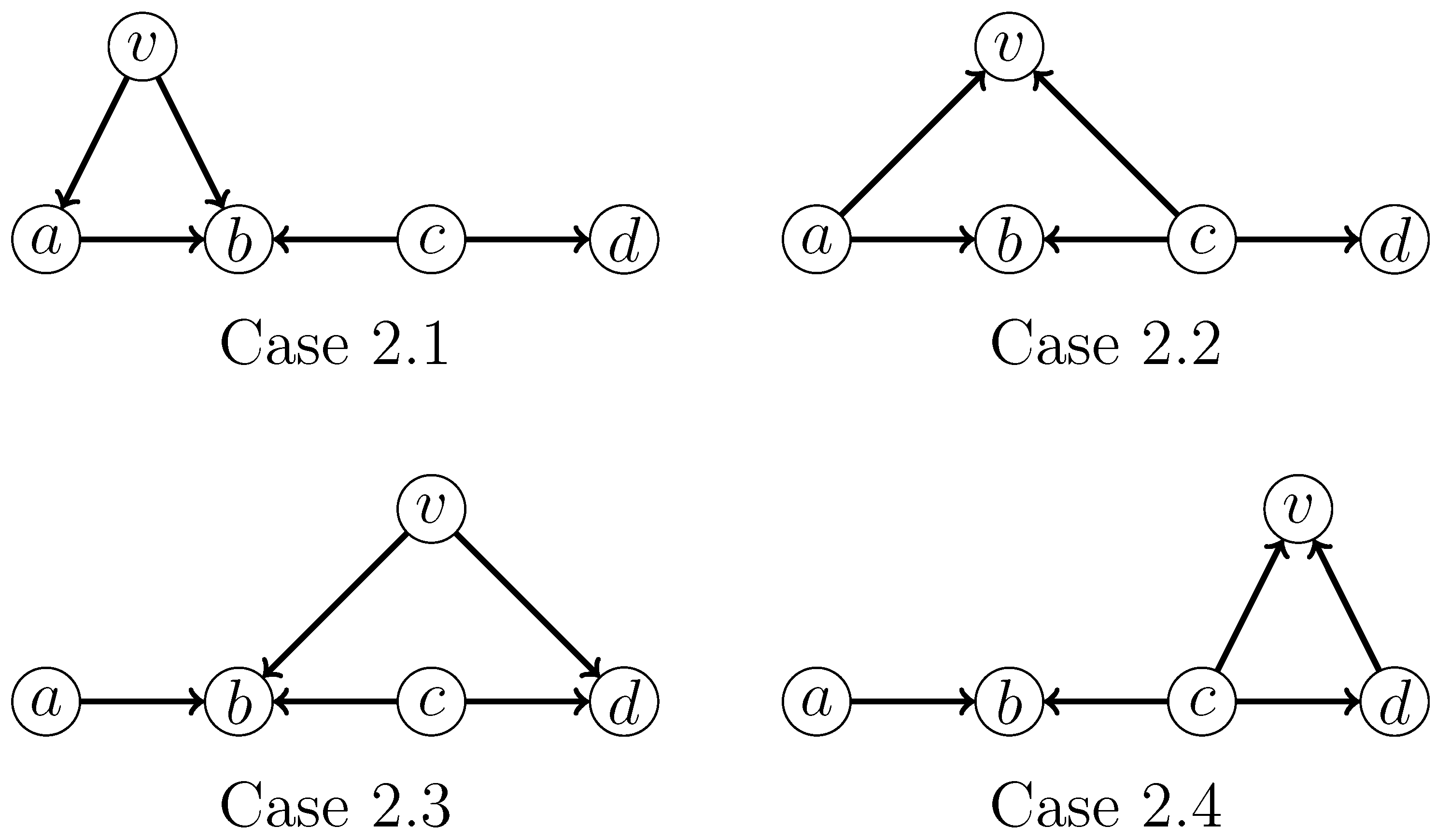
- 2: v has exactly two neighbors in H.We need to consider the four subcases shown in Figure 6.For Case 2.1, we apply the following branching rule, where the branching vector is , corresponding to the branching factor :For Case 2.2, we apply the following branching rule, where the branching vector is , corresponding to the branching factor :For Case 2.3, we apply the following branching rule, where the branching vector is and the branching factor is :For Case 2.4, we apply the following branching rule, where the branching vector is and the branching factor is :
- Case
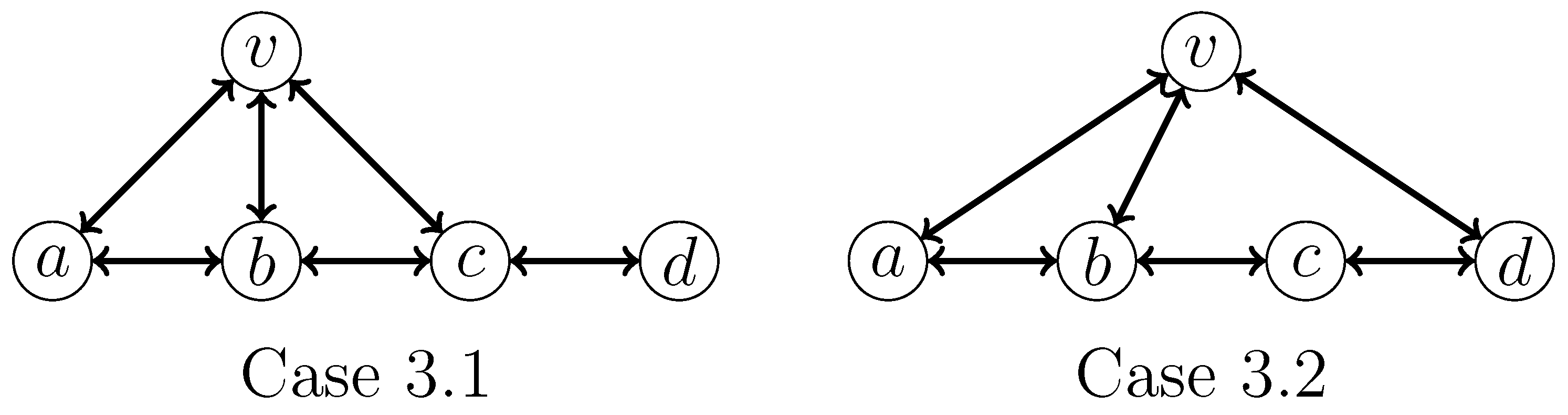
- 3: v has exactly three neighbors in H.Figure 7 depicts all subcases that we need to consider. For Case 3.1, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :For Case 3.2, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :
- Case
- 4: v is adjacent to all vertices of H.When none of the branching rules introduced above are applicable, if a vertex is adjacent to one vertex of H, then it is adjacent to all vertices of H, and, moreover, the subgraph induced by this vertex and all vertices of H is isomorphic to one of the graphs in Figure 8. Then, by the symmetry between the edges and , the branching cases and of branching factor 2 are sufficient in this case.
- Case
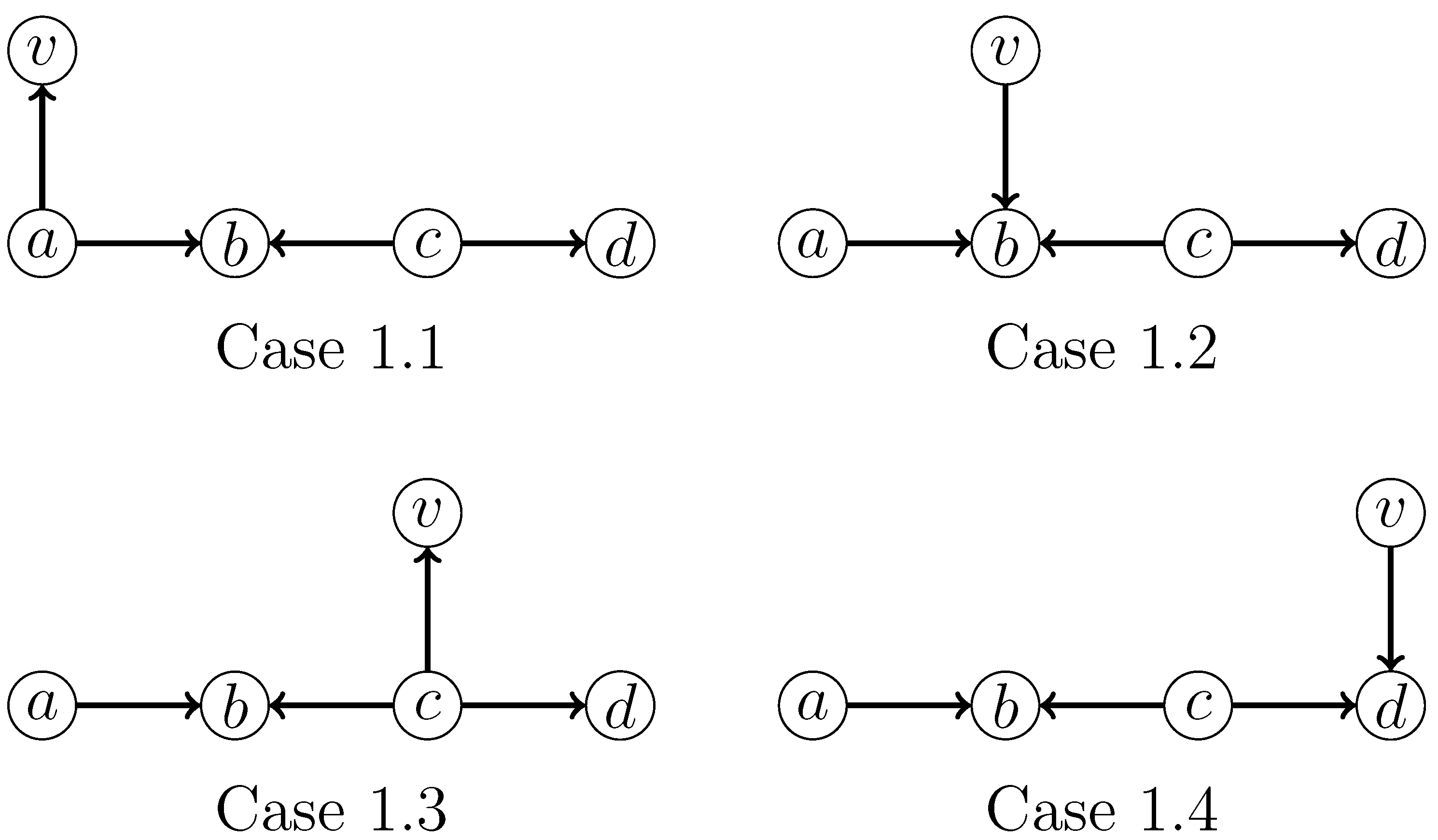
- 1: v is adjacent to exactly one vertex of H.All subcases that need to be considered are shown in Figure 9.For Case 1.1, we apply the branching rule:For Case 1.2, we apply the branching rule:For Case 1.3, we apply the branching rule:For Case 1.4, we apply the branching rule:The above four branching rules have the same branching vector of and a corresponding maximum branching factor of .
- Case
- 2: v has exactly two neighbors from H.All subcases that need to be considered are shown in Figure 10.For Case 2.1, we apply the following branching rule, where the branching vector is and the corresponding branching factor is :For Case 2.2, we apply the following branching rule, where the branching vector is and the corresponding branching factor is :For Case 2.3, we apply the following branching rule, where the branching vector is and the corresponding branching factor is :For Case 2.4, we apply the following branching rule, where the branching vector is and the corresponding branching factor is :
- Case
- 3: v has exactly three neighbors from H.All subcases that need to be considered are shown in Figure 11.For Case 3.1, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :For Case 3.2, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :For Case 3.3, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :For Case 3.4, we apply the following branching rule, which has a branching vector of and a corresponding maximum branching factor of :
- Case
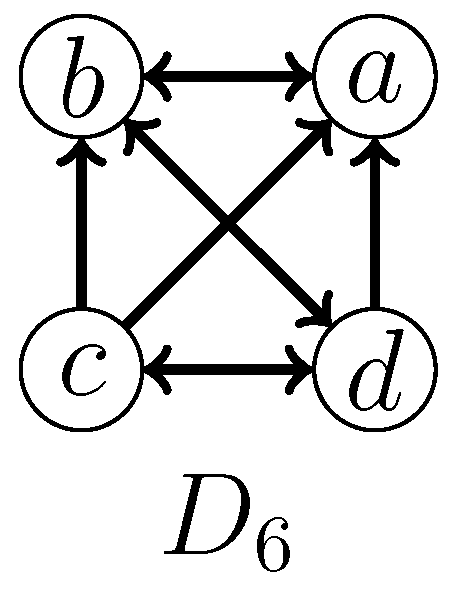
- 4: v is adjacent to all vertices of H.Let us consider a graph where none of the branching rules introduced so far are applicable, which is called a reduced graph. It is easy to verify that in a reduced graph, for any induced and any vertex v adjacent to all vertices of , the subgraph induced by the vertex v and the is isomorphic to one of the graphs in Figure 12. Two important observations are formulated below.Observation 1. Let G be a reduced graph. Then, all induced s in G are pairwise vertex disjoint.Observation 2. Let G be a reduced graph. Then, deleting any edge from an induced in G does not yield any new induced forbidden structures (–).Let i be the number of all induced in a reduced graph G. By Observation 1, we need to delete i edges to destroy all the induced s in G. By Observation 2, the resulting graph is a directed co-graph. In light of this fact, when we arrive at a reduced graph at a branching node, we determine that the given instance is a YES-instance if there are, at most, k induced s in the reduced graph.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Crespelle, C.; Drange, P.G.; Fomin, F.V.; Golovach, P.A. A Survey of Parameterized Algorithms and the Complexity of Edge modification. Comput. Sci. Rev. 2023, 48, 100556. [Google Scholar] [CrossRef]
- Li, W.; Tang, X.; Yang, Y. An Improved Branching Algorithm for the Proper Interval Edge Deletion Problem. Front. Comput. Sci. 2022, 16, 162401. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; You, J.; Chen, J.; Cao, Y. Edge Deletion Problems: Branching Facilitated by Modular Decomposition. Theor. Comput. Sci. 2015, 573, 63–70. [Google Scholar] [CrossRef]
- Béchet, D.; de Groote, P.; Retoré, C. A Complete Axiomatisation for the Inclusion of Series-Parallel Partial Orders. In Proceedings of the Rewriting Techniques and Applications, 8th International Conference, RTA-97, Sitges, Spain, 2–5 June 1997; Lecture Notes in Computer Science. Comon, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1232, pp. 230–240. [Google Scholar] [CrossRef]
- Crespelle, C.; Paul, C. Fully Dynamic Recognition Algorithm and Certificate for Directed Cographs. Discret. Appl. Math. 2006, 154, 1722–1741. [Google Scholar] [CrossRef]
- El-Mallah, E.; Colbourn, C.J. The Complexity of Some Edge Deletion Problems. IEEE Trans. Circuits Syst. 1988, 35, 354–362. [Google Scholar] [CrossRef]
- Nastos, J.; Gao, Y. Bounded Search Tree Algorithms for Parametrized Cograph Deletion: Efficient Branching Rules by Exploiting Structures of Special Graph Classes. Discret. Math. Algorithms Appl. 2012, 4, 1250008. [Google Scholar] [CrossRef]
- Guillemot, S.; Havet, F.; Paul, C.; Perez, A. On the (Non-)Existence of Polynomial Kernels for Pl-Free Edge Modification Problems. Algorithmica 2013, 65, 900–926. [Google Scholar] [CrossRef]
- Bretscher, A.; Corneil, D.G.; Habib, M.; Paul, C. A Simple Linear Time LexBFS Cograph Recognition Algorithm. SIAM J. Discret. Math. 2008, 22, 1277–1296. [Google Scholar] [CrossRef]
- Schmitz, Y.; Wanke, E. The Directed Metric Dimension of Directed Co-Graphs. arXiv 2023, arXiv:2306.08594. [Google Scholar]
- Gurski, F.; Komander, D.; Rehs, C. How to Compute Digraph Width Measures on Directed Co-Graphs. Theor. Comput. Sci. 2021, 855, 161–185. [Google Scholar] [CrossRef]
- Gurski, F. Dynamic Programming Algorithms on Directed Cographs. Stat. Optim. Inf. Comput. 2017, 5, 35–44. [Google Scholar] [CrossRef][Green Version]
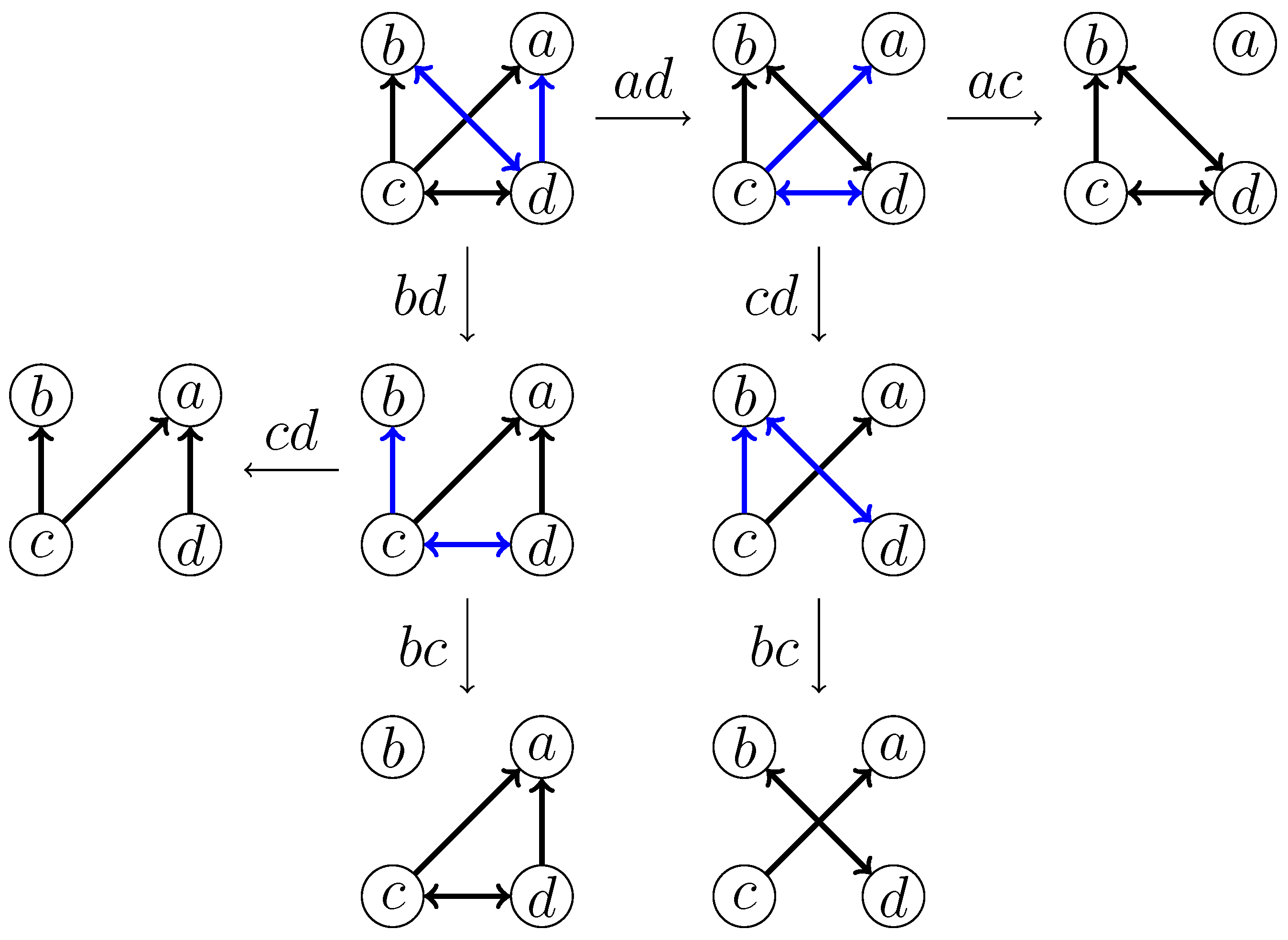





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Yang, X.; Xu, C.; Yang, Y. An FPT Algorithm for Directed Co-Graph Edge Deletion. Algorithms 2024, 17, 69. https://doi.org/10.3390/a17020069
Li W, Yang X, Xu C, Yang Y. An FPT Algorithm for Directed Co-Graph Edge Deletion. Algorithms. 2024; 17(2):69. https://doi.org/10.3390/a17020069
Chicago/Turabian StyleLi, Wenjun, Xueying Yang, Chao Xu, and Yongjie Yang. 2024. "An FPT Algorithm for Directed Co-Graph Edge Deletion" Algorithms 17, no. 2: 69. https://doi.org/10.3390/a17020069
APA StyleLi, W., Yang, X., Xu, C., & Yang, Y. (2024). An FPT Algorithm for Directed Co-Graph Edge Deletion. Algorithms, 17(2), 69. https://doi.org/10.3390/a17020069



