Abstract
The automated design of dispatching rules (DRs) with genetic programming (GP) has become an important research direction in recent years. One of the most important decisions in applying GP to generate DRs is determining the features of the scheduling problem to be used during the evolution process. Unfortunately, there are no clear rules or guidelines for the design or selection of such features, and often the features are simply defined without investigating their influence on the performance of the algorithm. However, the performance of GP can depend significantly on the features provided to it, and a poor or inadequate selection of features for a given problem can result in the algorithm performing poorly. In this study, we examine in detail the features that GP should use when developing DRs for unrelated machine scheduling problems. Different types of features are investigated, and the best combination of these features is determined using two selection methods. The obtained results show that the design and selection of appropriate features are crucial for GP, as they improve the results by about 7% when only the simplest terminal nodes are used without selection. In addition, the results show that it is not possible to outperform more sophisticated manually designed DRs when only the simplest problem features are used as terminal nodes. This shows how important it is to design appropriate composite terminal nodes to produce high-quality DRs.
1. Introduction
The unrelated parallel machine scheduling problem is an important combinatorial optimisation problem with frequent applications in the real world [1], such as task scheduling [2], device scheduling [3], and manufacturing [4]. Since the problem is NP-hard, it is traditionally solved using various metaheuristic optimisation methods [5,6]. However, since real-world problems are often dynamic in nature, traditional optimisation approaches that continuously improve potential solutions are usually not directly applicable. The reason for this is that not all information about the problem under consideration may be known, and in this case, it is not possible to construct a complete solution. This was the motivation for researching alternative methods that can be used to solve dynamic problems such as dispatching rules.
Dispatching rules (DRs) have emerged as an alternative solution method for solving various scheduling problems, mostly dynamic problem variants [7]. They represent simple constructive heuristics that solve the problem incrementally by making decisions about which job to schedule next based solely on the information currently available in the system. Therefore, such rules can react quickly to the changing problem environment, as they construct the solution based only on the currently available information. As new information becomes available, they can take it into account when constructing the solution. Although many DRs have been proposed over the years [7], they have been developed for a limited number of problem variants and scheduling criteria. In addition, the developed DRs perform scheduling decisions using simple heuristic strategies, which affects the quality of the plans they produce.
To address the above problems, various methods based on evolutionary computation and machine learning have been used over the years to automatically design new DRs for various problems [8,9,10]. One of the most commonly used methods for this purpose is genetic programming [11]. GP is an evolutionary computational method developed to enable the generation of various mathematical expressions and even computer programmes [12]. It has been applied in many fields, where it has achieved competitive results with humans [13], proving its effectiveness. In recent years, however, GP has established itself as the leading hyperheuristic method [14,15], a method used to automatically develop new heuristics.
In the context of DRs, GP is used to generate an expression, often referred to as a priority function, that is used by the DR to rank all decisions at each decision point and select the appropriate decision [16]. GP generates the expression based on a set of defined problem characteristics, which it attempts to combine in a meaningful way to determine the optimal scheduling decision at each decision point. Therefore, it is necessary to provide GP with all the relevant information about the problem in the form of terminal nodes representing certain features of the problem. However, an incomplete or wrong choice of terminal nodes can result in myopic DRs that offer poor performance [17]. Regardless, this step is often overlooked, and quite often only the most basic problem information is used as terminal nodes without a selection of appropriate nodes. Naturally, providing too many terminal nodes again has the drawback that the search space of the method grows exponentially, making it more difficult to find high-quality solutions. Although the definition and choice of appropriate terminal nodes is an important decision that significantly affects the quality and complexity of DRs, it has not yet been investigated in the context of the automated design of DRs for unrelated machine environments. Thus, there is no guarantee that the terminal nodes currently applied in the literature are really the most appropriate or whether the results could be improved by applying a different set of terminal nodes.
The aim of this study is to perform a detailed investigation of the influence of different problem properties on the quality of DRs automatically developed by GP for unrelated machine scheduling problems. The motivation for this is to determine the set of the most suitable terminal nodes, with which GP can generate DRs that perform well across a wide range of problem instances. This is done in a sequential manner, where first, simple atomic features are analysed, representing only the most basic information about the problem. Then, composite features are added to the set of terminals to investigate whether by including more sophisticated terminal nodes, either designed automatically or manually, they can improve the performance of the generated DRs. Naturally, only providing the terminal nodes is not enough, since a too-large terminal set can negatively affect the results simply due to a too-large solution space that the algorithm needs to traverse. Therefore, to select the appropriate feature set, we use the backward sequential feature selection method, which is commonly used in the literature for this purpose, but also investigate the ability of GP to perform feature selection by using the frequency of occurrence of nodes in the expressions as a criterion for selecting the appropriate features. From the obtained results, we investigate how the different node sets that were obtained influence not only the performance and complexity of the generated DRs but also the performance of different methods in selecting the appropriate features.
The contributions of this study can be summarised as follows:
- Analysis of how different types of terminal nodes influence the effectiveness of GP to generate good quality DRs and their complexity.
- Construction of new terminal nodes based on the frequency of occurrence of sub-expressions in the generated DRs.
- Application and comparison of two feature selection methods to determine appropriate terminal node sets.
The rest of this study is organised as follows. Section 2 outlines the relevant literature on the generation of DRs with GP. The necessary background information about the problem under consideration and the application of GP to generate DRs is given in Section 3. The methodology used to conduct the investigation in this paper is described in Section 4. Section 5 describes the design of the experimental study and discusses the results obtained. A more in-depth analysis of the results obtained is presented in Section 6. Finally, Section 7 concludes this paper and provides guidance for future research.
2. Literature Review
The automated generation of DRs has its roots in the pioneering studies of Miyashita [18] and Dimopoulos and Zalzala [19]. These studies showed that GP can be efficiently used to design new DRs for various scheduling problems. Since then, GP has been applied in numerous studies to generate DRs for various problems, such as the parallel machine scheduling problem [20], flexible job shop problem [21], resource-constrained project scheduling problem [22], and one-machine variable capacity problem [23].
Over the years, many research directions have been explored in the context of the automated design of DRs. One line of research has focused on investigating different representations for DRs. In [24], the authors compared three DR representations: one that generates an expression that selects an existing DR based on system properties to make the scheduling decision, one that generates a new DR from basic system information, and one that combines the previous two approaches. The results showed that the first approach was inferior to the other two approaches. In [25], the potential of GP to generate DRs was compared with that of artificial neural networks. The results showed that both methods performed similarly, but GP developed interpretable and more user-friendly DRs. In [26], the authors investigated several evolutionary algorithms for developing DRs and found that their performance was similar in most cases, although some resulted in simpler DRs. Another line of research focused on the generation of DRs for multi-objective scheduling problems, which were considered in [27,28,29] for the job shop problem and [30] for the unrelated machine scheduling problem.
Ensemble learning is one of the most widely considered topics related to DR creation, as it has the potential to significantly improve the performance of individual DRs. This topic has been studied from many aspects, including methods used to construct ensembles [31,32,33], methods used to aggregate the decisions of individual DRs in the ensemble [34,35], and the application of ensemble learning for multi-objective problems [36]. Another way to improve the performance of automatically generated DRs is the application of surrogate models [37,38] and local search [39], both of which have been shown to improve the performance of GP. Another recent research trend is the application of multitask learning in GP, which enables knowledge transfer between individuals to solve different types of problems [40].
Only limited attention has been given to the issues of feature selection and construction in the context of automatic generation of DRs, and this has focused mainly on the job shop scheduling problem. In [41], the authors proposed a feature selection algorithm that is embedded in GP and based on niching. This feature selection method takes into account both the fitness of the individuals in which the features occur and the frequency of occurrence of these features. The experimental results showed that the proposed approach can select features that lead to better results compared to using the entire feature set. In [42], the authors considered feature selection in the context of developing DRs for the flexible job shop problem. In this approach, two terminal sets are used and, therefore, features need to be selected for each of them simultaneously. A GP approach with adaptive search based on the frequency of features was proposed in [43] and was shown to perform better compared to standard GP in some scenarios. Another feature selection approach was proposed in [44], which led to simpler DRs that achieved comparable performance to those developed without feature selection. Finally, in [45], the authors considered feature construction in addition to feature selection, but no follow-ups or extensions to this original research were conducted. Overviews of the literature on the remaining studies dealing with the automated design of DRs for various scheduling problems can be found in [8,9,10].
The importance of selecting suitable problem features when using GP to create DRs was discussed in [17]. However, studies in this field rarely explore the definition of the features used in solving a particular problem. On the contrary, a particular set of features is usually defined based on previous user experiences, without further investigation into whether this terminal set is really the most appropriate. As can be seen from the previous literature review, although several studies deal with feature selection, they focus on the algorithmic aspect rather than on which features should be used or how they should be designed. Therefore, this study provides a deeper investigation into the definition and selection of features in the automated development of DRs for unrelated machine environments.
3. Background
As mentioned previously, the unrelated machine environment appears in many real-world scenarios, such as the manufacturing of pipes, manufacturing cells, distributing jobs in heterogeneous systems, and scheduling in the textile industry, among others [6]. Many of those problems are dynamic in nature, meaning that certain aspects of the problem are not known at the beginning of the system’s execution. In such cases, DRs represent the method of choice for solving such problems [7]. However, the performance of existing DRs is quite limited, and they are usually designed for very specific problem variants, thus limiting their performance and generalisation ability. This means that it is required to design DRs for all the different problem variants that are considered. Since it is difficult to manually design DRs for all the available problem variants, the concept of the automated design of DRs has garnered significant attention. One of the most prominent and commonly used approaches for this purpose is GP, which has been successfully used to generate new DRs for various problems.
3.1. Unrelated Parallel Machine Scheduling Problem
In the unrelated machine scheduling problem, a set of jobs must be scheduled and executed on a scarce set of machines [46]. Each job contains certain properties that are taken into account in scheduling decisions, such as:
- —the processing time of job j on machine i.
- —the release time of job j, which specifies the earliest time at which the job can be considered for scheduling.
- —the due date of job j, which specifies the time by which the job should finish with its execution.
- —the weight of job j, which indicates the importance of the job.
Each machine can only process one job at a time. As soon as a machine starts executing a job, it must complete it before it can start executing another job.
Many criteria can be considered and optimised for this problem. In this study, we focus on minimising the total weighted tardiness criterion (), defined as , which is one of the most frequently optimised criteria in the literature, especially when considering dynamic environments [6]. represents the tardiness of job j and is defined as , where indicates the time at which job j was completed. The tardiness, therefore, represents the time the job has been completed after its due date, whereas the total weighted tardiness is simply the combination of all tardiness values multiplied by the corresponding weights. By minimising , we effectively minimise the times jobs are completed after their due date.
Using the standard notation for scheduling problems [47], the problem considered in this study can be specified as . In this notation, represents the machine environment, which in this case, is the unrelated machine environment (denoted by R); represents the additional constraints, which in this case, include the release times of the jobs (denoted by ); and represents the optimised criterion, which in this case, is the total weighted tardiness (denoted by ). Moreover, the problem is considered under dynamic conditions, which means that not all information about the problem is available during the execution of the system. More precisely, no information about the jobs, including their arrival time, is known before they are released into the system. However, once they are released into the system, all their properties are known precisely, and the jobs can then be taken into account for scheduling.
The most suitable method for solving such dynamic problems is DRs [7]. DRs consist of two parts: a schedule generation scheme (SGS) and a priority function (PF) [48]. The SGS represents the algorithmic framework of the DR, which determines when and under what conditions it performs scheduling decisions. It also ensures that it only creates feasible schedules, for example, by checking that no machine executes two jobs at the same time. Algorithm 1 provides the definition of the SGS that is used by the automatically designed DRs. This SGS performs a scheduling decision every time at least one machine is available and there are unscheduled jobs in the system. It also ensures that no job is scheduled on a machine on which a job is already in progress.
| Algorithm 1 SGS used by generated DRs |
|
One of the most important parts of the SGS is determining which scheduling decision to make at each decision time, i.e., which job should be scheduled on which machine. The SGS uses a PF to evaluate all available decisions. The best decision, determined by the lowest or highest rank, is then selected and executed. Over the years, PFs of varying complexity have been proposed in the literature [7]. For example, the earliest due date (EDD) rule uses a PF defined as , which means that jobs are executed in order according to their due dates. The EDD selects the jobs with the earliest due dates first, where jobs that need to be completed as quickly as possible take priority. The PF can, of course, be much more complex than that defined by the EDD. In fact, the PF is the most important part of any DR, and, therefore, great care needs to be taken when developing new and efficient PFs. However, manually designing meaningful PFs has proven to be quite a difficult and tedious task, which is why only a limited number of existing PFs are available [7,8].
3.2. Genetic Programming and Generating DRs
GP is a metaheuristic method based on the concept of natural evolution [12]. It starts with a set, called the population, of randomly generated solutions, usually referred to as individuals. These individuals are evaluated using the fitness function, which calculates the fitness of each individual, i.e., a numerical measure of how well the individual solves a particular problem by optimising a certain criterion. GP then iteratively applies a series of genetic operators to these individuals in search of better solutions until a certain termination criterion is met. The operators that GP applies are selection, crossover, and mutation. With the selection operator, GP selects better individuals for the crossover operator and worse individuals to be eliminated from the population. The selected individuals are then used by the crossover operator, which combines their properties and creates a new individual that is potentially better than the individuals from which it was created. In addition, the newly created individual can be mutated with a certain probability to introduce random changes. The purpose of the mutation operator is to help the algorithm bypass local optima and restore lost genetic material in the population. This newly created individual then replaces one of the underperforming individuals in the population. With such a strategy, GP iteratively attempts to obtain better solutions through crossover and mutation and place them into the population, eliminating poor-quality individuals. The variant of the selection algorithm used in this study is described in Algorithm 2 [48], and the flow diagram of the algorithm is shown in Figure 1.
| Algorithm 2 The GP algorithm |
|
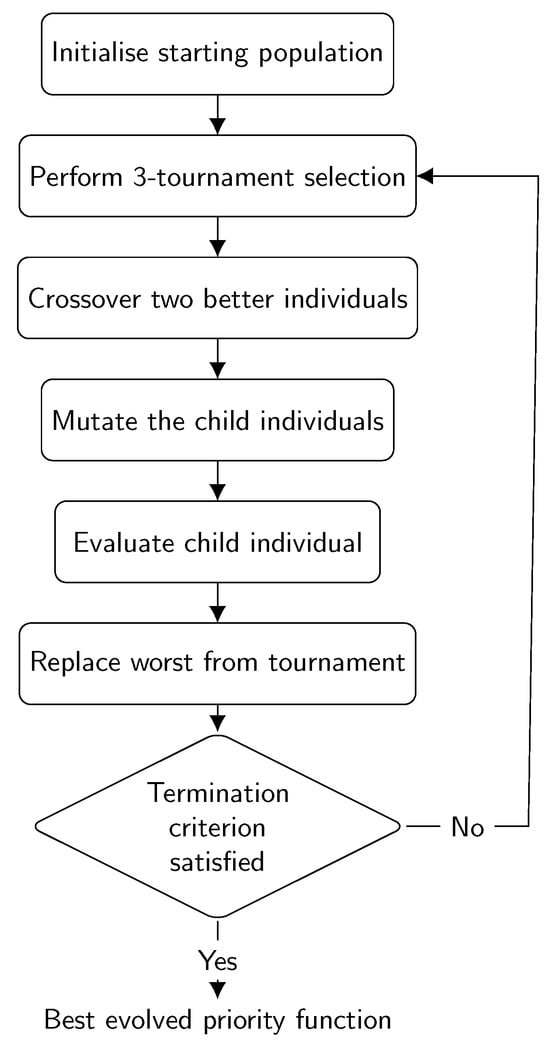
Figure 1.
Flowchart of the GP algorithm.
As already mentioned, solutions in GP are coded as expression trees consisting of function and terminal nodes. The function nodes are the inner nodes in the tree and represent various mathematical, logical, or other types of operations. The terminal nodes, on the other hand, appear as leaf nodes in the tree and represent different features of the problem. Therefore, the definition of terminal nodes is one of the most important decisions that must be made when applying GP to any problem. Through the evolutionary process, GP searches for the most appropriate expression to solve a given problem.
GP has been successfully used as a hyperheuristic method [14,49] to automatically generate heuristics for various types of combinatorial optimisation problems, such as scheduling problems [50,51], the travelling salesman problem [52,53], vehicle and arc routing problems [54,55,56], the container relocation problem [57], and the cutting stock problem [15,58]. When used to generate DRs for scheduling problems, GP has the task of finding a suitable PF that can be used by the DR to evaluate scheduling decisions. Each individual represents a potential PF, which is then used by the SGS, as defined in Algorithm 1, to evaluate its effectiveness for a given set of problem instances. To be able to meaningfully rank the various decisions in the scheduling problem, e.g., which job to schedule next, GP must have access to all relevant features of the problem via its terminal nodes. Therefore, the set of terminal nodes must contain relevant problem characteristics, such as the processing times of jobs, their due dates, weights, and so on.
The entire methodology for the automatic creation of DRs is shown in Figure 2. The figure shows that GP is used to generate PFs embedded in an SGS, as outlined in Algorithm 1. This combination represents a DR, which is then used to generate a schedule based on the characteristics of the scheduling problem (job processing times, due dates, etc.). The meaning of the symbols is outlined in Table 1 and Table 2. The schedule simply determines which job is assigned to which machine and the order in which they are executed on these machines. Finally, the quality of the created schedule can be evaluated using different performance criteria.
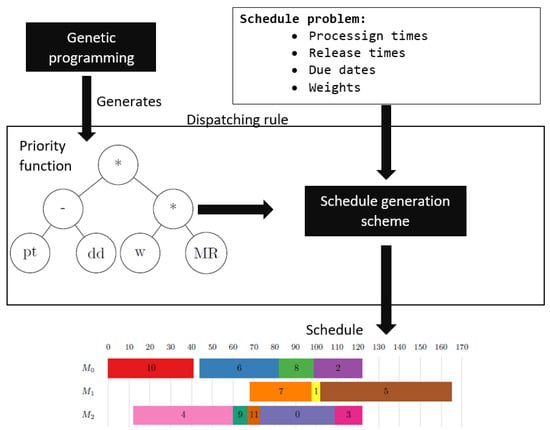
Figure 2.
Outline of the procedure for the automated generation of DRs.

Table 1.
The set of basic terminal nodes.

Table 2.
The set of extended terminal nodes.
4. Methodology
As described in the previous section, the definition and selection of suitable terminal nodes is an important step in applying GP to develop new DRs. This is probably also the most difficult step, as it requires a certain amount of expert knowledge about the problem in order to define these terminal nodes in a meaningful way. However, even with good expert knowledge, there is no guarantee that the defined nodes will enable GP to obtain good priority functions. Therefore, the aim of this study is to investigate the process of designing the terminal set in more detail and determine how the inclusion and construction of different features and nodes affect the performance of GP.
This investigation is divided into three phases, each focusing on the influence of the following factors: (1) atomic terminal nodes, (2) composite terminal nodes constructed based on the frequency of occurrence in the previous phase, and (3) composite terminal nodes designed manually. In the following, we describe each phase in detail.
4.1. Atomic Terminal Nodes
In the first phase, only atomic terminal nodes, labelled in Table 1, are used. These nodes are called atomic because they represent the most basic information about the problem at hand, such as the processing times of jobs, their due dates, weights, and so on. They cannot, therefore, be broken down into sub-expressions of simpler nodes or coded in any other way. GP can combine these nodes into more complex expressions that are interpreted as PFs to determine which scheduling decision should be selected at each decision point.
Even if the previously defined set of terminal nodes is sufficient to construct any complex expression, this might prove quite difficult for GP, since it is very likely that such expressions are easily perturbed by genetic operators. Therefore, it makes sense to define composite terminal nodes, i.e., nodes that are represented as a kind of expression computed from multiple atomic nodes. However, there are several ways to define compound terminal nodes, and these are analysed in the second and third phases of the study.
4.2. Frequency-Based Composite Terminal Nodes
In the second phase, we analyse whether it is possible to automatically construct new terminal nodes by using the frequency of occurrence of sub-expressions from previously developed PFs that work well. This phase is, therefore, based on the results of the first phase to determine which sub-expressions occur most frequently but only in the PFs with the best performance. From the best PFs, we calculate the frequency of occurrence of all sub-expressions and select the most frequent ones. We also define new terminal nodes that encode these sub-expressions and add them to the terminal set.
4.3. Manually Designed Composite Terminal Nodes
In the third phase, we investigate the influence of composite, manually designed terminal nodes that combine different basic information from Table 1 in different ways. The motivation for introducing these terminals arises from several existing manually designed DRs that use similar information to that presented in Table 2. For example, these nodes represent information such as the slack of the job, a feature often used in manually designed DRs developed to optimise the criterion, or the time until a particular machine is available. Since such information has proven valuable in various manually created DRs, there is reason to believe that it could also be useful in the context of automatically created DRs. Therefore, we have investigated their influence on the performance of GP.
4.4. Feature Selection Methods
Although we have defined various terminal nodes, not all of them are equally useful for GP in designing new DRs. The problem with including unnecessary terminal nodes is that the solution space in which GP searches for a suitable PF increases exponentially. Therefore, it becomes increasingly difficult for GP to converge to good solutions. Therefore, it is not sufficient to define only a set of terminal nodes that represent all features of the problem; it is also crucial to determine whether these features are relevant for GP.
Although various algorithms and methods for feature selection have been defined in the literature [59,60,61], we use two simple methods: backward sequential feature selection (BSFS) and frequency-based selection (FBS). Although simple, the BSFS method is commonly used in the machine learning community to select appropriate features. The reason we select only the above-mentioned methods is that our goal is to determine the best feature set for the problem under consideration rather than compare different feature selection methods.
BSFS starts with the complete feature set and removes one feature from the feature set in each iteration. GP is then executed with this reduced feature set, and the developed PFs are evaluated. The reduced set that results in the best performance for the generated DRs is selected, and the procedure is repeated until all features are removed. So, in each iteration, this method tests the effect of removing each feature on the results and removes the feature that has the least negative effect. This process requires a quadratic number of experiments to determine the appropriate terminal set.
The FBS method also starts with the complete feature set to generate a certain number of DRs. Based on the best DRs, the frequency of occurrence of each terminal node is determined. The node that occurs the least frequently is removed, and the process is repeated until all terminal nodes are removed from the terminal set. This method, therefore, removes the node that occurs least frequently in the generated PFs in each iteration. Compared to the BSFS method, this method only requires a linear number of experiments in relation to the terminal nodes. This is because only one experiment is performed in each iteration, on the basis of which the frequency of occurrence of terminal nodes can be determined to decide which node should be removed next.
5. Experimental Study
In this section, we present the experimental study. First, we describe the outline of the performed experiments, and then, we outline the obtained results.
5.1. Setup
To conduct the experimental study, we used the dataset proposed in [16], which consists of 180 problem instances of varying sizes and complexities. The instances involve between 3 and 10 machines and between 12 and 100 jobs. Moreover, the dataset contains instances of different difficulty levels considering the criterion, which means that some instances are easy to solve while others are more complex. The dataset is divided into three subsets: a training set, a validation set, and a test set. Each set contains 60 instances with similar characteristics. The training dataset was used by GP to generate new DRs. After the DRs were generated, the validation set was used by the feature selection procedures to determine the best feature sets. Finally, the test dataset was used to evaluate the DRs obtained for the best feature sets, assessing their generalisation performance on unseen problems. All the results presented below were obtained with the problem instances from the test dataset. Finally, we compared the results of the automatically generated DRs with three DRs proposed in the literature [7].
The parameters used to run GP are listed in Table 3. These parameters were optimised in a previous study [16]. For each experiment, GP was run 30 times to perform a statistical analysis of the results. Due to the large number of results, only the median values from these 30 executions are presented in the tables because the Shapiro–Wilk test for normality showed that not all results followed a normal distribution. To test the statistical difference between pairs of methods, we used the Mann–Whitney test. On the other hand, to test for a statistical difference between a group of methods, we used the Kruskal–Wallis test with Dunn’s post hoc test and the Bonferroni correction method. All statistical tests were conducted with a significance level of 0.05. All methods were coded in the C++ programming language using the ECF framework (http://ecf.zemris.fer.hr/, accessed on 1 May 2023). The experiments were conducted on a Windows 10 PC with an AMD Ryzen Threadripper 3990X 64-core processor and 128 GB of RAM.

Table 3.
GP parameters.
5.2. Results
The results in this section are presented in three phases, corresponding to the research phases described in the methodology section. In the first phase, the set of terminal nodes consists only of the atomic features of the problem. In the second phase, this terminal set is extended with composite terminal nodes consisting of the most frequent sub-expressions of the PFs developed in the first phase. Finally, in the last phase, the basic terminal set is extended with manually designed composite nodes.
5.2.1. Simple Terminal Set
In the first phase, the terminal set shown in Table 1 was used as the starting set for the construction of DRs. To determine which features were most important in this set, the BSFS and FBS methods were used to determine the optimised set of terminal nodes.
The results obtained using BSFS in this phase are shown in Table 4. The columns in the table denote the results where the corresponding feature was removed from the feature set, whereas the rows denote the steps of the algorithm. The first row indicates the results obtained when all features were used. In each subsequent row, the best result is indicated in bold, which also indicates which feature was removed from the feature set in the next iteration. In addition, each cell contains the results of the statistical test comparing the result presented in this cell with the result obtained with the entire terminal set. The symbol + means that significantly better results were achieved with the reduced set, − means that significantly worse results were achieved with the reduced set, and ≈ means that there was no significant difference between the results. We can see from the table that removing certain nodes almost always led to a significant deterioration in the results. The nodes where this happened were , , , and w. From this, we can conclude that these nodes represent the minimum set of features that the GP needs to construct meaningful PFs. By using only these four terminal nodes, GP achieved a value of 13.88, which was lower but not statistically better than the value obtained when using all terminal nodes. Removing all other nodes from the terminal set did not have a significant impact on the results, or in some cases, even led to a significant improvement. The best overall result was obtained for the node set that included the and nodes in addition to the four previously mentioned terminals. The nodes, in particular, seem to be important, as they provide information about the current time in the system, which can then be used in combination with other terminal nodes to determine when a job will become late and thus prioritise it.

Table 4.
Results obtained by BSFS for the feature set outlined in Table 1.
Table 5 shows the results GP achieved when the terminal nodes were removed based on the frequency of their occurrence in the generated PFs. The first row lists the removed terminal nodes, whereas the second row shows the corresponding fitness values. Again, each cell contains the result of the statistical test comparing the results of the entire set with the reduced sets. We can see that the best overall result was obtained with two terminal sets: a smaller one with the nodes , , , and w, and a larger one with the nodes and in addition to these nodes. In both cases, the results are significantly better than the results obtained with the entire terminal set. This shows that it is possible to make a meaningful selection of features depending on the frequency of the terminal nodes in the obtained expressions, especially since the four most important terminal nodes consistently have the highest frequency.

Table 5.
Results obtained by GP when selecting atomic features based on their frequency in the PFs.
5.2.2. Extended Terminal Set with Composite Features Determined by Frequency of Occurrence
Based on the best individuals from the first phase of the experiments, we calculated the frequency of sub-expressions. The sub-expressions with more than 30 occurrences are listed in Table 6. It is interesting to note that only sub-expressions of size 3 occurred, whereas larger sub-expressions were rare in several trees. This shows that there did not seem to be a larger, well-functioning sub-expression that could be reused; rather, the rules consisted of small, frequently repeated sub-expressions. The reason for this could be that either such a sub-expression did not exist or that GP had difficulty obtaining it with the given settings. If we examine which sub-expressions occurred most frequently, we can see that GP created certain sub-expressions that occurred frequently in manually created DRs. For example, the expression was often used to determine how quickly the job would be completed on each machine, using information about when the machine was available and how long the job would take on the machine. Sub-expressions such as and were also common, as the purpose was to schedule jobs with a lower processing time or due date adjusted for the weight of the job. Based on this frequency of occurrence, seven new terminal nodes were designed and included in the previously optimised terminal set.

Table 6.
Frequency of occurrence of most commonly appearing sub-expressions from Phase 1.
Table 7 provides an overview of the results obtained through the additional use of the seven features described in Table 6. In this section, the results obtained are statistically compared with the optimised terminal set from Phase 1, the results of which are also included in the first row of the table. The results show that the inclusion of these composite features in the terminal set did not have a positive influence on the results compared to the optimised terminal set from Phase 1. In most cases, the results either remained the same or even deteriorated, which was confirmed by the statistical tests performed. The only node that seemed to have some effect on this terminal set was , which occurred most frequently in the PFs from Phase 1. On the other hand, nodes such as , were the first to be removed, suggesting that they were the least informative.

Table 7.
Results obtained by BSFS for the extended terminal set with features created based on their frequency of occurrence.
Table 8 shows the selection process carried out by FBS. We can see that in this case, the order in which features were removed from the terminal set differed from that of BSFS. The results in this case showed no improvement over the terminal obtained at the end of Phase 1. Since neither method achieved a positive result, we can conclude that creating new composite features based on their frequency of occurrence in well-functioning rules does not generally lead to better results. These nodes, therefore, offer no advantages over the original set of atomic features identified in Phase 1.

Table 8.
Results obtained by GP when selecting automatically designed composite features based on their frequency in the PFs.
5.2.3. Extended Terminal Set with Manually Designed Composite Features
Table 9 shows the results obtained with the BSFS method when using manually designed composite terminal nodes. Again, the statistical tests were calculated using the optimised terminal set from Phase 1. The results show that no single combination of terminal nodes was able to achieve significantly better results compared to the terminal set obtained after Phase 1. With the set from Phase 1 extended with the nodes , , , , and , the median value of the results achieved was improved to 13.47. In all other cases, however, it was not possible to achieve a significant improvement. The results are either equally good or even significantly worse than those achieved with the terminal set obtained in Phase 1.

Table 9.
Results obtained using BSFS for the extended terminal set with features created based on their frequency of occurrence.
The results when using FBS are shown in Table 10. This table shows that in all cases, the results were as good as with the basic terminal set obtained after Phase 1. Again, we can see that the order in which the terminals were removed from the set is similar to that of BSFS.

Table 10.
Results obtained by GP when selecting manually designed composite features based on their frequency in the PFs.
Unfortunately, the results obtained when manually defined composite nodes were included are inconclusive. In most cases, there was no significant difference between the sets containing these features and the set obtained after Phase 1. However, some improvement in the results was observed for one feature set. This could indicate that the additional features were beneficial for GP and allowed it to generate better PFs, but at the same time, their inclusion also increased the search space, making it more difficult for GP to converge.
6. Analysis
6.1. Comparison of Results from Each Phase
Table 11 gives an overview of the best results obtained with the validation set for each terminal set, as well as the best manually developed DRs, namely EDD, COVERT, and ATC. The initial feature set from Table 1 is labelled as Phase 0, whereas Phase 2 + 3 refers to the combination of the best feature sets from Phase 2 and Phase 3, which was used to investigate whether the combination of these two feature sets led to an improvement in the results. In addition, the table shows the average rule size obtained when using each terminal set, which represents the average number of nodes in the expressions generated by GP. Compared to the manually generated DRs, we can see that GP achieved better DRs with the best terminal set obtained after each phase compared to the three manually generated ones. Only in the cases where no optimisation was performed, or when Phases 2 and 3 were combined, did GP fail to outperform the ATC rule. This shows that even for a terminal set with atomic terminal nodes, GP can reasonably combine them to outperform the existing rules. However, for more complex terminal nodes, GP can even increase the gap between manually and automatically created DRs.

Table 11.
Comparison of results from all phases on the validation set.
Figure 3 depicts the results from Table 11 as a box plot. The figure shows that the terminal node sets from Phase 1 and Phase 2 lead to the least scattered solutions. This is favourable, as it means that GP is more likely to produce a result close to the median. Therefore, the method is more reliable when it comes to generating solutions of expected quality. On the other hand, the solutions obtained when using the terminal node set obtained in Phase 3 are quite scattered. The results also show that GP is more likely to obtain better results with this terminal node set than with any other terminal node set.
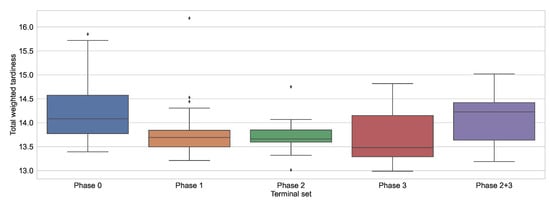
Figure 3.
Box plot of the best results obtained by each terminal set on the validation set.
To determine whether there was a significant difference between the results, the statistical tests described above were used, and a p-value close to 0 was determined. This shows that there was a significant difference between the results obtained. To determine which of the results were significantly different, the post hoc test was used, the results of which are shown in Table 12. The table shows that the results in the row are inferior to those in the column when indicated by “<”, superior when indicated by “>”, or equivalent when indicated by “≈”. We can see that the results obtained using only the atomic nodes, without optimising the terminal set, usually led to the worst results. In contrast, there was no significant difference between the results from Phases 1, 2, and 3.

Table 12.
Results of the statistical tests on the validation set.
The above results summarise the validation set. In order to more objectively evaluate the performance of GP with the different terminal sets, the rules obtained were evaluated using the test set. These results are listed in Table 13. It can be seen from the table that the performance of the rules obtained is now quite different from before. In this case, the results before feature selection only outperformed the simplest DR but not the two more complicated ones, namely COVERT and ATC. Even after Phases 1 and 2, GP could only find rules that performed similarly well to the manually designed rules. Only when the manually designed terminal nodes were finally introduced did GP generate rules that clearly outperformed the manually designed rules. The results are also shown as a box plot in Figure 4 to better illustrate the differences between the results. The figure illustrates that the introduction of manually designed composite terminal nodes led to the greatest increase in performance.

Table 13.
Comparison of results from all phases on the test set.
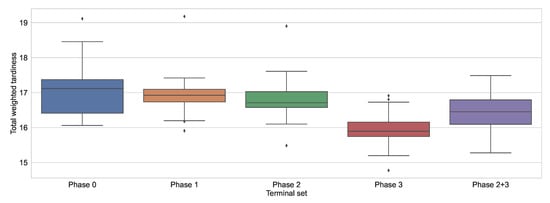
Figure 4.
Box plot of the best results obtained by each terminal set on the test set.
To confirm that the addition of manually designed composite nodes led to a significant improvement in the results, the Kruskal–Wallis test was used, and a p-value of 0 was obtained, meaning that there was a significant difference. The results of the post hoc tests performed are shown in Table 14. The table shows that although in most cases there was no significant difference between the terminal sets, the use of manually designed composite terminal nodes significantly improved the results compared to those obtained in Phases 0, 1, and 2.

Table 14.
Results of the statistical tests on the test set.
Based on the previous results, we can see that the manually designed terminal nodes actually provided the most valuable information about the problem, allowing the rules to generalise well to unseen problem instances. Presumably, all methods performed similarly on the validation set, as the best terminal sets were selected for them. However, it appears that this may have led to a slight overfitting to the validation set. Based on the previous observations, it is, therefore, safe to conclude that a mixture of simple and manually designed composite terminal nodes is required to create the best DRs.
6.2. DR Complexity Analysis
One could assume that a potential advantage of introducing composite features into the terminal set could be the generation of smaller expressions. To analyse this, Figure 5 presents a scatter plot in which the fitness of the DR (x-axis) is plotted against its size (y-axis) for each terminal set used. The figure illustrates that the solutions are very widely scattered and only a very small number of rules below size 30 were obtained. Furthermore, the smaller rules usually did not perform well, often reaching a Twt value of over 16. It seems that the generated DRs started to perform well at around size 35. However, the best overall rule had a size of more than 50, and some other well-performing rules also had sizes of more than 50 nodes. To determine whether there was a correlation between the rule size and its performance, Spearman’s rho test was used. Since values between −0.15 and 0.1 were obtained for the results of all phases, we can conclude that there was no obvious correlation between these two measures. Although it may seem counterintuitive as to why smaller expressions were not obtained for composite terminal nodes, as more complex expressions should be represented by a smaller number of nodes, this was most likely due to the bloating of GP, and could be mitigated by using different mechanisms to control the bloating [62,63].
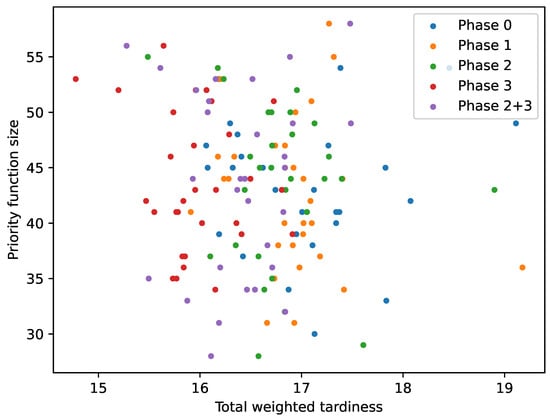
Figure 5.
Scatter plot of DR fitness values plotted against the size of the DRs.
6.3. Convergence Analysis
Another interesting aspect to investigate is the rate of convergence of GP when using different terminal node sets. For this purpose, the best individual was saved after every 10,000 evaluations and later evaluated on the validation set. This was done for all 30 executions, and the median values were calculated and then used to plot Figure 6. The figure illustrates that the terminal set significantly influenced the quality of the initial solution. The worst solution quality was obtained either with the initial terminal set (Phase 0) or the one obtained from Phase 2 + 3. The reason for this could be that these terminal node sets were larger and, therefore, it was more difficult for GP to generate a good initial solution. Interestingly, the terminal set from Phase 2 achieved the best initial solution, indicating that the node used contributed to the development of good solutions. Moreover, this terminal led to the fastest convergence of the algorithm in the first half of the evolutionary process, although the algorithm started to stagnate after a certain time. When using the terminal set obtained in Phase 3, GP started with quite poor solutions; however, in the end, it reached the best overall solutions. This suggests that this terminal set might have been the most meaningful, and GP was thus able to produce high-quality DRs. However, it also seemed to be much more difficult for GP to obtain these solutions, thus requiring a longer evolution process, as it can be seen that the quality of the solutions themselves had improved by the end of the assigned number of scores. Therefore, there is a possibility that with more time, GP could achieve even better solutions with this terminal set.
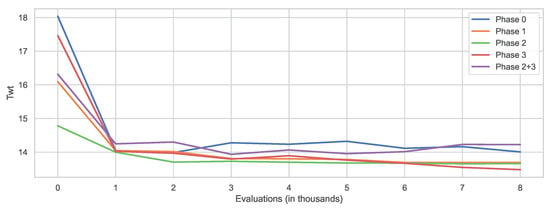
Figure 6.
Algorithm convergence on the validation set.
6.4. Removal-Sequence Similarity
To analyse how similar the order in which the terminal nodes were removed from the terminal set was, the Levenshtein distance measure was used to determine the similarity of the two removal sequences. For this purpose, the removal sequences of BSFS and FBS were determined, and the Levenshtein distance for these two sequences was calculated for each phase. The Levenshtein distance values obtained, scaled between 0 and 1, were 0.666, 0.571, and 0.666 for the removal sequences obtained in Phases 1, 2, and 3, respectively. The values obtained show that there were indeed large differences between the removal sequences of the two selection methods. Thus, even if FBS could determine the nodes to be removed, it still deviated significantly from the sequence obtained by a more thorough search for the optimal feature set.
6.5. Run-Time Analysis
In this section, we briefly analyse the running times of the two feature selection algorithms. The complexity of FBS is linear with the number of features, i.e., to determine the best set of terminals, experiments must be performed, where N denotes the number of features. The appears because it is not necessary to perform the last experiment with only a single feature. On the other hand, BSFS has a quadratic complexity and requires about experiments. This obviously represents a significant difference in execution time, as the execution time of GP for the 80,000 fitness evaluations was about 1 h. Thus, in the case where nine terminal nodes were included in the set, FBS required 8 experiments, whereas BSFS required 44. Since each experiment was executed 30 times, and each execution took 1 h, FBS was executed for a total of 240 h, whereas BFSF was executed for 1320 h. It is assumed that all experiments are run in series. However, in many cases they can be run in parallel, reducing the total execution time. Although a smaller number of evaluations could be used, this would likely lead to a degradation in performance, as previous studies have shown that GP performs best for the given number of feature evaluations [16].
7. Conclusions and Future Work
The aim of this study was to investigate the impact of different types of terminal nodes on the performance of GP in developing DRs for unrelated machine scheduling problems. The experimental results show that when GP is equipped with only atomic features to generate DRs, it can outperform simple DRs but has difficulty in evolving rules better than complex manually designed DRs. Therefore, two methods were used to construct composite terminal nodes and improve the performance of GP. In the first method, new terminals were constructed based on sub-expressions most commonly found in DRs developed with atomic terminals. Although with these terminals, GP matched the performance of manually constructed DRs, it still rarely outperformed them. However, the second approach, where composite terminal nodes were designed manually, proved to be more efficient and allowed GP to generate DRs that significantly outperformed manually designed DRs. Therefore, a certain level of expertise is required when designing terminal nodes, as it is necessary to define terminal nodes that provide more complex information about the scheduling problem. In addition to defining new terminals, it is also imperative to apply a feature selection method to determine the appropriate set of terminal nodes to prevent the search space from growing exponentially. The experiments showed that selecting terminal nodes based on their frequency of occurrence can help in selecting meaningful terminal nodes. However, this approach is not as robust as standard feature selection methods, such as backward sequential feature selection.
The results obtained in this study open up several avenues for future research. One possible research direction, which was only briefly explored, would be to introduce feature construction methods into the GP algorithm so that it can automatically design new features. In addition, better measures for identifying relevant features and sub-expressions are needed, aside from frequency of occurrence. Finally, another option would be to manually construct additional terminal nodes, as such nodes usually lead to better results compared to those constructed based on the frequency of occurrence.
Author Contributions
Conceptualization, M.Đ., D.J., S.P. and L.M.; methodology, M.Đ., D.J., S.P. and L. M.; software, M.Đ., D.J., S.P. and L.M.; validation, M.Đ., D.J., S.P. and L.M.; formal analysis, M.Đ., D.J., S.P. and L.M.; investigation, M.Đ., D.J., S.P. and L.M.; resources, M.Đ., D.J., S.P. and L.M.; data curation, M.Đ., D.J., S.P. and L.M.; writing—original draft preparation, M.Đ., D.J., S.P. and L.M.; writing—review and editing, M.Đ., D.J., S.P. and L.M.; visualization, M.Đ., D.J., S.P. and L.M.; supervision, M.Đ., D.J., S.P. and L.M.; project administration, M.Đ., D.J., S.P. and L.M.; funding acquisition, M.Đ., D.J., S.P. and L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Croatian Science Foundation under the project IP-2019-04-4333.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Leung, J.Y.T. (Ed.) Handbook of Scheduling; Chapman & Hall/CRC Computer and Information Science Series; Chapman & Hall/CRC: Philadelphia, PA, USA, 2004. [Google Scholar]
- Wu, L.; Wang, S. Exact and heuristic methods to solve the parallel machine scheduling problem with multi-processor tasks. Int. J. Prod. Econ. 2018, 201, 26–40. [Google Scholar] [CrossRef]
- Gedik, R.; Kalathia, D.; Egilmez, G.; Kirac, E. A constraint programming approach for solving unrelated parallel machine scheduling problem. Comput. Ind. Eng. 2018, 121, 139–149. [Google Scholar] [CrossRef]
- Yu, L.; Shih, H.M.; Pfund, M.; Carlyle, W.M.; Fowler, J.W. Scheduling of unrelated parallel machines: An application to PWB manufacturing. IIE Trans. 2002, 34, 921–931. [Google Scholar] [CrossRef]
- Hart, E.; Ross, P.; Corne, D. Evolutionary Scheduling: A Review. Genet. Program. Evolvable Mach. 2005, 6, 191–220. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Heuristic and metaheuristic methods for the parallel unrelated machines scheduling problem: A survey. Artif. Intell. Rev. 2022, 56, 3181–3289. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. A survey of dispatching rules for the dynamic unrelated machines environment. Expert Syst. Appl. 2018, 113, 555–569. [Google Scholar] [CrossRef]
- Branke, J.; Nguyen, S.; Pickardt, C.W.; Zhang, M. Automated Design of Production Scheduling Heuristics: A Review. IEEE Trans. Evol. Comput. 2016, 20, 110–124. [Google Scholar] [CrossRef]
- Nguyen, S.; Mei, Y.; Zhang, M. Genetic programming for production scheduling: A survey with a unified framework. Complex Intell. Syst. 2017, 3, 41–66. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Survey on Genetic Programming and Machine Learning Techniques for Heuristic Design in Job Shop Scheduling. IEEE Trans. Evol. Comput. 2023, 28, 147–167. [Google Scholar] [CrossRef]
- Poli, R.; Langdon, W.B.; McPhee, N.F. A Field Guide to Genetic Programming; Lulu Enterprises, UK Ltd.: London, UK, 2008. [Google Scholar]
- Koza, J.R. Genetic Programming; Complex Adaptive Systems; Bradford Books: Cambridge, MA, USA, 1992. [Google Scholar]
- Koza, J.R. Human-competitive results produced by genetic programming. Genet. Program. Evolvable Mach. 2010, 11, 251–284. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Ozcan, E.; Woodward, J.R. Exploring Hyper-heuristic Methodologies with Genetic Programming. Comput. Intell. 2009, 1, 177–201. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Woodward, J. Automating the Packing Heuristic Design Process with Genetic Programming. Evol. Comput. 2012, 20, 63–89. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D.; Knežević, K. Adaptive scheduling on unrelated machines with genetic programming. Appl. Soft Comput. 2016, 48, 419–430. [Google Scholar] [CrossRef]
- Hunt, R.; Johnston, M.; Zhang, M. Evolving “less-myopic” scheduling rules for dynamic job shop scheduling with genetic programming. In Proceedings of the GECCO ’14: 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014. [Google Scholar] [CrossRef]
- Miyashita, K. Job-Shop Scheduling with Genetic Programming. In Proceedings of the GECCO’00: 2nd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 10–12 July 2000; pp. 505–512. [Google Scholar]
- Dimopoulos, C.; Zalzala, A. Investigating the use of genetic programming for a classic one-machine scheduling problem. Adv. Eng. Softw. 2001, 32, 489–498. [Google Scholar] [CrossRef]
- Jakobović, D.; Budin, L. Dynamic Scheduling with Genetic Programming. In Proceedings of the Genetic Programming, Budapest, Hungary, 10–12 April 2006; Collet, P., Tomassini, M., Ebner, M., Gustafson, S., Ekárt, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 73–84. [Google Scholar]
- Ho, N.; Tay, J.C. Evolving Dispatching Rules for solving the Flexible Job-Shop Problem. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005. [Google Scholar] [CrossRef]
- Chand, S.; Huynh, Q.; Singh, H.; Ray, T.; Wagner, M. On the use of genetic programming to evolve priority rules for resource constrained project scheduling problems. Inf. Sci. 2018, 432, 146–163. [Google Scholar] [CrossRef]
- Gil-Gala, F.J.; Varela, R. Genetic Algorithm to Evolve Ensembles of Rules for On-Line Scheduling on Single Machine with Variable Capacity. In From Bioinspired Systems and Biomedical Applications to Machine Learning; Springer International Publishing: Cham, Switzerland, 2019; pp. 223–233. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. A Computational Study of Representations in Genetic Programming to Evolve Dispatching Rules for the Job Shop Scheduling Problem. IEEE Trans. Evol. Comput. 2013, 17, 621–639. [Google Scholar] [CrossRef]
- Branke, J.; Hildebrandt, T.; Scholz-Reiter, B. Hyper-heuristic Evolution of Dispatching Rules: A Comparison of Rule Representations. Evol. Comput. 2015, 23, 249–277. [Google Scholar] [CrossRef] [PubMed]
- Planinić, L.; Backović, H.; Đurasević, M.; Jakobović, D. A Comparative Study of Dispatching Rule Representations in Evolutionary Algorithms for the Dynamic Unrelated Machines Environment. IEEE Access 2022, 10, 22886–22901. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Johnston, M.; Tan, K.C. Dynamic Multi-objective Job Shop Scheduling: A Genetic Programming Approach. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; pp. 251–282. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Tan, K.C. Enhancing genetic programming based hyper-heuristics for dynamic multi-objective job shop scheduling problems. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 2781–2788. [Google Scholar] [CrossRef]
- Masood, A.; Mei, Y.; Chen, G.; Zhang, M. Many-objective genetic programming for job-shop scheduling. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 209–216. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Evolving dispatching rules for optimising many-objective criteria in the unrelated machines environment. Genet. Program. Evolvable Mach. 2017, 19, 9–51. [Google Scholar] [CrossRef]
- Park, J.; Nguyen, S.; Zhang, M.; Johnston, M. Evolving Ensembles of Dispatching Rules Using Genetic Programming for Job Shop Scheduling. In Proceedings of the Genetic Programming, Copenhagen, Denmark, 8–10 April 2015; Machado, P., Heywood, M.I., McDermott, J., Castelli, M., García-Sánchez, P., Burelli, P., Risi, S., Sim, K., Eds.; Springer: Cham, Switzerland, 2015; pp. 92–104. [Google Scholar]
- Hart, E.; Sim, K. A Hyper-Heuristic Ensemble Method for Static Job-Shop Scheduling. Evol. Comput. 2016, 24, 609–635. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Comparison of ensemble learning methods for creating ensembles of dispatching rules for the unrelated machines environment. Genet. Program. Evolvable Mach. 2017, 19, 53–92. [Google Scholar] [CrossRef]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An Investigation of Ensemble Combination Schemes for Genetic Programming based Hyper-heuristic Approaches to Dynamic Job Shop Scheduling. Appl. Soft Comput. 2017, 63, 72–86. [Google Scholar] [CrossRef]
- Đurasević, M.; Gil-Gala, F.J.; Planinić, L.; Jakobović, D. Collaboration methods for ensembles of dispatching rules for the dynamic unrelated machines environment. Eng. Appl. Artif. Intell. 2023, 122, 106096. [Google Scholar] [CrossRef]
- Đurasević, M.; Gil-Gala, F.J.; Jakobović, D.; Coello, C.A.C. Combining single objective dispatching rules into multi-objective ensembles for the dynamic unrelated machines environment. Swarm Evol. Comput. 2023, 80, 101318. [Google Scholar] [CrossRef]
- Nguyen, S.; Zhang, M.; Tan, K.C. Surrogate-Assisted Genetic Programming with Simplified Models for Automated Design of Dispatching Rules. IEEE Trans. Cybern. 2017, 47, 2951–2965. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M.; Tan, K.C. Surrogate-Assisted Evolutionary Multitask Genetic Programming for Dynamic Flexible Job Shop Scheduling. IEEE Trans. Evol. Comput. 2021, 25, 651–665. [Google Scholar] [CrossRef]
- Gil-Gala, F.J.; Sierra, M.R.; Mencía, C.; Varela, R. Genetic programming with local search to evolve priority rules for scheduling jobs on a machine with time-varying capacity. Swarm Evol. Comput. 2021, 66, 100944. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Tan, K.C.; Zhang, M. Multitask Genetic Programming-Based Generative Hyperheuristics: A Case Study in Dynamic Scheduling. IEEE Trans. Cybern. 2021, 52, 10515–10528. [Google Scholar] [CrossRef]
- Mei, Y.; Nguyen, S.; Xue, B.; Zhang, M. An Efficient Feature Selection Algorithm for Evolving Job Shop Scheduling Rules with Genetic Programming. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 339–353. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Zhang, M. A two-stage genetic programming hyper-heuristic approach with feature selection for dynamic flexible job shop scheduling. In Proceedings of the GECCO ’19: Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Genetic Programming with Adaptive Search Based on the Frequency of Features for Dynamic Flexible Job Shop Scheduling. In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; pp. 214–230. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Evolving Scheduling Heuristics via Genetic Programming with Feature Selection in Dynamic Flexible Job-Shop Scheduling. IEEE Trans. Cybern. 2021, 51, 1797–1811. [Google Scholar] [CrossRef]
- Yska, D.; Mei, Y.; Zhang, M. Feature construction in genetic programming hyper-heuristic for dynamic flexible job shop scheduling. In Proceedings of the GECCO ’18: Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018. [Google Scholar] [CrossRef]
- Pinedo, M.L. Scheduling; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Graham, R.; Lawler, E.; Lenstra, J.; Kan, A. Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. In Discrete Optimization II; Annals of Discrete Mathematics; Hammer, P., Johnson, E., Korte, B., Eds.; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar] [CrossRef]
- Đurasević, M.; Jakobović, D. Comparison of schedule generation schemes for designing dispatching rules with genetic programming in the unrelated machines environment. Appl. Soft Comput. 2020, 96, 106637. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Nguyen, S.; Mei, Y.; Xue, B.; Zhang, M. A Hybrid Genetic Programming Algorithm for Automated Design of Dispatching Rules. Evol. Comput. 2019, 27, 467–496. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Guided Subtree Selection for Genetic Operators in Genetic Programming for Dynamic Flexible Job Shop Scheduling. In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; pp. 262–278. [Google Scholar] [CrossRef]
- Duflo, G.; Kieffer, E.; Brust, M.R.; Danoy, G.; Bouvry, P. A GP Hyper-Heuristic Approach for Generating TSP Heuristics. In Proceedings of the 2019 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Rio de Janeiro, Brazil, 20–24 May 2019; pp. 521–529. [Google Scholar] [CrossRef]
- Gil-Gala, F.J.; Durasević, M.; Sierra, M.R.; Varela, R. Evolving ensembles of heuristics for the travelling salesman problem. Nat. Comput. 2023, 22, 671–684. [Google Scholar] [CrossRef]
- Jacobsen-Grocott, J.; Mei, Y.; Chen, G.; Zhang, M. Evolving heuristics for Dynamic Vehicle Routing with Time Windows using genetic programming. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1948–1955. [Google Scholar] [CrossRef]
- Wang, S.; Mei, Y.; Park, J.; Zhang, M. Evolving Ensembles of Routing Policies using Genetic Programming for Uncertain Capacitated Arc Routing Problem. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1628–1635. [Google Scholar] [CrossRef]
- Liu, Y.; Mei, Y.; Zhang, M.; Zhang, Z. A Predictive-Reactive Approach with Genetic Programming and Cooperative Coevolution for the Uncertain Capacitated Arc Routing Problem. Evol. Comput. 2020, 28, 289–316. [Google Scholar] [CrossRef]
- Đurasević, M.; Đumić, M. Automated design of heuristics for the container relocation problem using genetic programming. Appl. Soft Comput. 2022, 130, 109696. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G. Evolving Bin Packing Heuristics with Genetic Programming. In Parallel Problem Solving from Nature—PPSN IX; Springer: Berlin/Heidelberg, Germany, 2006; pp. 860–869. [Google Scholar] [CrossRef]
- DASH, M.; LIU, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Jovic, A.; Brkic, K.; Bogunovic, N. A review of feature selection methods with applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015. [Google Scholar] [CrossRef]
- Abiodun, E.O.; Alabdulatif, A.; Abiodun, O.I.; Alawida, M.; Alabdulatif, A.; Alkhawaldeh, R.S. A systematic review of emerging feature selection optimization methods for optimal text classification: The present state and prospective opportunities. Neural Comput. Appl. 2021, 33, 15091–15118. [Google Scholar] [CrossRef]
- Luke, S.; Panait, L. A Comparison of Bloat Control Methods for Genetic Programming. Evol. Comput. 2006, 14, 309–344. [Google Scholar] [CrossRef]
- Alfaro-Cid, E.; Merelo, J.J.; de Vega, F.F.; Esparcia-Alcázar, A.I.; Sharman, K. Bloat Control Operators and Diversity in Genetic Programming: A Comparative Study. Evol. Comput. 2010, 18, 305–332. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).