Variational Autoencoders-Based Algorithm for Multi-Criteria Recommendation Systems

Abstract

In recent years, recommender systems have become a crucial tool, assisting users in discovering and engaging with valuable information and services. Multi-criteria recommender systems have demonstrated significant value in assisting users to identify the most relevant items by considering various aspects of user experiences. Deep learning (DL) models demonstrated outstanding performance across different domains: computer vision, natural language processing, image analysis, pattern recognition, and recommender systems. In this study, we introduce a deep learning model using VAE to improve multi-criteria recommendation systems. Specifically, we propose a variational autoencoder-based model for multi-criteria recommendation systems (VAE-MCRS). The VAE-MCRS model is sequentially trained across multiple criteria to uncover patterns that allow for better representation of user–item interactions. The VAE-MCRS model utilizes the latent features generated by the VAE in conjunction with user–item interactions to enhance recommendation accuracy and predict ratings for unrated items. Experiments carried out using the Yahoo! Movies multi-criteria dataset demonstrate that the proposed model surpasses other state-of-the-art recommendation algorithms, achieving a Mean Absolute Error (MAE) of 0.6038 and a Root Mean Squared Error (RMSE) of 0.7085, demonstrating its superior performance in providing more precise recommendations for multi-criteria recommendation tasks.

1. Introduction

The advancement of online resources has led to a significant increase in online information, resulting in information overload that complicates users’ ability to acquire the items, information, and services they require. Such users are faced with the challenge of navigating a vast amount of available content and selecting from a wide range of items. To address this challenge, recommender systems (RSs) provide an efficient solution to this problem. RSs aid users in making correct decisions by analyzing their preferences and suggesting items that satisfy their preferences. In recent years, RSs attracted significant attention and are utilized across various online platforms, including e-learning, e-commerce, e-tourism, and others [1,2].

Collaborative filtering (CF) is a widely utilized method in RS. CF produces recommendations based on the user interactions with items. By analyzing such interactions, CF utilizes ratings to determine similarities between users or items and generate recommendations based on those similarities [3,4]. Despite its effectiveness, CF techniques face several limitations, including issues like the cold start problem, sparsity, inaccurate predictions, and scalability. In addition, most of the CF methods rely on a single criterion rating, an overall score, and based on that, recommendations are generated. This strategy does not effectively reflect user needs, leading to inaccurate recommendations as they do not take into consideration the various aspects of user preferences [5].

In practice, end users are inclined to assess an item with respect to many attributes at the same time. For example, one can evaluate a hotel by its location, amenities, food, and atmosphere. RSs can fail to predict this kind of preference if the end user is asked to provide a single overall rating. To address this limitation and extend the usability of the recommendation models, Multi-Criteria Recommender Systems (MCRSs) have emerged [6,7]. MCRSs improve the quality of the recommendations, in particular, the recommendation accuracy, by allowing the user to incorporate multiple criteria into the recommendation process instead of only one. Nonetheless, MCRSs have their own set of challenges. A significant issue is the need for accurate user preference modeling to capture user preferences across several aspects of an item. Without this, such recommendations will not take into consideration some of the tastes a user has. Additionally, the interdependencies among criteria can lead to multi-collinearity issues, complicating the modeling process and potentially degrading recommendation accuracy. Apart from that, another challenge comes from incomplete ratings across criteria. In most cases, users rate only a few of the criteria required, hence making it very hard to make models that can predict preferences accurately. Solving this sparsity while recommending relevant items is critical. Furthermore, the models should be biased to overfitting through joint training and regularization so that the representations learned are relevant to all the criteria and not just a select few [8,9,10]. To tackle these issues, this paper proposes a VAE-based model designed for multi-criteria recommendation systems (VAE-MCRS). The architecture of the VAE model is trained sequentially on many criteria, taking into account the complex relationship between users, their preferences, and the properties of the items. By integrating VAE with MCRS, the proposed model leverages the generative modeling capabilities of the VAE alongside MCRS interactions for capturing complex user preferences, and improves recommendation accuracy.

The major contributions of this study are outlined as follows:

• We propose a novel VAE-based model tailored for multi-criteria recommendation systems (VAE-MCRS), which incorporates both latent representation vectors and user–item interactions.
• We demonstrate that incorporating multiple item aspects (i.e., multi-criteria ratings) enables the proposed VAE-MCRS model to utilize its generative capabilities effectively within the multi-criteria recommendation framework. The proposed model is capable of capturing rather complex dependencies among the various criteria as well as the overall user preferences, thus enhancing recommendation accuracy.
• We conduct an extensive set of experiments on a real-world multi-criteria dataset (Yahoo! Movies), comparing the VAE-MCRS model with various stare-of-the-art recommendation models. The experimental results validate the effectiveness of the proposed model, highlighting its advantage over other baseline recommendation models in terms of recommendation accuracy.

The rest of the paper is organized as follows: Section 2 presents the background of deep learning models, VAE, and outlines relevant related works on VAE-based recommender systems. Section 3, details the design and development of the VAE-MCRS model. Section 4 presents and discusses the performance evaluation of the VAE-MCRS model through a series of experiments with related recommendation methods as benchmarks. Finally, Section 5 illustrates the conclusion of this study and proposes further research directions.

2. Background and Related Work

2.1. Deep Learning Models in Recommender Systems

Deep learning has transformed various fields within artificial intelligence and machine learning. These models resemble the structure and functioning of the human brain by using interconnected layers of artificial neurons to learn and recognize patterns in large amounts of data. The capabilities of deep learning have made it one of the most adopted tools, as they perform automated feature extraction and effectively handle time-series data as compared with traditional machine learning techniques. Deep learning models have proven to make remarkably accurate performance on large-scale data-driven tasks. The combination of pattern recognition, feature learning, and prediction performance makes deep learning have a transformative nature across a variety of industries and fields of research [11]. Deep learning models in recommender systems extract hidden patterns to alleviate common problems in traditional recommender systems: scalability, sparsity, and accuracy. Deep learning enhances recommender systems through the following:

• Capturing non-linear relationships: deep learning models effectively allow for the extraction of non-linear relationships between users and items, which are often overlooked by traditional methods. This is crucial for understanding nuanced preferences and providing more accurate recommendations [12,13].
• Handling high-dimensional data: deep learning models remain capable of handling extremely high-dimensional data, emerging as a challenge in recommender systems. Such models have the capacity to extract low-dimensional representations, thereby simplifying the complexity of problems while still preserving all informative contents, with a data sample size large enough to make conventional statistical methods ineffective [12,13].
• Addressing data sparsity: deep learning models can effectively deal with the problem of sparsity of data, which can occur when information about user preferences or item attributes is limited. They can learn from incomplete data and hence make accurate predictions even when user interactions are limited [12,13].
• Improving recommendation quality: deep learning models have generally surpassed traditional approaches in recommender systems, leading to more relevant and personalized recommendations [12,13].

Overall, deep learning models have become essential in modern recommender systems across numerous domains, including e-learning, e-commerce, e-health, e-tourism, and entertainment, increasingly enhancing their efficiency in delivering personalized user experiences [11,13].

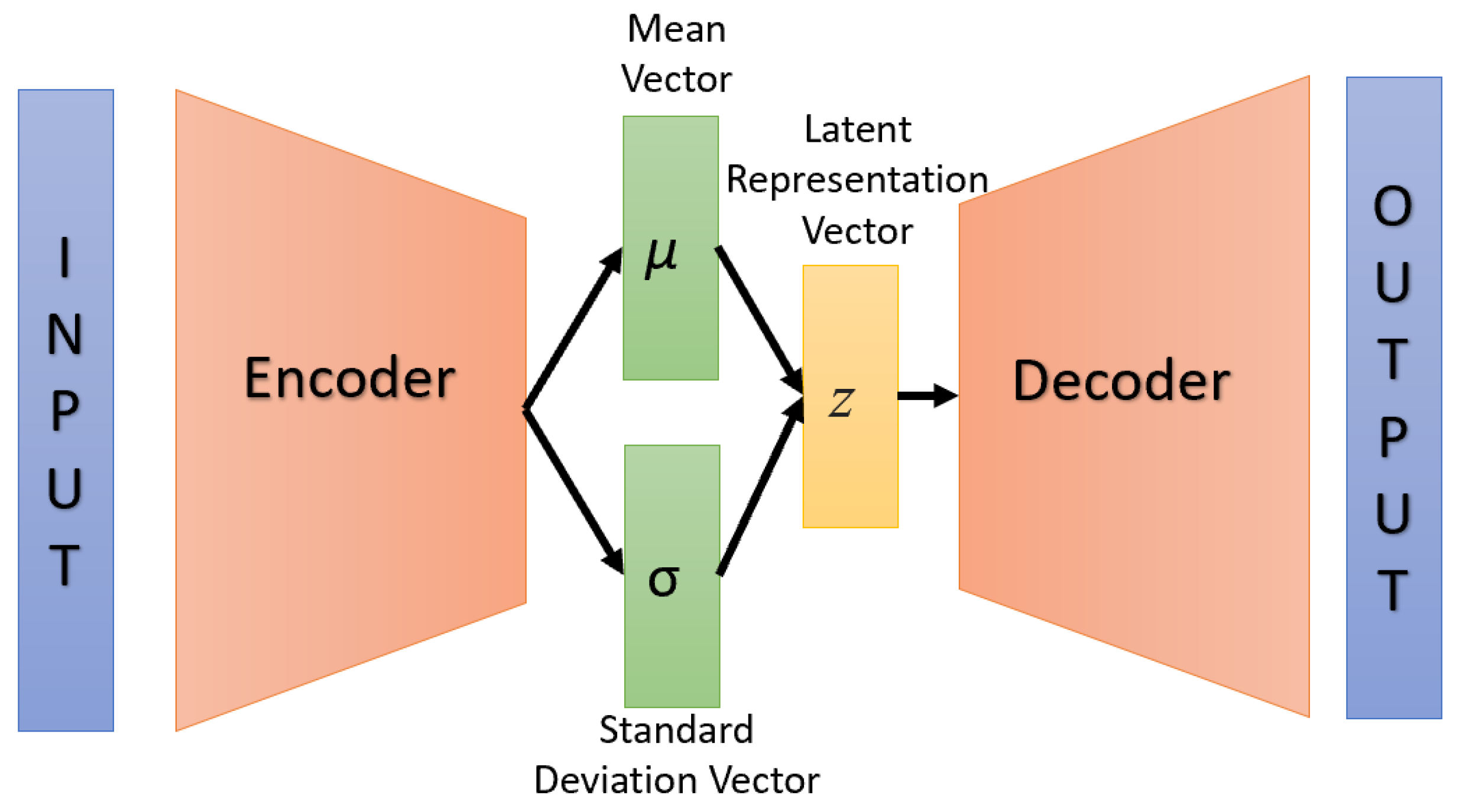
2.2. Variational Autoencoders

A variational autoencoder (VAE) is a deep learning generative model that merges the principles of autoencoders with probabilistic modeling, particularly variational inference, allowing for the generation of new data points by learning the underlying data distribution. It is commonly used for dimensionality reduction, data generation, and latent space exploration.

The main goal of a VAE is to learn a compressed representation, called the latent representation, of the input data that captures its underlying structure. The VAE achieves this by training an encoder and a decoder network sequentially.

As illustrated in Figure 1, in a VAE, the architecture and parameters for each layer are designed to achieve a balance between efficient data compression and accurate reconstruction. The VAE consists of two main components: the encoder and the decoder. The encoder reduces the input data to a low-dimensional latent representation. It begins with an input layer, with a number of neurons corresponding to the feature count. This is followed by several hidden layers that iteratively decrease the number of neurons. The latent layer, which is the final layer of the encoder, outputs latent variables z by estimating two parameters ($\mu$ mean and $\sigma$ standard deviation) of a multivariate Gaussian distribution. This allows for sampling from the latent space during training, introducing a stochastic element to the model.

Figure 1. Architecture of variational autoencoder model.

The latent variable z is computed as shown in the following Equation (1):

$$z=\mu +\sigma \odot ϵ$$

(1)

where $ϵ\sim \mathcal{N}(0,I)$ is sampled from a standard normal distribution, where 0 represents the mean and I is the identity matrix, ensuring that z follows a multivariate Gaussian distribution with zero mean and unit variance. ⊙ denotes element-wise multiplication.

The decoder mirrors the encoder’s structure, expanding the latent space back to the original input dimensions. It starts with a latent input layer that takes the latent variables as input. The decoder includes hidden layers that progressively increase the number of neurons, reflecting the encoder’s structure in reverse. Finally, the output layer reconstructs the original input dimensions to closely approximate the input data based on the compressed latent representation. Each layer is fully connected to the previous adjacent layer and employs chosen neuron counts and activation functions to ensure generalizability and mitigate the risk of overfitting.

During training, the VAE aims to optimize two objectives simultaneously: the reconstruction loss and the KL divergence loss.

The reconstruction loss measures how well the decoded output matches the original input by calculating the difference between the original input and its reconstruction, encouraging the decoder to generate accurate outputs. It is computed using the binary cross-entropy BCE or MSE between the original input x and its reconstruction $\widehat{x}$, as given in the following Equation (2):

$$\mathrm{Reconstruction}\mathrm{Loss}= \parallel x-\widehat{x}{\parallel }^2$$

(2)

The KL divergence loss ensures that the learned latent space distribution aligns with a prior distribution, usually a standard Gaussian. This regularization term encourages the latent space to be smooth and encourages the model to learn a useful and well-structured representation. This regularizes the learned latent space distribution by reducing the Kullback–Leibler (KL) distance between the approximate posterior distribution $q\left(z\right|x)$ (parametrized by $\mu$ and $\sigma$) and the prior distribution $p\left(z\right)$, which is usually a standard normal distribution $\mathcal{N}(0,I)$. It is computed as presented in the following Equation (3):

$$\mathrm{KL}\mathrm{Divergence}\mathrm{Loss}=-{\displaystyle \frac{1}{2}}\sum _{i=1}^d\left(1+log\left({\sigma }_i^2\right)-{\mu }_i^2-{\sigma }_i^2\right)$$

(3)

Thus, as displayed in the following Equation (4), the total VAE loss is the sum of the reconstruction loss and the KL divergence loss:

$$\mathrm{VAE}\mathrm{Loss}=\mathrm{Reconstruction}\mathrm{Loss}+\mathrm{KL}\mathrm{Divergence}\mathrm{Loss}$$

(4)

By training a VAE, new data records are generated by sampling the learned latent space distribution. This makes VAEs useful for tasks such as recommender systems, where they can generate prediction ratings for all items, including those that the user has not rated yet, by sampling from the latent space.

Overall, the VAE architecture combines the benefits of autoencoders, which can learn compact representations, with probabilistic modeling techniques, enabling the model to capture uncertainty and generate new data records.

In recommender systems, the VAE can be applied to effectively manage multi-criteria data by the extraction of user preferences and interactions. The VAE model starts by encoding multi-criteria ratings, such as Acting, Direction, Story, and Visualization, into a latent space through an encoder network. This process generates parameters ($\mu$ and $\sigma$) for a latent variable distribution, which allows the model to capture representative patterns of user preferences. The decoder network reconstructs the ratings from these latent variables, ensuring that the predicted ratings align with actual user data.

The VAE model can effectively handle data sparsity in recommender systems through several mechanisms. First, VAEs map sparse user–item interaction matrices into a latent space, capturing essential features despite missing entries. By minimizing reconstruction loss, VAEs focus on existing ratings to infer missing values based on correlations identified in the latent representation. The inclusion of a KL divergence term in the loss function encourages the latent space to follow a Gaussian distribution, enabling the model to sample values for missing entries. Additionally, VAEs can impute missing ratings by sampling from the learned latent distribution, allowing for the generation of potential ratings based on similarities with other users. In multi-criteria recommendation systems, the VAE model leverages relationships across different criteria to enhance the imputation of missing data. This capability makes VAEs a robust tool in real-world applications where data sparsity is prevalent, improving the accuracy and relevance of recommendations.

2.3. Variational Autoencoder-Based Recommender Systems

Among deep learning-based models, autoencoders and VAEs are enormously popular because they serve daily purposes in multiple domains and applications of deep learning-based algorithms in various tasks of unsupervised learning [14]. VAEs, which are improved-upon versions of autoencoders, work through nonlinear techniques alongside probabilistic modeling of latent variables to build compact representations of data. These probabilistic models let VAEs infer latent user preferences and intrinsic semantics of items without the need for explicit labels. The uncertainty captured by VAEs in user–item interactions allows them to make more refined recommendations [15,16,17,18,19,20,21,22]. Consequently, several researchers have leveraged autoencoder and VAE architectures to further improve the effectiveness of their recommendation systems. However, these works reveal several gaps and opportunities for improvement in terms of architectural design, multi-criteria handling, and the integration of probabilistic modeling.

Batmaz and Kaleli in [22] proposed a multi-criteria CF algorithm (AE-MCCF) that is based on autoencoders. This algorithm is designed to improve the accuracy of the recommendations. This occurs as AE-MCCF uncovers latent, complex, and nonlinear relationships between user and item profiles. Initially, an autoencoder is developed for the user–item data associated with specific criteria. Then, a feedforward neural network is utilized to model the nonlinear relationships between the criteria and the overall user evaluations. Finally, an aggregation function is employed to aggregate criterion-based predictions to generate the overall predictions. Empirical results showed that AE-MCCF improved the accuracy of the predictions generated in comparison with the baseline recommendation methods. Shambour [21] proposed a multi-criteria recommendation algorithm based on deep autoencoders (AEMC) to capture the intricate, non-linear, and latent relations among users with respect to multiple criteria preferences to produce more relevant recommendations. The AEMC model supports the encoding of complex abstractions as data representations in the encoder layers while integrating users’ multi-criteria preferences. This model will therefore be able to understand and extract fine-grained interactions between users and items. This is validated by experimental results on multi-criteria datasets, TripAdvisor and Yahoo! Movies, which demonstrated better performance of the AEMC model in comparison with various benchmark recommendation models. Although AE-MCCF and AEMC demonstrated enhanced performance compared with baseline methods, their reliance on conventional autoencoders prevented them from exploiting the uncertainty modeling capabilities inherent in VAEs.

Shenbin et al. [19] presented a variational autoencoder-based recommender system, referred to as RecVAE. It includes multiple improvements for the foundational Multi-VAE model [23], such as an updated encoder architecture, a novel composite prior distribution for the latent codes, a novel method to set the hyperparameter $\beta$, and an innovative method for RecVAE training through interchanging updates of the encoder and decoder. Experimental results on the Netflix Prize, MovieLens-20M, and Million Songs datasets showed that RecVAE significantly outperforms other autoencoder-based recommendation models. While RecVAE demonstrated significant performance improvements on the Netflix Prize, MovieLens-20M, and Million Songs datasets, it was limited to single-criterion recommendations.

Askari et al. [15] introduced the Joint Variational Autoencoder (JoVA) model, an ensemble of two VAEs, for Top-K recommendations with implicit feedback. JoVA predicts user preferences by extracting both user and item representations. This architecture enables JoVA to gather correlations between users and items. The authors also introduced JoVA-Hinge, an enhanced version of JoVA aimed to improve the use of implicit feedback in recommendations. Experiments conducted on four datasets show the effectiveness of JoVA-Hinge in outperforming a set of related recommendation approaches. While JoVA demonstrated strong performance across multiple datasets, it was primarily designed for single-criterion implicit feedback scenarios.

Spoorthy and Sanjeevi [20] proposed an integrated MC model that features autoencoder and deep neural networks, wherein the initial weights of the model were optimized using the Firefly algorithm, labeled MCAE-FADNN. The model is broken down into three phases. The first phase aims to use the autoencoder to fill in the gaps by predicting the missing ratings of the criteria. The second phase entails making up the gaps concerning the overall ratings of criteria that are missing in the current training data. Finally, the third phase involves generating recommendations and measuring the effectiveness of the model. The model helps address the challenges of data sparsity while providing accurate recommendations. Experiments conducted using two datasets, as well as evaluation metrics of MAE, RMSE, Precision, Recall, F2, and MAP, showed that the proposed MCAE-FADNN model performed better than relevant baseline models. Rajput et al. [18] introduced a multi-criteria recommendation approach that utilizes deep learning and matrix factorization to alleviate the sparsity problem. To perform nonlinear and hidden connections among users’ multi-criteria data, deep AEs are used together with single-value decomposition, which improves the overall accuracy of recommendations. Using the latent vector obtained from the autoencoder and the dimensionality reduction performed by singular-value decomposition, the proposed method can accordingly render accurate predictions of the missing ratings for the users. The experimental results on the Yahoo! Movies multi-criteria dataset indicate that the proposed approach surpasses existing recommendation methods by addressing data sparsity and resulting in more accuracy in recommendations as described by RMSE and MAE values. While these works showed promising results in addressing data sparsity and improving recommendation accuracy, they did not fully exploit VAE’s capability to model uncertainty in user preferences.

Liu et al. made notable contributions in addressing the limitations of VAE-based models, particularly in the context of implicit feedback and Top-N recommendations. In their first work [16], they introduced a self-adapting credibility weight technique that re-evaluates the positive samples and utilizes higher-order relationships to identify key negative samples within the item–item matrix. In addition, the authors simplify the complex nonlinear structure and instead create a straightforward, efficient VAE framework with a linear structure. Integrating reconstruction loss functions for positive samples and key negative samples, VAE++ outperformed the VAE-based models by a great margin, as is shown by extensive experiments conducted on four publicly available real-world datasets. Building on this, Liu et al. [17] addressed a central issue with collaborative filtering recommender systems that rely on implicit feedback, especially in the context of Top-N recommendation. They challenge the common practice of treating all interacted items as equal positives and all non-interacted items as negatives, stating that this underscores the complexity of user preferences. To address this issue, they designed a simple effective linear VAE framework, named VAE*, that essentially adapts the credibility weight mechanism for positive samples and higher-order interactions for identifying relevant negative samples. They also streamlined the VAE framework into a linear specification by removing the non-linear components. Their theoretical justification and extensive empirical tests on six datasets show that their method considerably outperforms existing VAE-based models. The authors conclude that careful handling of implicit feedback can dramatically enhance system performance rather than constructing complicated model architectures. However, the linear nature of these VAE frameworks proposed by Liu et al. may limit their ability to capture the complex non-linear relationships in multi-criteria recommendation contexts.

In summary, recent studies have demonstrated the potential of VAEs in tackling the inherent accuracy and other challenges involved in traditional recommender systems. By leveraging non-linear probabilistic latent-variable approaches, VAE-based models can identify users’ involved preferences across various criteria, leading to more accurate recommendations. However, major gaps still exist in the research landscape. First, the research focus has largely been limited to single-criterion recommendation scenarios, leaving the potential of VAEs in multi-criteria settings mostly unexplored. This oversight is significant, as VAEs’ probabilistic approach makes them uniquely qualified to capture and model the interdependencies between different criteria in user preference patterns. Second, most of the proposed VAE-based architectures have concentrated mostly on model complexity, aiming to capture increasingly complex relationships. Nevertheless, model complexity does not always accompany an increase in performance. Instead, there is a need for simpler, more efficient VAE frameworks that can deliver accurate recommendations. In view of these research gaps, the current study aims to investigate the capability of the proposed VAE-MCRS model to enhance prediction accuracy within multi-criteria recommendation frameworks. By combining the advantages of probabilistic VAEs with explicit handling of multiple criteria, this work seeks to improve the understanding and application of VAEs to more performant modern recommender systems.

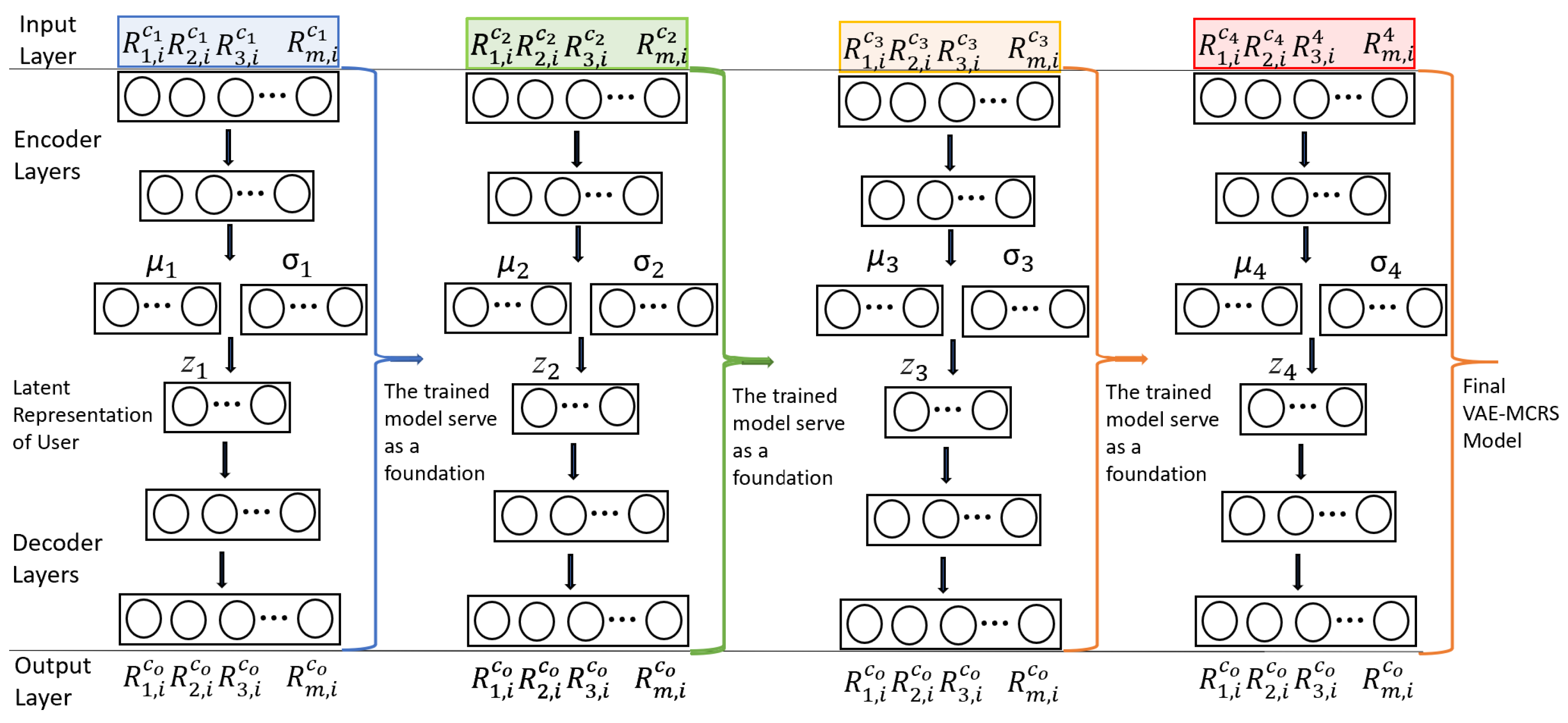
3. Proposed Variational Autoencoder Model

As presented in Figure 2, the proposed VAE-MCRS model is built on two core concepts: first, the sequential training of the VAE model on different datasets, and second, utilizing the VAE model for prediction.

Figure 2. The proposed VAE-MCRS model architecture. R: Rating, C: Criterion, m: Movie, i: User.

As shown in Figure 2, the VAE architecture comprises three main components: encoder, latent, and decoder layers. The encoder begins with an input layer containing m neurons, representing the number of movies. It includes a hidden layer with a reduced number of neurons, with several configurations tested in the experiment section to determine the optimal structure for the model. The latent layers contain parameters for the mean ($\mu$), standard deviation ($\sigma$), and latent variable (z).

The decoder mirrors the encoder structure in reverse. It starts with z as the input layer, followed by a hidden layer, and concludes with an output layer that has the same number of neurons as the encoder’s input layer.

The proposed VAE-based model VAE-MCRS is trained sequentially on multiple criteria datasets to enhance the model’s ability to understand complex user preferences in a collaborative filtering recommendation system. The use of multiple criteria ratings like Acting, Story, Direction, and Visuals helps the model to capture the dependencies and correlations between these criteria, which leads to more personalized and accurate recommendations.

The interaction between criteria is modeled by leveraging the latent feature space in the VAE. Specifically, after training on a criterion, the learned representations capture the unique patterns of that criteria. When the model moves to the next criterion, the previously learned latent features provide a foundation that enhances the model’s ability to capture correlations between criteria, as these are inherently influenced by the patterns established in the earlier training stages. During training, each criterion-specific dataset is passed through the VAE, which consists of an encoder and a decoder. The encoder compresses the user–item interactions into a latent representation, while the decoder reconstructs these interactions, refining the latent features as it iterates through each criterion. This sequential training across multiple criteria progressively enhances the model’s capability to learn complex interactions that might exist across different aspects of user preferences.

As shown in Figure 2, the VAE-MCRS learning process begins with training the VAE model on the dataset for the first criterion. During this phase, the model parameters are optimized to identify the patterns between the first criterion ratings and the overall ratings, which serve as the output to be predicted by the model. Once the training with the first criterion dataset is complete, the model is then trained on the dataset for the next criterion. This process continues in sequence for each criterion dataset.

The sequential aspect of the proposed approach enables the VAE-MCRS model to identify patterns where a user preference for one criterion might influence or correlate with another. For example, a user who prefers to always rate movies highly based on the visuals criteria might also prefer movies with strong direction criteria. By training the model with all criteria sequentially, it learns these multi-dimensional patterns, improving its ability to predict overall user preferences more effectively. In addition, training the same model sequentially on all criteria leads to more robust recommendations instead of training a distinct model for each criterion task. The model can predict a user overall movie rating by combining the criteria. This helps the model to generalize better across various types of movie ratings and provide recommendations that reflect user preferences.

This approach can also better handle situations where users may not have provided ratings for all criteria. By learning relationships between the different criteria, the model can deduce a user preference for certain criteria even when explicit ratings are missing, leading to more accurate predictions.

Algorithm 1 represents the general pseudocode for the VAE-MCRS model. As indicated after step 9, the model is trained, enabling the VAE-MCRS model to generate recommendations by sampling from the latent space and employing the decoder to predict ratings for unrated user–movie pairs. These predictions are derived from the learned relationships among various criteria and user preferences. The VAE-MCRS model is subsequently evaluated using the testing dataset.

Algorithm 1 Multi-criteria variational autoencoder for collaborative filtering-based recommender systems VAE-MCRS.

Input: Multi-criteria dataset.      Output: Recommendation prediction. First stage: Dataset and VAE-MCRS model preparation      Step 1: Clean missing values, duplication, standardization (rating range [1–5]) ▹ Data preprocessing      Step 2: For each criterion, construct a matrix where N rows represent N users and M columns represent M movies.                     ▹ Construct User–Movie Matrix      Step 3: Split dataset on 80% for training and 20% for testing.      Step 4: Initialize the hyper-parameters of the VAE-MCRS encoder and decoder networks.                     ▹ Initialization phase. Second stage: Train VAE-MCRS model Step 5: Maps the user’s ratings to two vectors: mean and standard deviation of the latent space (representing latent features).                     ▹ Encoding phase.      Step 6 The encoder produces two vectors: $\mu$ (mean): The center of the distribution in latent space. $\sigma$ (variance): The spread or uncertainty in the latent space.                             ▹ Latent representation phase.      Step 7: Construct the latent representation vector z using the mean and the standard deviation vectors.                   ▹ Reparameterization phase.      Step 8: Decodes the latent vector z back into predicted ratings for all movies, including those that the user has not rated.                   ▹ Decoding phase.      Step 9: For each new criterion, go back to Step 5 to train the trained VAE-MCRS model with the rating matrix of the new criteria.      Step 10: Feed VAE-MCRS with testing data for prediction.

The second key motivation for using a variational autoencoder in the development of the proposed VAE-MCRS model is its ability to significantly improve the performance of collaborative filtering approaches in several critical aspects:

• When trained sequentially on a multiple criteria ratings dataset (for example, Acting, Story, Direction, and Visuals), the VAE can learn a shared latent space that effectively captures users’ preferences across all the criteria. This process results in a compact latent representation of a user’s overall preferences, considering how preferences for one criterion (e.g., Acting) may relate to others (e.g., Direction). For example, the VAE might learn that users who rate Acting highly also tend to rate Direction highly, or that users with strong Visuals preferences might not care as much about the Story. This shared latent space enables the model to gain a deeper understanding of user behavior across all criteria, ultimately improving its predictive accuracy and recommendation effectiveness.
• In a multi-criteria recommendation system, user preferences are not always independent. There may be complex, nonlinear interactions between different criteria. For example, a user might only value strong Direction if the Story is equally compelling. Traditional linear models may struggle to capture these relationships. However, the VAE is designed to handle such nonlinear interactions through the learning of the compressed latent vector. The VAE can learn how different criteria influence each other and combine them into one preference profile that reflects the complex dynamics of user preferences.
• In a real case, users do not provide ratings for all criteria (for example, a user may rate Acting and Visuals, but omit Story and Direction). The VAE model, well regarded for handling missing data, addresses this challenge by inferring missing ratings based on the ratings provided. By learning the distribution of preferences across all users and criteria, the VAE can estimate likely values for unrated criteria. For instance, if a user rates highly on Acting and Direction but leaves Visuals unrated, the VAE can predict the likely Visuals rating based on patterns learned from similar users. This ability is crucial when training the model on multiple criteria datasets sequentially, as it ensures robust performance even when full information is not available for every user or criterion.
• The VAE applies Gaussian distribution to the latent space for regularization. This regularization helps prevent overfitting to specific criteria and encourages the model to generalize across the dataset. As a result, the VAE balances the influence of each criterion and achieves a balanced representation of user preferences across all criteria (i.e., no single criterion dominates).
• By training on all criteria datasets sequentially, the VAE can generate personalized recommendations that reflect users’ true preferences across different aspects. Rather than optimizing the model for each criterion independently (which may lead to partial or less coherent recommendations), the VAE enables the model to understand how user ratings for criteria such as Acting, Story, Direction, and Visuals are correlated. For example, if a user rates Visuals ‘very good’ but has moderate preferences for Acting, the VAE will use the learned latent representation to recommend movies that balance these preferences, like movies with strong visuals but average acting. It also enables the model to make a list of recommendations by understanding user preferences across different combinations of criteria.
• When VAE is trained on a multi-criteria dataset, it can suggest items based on different aspects. For example, if a user favors Story and Visuals, the VAE might recommend a movie that excels in these aspects or suggest a movie with strong Direction and Acting, providing diverse relevant options.

The proposed VAE-MCRS model is well suited for deployment across various real-world recommendation systems, making it practically relevant in industries such as e-commerce, streaming platforms, and tourism. Its flexible architecture allows for simple adaptation to specific domains by adjusting criteria to reflect domain-specific aspects. For example, in e-commerce, criteria could include product quality, price, brand, and customer reviews, enabling the model to deliver recommendations that more accurately match user preferences. The model can be integrated as a backend recommendation engine, processing user interactions and historical data to generate recommendations in real time. This adaptability and ease of integration demonstrate the model’s utility for businesses looking to offer tailored, data-driven recommendations to their users.

4. Experimental Results and Discussion

To assess the performance of the proposed VAE-MCRS model, different experiments were conducted. The results were benchmarked against various multi-criteria and single-criterion recommender systems: MCEDSL [24], MMEDSL [24], AEMC [21], MovieANN [25], MC-UCF [6], and SC-UCF [26].

MCEDSL and MMEDSL refer to Multi-Criteria and Multi-Modal Deep Encoder–Decoder-based Shared Learning systems. AEMC is based on deep autoencoder architectures tailored for multi-criteria recommendations. MovieANN utilizes a multi-layer feedforward artificial neural network to leverage multi-criteria ratings for overall rating predictions. MC-UCF serves as a multi-criteria user-based collaborative filtering recommender system, whereas SC-UCF is a single-criterion user-based collaborative filtering model.

4.1. Evaluation Metrics

The proposed models’ and other algorithms’ performances are measured by evaluating their prediction accuracies through statistical metrics, specifically MAE (Equation (5)) and RMSE (Equation (6)).

$$MAE={\displaystyle \frac{1}{N}}\sum _{u,i}^N|P_{u,i}-r_{u,i}|$$

(5)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{u,i}^N{(P_{u,i}-r_{u,i})}^2}$$

(6)

Here, N is the total number of ratings, $P_{u,i}$ is the predicted rating provided by user u for item i, and $r_{u,i}$ is the actual rating given by user u for the same item i.

4.2. Dataset

The experimental dataset used is the Yahoo! Movies multi-criteria dataset [27]. This dataset includes 34,800 ratings from 1716 users across 965 movies. Each user rates a movie based on four specific criteria: acting, story, visuals, and direction, along with an overall rating. Figure 3 presents a sample of the Yahoo! Movies multi-criteria with four different criteria and an overall rating for each user–movie pair.

Figure 3. Yahoo dataset sample.

As detailed in Algorithm 1, each criterion dataset is used to generate a 2D $M\times N$, M is the number of items (movies), and N is the number of users. Regarding these dimensions, as shown in Figure 2, the input layer of the VAE-MCRS model consists of 965 neurons, corresponding to the number of movies. The output layer of the VAE-MCRS model is similarly structured, with 965 neurons, reflecting the number of movies based on the overall ratings dataset.

4.3. Sensitivity Analysis

Multiple assessments were performed to identify the best values for the VAE-MCRS model hyperparameters, such as the number of hidden layers, optimization algorithms, and activation functions.

Table 1 displays the hyperparameter values tested in the experiments to find the optimal settings for the proposed model. Table 2 illustrates the optimal hyperparameters of the VAE-MCRS model.

Table 1. Hyperparameters of the VAE-MCRS model.

Hyperparameters	Experiments Using
Optimizer	Adagrad, SGD, Adam, RMSprop
Activation Functions	Softmax, ELU, RELU, Sigmoid
Hidden Layers	7, 5, 3

Table 2. Tuned hyperparameters of VAE-MCRS.

Hyperparameters	VAE-MCRS
Output Layer Activation Function	Sigmoid
Hidden Layers Activation Function	ELU
Number of Hidden Layers	3
Optimizer	Adam
dropout	0.5
Learning Rate	0.01
Epochs with Early Stopping	100
Batch Size	32

Table 3 demonstrates the impact of different values of the number of hidden layers on VAE-MCRS’s effectiveness. The findings show that three hidden layers provide the most optimal performance for VAE-MCRS. Increasing the number of hidden layers leads to higher MAE and RMSE, indicating potential overfitting with deeper architectures.

Table 3. Effect of hidden layer on the model performances.

Hidden Layers	VAE-MCRS
	MAE	RMSE
3 Layers	0.6038	0.7085
5 Layers	0.6691	0.8099
7 Layers	0.7016	0.8849

Bold values highlight the best performance.

The results of the sensitivity analysis in Table 4 highlight the impact of various activation functions on the VAE-MCRS model effectiveness. Combining the ELU activation function in the hidden layers and the Sigmoid function in the output layer yields the best performance, with an MAE of 0.6038 and an RMSE of 0.7085. In contrast, using ELU in both layers results in higher errors, while the ELU–Softmax combination improves performance but does not surpass the ELU–Sigmoid configuration. The results demonstrate that the Sigmoid activation function is most effective for mapping discrete ratings to the discrete range of [1, 5].

Table 4. Effect of activation functions on the model performances.

Activation Function		VAE-MCRS
Hidden Layers	Output Layer	MAE	RMSE
ELU	ELU	0.7231	1.054
ELU	Softmax	0.6709	0.7903
ELU	Sigmoid	0.6038	0.7085
RELU	Sigmoid	0.6102	0.7125

Bold values highlight the best performance.

Table 5 summarizes the results obtained by applying VAE-MCRS with four different optimizers. The analysis reveals that the VAE-MCRS model achieved its best performance using the Adam optimizer, while the RMSprop optimizer provided the optimal results for the VAE-MCRS model with the highest performance metrics.

Table 5. Effect of the optimizer on the model performances.

Optimizer	VAE-MCRS
	MAE	RMSE
Adagrad	0.9236	1.2086
Adam	0.6038	0.7085
RMSprop	0.6795	0.8604
SGD	1.3558	1.7642

Bold values highlight the best performance.

4.4. Results and Discussion

Table 6 provides a detailed evaluation of prediction accuracy using the VAE-MCRS model and other recommender systems on the Yahoo! dataset. The proposed VAE-MCRS model demonstrates the highest accuracy with an MAE of 0.6038 and an RMSE of 0.7085, showing its superiority to predict ratings accurately. The MCEDSL and MMEDSL methods show strong performance. These results indicate that both methods effectively utilize autoencoder-based frameworks for multi-criteria data, with the VAE demonstrating superiority over the traditional AE in learning from multi-criteria inputs. The ability of the VAE to capture complex latent representations and handle the variability inherent in multi-criteria ratings allows it to provide more accurate predictions. This good performance shows that the VAE can understand the relations between different criteria, which makes it helpful for collaborative filtering tasks where many factors affect what users like.

Table 6. Prediction accuracy across all methods.

Approach	RMSE	MAE
SC-UCF [26]	0.9843	0.8720
MC-UCF [6]	0.8617	0.7722
MMEDSL [24]	0.8133	0.6881
MovieANN [25]	0.7834	0.7190
AEMC [21]	0.7257	0.6435
MCEDSL [24]	0.7202	0.6077
Proposed VAE-MCRS	0.7085	0.6038

Bold values highlight the best performance.

We also compared our proposed model with SC-UCF, a single-criterion model, which performs less effectively with an MAE of 0.8720 and an RMSE of 0.9843, highlighting its limitations in capturing complex user preferences compared with multi-criteria methods. MC-UCF, which uses a multi-criteria CF approach, shows an MAE of 0.7722 and an RMSE of 0.8617, indicating better accuracy than SC-UCF but still not as satisfactory as the other advanced models. For MovieANN, which uses a multilayer feedforward neural network for multi-criteria ratings and has an MAE of 0.7190 and an RMSE of 0.7834, the performance is good but not like the precision of the VAE-MCRS model. For AEMC, utilizing a deep autoencoder-based approach achieves an MAE of 0.6435 and an RMSE of 0.7257, which is considered a very good result but does not perform as well as the VAE-MCRS model. In summary, the VAE-MCRS model excels in the integration of multi-criteria data with deep learning techniques, with the most accurate predictions compared with the other methods tested.

The VAE-MCRS model presents several advantages alongside some limitations when compared with the techniques outlined in Table 6. One of its key strengths is its ability to capture complex, nonlinear patterns in user preferences, allowing for a nuanced representation of user–item interactions across multiple criteria. This model is particularly adept at handling data sparsity, as it learns a probability distribution over the latent space, making it effective in scenarios where users have rated only a small subset of items. Furthermore, VAE-MCRS utilizes a sequential training approach, uncovering relationships where preferences in one criterion may influence another, leading to a more comprehensive understanding of user behavior. Its generative capability also allows for the prediction of ratings for unrated items, effectively addressing the “cold start” problem. Experimental results indicate that VAE-MCRS outperforms baseline models in terms of accuracy, as evidenced by MAE and RMSE. On the other hand, the main disadvantage of the VAE-MCRS model is its computational complexity, as the iterative training across multiple criteria can increase resource demands, particularly with large datasets.

5. Conclusions

This research paper introduces VAE-MCRS, a variational autoencoder-based algorithm for multi-criteria recommendation systems. The VAE-MCRS model uses a sequential learning process that adapts its internal representations. The experiment results demonstrate its effectiveness in identifying the relationships between individual criteria and the overall rating. This method improves prediction accuracy and offers a deep understanding within a multi-criteria framework. By combining collaborative filtering with this VAE-based approach, the system utilizes both latent representation vector and user–item interactions, resulting in more precise recommendations and offering users personalized and relevant suggestions.

The experimental results reveal that the proposed VAE-MCRS model improves recommendation accuracy compared with leading baseline recommendation algorithms. This enhancement stems from the model’s capacity to capture complex, nonlinear patterns in user preferences, resulting in a more effective representation of user–item interactions across multiple criteria. However, a significant drawback of the VAE-MCRS model is its computational complexity; the iterative training process across multiple criteria can lead to increased resource requirements, especially when working with large datasets.

In future work, we plan to explore the use of temporal data to study how user preferences change over time. By investigating the change in user preferences and understanding how past behaviors influence current recommendations, we can develop more adaptive and precise recommendation systems.