New Insights into Fuzzy Genetic Algorithms for Optimization Problems
Abstract
1. Introduction
- An NNC strategy is discussed as a way to significantly speed up the fuzzy inference in two promising FGAs, from the explainability perspective, i.e., GFGA and EFGA, without any performance losses;
- Variants of the original GFGA and EFGA, in terms of fuzzy logic settings, are explored;
- A comparison against traditional and state-of-the-art techniques, which are both fuzzy and non-fuzzy, is presented over benchmark cases and a real-world application problem.
2. Fuzzy Genetic Algorithms: Dealing with Individuals and Fitness
2.1. Preliminaries
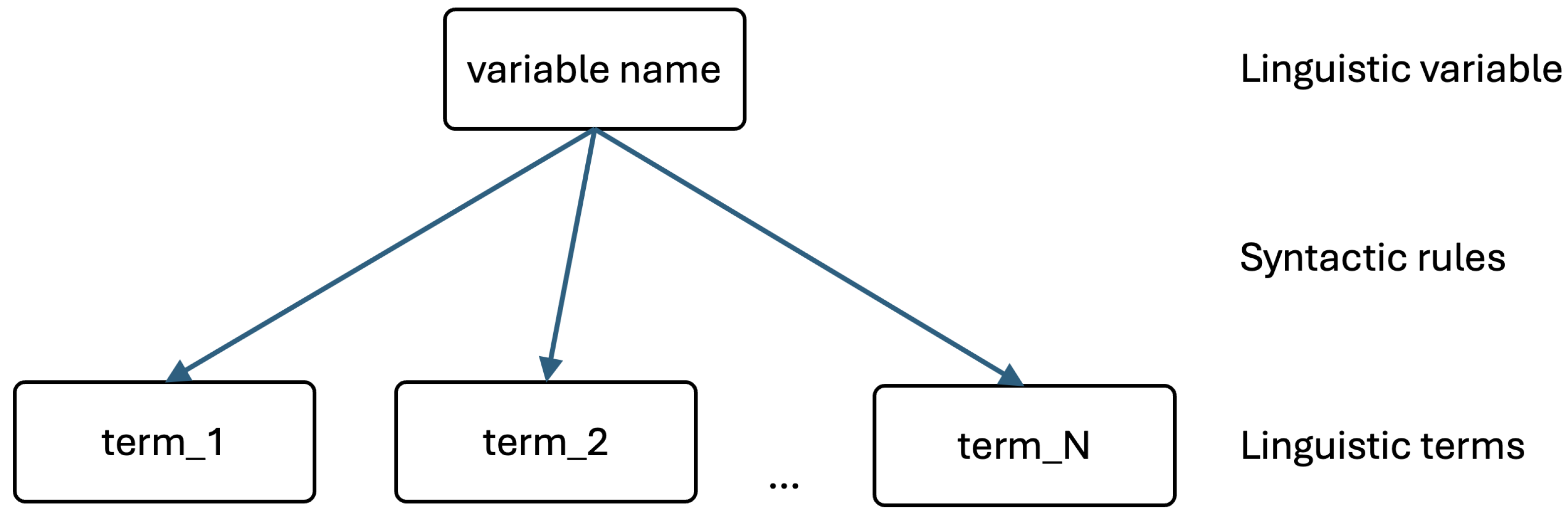
2.1.1. Fuzzy Sets
2.1.2. Genetic Algorithms
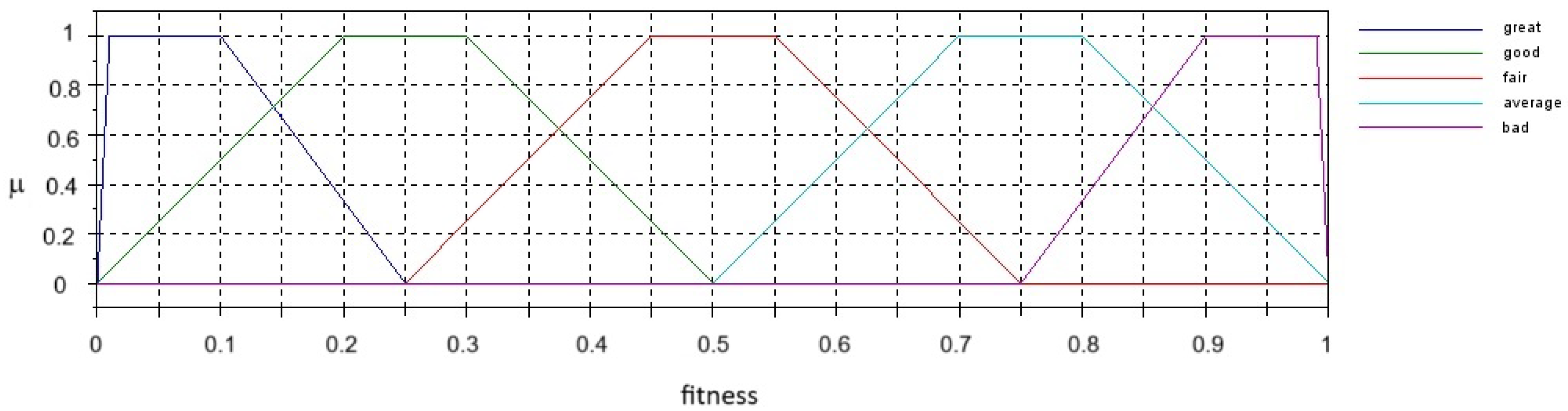
2.2. EFGA
- {Great, Good, Fair, Average, Bad} and {Very Low, Low, Moderate, Medium, High, Very High, Extremely High, Exceptionally High, Extraordinary}, i.e., ;
- {Exceptional, Great, Good, Average, Mediocre, Poor, Terrible} and {Very Low, Low, Moderately Low, Below Average, Average, Above Average, Moderate, High, Very High, Extremely High, Exceptionally High, Extraordinary, Exceptional}, i.e., ;
- where and are the fitness of the parent genomes.
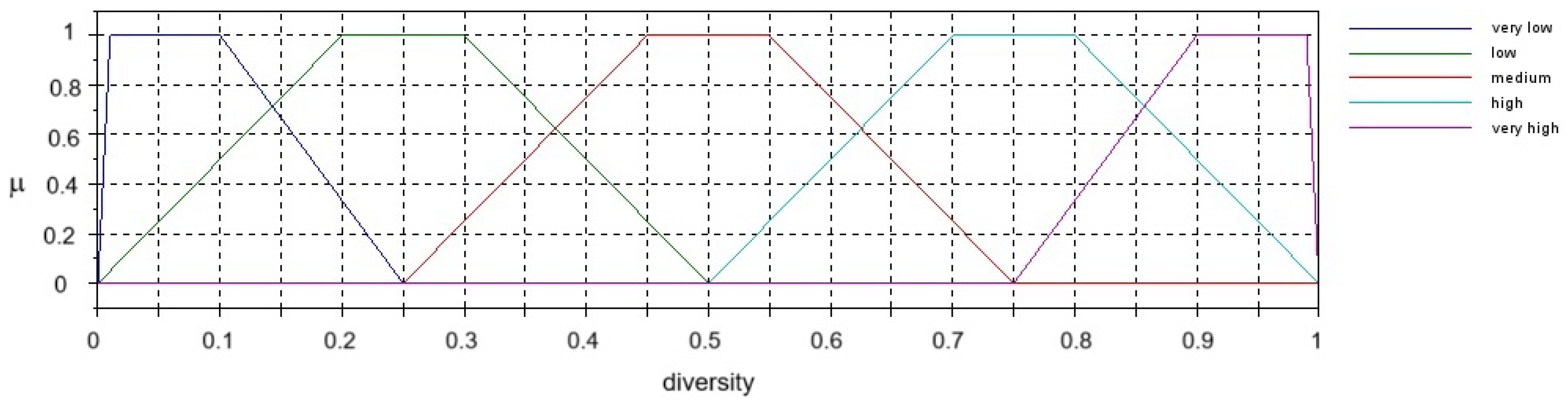
2.3. GFGA
- {Infant, Child, Teenager, Adult, Elderly};
- {Newborn, Infant, Toddler, Child, Teenager, Adult, Elderly};
- {Very Low, Low, Medium, High, Very High};
- {Extremely Low, Very Low, Low, Medium, High, Very High, Extremely High};
- except for the lowest diversity term or the highest age term and second-lowest diversity term:
- since the index of the age and diversity terms is 4, resulting in an index for the partner age, which equals 4.
- since the index of the age and diversity terms is 5, resulting in an index for the partner age, which equals 6.
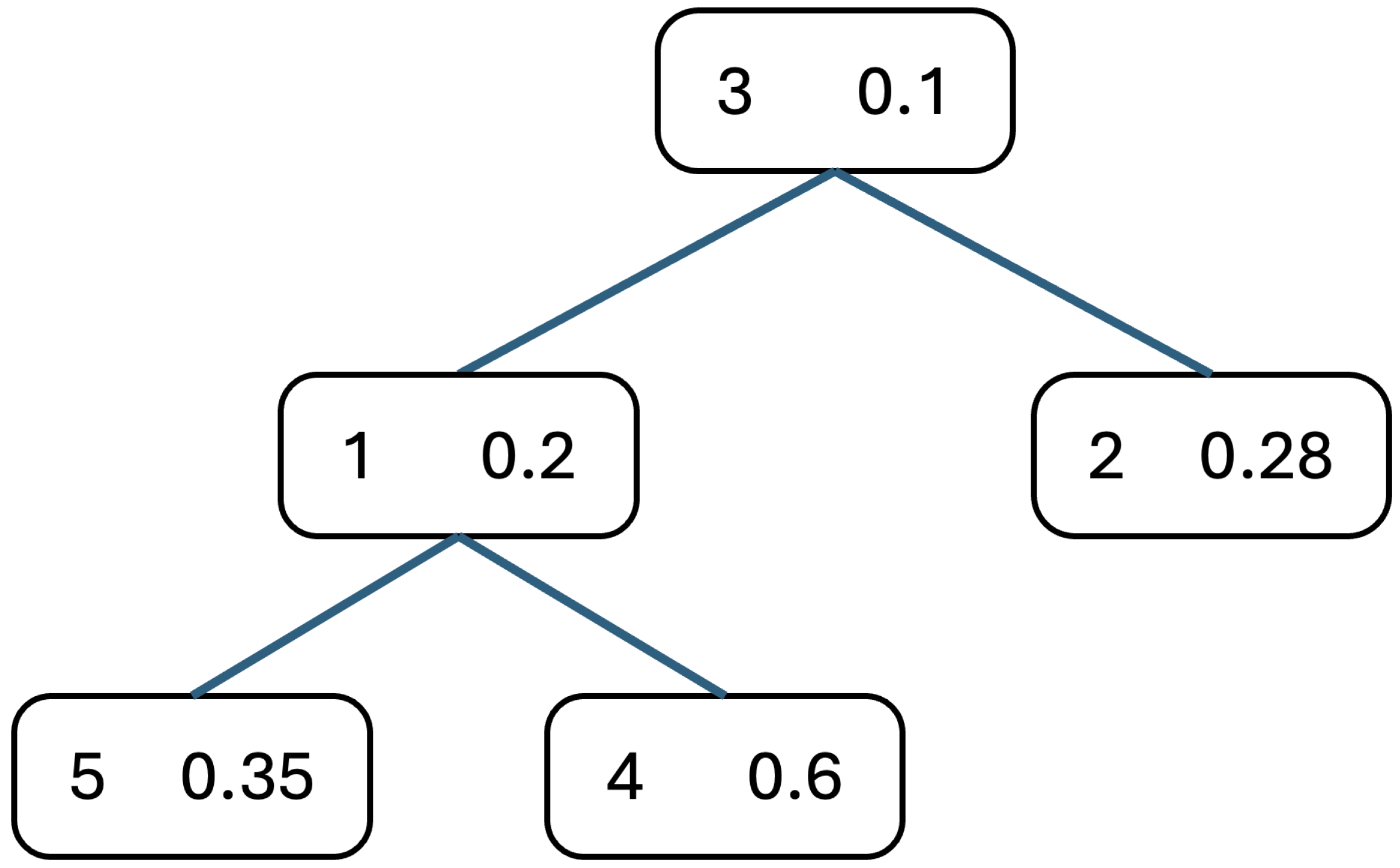
3. Nearest-Neighbor Caching
4. Experiments and Discussion
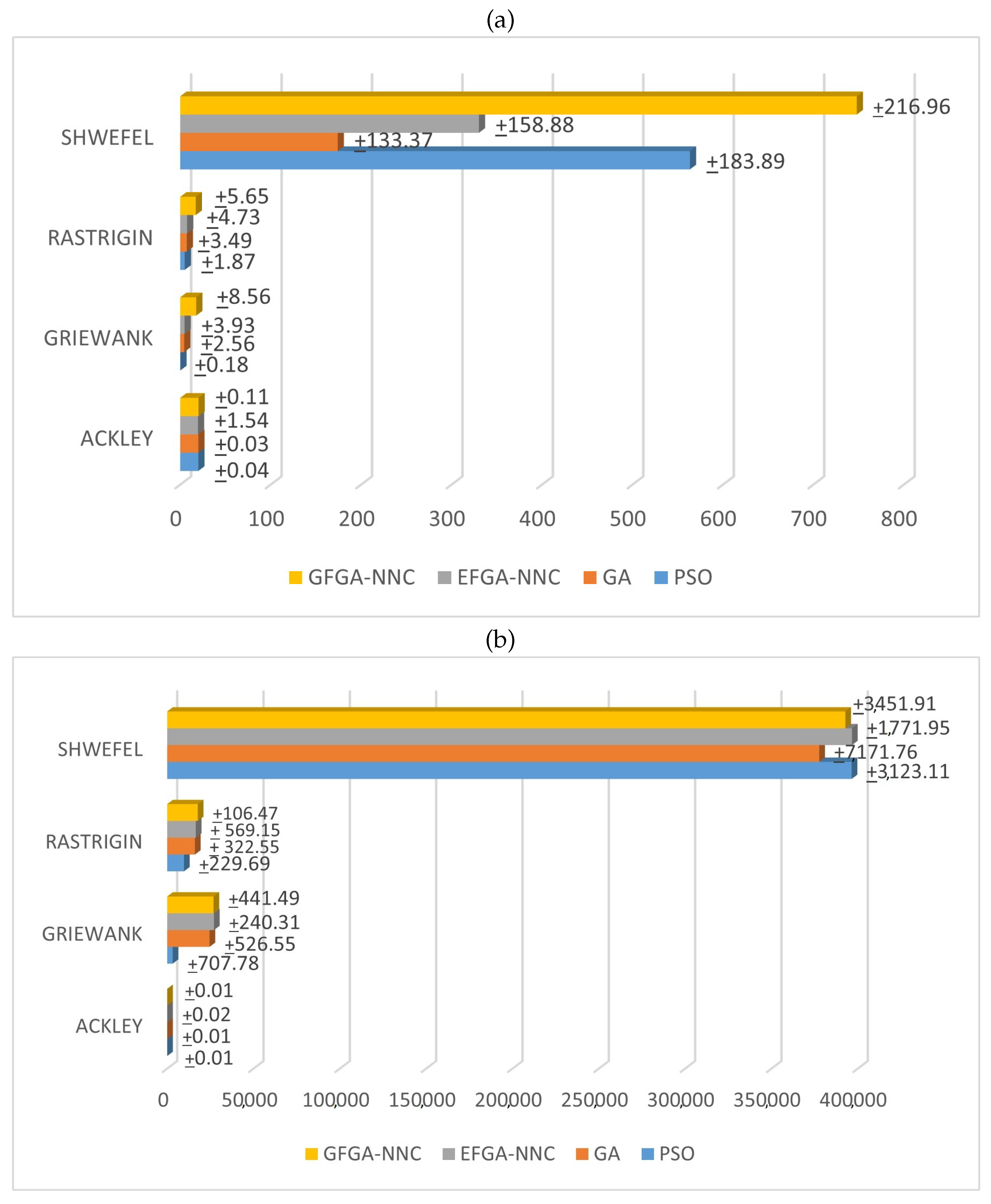
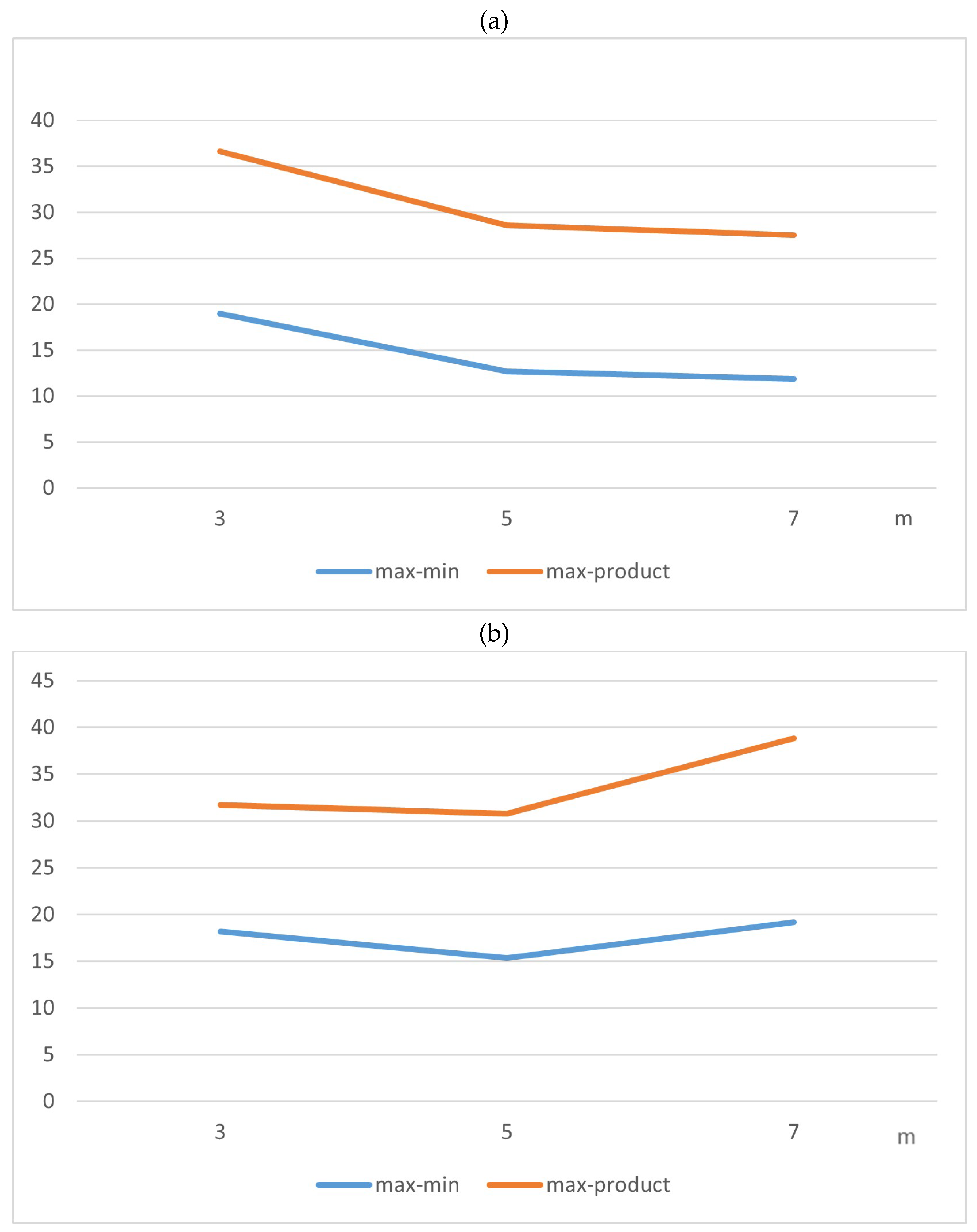
4.1. Initial Experiments on Popular Benchmarks
- The Schwefel function
- The Rastrigin function
- The Griewank function
- The Ackley function
4.2. Additional Benchmarks from the Literature
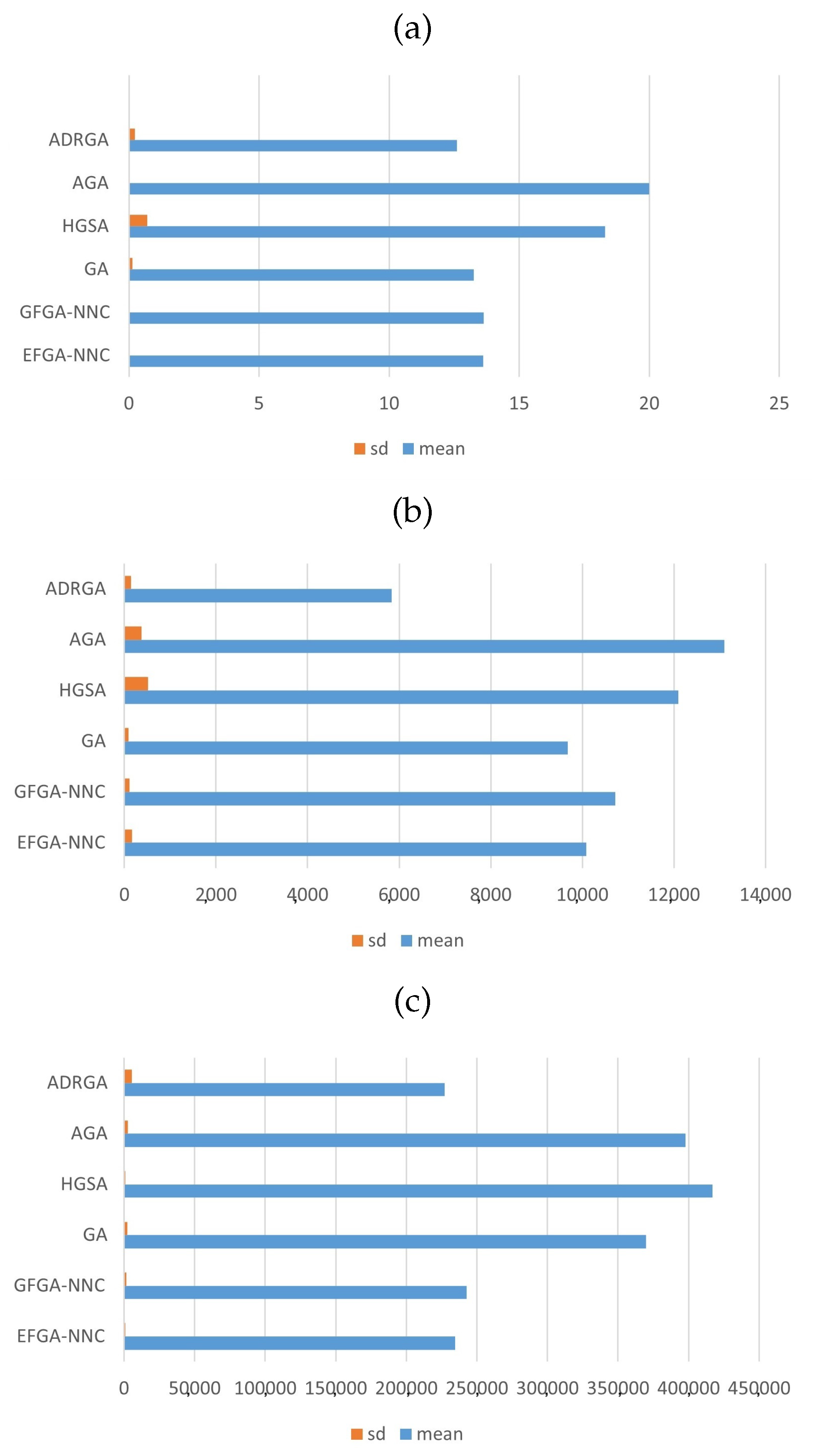
4.3. Traveling Salesman Problem
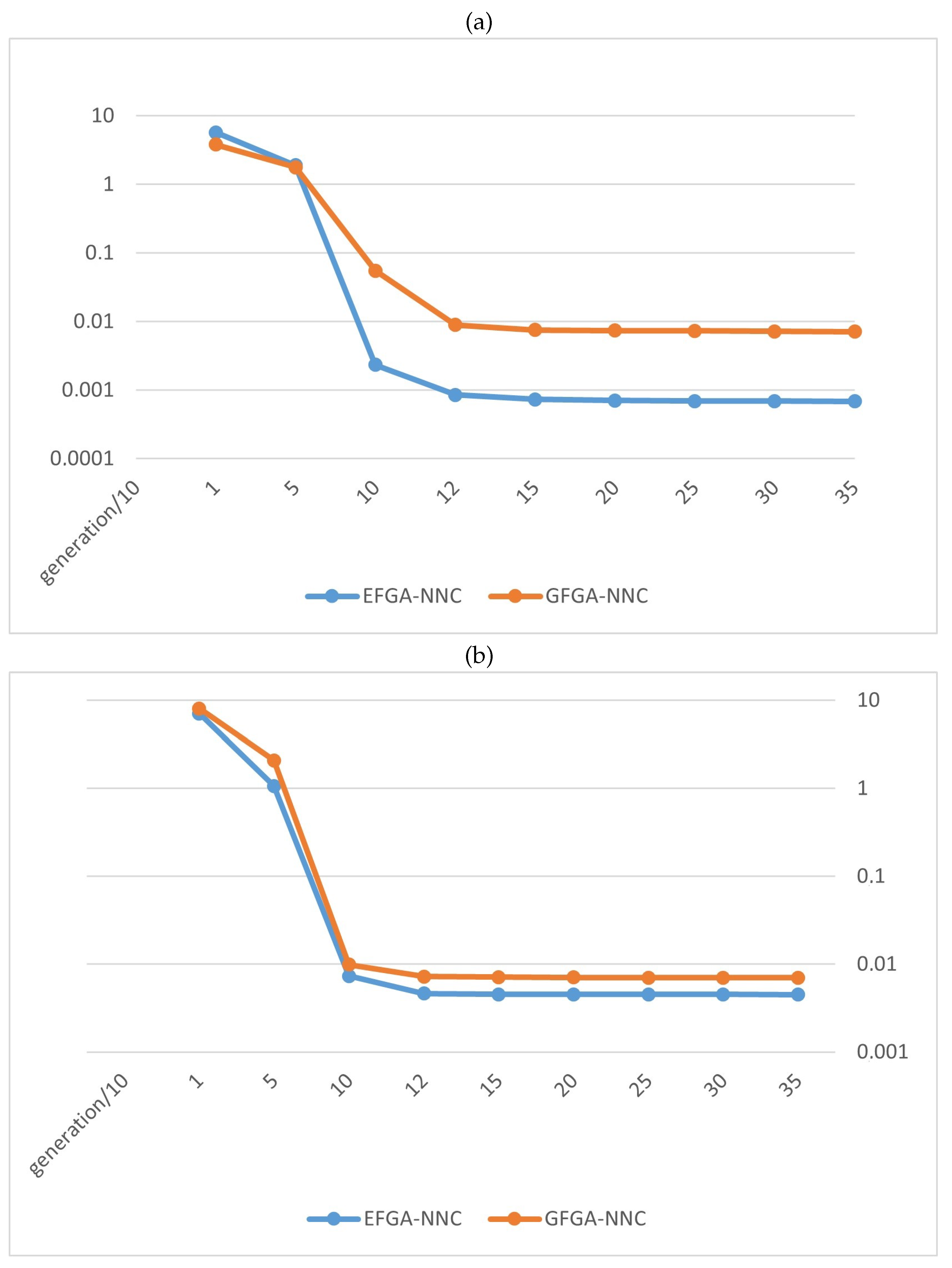
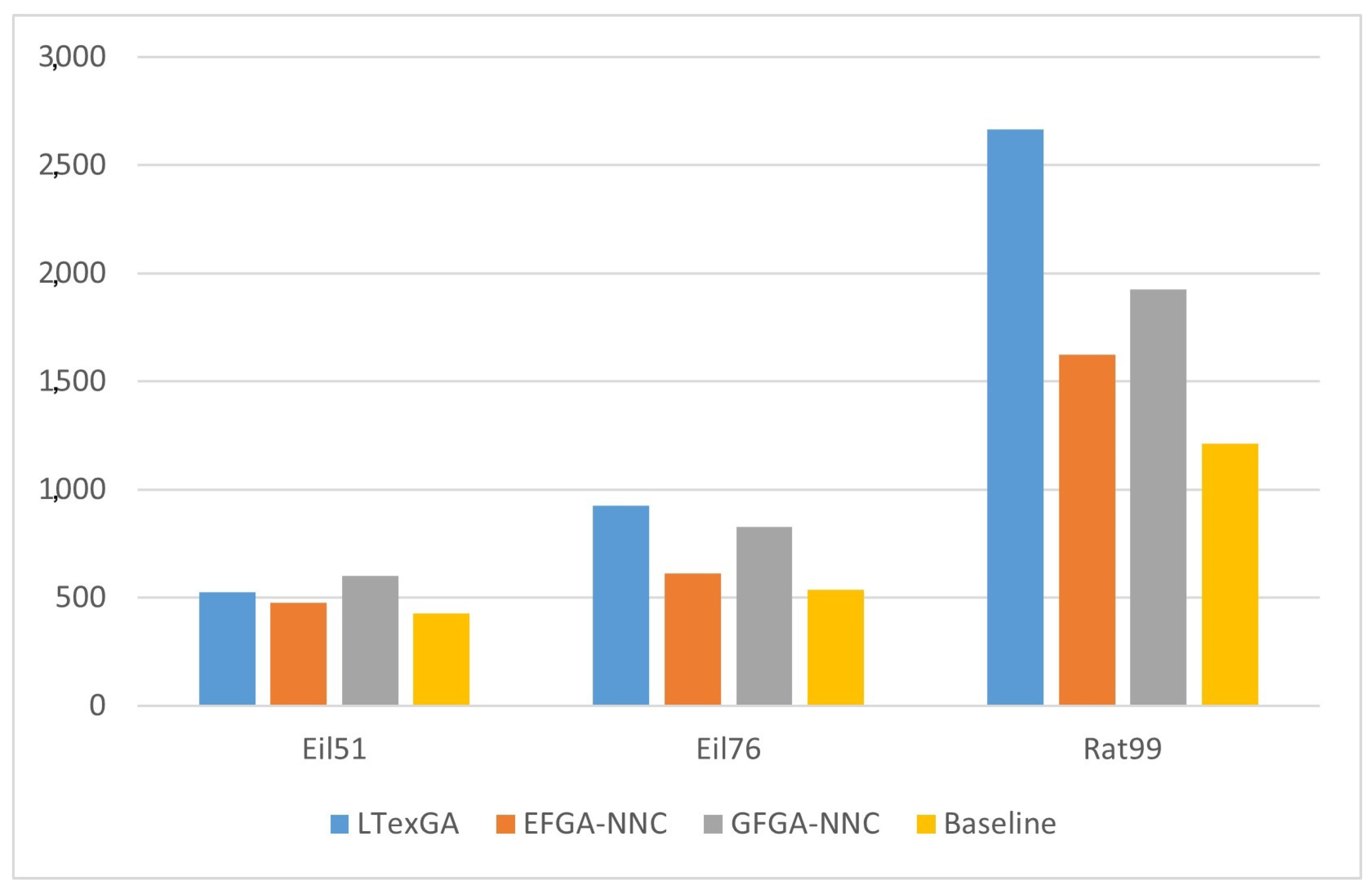
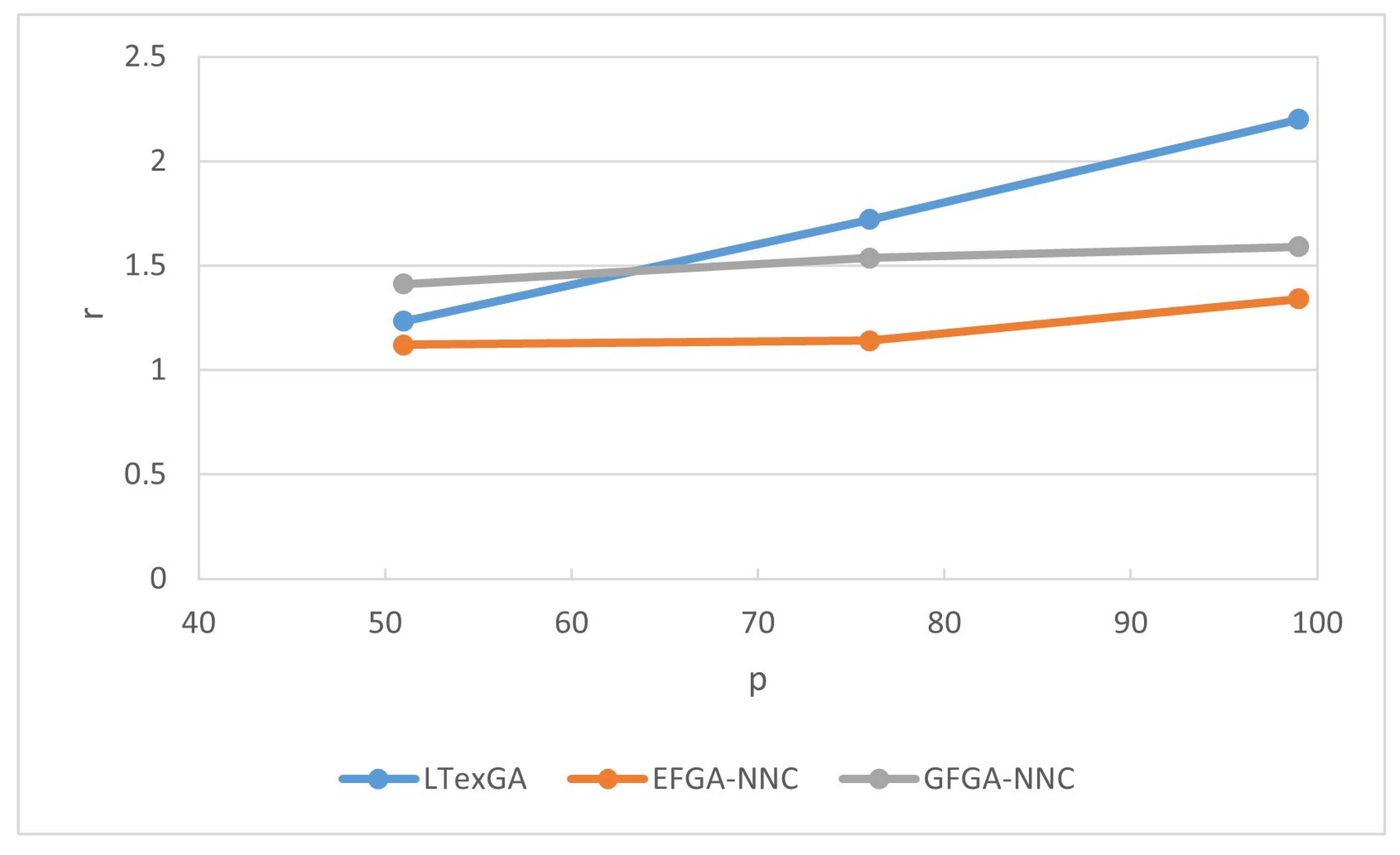
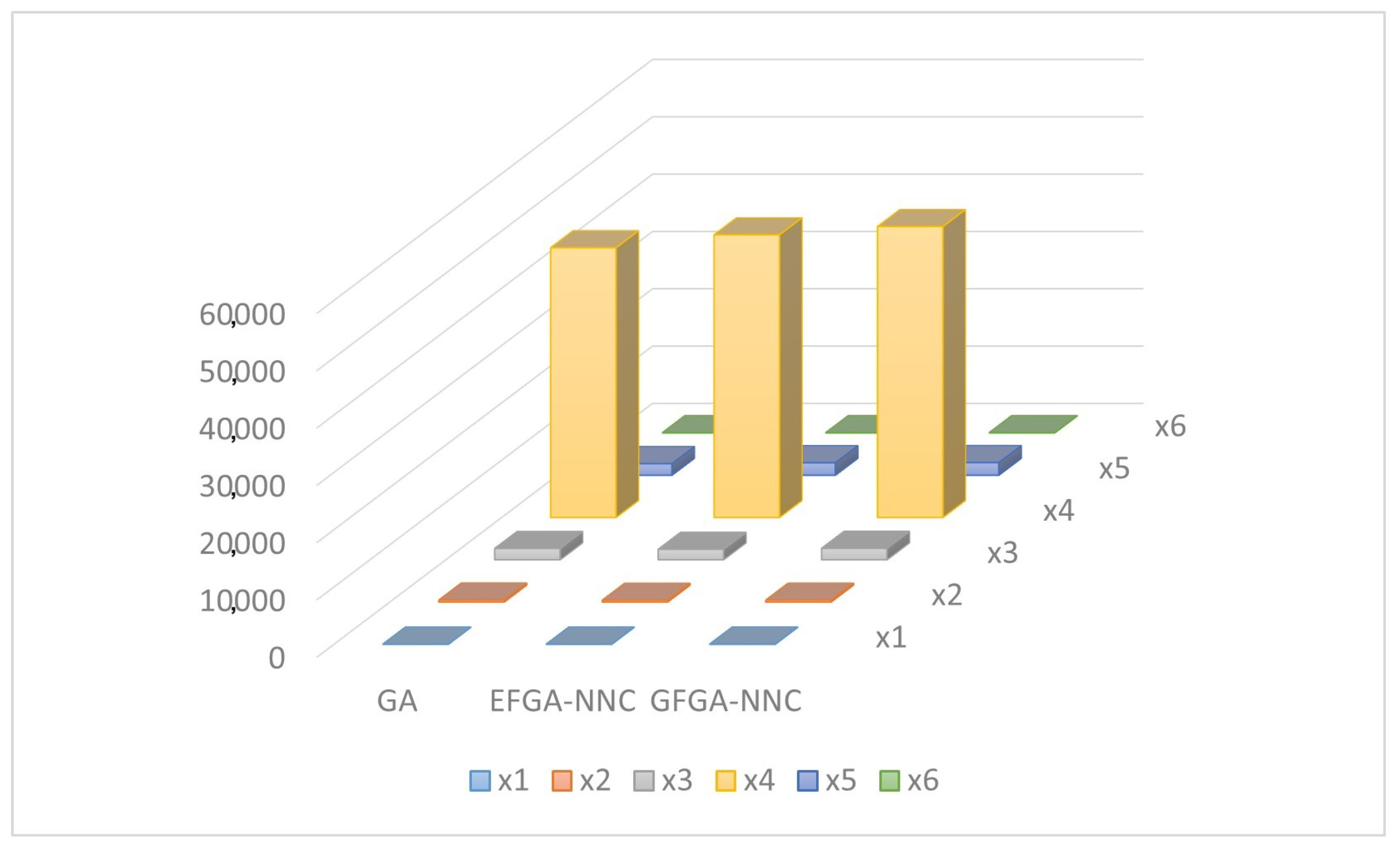
4.4. A Real-World Problem: The Case of Rice Production
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, S.; Chen, H. Security Protection Technology in Multi-Attribute Data Transmission Based on Fuzzy Genetic Algorithm. Wirel. Pers. Commun. 2022, 127, 897–917. [Google Scholar] [CrossRef]
- Rajasekar, V.; Predić, B.; Saracevic, M.; Elhoseny, M.; Karabasevic, D.; Stanujkic, D.; Jayapaul, P. Enhanced multimodal biometric recognition approach for smart cities based on an optimized fuzzy genetic algorithm. Sci. Rep. 2022, 12, 622. [Google Scholar] [CrossRef] [PubMed]
- Ashtari, P.; Karami, R.; Farahmand-Tabar, S. Optimum geometrical pattern and design of real-size diagrid structures using accelerated fuzzy-genetic algorithm with bilinear membership function. Appl. Soft Comput. 2021, 110, 107646. [Google Scholar] [CrossRef]
- Jahan, A.; Mollazadeh, M.; Akbarpour, A.; Khatibinia, M. Health monitoring of pressurized pipelines by finite element method using meta-heuristic algorithms along with error sensitivity assessment. Struct. Eng. Mech. 2023, 87, 211–219. [Google Scholar]
- Song, P.; Chen, C.; Zhang, L. Evaluation Model of Click Rate of Electronic Commerce Advertising Based on Fuzzy Genetic Algorithm. Mob. Netw. Appl. 2022, 27, 936–945. [Google Scholar] [CrossRef]
- Wang, S.; Hui, J.; Zhu, B.; Liu, Y. Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production. Sustainability 2022, 14, 5072. [Google Scholar] [CrossRef]
- Song, Y.H.; Wang, G.S.; Wang, P.Y.; Johns, A.T. Environmental/economic dispatch using fuzzy logic controlled genetic algorithms. Gener. Transm. Distrib. 1997, 144, 377. [Google Scholar] [CrossRef]
- Subbu, R.; Sanderson, A.C.; Bonissone, P.P. Fuzzy logic controlled genetic algorithms versus tuned genetic algorithms: An agile manufacturing application. In Proceedings of the 1998 IEEE International Symposium on Intelligent Control (ISIC) Held Jointly with IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA), Piscataway, NJ, USA, 17 September 1998; pp. 434–440. [Google Scholar]
- Wang, K. A new fuzzy genetic algorithm based on population diversity. In Proceedings of the 2001 IEEE International Symposium on Computational Intelligence in Robotics and Automation (Cat. No.01EX515), Banff, AB, Canada, 29 July–1 August 2001; pp. 108–112. [Google Scholar]
- Yun, Y.; Gen, M. Performance analysis of adaptive genetic algorithms with fuzzy logic and heuristics. Fuzzy Optim. Decis. Mak. 2003, 2, 161–175. [Google Scholar] [CrossRef]
- Last, M.; Eyal, S. A fuzzy-based lifetime extension of genetic algorithms. Fuzzy Sets Syst. 2005, 149, 131–147. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Z.; Abraham, A. Hybrid fuzzy-genetic algorithm approach for crew grouping. In Proceedings of the 5th International Conference on Intelligent Systems Design and Applications (ISDA05), Wroclaw, Poland, 8–10 September 2005; pp. 332–337. [Google Scholar]
- Li, Q.; Tong, X.; Xie, S.; Liu, G. An improved adaptive algorithm for controlling the probabilities of crossover and mutation based on a fuzzy control strategy. In Proceedings of the 2006 Sixth International Conference on Hybrid Intelligent Systems (HIS06), Rio de Janeiro, Brazil, 13–15 December 2006; pp. 50–56. [Google Scholar]
- Jafari, S.A.; Mashohor, S.; Varnamkhasti, M.J. Committee neural networks with fuzzy genetic algorithm. J. Pet. Sci. Eng. 2011, 76, 217–223. [Google Scholar] [CrossRef]
- Venkatanareshbabu, K.; Nisheel, S.; Sakthivel, R.; Muralitharan, K. Novel elegant fuzzy genetic algorithms in classification problems. Soft Comput. 2018, 23, 5583–5603. [Google Scholar] [CrossRef]
- Singh, M.; Brownlee, A.E.I.; Cairns, D. Towards Explainable Metaheuristic: Mining Surrogate Fitness Models for Importance of Variables. In Proceedings of the GECCO22, Boston, MA, USA, 9–13 July 2022; pp. 1785–1793. [Google Scholar]
- Pandey, S.; Broder, A.; Chierichetti, F.; Josifovski, V.; Kumar, R.; Vassilvitskii, S. Nearest-Neighbor Caching for Content-Match Applications. In Proceedings of the International World Wide Web Conference (WWW 2009-ACM), Madrid, Spain, 20–24 April 2009; pp. 441–451. [Google Scholar]
- Niesen, U.; Shah, D.; Wornell, G.W. Caching in Wireless Networks. IEEE Trans. Inf. Theory 2012, 58, 6524–6540. [Google Scholar] [CrossRef]
- Bagheri, E.; Deldari, H. Dejong Function Optimization by means of a Parallel Approach to Fuzzified Genetic Algorithm. In Proceedings of the 11th IEEE Symposium on Computers and Communications (ISCC’06), Cagliari, Italy, 26–29 June 2006; pp. 675–680. [Google Scholar]
- Nabavi-Pelesaraei, A.; Rafiee, S.; Mohtasebi, S.S.; Hosseinzadeh-Bandbafha, H.; Chau, K.W. Assessment of optimized pattern in milling factories of rice production based on energy, environmental and economic objectives. Energy 2019, 169, e1259–e1273. [Google Scholar] [CrossRef]
- Chierichetti, F.; Kumar, R.; Vassilvitskii, S. Similarity Caching. In Proceedings of the 28th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS-09), San Diego, CA, USA, 9–12 June 2009; pp. 127–135. [Google Scholar]
- Li, Q.; Yin, Y.; Wang, Z.; Liu, G. Comparative Studies of Fuzzy Genetic Algorithms. In Proceedings of the Advances in Neural Networks—ISNN 2007: 4th International Symposium on Neural Networks, ISNN 2007, Nanjing, China, 3–7 June 2007. [Google Scholar]
- Li, Q.; Zheng, D.; Tang, Y.; Chen, Z. A New Kind of Fuzzy Genetic Algorithm. J. Univ. Sci. Technol. 2001, 1, 85–89. [Google Scholar]
- Kuang, T.; Hu, Z.; Xu, M. A Genetic Optimization Algorithm Based on Adaptive Dimensionality Reduction. Available online: https://onlinelibrary.wiley.com/doi/10.1155/2020/8598543 (accessed on 5 November 2024).
- Available online: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/ (accessed on 5 November 2024).
- Faostat-Crops and Livestock Products. Available online: www.fao.org/faostat/en/#data/QCL (accessed on 5 November 2024).
- Tomasiello, S.; Uzair, M.; Liu, Y.; Loit, E. Data-driven approaches for sustainable agri-food: Coping with sustainability and interpretability. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 16867–16878. [Google Scholar] [CrossRef]
- D’Arienzo, M.P.; Raritá, L. Management of Supply Chains for the Wine Production. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics 2019, ICNAAM 2019, Rhodes, Greece, 23–28 September 2019. [Google Scholar]
- Raritá, L. A Genetic Algorithm to Optimize Dynamics of Supply Chains; AIRO Springer Series; Springer: Berlin/Heidelberg, Germany, 2022; Volume 8, pp. 107–115. [Google Scholar]
- Naderi, R.; Nikabadi, M.S.; Tabriz, A.A.; Pishvaee, M.S. Supply chain sustainability improvement using exergy analysis. Comput. Ind. Eng. 2021, 154, 107142. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syzonov, O.; Tomasiello, S.; Capuano, N. New Insights into Fuzzy Genetic Algorithms for Optimization Problems. Algorithms 2024, 17, 549. https://doi.org/10.3390/a17120549
Syzonov O, Tomasiello S, Capuano N. New Insights into Fuzzy Genetic Algorithms for Optimization Problems. Algorithms. 2024; 17(12):549. https://doi.org/10.3390/a17120549
Chicago/Turabian StyleSyzonov, Oleksandr, Stefania Tomasiello, and Nicola Capuano. 2024. "New Insights into Fuzzy Genetic Algorithms for Optimization Problems" Algorithms 17, no. 12: 549. https://doi.org/10.3390/a17120549
APA StyleSyzonov, O., Tomasiello, S., & Capuano, N. (2024). New Insights into Fuzzy Genetic Algorithms for Optimization Problems. Algorithms, 17(12), 549. https://doi.org/10.3390/a17120549






