Realistic Simulation of Dissolution Process on Rock Surface

Abstract

Hydraulic dissolution, driven by carbon dioxide-rich precipitation and runoff, leads to the gradual breakdown and removal of soluble rock materials, creating unique surface and subsurface features. Dissolution is a complex process that is related to numerous factors, and the complete simulation of its process is a challenging problem. On the basis of deep investigation of the theories of geology and rock geomorphology, this paper puts forward a method for simulating the dissolution phenomenon on a rock surface. Around the movement of water, this method carries out dissolution calculations, including processes such as droplet dissolution, water flow, dissolution, deposition, and evaporation. It also considers the lateral dissolution effect of centrifugal force when water flows through bends, achieving a comprehensive simulation of the dissolution process. This method can realistically simulate various typical karst landforms such as karst pits, karst ditches, and stone forests, with interactive simulation efficiency.

1. Introduction

The dissolution process on a rock surface is a common and complex geological phenomenon in nature [1]. Simulation techniques can visualize the evolution of this process over long time scales and predict future geomorphologic trends. This is of great significance for geological disaster forecasting and land use planning. There is also an urgent need for the continuous development and refinement of simulation technology in fields such as engineering safety assessments, environmental protection, resource management, education, and popularization of science.

Rock surface dissolution refers to the chemical dissolution and physical erosion of soluble rocks (such as carbonate rocks) under the action of precipitation, resulting in the gradual erosion of the rock surface. Its main causes include the solubility of rock and dissolution ability of water. When falling on the rock surface, the carbon dioxide in water will react with the carbonate or other substances to dissolve the rock, resulting in a dissolution effect. This process has a greater impact on halide, sulfate, and carbonate rocks. The dissolution rate is affected by climate, rock properties, terrain, vegetation cover, and other factors. We simplify real-world dissolution phenomena by allowing users to interactively set different dissolution rates to represent different rock properties and environmental factors.

Most studies are devoted to simulating the physical movement of hydraulic erosion, such as the erosion and transport of soil substances by water bodies, and the sliding of soil substances. Only few studies involve chemical changes of substances. For rock landforms, their stability and solidity make the physical impact of water not obvious. On the contrary, the carbonate in the rock will react with the carbon dioxide in water and then dissolve in the water. This chemical action often has a significant impact on rocks, forming a special karst landform. In the field of computer graphics, there is still a lack of in-depth research on dissolution. A few researchers have simulated the rust on metal surfaces [2,3], the corrosive effect of strong acid on materials [4], and the phenomenon of karst caves inside rock bodies [5,6,7]. However, the above work does not involve the simulation of rock surface dissolution, and the relevant calculation process does not refer to the theory of geology, which lacks theoretical authenticity.

Based on the relevant theories of geology and rock geomorphology, we construct a relatively complete framework for dissolution simulation. In this framework, centering on the calculation of water’s movement trajectory, we simulated a series of key processes such as splash, dissolution, deposition, and water evaporation, and we achieved a complete simulation of the dissolution process. The calculation has a professional theoretical basis, and the simulation results are realistic. In addition, we also considered the effect of centrifugal force on dissolution, simulating the effect of centrifugal force on the side wall of the curved channel when water flow flows through it. Using the simulation framework proposed in this paper, we can simulate various geomorphic forms under dissolution, including karst pits, karst ditches, and stone forest landscapes (as shown in Figure 1). With our method, users will be able customize relevant parameters in the system, restore specific real landforms, simulate the change of a rock’s surface erosion development state in real scenarios, and observe the changes of real rock layers under hydraulic dissolution. This will provide an important reference for geomorphic prediction in geology.

2. Related Work

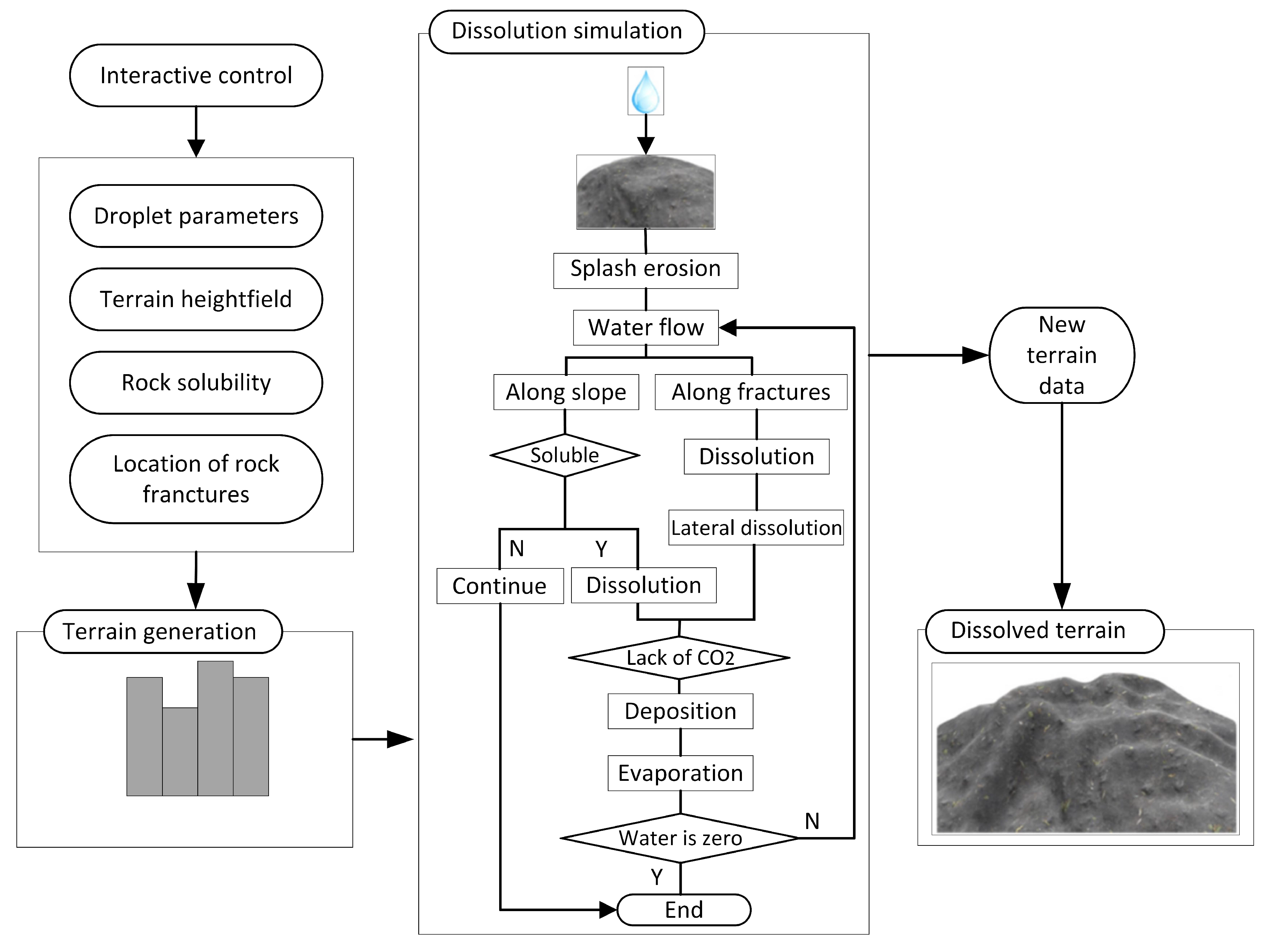
2.1. Simulation of Hydraulic Erosion and Dissolution

Hydraulic erosion is a common phenomenon on the terrain surface, which has a significant impact on the surface morphology. Many researchers have carried out research on the simulation of hydraulic erosion and are committed to simulating realistic eroded terrain. This research can be traced back to 1998. Musgrave et al. [8], striving to make the virtual terrain have a more natural and realistic appearance, first introduced thermal erosion and hydraulic erosion calculation on three-dimensional terrain. Subsequently, on this basis, Chiba et al. [9] proposed a hydraulic erosion model based on the flow velocity field in 1998. The model simulates the flow process of water to calculate the impact of hydraulic erosion on the whole terrain. In 2002, Benes et al. [10] summarized the erosion process into four independent steps: water flow, erosion, transportation, and deposition. Anh et al. [11] proposed a fast and efficient 2.5D hydraulic erosion simulation method in 2007, aiming to use the computing power of GPU to produce high-resolution erosion effects on terrain. Inspired by Wojtan et al. [4]’s simulation of fluid with Euler’s method, Kristof et al. [12] combined smooth particle hydrodynamics with Euler’s erosion model and proposed a particle-based hydraulic erosion simulation method, which achieved better performance with lower memory. In addition, to consider the impact of water on terrain, Cordonnier et al. [13] added vegetation to the erosion simulation, considering the effects between vegetation and soil. Recently, in 2022, supported by the professional theory of soil and water conservation, Yu et al. [14] added the simulation of water infiltration, channel widening, and soil fixation of plant roots to the basic framework of hydraulic erosion, and they also built a more complete simulation framework.

The above studies have achieved great hydraulic erosion simulation results; however, these studies mainly focus on the physical erosion of water on the surface. However, for rock layers, its shear resistance is extremely strong, and the physical erosion of water can only have a slight impact. On the contrary, chemical dissolution can make it produce more obvious changes.

In the simulation of chemical action, some scholars of computer graphics are committed to simulating the dissolution effect of metal surfaces. For example, Merillou [2] and Chang [3], respectively, simulated the corrosion effect of the atmosphere and seawater on metal. In addition, Wojtan et al. [4] constructed a corroded object based on the voxel model and simulated physical erosion, deposition, and chemical corrosion. However, in Wojtan’s simulation, they only discussed the action of strong acid on materials. The chemical reaction generated by this action is irreversible, and the material will not precipitate again after being dissolved by acid, so their simulation work is one-sided. In addition, a few researchers have focused on the simulation of caverns inside rock bodies. In 2019, Paris et al. [5] completed a construction of terrain using the voxel model and completed the modeling of the cave features inside a rock using the tree structure by combining various topographic primitives. Two years later, the team proposed a geology-based method for generating karst underground caves, which used the meshless anisotropic shortest path algorithm to obtain the skeleton of an underground karst network according to the entrance and exit data of underground caves and geomorphic feature parameters [6]. In the same year, Frank et al. [7] also proposed a method to generate natural karst cave landscapes, which realized the generation of a cave network and had a cave passage shape. They also simulated the cave’s inner wall details and stalactite phenomena. These simulation works of karst cave landscapes focus on the construction of cave morphology and do not carry out in-depth simulations of the dissolution process itself.

In summary, the current dissolution simulation work either focuses on the corrosion effect of acid substances on metals or focuses on the construction of cave morphologies formed by dissolution, and there is no detailed simulation work on the dissolution process of rock surfaces. In addition, the calculation processes of previous works are not fully supported by geological theories and formulas, and the simulation results lack theoretical authenticity: they are not suitable for the construction of real karst surface geomorphology.

2.2. Studies on Dissolution Process in Geology

In nature, some rock terrains are composed of soluble rocks, and the surface of such rocks will be significantly affected by hydraulic dissolution, forming a unique karst landform. The dissolution process has been deeply studied in geology, mainly including the occurrence conditions, action process, classification, and main factors affecting the dissolution process.

After a lot of experiments and research, researchers believe that the main cause of dissolution is water. Yang Mingde [15] and Zhang Huiling [16] discussed the development process of karst landforms from the perspective of hydrogeology. They found that after rainfall, the raindrops will splash and erode holes after dropping onto rock surfaces. Subsequently, the water flow will converge to these holes and continue to penetrate and dissolve downward in the process of flow, making the hole expand and deepen. For some rock strata, fractures with different shapes are distributed on them. Under gravity, runoff seeps into the fissures for dissolution, which will gradually expand the fissures and form dissolution channels. The above description roughly reduces the overall process of dissolution.

In terms of the classification of karst landforms, their morphology mainly shows the network structures of holes and cracks. Among them, the typical karst surface morphology includes karst pits, karst ditches, and stone forests [17]. In order to clarify the definition of these three landscapes, researchers have defined their forms.

Karst pits refer to depressions with butterfly or inverted cones on a rock surface. After investigation and measurement, Cai Hulin concluded that the depth and width of karst pits are about several centimeters, and some large karst pits or karst funnels can be in a steep side wall state [18].

The dissolution ditch refers to the gully on the rock surface, which is formed by the dissolution of runoff along the rock surface [19]. After investigation and measurement, Cai Hulin concluded that the length of the dissolution ditch is about several centimeters to ten centimeters, the depth and width are about several centimeters [18]. Some dissolution ditches are developed from rock fractures, so their shape is affected by the fracture trend, and most of them are parallel, dendritic and other cross shapes [20].

Stone forests refer to landscapes composed of a large number of dense columnar or conical rocks, which can also be interpreted as a concave/convex rock landscape composed of a large number of tall stone buds. The side walls of ditches are mostly steep and straight, with a height of about 10 m [18]. Under the continuous action of strong rainfall, the scouring and dissolution of water flow on the rock body will form deep-cut karst pits and ditches. After a long time of development, these karst pits and ditches will come in contact and merge with each other and then form a stone forest landscape.

In order to understand the mechanism of the dissolution process more deeply, researchers have studied the important factors that affect the dissolution process, and they are committed to exploring the influence of various factors on the dissolution process. The main factors include rock fracture, precipitation intensity, carbonate ion content in water, etc.

In terms of rocks, fractures in rocks can directly determine the trend of dissolution ditches. Tao Zhenyu [21] defined fractures as cracks that occur after a rock is fractured under stress. It is a very common geological phenomenon and can also be understood as the crack of a rock.

In terms of water, precipitation intensity and carbonate ion content in water will affect the dissolution process. Corbel et al. [22] proposed the hydrochemical runoff method in 1959 and summarized the relationship between hydrochemistry and the dissolution rate. In this relationship, the dissolution rate is determined by the water depth and the calcium carbonate content in water. This also provides a quantitative formula for our subsequent simulation work.

To sum up, in the related fields of geology and rock geomorphology, researchers have carried out sufficient experiments and analyses on the phenomenon of dissolution, and summarized the definition, occurrence conditions, occurrence process, and definition of typical landscapes, providing strong support for our simulation work.

3. Framework Overview

The complete dissolution simulation process is based on the movement of water. We regard water as an individual particle and simulate the distribution and trajectory of water according to the rock surface morphology and fracture shape (see Section 4.1). Figure 2 shows the framework of the dissolution simulation process in this paper. In this framework, referring to geological research results [15,16], we mainly divide the dissolution process into splash dissolution, water flow, dissolution, lateral dissolution under centrifugal force, deposition, and water evaporation. The above processes are explained separately in the following:

• Splash dissolution: After dropping onto the rock surface, droplets will play a splash role first, forming a shallow hole-like landscape on the surface; in the splash dissolution process, we mainly calculate the splash dissolution amount based on the maximum material-carrying capacity and splash erosion rate of droplets (see Section 4.2).
• Water flow: In the process of water flow, droplets will flow along the slope, but if they are in the rock fractures, they will flow along the shape of fracture. If water droplets encounter carbonate content during the flow process, they will undergo a chemical reaction, resulting in dissolution. Rock fractures can affect the flow route of water and thus significantly affect the dissolution effect.
• Dissolution: In the dissolution process, we will use the carbonate content and water volume to calculate the dissolution rate, and we will then calculate the dissolution amount according to the rate and material volume that water can still carry (see Section 4.3).
• Lateral dissolution: When the dissolution ditch is obviously curved, the centrifugal force of a droplet will also play a dissolution role on the side wall of a ditch to expand and deepen the fracture. In the horizontal dissolution process under the action of centrifugal force, we calculate the influence area of centrifugal force according to the direction of water velocity, and we calculate the dissolution amount according to water volume, carbonate content, velocity, and centrifugal radius (see Section 4.4).
• Deposition: In the process of dissolution, the replacement reaction reduces the carbon dioxide content in the droplets. When the content reaches the lower limit, the deposition phenomenon will occur. We will use the deposition rate and the carbonate ion content of water to determine the value of sediment (see Section 4.5).
• Evaporation: Evaporation will reduce the amount of water. We calculate the amount of water after evaporation based on the evaporation rate and the minimum threshold value (see Section 4.6).

In the terrain generation module, we use an elevation model as the representation method of terrain information. The elevation data store the information of each point on the terrain surface, which makes it easier to calculate terrain morphology in detail, and it is also suitable for our calculation framework. In addition, the elevation model can be easily converted into a mesh model for rendering. In order to increase a change in surface morphology, we use the method of SimpleX noise function [23] to perturb terrain data, so as to generate random surface morphology.

In the interactive control interface, users can set parameters related to rainfall, terrain height field, rock solubility, and rock fractures to generate customized dissolution effects. The so-called ”rock solubility” refers to the proportion of soluble substances (carbonates) in a rock. According to this value, we sample the rock surface randomly to determine the soluble area. Rock fractures will directly affect the trend of water flow, and users can draw it by mouse sketching.

4. Dissolution Simulation

In the process of dissolution, droplets are the main body, affecting the surface of the area where they are located and changing their morphology. As a result, their movement trajectory also determines the position of the holes created by dissolution and the trend of ditches after dissolution.

Therefore, the whole simulation process is carried out around the movement of droplets. Based on the theoretical reference of the dissolution process summarized by Yang Mingde [15] and Zhang Huiling [16], we realized the simulation of splash erosion, dissolution ditch, and other effects by calculating the interaction between water droplets and rocks during their movement. In our method, water is represented by several water particles that store the properties of position, velocity, carbonate ion content, carbon dioxide content, etc. We simulate the dissolution effect by calculating the movement trajectory of each droplet in its life cycle and the interaction between it and the surface in parallel, so as to achieve the generation of dissolved terrain. The life cycle of droplet particles refers to the process from the appearance of a droplet to its demise—when the amount of water becomes zero.The amount of water will gradually become zero due to evaporation.

In the preparation process of the simulation, we first obtain the terrain height field through the elevation data file or SimpleX noise to complete the construction of the initial terrain. Then, we obtain the soluble part of rocks by randomly sampling their surface according to the value of rock solubility. After that, the user can also interactively draw the fracture shape on the rock surface through a mouse sketch. These rock fractures can affect the trend of flow water and thus affect the dissolution results. The information of the dissoluble region and rock fractures is stored in the corresponding data structure. On the basis of the above work, the calculation of dissolution can be started. The calculation process is

Algorithm 1. Dissolution simulation.

Input: Terrain height field data and various parameters.

Output: New terrain height field data.

Algorithm 1.1. Splash calculation:

Calculate the amount of splash dissolution $\Delta M_r$ and update the carbonate ions content in droplets and terrain height.

Algorithm 1.2. Dissolution calculation:

Calculate the amount of rock dissolution and lateral dissolution $\Delta M_r$ and update the carbonate ions content in droplets and terrain height.

Algorithm 1.3. Deposition calculation:

According to the carbonate ion content in droplets, calculate the sedimentation amount $\Delta M_d$ and update the carbonate ions content in droplets and terrain height.

Algorithm 1.4. Flow trajectory calculation:

Calculate the movement of water droplets along rock fractures or based on gradients and inertia, and update the position of droplets.

Algorithm 1.5. Evaporation calculation:

Calculate the amount of evaporation and update the water volume. If the water volume is not zero, return to Algorithm 1.2; otherwise, end Algorithm 1.

Algorithm 1.1. Splash calculation.

Input: Terrain height field data and various parameters.

Output: New terrain height field data and carbonate ion content in droplets.

Splash calculation:

For all particles, complete the following:

Calculate splash dissolution amount $\Delta M_r=M_c\times R_s$.

Increase the content M of carbonate ion in water by $\Delta M_r$.

Decrease the height of terrain by $\Delta M_r$.

End.

Algorithm 1.2. Dissolution calculation.

Input: Terrain height field data and various parameters.

Output: New terrain height field data and carbonate ion content in droplets.

Dissolution calculation:

For all particles, complete the following:

Calculate dissolution amount $\Delta$$M_r=(Mc-M)$×$R_r$.

Increase the content M of carbonate ion in water by $\Delta M_r$.

Decrease the height of terrain by $\Delta M_r$.

End.

For all particles, complete the following:

Calculate lateral dissolution amount $\Delta M_r=(Mc-M)\times R_{r^{\prime }}$.

Increase the content M of carbonate ion in water by $\Delta M_r$.

Decrease the height of terrain decreased by $\Delta M_r$.

End.

Algorithm 1.3. Deposition calculation.

Input: Terrain height field data and various parameters.

Output: New terrain height field data and carbonate ion content in droplets.

Deposition calculation:

For all particles, complete the following:

Calculate deposition amount $\Delta M_d=M\times R_d$.

Decrease the content M of carbonate ion in water by $\Delta M_d$.

Increase the height of terrain by $\Delta M_d$.

End.

Algorithm 1.4. Flow trajectory calculation.

Input: Terrain height field data and various parameters.

Output: New position of droplets.

Flow trajectory calculation:

For all particles, complete the following:

If the current position $P_k$ is a rock fracture, then

$P_{k+1}$ is the point closest to the direction vector in the fracture sequence.

Else,

Calculate direction vector $V_{new}=V_{old}\times Inertia-G\times (1-Inertia)$.

Calculate the particle’s position $P_{k+1}$.

End if

End for

Algorithm 1.5. Evaporation calculation.

Input: Water volume of droplets and rate of evaporation.

Output: New water volume of droplets.

Evaporation calculation:

For all particles, complete the following:

Calculate water volume $W_t=W_0\times e^{R_e\times t}-W_H$.

If $W_t\ne$ 0, then return to Algorithm 1.2.

Else, stop calculating the particle.

End if

End for

The above whole simulation process is carried out around the movement of raindrops, so we first introduce the calculation of the trajectory of raindrops in Section 4.1. Then, around its movement, the simulation methods of splash erosion, dissolution, deposition and water evaporation are introduced in Section 4.2, Section 4.3, Section 4.4, Section 4.5 and Section 4.6, respectively.

4.1. Calculation of Flow Trajectory

In the process of dissolution, the movement track of raindrops will be affected by many factors, including the current movement direction, flow velocity, terrain slope, and fracture sequence in rocks. In this paper, these factors are comprehensively considered, and the motion trajectory of raindrops is formed by continuously calculating the position of droplets at the next moment.

The following attributes are stored in each droplet: position P, flow velocity V, water volume W, carbonate ion content M, and carbon dioxide content C. Water is reduced by evaporation, and the reduction depends on the evaporation rate. When the water volume W = 0, the droplet will ceases to exist. When W is not zero, droplets either flow along the rock fracture or slide along the slope in the direction of the maximum gradient.

Assume the current position of a droplet is $P_k$. When the droplet is just in a rock fracture, its movement path is completely affected by the fracture trend. According to its current movement direction $V_{old}$, we select the point closest to the direction vector in the fracture sequence as the alternative point $P_{k^{\prime }}$. Considering that the water droplet cannot flow to a position with an altitude higher than the current position, we can determine the position $P_{k+1}$ of the droplet at the next moment by comparing the current height and the height of the alternative position, as follows:

$$P_{k+1}=Max\_height(P_k,P_{k^{\prime }})$$

(1)

If the height of the current position $P_k$ is higher than the height of the alternative position $P_{k^{\prime }}$, it means that the droplet will continue to stay at the current position for dissolution.

When the droplet is not in the rock fracture, we calculate gradient G at $P_k$, thus obtaining the next position $P_{k+1}$. Considering that the position of the water droplet may not necessarily fall exactly on the grid point, there might be a deviation. We use the distance difference (u,v) between its current position and the integer coordinate point to perform bilinear interpolation on the three grid points adjacent to $P_k$, so as to obtain the gradient G of the current position, as follows:

$$G\left(P_k\right)=\left(\begin{array}{c}(P_{x+1,z}-P_{x,z})\times (1-v)+(P_{x+1,z+1}-P_{x,z+1})\times \left(v\right)\\ (P_{x,z+1}-P_{x,z})\times (1-u)+(P_{x+1,z+1}-P_{x+1,z})\times \left(u\right)\end{array}\right)$$

(2)

where u and v are the offset of the position of the water droplet with respect to the coordinate value of the grid point, and $P_{x,z}$ is the position of the grid point closest to $P_k$.

Considering that the water droplet has inertia, its motion is not only affected by the slope of terrain but also by its current direction. Therefore, we can obtain the new direction $V_{new}$ via linear interpolation of the current direction $V_{old}$ and gradient G.

$$V_{new}=V_{old}\times Inertia-G\times (1-Inertia)$$

(3)

where $Inertia$∈(0, 1) is the user-defined coefficient. Inertia = 1 means that the raindrop will always move in the initial direction, without considering the influence of the gradient. Inertia = 0 means that the direction of the raindrop is only affected by the gradient. The next position $P_{k+1}$ can be obtained by adding the flow direction $V_{new}$ and the current position $P_k$. The directions mentioned above are normalized. Since the flow direction is a normalized value, the distance that the raindrop moves across will not exceed one unit, so the position of the raindrop at the next moment will only be its adjacent point.

4.2. Splash Dissolution

This section will introduce Algorithm 1.1.

When raindrops fall from clouds to the surface of rocks, they absorb carbon dioxide in the atmosphere, and thus have the ability to react with soluble substances, such as limestone.

At the moment when the raindrop contacts a rock surface, its impact and solubility on the surface will make the rock surface sag and form a hole-like karst pit. This is also known as splash dissolution. In the process of dissolution, carbon dioxide and the rock react, resulting in a decrease in terrain height, while the content of carbonate ions in water increases and the content of carbon dioxide decreases. Inspired by Hans [24], it can be seen that the dissolution amount $\Delta$$M_r$ is jointly affected by the amount of material that raindrops can still carry and the splash erosion rate. Considering that the content of carbonate ions in water is zero at the beginning, the amount of material that raindrops can carry at this time is the maximum value $M_c$. The amount of dissolved material can be expressed as

$$\Delta M_r=M_c\times R_s$$

(4)

where $R_s$ is the splash erosion rate, which is determined by user customization. At the same time, the change of carbon dioxide content will also be affected by the amount of dissolved material.

4.3. Dissolution

This section will introduce Algorithm 1.2.

After the raindrops fall to the rock surface, they begin to move along the slope. If its current position contains soluble rock, and the carbonate ion content in the raindrop does not reach the upper limit, the raindrop will dissolve the material here, and the terrain height will descend accordingly, the carbonate ion content in water will increase, and the carbon dioxide content will decrease. The change in these three properties is determined by the amount of dissolution. The dissolution amount $\Delta$$M_r$ in this state is still related to the material that a raindrop can still carry and the dissolution rate. The formula for this is as follows:

$$\Delta M_r=(M_c-M)\times R_r$$

(5)

where $R_r$ is the dissolution rate. In geology, most scholars use the simplified formula [22] proposed by Corbel to calculate the dissolution rate, which is determined by the water volume W and the content of carbonate ions in water M, as shown below:

$$R_r=4\times W\times {\displaystyle \frac{M}{100}}$$

(6)

If the material at the current position is insoluble, it means that the rock here cannot react with the carbon dioxide in water, so no dissolution calculation is required.

4.4. Lateral Dissolution

The above dissolution phenomenon only occurs at the current position of the raindrop. Due to the different shapes and trends of rock fractures, the movement direction of raindrops may be completely changed when flowing along the fractures. That is, the motion direction of droplets at the current time and its motion direction at the previous time are different in a certain space. For example, as shown in Figure 3, the droplet starts flowing in the southwest direction ($V_{old}$) at the last moment, but it flows to the southeast ($V_{new}$) at the current moment.

When the direction changes, raindrops will dissolve curved ditches on the rock surface. When water flows into a curved ditch, it generates centrifugal force at the same time. Under the action of centrifugal force, water will also have a lateral dissolution effect on the side wall of the concave bank of the ditch, which will dissolve the material of the concave bank and reduce its height.

When simulating this phenomenon, we obtain the previous direction $V_{old}$ and the current direction $V_{new}$, respectively, and judge whether they have changed. If there is a change, multiply the two direction vectors to obtain the vector $V_l$. Then, find the grid point $P_n$ that is nearest to the direction vector in the eighth neighborhood as the grid point of a concave bank; moreover, reduce its height to simulate the dissolution effect on a concave bank. During the dissolution process described in Section 4.3, the amount of dissolution is affected by water volume. However, the dissolution in this section is affected by centrifugal force. Therefore, the calculation method is different from the one described in Section 4.3. According to physics, the calculation formula of centrifugal force is

$$F={\displaystyle \frac{m\times |V^2|}{2}}$$

(7)

Therefore, in combination with Formula (6), we have obtained the calculation formula of the dissolution rate $R_{r^{\prime }}$ under centrifugal force, as follows:

$$R_{r^{\prime }}={\displaystyle \frac{4\times W\times M\times |V^2|}{100\times r}}$$

(8)

where we use water volume W to represent the mass of droplet m, $\left|V\right|$ is the velocity of the droplet, and r is the radius of centrifugal motion.

4.5. Deposition

Deposition is one of the important processes in dissolution. The reduction in carbon dioxide content in water will cause the chemical reaction to proceed in the opposite direction, and the carbonate material in water will precipitate and settle to the rock surface, leading to a rise in terrain height. This process is called deposition. The simulation of this phenomenon corresponds to Algorithm 1.3. We can obtain the change value in height by calculating the amount of carbonate material exchanged between the raindrops and the rock.

It can be seen from Section 4.2, Section 4.3 and Section 4.4 that the splash and dissolution effect will reduce the carbon dioxide content in water. When the carbon dioxide content is lower than the threshold $C_{min}$, the raindrops will precipitate some salt substances and discard them at the current position $P_k$, and the terrain will rise accordingly. Inspired by Hans [24], we found that the amount of material exchange between droplets and rocks caused by deposition can be determined by the content of carbonate ions in the water and the deposition rate $R_d$. Therefore, the amount of material exchange caused by deposition $\Delta$$M_d$ can be expressed by Formula (9), as follows:

$$\Delta M_d=M\times R_d$$

(9)

where M is the content of carbonate ions in water. The proportion of deposition material is determined by the sedimentation rate $R_d$. After analyzing the theory introduced by Feng Bei [25], we set the minimum threshold of carbon dioxide $C_{min}$ as 10% of the initial content of carbon dioxide in the simulation process.

4.6. Evaporation

As time goes on, the amount of water in the droplets will decrease due to evaporation. Water evaporation corresponds to Algorithm 1.5. In previous hydraulic erosion simulation studies, most researchers only expressed evaporation by subtracting the evaporation value from the current water volume. This is a simplified empirical model and is not accurate. After a full investigation, Benes et al. [11] used a more accurate water volume representation method for simulations. Inspired by them, we learned that under the condition of constant temperature, the evaporation process of water can be expressed as

$${\displaystyle \frac{dW}{dt}}=(-1)\times W\times R_e$$

(10)

where $R_e$ is the rate of evaporation. After a deduction of Formula (10), it can be seen that the evaporation of water is determined by the water volume, time, and evaporation rate. The water volume after evaporation can be calculated with the following formula:

$$W_t=W_0\times e^{-R_e\times t}$$

(11)

When using Formula (11) to calculate the water volume after evaporation, we found that the water volume will never return to zero in the process of an exponential decline, which obviously does not conform to the natural law. Therefore, we simply introduce a minimum threshold $W_H$ to solve this problem. The optimized formula can be expressed as

$$W_t=W_0\times e^{-R_e\times t}-W_H$$

(12)

5. Results

We implemented our algorithm in Unity3D (version 2019.4.29f1) using the C# language. The calculation of the dissolution algorithm was completed in Compute Shader. We generated our simulation results on a laptop equipped with the Windows 10 system and Intel Core i7, clocked at 2.40GHz with 8GB of RAM.

5.1. Simulation Results

According to the theories of geology, the rock body contains both soluble carbonate rocks and other rock substances that are not soluble in water. Water will dissolve easily soluble substances, forming various landscapes such as karst pits, karst ditches, and stone forests. In order to simulate more rich and realistic effects, we built a rock terrain composed of soluble rock and insoluble rock material, and we customized different fracture trends on the surface of rocks through mouse interactions. Next, we will show the simulation effects of three typical dissolution landscapes.

• Karst pit
  A karst pit refers to the hole-like landscape that is dissolved after the raindrops drop vertically on a rock surface. A raindrop falls under the action of gravity and absorbs carbon dioxide continuously in the air during the falling process. Its dissolution will cause splash dissolution to the rock, forming shallow holes, constituting to the initial form of a karst pit. Under the continuous dissolution of water flow, the holes gradually expand and deepen, forming a more obvious karst pit landscape. Figure 4 shows our simulated effect of a karst pit.
• Karst ditch
  A karst ditch refers to a ditch-shaped depression carved by the movement of water on the surface of a rock. During the flowing of water, its direction will be affected by the slope, and then it will dissolve out curved ditches. However, when encountering a rock fracture, the water flow will penetrate into the fracture and move along its trend, making the fracture expand and deepen continuously, forming a parallel or dendritic karst ditch landscape developed from a rock fracture. Figure 5 and Figure 6 show our simulated karst ditches.
• Stone forest
  A stone forest refers to a landscape composed of a large number of dense columnar or conical rock bodies, which are generally concave and convex. After heavy rainfall dissolves the rock body, a large number of karst pits and ditches will be formed. After a long time of development, dense columnar or conical rocks will be formed, which together constitute a stone forest landscape. Figure 7 shows our simulated stone forest landscape.

In addition, we compared our simulation results with a real dissolution landscape, as shown in Figure 8, Figure 9 and Figure 10. The three real dissolution landscapes are from a Zhongshan landform from Guilin County, Luzhou City, Sichuan Province, and Xingwen County, Yibin City, Sichuan Province. The trend of the erosive network in the analyzed sites is defined by interactive mouse clicking (red dots). It can be seen from the comparison results that the simulation effect in this paper has a good sense of reality.

5.2. Dissolution Effect Under Different Parameters

The dissolution process depends on many parameters, such as precipitation intensity, maximum material-carrying capacity of raindrops, water evaporation rate, etc. Using this method, users can interactively set various parameters to produce different simulation effects.

• Precipitation intensity
  Precipitation is the main body of the dissolution effect on a rock surface. In our dissolution simulation framework, the precipitation intensity is marked by the number of raindrops. Like the natural law, the greater the precipitation intensity, the more raindrops will act on the terrain, thus forming a more obvious dissolution effect. Figure 11 shows this.
• Maximum material-carrying capacity of raindrop
  Raindrops will flow together with carbonate materials during transportation. It can be seen from Formulas (4) and (5) that the larger maximum material-carrying capacity of a raindrop, the higher the dissolution amount, and the more obvious the dissolution effect. Figure 12 can prove this.
• Evaporation rate
  According to Formula (12), the evaporation of water is affected by the evaporation rate. The greater the evaporation rate, the faster the water volume decreases. Therefore, under the same conditions, the greater the water evaporation rate, the weaker the dissolution effect. Figure 13 can prove this phenomenon.

5.3. Operation Efficiency

Table 1. Running time in (sec).

	Rain	5000	10,000	20,000	50,000
Grid
10,000		0.049	0.053	0.058	0.068
22,500		0.086	0.092	0.102	0.116
40,000		0.132	0.152	0.172	0.197
57,600		0.183	0.205	0.228	0.258

lists the running time required by the simulation method in this paper under different conditions. The precipitation intensity (rain) is marked by the number of raindrops per unit time, and the terrain resolution determines the number of terrain grid points (grid). It can be seen from the data below that the increase in the precipitation intensity and terrain resolution will increase the time required for the calculation. However, relatively speaking, our algorithm can run interactively or in real time, and it has a strong application value.

6. Discussion

We presented a dissolution simulation framework for rock surfaces. By simplifying the process of dissolution in nature, we chose the movement trajectory of raindrops as the main simulation parameter. We introduced formulas of geology to account for simulating the splashing dissolution, dissolution under different conditions, deposition, and evaporation phenomena. Users can interactively set parameters related to rainfall, terrain height fields, rock solubility, and rock fissures to generate custom dissolution effects. The algorithm performs well in simulating the dissolution effect under different conditions, has good visual fidelity, and can achieve an interactive simulation efficiency.

There are many possible avenues for future works. We presented a general solution, but we only experimented with dissolution rates to represent different rock properties and environmental factors. One important future direction is an extension to a representation of full rock properties, which would allow for accurate simulations. Another possible future aim would be to focus on a better method for constructing internal cave structures formed by the dissolution of underground rivers inside rocks. We may use the volume model to represent terrain information, so that it can support the carving operation of caves and ditches in rocks. In addition, a change in a rock’s height may lead to the destruction of its stability, and then it may collapse. We also want to consider the collapse phenomenon of rock surfaces in a simulation process, which may be one of our research directions in the future.