Abstract
The minimum spanning tree problem in graphs under budget-type degree constraints (DCMST) is a well-known NP-hard problem. Spanning trees do not always exist, and the optimum can not be approximated within a constant factor. Recently, solutions have been proposed to solve degree-constrained spanning problems in the case of limited momentary capacities of the nodes. For a given node, the constraint represents a limited degree of the node for each visit. Finding the solution with minimum cost is NP-hard and the related algorithms are not trivial. This paper focuses on this new spanning problem with heterogeneous capacity-like degree bounds. The minimum cost solution corresponds to a graph-related structure, i.e., a hierarchy. We study the conditions of its existence, and we propose its exact computation, a heuristic algorithm, and its approximation.
1. Introduction
It is important to cover node sets in graphs with minimum cost in several domains, for instance, for efficient broadcast/multicast communications in networks. The sub-graph that spans the set of nodes with minimum cost is a minimum spanning tree (MST), and several polynomial-time algorithms to compute it are known. The partial spanning with minimum cost (the Steiner problem in graphs) is NP-hard. Some applications must meet additional constraints. We are interested in the degree-constrained spanning problem. Each node of the graph is assigned a positive integer value which represents the maximum degree of v in any spanning structure. This degree is potentially different from the degree of (). In the literature, proposals can be found to span the node set of a graph adhering to budget type degree bounds [1,2]. In these problems, nodes have limited budgets and cannot exceed the given limits in the spanning structures (in the spanning trees). Degree Constrained Minimum Spanning Tree (DCMST) problems are hard to solve, and unfortunately, constant factor approximations do not exist for them [3].
Degree bound does not always correspond to a definitive budget but to a momentary limited capacity. For example, in optical networks, the capacity of duplication of the switches may be limited for each incoming light, but a wavelength can pass through a switch many times (cf. [4]). As a result, the optical broadcast/multicast route may be different from a spanning tree. In [5], a special walk returning to some nodes is proposed when spanning trees are impossible due to the absence of nodes having a degree bound greater than two. If the constraints can be greater than two, branching nodes are possible, and the spanning structure could be a hierarchy crossing certain nodes several times. For the case of homogeneous capacity constraints, a hierarchy-based optimum and its approximation have been proposed in [6]. The analysis of this NP-hard problem shows that this kind of solution still exists and can be approximated. The most important results of the related work can be found in Section 3.
Here, we propose the analysis of cases presenting heterogeneous momentary capacity constraints.
We are studying the following questions: In which cases does the solution exist? How can the optimum be calculated? Can it be approximated?
As in the case of homogeneous capacity bounds, the optimal solution to the problem is a hierarchy. As a new result, we formulate necessary and sufficient conditions for its existence. The problem is NP-hard, and we highlight that, in some cases, the optimal solution can be approximated. We propose a special heuristic algorithm for this. In the following section, we present the definition of hierarchies. Section 3 offers a quick overview of DCMST issues, followed by the formulation of capacity-constrained spanning problems. The necessary and sufficient conditions for a solution to exist are formulated in Section 4. An ILP-based exact computation (cf. Section 5.1) and a heuristic algorithm (cf. Section 5.2) are also proposed. Section 6 presents some approximations. Performance is compared in Section 7.
2. Notations and Definitions
The most important notations used in the paper are in Table 1.

Table 1.
Notations.
A brief review of the hierarchy concept corresponding to the minimum cost solutions follows.
Hierarchies
The generalization of trees is based on graph homomorphism. The homomorphic mapping of nodes between a tree T and a graph G can be used to define an eventually non-elementary tree in G. To simplify, let us suppose undirected graphs but the definition in digraphs is trivial.
Definition 1 (Hierarchy).
Let be an arbitrary graph and let be a tree. Let be a homomorphic function that associates a node to each node . The application defines a hierarchy in G.
Definition 2 (Image of a hierarchy).
The sub-graph defined by the set of nodes and edges in G associated by h to T is the image of the hierarchy.
Since a node can be associated with several nodes in P, a hierarchy can contain multiple occurrences of a node and an edge. A hierarchy can be considered as a ”non-elementary tree” in G. Certain nodes in the hierarchy can eventually be branching nodes; they are the node occurrences corresponding to the branching nodes of the tree T. Figure 1 illustrates with discontinuous lines a hierarchy in a graph and the associated tree. The labels of the nodes in T are the labels of the corresponding nodes in G. Dotted lines with arrows indicate the associations between these nodes. Some nodes of G (namely the nodes c and d) participate on different levels of the hierarchy as shown in the labeled tree T.
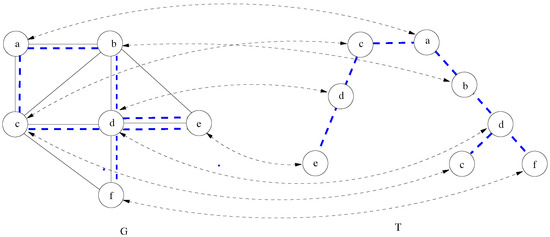
Figure 1.
Illustration of a hierarchy with discontinuous lines in an undirected graph G and the corresponding labeled tree T.
Hierarchies generalize trees. Trees are special hierarchies without repetition of nodes (when the mapping h is injective), and therefore, inherit the properties of hierarchies. Note that the image of a hierarchy can contain cycles in G but the hierarchy itself preserves the structure of a tree. Hierarchies allow the exact definition of the optimum in the case of capacity-like constraints.
3. Degree-Constrained Spanning Problems
We propose a clear distinction between two categories of degree constraints:
- budget-like constraints: in this case, the total number of adjacent nodes of the constrained node is limited,
- capacity-like constraints: the number of adjacent nodes is limited for each occurrence of the node.
3.1. Minimum Spanning Trees Under Budget-Like Degree Constraints
Any minimum cost solution of spanning problems under budget-like degree constraints, if it exists, is a tree. Trivially, cycles are useless in any optimum. Deleting an edge from a cycle, the node set remains covered. The basic problem was formulated as follows.
Definition 3 (Degree-constrained minimum spanning tree (DCMST) problem).
In an undirected graph G with non-negative costs on the edges and with positive integer degree bounds the problem consists in finding a spanning tree in which the degree of any node v is at most and the total cost is minimized.
The degree bounds can be uniform or not in the node set.
The DCMST problem is NP-hard [7], and there is not always a solution. As observed in [8], a spanning tree can exist if and only if . The hardness of the problem has also been demonstrated using a reduction from the traveling salesman problem. In [3], the authors present the problem as a generic bi-criteria optimization where the first objective corresponds to the respect of the budget (degree) constraints and the second to the cost minimization. The paper also specifies the sub-graphs to solve the problem. The investigated classes are spanning trees, Steiner trees, and generalized Steiner trees. The authors give some negative results on the approximations. There is no polynomial-time -approximation algorithm for the DCMST problem minimizing the cost when respecting the degree constraint, even when the same upper bound is supposed for all nodes. Heuristic solutions were proposed in several works (cf. [2,3,9,10,11,12,13]). In unweighted graphs constrained by a uniform degree bound , an -approximation algorithm has been proposed by Fürer and Raghavachari [14]. The results are generalized to weighted graphs in [13].
An interesting idea to compute the solution can be based on uniformly generated spanning trees (cf. [15]) followed by the selection of the tree satisfying the constraints. In [16] the DCMST problem in uncertain networks is discussed. The nondeterministic model mainly concerns the edge costs. Note that uncertainties can characterize the degree bounds.
In the mentioned papers, the constraints are budget constraints, and spanning trees are the solutions. In the case of degree bounds corresponding to capacities of the nodes, we suppose that the solution can contain several times any node, and the capacity of each occurrence of a node is the same. The model has been presented in [6] for uniform degree bounds.
3.2. Minimum Spanning Problem Under Capacity-Like Degree Constraints
Definition 4 (Node capacity constrained minimum spanning problems).
In a graph G, the degree bounds associated with nodes represent the maximum degree capacities. The problem consists of finding the minimum cost solution spanning the node set V such that the degree constraints are respected for each occurrence of the nodes.
Property 1.
The minimum cost solution spanning the set of nodes of a connected graph under limited node capacities is a hierarchy.
Proof.
Let us assume the solution exists (the reader can find the conditions in Section 4). Since homomorphism preserves adjacency, any solution can be given by a homomorphism-based triplet . For a connected solution, S must be a connected graph. Suppose there is an optimal solution respecting the degree constraints, which is not a hierarchy. In this case, S is not a tree but another connected graph. Therefore, it contains cycles. Trivially, some edges can be removed from the cycles in S without removing nodes thus preserving the node coverage in G with a lower cost. In the minimum cost solution, S is a tree, and the triplet defines a hierarchy. □
A degree-constrained minimum spanning hierarchy (DCMSH) is illustrated in Figure 2. The cost of any edge in G is unitary, and the capacity constraints are indicated. Trivially, no DCMST exists but there is a spanning hierarchy satisfying the constraints. It contains the node b twice, and each occurrence of this node respects the degree constraint as shown by the labeled tree T of the solution. The image of the solution is the graph G itself.
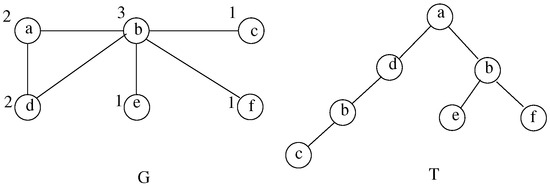
Figure 2.
A DCMSH represented by its labeled tree T in the graph G.
The case of uniform capacity bounds and its approximation have been presented in [6]. Spanning hierarchies satisfying homogeneous degree constraints always exist. An ILP-based exact computation of the optimum can be found in [17]. The approximation has been improved in [18].
Since the problem of uniform degree constraints is NP-hard (cf. [17]), the more general problem of non-uniform constraints is NP-hard.
The following section discusses the conditions for the existence of a feasible solution in the case of non-uniform bounds.
4. Necessary and Sufficient Conditions for the Existence of a Solution
Degree-constrained spanning hierarchies do not always exist in the case of heterogeneous degree bounds. In this section, we formulate conditions for their existence.
Remember, we suppose a connected graph and indicates the subset of nodes with degree bound m. Trivially, the nodes in must be leaves in any solution.
Lemma 1.
If the specified leaf node set is empty, hierarchies spanning V and satisfying the degree constraints exist.
Proof.
A simple solution can be constructed as follows. Let W be a walk following an MST in G. In W each node occurrence has a degree of at most two. The degree constraints are satisfied and the node set is covered. □
Trivially, Lemma 1 gives a sufficient condition. The complementary case is when is not empty. The necessary and sufficient conditions for this case are discussed next.
Lemma 2.
If contains a separator (removing a separator makes a connected graph disconnected), there is no hierarchy spanning V and satisfying the degree constraints.
Proof.
Let A and B be two non-empty subsets of nodes separated by a separator . Any path from a node in A to a node in B must pass through S but nodes in S can not be internal nodes in any path. Trivially, no paths exist between nodes in A and nodes in B satisfying the degree constraints in . □
A necessary condition can be formulated: must be free of any separator. If is not a separator but a subset of is a separator, this later isolates some nodes in . Consequently, a spanning hierarchy satisfying the degree constraints does not exist. Figure 3 illustrates this case. Here, is not a separator but the subset is.
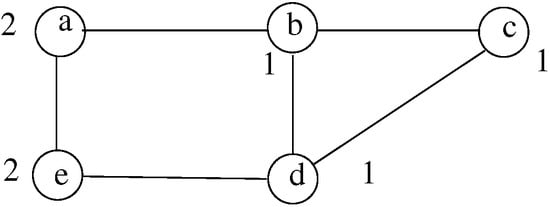
Figure 3.
is not a separator, but contains a separator.
Suppose there is no separator in . Lemmas 3 and 5 indicate that a set without a separator is necessary but not sufficient for the existence of a spanning hierarchy satisfying the degree constraints. Further sufficient conditions are given by Lemmas 4, 6 and 7.
Lemma 3.
If there is no node with a degree bound greater than 2 and there are more than two nodes with a degree bound 1 (), there is no hierarchy spanning V and satisfying the constraints.
Proof.
Each node in must be a leaf in the spanning hierarchy (and trivially in the corresponding tree T). Since , the tree T and the hierarchy must have more than two leaves. Because , the degree of internal nodes in T is equal to 2. T is a path and as such it can not have more than two leaves. □
Lemma 4.
If , hierarchies spanning V and satisfying the constraints exist.
Proof.
Suppose there are two nodes a and b with degree bound 1. A complete graph can be constructed in which the edges represent the shortest paths in G that contain neither a nor b as an internal node. These paths exist because does not contain any separators.
In , Hamiltonian paths exist whose endpoints coincide with a and b. Each Hamiltonian path corresponds to a Hamiltonian walk (a Hamiltonian walk covers the node set and can return several times to certain nodes) in the original graph covering the node set and respecting the degree constraints. These walks are solutions. The same demonstration is trivial with only one node in . In this case, one end of the Hamiltonian paths can be freely chosen in . □
Lemma 5.
Let us suppose that and let the node in . If the degree bound , there is no hierarchy spanning V and respecting the constraints.
Proof.
Since there is no separator in , the nodes in are connected to . (suppose that a node is not connected to but to another node . b separates a from the other nodes) The nodes in must be leaves in any spanning hierarchy. Since there is no return from leaves, there is only one occurrence of in any hierarchy. This occurrence of can have at most neighbors, but . □
Lemma 6.
If , and of the node , a spanning hierarchy respecting the degree constraints exists.
Proof.
The graph G contains a star with a central node and the nodes in are connected to it (there is no separator in ). Since , and the star satisfies the degree constraints. □
Lemmas 3 and 5 indicate cases where there are several nodes in and there is no spanning hierarchy respecting the degree constraints. The following lemma formulates a sufficient condition.
Lemma 7.
If (there are at least two nodes with a degree bound greater than 1) and (there is at least one node with a degree bound greater than 2), a spanning hierarchy respecting the degree constraints exists.
Proof.
Let b be a node with , and another c with . A degree-constrained spanning hierarchy can be constructed as follows. Because there is no separator in , each node in can be connected to c with a path satisfying the degree constraints. The set of paths can be partitioned such that there are at most paths in every group. Since one endpoint of the paths is the node c, each group corresponds to a ”spider” respecting the degree constraints and having an occurrence of c as the central node. The different occurrences of c can be chained by a walk visiting the node b (having a degree bound at least 2) such that the degree of each central node is at most . The obtained structure is a degree-constrained hierarchy spanning the node-set. □
Figure 4 illustrates a spanning hierarchy corresponding to Lemma 7. The occurrences of the node c are the central nodes of spiders which are connected by paths passing through the node b. Notice that it is not the ”best” spanning hierarchy. The reader can easily find hierarchies containing fewer edges while respecting the constraints.
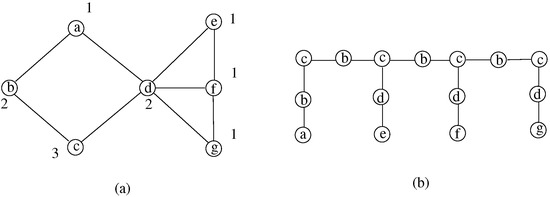
Figure 4.
Illustration of Lemma 7. (a) indicates the graph and (b) its spanning hierarchy.
The following theorem formulates necessary and sufficient conditions for the existence of degree-constrained spanning hierarchies.
Theorem 1.
Let the set of conditions be as follows:
A: is empty
B: there is no separator in
C: (there are at most two nodes with degree bound 1)
D: and the nodes in are neighbor nodes of a node v s.t.
E: (there are at least two nodes with degree bound greater than 1) and
(there is at least one node with a degree bound greater than 2).
A hierarchy spanning all the nodes of a connected graph and respecting non-uniform capacity degree constraints can be found, if
Proof.
Following Lemma 1, condition A is sufficient.
If A is not true, the second part of the expression, i.e., ) gives a sufficient condition for the existence of a solution as it can be proven easily. In any case, cannot contain a separator (condition B is necessary, as a consequence of Lemma 2), and one of the cases or E must be true. Following Lemmas 4, 6 and 7 these conditions together with B are sufficient. If is not empty () and there is no separator in it (B), the expression gives also a necessary condition, that is one of them should be true for the existence. We prove that if none of them are true, there is no spanning hierarchy respecting the constraints. Let us suppose that none of them are true: there are more than two nodes in (), and they are not neighbors of a node with a sufficiently large degree bound (), and there is no node with a degree bound greater than 2 or another with degree bound 2 (). We start our proof by . If there is a single node with a degree bound greater than 2, it must be the neighbor node of the nodes in , but following , its bound is not sufficiently large. If there is no node with a degree bound greater than 2, there are only nodes in and in . Following , there are more than two nodes in . Therefore, the three conditions cannot be false together (and another fourth condition cannot guarantee the spanning hierarchy) when . □
5. Algorithm Design
5.1. Exact Solution
We propose an ILP-based computation in several steps. It is an improved version of the procedure in [17] using a flow model in a directed graph. Since an arc can be used multiple times by a directed DCMSH, the flow computation must be adapted to this. We will show that the result of the ILP is not the optimal hierarchy but its image. Each arc in the image is associated with an integer value indicating how many times the arc is used. The computed image permits the reconstruction of the DCMSH. The procedure is illustrated by Figure 5 and detailed as follows.
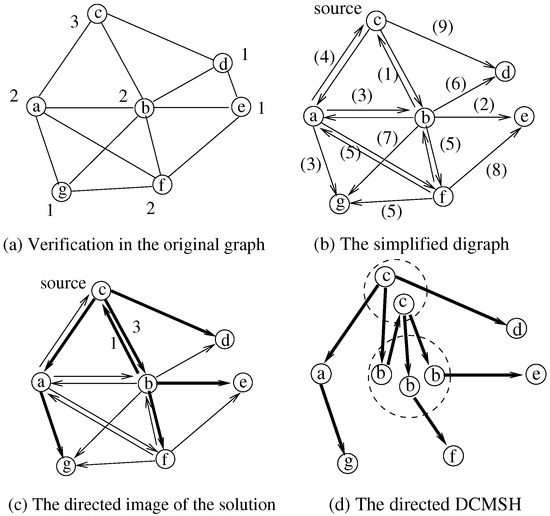
Figure 5.
The steps of the construction of a DCMSH.
5.1.1. Verification for the Existence
Theorem 1 gives the necessary and sufficient conditions for the existence of any solution. These conditions must be verified.
- (1)
- At first, it is checked that there is no node separated in itself. If there is at least one node in s.t. all its neighbors are also in , it is isolated.
- (2)
- cannot correspond to any separator in G. After removing from G, the number of connected components is calculated. If it is greater than 1, there is a separator and the solution does not exist.
- (3)
- If there is a single node and , there is no solution.
- (4)
- If and the nodes in are in , there is no solution.
Figure 5a shows an undirected graph and the degree constraints on the nodes. The graph does not contain any separators.
5.1.2. Creation of a Digraph
If the solution exists, a directed graph is created for the computation of the image of the optimum.
- (1)
- At first, each edge of G is replaced by two arcs, one in each direction and having the same cost as the edge.
- (2)
- A node s is selected as the source of flows. (in the computation a set of flows will be used, one flow to each destination from s)
- (3)
- Potential simplifications of the digraph are possible. If , it can have only one successor and its incoming arcs can be deleted. The other nodes in can have only incoming arcs. Their outgoing arcs can be deleted.
The simplified digraph of the example is illustrated in Figure 5b. The costs of the arcs are also indicated.
5.1.3. Computation of the Image of the Solution
In the next step, a valued, directed image of the DCMSH is computed in the digraph. Integer values are associated with the arcs indicating the number of transited flows. The set of arcs with non-zero flows determines the image. Note that the number of flows is not equal to the number of occurrences of the arc in the directed DCMSH.
ILP variables:
| : Integer variable. It is equal to the number of occurrences of | |
| arc in the resulted hierarchy. | |
| : Commodity flow variable. It denotes the quantity of flow | |
| transiting on arc . |
Objective:
The cost of the image must be minimized.
The values associated with the arcs indicate the number of incoming/outgoing arcs in the DCMSH. In an optimal hierarchy, there is a strictly minimal number of occurrences of any node. In our directed model, the number of occurrences of a non-source node is equal to the number of its predecessors. If there are multiple occurrences of the source node, the first one has no predecessor. Respecting the constraints, the number of occurrences must be sufficient to connect the successor nodes by the outgoing arcs. The degree constraints can be formulated as follows. At the arbitrarily selected source s, there are returns if and only if the degree is not sufficient to be the start point of the outgoing arcs:
Especially, if , is empty and there is only one outgoing arc.
For an arbitrary non-source node m, each occurrence of m can be the start point of at most outgoing messages:
Trivially, for nodes in , no outgoing arc is used.
The following lower bounds are not necessary but practical.
At the source:
In a non-source node m with degree bound :
Every node except the source has a predecessor in the hierarchy. This condition guarantees the full coverage as follows.
Full coverage does not mean full connectivity. Flows can be used to guarantee the connectivity. The arbitrary source is the start point of one flow per destination. (the destinations are the other nodes). We have
Each non-source node is the destination of one and only one flow. We require
The conditions of flow transit by occurrences of arcs are as follows.
If an arc does not belong to the solution, it does not carry any flow. Moreover, each arc should carry a non-zero flow if it belongs to the DCMSH, and the value of this flow must not be less than the number of occurrences of the arc.
The number of occurrences of an edge in a DCMSH (and the number of occurrences of an arc in the directed model) is limited:
The upper bound can be calculated in advance.
Remember, solving our linear program does not give a DCMSH but its image. Figure 5c illustrates the valued image of the solution in our example. A last phase is needed to construct an optimal "non-elementary tree" from its image.
5.1.4. Reconstruction of the Optimal Hierarchy
The variable indicates how many times the arc is used in the directed solution. From the image, a directed DCMSH can be built. A directed, labeled tree can be first reconstructed, and then an undirected version can be obtained. Several directed trees can correspond to the image if the number of occurrences of some arcs is different from one. Let and be the numbers of incoming and outgoing arcs, respectively. Each node occurrence has one and only one predecessor (except the source). A node n must be duplicated times in the labeled tree (i.e., in the DCMSH). For each occurrence of n, there is one and only one incoming arc. For the source, one occurrence has no predecessor and the number of occurrences is .
The successors can be arbitrarily associated with the occurrences of n, but to respect the degree constraints, each occurrence of n can have at most successors. Property 4.3 in [17] indicates that for a node n, an optimal hierarchy exists in which all occurrences of n except one have the maximal degree . Following this property, the successors can be distributed between the occurrences of n such that successors are connected to each first occurrences of n. A depth-first search type recursive algorithm can be used for the construction of a directed, labeled tree . Figure 5d shows the directed DCMSH built in the given graph. The labels of the nodes in the tree are the labels of the nodes in the image.
Omitting the direction of arcs from , an undirected, labeled tree is obtained.
Theorem 2.
The labeled tree corresponds to a DCMSH.
Proof.
Since the directed tree (and consequently ) refers to the nodes in G, and the arcs (the edges) in (in ) correspond to arcs (to edges) in (in G), neighbor nodes in (in ) are neighbors in (in G). As a result and are hierarchies.
The computed image covers the whole graph . Each node in V is associated with at least one node of (and with at least one node of ). The hierarchy H spans the node set V. By the construction, the nodes in the tree respect the degree constraints (a node occurrence of the node has at most neighbors). So, H is a degree-constrained hierarchy spanning V. It is with minimum cost. Its cost is the sum of the cost of edge occurrences. Because an edge is present times in H:
This sum is minimized by the ILP. □
5.2. A Heuristic
An approximation of the DCMSH under homogeneous capacity degree bounds has been presented in [6] and improved in [18]. The proposed approximation scheme can not directly be used for our case with in-homogeneous degree bounds. In the present paper, possible approximations under non-uniform degree bounds are analyzed, and a heuristic is proposed. First of all, a lower bound of the cost of any optimal solution is presented.
5.2.1. A Lower Bound
Consider the following spanning tree.
Definition 5 (Minimum spanning tree with specified leaves—MSTSL).
Let be the subset of desired leaves. The MSTSL is a minimum cost spanning tree covering the node set such that the nodes in are leaves in the tree.
The degrees of the nodes in are not limited in the tree. An MSTSL in G can be computed in polynomial time as follows:
- Delete the nodes in .
- Compute an MST in the remaining graph.
- Reconnect the nodes in to the MST using the best cost adjacent edges.
A more complex study can be found in [19], which gives sufficient conditions for a graph to have a spanning tree with a specified set of leaves.
Theorem 3.
Suppose that spanning hierarchies corresponding to the given degree constraints exist in a graph G. Then, an MSTSL exists and its cost is a lower bound for the cost of any DCMSH.
Proof.
Satisfying the conditions in Theorem 1 guarantees that there is no separator in and the MSTSL exists. In a DCMSH H, each node in is present only once (nodes in must be leaves in H). By deleting the leaf nodes in and the set of their adjacent edges from H, a hierarchy is obtained. The image of in G may contain cycles. Since a node of can be associated with several node occurrences in H and in , it can have more than neighbors in the image. does not necessarily respect the degree constraint. From each possible cycle in , an edge can be deleted and a tree in G covering the node set is obtained (it is possible that does not respect the degree constraints). By adding the deleted nodes in using the edges in to a spanning tree is created. It respects the constraints for the specified leaf nodes in . Since contains the edges that are present in H only once and some edges are eventually deleted from the image : . Since an MSTSL exists and is also a spanning tree respecting the constraints given by , . Finally, . □
The main features of the proposed heuristic are as follows.
- An MSTSL is created.
- The MSTSL is decomposed into a set of edge-disjoint stars.
- A degree-constrained spanning hierarchy with low cost is computed in each star.
- Finally, these spanning hierarchies are connected to form a unique hierarchy spanning the MSTSL. (cf. Figure 6).
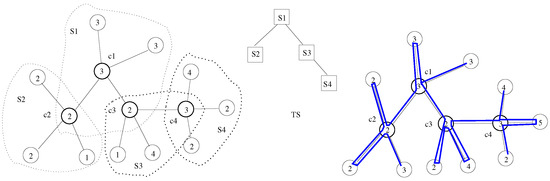 Figure 6. The decomposition of an MSTSL, the tree of stars and its spanning hierarchy.
Figure 6. The decomposition of an MSTSL, the tree of stars and its spanning hierarchy.
5.2.2. Decomposition of the MSTSL into a Set of Edge-Disjoint Stars
Let us suppose there are more than three nodes in the tree; otherwise, the tree is a path and decomposition is useless. The decomposition starts with the unique neighbor node of an arbitrary leaf of the MSTSL (e.g., node in Figure 6). This node is considered the first star’s central node, and the nodes related to this central node are leaves in the star ( in the figure). If a leaf in the star is not a leaf in the MSTSL, it is considered the central node of a following star. In our example, the nodes and are such nodes in . The decomposition continues in the newly detected stars until there are no more leaves eligible for new centers.
The decomposition can be seen as a rooted tree of stars in which each star (except the first) has a “parent”. Each star is connected to its “parent” via its central node (which is a leaf in the “parent” star).
5.2.3. Computation of a Degree-Constrained Hierarchy Spanning a Star
A polynomial-time algorithm computes a spanning hierarchy in a star S with a central node c satisfying the degree constraints. The outline is as follows:
- If , the star itself satisfies the degree constraint; there is nothing to do.
- If and there are more than two leaves with degree bound one in S and there is no node with a degree bound greater than two, there is no solution (cf. Theorem 1).
- Otherwise, we propose to cover S by a set of connected, degree constrained small stars.
In the last case, multiple occurrences of c are needed, and some edges are duplicated. Trivially, edges going to nodes in are not duplicated. For the duplication, the best cost edges are selected in ascending order. Each duplication of an edge links two occurrences of c. At most adjacent edges of w are possible. Each small star can cover at most leaves different from w. Some adjacent edges of the occurrences of c must be reserved for the connection to the parent star. An example of these small stars in a star is illustrated in Figure 7. The dotted lines indicate the connections to the parent star.
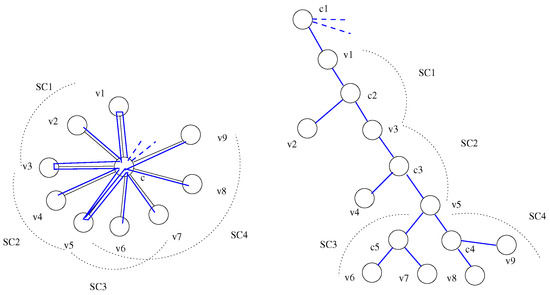
Figure 7.
Degree-constrained spanning hierarchy of a star.
5.2.4. The Connection of the Hierarchies
Let us suppose, that the spanning hierarchy of S with the central node c must be connected to the hierarchy spanning the parent star with the central node p. The edge is used times in . It is the number of adjacent edges of c in . Moreover, c has adjacent edges in . Finally, neighbor edges must be connected to c. If , a unique occurrence of c is sufficient for the connections. If , the first occurrence of c ensures the connections to the parent node p and edges in . The remaining edges in must be connected to the next occurrences of c in the defined order. If , the first occurrence of c can have only times occurrences of as adjacent edges and the last occurrence of is connected to the second occurrence of c, etc. In the example of Figure 7, and . The first occurrence of c is connected twice to (these connections are indicated with dashed lines).
As stated before, the heuristic does not work in cases where the conditions in Theorem 1 are not met in a star. This means that the proposed heuristic does not work in these cases, even if an eventual degree-constrained spanning hierarchy exists in the MSTSL.
6. Approximations
If there are only a small number of nodes in , guaranteed ratios can be found.
6.1. Case of
Theorem 4.
Let us suppose there is no node with a degree bound 1. The cost of a DCMSH can be approximated within a ratio , where .
Proof.
The proposed heuristic gives an approximation. Remember, the MSTSL T is decomposed into a set of edge-disjoint stars. Let us recall that in each star , a spanning hierarchy satisfying the degree constraint of the (possibly multiplied) central node can be built. Since , possible duplicates concern the best cost edges in . In the worst case, the leaves are in and only one return is possible from each leaf. The cost of the hierarchy spanning the star is bounded by where is the cost of the star (cf. [6]). The hierarchies spanning the k different stars can be connected, and a hierarchy H spanning the node set V and satisfying the degree constraints is obtained. With , since the cost of the spanning hierarchy is bounded:
□
In the worst case, the degree bound of all nodes is two, and the ratio of costs is also two. If there are nodes with large degree bounds, the heuristic computes hierarchies close to the optimum.
6.2. Case of
In this case, we suppose that is not empty but it contains at most two nodes that are not separators. We propose to analyze the case of , but the result is trivially true if there is only one node in .
Theorem 5.
In the case of at most two specified leaves in , the cost of a DCMSH can be approximated within a factor 2.
Proof.
Let a and b be the two nodes in and let T be an MSTSL having nodes a and b as leaves. Following T, a walk can be computed starting from a and ending at b. This walk W contains the edges of T at most twice and corresponds to a spanning hierarchy satisfying the degree constraints (the internal nodes in W have only degree 2). Finally, . □
If there are nodes with a degree bound greater than two, the heuristic proposed in Section 5.2 can return hierarchies with lower cost.
6.3. Case of
Unfortunately, in arbitrary graphs with , a bounded approximation ratio related to an MSTSL can not be guaranteed.
Remark 1.
Even if a DCMSH exists, it can not always be approximated by a constant factor compared to an MSTSL when .
To illustrate this remark, let us consider a simple star as follows. Let a be a leaf with a degree bound 3 and b the central node in the star with a degree bound 2. Let k nodes in be connected to the node b. So there is a feasible solution. Consider the cost of the edges leading to leaves in being w negligible compared to the cost of the edge . In this graph (cf. Figure 8), the MSTSL corresponds to the graph itself, and its cost is equal to . In the DCMSH (indicated in the figure), the possible branching nodes are occurrences of a. The cost of a path from a to an arbitrary leaf is . Since there are k leaves: . The ratio between the costs is as follows:
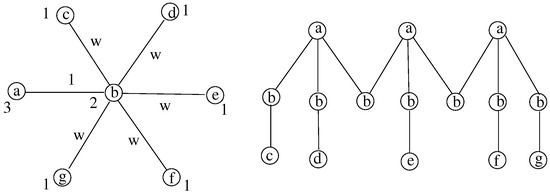
Figure 8.
A particular star and its DCMSH.
When w tends to zero, the lower bound tends to k. When k tends to infinity, the lower bound cannot be bounded by a constant.
Note that MSTSLs are not the only possible lower bounds of our problem. Whether or not an approximation related to another sub-graph (tree or spanning hierarchy computable in polynomial time) can be found is an open question.
7. Results, Evaluation of the Solutions
We compare four solutions (the MSTSL, the DCMSH, the DCMST, and the result of the heuristic) if they exist.
7.1. Materials and Methods
For the analysis, random graphs based on the model of Albert-Barabási [20] were generated. The algorithms are implemented in C++ using the Leda library [21]. The DCMSHs and DCMSTs were computed using the CPLEX Ilog server [22]. The heuristic and the computation of the MSTSL are in polynomial time, but the exact solutions need expensive computations. Fortunately, in the tested random graphs the computation of the exact solutions required from a few seconds to a few hours and was feasible.
Parameter Settings
In the experiment, some parameters were variable: the number of nodes in the random graphs, the degree bounds on the nodes, and the edge costs. Medium-size topologies were generated containing 80–170 nodes. Notice that the number of edges in the graphs was not deterministic, since the edges were generated randomly. In each experiment presented hereafter, we indicate the average number of edges. The degree bounds were set randomly from an interval using a uniform) distribution. The edge costs were also uniformly generated from the interval .
7.2. Discussion
7.2.1. Effect of the Degree Bounds
In the first experiment, we show the effect of the maximal degree bound varied from 3 to 12 when . The edge costs were randomly generated with . Table 2 resumes the graph properties, and also the number of cases in which trees and hierarchies corresponding to the constraints exist. In each run, 100 random graphs with 100 nodes were created.

Table 2.
Results by varying .
The average number of randomly generated edges was in each run. Trivially, the average number decreases by increasing . The column indicates the average number of arcs in the simplified digraph. The next two columns indicate the number of graphs satisfying the conditions for the existence of the DCMSHs (the number of hierarchies) and the number of DCMSTs, respectively. With a large set , there are fewer possible trees. The last columns contain the average costs of the four structures. It is clear that as increases, the costs converge to the same value. Probably, the cost converges towards the cost of the . The cost of the optimal hierarchies is always better or equal to the cost (if these solutions exist). By increasing , the probability of degree bounds one (and also of the other small degree bounds imposing real constraints on the degrees) decreases. Consequently, the difference between trees and hierarchies decreases and their costs tend to the cost of the MSTSL. Notice that the heuristic also provides good costs.
7.2.2. Effect of the Edge Costs
In this case, the number of nodes was fixed at 100 and was equal to 3. The edge costs were randomly generated from the interval , and the value of varied as indicated in Table 3.

Table 3.
Results by varying the edge costs.
Independently from the edge costs, the obtained typologies are relatively stable; and show a small variation. DCMST does not exist in 50–60% of cases and DCMSH does not exist in 10% of cases. The first lines of the results need explanation. Let us analyze the first line. If the DCMST exists (in 57 cases of 100 runs) the cost is equal to 99, which is the cost of the 99 edges needed to cover the 100 nodes. The average cost of DCMSHs is greater, but it is the average of 91 cases that contain hierarchies returning several times to some nodes (cases not covered by trees). The average of the maximal number of edge duplication is indicated in the column .
7.2.3. Varying the Size of the Graphs
A third series allows us to see the effect of the size of Albert-Barabási random graphs on the minimum spanning structures. The experiment is summarized in Table 4. The number of nodes varied from 80 to 170 nodes. was equal to 3 and to 5. It can be seen that the observed values increase almost linearly with the size of the graphs. For instance, let us compare the lines with 80 and 160 nodes. The average number of edges, the number of desired leaves in , and the cost are almost double. The number of DCMSHs and DCMSTs are mainly the same. Note that trees are 5–10% more expensive than hierarchies.

Table 4.
Results by varying the graph size.
8. Conclusions and Perspectives
In our study, new results on degree-constrained minimum spanning hierarchies in graphs with non-uniform capacity constraints are presented. DCMSHs can be built in several cases, where DCMSTs do not exist. An ILP-based exact solution and a heuristic are proposed for the NP-hard DCMSH problem. Certain approximation ratios are also discussed. As the solution does not always exist, the necessary and sufficient conditions for the existence are formulated.
Our study shows that the set of specified leaves with degree bound 1 is crucial for the properties of the solutions. If this set is large, the solution may not exist and the approximation within a constant is not trivial (we consider, it to be an open question). The DCMSH exists in several cases where the DCMST does not exist. The average cost of DCMSHs is lower than the average cost of DCMSTs. The weaker the constraints, the more the solution converges to the MST (or to the MSTSL). Note that the heuristic provides good results relatively close to the optimum.
In future work, the approximation of spanning hierarchy problems with different degree constraints in various graphs should be analyzed. We conjecture that in some cases, depending on the positions of leaves in , approximations can be found even if . Another important perspective is the analysis of partial spanning problems like degree-constrained Steiner problems. We believe that an important part of the results presented in this paper can be applied to partial spanning problems. Applications of the degree-constrained spanning hierarchies can be found, for instance in optical broadcast/multicast routing. In these applications, additional constraints (e.g., the uniqueness of the used wavelength in the fibers, limited length of paths, etc) exist, and various constraints must be fully satisfied. Analyzing these issues promises further interesting challenges.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Deo, N.; Hakimi, S. The shortest generalized Hamiltonian tree. In Proceedings of the Sixth Annual Allerton Conference, Monticello, IL, USA, 2–4 October 1968; pp. 879–888. [Google Scholar]
- Boldon, B.; Deo, N.; Kumar, N. Minimum-Weight Degree-Constrained Spanning Tree Problem: Heuristics and Implementation on an SIMD Parallel Machine. Parallel Comput. 1996, 22, 369–382. [Google Scholar] [CrossRef]
- Ravi, R.; Marathe, M.V.; Ravi, S.S.; Rosenkrantz, D.J.; Iii, H.B.H. Approximation algorithms for degree-constrained minimum-cost network-design problems. Algorithmica 2001, 31, 58–78. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, B. Optical WDM Networks (Optical Networks); Springer: Berlin/Heidelberg, Germany, 2006; pp. 26–27. [Google Scholar]
- Ali, M.; Deogun, J. Cost-effective implementation of multicasting in wavelength-routed networks. IEEE J. Light. Technol. Spec. Issue Opt. Netw. 2000, 18, 1628–1638. [Google Scholar] [CrossRef]
- Molnár, M.; Durand, S.; Merabet, M. Approximation of the Degree-Constrained Minimum Spanning Hierarchies. In Proceedings of the SIROCCO, Takayama, Japan, 23–25 July 2014; pp. 96–107. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Cieslik, D. The vertex degrees of minimum spanning trees. Eur. J. Oper. Res. 2000, 125, 278–282. [Google Scholar] [CrossRef]
- Könemann, J.; Ravi, R. A Matter of Degree: Improved Approximation Algorithms for Degree-Bounded Minimum Spanning Trees. SIAM J. Comput. 2002, 31, 1783–1793. [Google Scholar] [CrossRef]
- Könemann, J.; Ravi, R. Primal-Dual Meets Local Search: Approximating MSTs With Nonuniform Degree Bounds. SIAM J. Comput. 2005, 34, 763–773. [Google Scholar] [CrossRef]
- Ravi, R. Matching Based Augmentations for Approximating Connectivity Problems. In Proceedings of the 7th Latin American Symposium on Theoretical Informatics (LATIN’06), Valdivia, Chile, 20–24 March 2006; pp. 13–24. [Google Scholar]
- Ravi, R.; Singh, M. Delegate and Conquer: An LP-Based Approximation Algorithm for Minimum Degree MSTs. In Proceedings of the ICALP, Venice, Italy, 10–14 July 2006; pp. 169–180. [Google Scholar]
- Singh, M.; Lau, L.C. Approximating minimum bounded degree spanning trees to within one of optimal. In Proceedings of the STOC ’07: Proceedings of the Thirty-Ninth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 11–13 June 2007; pp. 661–670. [Google Scholar] [CrossRef]
- Fürer, M.; Raghavachari, B. Approximating the minimum-degree Steiner tree to within one of optimal. J. Algorithms 1994, 17, 409–423. [Google Scholar] [CrossRef]
- Russo, L.M.S.; Teixeira, A.S.; Francisco, A.P. Linking and Cutting Spanning Trees. Algorithms 2018, 11, 53. [Google Scholar] [CrossRef]
- Gao, X.; Jia, L. Degree-constrained minimum spanning tree problem with uncertain edge weights. Appl. Soft Comput. 2017, 56, 580–588. [Google Scholar] [CrossRef]
- Merabet, M.; Molnár, M.; Durand, S. ILP formulation of the degree-constrained minimum spanning hierarchy problem. J. Comb. Optim. 2018, 36, 789–811. [Google Scholar] [CrossRef]
- Singh, M.; Zenklusen, R. k-Trails: Recognition, Complexity, and Approximations. In Integer Programming and Combinatorial Optimization; Louveaux, Q., Skutella, M., Eds.; Springer: Liège, Belgium, 1–3 June 2016; pp. 114–125. [Google Scholar]
- Egawa, Y.; Matsuda, H.; Yamashita, T.; Yoshimoto, K. On a Spanning Tree with Specified Leaves. Graphs Comb. 2008, 24, 13–18. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Mehlhorn, K.; Näher, S. LEDA: A Platform for Combinatorial and Geometric Computing; Cambridge University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Cplex, I.I. V12. 1: User’s Manual for CPLEX. Int. Bus. Mach. Corp. 2009, 46, 157. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).