Abstract
The presented work outlines a new genetic crossover operator, which can be used to solve problems by the Grammatical Evolution technique. This new operator intensively applies the one-point crossover procedure to randomly selected chromosomes with the aim of drastically reducing their fitness value. The new operator is applied to chromosomes selected randomly from the genetic population. This new operator was applied to two techniques from the recent literature that exploit Grammatical Evolution: artificial neural network construction and rule construction. In both case studies, an extensive set of classification problems and data-fitting problems were incorporated to estimate the effectiveness of the proposed genetic operator. The proposed operator significantly reduced both the classification error on the classification datasets and the feature learning error on the fitting datasets compared to other machine learning techniques and also to the original models before applying the new operator.
1. Introduction
Genetic algorithms are stochastic optimization algorithms originated in the work of Holland [1]. They belong to a wide area of optimization algorithms called evolutionary techniques [2]. Genetic algorithms initiate by formulating candidate solutions of the objective problem. These solutions are evolved through a series of processes that mimic natural evolution, such as selection, crossover and mutation [3,4,5]. The genetic algorithms were incorporated in a variety of problems, such as networking problems [6], problems arising in robotics [7,8], energy problems [9,10], medicine problems [11,12], agriculture problems [13], etc.
Grammatical Evolution [14] is an integer-based genetic algorithm, where each chromosome represents a series of production rules derived from a Backus–Naur form (BNF) grammar [15]. Grammatical Evolution can be utilized to produce programs in the provided programming language. This method was used in a series of cases derived from real-world problems, such as data fitting [16,17], credit classification [18], detection of network attacks [19], solving differential equations [20], monitoring the quality of drinking water [21], construction of optimization methods [22], application in trigonometric problems [23], composition of music [24], constructing neural networks [25,26], computer games [27,28], problems regarding energy demand [29], combinatorial optimization [30], security topics [31], automatic construction of decision trees [32], circuit design [33], discovering taxonomies in Wikipedia [34], trading algorithms [35], bioinformatics [36], modeling glycemia in humans [37], etc.
Grammatical Evolution has been extended by many researchers in the recent bibliography. Among these extensions there are works, such as the Weighted Hierarchical Grammatical Evolution [38], which proposed a novel technique to map genotypes to phenotypes, or the method of Structured Grammatical Evolution [39,40]. Also, O’Neill et al. suggested the usage of shape grammars in the Grammatical Evolution for evolutionary design [41]. Also, the Grammatical Evolution method [42] was suggested as a modification of the Grammatical Evolution, where a position-independent mapping was proposed. Another interesting work was the incorporation of Particle Swarm Optimization (PSO) [43] to create expressions in Grammatical Evolution. This method was named Grammatical Swarm [44,45] in the relevant literature. Moreover, the method of Probabilistic Grammatical Evolution [46] has been introduced recently, where a stochastic procedure was used as a mapping mechanism. Recently, the optimization method of the Fireworks algorithm [47] was applied as a learning algorithm for the Grammatical Evolution procedure [48]. Contreras et al. suggested the combination of Grammatical Evolution and some ideas from interval analysis to solve problems with uncertainty [49]. Grammatical evolution has also been extended using programming techniques [50,51] or Christiansen grammars [52].
Additionally, many researchers have developed and published open source software for Grammatical Evolution, such as the graphical user interface (GUI) application of Grammatical Evolution in Java (GEVA) [53], a Java implementation called jGE [54], an R implementation of Grammatical Evolution under the name gramEvol [55], the GRAPE software version 1.0 that implemented Grammatical Evolution in Python [56], the GeLab [57] software that suggested a Matlab toolbox for Grammatical Evolution, a software which produced classification programs with Grammatical Evolution called GenClass [58], the QFc software version 1.0 [59] was incorporated for feature construction, etc.
In this work, a new genetic operator for Grammatical Evolution is introduced, which is derived from the one crossover technique. The new genetic operator is stochastically applied to the genetic population, randomly selecting a set of chromosomes on which to apply it. For each randomly selected chromosome, a group of chromosomes is stochastically formed from the current genetic population. Afterwards, a one-point crossover operation is performed between the selected chromosome and each of the generated groups to search for a lower value of the fitness function. The new genetic operator was applied in two distinct cases of Grammatical Evolution methods: in the rule construction technique introduced recently [60] and in the neural network construction technique [61]. These machine learning tools were applied on some classification and regression datasets proposed in the recent literature, and the experimental results indicated a reduction in classification or regression error from the application of the new genetic operator.
The main components of the proposed technique are outlined below:
- The method can be applied as a genetic operator to all problems solved by the Grammatical Evolution technique, and the only information it exploits is the fitness function of the problem.
- The method has no dependence on the grammar of the objective problem.
- By using an application rate, the user can require fewer or more applications of the new operator.
- Although this operator requires significant computing time for its execution, its application between chromosomes can be made using parallel techniques, since there is no dependency between its successive applications.
- Simple linear operations are required for its implementation, such as crossing a point between chromosomes.
- The new genetic operator could theoretically be applied to other forms of genetic algorithms beyond Grammatical Evolution.
2. Materials and Methods
2.1. Basics of the Grammatical Evolution Method
Grammatical Evolution considers chromosomes as a set of production rules in the provided BNF grammar. BNF grammar is usually denoted as a set with the following assumptions:
- N defines the set of non-terminal symbols.
- T is a set that contains the terminal symbols.
- S is a non-terminal symbol that corresponds to the start symbol of the grammar.
- P is the set of the rules used during production. These rules are in the form or . In the Grammatical Evolution procedure, a sequence number is assigned to every production rule.
The grammar used for the rule machine learning method is outlined in Figure 1 and the corresponding grammar for the neural network construction technique is displayed in Figure 2.

Figure 1.
The BNF grammar used in the method that constructs rules using the Grammatical Evolution procedure.

Figure 2.
The BNG grammar for the procedure of creating artificial neural networks with Grammatical Evolution.
The notation < > is used to enclose non-terminal symbols. The numbers at the end of the production rules represent the sequence number of each rule. The parameter d is the dimension of the used dataset (number of features). Grammatical Evolution produces valid expressions by starting from the starting symbol S and by following the production rules. The method selects the following production rules according to the following scheme:
- The next element denoted as V from the chromosome to be processed is retrieved.
- The next production rule is selected according to the formula.where the value NR represents the total number of production rules for the under processing non-terminal symbol.
For a dataset with three features , the following possible expression could be created for the case of the rule method:
The terminal symbol value is used to denote the final outcome of the rule method. For the same case, the following constructed neural network could be created:
This grammar of Figure 2 is able to produce artificial neural networks using this form:
The vector indicates the input vector and the vector stands for the parameter set of the neural network. The integer constant H denotes the number of weights or processing units. These networks have one processing level, but the grammar could be easily extended to produce neural networks of additional levels. The function used in the previous example denotes the sigmoid function given by
used in the majority of cases of neural networks. Of course, the Grammatical Evolution procedure can construct neural networks with different activation functions or neural networks that use a mix of activation functions.
2.2. The Genetic Algorithm
The two machine learning techniques, in which the new genetic operator was applied, follow a series of similar execution steps, which are presented in detail below:
- Initialization step.
- (a)
- Set as the generation counter.
- (b)
- Denote with the generations allowed and with the amount of chromosomes in the genetic population.
- (c)
- Denote with the used selection rate and with the used mutation rate .
- (d)
- Set as the rate for the application of the new crossover operator, where 1.
- (e)
- Set as the amount of chromosomes that will be chosen for each chromosome where the new crossover operator will be applied.
- Fitness step.
- Genetic operations.
- (a)
- Apply the selection procedure: In the first phase, a sorting is performed for the members of the genetic population according to the fitness of each chromosome. The best of these are transmitted unchanged to the next generation, while the rest will be replaced by chromosomes produced through crossover and mutation.
- (b)
- Execute the crossover procedure: During this procedure, offsprings are produced from the population under processing. For every set of produced children, two distinct chromosomes are chosen from the current population with tournament selection. The offsprings are formulated using the one-point crossover procedure, which is graphically outlined in Figure 3.
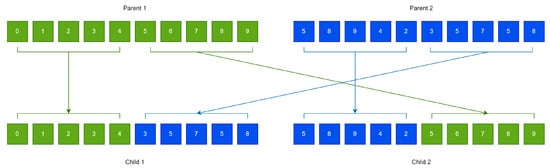 Figure 3. A working example for the production of children using the method of one-point crossover.
Figure 3. A working example for the production of children using the method of one-point crossover. - (c)
- Perform the mutation procedure. During this procedure, a random number is selected for each element of every chromosome, and this element is changed randomly if .
- (d)
- Apply the new crossover operator: For each chromosome , a random number is selected. If , then we execute the procedure described in Section 2.3 on .
- Termination step.
- (a)
- Set .
- (b)
- If go to Step 2, else terminate.
The previous algorithm is also graphically illustrated in the flowchart of Figure 4.
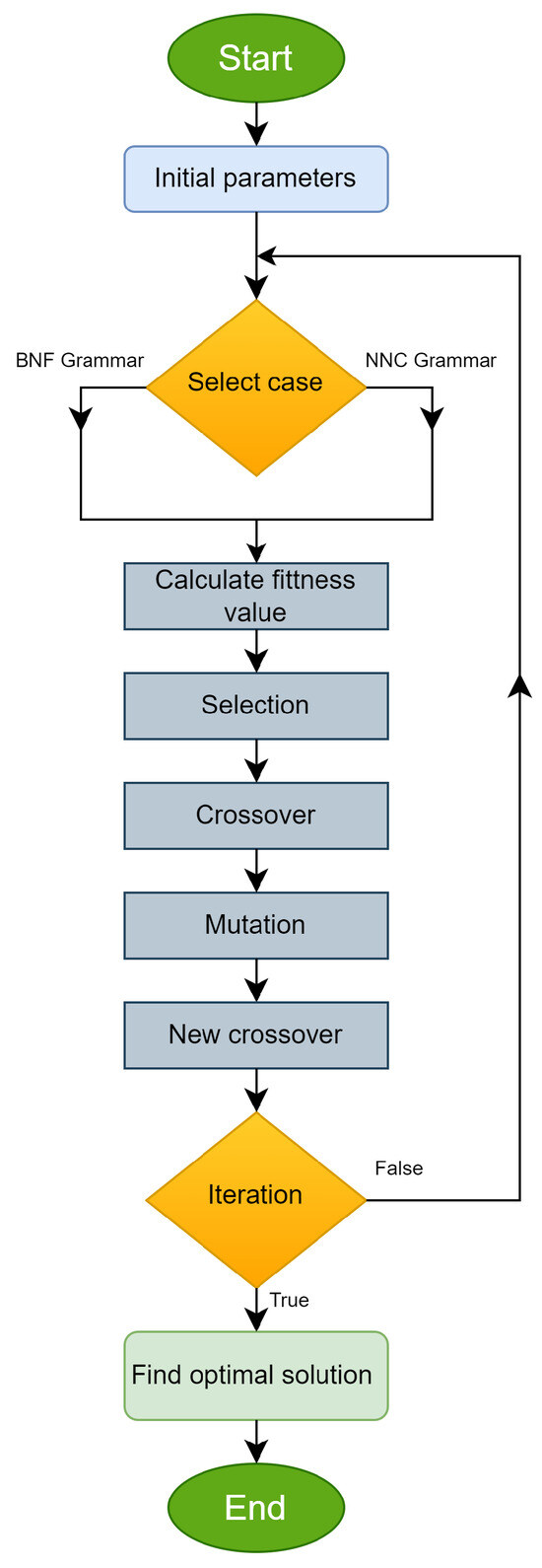
Figure 4.
The main steps of the incorporated genetic algorithm are presented as a flowchart.
2.3. The New Crossover Operator
The new crossover operator executes the one-point crossover method on a selected chromosome using a set of chromosomes that was selected randomly from the current population. The steps of the proposed operator are outlined below:
- Set as g the chromosome where the operator will be applied and as the corresponding fitness value.
- Create the set of randomly selected chromosomes.
- For do
- (a)
- Perform one-point crossover between g and . This procedure produces the offsprings and with associated fitness values and .
- (b)
- If then
- (c)
- else if then
- (d)
- Endif
- EndFor
3. Results
The suggested genetic operator was tested on a set of classification and regression datasets obtained from the recent bibliography and relevant websites. The internet sources for these datasets are the following websites:
- The UCI dataset repository, https://archive.ics.uci.edu/ml/index.php (accessed on 10 October 2024) [62];
- The Keel repository, https://sci2s.ugr.es/keel/datasets.php (accessed on 10 October 2024) [63];
- The Statlib URL http://lib.stat.cmu.edu/datasets/ (accessed on 10 October 2024).
3.1. The Used Classification Datasets
A wide series of datasets presenting classification problems is used here:
- Appendictis proposed in [64].
- Australian dataset proposed in [65].
- Balance dataset [66] used in a series of psychological experiments.
- Circular dataset, which is a dataset produced artificially.
- Cleveland dataset [67,68].
- Dermatology dataset [69], which is related to dermatological deceases.
- Ecoli dataset, which is related to protein problems [70].
- Fert dataset for the detection of possible relations between fertility and sperm concentration.
- Haberman dataset, which is used for breast cancer detection.
- Hayes roth dataset [71].
- Heart dataset [72], which is proposed for the detection of heart diseases.
- HeartAttack dataset, which is a medical dataset related to heart diseases.
- HouseVotes dataset [73], which contains the votes in the U.S. House of Representatives for various cases.
- Glass dataset, which contains glass component analysis for glass pieces that belong to six classes.
- Liverdisorder dataset [74], which is a medical dataset for the detection of liver disorders.
- Mammographic dataset [75], which is used in breast cancer detection.
- Parkinsons dataset, which is proposed in [76].
- Pima dataset [77], which is used in the detection of diabetes.
- Popfailures dataset [78], which is to do with climate-related measurements.
- Regions2 dataset, which is proposed in [79].
- Saheart dataset [80], which is proposed to detect heart diseases.
- Segment dataset [81], which contains information regarding image processing.
- Spiral dataset, which is a dataset created artificially.
- Student dataset [82], which is a dataset for measurements in schools.
- Wdbc dataset [83], which is used in cancer detection.
- Wine dataset, which contains information about wines [84,85].
- Eeg datasets, which is a medical dataset that contains measurements from various experiments regarding EEG [86]. The following subdatasets were extracted from this dataset: Z_F_S, Z_O_N_F_S, ZO_NF_S and ZONF_S.
- Zoo dataset [87], which is proposed to estimate the category of some animals.
3.2. The Used Regression Datasets
A series of datasets from this category was utilized in the current work:
- Abalone dataset [88].
- Airfoil dataset, which is provided by NASA [89].
- BK dataset [90], which is related to the prediction of points in a basketball game.
- BL dataset, which is related to calculations from electricity experiments.
- Baseball dataset, which is used to estimate the income of baseball players.
- Concrete dataset [91], which is a dataset related to the durability of cements in public works.
- Dee dataset, which is related to the prices of electricity.
- FY, which is a dataset that contains measurements for the longevity of fruit flies.
- HO dataset, which is provided from the the STALIB repository.
- Housing dataset [92].
- Laser dataset, which contains measurements from laser experiments.
- LW dataset, which contains measurements regarding the weight of babies.
- MORTGAGE, which contains economic measurements from USA.
- MUNDIAL, which is used from the STALIB repository.
- PL dataset, which is used from the STALIB repository.
- QUAKE dataset, which is used in measurements from earthquakes.
- REALESTATE, which is from the STALIB repository.
- SN dataset, which is used in an experiment related to trellising and pruning.
- Treasury dataset, which is a dataset regarding the economy of USA.
- TZ dataset, which is founded in the STALIB repository.
- VE dataset, which is from the STALIB repository.
3.3. Experimental Results
ANSI C++ was used to code the software for the conducted experiments using also the Optimus optimization environment, which is available from https://github.com/itsoulos/GlobalOptimus/ (accessed on 10 October 2024). The experiments were executed 30 times for each case, and the random number generator was initialized using different seeds in every execution. For the case of classification problems, the average classification error as measured on the test set was recorded and, for the case of regression datasets, the average regression error as measured on the test set was recorded. The validation of experiments was carried out using the method of ten-fold cross-validation. Table 1 depicts the experimental settings for the performed experiments.

Table 1.
This table presents the values used for the experimental parameters, which are used in the conducted experiments.
Table 2 outlines the results for the performed experiments on the classification datasets while Table 3 holds the results for the mentioned regression datasets. The following notations are used in the experimental tables:

Table 2.
This table shows the average classification error as calculated on the corresponding test set for the classification datasets using all machine learning models.

Table 3.
This table shows the experimental results when the regression datasets were used and the numbers stand for the average regression error as measured on the corresponding test set.
- The column BFGS represents the incorporation of the BFGS method [93] to train an artificial neural network with H hidden nodes.
- The column GEN outlines the experimental results using a genetic algorithm [94] to train an artificial neural network with H hidden nodes. The values for the critical parameters of the genetic algorithm are included in Table 1.
- The column RULE refers to the simple rule construction method [60] without the incorporation of the new crossover operator.
- The column NNC refers to the method of neural network construction [61]. This method was applied without the new operator.
- The column RULE_CROSS represents the application of the new crossover operator and the rule construction machine learning model.
- The column NNC_CROSS depicts the results for the neural construction method with the assistance of the new genetic operator.
- The average error is depicted in the row under the name AVERAGE.
There is a clear indication from the experimental results that there is a significant reduction in the mean error using the new genetic operator in both machine learning models. In a wide range of datasets, the proposed technique drastically reduces the error of data classification or fitting, as it is also represented in Figure 5 and Figure 6. These graphs show the number of datasets in which the application of the new genetic operator resulted in a drastic reduction in the corresponding error.
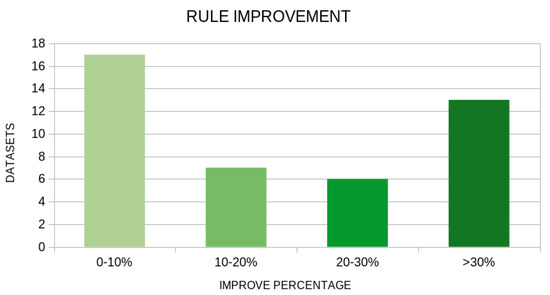
Figure 5.
Number of datasets that improved in the rule machine learning model using the proposed method. The vertical axis represents the number of datasets and the horizontal axis represents the percentage of reduction in error.
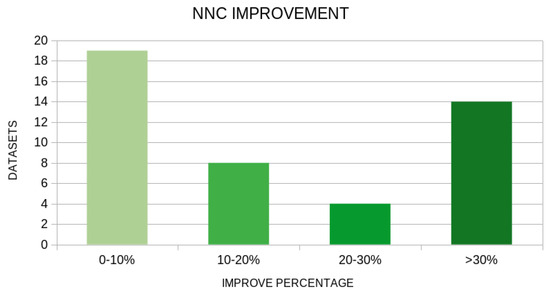
Figure 6.
Number of datasets that improved in the NNC machine learning model using the proposed method. The vertical axis represents the number of datasets and the horizontal axis represents the percentage of reduction in error.
Furthermore, the box plots for the classification cases are shown in Figure 7 and Figure 8 for the rule construction model and the network construction model, respectively.
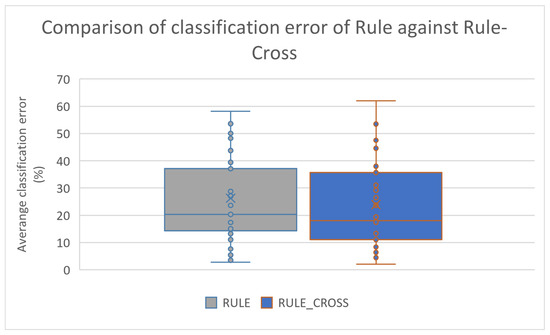
Figure 7.
Box plot for the comparison between the original rule construction model and the improved one that utilizes the new crossover operator.
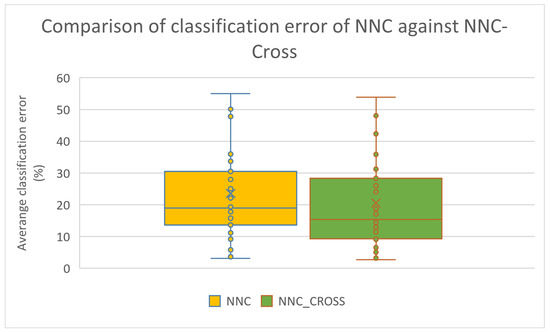
Figure 8.
Box plot used to compare the original rule construction model and the improved one that utilizes the new crossover operator.
Box plots for the same comparisons as deduced from the results using the series of regression datasets are shown in Figure 9 and Figure 10, respectively.
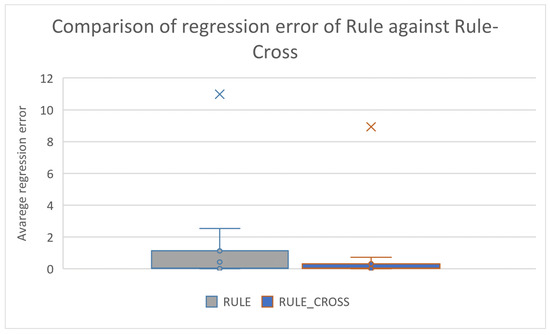
Figure 9.
Box plot used to compare the original rule construction model and the improved one that utilizes the new crossover operator for the regression datasets.
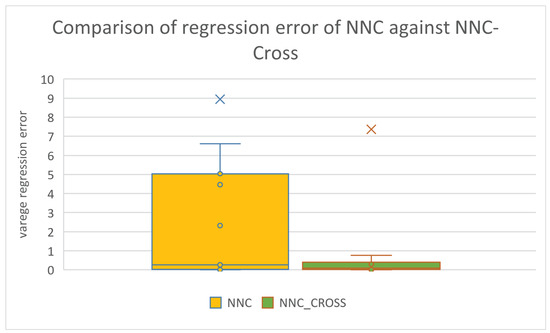
Figure 10.
Box plot used to compare the original neural network construction model and the improved one that utilizes the new crossover operator for the regression datasets.
These figures confirm the significant improvement brought about by the use of the new operator in the effectiveness of the two techniques that utilize Grammatical Evolution. This improvement appears to be greater in the datasets used in data fitting.
Also, a statistical comparison was performed using the two machine learning methods and the enhanced ones that use the new crossover operator. This comparison was performed using the classification datasets, and it is shown in Figure 11.
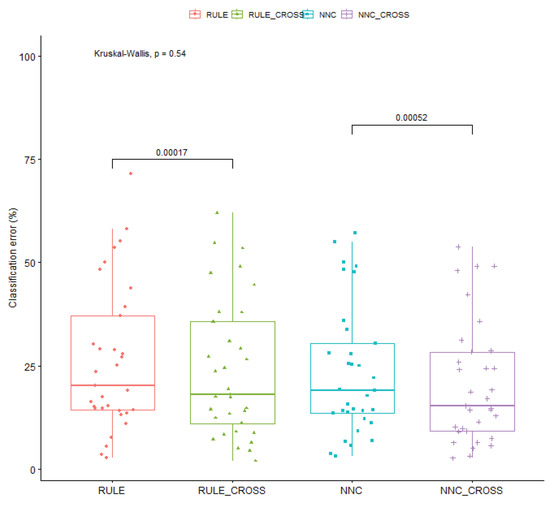
Figure 11.
Statistical test for all the improved machine learning methods and the original methods. The methods were tested on the classification datasets.
Moreover, an additional test was executed in order to estimate the effectiveness of the new crossover rate parameter denoted as . In this experiment, the rule construction machine learning model was applied on the classification datasets using a series of values for , and the results are shown in Table 4.

Table 4.
The effect of a series of values of to the rule model with application on the classification datasets.
Looking at the table of results, one can see a significant decrease in the average classification error when the application rate of the genetic operator increases from 2.5% to 5%. However, the rate of reduction of the average error decreases significantly when the application rate increases to 7.5%. This finding reinforces the idea of implementing the new genetic operator at a rate of 5%.
Another experiment was performed in order to estimate the importance of the parameter , which controls the number of chromosomes participating in the new crossover operator. In this experiment, the neural network construction method was tested on the classification datasets using a series of values for the parameter , while the parameter was fixed to 2.5%. The outcomes obtained from this experiment are depicted in Table 5.

Table 5.
The effects of the parameter to the NNC machine learning model. The classification datasets were used in this experiment. In all experiments, the value was set to 0.025.
The lowest average classification error is observed for ; however, no major changes are observed in the classification errors as the parameter increases. Furthermore, we expected the average execution time to increase as the value increases, and this is demonstrated in Figure 12, where the computation time for the neural network construction method is plotted with respect to the .
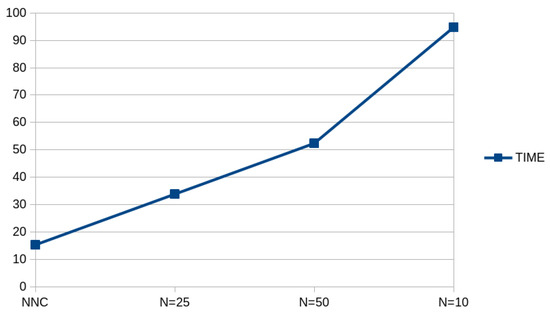
Figure 12.
Average execution time for the NNC machine learning model using different values of the value.
The average computation time increases dramatically as the critical parameter increases, which is something that is expected, since the crossings increase significantly with the increase in this parameter. This dramatic increase in required execution time can be reduced by incorporating modern parallel libraries. These programming techniques may include the application of the Message Passing Interface (MPI) library [95] or the incorporation of the OpenMP library [96].
4. Conclusions
A new genetic operator for tasks based on Grammatical Evolution is introduced in this article. This operator is applied to randomly selected chromosomes of the genetic population. On each application, a group of randomly selected chromosomes is formulated for every chromosome, and one-point crossover is executed between each member of the group and the selected chromosome, aiming to reduce the associated fitness value. In order to measure the effectiveness of the new operator, it was applied with success in two machine learning models from the recent bibliography that utilizes the Grammatical Evolution method:
- A rule construction method that constructs rules in language similar to the C programming language for data classification or regression problems.
- A method that constructs artificial neural networks.
Several datasets from the literature were used to test the proposed method. In the vast majority of cases, the application of the new genetic operator resulted in a drastic reduction in the corresponding classification or data fitting error. Furthermore, to asses the sensitivity of the proposed method to some critical parameters, more experiments were conducted in which these parameters were changed inside a wide range of values. Boosting these values improves the performance of machine learning methods by applying the new genetic operator but only up to a point. In addition, an increase in the chromosomes involved in the genetic operator has a significant increase in the required execution time, as was also seen in the performed experiments. However, with the use of recent techniques that can utilize modern parallel computing structures, this additional time can be significantly reduced.
Improvements of the proposed operator in future studies may include the application of the new crossover in other machine learning methods based on Grammatical Evolution, a parallel implementation of the operator or even the usage of this operator in other tasks involving Genetic Algorithms.
Author Contributions
V.C. and I.G.T. conducted the experiments, employing several datasets and provided the comparative experiments. D.T. and V.C. performed the statistical analysis and prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This research has been financed by the European Union: Next Generation EU through the Program Greece 2.0 National Recovery and Resilience Plan, under the call RESEARCH–CREATE–INNOVATE, project name “iCREW: Intelligent small craft simulator for advanced crew training using Virtual Reality techniques” (project code:TAEDK-06195).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Yusup, N.; Zain, A.M.; Hashim, S.Z.M. Evolutionary techniques in optimizing machining parameters: Review and recent applications (2007–2011). Expert Syst. Appl. 2012, 39, 9909–9927. [Google Scholar] [CrossRef]
- Stender, J. Parallel Genetic Algorithms: Theory & Applications; IOS Press: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Santana, Y.H.; Alonso, R.M.; Nieto, G.G.; Martens, L.; Joseph, W.; Plets, D. Indoor genetic algorithm-based 5G network planning using a machine learning model for path loss estimation. Appl. Sci. 2022, 12, 3923. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Chen, B. Genetic algorithm-based trajectory optimization for digital twin robots. Front. Bioeng. Biotechnol. 2022, 9, 793782. [Google Scholar] [CrossRef]
- Nonoyama, K.; Liu, Z.; Fujiwara, T.; Alam, M.M.; Nishi, T. Energy-efficient robot configuration and motion planning using genetic algorithm and particle swarm optimization. Energies 2022, 15, 2074. [Google Scholar] [CrossRef]
- Liu, K.; Deng, B.; Shen, Q.; Yang, J.; Li, Y. Optimization based on genetic algorithms on energy conservation potential of a high speed SI engine fueled with butanol–gasoline blends. Energy Rep. 2022, 8, 69–80. [Google Scholar] [CrossRef]
- Zhou, G.; Zhu, S.; Luo, S. Location optimization of electric vehicle charging stations: Based on cost model and genetic algorithm. Energy 2022, 247, 123437. [Google Scholar] [CrossRef]
- Doewes, R.I.; Nair, R.; Sharma, T. Diagnosis of COVID-19 through blood sample using ensemble genetic algorithms and machine learning classifier. World J. Eng. 2022, 19, 175–182. [Google Scholar] [CrossRef]
- Choudhury, S.; Rana, M.; Chakraborty, A.; Majumder, S.; Roy, S.; RoyChowdhury, A.; Datta, S. Design of patient specific basal dental implant using Finite Element method and Artificial Neural Network technique. J. Eng. Med. 2022, 236, 1375–1387. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, X. Design of intelligent control system for agricultural greenhouses based on adaptive improved genetic algorithm for multi-energy supply system. Energy Rep. 2022, 8, 12126–12138. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Backus, J.W. The Syntax and Semantics of the Proposed International Algebraic Language of the Zurich ACM-GAMM Conference. In Proceedings of the International Conference on Information Processing, UNESCO, Paris, France, 15–20 June 1959; pp. 125–132. [Google Scholar]
- Ryan, C.; Collins, J.; O’Neill, M. Grammatical evolution: Evolving programs for an arbitrary language. In Genetic Programming. EuroGP 1998; Lecture Notes in Computer Science; Banzhaf, W., Poli, R., Schoenauer, M., Fogarty, T.C., Eds.; Springer: Berlin/Heidelberg, Geremany, 1998; Volume 1391. [Google Scholar]
- O’Neill, M.; Ryan, M.C. Evolving Multi-line Compilable C Programs. In Genetic Programming. EuroGP 1999; Lecture Notes in Computer, Science; Poli, R., Nordin, P., Langdon, W.B., Fogarty, T.C., Eds.; Springer: Berlin/Heidelberg, Geremany, 1999; Volume 1598. [Google Scholar]
- Brabazon, A.; O’Neill, M. Credit classification using grammatical evolution. Informatica 2006, 30, 325–335. [Google Scholar]
- Şen, S.; Clark, J.A. A grammatical evolution approach to intrusion detection on mobile ad hoc networks. In Proceedings of the Second ACM Conference on Wireless Network Security, Zurich, Switzerland, 16–18 March 2009. [Google Scholar]
- Tsoulos, I.G.; Lagaris, I.E. Solving differential equations with genetic programming. Genet. Program Evolvable Mach. 2006, 7, 33–54. [Google Scholar] [CrossRef]
- Chen, L.; Tan, C.H.; Kao, S.J.; Wang, T.S. Improvement of remote monitoring on water quality in a subtropical reservoir by incorporating grammatical evolution with parallel genetic algorithms into satellite imagery. Water Res. 2008, 42, 296–306. [Google Scholar] [CrossRef]
- Tavares, J.; Pereira, F.B. Automatic Design of Ant Algorithms with Grammatical Evolution. In Genetic Programming. EuroGP 2012; Lecture Notes in Computer Science; Moraglio, A., Silva, S., Krawiec, K., Machado, P., Cotta, C., Eds.; Springer: Berlin/Heidelberg, Geremany, 2012; Volume 7244. [Google Scholar]
- Ryan, C.; O’Neill, M.; Collins, J.J. Grammatical evolution: Solving trigonometric identities. Proc. Mendel 1998, 111–119. [Google Scholar]
- Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic composition of music by means of grammatical evolution. In Proceedings of the 2002 Conference on APL: Array Processing Languages: Lore, Problems, and Applications, Madrid, Spain, 22–25 July 2002; pp. 148–155. [Google Scholar]
- De Campos, L.M.L.; de Oliveira, R.C.L.; Roisenberg, M. Optimization of neural networks through grammatical evolution and a genetic algorithm. Expert Syst. Appl. 2016, 56, 368–384. [Google Scholar] [CrossRef]
- Soltanian, K.; Ebnenasir, A.; Afsharchi, M. Modular Grammatical Evolution for the Generation of Artificial Neural Networks. Evol. Comput. 2022, 30, 291–327. [Google Scholar] [CrossRef]
- Galván-López, E.; Swafford, J.M.; O’Neill, M.; Brabazon, A. Evolving a Ms. PacMan Controller Using Grammatical Evolution. In Applications of Evolutionary Computation. EvoApplications 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Geremany, 2010; Volume 6024. [Google Scholar]
- Shaker, N.; Nicolau, M.; Yannakakis, G.N.; Togelius, J.; O’Neill, M. Evolving levels for Super Mario Bros using grammatical evolution. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 304–331. [Google Scholar]
- Martínez-Rodríguez, D.; Colmenar, J.M.; Hidalgo, J.I.; Micó, R.J.V.; Salcedo-Sanz, S. Particle swarm grammatical evolution for energy demand estimation. Energy Sci. Eng. 2020, 8, 1068–1079. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Grammatical Evolution Hyper-Heuristic for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 840–861. [Google Scholar] [CrossRef]
- Ryan, C.; Kshirsagar, M.; Vaidya, G.; Cunningham, A.; Sivaraman, R. Design of a cryptographically secure pseudo random number generator with grammatical evolution. Sci. Rep. 2022, 12, 8602. [Google Scholar] [CrossRef]
- Pereira, P.J.; Cortez, P.; Mendes, R. Multi-objective Grammatical Evolution of Decision Trees for Mobile Marketing user conversion prediction. Expert Syst. Appl. 2021, 168, 114287. [Google Scholar] [CrossRef]
- Castejón, F.; Carmona, E.J. Automatic design of analog electronic circuits using grammatical evolution. Appl. Soft Comput. 2018, 62, 1003–1018. [Google Scholar] [CrossRef]
- Araujo, L.; Martinez-Romo, J.; Duque, A. Discovering taxonomies in Wikipedia by means of grammatical evolution. Soft Comput. 2018, 22, 2907–2919. [Google Scholar] [CrossRef]
- Martín, C.; Quintana, D.; Isasi, P. Grammatical Evolution-based ensembles for algorithmic trading. Appl. Soft Comput. 2019, 84, 105713. [Google Scholar] [CrossRef]
- Moore, J.H.; Sipper, M. Grammatical Evolution Strategies for Bioinformatics and Systems Genomics. In Handbook of Grammatical Evolution; Ryan, C., O’Neill, M., Collins, J., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Hidalgo, J.I.; Colmenar, J.M.; Risco-Martin, J.L.; Cuesta-Infante, A.; Maqueda, E.; Botella, M.; Rubio, J.A. Modeling glycemia in humans by means of grammatical evolution. Appl. Soft Comput. 2014, 20, 40–53. [Google Scholar] [CrossRef]
- Bartoli, A.; Castelli, M.; Medvet, E. Weighted Hierarchical Grammatical Evolution. IEEE Trans. Cybern. 2020, 50, 476–488. [Google Scholar] [CrossRef]
- Lourenço, N.; Pereira, F.B.; Costa, E. Unveiling the properties of structured grammatical evolution. Genet. Program. Evolvable Mach. 2016, 17, 251–289. [Google Scholar] [CrossRef]
- Lourenço, N.; Assunção, F.; Pereira, F.B.; Costa, E.; Machado, P. Structured grammatical evolution: A dynamic approach. In Handbook of Grammatical Evolution; Springer: Cham, Switzerland, 2018; pp. 137–161. [Google Scholar]
- O’Neill, M.; Swafford, J.M.; McDermott, J.; Byrne, J.; Brabazon, A.; Shotton, E.; Hemberg, M. Shape grammars and grammatical evolution for evolutionary design. In Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation, Montreal, QC, Canada, 8–12 July 2009; pp. 1035–1042. [Google Scholar]
- O’Neill, M.; Brabazon, A.; Nicolau, M.; Garraghy, S.M.; Keenan, P. πGrammatical Evolution. In Genetic and Evolutionary Computation—GECCO 2004; GECCO 2004; Lecture Notes in Computer Science; Deb, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3103. [Google Scholar]
- Poli, R.; Kennedy, J.K.; Blackwell, T. Particle swarm optimization: An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- O’Neill, M.; Brabazon, A. Grammatical swarm: The generation of programs by social programming. Nat. Comput. 2006, 5, 443–462. [Google Scholar] [CrossRef]
- Ferrante, E.; Duéñez-Guzmán, E.; Turgut, A.E.; Wenseleers, T. GESwarm: Grammatical evolution for the automatic synthesis of collective behaviors in swarm robotics. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 17–24. [Google Scholar]
- Mégane, J.; Lourenço, N.; Machado, P. Probabilistic Grammatical Evolution. In Genetic Programming. EuroGP 2021; Lecture Notes in Computer Science; Hu, T., Lourenço, N., Medvet, E., Eds.; Springer: Cham, Switzerland, 2021; Volume 12691. [Google Scholar]
- Tan, Y.; Zhu, Y. Fireworks algorithm for optimization. In ICSI 2010; Tan, Y., Shi, Y., Tan, K.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Part I, LNCS; Volume 6145, pp. 355–364. [Google Scholar]
- Si, T. Grammatical Evolution Using Fireworks Algorithm. In Proceedings of the Fifth International Conference on Soft Computing for Problem Solving; Advances in Intelligent Systems and Computing. Pant, M., Deep, K., Bansal, J., Nagar, A., Das, K., Eds.; Springer: Singapore, 2016; Volume 436. [Google Scholar] [CrossRef]
- Contreras, I.; Calm, R.; Sainz, M.A.; Herrero, P.; Vehi, J. Combining Grammatical Evolution with Modal Interval Analysis: An Application to Solve Problems with Uncertainty. Mathematics 2021, 9, 631. [Google Scholar] [CrossRef]
- Popelka, O.; Osmera, P. Parallel Grammatical Evolution for Circuit Optimization. In Evolvable Systems: From Biology to Hardware. ICES 2008; Lecture Notes in Computer Science; Hornby, G.S., Sekanina, L., Haddow, P.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5216. [Google Scholar] [CrossRef]
- Ošmera, P. Two level parallel grammatical evolution, In Advances in Computational Algorithms and Data Analysis; Springer: Dordrecht, The Netherlands, 2009; pp. 509–525. [Google Scholar]
- Ortega, A.; de la Cruz, M.; Alfonseca, M. Christiansen Grammar Evolution: Grammatical Evolution with Semantics. IEEE Trans. Evol. Comput. 2007, 11, 77–90. [Google Scholar] [CrossRef]
- O’Neill, M.; Hemberg, E.; Gilligan, C.; Bartley, E.; McDermott, J.; Brabazon, A. GEVA: Grammatical evolution in Java. ACM SIGEVOlution 2008, 3, 17–22. [Google Scholar] [CrossRef]
- Georgiou, L.; Teahan, W.J. jGE-A java implementation of grammatical evolution. In Proceedings of the 10th WSEAS International Conference on Systems, Athens, Greece, 10–12 July 2006. [Google Scholar]
- Noorian, F.; de Silva, A.M.; Leong, P.H.W. gramEvol: Grammatical Evolution in R. J. Stat. Softw. 2016, 71, 1–26. [Google Scholar] [CrossRef]
- de Lima, A.; Carvalho, S.; Dias, D.M.; Naredo, E.; Sullivan, J.P.; Ryan, C. GRAPE: Grammatical Algorithms in Python for Evolution. Signals 2022, 3, 642–663. [Google Scholar] [CrossRef]
- Raja, M.A.; Ryan, C. GELAB—A Matlab Toolbox for Grammatical Evolution. In Intelligent Data Engineering and Automated Learning—IDEAL 2018; IDEAL, 2018; Lecture Notes in Computer Science; Yin, H., Camacho, D., Novais, P., Tallón-Ballesteros, A., Eds.; Springer: Cham, Switzerland, 2018; Volume 11315. [Google Scholar] [CrossRef]
- Anastasopoulos, N.; Tsoulos, I.G.; Tzallas, A. GenClass: A parallel tool for data classification based on Grammatical Evolution. SoftwareX 2021, 16, 100830. [Google Scholar] [CrossRef]
- Tsoulos, I.G. QFC: A Parallel Software Tool for Feature Construction, Based on Grammatical Evolution. Algorithms 2022, 15, 295. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Learning Functions and Classes Using Rules. AI 2022, 3, 751–763. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Kelly, M.; Longjohn, R.; Nottingham, K. The UCI Machine Learning Repository. 2023. Available online: https://archive.ics.uci.edu (accessed on 18 February 2024).
- Alcalá-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: Burlington, VT, USA, 1991. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Horton, P.; Nakai, K. A Probabilistic Classification System for Predicting the Cellular Localization Sites of Proteins. In Proceedings of the International Conference on Intelligent Systems for Molecular Biology, St. Louis, MO, USA, 12–15 June 1996; Volume 4, pp. 109–115. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, F. Concept learning and the recognition and classification of exemplars. J. Verbal Learn. Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Symposium on Computer Applications and Medical Care; IEEE Computer Society Press: Washington, DC, USA, 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 5 November 2015; pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C (Appl. Stat.) 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Cortez, P.; Silva, A.M.G. Using data mining to predict secondary school student performance. In Proceedings of the 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008), EUROSIS-ETI, Porto Alegre, Brazil, 9–11 April 2008; pp. 5–12. [Google Scholar]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef]
- Raymer, M.L.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. Publ. IEEE Syst. Cybern. Soc. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 1–8. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (Haliotis species) in Tasmania. I. Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait; Sea Fisheries Division; Technical Report 48; Sea Fisheries Division, Department of Primary Industry and Fisheries: Orange, NSW, Australia, 1994.
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction. Technical Report; NASA RP-1218; NTRS: Hampton, VA, USA, 1989. [Google Scholar]
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Yeh, I.C. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Chandra, R. Parallel Programming in OpenMP; Morgan Kaufmann: Cambridge, MA, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).