Abstract
Advances in the early detection of breast cancer and treatment improvements have significantly increased survival rates. Traditional screening methods, including mammography, MRI, ultrasound, and biopsies, while effective, often come with high costs and risks. Recently, thermal imaging has gained attention due to its minimal risks compared to mammography, although it is not widely adopted as a primary detection tool since it depends on identifying skin temperature changes and lesions. The advent of machine learning (ML) and deep learning (DL) has enhanced the effectiveness of breast cancer detection and diagnosis using this technology. In this study, a novel interpretable computer aided diagnosis (CAD) system for breast cancer detection is proposed, leveraging Explainable Artificial Intelligence (XAI) throughout its various phases. To achieve these goals, we proposed a new multi-objective optimization approach named the Hybrid Particle Swarm Optimization algorithm (HPSO) and Hybrid Spider Monkey Optimization algorithm (HSMO). These algorithms simultaneously combined the continuous and binary representations of PSO and SMO to effectively manage trade-offs between accuracy, feature selection, and hyperparameter tuning. We evaluated several CAD models and investigated the impact of handcrafted methods such as Local Binary Patterns (LBP), Histogram of Oriented Gradients (HOG), Gabor Filters, and Edge Detection. We further shed light on the effect of feature selection and optimization on feature attribution and model decision-making processes using the SHapley Additive exPlanations (SHAP) framework, with a particular emphasis on cancer classification using the DMR-IR dataset. The results of our experiments demonstrate in all trials that the performance of the model is improved. With HSMO, our models achieved an accuracy of 98.27% and F1-score of 98.15% while selecting only 25.78% of the HOG features. This approach not only boosts the performance of CAD models but also ensures comprehensive interpretability. This method emerges as a promising and transparent tool for early breast cancer diagnosis.
1. Introduction
Breast cancer is a profoundly distressing disease. Screening programs for early breast disease detection significantly contribute to reductions in the mortality rate among women. These programs save lives by detecting conditions at their initial stages when treatment is more effective and less costly. Medical imaging modalities are employed for breast cancer diagnosis, as well as the differentiation of malignant from benign breast tumors, including mammography, magnetic resonance imaging (MRI), ultrasound, computed tomography (CT), positron emission tomography (PET), and thermography. Mammography, while widely used, presents specific limitations. These include challenges in visualizing smaller tumors [1], inadvisability for use in younger women and those with dense breast tissues [2], considerable cost and time requirements [3], and physical discomfort due to breast compression. Moreover, concerns about the potential carcinogenic effects of cumulative ionizing radiation exposure have been raised [4]. The high incidence of false-positive results further contributes to patient anxiety and unnecessary procedures [5]. In this context, Infrared Thermography has emerged as a promising and robust screening tool for early cancer detection [6,7]. Thermography offers distinct advantages, such as being painless, non-invasive, non-contact, and cost-effective [8]. Notably, it is particularly well suited for screening younger women, patients with dense breast tissue, and pregnant or nursing women, as it does not involve ionizing radiation exposure [9].
In health systems, breast cancer diagnostics have benefited from computer-aided diagnosis (CAD) systems, streamlining the analysis process and minimizing errors. These systems typically consist of several steps, from image preprocessing to classification, where feature extraction and selection play vital roles. Extracting pertinent features is essential for capturing subtle patterns indicative of early-stage breast cancer, whether through meticulously crafted methods or advanced deep learning approaches [10]. However, the current narrative predominantly emphasizes the accuracy and automation aspects of these systems, often achieved by training models on extensive datasets to recognize patterns in medical data. Yet, amid these advancements, there exists a notable gap in the discourse—the lack of attention to model interpretability [11]. In this paper, we proposed an interpretable computer-aided diagnosis (CAD) while delving into the relationship between pattern recognition and machine learning. Understanding this connection is paramount in addressing the complexity of medical data. Pattern recognition, within its broader domain, is fundamentally concerned with identifying regularities or inherent patterns within datasets. This field embraces a wide array of techniques and methods designed to identify patterns across various data types, spanning images, signals, and sequences. The attainment of pattern recognition can be realized through two primary approaches: manual and automated. Manual pattern recognition often relies on human expertise and heuristic approaches [12], depending on the nuanced judgment of experts to identify patterns, while automated pattern recognition employs computational methods to autonomously detect and outline patterns embedded within the data [13]. Machine learning, a subset of artificial intelligence, is exclusively dedicated to developing algorithms and statistical models that empower computers to learn from data and subsequently make predictions or decisions, encompassing a vast spectrum of techniques, including supervised learning, unsupervised learning, reinforcement learning, and hybrid methodologies.
On the other hand, healthcare professionals need to understand how AI systems arrive at their recommendations or decisions, especially when these decisions can have significant real-world impacts. In the context of synergy between pattern recognition and machine learning, Explainable Artificial Intelligence (XAI) can be used to understand the rules that are generated. The inherent non-human-interpretable nature of AI models has led to limited work aimed at developing models that can effectively elucidate their decision-making processes and actions [14].
The evolution and role of XAI have significantly shaped the healthcare industry, offering transparency and trustworthiness in AI-assisted medical diagnoses [15], which is essential for gaining acceptance and facilitating collaboration between AI systems and medical professionals (Figure 1)
Figure 1.
The evolution and role of XAI in decision making by stakeholders.
The insights gained by leveraging the integration of machine learning, pattern recognition, and XAI hold significant potential in the domain of medical image analysis for breast cancer detection; each of these fields consists of several processes. One approach that enhances this integration is the use of metaheuristics, which employ techniques inspired by nature to perform abstract optimization [16]. Although a limited number of studies have explored breast cancer thermogram diagnosis using optimization algorithms, the review article [17] presents an overview of advancements in this field.
The authors of this paper are also aware of the ongoing debate surrounding metaheuristic-based optimization [18]. In order to address some of those concerns while employing these algorithms, our work stands as a significant contribution to this research area:
- Our primary goals encompass the comprehensive solution to the challenges of achieving dynamic optimization problems. The development of Hybrid PSO (HPSO) and Hybrid SMO (HSMO) methodologies for tackling continuous variable optimization and discrete problems. The proposed approaches allow the optimization algorithm to ensure effective solutions in a varied search space.
- Harnessing the power of multi-objective optimization techniques, the proposed optimizers aim to provide a deeper understanding of model behavior across varying problem formulations. We used multi-objective ML approaches to strive to optimize multiple aspects of model performance simultaneously. These include hyperparameter optimization, prediction performance, sparseness, and interpretability.
- Through our research, the automated aspects on finding textures and features through machine learning-based optimization functions that best represent breast cancer classification patterns by producing handcrafted features from breast thermogram images using different methods, such as LBP, HOG, Gabor and canny edge and SVM for classification, are employed.
- Using visual explanation techniques that generate interpretable graphical representations enables healthcare practitioners to intuitively grasp the rationale behind each classification, making complex patterns associated with breast thermograms more comprehensible.
- The proposed HSMO and HPSO optimizer incorporates the SHapley Additive exPlanations (SHAP) framework into the evaluation process; this method ensures that the importance of different features is considered. This method adds another layer of complexity and variation to the solutions being explored.
- The other goal of this paper is to evaluate the convergence behaviors of distinct metaheuristic algorithms (HPSO, HSMO, Binary Particle Swarm Optimization algorithm (BPSO), and Binary Spider Monkey Optimization algorithm (BSMO) to identify similarities and differences in their solutions and second, to ensure consistent results upon repeated runs.
2. Related Work
Machine learning models and deep neural networks are often characterized as “black box” models due to their high complexity, resulting in a lack of readily available explanations for their predictions [15]. While these models excel in accuracy, understanding the rationale behind a specific prediction can be a formidable challenge.
Many papers focus on the automation aspects of using AI for breast cancer classification through thermal imaging. For example, Abdel-Nasser et al. [19] introduced a novel learning-to-rank (LTR) method combined with handcrafted features. By utilizing HOG with 288 feature vectors, their method achieved an accuracy of 95.80% using a Multi-Layer Perceptron (MLP) classifier. Different DL methods have been applied to the DMR-IR dataset. Resmini et al. [20] used textural and spectral features. The relevant features were selected by a Genetic Algorithm (GA). The model achieved an accuracy of 96.15% on the DMR-IR dataset. Gonçalves et al. [21] applied Particle Swarm Optimization (PSO) to optimize the hyperparameters of a CNN model named VGG-16. Pramanik et al. [22] extracted features using a SqueezeNet 1.1 model and a hybrid of the Genetic Algorithm (GA) and Grey Wolf Optimizer (GWO) for feature selection, achieving an accuracy of 100%. Ensaafi et al. [23] applied transfer-based deep learning methods on a static DMR-IR dataset, trained by fusing several views of thermograms. The dataset included 239 images of healthy individuals and 232 images of sick individuals. Their model achieved an accuracy of 93%.
Nevertheless, there are relatively few papers focusing on methods used to aid and assist healthcare professionals or lay individuals in understanding the predictions of machine learning models in breast thermogram images. In a recent study [24,25], authors proposed an approach based on Bayesian networks (BNs) with CNNs. The authors emphasize the utilization of a BN, which is renowned for its probabilistic and graphical data representation to enhance the interpretability of model predictions. These models extract relevant features from thermography images, which Bayesian networks can then interpret to make informed and explainable diagnostic decisions. In a study conducted by Nicandro et al. [26], the goal was to evaluate the diagnostic capability of thermographic variables for distinguishing patients suspected of having breast cancer from healthy individuals. The paper employs Bayesian networks for analysis, chosen for their ability to reveal interactions between attributes and classes and interactions among attributes themselves. This unique capability allows for a visual identification of which attributes influence the outcome and how they are interconnected. The results indicate that, while other models like Multi-Layer Perceptrons (MLP) and decision trees demonstrate a comparable performance, they lack explanation power. The paper suggests that a deep CNN with transfer learning achieves sensitivity levels similar to those of human experts, even in datasets with a low prevalence of breast cancer. A paper by Dey et al. [27] suggests that a hybrid of deep CNNs and edge detectors can achieve sensitivity levels comparable to those of human experts, even in datasets with a low prevalence of breast cancer. Additionally, they utilized Class Activation Mapping (CAM) into the model. While the paper does not explicitly mention the integration of external interpretability beyond CAM, CAM itself serves as a form of explainability by highlighting the regions of interest in the thermograms that contribute to the network’s decision-making process.
Considering the advancements of AI for breast cancer detection using thermography, there remains a crucial avenue for improvement, where the scope is placed on optimization-based metaheuristics, a research topic that has garnered significant public attention. Furthermore, the demand for elucidating the distinctive contributions of specific models to predictions is more critical than ever. This paper undertakes the challenge of addressing these pivotal aspects and aims to open new research directions by providing an interpretable CAD system capable of handling complex, evolving problems, human interpretability, and feature attributions.
3. Methodology
A multi-step methodology is involved in the proposed CAD architecture. While using LBP as a feature extractor, the complete pipeline is indicated in Figure 2 as follows. The preprocessing of breast thermograms is followed by a feature extraction using various texture analysis methods. Next, the extracted features and their histograms are visualized to understand the initial feature vector distribution. Subsequently, the multi-objective function can be used with the proposed optimizers HPSO and HSMO to identify the optimal model contributing significantly to the classification task.
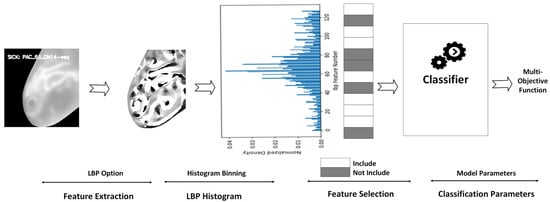
Figure 2.
Pipeline representation.
Furthermore, recognizing the importance of optimizing model parameters to enhance classification performance, we employed an objective function to ensure optimal performance.
3.1. Dataset Description
This research used images sourced from the Database for Mastology Research with Infrared Image (DMR-IR) developed by silva et al. [28]. This database contains both Static Infrared Thermography (SIT) and Dynamic Infrared Thermography (DIT) images, with our focus on DIT images. The imaging protocol involves patients standing with their hands on their heads for five minutes. During this period, an electric fan cools the breast and armpit regions in a controlled temperature environment ranging from 20 °C to 22 °C. Following the cooling phase, a FLIR thermal camera (model SC620) captures 20 DIT images, each with dimensions of 640 × 480 pixels.
This dataset is a comprehensive collection of individual cases designed for breast cancer detection, with each case linked to a unique ID. It offers diversity in terms of age and demographics, encompassing a broad spectrum of breast cancer risk factors. Each case comprises multiple images. The dataset is segregated into two folders: “old” cases (Desenvolvimento da Metodologia) and “new” cases (12 Novos Casos de Testes), as shown in Table 1. Notably, each ID in the dataset is labeled as either “healthy” or “sick”. Healthy IDs feature images from both the right and left sides of the chest, whereas sick IDs exclusively contain images of the affected side due to the differences in temperature gradients between healthy and sick breasts. The conventional approach treats the data as a collection of images split into train/test/validation sets based on predefined ratios [29]. However, this approach introduces a level of data leakage into trained models since each patient ID can have images in multiple sets, potentially causing overlap between the test and training sets. To mitigate this data leakage issue, we propose creating splits based on patient IDs, where each ID’s images are associated with one of the possible data splits. The division into test and training sets is initially performed based on IDs and subsequently on their associated images. To achieve this goal with our proposed approach, we initially gather the IDs and subsequently divide the ID pool into train/test sets, as illustrated in Figure 3. The dataset was split using a 70–30 train–test split ratio. This split resulted in 1060 samples allocated for training and 462 samples allocated for testing.

Table 1.
Details about dataset classes.
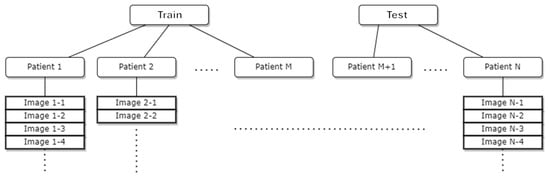
Figure 3.
Process of gathering IDs and division into train–test sets in DMR-IR database.
3.2. Data Pre-Processing
The pre-processing steps involved several stages to prepare the images for analysis and interpretability. Initially, the heat gradient files were converted into an image format to ensure consistency and compatibility with standard image processing techniques. Next, experts manually segmented the full thermogram images into the chest region, a step included with the dataset. Subsequently, previously segmented grayscale images were cropped to eliminate extraneous regions along each axis. Before feature extraction, the grayscale version of the input image was resized to a standardized dimension of 240 × 240 pixels to ensure uniformity. Post-feature extraction, an optional normalization, and a rounding step were included, where the features were scaled based on a precomputed scaler from a training dataset. Finally, the selected features were fed into downstream machine learning models for classification.
3.3. Feature Extraction
The feature extraction process is a crucial step in our methodology, enabling the transformation of raw image data into a structured format suitable for machine learning models. We utilize a range of algorithms, namely Histogram of Oriented Gradients (HOG) [30], Local Binary Pattern (LBP) [31], Gabor Filters [32], and Canny Edge Detection [33]. This diversified strategy aims to capture a comprehensive set of features, taking advantage of each algorithm’s unique characteristics. The Local Binary Pattern (LBP) encodes the local structure of an image by comparing the intensity of each pixel with its neighboring pixels, providing a robust representation of texture patterns. Gabor Filters analyze an image’s spatial features by capturing the occurrences of pixel patterns with particular intensity values at specific orientations and scales, providing valuable information about the image’s texture and structure. The Histogram of Oriented Gradients (HOG) divides an image into small regions, computes the gradient and orientation information for each pixel, and then creates a histogram of gradient orientations, capturing the underlying structure of objects. The Canny Edge Detection employs a multi-stage algorithm involving gradient computation, non-maximum suppression, and edge tracking with hysteresis to accurately identify and trace edges in an image.
It is important to note that the parameters associated with each algorithm are not fixed but are subject to optimization. This flexible approach recognizes the complexity of the dataset, allowing for the fine-tuning of parameters to enhance the performance of the feature extraction process.
Depending on the extractor, the feature vectors are subsequently extracted by dividing all values into N histogram bins, translating each image in the dataset to a feature vector of N length, and a feature length of 128 is constructed where each feature is a bin of values representing the frequency or count of a specific pattern in the image. Figure 4 offers sample extractions from each method and their captured data distribution, visually depicting their differences.
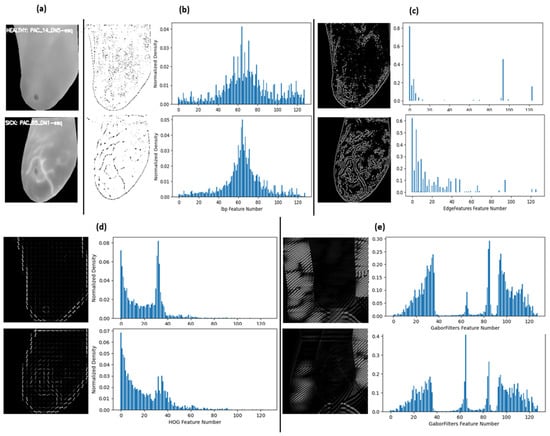
Figure 4.
Sample feature extract image and their distributions (a) original cropped image: top left healthy sample and bottom left sick sample; (b) LBP; (c) Canny edges; (d) HOG; and (e) Gabor filter.
The most notable aspect in these samples is that each extractor converted the images into unique sets of feature distributions as well, where the distinctive patterns of classification became varied. This variety was intentional to determine whether the features would align visually when different extractors undergo optimization through metaheuristic algorithms.
3.4. The Proposed Metaheuristic-Based Feature and Hyperparameter Optimization
The metaheuristic algorithms used in our study consist of Spider Monkey optimization [34] and Particle Swarm [35]. The Spider Monkey Optimization (SMO) is a nature-inspired algorithm that draws inspiration from the cooperative foraging behavior of spider monkeys. The SMO leverages the concepts of exploration and exploitation to search for optimal solutions in a solution space. The algorithm involves the establishment of a population of potential solutions, and through successive iterations, it refines and evolves these solutions based on the fitness of each candidate. In its binary version, a Boolean operator is used to accomplish this task of transferring continuous solutions in each dimension, which forces the monkey to discretize their movement, representing the presence or absence of a certain feature or decision. The Binary SMO (BSMO) was proposed by Singh et al. [36].
Particle Swarm Optimization (PSO) is a population-based optimization algorithm that simulates the social behavior of birds or fish. Individuals in the population, referred to as particles, traverse the search space, adjusting their positions based on personal experience and the best positions found by their peers. PSO is particularly effective for continuous optimization problems, where variables can take any real value. This algorithm was adapted to work in the binary search space using Binary (BPSO) [37]. The algorithm is known for its simplicity and ability to explore the solution space efficiently. To find a diverse set of optimal solutions for multi-objective problems, our research employs hybrid versions of these algorithms, integrating both their continuous and binary variables within each algorithm. This hybrid approach allows for a more flexible and adaptable optimization process, addressing the problem of feature selection as well as extractor parameter optimization that involves a mix of discrete and continuous decision variables. In the following, both the SMO and the PSO algorithms are presented along with the mathematical formulation of the proposed HPSO and HSMO in detail. Then, the complete framework of HPSO and HSMO are depicted in Algorithm 1 and Algorithm 2, respectively.
3.4.1. HPSO Optimizer
Initialization:
The algorithm begins by randomly initializing particle positions for analog parameters from a uniform distribution and for Boolean parameters from a Bernoulli distribution . Velocities are also initialized, where is the position of the particle, and is the velocity of the particle.
Velocity Update Equation:
For each particle , the velocity update equation is given by:
where is inertia weight, are acceleration coefficients that control the influence of the particle’s best position , and the global best and are random values.
Position Update:
In HPSO, we introduce a hybrid approach to manage both continuous and Boolean parameters. The position update differs for analog and Boolean parameters.
For analog parameters:
For Boolean parameters, the sigmoid transformation is applied to map velocities to a range between 0 and 1.
Positions are updated based on the sigmoid output, where the positions are adjusted according to the likelihood of switching between binary states. This action is achieved by applying a threshold on the sigmoid-transformed velocities. The activation value for each boolean parameter can be defined as:
This activation value guides the decision of whether a binary feature should be flipped (0 to 1 or 1 to 0) based on the following equation:
where is a random variable for each boolean parameter, and ⊕ is the logical XOR operation.
Thus:
Fitness Evaluation:
The fitness of each particle is evaluated using the objective function . The personal best found by the particle is updated if the current fitness is better:
Then, the global best position found by the swarm is updated as:
3.4.2. HSMO Optimizer
The SMO is a population-based optimization technique that contains six stages to complete its work. The algorithm operates by dividing the population into groups to search for food and exploring different regions of the solution space, with at least two population sizes in each group. During an iteration process, a sequence of local and global steps is performed to update the solution thoroughly. The local steps take into account only the group population solution when updating individual solution, and the global steps are performed by considering the best solution among all the groups. The sequence is fixed twice in each iteration because the solutions are altered through both the local groups as well as the global leader until the optimum solution is achieved. The fission–fusion behavior helps the algorithm to explore the search space and to find the optimal solution.
Initialization phase:
A population of spider monkeys is randomly distributed. For the parameter N and population P, we had P solutions (monkey/point), where each solution contained N parameters, . The parameters were then given as input to the objective function resulting in a fitness value that represents the quality or performance of the solution. The initialized population of spider monkeys is now ready for the subsequent optimization phases of the SMO algorithm.
Equation (9) represents the calculation of the parameter value for the spider monkey and the jth parameter (dimension). The lower and upper bounds in the j direction are denoted as and , respectively, while is a random value generated within a predefined range.
Local Leader Phase:
In the local leader phase of the SMO algorithm, the monkeys within each group explored the search space by updating their positions. This was achieved by randomly selecting a subset of dimensions for each monkey and perturbing their positions in those dimensions using random weights. If the new position led to an improved fitness value compared to the old one, then the new position of the current spider monkey was updated using Equation (10), Otherwise, the current element remained unchanged. After this process was completed for all randomly selected monkeys within the group, the local leader phases end.
where is the ith monkey’s positions in jth dimension, is its current position, represents the jth dimension of local leader of the kth group, and is the jth dimension of a randomly selected from the kth group, such that . Here, and represent random values.
From Equation (10), monkeys always take parameter weights from the local leader in addition to a random group member from the population, and because the local leader usually has a better solution in its group, it gives direction for improving the solution. This process encourages an exploration of the search space.
Global Leader Phase:
In this phase, each monkey drifts towards global leader. If any group of monkeys consist of G members, then within that group G-1 updates will be made. However, unlike the previous phase, for the selected monkey to update, one more parameter of that monkey is marked for updating instead of the whole set of parameters. This action helps in selecting the best parameters. In this phase, each spider monkey updates its position using a combination of its own persistence, knowledge of the global leader position, and experience of neighboring spider monkeys. The position update equation is given by Equation (11).
is the position of the global leader in the jth dimension. The spider monkey that is updated may depend on the specific probabilistic value of each monkey , which is calculated based on its fitness value and the maximum fitness value based on Equation (12). This is conducted using the fitness function, which calculates the fitness value for each spider monkey based on its objective function value using Equation (13). A monkey with high fitness will receive more of a chance for the update, and this value may change over time as the simulation progresses.
Once G-1 attempts at modification have been made in all groups, then the phase concludes.
Local Leader Learning Phase:
In the local learning phase, each group identifies the new local leader. But there are some additional variables that are used during the phases, when the values are updated and then we measure the change in each updated group’s fitness if the change is smaller than a certain threshold error. Then we increment a counter of that group. These increments are stored in local counters and are compared with the local leader limit. This comparison is made in a later phase, but when all local leaders are identified and group increments have been made, this phase is concluded.
Global Leader Learning Phase:
Global learning is very similar to local learning. We mark the new global leader and update the fitness as well. And this time, if the change in fitness is too small, we increment a global counter and compare with the global leader limit.
Local Leader Decision Phase:
In the local leader decision phase, the algorithm checks if the local leader has improved the fitness function based on the local counters. If it has improved, then the local leader is retained and the other members of the group are updated to be closer to the local leader. But when group limits exceed the local limit threshold, then it indicates a saturation in solution and all the monkeys of that group are marked for a decision update.
These group updates can occur after at least some iterations have been completed because in each iteration, the increments are made only once. If these updates are not made before the incremented values exceed the local leader limit, it indicates that the local leader has not improved the solution for a certain number of iterations. Then, the algorithm resets the counter to 0, and the positions of all the members of that group are updated with parameters from local and global leaders using Equation (14), or it is completely randomly reinitialized using Equation (9). This update is based on the change threshold value.
The purpose of this phase is to strike a balance between exploration and exploitation. By periodically updating the positions of all group members, the algorithm aims to overcome potential stagnation and encourage further exploration of the solution space.
Global Leader Decision Phase:
In the global decision phase, if a global solution is saturating, then all the groups are dissolved. If the M groups had existed, then groups are created from scratch and decide fission process. Each group is marked a new local leader based on the fitness value of members of the groups, and the local limit counts for each group are also reset. However, if M + 1 is greater than the number of maximum groups (MGs) that can exist, then M is set to 1, meaning that all monkeys become part of the same group, e.g., fusion.
Perturbation rate:
The perturbation rate pr is a significant parameter in the metaheuristic algorithm as it determines the likelihood of perturbing the parameters and plays a crucial role during the balancing of exploration and exploitation in the optimization process. Finding the appropriate degree of perturbation is often a matter of experimentation and tuning [38]. In the proposed HSMO, the pr value is modified to dynamically updated at each iteration using Equation (7). The value of is typically a value between 0 and 1.
Equation (15) states that the will increase by a fixed increment value divided by the current iteration number. This action can help to reduce the likelihood of making drastic changes in the search process, which could lead to premature convergence or instability.
The perturbation rate parameter has an impact on both the local leader phase and the local leader decision phase. The purpose of gradually increasing over iterations is to taper off updates. As the algorithm progresses, the focus shifts more towards exploitation rather than exploration, allowing the algorithm to converge towards promising solutions and avoid excessive exploration.
In the local leader phase, the initial selection of monkeys is random. However, it is important to understand that at the beginning of this phase, when is small, monkeys are selected for position updates with high perturbation rates in all dimensions, which promotes exploration. But over time as the pr value increases, the frequency of picked monkeys reduces, resulting in fewer and fewer updates, and the algorithm focuses more on exploitation to refine and improve the quality of the solutions.
During the local leader decision phase, the pr value, which increases in each successive iteration, influences the probability in determining different update strategies for the monkeys in a group. When the pr value is smaller (specifically, if the generated random number is greater than or equal to pr), there is a possibility that a non-optimal minima has been reached, and the solution may be stuck there. In such cases, random initialization is used to introduce exploration and to prevent the solution becoming stuck by using Equation (9). On the other hand, when the value is large, it suggests that the group has exceeded the local leader limit (threshold), indicating that the global and local leaders have likely converged to a desirable solution, so their parameters have more of a chance of being used for the updates, promoting exploitation of the current best solutions using Equation (14).
Particle Probability:
Particle probability controls the update of a position value during the optimization process and then generates a trial vector by mutating and recombining the population vectors. The probability is a value between 0 and 1, where a higher value indicates a higher probability of changing a parameter value.
Binary SMO:
As previously stated, because the new monkey locations are values in continuous form, the continuous values were translated to binary values that correspond to each other. A Boolean operator is used to accomplish this task of transferring continuous solutions in each dimension, which forces the monkey to discretize their movement.
For Boolean parameters, the basic equations of the continuous SMO algorithm are modified using the logical operators AND, OR, and XOR.
| Algorithm 1. Proposed HPSO |
| 1. Initialize: - Initialize the particle positions and velocities. - Set parameters like inertia weight (w), cognitive parameter (c1), social parameter (c2), and the number of particles (N). - Randomly generate initial positions and velocities for particles. - Create a DataFrame to store particle information: ID of particle, objective function value, global best position g, and parameters (analogic and continuous). - Calculate the initial objective function values for particles. - Set the best positions for each particle and global best position. 2. Iterative Optimization: - For a specified number of iterations or until an iteration is met: a. Update Velocities: - Calculate new velocities for each particle using the formula in Equation (8) b. Update Positions: - Update the positions of particles using the new velocities. - For continuous parameters, add the velocity to the position, as defined in Equation (2). - For binary parameters, use a sigmoid function to determine whether to flip the bit based on the velocity as defined in Equation (6). c. Evaluate Objective Function: - Calculate the objective function values for the updated positions of the particles. - Update the DataFrame with the new positions and objective function values. - Update the best positions for each particle if the new position is better. d. Update Global Best: - Determine if any particle’s current position is better than the global best position. - Update the global best position if necessary, as defined in Equation (8). 3. Final Output: - Return the best solution found and its corresponding objective function value. |
| Algorithm 2. Proposed HSMO |
| 1. Initialize: - Set parameters like population, parameters (analogic and continuous), groups, max groups, pr, acc_err_delta_threshold, global_lim_thresh, local_lim_thresh, target_value, debug_mode, and pr increment - Initialize spider monkeys’ positions and IDs - Initialize DataFrame to store positions, fitness, probabilities, etc. - Calculate the initial objective function values and fitness values - Assign initial probabilities - Create initial groups - Identify local leaders and the global leader 2. Iterative Optimization: - For each iteration: a. Local Leader Phase: - Randomly select spider monkeys based on pr - Randomly select group members for the value update - Update positions using local leader and selected group members - Update fitness values - Swap positions if fitness improves b. Global Leader Phase: - Identify the global leader - For each group, update positions using the global leader and selected group members - Update fitness values - Swap positions if fitness improves c. Local Decision Phase: - Check if local leader performance improves - Increment limit count if no improvement - Reset group if limit count exceeds threshold d. Global Decision Phase: - Check if global leader performance improves - Increment global limit count if no improvement - Increase the number of groups or reset groups if limit count exceeds threshold e. Update pr 3. Final Output: - Return the best solution found and its corresponding objective function value |
3.5. XAI Models through Metaheuristic Optimization
The XAI model under consideration hinges on the interpretation of features that have undergone a metaheuristic-based optimization process. This optimization ensures that the selected features are not only relevant but also contribute significantly to the model’s overall performance. The feature interpretation within our framework is a two-pronged approach aimed at enhancing both robustness and interpretability. First, we utilize Shapley Additive exPlanations (SHAP) to quantify the importance of individual features. This provides a metric for assessing the robustness of the selected features in influencing model outcomes. Second, we implement a visual interpretation strategy by mapping the selected features back onto the original images. This visual mapping facilitates a more intuitive understanding of the role played by specific features in the model’s decision-making process. By juxtaposing selected features against their corresponding images, this method provides a tangible link between abstract mathematical representations and real-world visual elements. The combination of these two approaches—quantitative assessment through SHAP and qualitative understanding through visual mapping—not only fortifies the robustness of the XAI model but also introduces a layer of interpretability. Observing and comprehending the features that underpin model decisions is paramount for building trust and facilitating informed decision-making in applications, especially ones related to diagnostic systems such as breast cancer detection, for which this study is undertaken.
Figure 5a–c below illustrate the feature interpretation process. Figure 5b shows the Canny Edge and LBP extraction for given sample images. Figure 5c portrays the same features post feature selection, effectively mapped back for interpretation. This juxtaposition allows for a direct comparison, showcasing the impact of the feature selection process on the extracted features. It serves as a visual narrative of how the model prioritizes and refines features, shedding light on the interpretability of the chosen features.
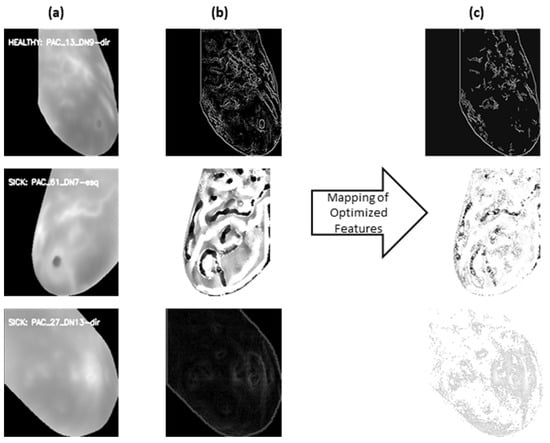
Figure 5.
(a) Original cropped image; (b) feature extract image: top using canny edges, middle LBP extractor and bottom using HOG; and (c): selected features mapped back to extracted features.
Figure 6 and Figure 7 show the quantifiable aspects of features in the image data. The upper part of Figure 6 presents a chart depicting the extracted features. Complementing these features, the lower part of Figure 6 exhibits a feature graph of the selected features after the metaheuristic-based optimization process. This clear differentiation between the extracted and selected features allows for a look into the model’s preference for certain features over others. Within both figures, the blue bars represent features of the sample healthy image, while the red bars are for a different sample image of the sick category.
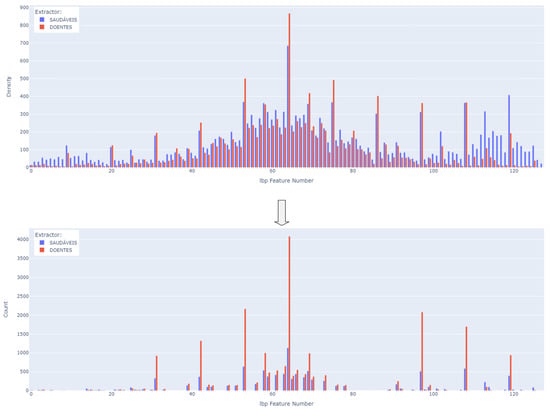
Figure 6.
Example feature selection; top: extracted features using LBP extractor; bottom: selected features using HSMO.
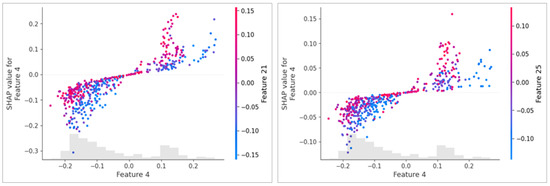
Figure 7.
Example of explaining prediction using SHAP plot: the left side after applying HSMO optimization; the right side without optimization, both using an HOG feature extractor. The X-axis represents the value of Feature 4, and the Y-axis shows its SHAP value, indicating its contribution to the model’s prediction. The color gradient represents secondary features (Feature 21 in the left plot and Feature 25 in the right plot), showing their interaction with Feature 4. The optimized model (left) displays a clearer and more structured relationship between features.
The integration of SHAP values into the optimization process allows for a more informed selection of features based on the importance of individual features as determined for distinguishing between classes. Figure 7 is an example of a feature impact visualization, using a SHAP dependency plot.
4. Experimental Setup
The experimental setup consists of multiple parts, each with respective configurations and settings. Data loading, dataset preprocessing, and feature extractors have previously been discussed in earlier sections.
Following the extraction of features, they undergo a feature selection stage where each feature is treated as a Boolean variable. Depending on whether the value is true or false, the corresponding feature is either retained or discarded. These Boolean variables are collectively optimized by the optimization algorithms as well. The retained features are then used for the training of classifiers and subsequent testing. The resulting accuracy and other metrics such as the F1-score, precision, and recall are then fed into an objective function, which includes the number of selected parameters into computing a final resulting metric that is used by optimizers.
The objective function is designed to equally prioritize both high accuracy and a lower number of selected features through the use of the geometric mean, detailed as follows:
In this formulation, the fitness score represents the assessment of a specific solution set offered by the proposed optimization algorithm. The multi-objective function in Equation (16) denotes the geometric mean of two components: accuracy and feature loss . quantifies the proportion of features that are not retained for the classification task. It is calculated by subtracting 1 from the ratio of the number of selected features to the total number of features . To align with the convention in optimization problems, where the objective is typically aimed towards zero, the fitness score is subtracted from 1. This approach yields a better potential solution in our optimization problem, achieving a desirable trade-off between accuracy and feature selection simultaneously.
For each experiment, the optimization algorithms consist of the HSMO, HPSO, BPSO, and BSMO. This section includes a discussion and details of each of the remaining experiment components. The process illustrated in Figure 8 includes the remaining experimental setup block of the XAI framework. This framework takes parameters from each stage as indicated in order to provide the two-pronged interpretability functions. The classification stage XAI inputs correspond to the utilization of SHAP to calculate the feature importance, while the feature selection and extraction stage XAI inputs correspond to the backwards-mapped selection of features to make the decision more interpretable. The optimization flow pipeline indicates one iteration of the complete process. In effect, as metaheuristic algorithms are designed, the optimization process of both continuous and binary variables is carried out in multiple iterations so that the process improves iteratively (see Figure 9). Visualizing the process itself over each stage can be thought of as modifying the values of all optimization variables over the iterations.
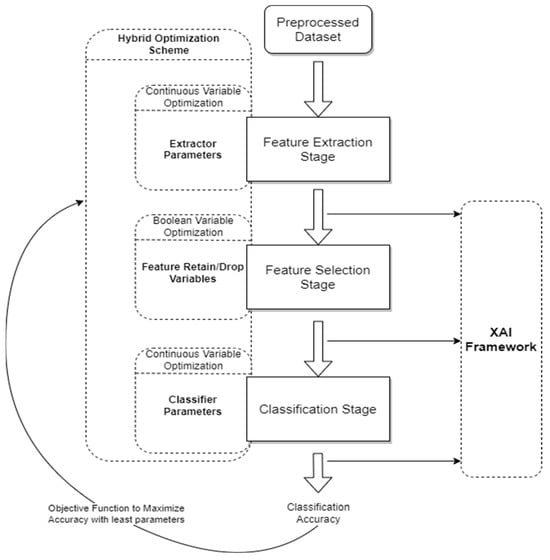
Figure 8.
Optimization process flow. Solid Arrows represent the flow of the process between the stages of the CAD system, while Dashed Boxes represent the Hybrid Optimization Scheme and the XAI Framework, which operate in parallel with the process to optimize various parameters at its different stages. The Objective Function evaluates the model’s classification accuracy.
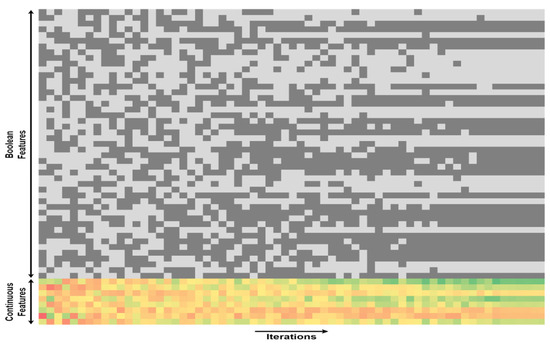
Figure 9.
The overall HSMO optimization process. The widening search space at the beginning of the iterations illustrates the diverse solutions explored by the population. Both regions pertaining to binary feature selection and continuous parameter optimization demonstrate convergence as the algorithm iterates. This convergence signifies the collaborative nature of the HSMO algorithm, where local leaders and the global leader guide the population towards more optimal solutions.
The following Table 2 describes the parameters where Boolean variables switch between True/False states, and continuous variables are adjusted over their ranges.

Table 2.
Details about the method used in different stages with arguments and hyperparameters range.
5. Results and Discussion
The presentation of our research findings is structured into two distinct parts, both offering valuable insights into the performance and characteristics of the applied methodologies and conducted experiments. In the first segment, we explore the effectiveness of metaheuristic algorithms with the novel hybrid approach HSMO and HPSO coupled with feature extraction methods. The aim was to evaluate the consistency of results across diverse optimization strategies. Multiple experiments were tested on the DMR-IR dataset. The positive class represents instances of sick breasts (red color). Therefore, to optimize the balance between computational resources and the desired level of performance, it was deemed sufficient to limit the optimization process to 60 iterations, as the incremental benefits beyond this point were deemed negligible. The experiment was conducted using Google Colab, powered by a Tesla4 GPU accelerator.
Figure 10 shows a chart indicating the resulting reduction in samples, as well as what the reduction translates to in terms of a visual interpretation of the LBP, HOG, Gabor, and edge features. It can be seen that the histogram of the feature importance distribution using HSMO and HPSO show similar shapes. In the case of an HOG extractor, the feature counts range between 0 and 0.27. The highest peaks occur within bins 13 to 25 for both healthy and sick instances. For the HSMO, the majority of counts fall within the lower end of this range, indicating that the HSMO tends to favor a sparse selection of features by focusing on those that significantly contribute to the model’s prediction. The HSMO optimizer demonstrates a more defined feature density distribution, due to its inherent properties to balance exploration and exploitation. On the other hand, the HPSO demonstrates a more active exploration approach. The presence of higher counts beyond the primary peak range reflects HPSO’s tendency toward broader exploration, driven by its selection of pressure mechanisms.
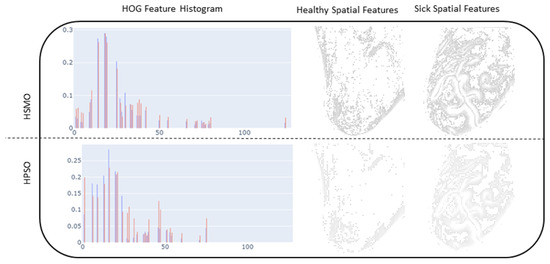
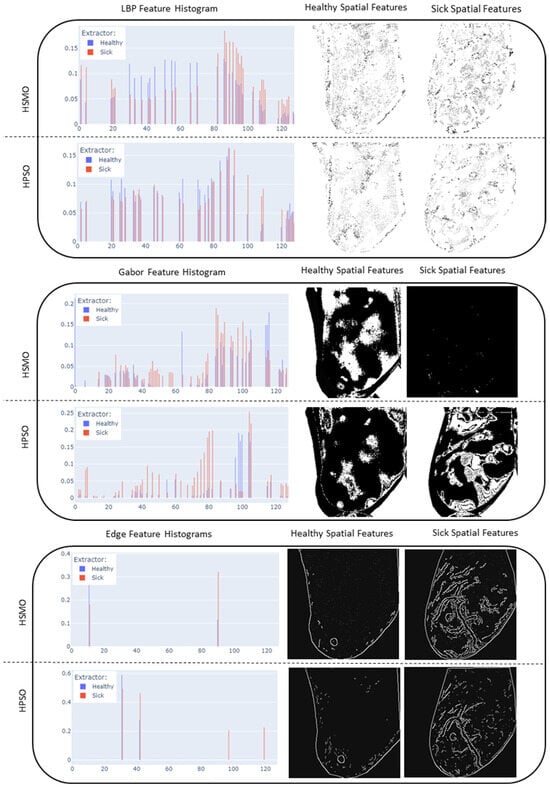
Figure 10.
Resulting feature histograms and optimized feature mapping for LBP, HOG, edge extractors, and Gabor.
The aggregated results across 60 optimizer runs for each extractor, as illustrated in Table 3, indicate that the HSMO achieves a leading performance in accuracy while maintaining a similar reduction in features compared to the HPSO. Notably, the HSMO-based HOG achieved a maximum geometric mean of 85.40%, an accuracy of 98.27%, and F1-score of 98.15%, with only 25.78% of features. In comparison, the HPSO achieved a slightly lower accuracy of 95.02% and an F1-score of 94.71%.

Table 3.
Results of optimization process using diverse feature extraction methods.
Although the HPSO provides a balanced outcome, it tends to a more aggressive feature reduction and still achieves competitive accuracy, for example, 95.89% for LBP with only 23.44% of features.
The lower accuracy observed with the BPSO and BSMO compared to the proposed hybrid approach of HPSO and HSMO stems from the fact that these methods are restricted to their fixed search space and limited dynamic capability, which results in suboptimal solutions, limited exploration, and an inability to handle continuous variables effectively. For instance, the best accuracy achieved for LBP–BSMO is 93.94% with a higher feature retention of 28.91%. This result underscores that binary optimization methods lack the flexibility needed to adapt continuously and refine solutions effectively.
Additionally, in order to include another layer of explainability at this stage, SHAP was used to analyze the distribution of feature importance of selected features across the dataset. This step allowed us to assess whether the use of metaheuristic algorithms had an impact on the importance distribution of selected features. Figure 11 indicates the respective feature importance charts of LBP features using a BSMO, BPSO, HSMO, and HPSO optimizer.
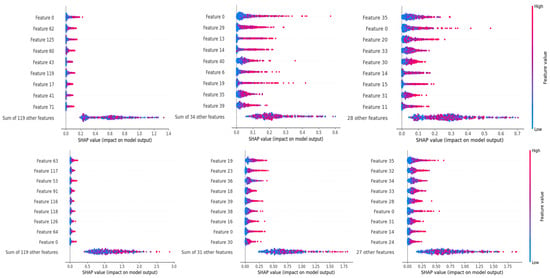
Figure 11.
Top: without optimization; left full features; middle BSMO and right BPSO; bottom: with optimization; left full features; and middle HSMO and right HPSO features.
A visible difference can be seen, where the distribution of remaining features in each metaheuristic algorithm tends to move towards greater importance scores. The most notable change occurs for HSMO and HPSO optimizers. These results also re-establish the fact that importance scores alone cannot be used as a metric for feature selection, as evident from Figure 11 in which almost none of the features deemed most important in a full feature set were selected during optimization by all the optimization algorithms. However, the distribution of importance scores still holds an effective role to assess how well the selection process performed for each algorithm comparatively.
Moving on to the second part of our results, we focused on the application of the leading optimization algorithm, HSMO, with various feature extractors. As the features still remain numerous even after being optimized, in order to gain this insight, SHAP was once again used to distinctly map the per instance ranked distribution of impact score from each top feature of each extractor as indicated in Figure 12 for Edge Filters, Gabor Filters, HOG, and LBP, respectively. The feature importance illustrations are presented in the form of heatmaps, with their placement logically controlled through SHAP in order to highlight any arising patterns. The bars on the right of each heatmap indicate the individual impact of the listed feature in the classification as a whole. The feature distribution becomes unique for each extractor; therefore, in order to assess the impact of optimization, each of the heatmaps is shown in pairs, where the right heatmap indicates the heatmap of all features and the left indicates the heatmap of optimized features.
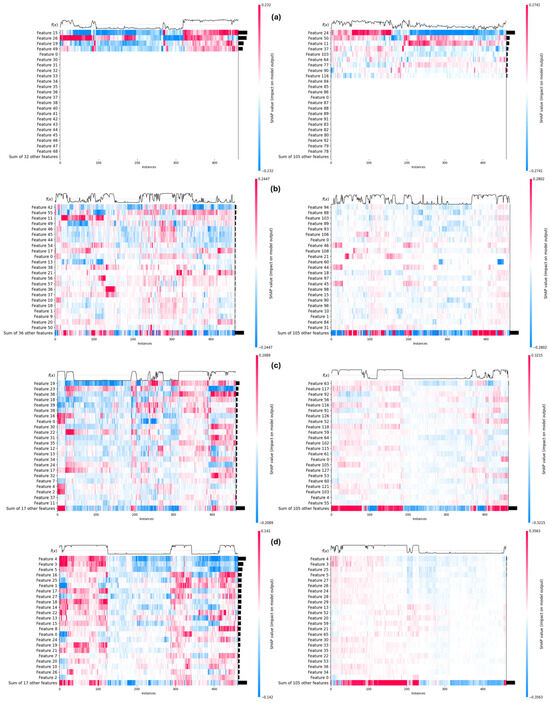
Figure 12.
Feature heatmap using HSMO optimizer: (a) canny edge detector, (b) Gabor filters, (c) LBP; and (d) HOG—full and optimized feature heatmaps in right and left, respectively.
As can be seen in Figure 12a, the most distinctive features were extracted through Edge Detection. The optimization of these extracted features resulted in a selection of key features, which can be seen from the top few optimized features being almost as important as all the low ranked features.
Gabor Filters fared the worst out of these, perhaps due to limited search space (Figure 12b), as their ability to gauge textures requires a much larger explorative search. Another possible reason is that the extractor is applied on the thermal gradient rather than the images themselves. The full feature set heatmap indicates the scattered impact across features with no specific descriptors arising. Nonetheless, the optimization of these features improves the situation by shedding features that might have served as noise to features that held valuable information and impact.
In Figure 12c,d, the HOG and LBP extractors enable the model to capture the most significant features, leading to clear and decisive predictions. The structure of their full feature heatmaps reflects this prediction, particularly in the confidence function at the top of the heatmaps, which shows a transition from the instances classified as healthy to those classified as sick in a much more defined way. The transition is especially sharp in the HOG heatmap, where the most distinctive features were extracted, which allowed for an evident increase in accuracy. The optimization process further refined these features, selecting key ones that contribute significantly to the model’s performance. This is evident as the top optimized features hold nearly as much importance as all the low-ranked features combined. As a result, the model’s confidence transition becomes steeper as it crosses the boundary where the instance changes class, indicating a well-learned, generalizable pattern. This consistent and precise decision boundary is crucial in a CAD system, as it enhances the trust that medical professionals place in the system’s outputs, ultimately improving the system’s reliability in clinical settings.
6. Comparison with State-of-the-Art Methodologies
To conduct a fair comparison of the proposed model, we selected related studies that applied machine learning, deep learning, and metaheuristic techniques to the DMR-IR thermogram dataset. The results are tabulated in Table 4, demonstrating our model’s effectiveness, when compared to studies that produced textural features from thermal images [19,20] and those that utilized CNN-based approaches [23,29]. It is important to highlight that the splitting approach employed by the studies [19,29] prevents data leakage, an issue some other studies have not addressed.

Table 4.
Performance comparison of the proposed method with related work.
While our method slightly underperforms compared to models leveraging deep learning and hybrid feature selection techniques [22], it offers several distinct advantages. CNN models are often more complex and computationally expensive, whereas our approach, which relies on handcrafted feature extraction, reduces feature dimensionality by 74.22% while still achieving a 98.27% accuracy. Additionally, our method provides interpretable features, which can be highly beneficial in clinical or real-world applications where transparency is critical for decision making.
Furthermore, our model automates the parameter-tuning process, eliminating the need for manual tuning and facilitating broader adoption in practical scenarios where ease of use and computational efficiency are essential.
7. Conclusions
This research resulted in insights into the synergy between metaheuristic algorithms and Explainable Artificial Intelligence (XAI) for addressing multi-objective problems involving both continuous and Boolean variables. The metaheuristic algorithm comparison revealed that the HPSO and HSMO consistently outperformed others in diverse problem scenarios. This superiority was further validated through XAI techniques, which helped illuminate the decision-making processes behind the algorithms.
The impact of feature extractors using handcrafted feature methods was investigated. Gabor Filters performed the least favorably, Edge Filters offered distinctive features, and LBP/HOG provided comprehensive feature sets. These findings were substantiated by a SHAP analysis, which highlighted the importance of feature selection and extraction. Interestingly, the metaheuristic optimization surpassed the direct use of SHAP importance values, underscoring the intricate relationship between optimization and interpretability.
This research lays the groundwork for continued exploration in the collective domain’s Explainable AI, metaheuristics, and medical image analysis. Our findings contribute to ongoing efforts to make computational models and metaheuristic algorithms more transparent, interpretable, and applicable to real-world problems.
For future work, this study can be expanded to multiple imaging modalities beyond breast cancer detection to ensure the robustness of the proposed approach. Additionally, incorporating domain experts in the interpretability loop analysis can result invaluable insights to the decision-making process of both experts and learning acquired by ML models. Additionally, we plan to explore the application of HSMO and HPSO collectively optimized with deep learning, which also holds promise for further enhancing the proposed framework’s efficacy.
Author Contributions
Conceptualization, H.D.; methodology, H.D.; software, H.D.; validation, H.D., O.B. and A.B.; formal analysis, H.D.; investigation, H.D.; resources, H.D., O.B. and A.B.; data curation, H.D.; writing—original draft preparation, H.D.; writing—review and editing, H.D., O.B. and A.B.; visualization, H.D.; supervision, O.B.; project administration, O.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ciatto, S.; Rosselli Del Turco, M.; Zappa, M. The detectability of breast cancer by screening mammography. Br. J. Cancer 1995, 71, 337–339. [Google Scholar] [CrossRef][Green Version]
- Foxcroft, L.M.; Evans, E.B.; Joshua, H.K.; Hirst, C. Breast cancers invisible on mammography. ANZ J. Surg. 2000, 70, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Pataky, R.; Phillips, N.; Peacock, S.; Coldman, A.J. Cost-effectiveness of population-based mammography screening strategies by age range and frequency. J. Cancer Policy 2014, 2, 97–102. [Google Scholar] [CrossRef]
- Pauwels, E.K.J.; Foray, N.; Bourguignon, M.H. Breast Cancer Induced by X-Ray Mammography Screening? A Review Based on Recent Understanding of Low-Dose Radiobiology. Med. Princ. Pract. 2015, 25, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Dabbous, F.M.; Dolecek, T.A.; Berbaum, M.L.; Friedewald, S.M.; Summerfelt, W.T.; Hoskins, K.; Rauscher, G.H. Impact of a False-Positive Screening Mammogram on Subsequent Screening Behavior and Stage at Breast Cancer Diagnosis. Cancer Epidemiol. Biomark. Prev. 2017, 26, 397–403. [Google Scholar] [CrossRef] [PubMed]
- Bansal, R.; Collison, S.; Krishnan, L.; Aggarwal, B.; Vidyasagar, M.; Kakileti, S.T.; Manjunath, G. A prospective evaluation of breast thermography enhanced by a novel machine learning technique for screening breast abnormalities in a general population of women presenting to a secondary care hospital. Front. Artif. Intell. 2023, 5, 1050803. Available online: https://www.frontiersin.org/articles/10.3389/frai.2022.1050803 (accessed on 25 February 2023). [CrossRef] [PubMed]
- Da Luz, T.G.R.; Coninck, J.C.; Ulbricht, L. Comparison of the Sensitivity and Specificity Between Mammography and Thermography in Breast Cancer Detection. In XXVII Brazilian Congress on Biomedical Engineering, Proceedings of the CBEB 2020, Vitória, Brazil, 26–30 October 2020; Bastos-Filho, T.F., de Oliveira Caldeira, E.M., Frizera-Neto, A., Eds.; IFMBE Proceedings; Springer International Publishing: Cham, Switzerland, 2022; Volume 83, pp. 2163–2168. ISBN 978-3-030-70600-5. [Google Scholar]
- Head, J.F.; Elliott, R.L. Infrared imaging: Making progress in fulfilling its medical promise. IEEE Eng. Med. Biol. Mag. 2002, 21, 80–85. [Google Scholar] [CrossRef]
- Sarigoz, T.; Ertan, T.; Topuz, Ö.; Sevim, Y.; Cihan, Y. Role of Digital Infrared Thermal Imaging in the Diagnosis of Breast Mass: A Pilot Study. Infrared Phys. Technol. 2018, 91, 214–219. [Google Scholar] [CrossRef]
- Guetari, R.; Ayari, H.; Sakly, H. Computer-aided diagnosis systems: A comparative study of classical machine learning versus deep learning-based approaches. Knowl. Inf. Syst. 2023, 65, 3881–3921. [Google Scholar] [CrossRef]
- Retson, T.A.; Eghtedari, M. Expanding Horizons: The Realities of CAD, the Promise of Artificial Intelligence, and Machine Learning’s Role in Breast Imaging beyond Screening Mammography. Diagnostics 2023, 13, 2133. [Google Scholar] [CrossRef]
- Skjong, R.; Wentworth, B.H. Expert Judgment and Risk Perception. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; OnePetro: Richardson, TX, USA, 2001. [Google Scholar]
- Park, H.; Megahed, A.; Yin, P.; Ong, Y.; Mahajan, P.; Guo, P. Incorporating Experts’ Judgment into Machine Learning Models. Expert. Syst. Appl. 2023, 228, 120118. [Google Scholar] [CrossRef]
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.M.; Confalonieri, R.; Guidotti, R.; Del Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable Artificial Intelligence (XAI): What we know and what is left to attain Trustworthy Artificial Intelligence. Inf. Fusion. 2023, 99, 101805. [Google Scholar] [CrossRef]
- Yang, G.; Ye, Q.; Xia, J. Unbox the black-box for the medical explainable AI via multi-modal and multi-centre data fusion: A mini-review, two showcases and beyond. Inf. Fusion. 2022, 77, 29–52. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.-W.; Chiang, M.-C.; Ksentini, A.; Chen, M. Metaheuristic Algorithms for Healthcare: Open Issues and Challenges. Comput. Electr. Eng. 2016, 53, 421–434. [Google Scholar] [CrossRef]
- Dihmani, H.; Bousselham, A.; Bouattane, O. A Review of Feature Selection and HyperparameterOptimization Techniques for Breast Cancer Detection on thermograms Images. In Proceedings of the 2023 IEEE 6th International Conference on Cloud Computing and Artificial Intelligence: Technologies and Applications (CloudTech), Marrakech, Morocco, 21–23 November 2023; pp. 01–08. [Google Scholar]
- Del Ser, J.; Osaba, E.; Molina, D.; Yang, X.-S.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.N.; Coello Coello, C.A.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019, 48, 220–250. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Moreno, A.; Puig, D. Breast Cancer Detection in Thermal Infrared Images Using Representation Learning and Texture Analysis Methods. Electronics 2019, 8, 100. [Google Scholar] [CrossRef]
- Resmini, R.; Silva, L.; Araujo, A.S.; Medeiros, P.; Muchaluat-Saade, D.; Conci, A. Combining Genetic Algorithms and SVM for Breast Cancer Diagnosis Using Infrared Thermography. Sensors 2021, 21, 4802. [Google Scholar] [CrossRef]
- Gonçalves, C.B.; Souza, J.R.; Fernandes, H. CNN architecture optimization using bio-inspired algorithms for breast cancer detection in infrared images. Comput. Biol. Med. 2022, 142, 105205. [Google Scholar] [CrossRef]
- Pramanik, R.; Pramanik, P.; Sarkar, R. Breast cancer detection in thermograms using a hybrid of GA and GWO based deep feature selection method. Expert. Syst. Appl. 2023, 219, 119643. [Google Scholar] [CrossRef]
- Ensafi, M.; Keyvanpour, M.R.; Shojaedini, S.V. A New method for promote the performance of deep learning paradigm in diagnosing breast cancer: Improving role of fusing multiple views of thermography images. Health Technol. 2022, 12, 1097–1107. [Google Scholar] [CrossRef]
- Aidossov, N.; Zarikas, V.; Zhao, Y.; Mashekova, A.; Ng, E.Y.K.; Mukhmetov, O.; Mirasbekov, Y.; Omirbayev, A. An Integrated Intelligent System for Breast Cancer Detection at Early Stages Using IR Images and Machine Learning Methods with Explainability. SN Comput. Sci. 2023, 4, 184. [Google Scholar] [CrossRef] [PubMed]
- Aidossov, N.; Zarikas, V.; Mashekova, A.; Zhao, Y.; Ng, E.Y.K.; Midlenko, A.; Mukhmetov, O. Evaluation of Integrated CNN, Transfer Learning, and BN with Thermography for Breast Cancer Detection. Appl. Sci. 2023, 13, 600. [Google Scholar] [CrossRef]
- Nicandro, C.-R.; Efrén, M.-M.; María Yaneli, A.-A.; Enrique, M.-D.-C.-M.; Héctor Gabriel, A.-M.; Nancy, P.-C.; Alejandro, G.-H.; Guillermo de Jesús, H.-R.; Rocío Erandi, B.-M. Evaluation of the Diagnostic Power of Thermography in Breast Cancer Using Bayesian Network Classifiers. Comput. Math. Methods Med. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Dey, S.; Roychoudhury, R.; Malakar, S.; Sarkar, R. Screening of breast cancer from thermogram images by edge detection aided deep transfer learning model. Multimed. Tools Appl. 2022, 81, 9331–9349. [Google Scholar] [CrossRef]
- Silva, L.; Saade, D.; Sequeiros Olivera, G.; Silva, A.; Paiva, A.; Bravo, R.; Conci, A. A New Database for Breast Research with Infrared Image. J. Med. Imaging Health Inform. 2014, 4, 92–100. [Google Scholar] [CrossRef]
- Zuluaga-Gomez, J.; Masry, Z.A.; Benaggoune, K.; Meraghni, S.; Zerhouni, N. A CNN-based methodology for breast cancer diagnosis using thermal images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2020, 9, 1–15. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Daugman, J.G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. J. Opt. Soc. Am. A JOSAA 1985, 2, 1160–1169. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider Monkey Optimization algorithm for numerical optimization. Memetic Comp. 2014, 6, 31–47. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Singh, U.; Salgotra, R.; Rattan, M. A Novel Binary Spider Monkey Optimization Algorithm for Thinning of Concentric Circular Antenna Arrays. IETE J. Res. 2016, 62, 736–744. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the Computational Cybernetics and Simulation 1997 IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Gupta, K.; Deep, K. Investigation of Suitable Perturbation Rate Scheme for Spider Monkey Optimization Algorithm. In Proceedings of Fifth International Conference on Soft Computing for Problem Solving; Pant, M., Deep, K., Bansal, J.C., Nagar, A., Das, K.N., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2016; pp. 839–850. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).