RooTri: A Simple and Robust Function to Approximate the Intersection Points of a 3D Scalar Field with an Arbitrarily Oriented Plane in MATLAB
Abstract
:1. Introduction and Related Work
2. Modeling and Implementation
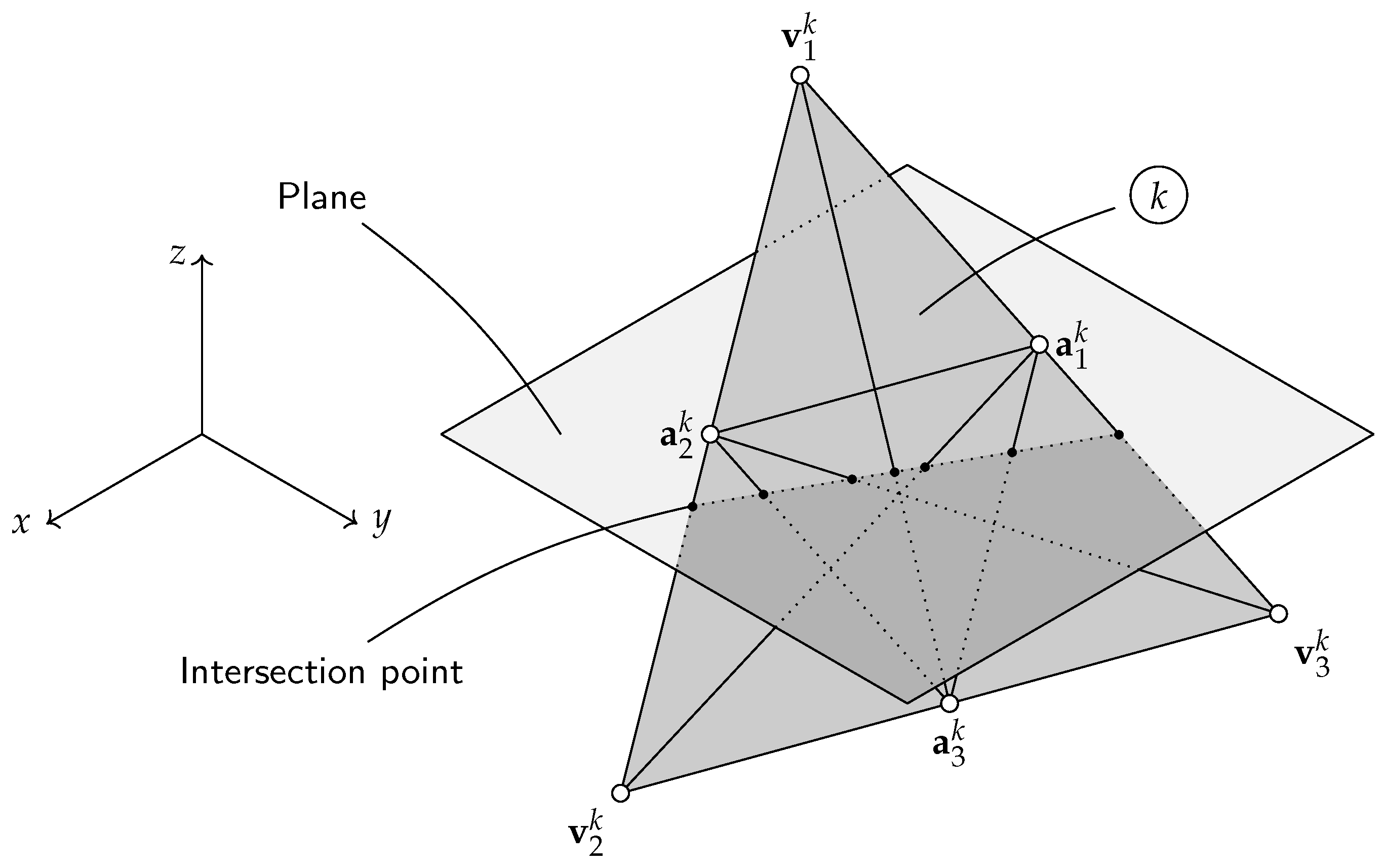
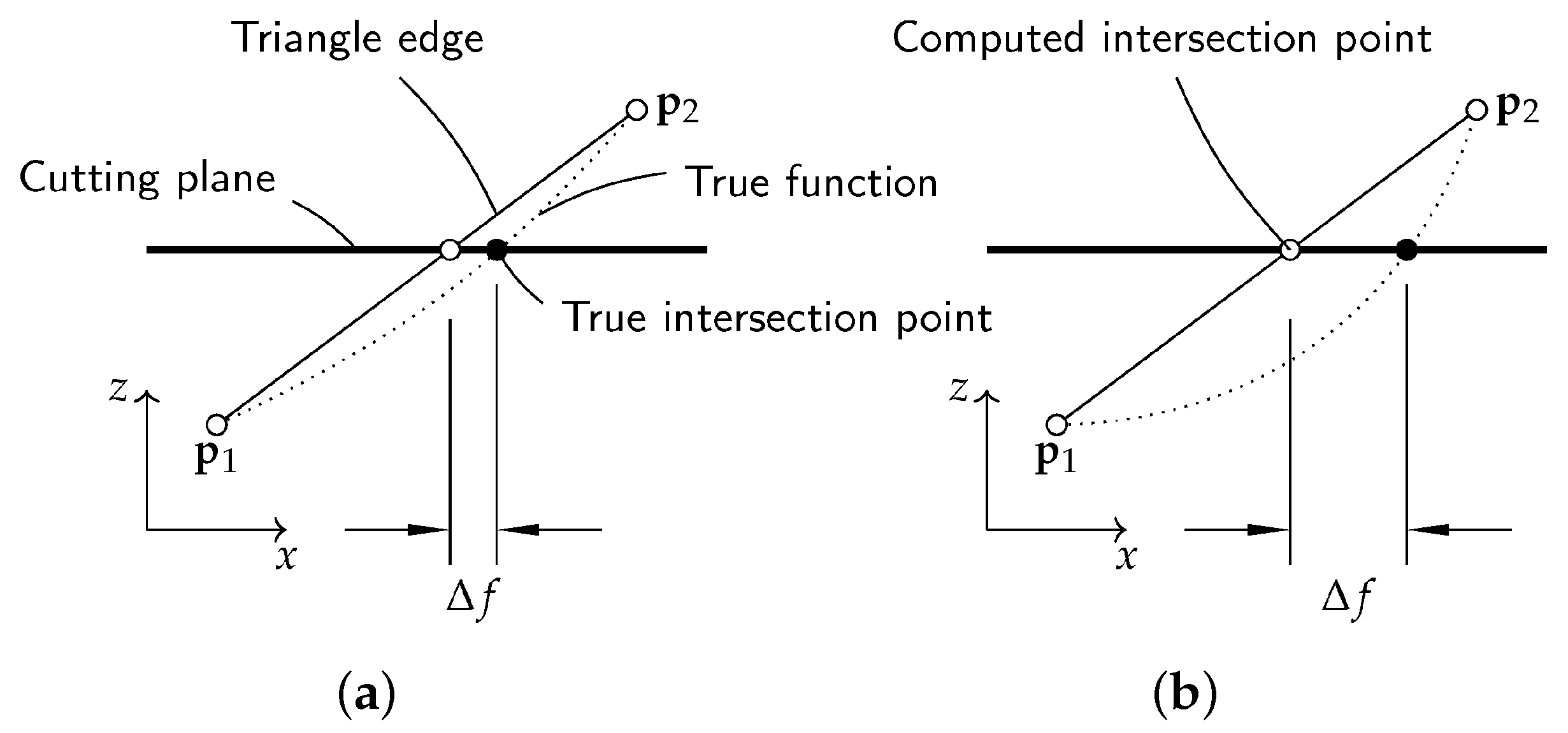
2.1. Mathematical Modeling
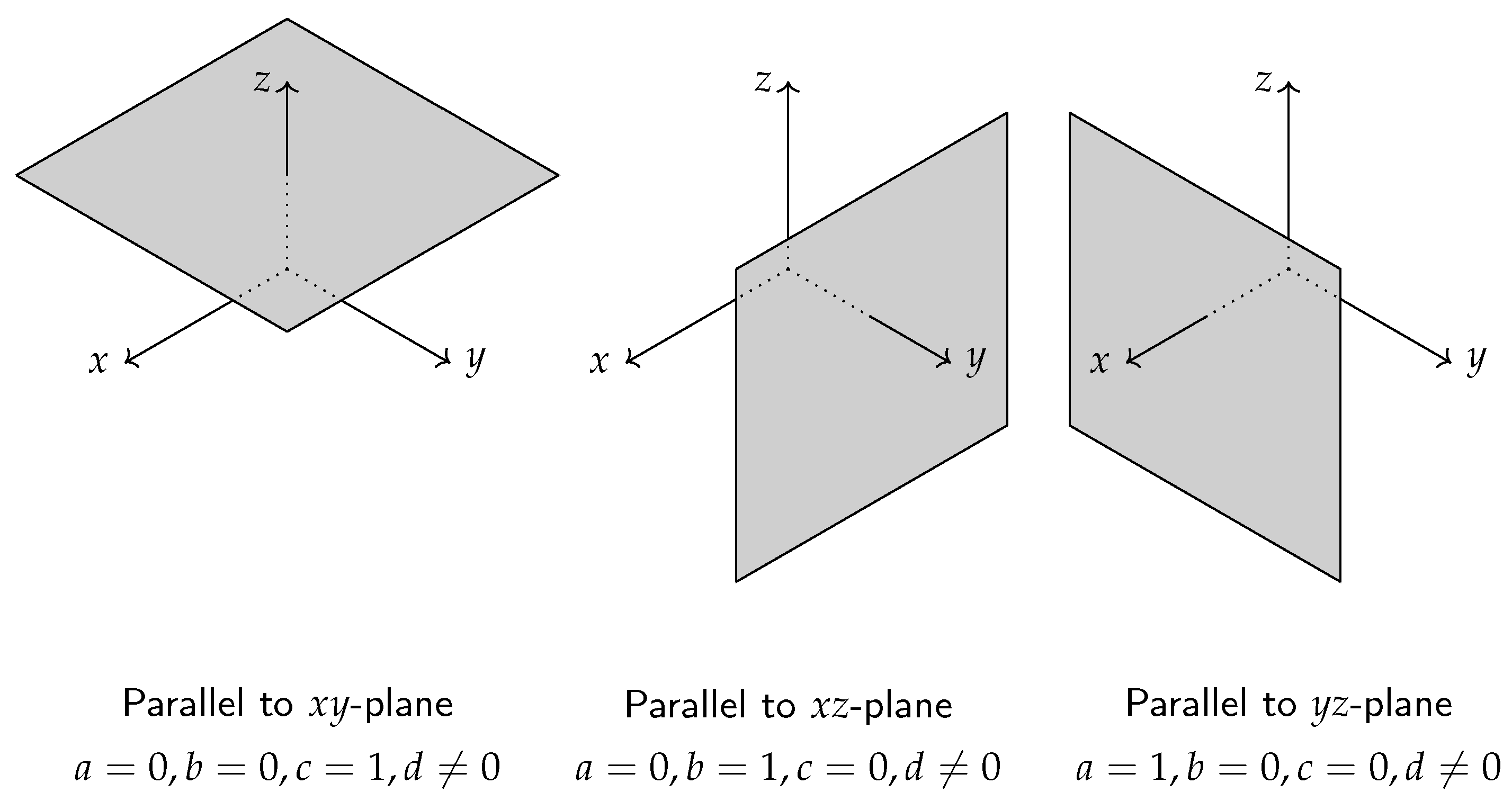
2.2. Note on the Determination of Plane Parameters
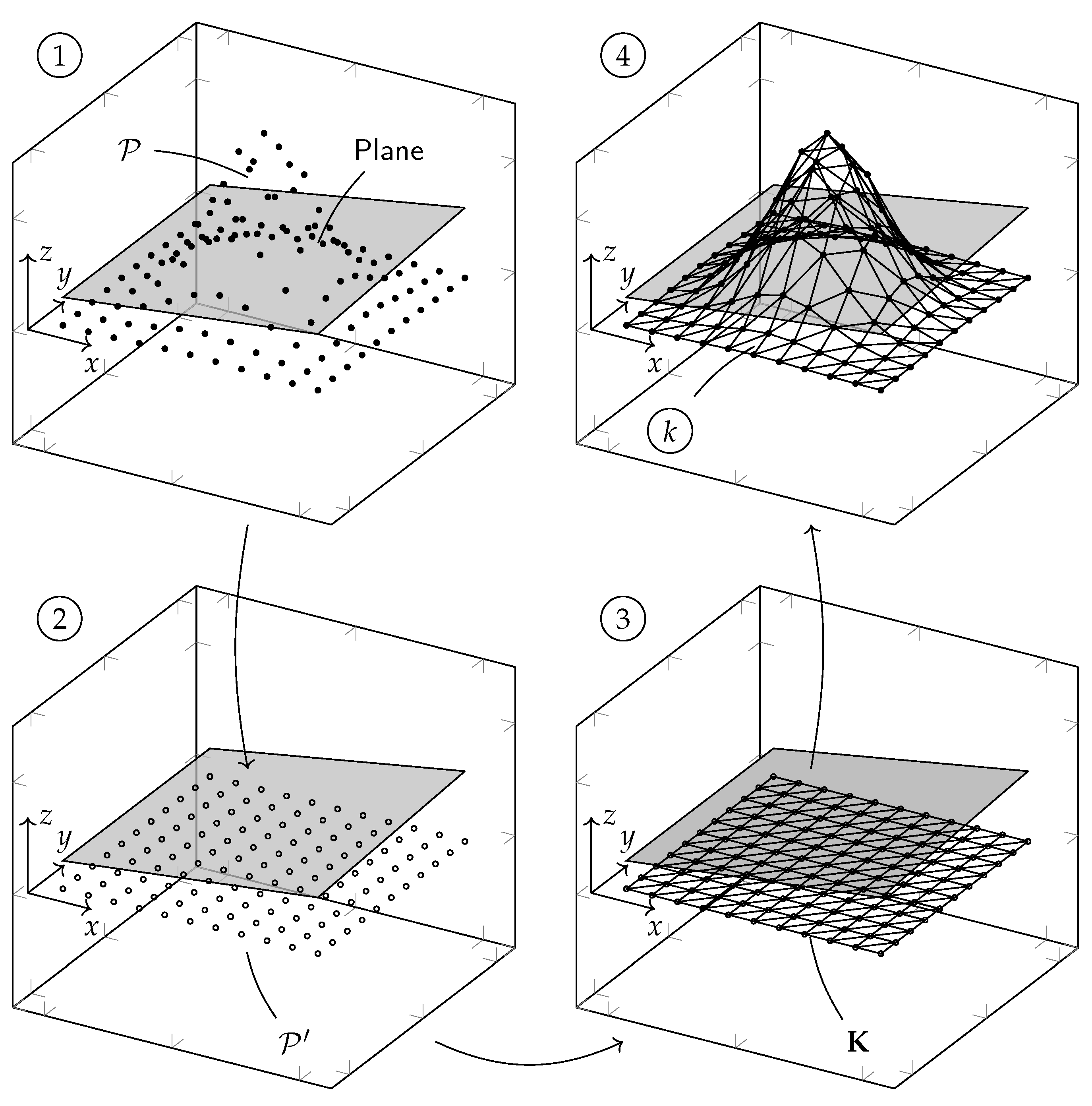
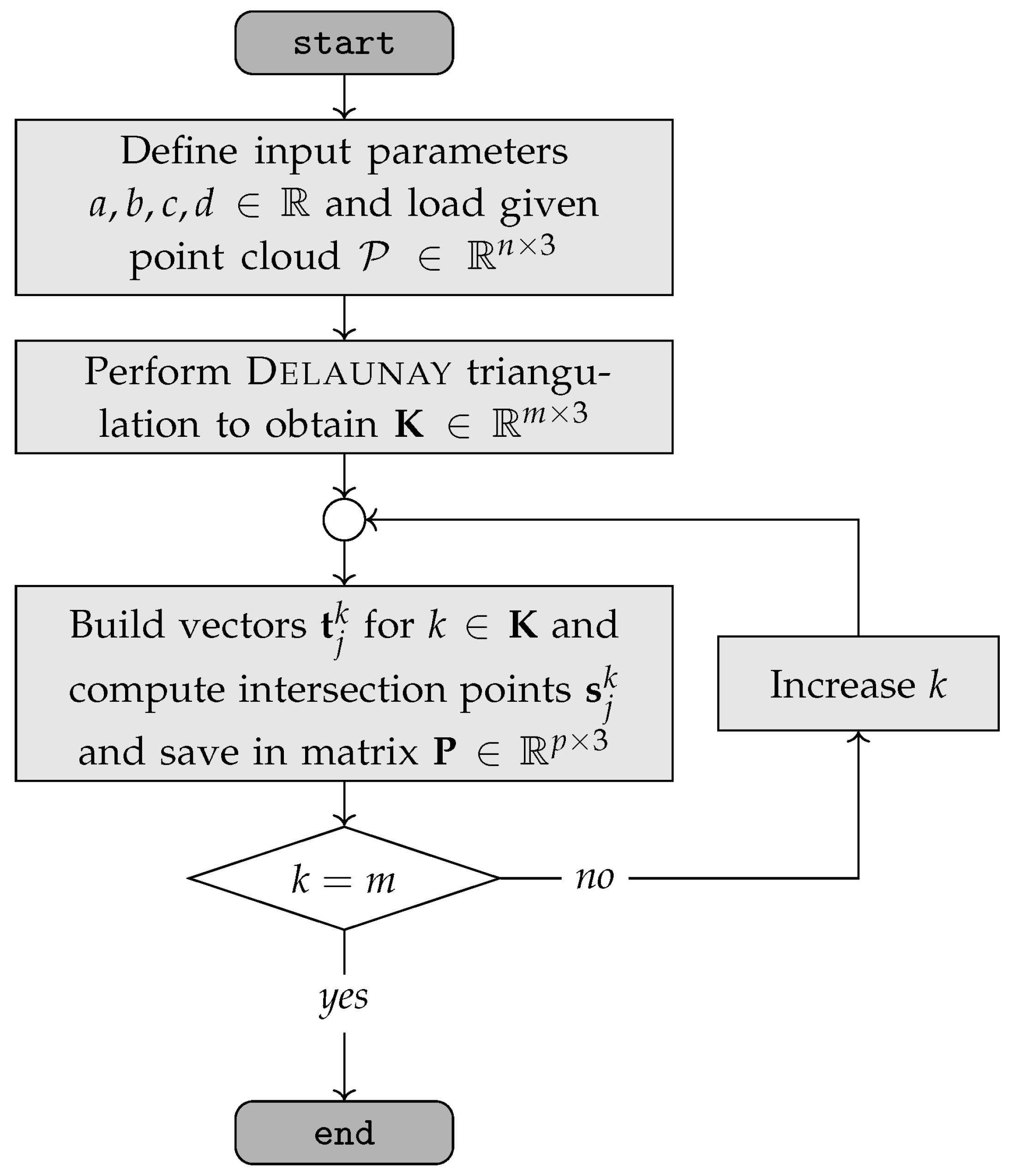
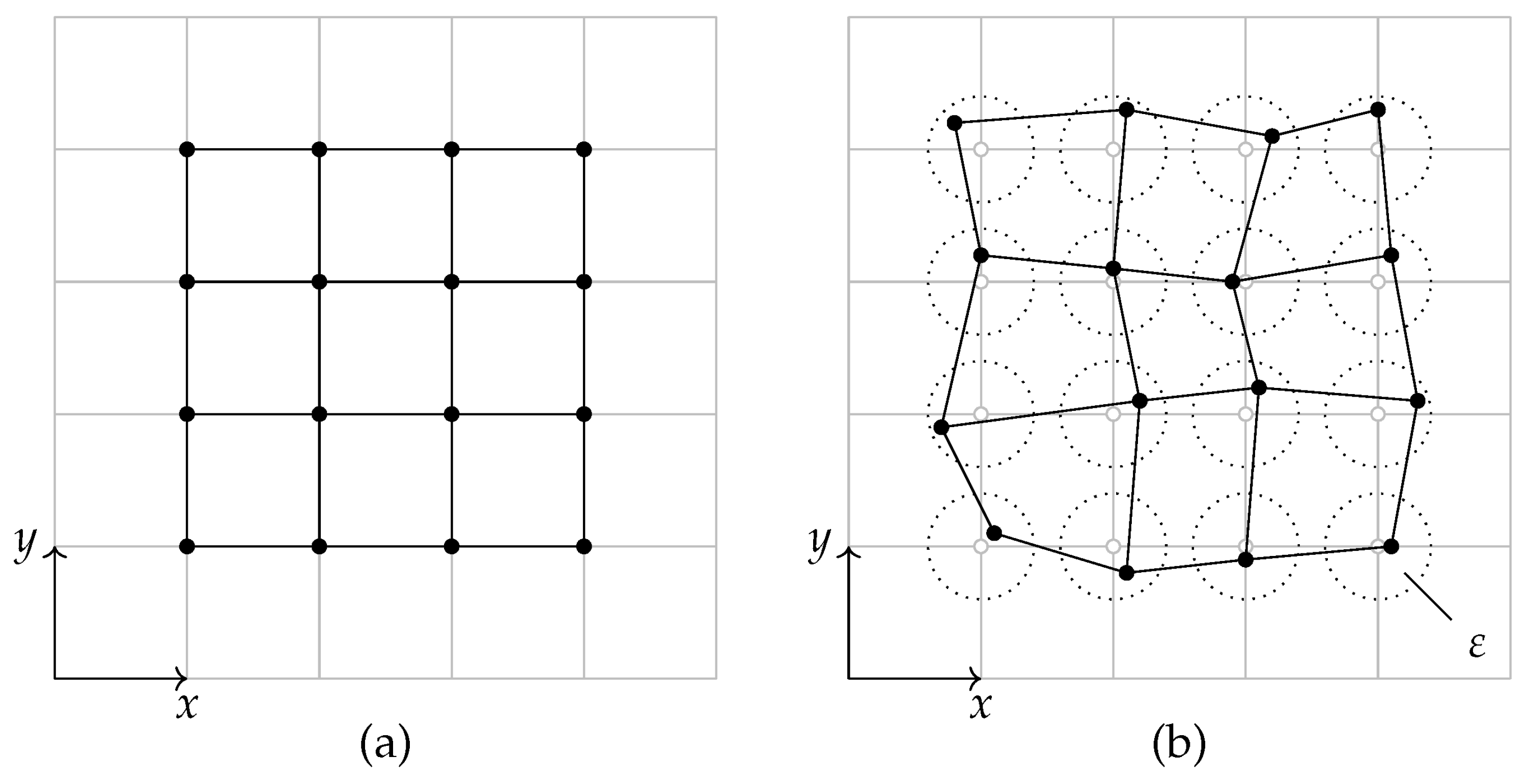
2.3. Numerical Implementation and Code Description
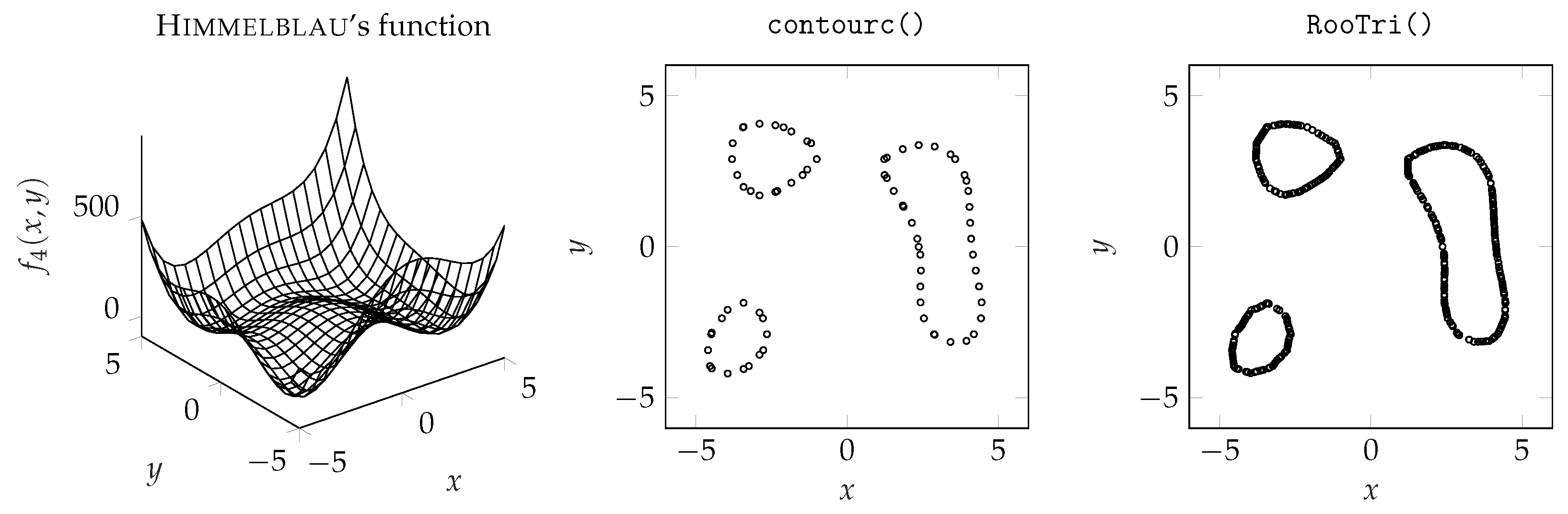
3. Experiments and Validation
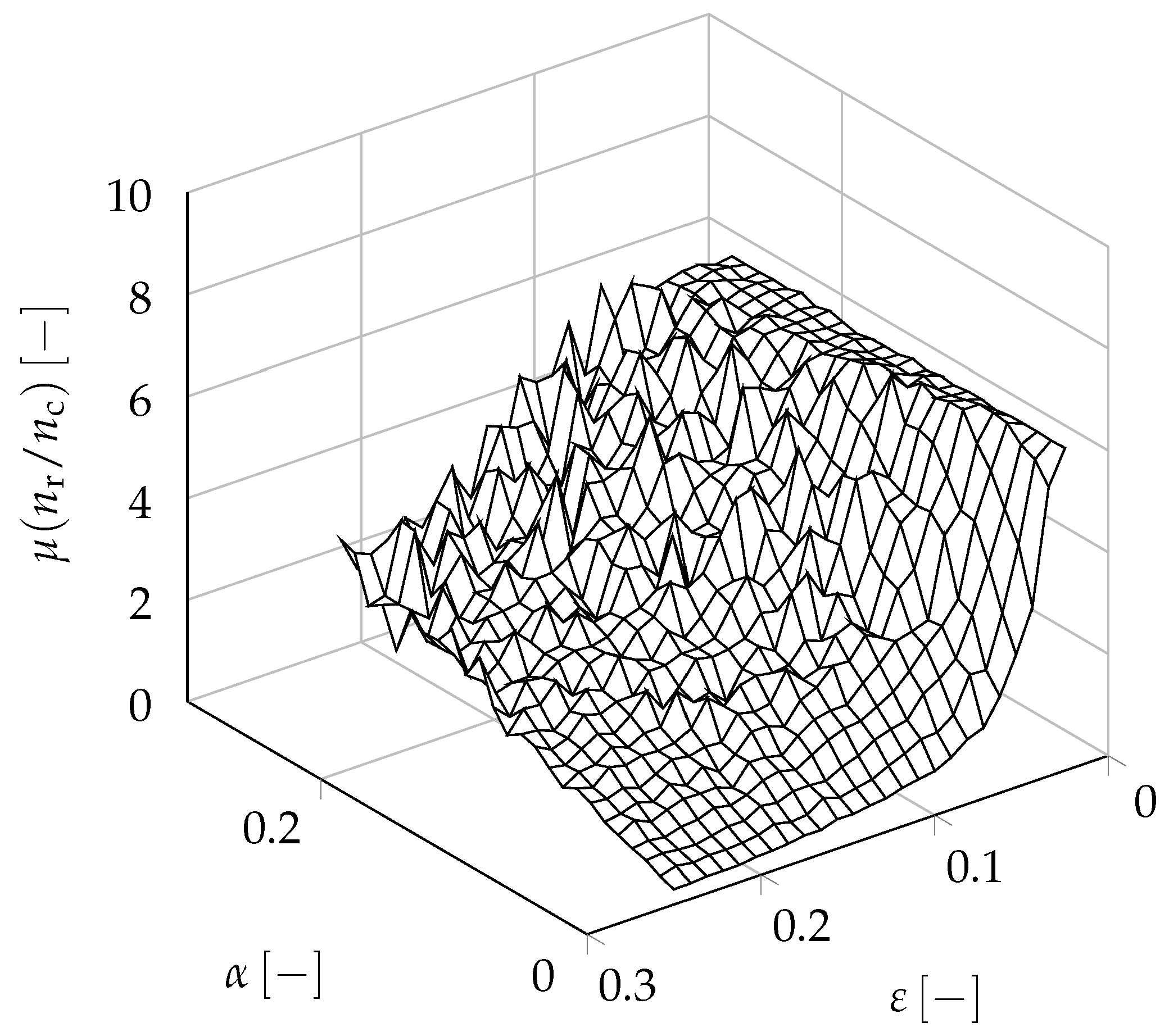
3.1. Design of Experiments
- Quality of the results;
- Number of computed intersection points;
- Time consumption;
- Required memory.
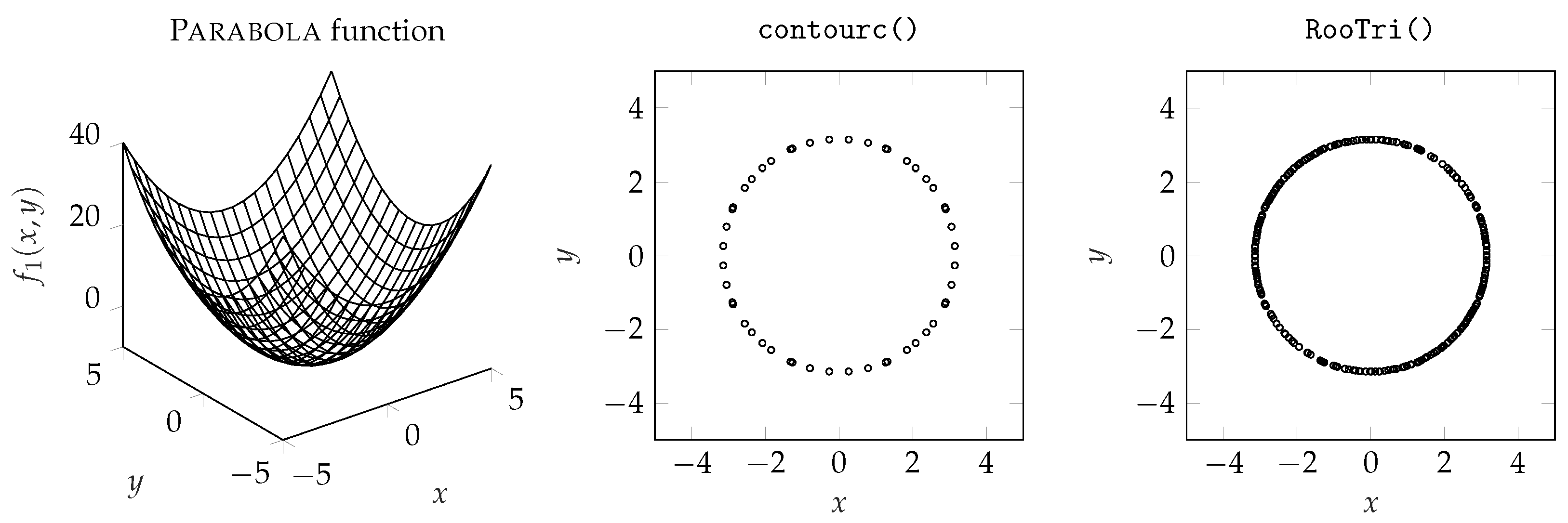
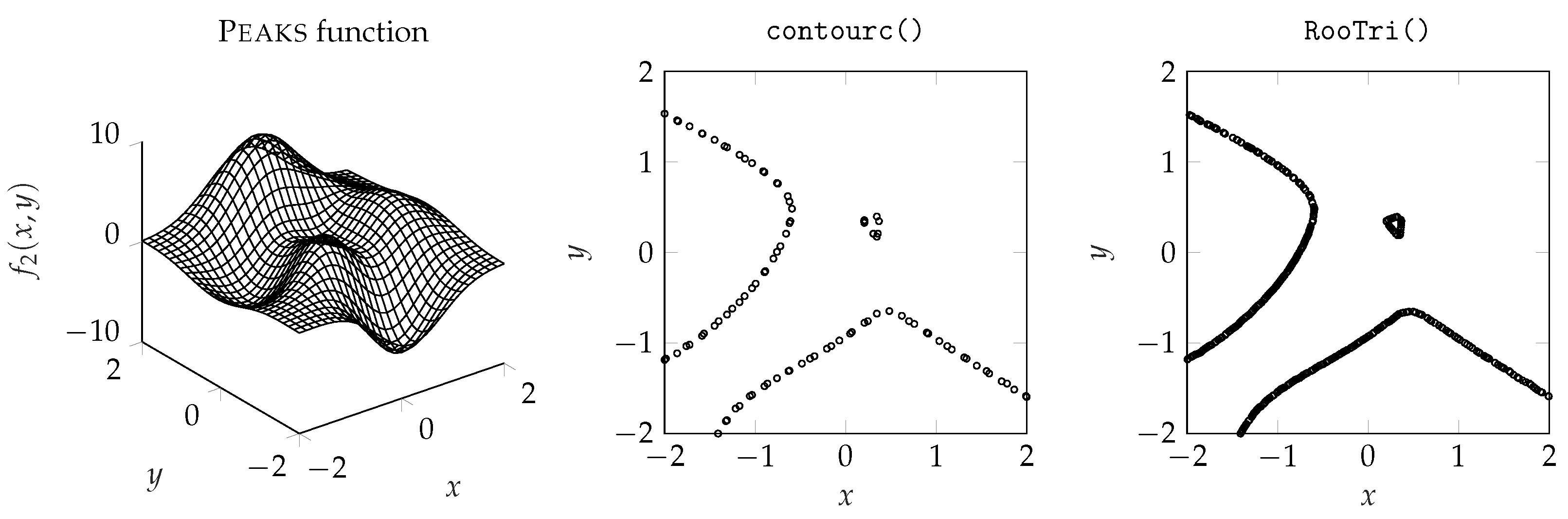
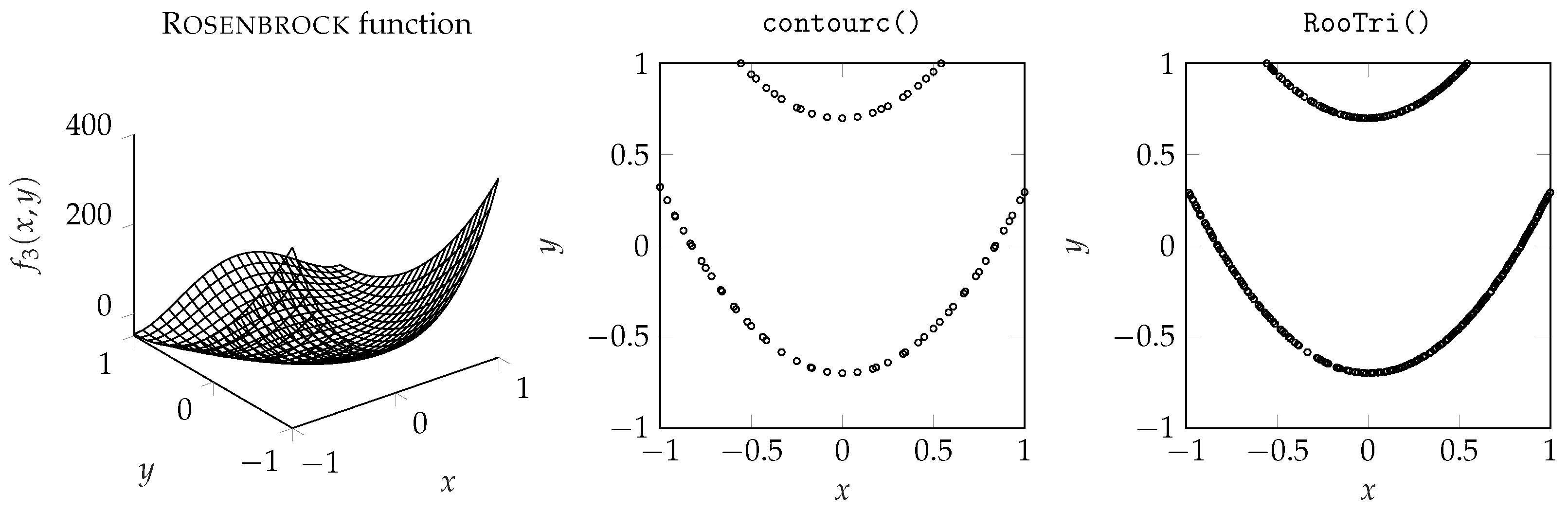
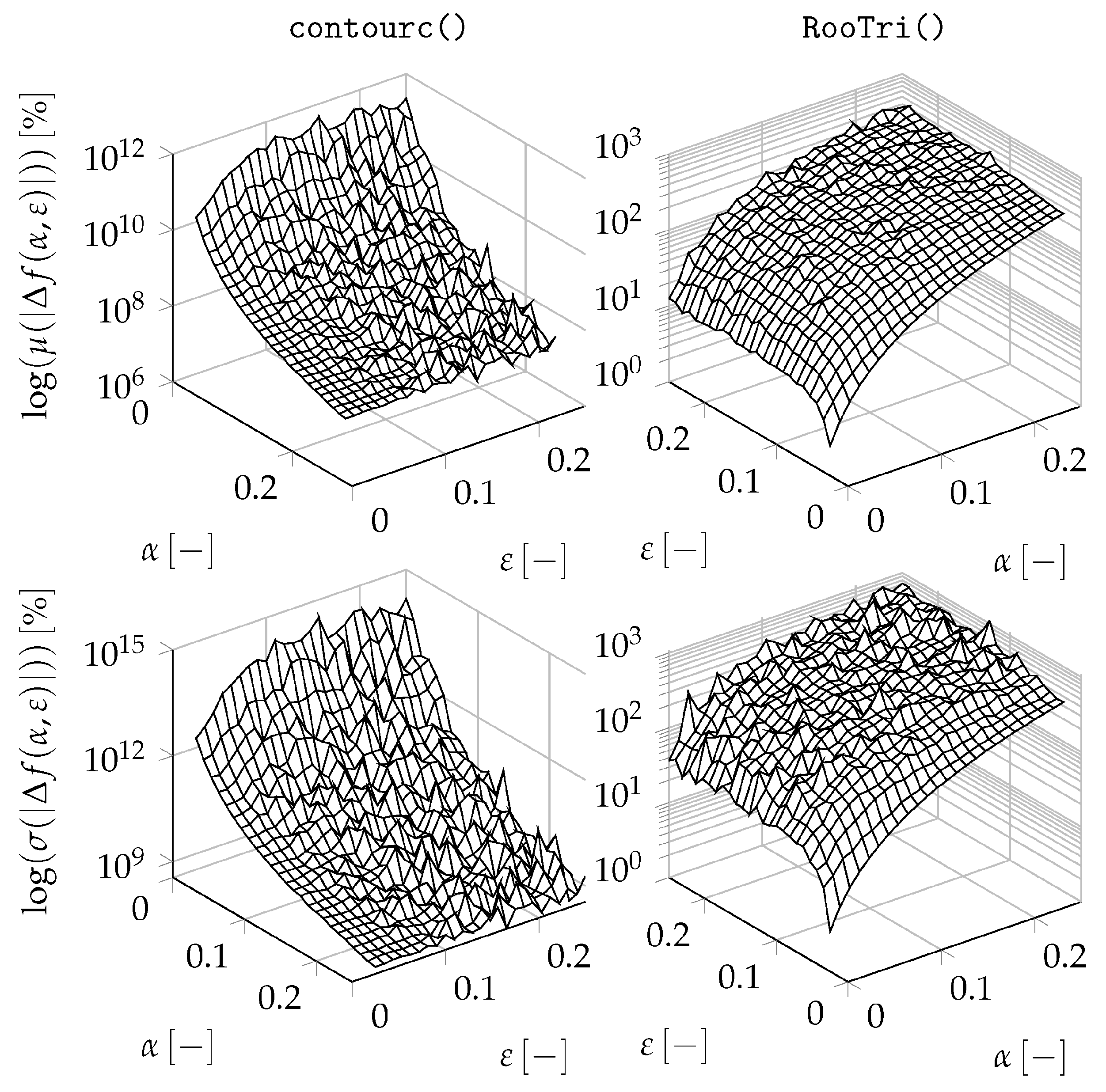
3.2. Evaluation of Computed Results
3.3. Quality of Computed Intersection Points
3.4. Number of Computed Roots
3.5. Time Consumption
3.6. Estimation of Required Memory
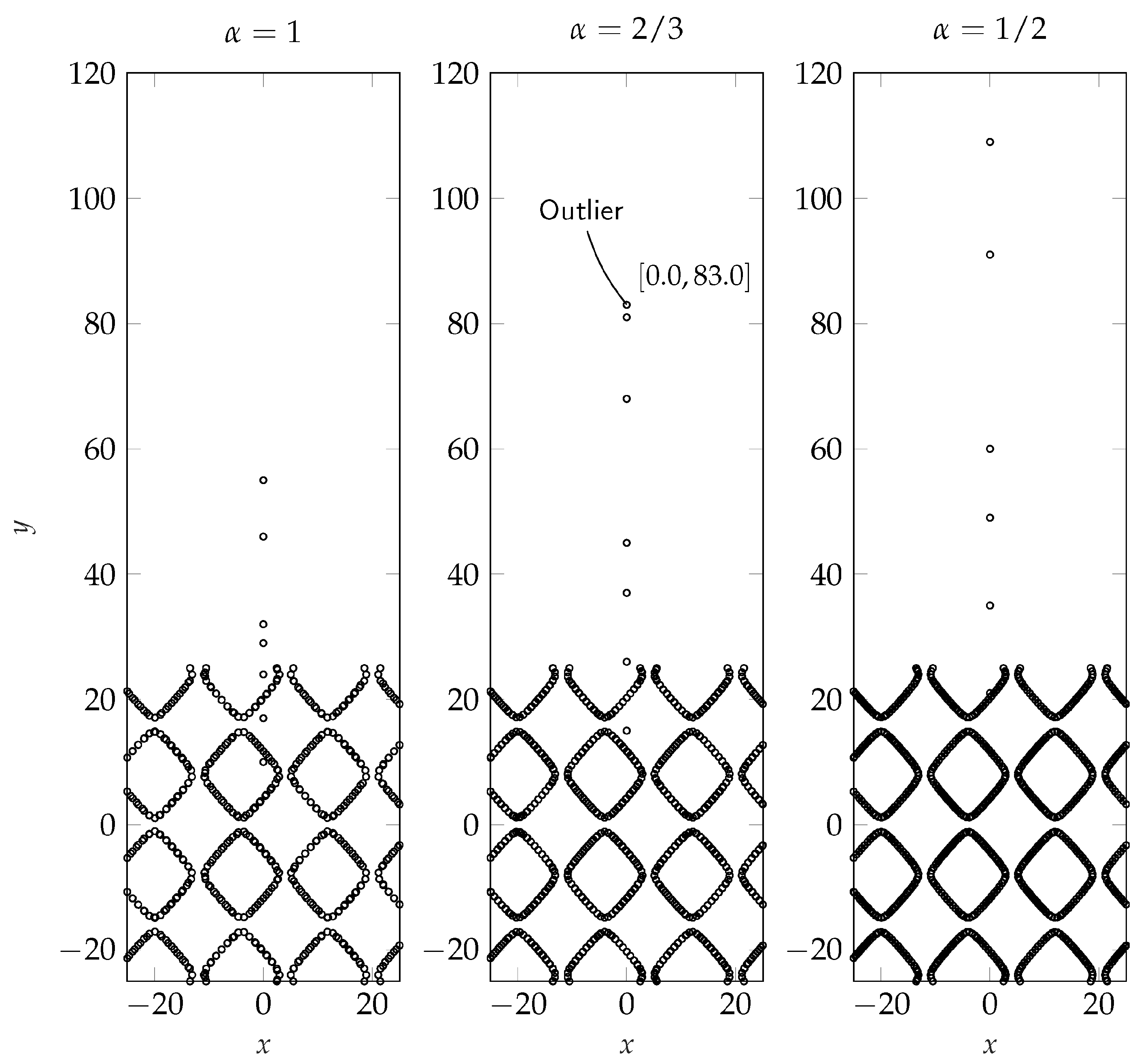
3.7. Limits of Application
4. Practical Application
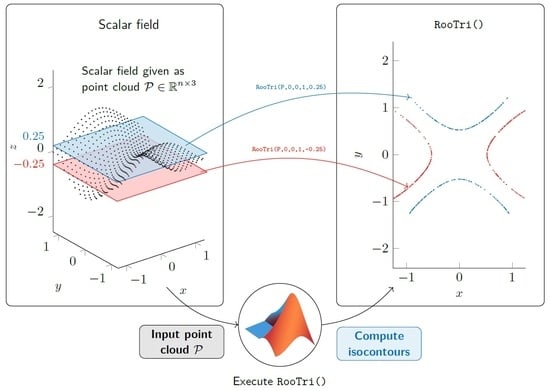
4.1. Exemplary Function Operation
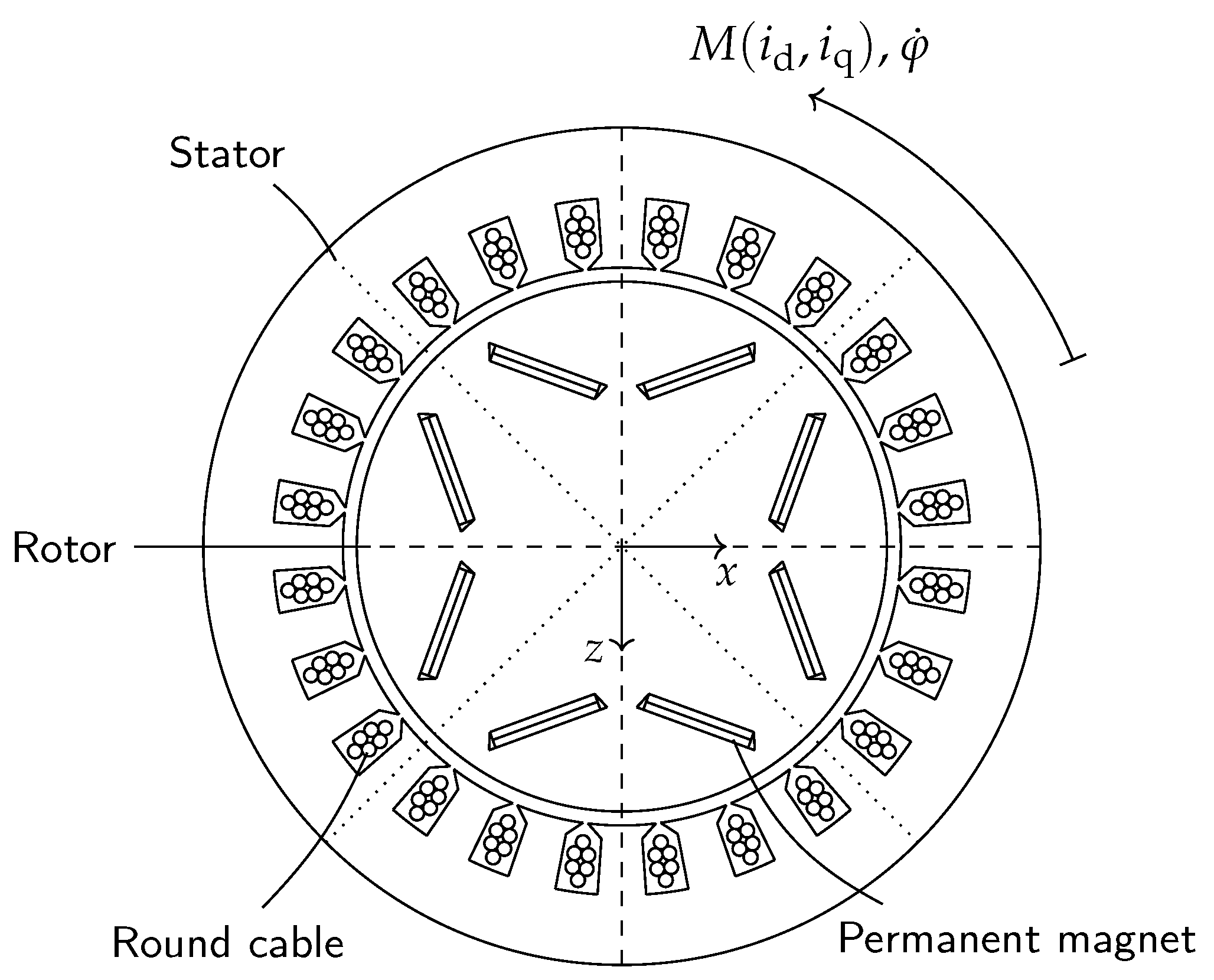
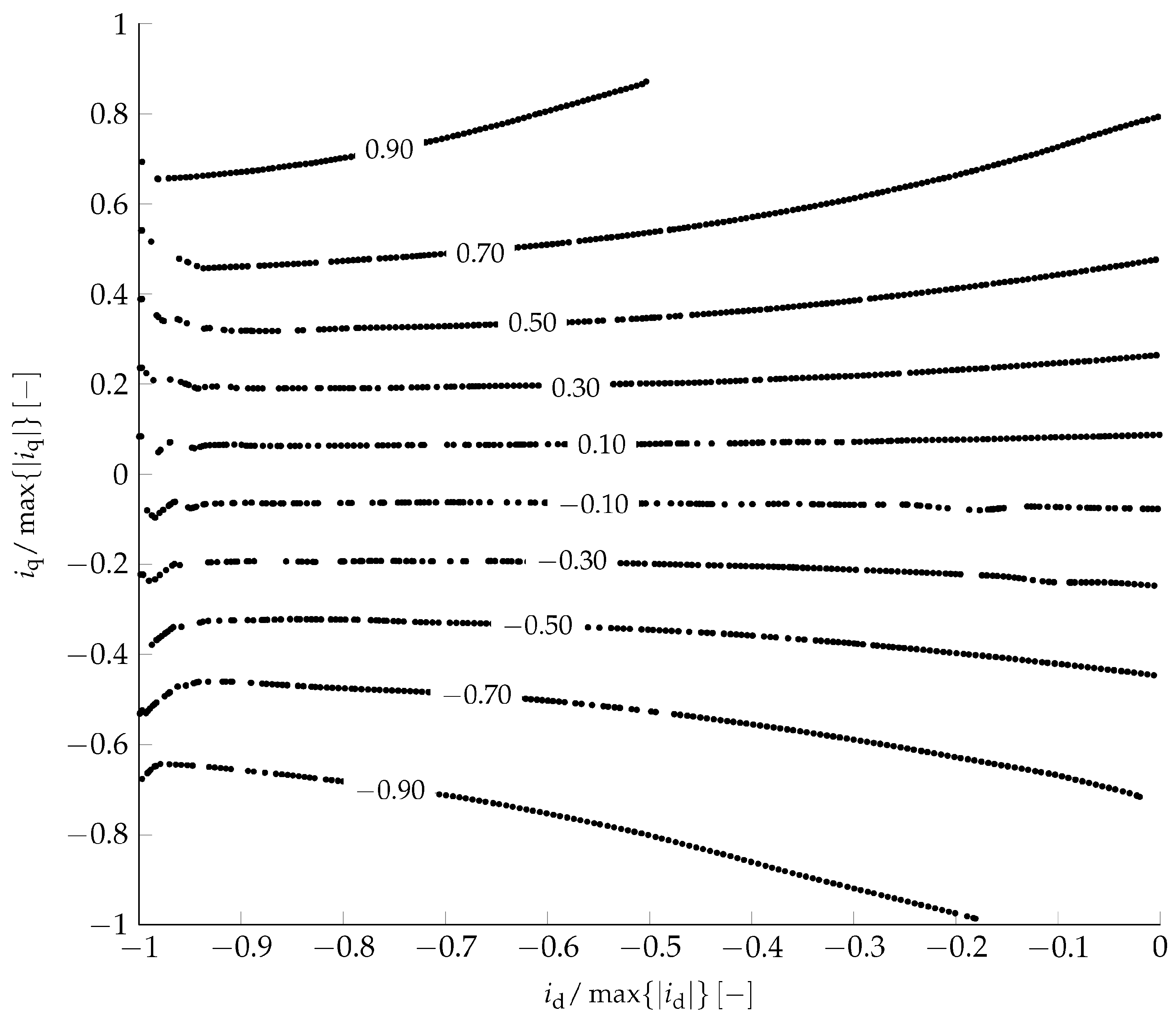
4.2. Measuring Electrical Machines
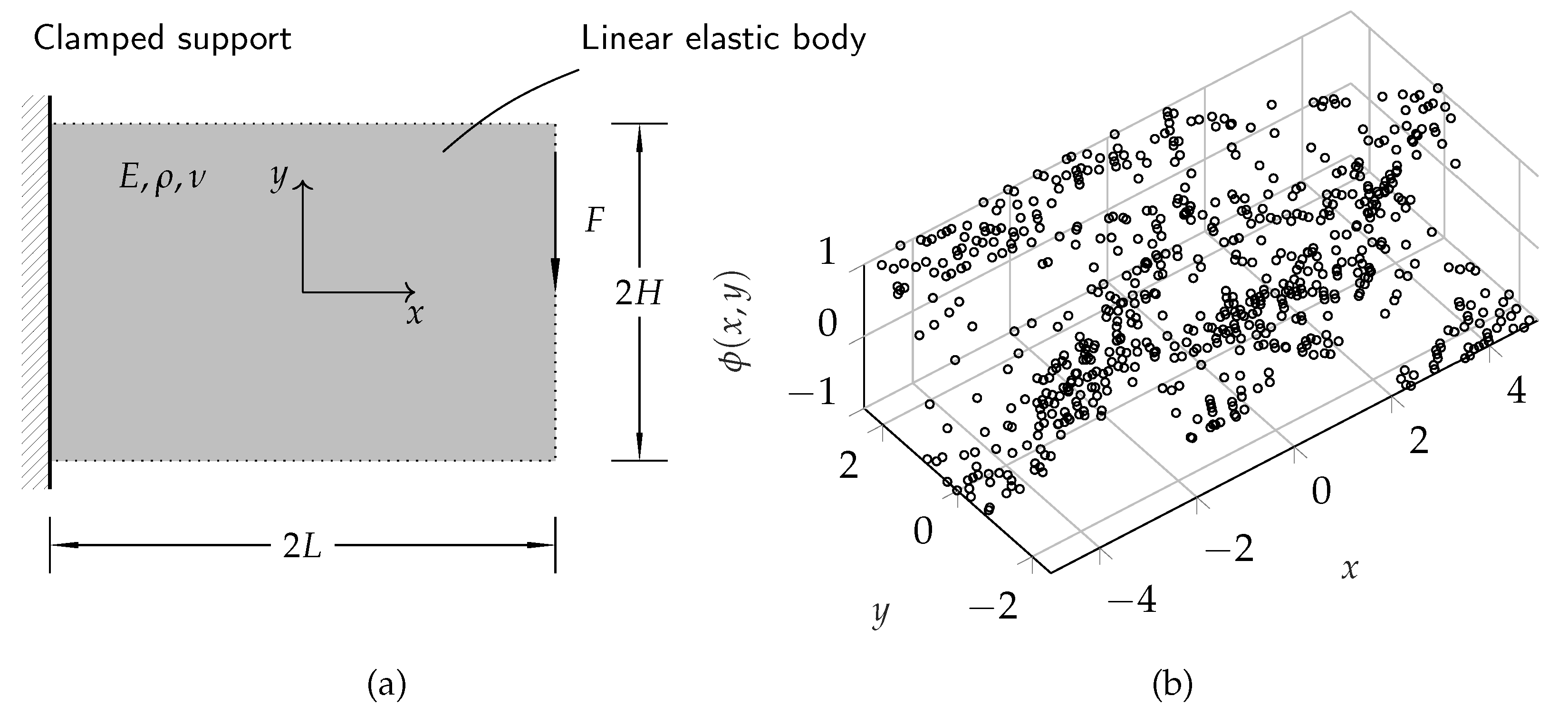
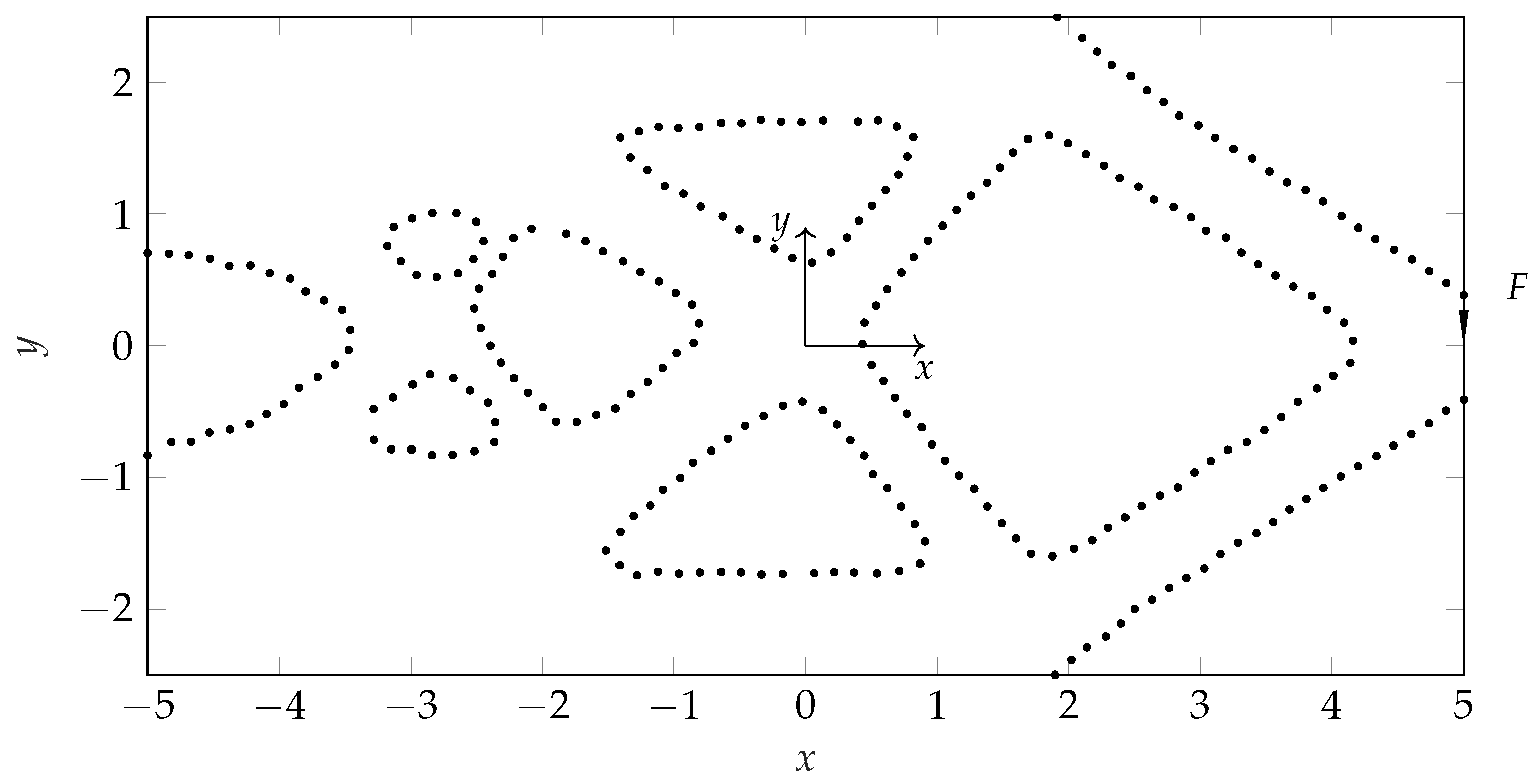
4.3. Structural Optimization
4.4. Further Impact
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. MATLAB Code Containing the RooTri Function
%...........................................................
% RooTri
% v1.0
%
% by Jan Oellerich & Keno Jann Buescher & Jan Philipp Degel
% 2023
%...........................................................
function [ipmat] = RooTri(arg1, arg2, arg3, arg4, arg5)
% INSTRUCTIONS
% add RooTri to your current working folder
% determine inputs as follows
% ouput m x 2 matrix called ‘ipmat’
% INPUTS
% arg1 point cloud as n x 3 matrix
% arg2 a of parameter plane equation, default = 0
% arg3 b of parameter plane equation, default = 0
% arg4 c of parameter plane equation, default = 1
% arg5 d of parameter plane equation, default = 0
% perform delaunay triangulation
T = delaunay(arg1(:,1),arg1(:,2));
a_vec = arg2 * ones(length(T(:,1)),1);
b_vec = arg3 * ones(length(T(:,1)),1);
c_vec = arg4 * ones(length(T(:,1)),1);
d_vec = arg5 * ones(length(T(:,1)),1);
p1_mat = [arg1(T(:,1),1) arg1(T(:,1),2) arg1(T(:,1),3)];
p2_mat = [arg1(T(:,2),1) arg1(T(:,2),2) arg1(T(:,2),3)];
p3_mat = [arg1(T(:,3),1) arg1(T(:,3),2) arg1(T(:,3),3)];
vec_1 = p2_mat - p1_mat; % main vector 1: p1 -> p2
vec_2 = p3_mat - p2_mat; % main vector 2: p2 -> p3
vec_3 = p1_mat - p3_mat; % main vector 3: p3 -> p1
aux_p12 = p1_mat + 0.5 * vec_1; % aux. point on vector 1
aux_p23 = p2_mat + 0.5 * vec_2; % aux. point on vector 2
aux_p31 = p3_mat + 0.5 * vec_3; % aux. point on vector 3
aux_vec_12_3 = p3_mat - aux_p12;
aux_vec_23_1 = p1_mat - aux_p23;
aux_vec_31_2 = p2_mat - aux_p31;
aux_vec_12_23 = aux_p23 - aux_p12;
aux_vec_23_31 = aux_p31 - aux_p23;
aux_vec_31_12 = aux_p12 - aux_p31;
lambda_mat(:,1) = (d_vec - (p1_mat(:,1).* a_vec + ...
p1_mat(:,2).* b_vec + p1_mat(:,3).* c_vec)) ./ ...
(vec_1(:,1).* a_vec + vec_1(:,2).* b_vec + ...
vec_1(:,3).* c_vec);
lambda_mat(:,2) = (d_vec - (p2_mat(:,1).* a_vec + ...
p2_mat(:,2).* b_vec + p2_mat(:,3).* c_vec)) ./ ...
(vec_2(:,1).* a_vec + vec_2(:,2).* b_vec + ...
vec_2(:,3).* c_vec);
lambda_mat(:,3) = (d_vec - (p3_mat(:,1).* a_vec + ...
p3_mat(:,2).* b_vec + p3_mat(:,3).* c_vec)) ./ ...
(vec_3(:,1).* a_vec + vec_3(:,2).* b_vec + ...
vec_3(:,3).* c_vec);
lambda_mat(:,4) = (d_vec - (aux_p12(:,1).* a_vec + ...
aux_p12(:,2).* b_vec + aux_p12(:,3).* c_vec)) ./ ...
(aux_vec_12_3(:,1).* a_vec + aux_vec_12_3(:,2).* ...
b_vec + aux_vec_12_3(:,3).* c_vec);
lambda_mat(:,5) = (d_vec - (aux_p23(:,1).* a_vec + ...
aux_p23(:,2).* b_vec + aux_p23(:,3).* c_vec)) ./ ...
(aux_vec_23_1(:,1).* a_vec + aux_vec_23_1(:,2).* ...
b_vec + aux_vec_23_1(:,3).* c_vec);
lambda_mat(:,6) = (d_vec - (aux_p31(:,1).* a_vec + ...
aux_p31(:,2).* b_vec + aux_p31(:,3).* c_vec)) ./ ...
(aux_vec_31_2(:,1).* a_vec + aux_vec_31_2(:,2).* ...
b_vec + aux_vec_31_2(:,3).* c_vec);
lambda_mat(:,7) = (d_vec - (aux_p12(:,1).* a_vec + ...
aux_p12(:,2).* b_vec + aux_p12(:,3).* c_vec)) ./ ...
(aux_vec_12_23(:,1).* a_vec + aux_vec_12_23(:,2).* ...
b_vec + aux_vec_12_23(:,3).* c_vec);
lambda_mat(:,8) = (d_vec - (aux_p23(:,1).* a_vec + ...
aux_p23(:,2).* b_vec + aux_p23(:,3).* c_vec)) ./ ...
(aux_vec_23_31(:,1).* a_vec + aux_vec_23_31(:,2).* ...
b_vec + aux_vec_23_31(:,3).* c_vec);
lambda_mat(:,9) = (d_vec - (aux_p31(:,1).* a_vec + ...
aux_p31(:,2).* b_vec + aux_p31(:,3).* c_vec)) ./ ...
(aux_vec_31_12(:,1).* a_vec + aux_vec_31_12(:,2).* ...
b_vec + aux_vec_31_12(:,3).* c_vec);
% compute intersection matrices
intersec_mat_1 = p1_mat + lambda_mat(:,1).* vec_1;
intersec_mat_2 = p2_mat + lambda_mat(:,2).* vec_2;
intersec_mat_3 = p3_mat + lambda_mat(:,3).* vec_3;
intersec_mat_4 = aux_p12 + lambda_mat(:,4).* aux_vec_12_3;
intersec_mat_5 = aux_p23 + lambda_mat(:,5).* aux_vec_23_1;
intersec_mat_6 = aux_p31 + lambda_mat(:,6).* aux_vec_31_2;
intersec_mat_7 = aux_p12 + lambda_mat(:,7).* aux_vec_12_23;
intersec_mat_8 = aux_p23 + lambda_mat(:,8).* aux_vec_23_31;
intersec_mat_9 = aux_p31 + lambda_mat(:,9).* aux_vec_31_12;
ipmat = intersec_mat_1(...
lambda_mat(:,1) <=1 & lambda_mat(:,1) >= 0,:,:);
ipmat = [ipmat; ...
intersec_mat_2(...
lambda_mat(:,2) <=1 & lambda_mat(:,2) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_3(...
lambda_mat(:,3) <=1 & lambda_mat(:,3) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_4(...
lambda_mat(:,4) <=1 & lambda_mat(:,4) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_5(...
lambda_mat(:,5) <=1 & lambda_mat(:,5) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_6(...
lambda_mat(:,6) <=1 & lambda_mat(:,6) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_7(...
lambda_mat(:,7) <=1 & lambda_mat(:,7) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_8(...
lambda_mat(:,8) <=1 & lambda_mat(:,8) >= 0,:,:)];
ipmat = [ipmat; ...
intersec_mat_9(...
lambda_mat(:,9) <=1 & lambda_mat(:,9) >= 0,:,:)];
if isempty(ipmat)
ipmat = [];
disp(‘ERROR: no intersection points found’)
else
% clean matrix
ipmat = unique(ipmat,‘rows’);
end
end
Appendix B. Exemplary Application of Contourc
%........................................................... % Exemplary Application of contourc % % by Jan Oellerich & Keno Jann Buescher & Jan Philipp Degel % 2023 %........................................................... % INSTRUCTIONS % l as interval limits % n as number of increments clc clear close all l = 25; n = 50; % define vectors x and y x = linspace(-l,l,n); y = linspace(-l,l,n); % build mesh grid [X,Y] = meshgrid(linspace(-l,l,n)); % generate matrix Z = sin(pi * X / 8) + cos(pi * Y / 8) + 0.1; % perform contourc function P1 = contourc(x,y,Z,[0,0]); plot(P1(1,:),P1(2,:),‘o’,‘MarkerSize’,2) axis equal; xlabel(‘x’); ylabel(‘y’)
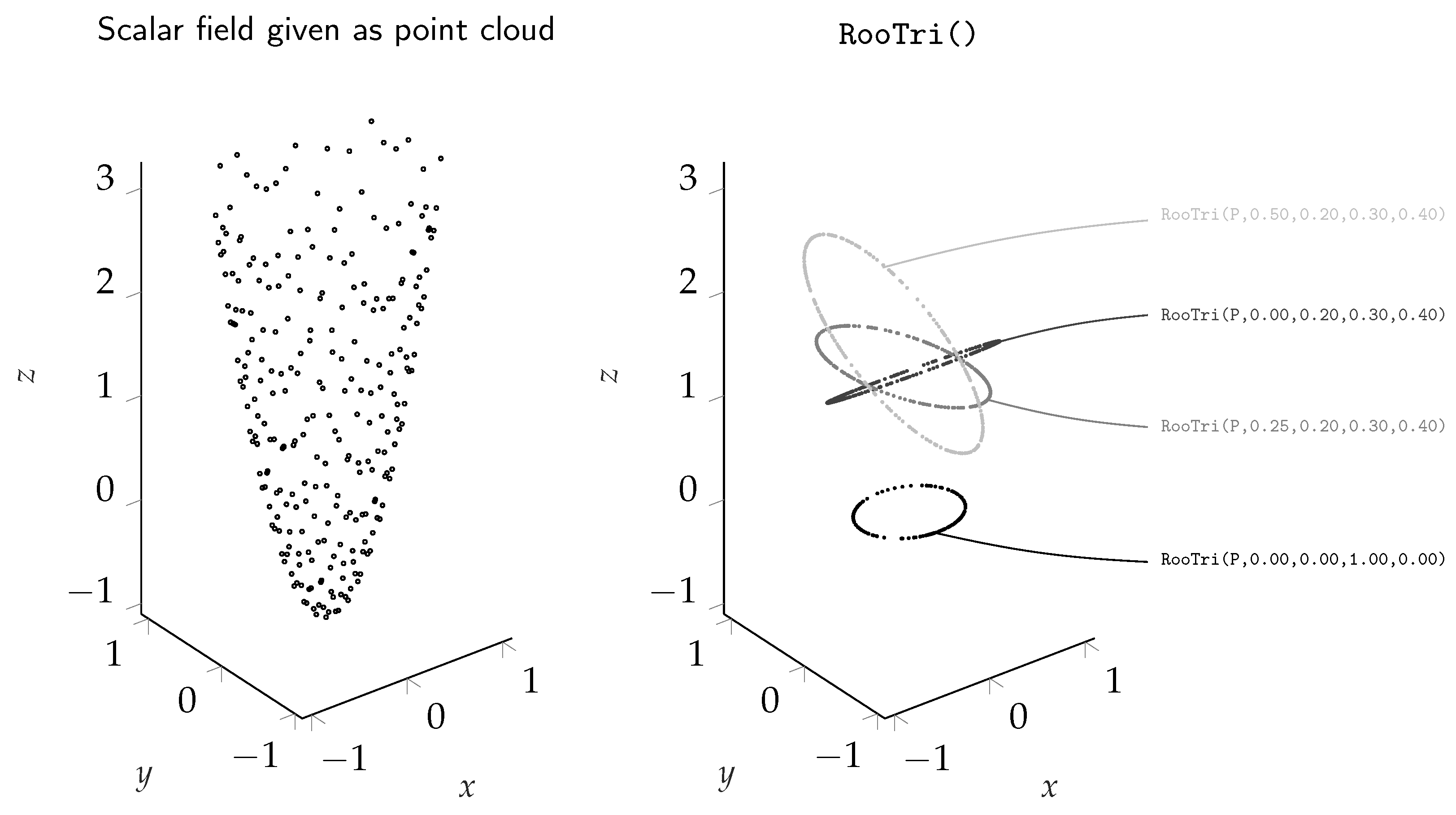
Appendix C. Exemplary Application of RooTri
%........................................................... % Exemplary Application of RooTri % % by Jan Oellerich & Keno Jann Buescher & Jan Philipp Degel % 2023 %........................................................... % INSTRUCTIONS % add RooTri to your current working folder % add RooTriExample.txt to your current working folder clc clear close all % load RooTriExample.txt file as point cloud P = readmatrix(‘RooTriExample.txt’); % define plane parameters a = 0.50; b = 0.20; c = 0.40; d = 0.30; % run RooTri() ipmat = RooTri(P,a,b,c,d); % plot results scatter3(ipmat(:,1),ipmat(:,2),ipmat(:,3),1,‘k’) axis equal title(‘Intersection points’) xlabel(‘x’); ylabel(‘y’); zlabel(‘z’)
References
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics, 2nd ed.; Texts in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ryaben’kii, V.; Tsynkov, S. A Theoretical Introduction to Numerical Analysis, 1st ed.; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Brent, R.P. An algorithm with guaranteed convergence for finding a zero of a function. Comput. J. 1971, 14, 422–425. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. SIGGRAPH Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Maple, C. Geometric design and space planning using the marching squares and marching cube algorithms. In Proceedings of the 2003 International Conference on Geometric Modeling and Graphics, London, UK, 16–18 July 2003; pp. 90–95. [Google Scholar] [CrossRef]
- Sin, Z.P.T.; Ng, P.H.F. Planetary Marching Cubes: A Marching Cubes Algorithm for Spherical Space. In Proceedings of the 2018 2nd International Conference on Video and Image Processing, Hong Kong, China, 29–31 December 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 89–94. [Google Scholar] [CrossRef]
- Custodio, L.; Pesco, S.; Silva, C. An extended triangulation to the Marching Cubes 33 algorithm. J. Braz. Comput. Soc. 2019, 25, 6. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S.; Wang, M.; Duan, Z. A marching cube algorithm based on edge growth. Virtual Real. Intell. Hardw. 2021, 3, 336–349. [Google Scholar] [CrossRef]
- Nielson, G.; Hamann, B. The asymptotic decider: Resolving the ambiguity in marching cubes. In Proceedings of the Visualization ’91, San Diego, CA, USA, 22–25 October 1991; pp. 83–91. [Google Scholar] [CrossRef]
- Grosso, R. An Asymptotic Decider for Robust and Topologically Correct Triangulation of Isosurfaces: Topologically Correct Isosurfaces. In Proceedings of the CGI ’17 Computer Graphics International Conference, Yokohama, Japan, 27–30 June 2017; Association for Computing Machinery: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Athawale, T.M.; Johnson, C.R. Probabilistic Asymptotic Decider for Topological Ambiguity Resolution in Level-Set Extraction for Uncertain 2D Data. IEEE Trans. Vis. Comput. Graph. 2019, 25, 1163–1172. [Google Scholar] [CrossRef] [PubMed]
- Wilhelms, J.; Van Gelder, A. Octrees for Faster Isosurface Generation. SIGGRAPH Comput. Graph. 1990, 24, 57–62. [Google Scholar] [CrossRef]
- Livnat, Y.; Shen, H.W.; Johnson, C. A near optimal isosurface extraction algorithm using the span space. IEEE Trans. Vis. Comput. Graph. 1996, 2, 73–84. [Google Scholar] [CrossRef]
- Redfern, D.; Campbell, C. The Matlab® 5 Handbook; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Demirkaya, O.; Asyali, M.; Sahoo, P. Image Processing with MATLAB: Applications in Medicine and Biology; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Sheikh, A. Matrix and Finite Element Analyses of Structures, 1st ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- de Berg, M.; Cheong, O.; van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Santner, T.; Williams, B.; Notz, W. The Design and Analysis of Computer Experiments, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Loeppky, J.; Sacks, J.; Welch, W. Choosing the Sample Size of a Computer Experiment: A Practical Guide. Technometrics 2009, 51, 366–376. [Google Scholar] [CrossRef]
- Shang, Y.W.; Qiu, Y.H. A Note on the Extended Rosenbrock Function. Evol. Comput. 2006, 14, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Naresh Babu, A.; Ramana, T.; Sivanagaraju, S. Analysis of optimal power flow problem based on two stage initialization algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 91–99. [Google Scholar] [CrossRef]
- Degel, J.P.; Gullone, G.; Doppelbauer, M.; Klöffer, C.; Wondrak, W. A Novel Approach of High Dynamic Current Control of Interior Permanent Magnet Synchronous Machines. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Zhuang, Z.; Xie, Y.; Zhou, S. A Reaction Diffusion-based Level Set Method Using Body-fitted Mesh for Structural Topology Optimization. Comput. Methods Appl. Mech. Eng. 2021, 381, 113829. [Google Scholar] [CrossRef]
| Argument | Description |
|---|---|
| arg1 | Point cloud |
| arg2 | Plane parameter |
| arg3 | Plane parameter |
| arg4 | Plane parameter |
| arg5 | Plane parameter |
| Lenovo T480s |
| Matlab© R2022b |
| Microsoft Windows 10 Enterprise LTSC |
| Intel(R) Core (TM) i7-8550U CPU @ 1.80 GHz, 1992 MHz, 4 cores, 8 logical processors |
| Installed physical memory 16.0 GB |
| Name | Equation |
|---|---|
| Parabola function | |
| Peaks function | |
| Rosenbrock function | |
| Himmelblau’s function |
| Experiment | Function | Experiment | Function | ||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2.0 | 4.3 | 16 | 3 | −3.0 | 8.2 |
| 2 | 1 | 3.5 | 4.9 | 17 | 3 | 1.3 | 8.1 |
| 3 | 1 | −2.1 | 2.9 | 18 | 3 | −1.6 | 4.8 |
| 4 | 1 | 4.9 | 9.6 | 19 | 3 | 1.4 | 3.5 |
| 5 | 1 | −4.1 | 6.7 | 20 | 3 | 2.7 | 3.1 |
| 6 | 2 | 2.6 | 4.4 | 21 | 3 | 4.6 | 6.0 |
| 7 | 2 | 3.3 | 7.1 | 22 | 4 | 3.8 | 8.6 |
| 8 | 2 | 0.6 | 6.9 | 23 | 4 | −2.7 | 3.0 |
| 9 | 2 | −3.6 | 3.8 | 24 | 4 | 0.7 | 1.7 |
| 10 | 2 | −0.2 | 9.8 | 25 | 4 | −4.6 | 7.4 |
| 11 | 2 | −3.7 | 1.6 | 26 | 4 | 0.1 | 9.3 |
| 12 | 2 | −2.9 | 2.0 | 27 | 4 | −4.8 | 6.3 |
| 13 | 3 | −0.6 | 2.6 | 28 | 4 | −1.3 | 5.6 |
| 14 | 3 | 4.2 | 7.7 | 29 | 4 | −2.0 | 5.5 |
| 15 | 3 | −1.0 | 4.3 | 30 | 4 | 1.9 | 8.8 |
| 2029 | 2496 | 2565 | 2581 | 2595 | 2850 | 2875 | 2940 | 2970 | 1479 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oellerich, J.; Büscher, K.J.; Degel, J.P. RooTri: A Simple and Robust Function to Approximate the Intersection Points of a 3D Scalar Field with an Arbitrarily Oriented Plane in MATLAB. Algorithms 2023, 16, 409. https://doi.org/10.3390/a16090409
Oellerich J, Büscher KJ, Degel JP. RooTri: A Simple and Robust Function to Approximate the Intersection Points of a 3D Scalar Field with an Arbitrarily Oriented Plane in MATLAB. Algorithms. 2023; 16(9):409. https://doi.org/10.3390/a16090409
Chicago/Turabian StyleOellerich, Jan, Keno Jann Büscher, and Jan Philipp Degel. 2023. "RooTri: A Simple and Robust Function to Approximate the Intersection Points of a 3D Scalar Field with an Arbitrarily Oriented Plane in MATLAB" Algorithms 16, no. 9: 409. https://doi.org/10.3390/a16090409
APA StyleOellerich, J., Büscher, K. J., & Degel, J. P. (2023). RooTri: A Simple and Robust Function to Approximate the Intersection Points of a 3D Scalar Field with an Arbitrarily Oriented Plane in MATLAB. Algorithms, 16(9), 409. https://doi.org/10.3390/a16090409