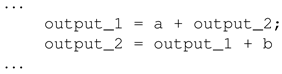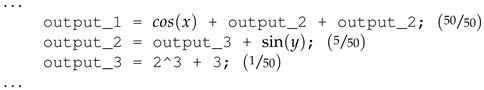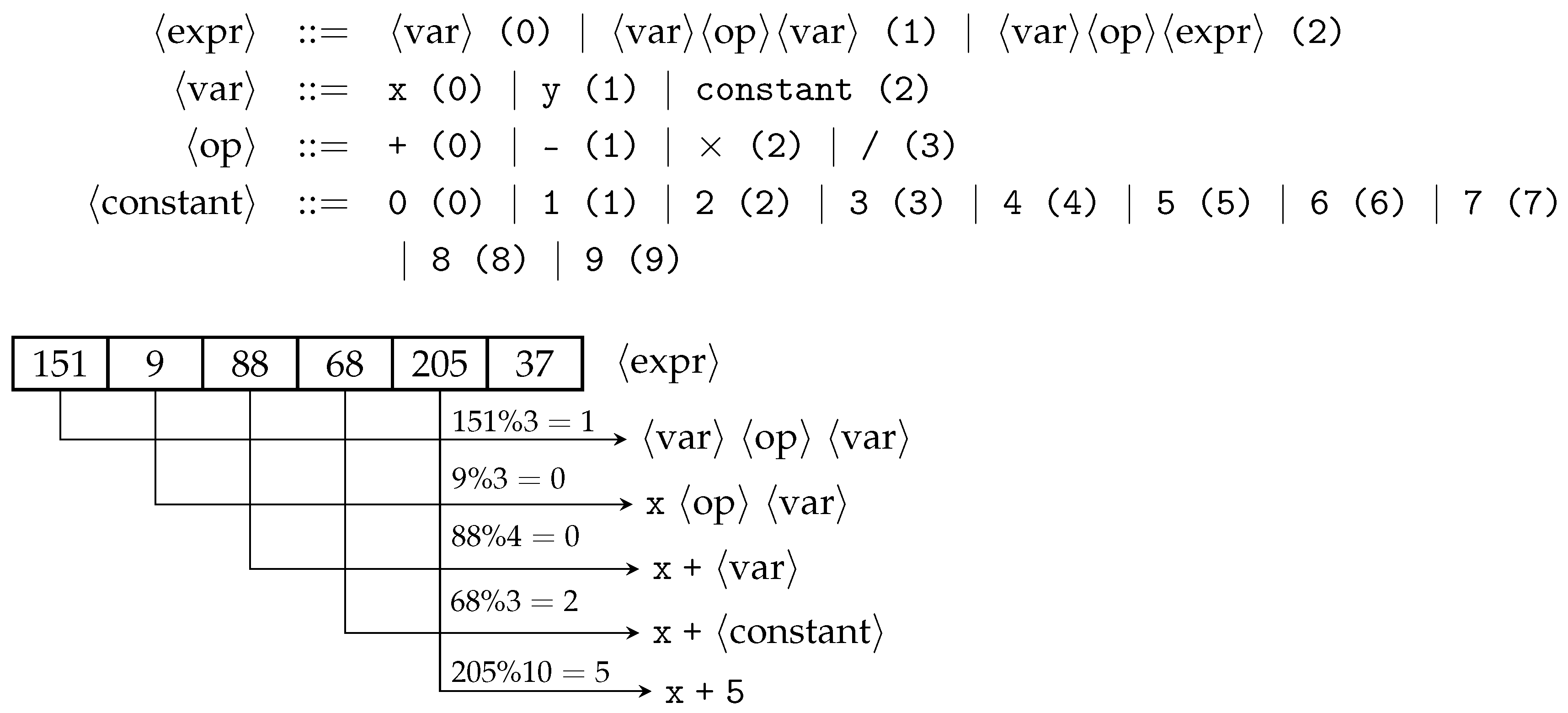1. Introduction
Evolvable Hardware (EWH) encompasses the application of evolutionary algorithms (EAs) to the design of re-configurable hardware and conventional circuits. Since its inception, circuits such as adders and multipliers have been evolved. Some EAs used in EHW include Genetic Algorithms, Genetic Programming (GP), Cartesian Genetic Programming, and Grammatical Evolution (GE). Confronting the field are two significant challenges: scalability of fitness evaluation and representation. The former deals with the required testing as circuit inputs increase (complex circuits). The latter, which is also a consequence of increasing inputs, requires longer chromosomes to represent individuals. Hence, due to the destructive nature of search operators (crossover and mutation), evolving circuits of such complexity is non-trivial.
Some existing approaches proposed to address the issue of representation scalability are decomposition [
1,
2] and more efficient genetic operators [
3]. Existing decomposition approaches break complex circuits down into evolvable sub-circuits either via inputs [
2] or outputs [
1] and merge them into a complete circuit using varying strategies. Other research efforts have also been directed toward efficiently reducing the computational cost of circuit evaluation. Some of these include parallel implementations of EAs, using different representations for evaluation and, more recently, corner case testing, a well-known technique used in industry to reduce the amount of testing, combined with a uniform sampling of training/testing cases [
4].
A major benefit of GE’s mapping process is the separation of the genotypic space from the phenotypic space, which facilitates an unconstrained evolutionary search [
5]. While there has been some suggestion that the low locality, i.e., the measure of the correlation between neighbouring genotypes and their corresponding neighbouring phenotypes brings about an issue [
6], other works [
7,
8,
9] suggest genetic operations at the beginning regions of GE’s genome are destructive but may serve as a good region for genetic operations.
Generally, a multi-output problem requires modeling complex input-output relationships and/or inter-output dependencies. Multi-output problems requiring the simultaneous modeling of these relationships are very challenging to deal with [
10]. Hence, decomposing such problems into single-output problems and solving each using a single-output algorithm of choice may prove very challenging as such approaches do not consider inter-output correlations [
10]. This paper proposes a Multi-Genome GE (MG-GE) for solving multi-output or multi-target problems, such as circuit problems, efficiently. Each genome encodes a solution to a single and unique output. Second, custom grammar syntax rules are introduced to facilitate the evolution of inter-output correlations by evolution. Third, we speculate that using Multi-Genome (MG) reduces the destructive effect of genetic operators by using a genome per output variable while benefiting from their ability to escape local optima. Fourth, MG-GE keeps track and stops the search for a solved output variable which is made available to all individuals in the population, thereby reducing the overall computational cost as evolution progresses. Finally, MG-GE is better suited for multi-output circuit problems than approaches that decompose such problems into single-output circuit problems using various decomposition techniques before merging the evolved sub-circuits into a complete circuit.
The contributions of this work are summarised as follows:
We present a multi-genome implementation of GE better suited for tackling multi-output problems;
We adapt genetic operators, initialisation routine, and mapping mechanism and implement a wrapping operator well-suited for MG-GE;
We introduce custom grammar syntax rules and a cyclic dependency-checking algorithm that facilitates the evolution of inter-output dependencies;
We investigate the performance of MG-GE with and without using our custom grammar syntax rules on multi-output combinational circuit problems.
2. Background
2.1. Grammatical Evolution
GE is a GP variant that evolves programs in any arbitrary Backus–Naur form (BNF) compliant language. GE has been used in different application domains such as game content design [
11], architecture design [
12], financial modelling [
13], music [
14] and software testing [
15].Standard GE uses a single linear genome. The genome is a sequence of codons (usually 8-bit unsigned numbers) that encode the genetic information of an individual. The corresponding phenotype is derived from a genome using a mapper. The mapper requires a grammar, usually a subset of the target language, sufficient to evolve an optimal solution to a problem potentially. A valid phenotype is derived only when all non-terminal symbols have been re-written regarding terminal symbols (any term without angle brackets). To expand a non-terminal into a string of terminals only, a derivation formula (
) is applied. Each phenotype is evaluated using the defined fitness function. The fitness score returned by the fitness function is assigned as the individual’s fitness.
BNF is a meta-syntax notation used for expressing grammars of formal languages, such as Context-Free Grammars (CFG). Grammars most commonly used within GE are CFGs. A CFG denoted by G is defined by a quadrupled tuple . N represents the set of non-terminal symbols which are enclosed within < >. For example, is a non-terminal symbol. Non-terminal symbols are placeholders and replaced by another symbol according to production rules. Production rules appear after the replacement symbol on the right-hand side. All non-terminal symbols are replaced, or expanded, until they become terminal symbols. T represents the set of terminal symbols which are not enclosed within < >. For example, variable names and operators (e.g., +, −) of a programming language are considered terminals. P represents production rules which are alternatives or choices to replace a non-terminal and are separated by|symbol. S represents the start symbol which is part of N and serves as the initial symbol from which a legal sentence in the target language can be derived.
2.2. Multi-Output Problems
Multiple output or target variables characterise multi-output (also known as multi-target or multi-variate) problems. Multi-variate regression and multi-label classification are categories of multi-output problems. Multi-variate regression deals with the estimation of a single regression model which models how multiple independent and dependent variables are linearly related. Multi-variate regression is used in different domains such as economics and finance, health care, social sciences, environmental studies and market research. For example, in economics and finance multi-variate regression is used to investigate the factors that affect inflation rates, stock prices, housing prices and GDP growth rate. In multi-label classification, zero or multiple labels are required as output per input sample [
16]. Gene classification in bio-informatics, text categorisation and image classification are real-world applications of Multi-label classification. These problems are challenging to deal with, mainly due to their multi-variate nature and possible dependencies between target variables [
17].
Methodologies designed for tackling multi-output regression problems are categorised into two groups:
problem transformation and
algorithm adaptation methods [
17]. Problem transformation methods transform multi-output problems into single-output problems, each uniquely solving one of the target variables using any single regression algorithm of choice [
17]. Algorithm adaptation methods adapt existing single-target algorithms to handle multi-target problems [
17]. Some advantages of the latter approach are better performance, better representation & interpretability, and computationally more efficiency compared to single-target methods [
17].
2.3. Hardware Description Languages
Hardware Description Languages (HDLs) such as Verilog and VHDL are the de facto standard for circuit design in the industry due to several benefits [
18]. Notable among these are the design of circuits at higher abstraction—Register Transfer Level (RTL), other than gate level [
19]. Additionally, RTL designs are more interpretable, require less time to modify and easier to verify [
20]. RTL designs employ programming constructs such as conditional statements, synthesisable for-loops, proceedural blocks, case statements, asynchronous and synchronous constructs to provide a human readable description of a circuit’s behaviour. As a result, RTL designs must undergo logic synthesis where these high level descriptions of circuits are converted to basic building blocks such as logic gates (AND, NOT, NAND, NOR and XOR)and flip-flops (or storage elements). GE has successfully evolved complex and accurate multiplier, adder, and parity using SystemVerilog [
4].
2.4. Related Work
Digital circuit designs like adders and multipliers require multiple output signals to be correct for their output to be accurate. Some of these output signals can be independent of one another, meaning that only a sub-section of an individual needs to be modified. These sub-modifications can be difficult for a classical GA with a single chromosome to perform as the genetic operators do not know how the modifications will affect the candidate design.
Multiple chromosomes have been used in various evolutionary hardware problems to tackle this problem. Cartesian Genetic Programming (CGP) is often used with gate-level evolutionary hardware problems as its column and row structure is ideal for connecting Boolean logic gates. Multiple codons in the chromosome are consumed when choosing a gate and its connections, which can lead to issues when performing crossover, as different gates can have a different number of connections. Slowik and Bialko [
21] address this by using a multi-chromosome genome that groups the logic gates with their input connections. This allows for the crossover method only select crossover points that would not produce an unconnected input and thus produce only valid individuals.
Walker et al. [
22] introduced a method called Multi-Chromosome CGP (MC-CGP) for Evolutionary Hardware. This approach uses a multi-chromosome where each chromosome is used in a separate CGP evolution to evolve a partial solution for a single output. When a solution is found for each output, they are then combined to produce the final solution. This approach allows the evolution to be performed in parallel but can produce redundant circuitry. To address this problem, Coimbra and Lamar [
23] used a hybrid approach of running an MC-CGP followed by a standard CGP where the multi-chromosome is treated as a single chromosome. This approach allowed them to reduce the gate count of the evolved individuals significantly.
CGP is generally only employed at the gate-level and thus cannot enjoy the benefit of HDLs. Work that has looked at higher-level problems includes a multi-objective approach that was taken to evolve a Proportional-Plus-Derivative fuzzy logic controller. In this work, Baine [
24] used four separate chromosomes to describe the input and output fuzzy sets for both the proportional and derivative parts of the controller. He found that the multi-chromosome approach converged around 20% faster than a single-chromosome approach.
In [
25], standard Gene Expression Programming (GEP) is adapted to directly handle multi-target regression problems without resorting to any transformation or decomposition approaches. A multi-gene chromosome representation is adopted. An
N-target regression problem requires a chromosome with
N genes. Each gene codes a solution to a single and unique target variable. Hence, the number of genes contained in a chromosome is problem-dependent. Individual initialisation remains the same as in standard GEP but is subject to a metric that ensures an individual is only added to the initial population if its similarity compared to other individuals in the population is below a threshold. Three different transposition operators are used to transpose gene fragments within the same gene, between two genes (of the same chromosome), and move a gene to the beginning of the chromosome. Also, three recombination operators are used to create offspring. Tested on eight multi-target regression datasets in comparison to two other methods, Gene Expression Programming for Multi-target Regression (GEPMTR) significantly outperformed the two state-of-the-art methods in seven of the eight multi-target datasets employed.
These works show that using a multi-chromosome approach for multi-target problems can significantly help find solutions. In addition, it helps address the issue of locality that Grammatical Evolution can experience.
3. Proposed Approach: Multi-Genome GE
3.1. Problem Description
GE mapping process starts from a start symbol. Usually, the first rule’s non-terminal is designated as the start symbol. For example in
Figure 1,
is the start symbol. GE iteratively expands or rewrites all non-terminals by using a modulus rule to select a production each time a choice needs to be made. This process continues until the sentence consists solely of terminals. In
Figure 1, using the sample genome provided, the sentence
is obtained.
Assuming a mutation event affects the first codon, changing its value from 151 to 150, this means the first production gets chosen after applying the mod rule (). As a result, the resultant sentence is now x after the mutation event. As described, a totally different phenotype is obtained after a simple codon alteration in GE’s genome, with all potentially evolved building blocks lost after genetic operations. This phenomenon is referred to as ripple effect.
As mentioned earlier, multi-output problems require all outputs to be simultaneously evolved. Assuming a standard GE individual (single genome representation) solves two of the three output variables due to the ripple effect caused by genetic operators, solving the remaining output variable may be challenging. It is also computationally expensive as there is no mechanism in place to stop searching for output variables that other individuals in the population have successfully evolved. Furthermore, standard GE does not have the necessary functionality to evolve inter-target dependencies properly.
3.2. Problem Formulation
Assuming a combinational circuit denoted as C has multiple inputs and outputs, the training/testing vectors for C can be denoted as and representing inputs and expected outputs respectively. Each circuit output in can depend on one to m input variables () as well as from zero to circuit outputs ; as far as no cyclic dependencies are formed between output variables in the case of combinational circuits. In certain instances, a circuit output may depend on one or more outputs as inputs.
Given that multi-output circuit problems (and multi-output problems in general) generally exhibit a more complex behaviour compared to a single-output circuit problem, evolving such circuits, especially at a low level of design—gate-level, using standard GE is intractable. To help cope with the challenges associated with evolving multi-output circuit problems using standard GE, a novel Multi-Genome GE is proposed.
3.3. Multi-Genome GE
MG-GE uses a multiple genome representation consisting of
n genomes, where
n represents the number of outputs or targets. Each genome evolves a circuit functionality that satisfies a single and unique circuit output. An example of a multi-genome for a multi-output problem with three output variables or target variables is shown in
Figure 2. An output or target variable is a variable to be predicted by other variables.
A new genome representation requires suitable initialisation routines, mapping mechanisms, selection, replacement, wrapping mechanisms, and genetic operators. Furthermore, we introduce grammar design specifications which must be adhered to for proper parsing of the grammar to ensure the adapted initialisation routine and mapper algorithms work properly. These adapted, and new operators are described in detail in subsequent sections.
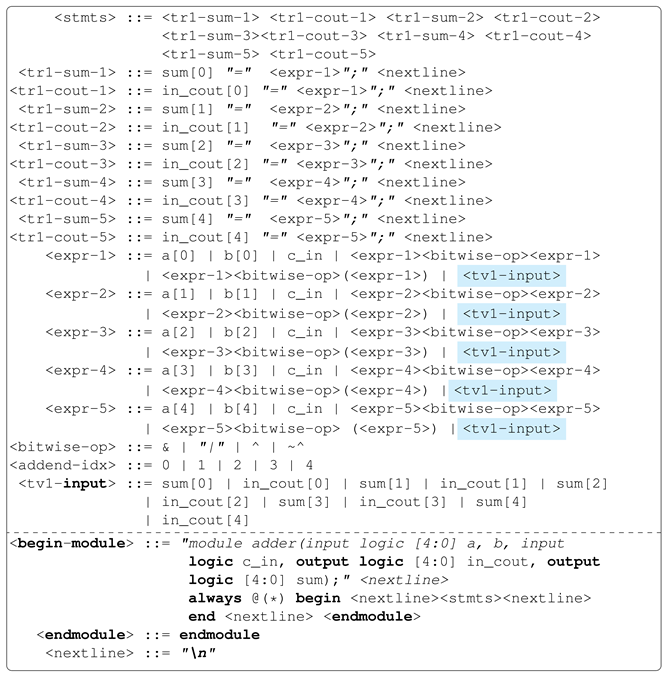
3.4. Grammar Design
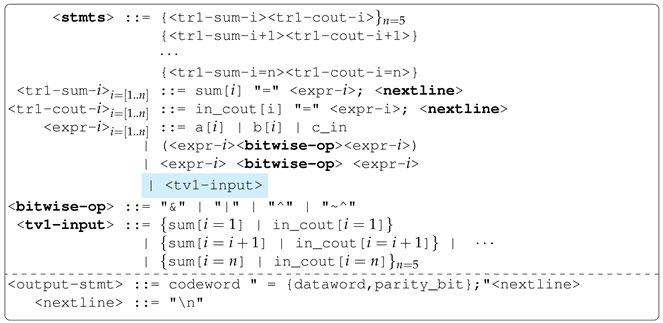
In MG-GE, each genome is mapped to its output expression or subprogram to model and predict its corresponding output variable. MG-GE requires a single grammar, just like standard GE. However, custom grammar rules have been introduced and must be adhered to. There are two main custom rules:
output rule and
output variable rule. These rules are illustrated by a sample grammar in
Figure 3. These custom rules allow for grammar rules to be annotated with required details which are parsed and used by the mapper, wrapper, selection, initialisation and genetic operators.
An
output rule (or
target rule) is a rule that codes a solution to one of the output variables in a multi-output problem. To define an output rule, the rule’s name must be preceded by
tr followed by an output group number. During the mapping process, whenever such a rule is encountered, a sub-mapping process is spawned. For example, in
Figure 3, there are four output rules:
,
,
and
. Also, in
Figure 3, there are two groups of output variables:
and
. In other words, there should be an output variable rule for each output group number as illustrated in
Figure 3.
The purpose of the group numbers is to facilitate modelling dependencies between output variables while avoiding cyclic dependencies, which is very key for the evolution of combinational circuit designs. Recall in
Section 3.2, we stated there might exist dependencies between outputs in some multi-output problems; hence, the group number allows outputs (represented by the output variable names as productions of output variable rules) to be grouped to allow evolution to evolve the potential dependencies which may exist between outputs belonging to the same group. For example, in combinational circuit problems, there may exist dependencies between outputs, but we need to ensure there exist no cyclic dependencies between these outputs. Failing to do so will result in circuit synthesis tools synthesising memory elements to store past/present output values, which render such a sequential circuit.
Illustrated in Listing 1 is an example of a program with an existing cyclic dependency. Assuming the program in Listing 1 is a combinational circuit design in SystemVerilog, both outputs depend on each other, which will cause memory elements to be synthesised by circuit synthesis tools rendering the circuit a sequential circuit instead of a combinational circuit. The cyclic dependency checker in Algorithm 3 is used to ensure that during the initialisation and mapping processes, such cyclic dependencies do not occur.
| Listing 1. A sample program with cyclic dependency. |
![Algorithms 16 00365 i001 Algorithms 16 00365 i001]() |
An output variable rule is defined by preceding the outputs group name by
tv followed by the output group number (e.g.,
and
). Essentially, an output variable rule’s productions are output variables (e.g.,
output_1 and
output_2) as shown in
Figure 3. Also, note that the exact order in which output rules are defined for each corresponding output variable must be followed when defining an output variable rule as observed in
Figure 3. For implementation purposes, extra attributes (corresponding output rule) are used to differentiate these outputs (e.g.,
output_1 and
output_2), which are terminals from other terminals in the grammar during initialisation and mapping processes. An output variable rule is how evolution evolves dependencies that may potentially exist between outputs. During the initialisation and mapping process of each output rule (in other words, when an output variable is being modelled), the cyclic dependency checker algorithm ensures only choices of output variables that do not cause cyclic dependency can be chosen whenever an output variable rule non-terminal is encountered. The cyclic dependency checker algorithm is described in
Section 3.7.
3.5. Initialisation
The initialisation of the multi-genome representation is dependent on the type of initialisation scheme required. In the case of random initialisation, each genome is randomly initialised. In other words,
n number (
n equals the number of outputs) of random initialisation events. However, sensible initialisation (SI) is preferred, as it creates diverse and valid individuals. SI is an adaptation of the ramped half-and-half GP initialisation scheme introduced by Koza [
26]. To benefit from SI’s desirable properties, we adapt sensible initialisation for use with the multi-genome representation. First, SI requires the grammar to be labelled. Each production of a rule is required to be labelled with the minimum depth to expand all non-terminals to terminals fully and whether or not the production is recursive or not. Each rule is then labelled recursive if any of its productions is recursive and the rule’s minimum depth equals the minimum of the minimum depth of its productions. During initialisation, SI applies grow and full methods when constructing the derivation tree. When applying the Grow method, any production with a minimum depth less than the remaining depth is eligible for selection. The remaining depth is obtained by subtracting the current depth from the specified maximum depth. The full method behaves similarly, except recursive productions are preferable if the remaining depth can accommodate it.
During MG-GE SI,
n genomes in the multi-genome will require
n SI events. The start symbol for each SI event is an output rule. The order of definition of the output rules in the grammar determine which genome to use during initialisation. The first genome is initialised by fully mapping the first output rule encountered, including any other rules occurring before the first output rule. The
genome is initialised when the
rule is encountered. The
genome is initialised with codons used to completely map the
output rule encountered and any remaining rules appearing after the
output rule. However, during the initialisation of an output rule, if an output variable rule is encountered, its corresponding dependency graph must be checked using the cyclic dependency checking algorithm to ensure only production choices not resulting in cyclic dependency are valid for selection. Recall from
Section 3.4 productions of output variable rules are essentially output variable names.
3.6. Multi-Genome Mapping
MG consists of
n genomes, where
n equals the number of output variables that must be simultaneously predicted. Given that there are
n genomes, the mapping process involves
n sub-mapping processes. Each genome encodes a solution to a single and unique output or output variable. As mentioned in
Section 3.4, the MG mapper requires a rule to be defined for each output variable termed
output rule. Output rule non-terminals serve as the start symbols for the sub-mapping processes. The order of output rule definitions dictates which genome to use during the sub-mapping process. The MG-GE mapping algorithm is shown in Algorithm 1.
The algorithm uses the first genome in MG to map the first output rule encountered during the mapping process. In other words, the order of definition of the output rules dictates which genome in MG to use. In addition, if non-terminals exist before the first and last output rules during the mapping process, codons are consumed from the first genome. Also, ideally, an output rule non-terminal must be used only once in the grammar.
MG-GE mapping process starts off by using the first genome, as can be seen on Line 6 in Algorithm 1. Lines 7–10 check if the genome contains any codons and terminates the mapping process if empty, as this indicates an invalid individual. Otherwise, if the genome contains codons, the mapping process continues as normal. The sub-mapping process is spawned as shown on line 16 in Algorithm 1, which maps the first output rule encountered, including all prior non-terminals, as stated in the previous paragraph. The sub-mapping process algorithm is shown in Algorithm 2. The sub-mapping algorithm is the same as the standard GE mapping process, with additional logic to accommodate the MG representation. The algorithm is recursive as it spawns a sub-mapping process whenever it encounters an unmapped output rule non-terminal by checking the set of
mapped_output_rules. Otherwise, it continues the mapping process consuming codons from the first genome (lines 13–18 in Algorithm 2). Lines 21–55 remain the same as standard GE mapping where symbols belonging to selected rule production are placed on a stack for subsequent derivation steps. Wrapping events are checked and applied accordingly.
| Algorithm 1: Multi-Genome GE Mapper |
![Algorithms 16 00365 i002 Algorithms 16 00365 i002]() |
| Algorithm 2: Output Rule Sub-Mapping |
![Algorithms 16 00365 i003 Algorithms 16 00365 i003]() |
3.7. Cyclic Dependency Checking Algorithm
Algorithm 3 shows the pseudo-code for the cyclic dependency checking. A 2D matrix is used as a graph to model the dependencies between each group of output variables. For each position
of matrix A, if
, it means that the output variable represented at position
i depends on the output variable at position
j. The function
UpdateGraphMatrix is a recursive function, which has the inputs
M, a square matrix with shape
, and
pos, the respective position to be updated. This function assigns 0 to the position
pos in the matrix
M, but this assignment triggers subsequent updates in its consequence. Subsequent calls of this function are recursive to ensure the necessary updates are made to prevent cyclic dependencies between output variables. For example, if output variable
a depends on output variable
b, then output variable
b cannot depend on output variable
a. Subsequently, any output variable which depends on output variable
b cannot depend on output variable
a.
| Algorithm 3: Cyclic Dependency Checking |
![Algorithms 16 00365 i004 Algorithms 16 00365 i004]() |
The main function FillMatrix initialises an empty matrix M with shape . Since the variables cannot depend on themselves, the positions , where , are initialised with 0. The input dependencies is a list with the respective dependencies to be filled in the matrix. In the next step, the positions regarding each dependency are filled with 1 (if possible), and the updates in consequence of that are made by calling the function UpdateGraphMatrix.
3.8. Perfect Wrapping
Given that multiple output variables are evolving simultaneously, a partially mapped output rule will render the entire individual invalid, negatively impacting the evolutionary performance. This means performing genetic operations in MG-GE will record higher invalid individuals than standard GE. In other words, the higher the number of output variables in a multi-output problem, the higher the number of invalid individuals created by genetic operations.
To mitigate this effect, we implement a new wrapping operator called
perfect wrapping. Perfect wrapping requires the grammar rules and productions to be labelled with the minimal number of codons required to map fully. The perfect wrapping operator requires a list of eligible productions as input. If the derived rule is an output variable rule, its corresponding dependency graph must be checked to determine its eligible productions. First, the list is populated with eligible productions which are non-recursive and require the minimum number of codons to expand fully. If the list is empty, then recursive productions requiring the minimum number of codons to expand are considered. Second, the mod rule is applied to determine if the chosen production is part of the list of eligible productions. If not, one of the productions in the list is uniformly selected at random, and Equation (
1) is used to generate a new codon to replace the current codon, which, when used with the mod rule, dictates the same choice. This process continues while codons are reused from the genome until a valid sentence is attained.
3.9. Selection
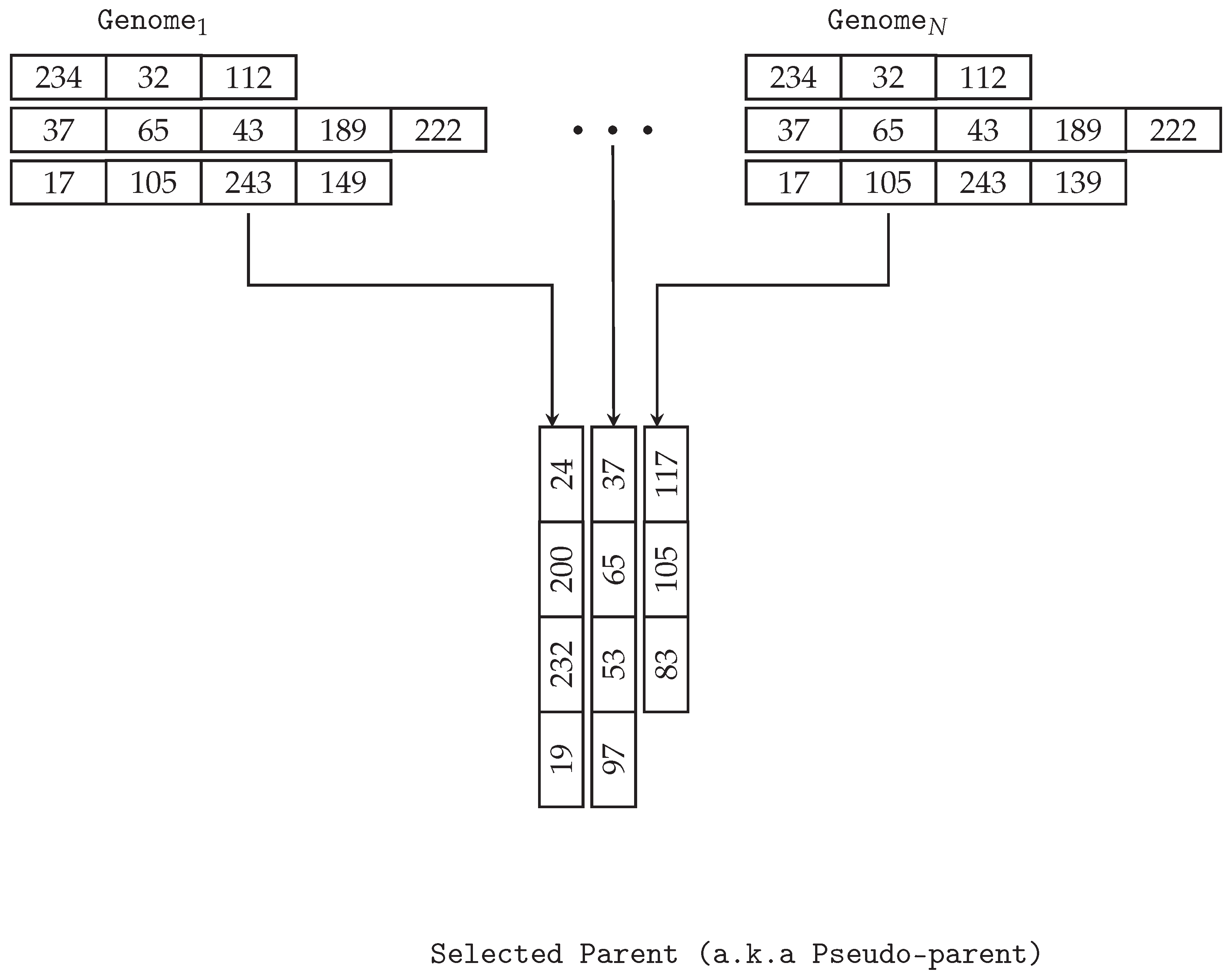
The selection operator implemented for MG-GE does not rely on the total aggregated fitness of all genomes in MG. This is because it is possible the worst-performing parent might have completely solved one of the output variables but will rarely or never be selected as a parent. Instead, a pseudo-parent is created by performing n number of selection events, where the best-performing genome per output variable is selected from the pool of potential parents. Any selection operator, such as tournament, lexicase, and roulette-wheel selections, can be used to select each genome.
For example, in a standard crossover event, two pseudo-parents are created and used to create two offspring. The selection process is illustrated in
Figure 4.
3.10. Well-formed Crossover and Mutation
Each genome in MG evolves a solution to a single and unique target variable. As a result, crossover operations occur between genomes that evolve the same output variable. Mutation operations are applied per genome in MG.
These genetic operations can be performed in several ways. Three types of events are currently implemented for genetic operation purposes. These include: random single-event, binary mask-event and all-event. In a random single event, only a single genome is randomly chosen for crossover and mutation. For a random single event, a binary mask of bit size equal to the number of genomes is randomly generated. All genomes in MG with bit positions in the binary mask whose bit values are one are chosen for mutation and crossover. In all-event, all genomes undergo genetic operations subject to the specified probability of these events occurring by the user.
3.11. Substitution Operator
In solving multi-output problems, there may exist inter-output dependencies as noted in
Section 1. To facilitate the evolution of these dependencies, we introduced custom grammar rules as described in
Section 3.4. Also, recall each genome in MG is meant to evolve a solution to a single unique output. Evolution is creative and can potentially exploit the inter-output dependency feature by using other sub-optimal output variable expressions as building blocks to solve another output perfectly. However, before extracting the solved output from an individual, if there exists a dependency on sub-optimal or optimal output variables, it is necessary to rewrite/substitute such output variables with their corresponding expression to obtain the final perfect expression for the solved output.
From Listing 2, assuming output variable
output_1 has completely been solved. Recall the best-evolved solution is a combination of the best-performing genome per output variable. Given that
output_1 is dependent on
output_2 and
output_2 is, in turn, dependent on
output_3, if we extract
output_1 without recursively substituting output variables with their corresponding expressions to obtain an expression devoid of output variables,
output_1 will no longer be regarded as solved, as
output_2 and
output_3 are very likely to be different in the created best individual. Applying the substitution operator, we will obtain the solved expression devoid of any output variables as shown in Listing 3. Hence, the importance of the cyclic dependency checking algorithm is to ensure the substitution operator does not get stuck in a non-terminating loop as a result of cyclic dependency existing between output variables.
| Listing 2. An individual that completely evolves the solution to output_ 1 (50 out of 50 total cases). |
![Algorithms 16 00365 i005 Algorithms 16 00365 i005]() |
| Listing 3. Final perfect output_ 1 statement after applying the substitution operator. |
![Algorithms 16 00365 i006 Algorithms 16 00365 i006]() |
In Listing 3, a typical iteration of the substitution operator to rewrite the solved output_1 variable before it is extracted. As can be observed from Listing 3, output variable output_1 used output variable output_2 twice which were replaced by the same expression at the end of the substitution operation. That is, in cases where an output variable uses another output variable multiple times will result in an increase in the size of the phenotype. In the case of digital circuits, such a scenario will increase the total number of gates required to realise the gate-level design of the circuit. However, this is a post-processing issue and is not addressed in this work.
3.12. Evolutionary Cycle
A steady-state EA is used to run the benchmark problems in this work. Unlike standard GE, where the best-performing individual is returned as the best-evolved solution, MG-GE creates its best individual by combining the best-performing genome for each output variable. However, when an output variable solution has been evolved, we perform substitution operations at the phenotype level described in
Section 3.11. The function of the substitution operator is to rewrite an expression in terms of variables other than the output variables.
Once an output variable has been solved, its solution is made available to all individuals in the population, and evolution no longer searches for it. However, this functionality can be modified if required for evolution to continue the search but for solutions with additional desirable properties, such as shorter expressions.
4. Experiments
Two combinational benchmark problems are used in this work: ripple carry adder and hamming code encoder. Two instances of each problem are considered based on the number of inputs and outputs, Hamming Code (7,4) and (15,11) Encoders, and 5-bit + 5-bit and 10-bit + 10-bit Adders.
Experiments are conducted to investigate the performance of standard GE versus MG-GE on these benchmark problems. For each experiment, we design two grammars. The first grammar variant, which we refer to as Grammar with Output Variable Sharing, allows output variables to use other output variables as building blocks as long as no cyclic dependency between output variables is formed. This is achieved by the definition of Output Variable Rules as described in
Section 3.4. In other words, Output Variable Rules, together with the cyclic dependency algorithm, are how MG-GE evolves inter-output dependencies that may exist. This feature is modelled in the grammar by adding the Output Variable Rule non-terminal to the
rules as the last production (highlighted in both grammars). The second version of the grammar, which we refer to as Grammar with No-Output Variable Sharing, follows the same structure as the previous grammar but simply omits the Output Variable Rule. Hence, with this grammar variant, if inter-output dependency exists between two output variables, evolution will have to evolve the expression/functionality of the independent output variable.
We speculate that for problems with inter-output dependencies, the Grammar with Output Variable Sharing will perform better than the Grammar with No-Output Variable Sharing and vice versa.
4.1. Ripple Carry Adder
Adder circuits perform addition in digital electronic devices. There are several types of digital adders, such as ripple-carry, carry-save and carry-lookahead adders. In this work, we use the ripple-carry adder, as its operation follows elementary addition, which is ideal for exploiting the concept of output variable sharing.
Illustrated in
Figure 5 is the elementary addition of two numbers. The addition operation starts from the last column (or the least significant numbers) and propagates any carry to the next least significant numbers up until the most significant numbers (first column). As can be observed, the
column addition depends/requires the carry from the
column addition. This problem can be modelled as an 8-output problem: four carry and four sum digits. Each sum digit (in other words, output) will require/depend on the carry from the previous addition stage as input. Without the inter-output dependency feature, each column addition to obtaining a sum digit will additionally require evolving the expression to generate the appropriate carry, taking into account all the carries propagated starting from the addition of the least significant digits of the addends.
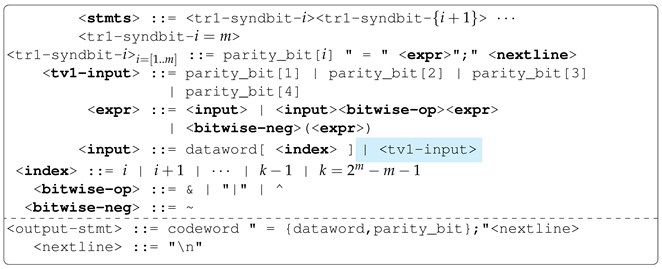
4.2. Hamming Code Encoder
Hamming codes belong to the family of Linear Block Codes [
27]. They are linear error-correcting codes capable of detecting a single error and, at most, two errors but can only correct one. For example, Hamming Code (7,4) Encoder encodes a 4-bit data word into a 7-bit code word before transmission. It does so by generating and adding three parity bits to the data word. Hamming Codes can be grouped into two categories based on the structure of the code words. These are
systematic and
non-systematic encodings. In systematic encoding, the data word and code word are separated while in non-systematic encoding, the data word and parity bits are interspersed. We adopt systematic encoding, as its structure is easier—data-word followed by the parity bits to obtain the code-word.
For example, the Hamming Code (7,4) Encoder can be modelled as a 3-output problem; each output represents the redundant bit generated and added to the data word to obtain the code word. Each redundant bit is generated by applying bit operations to a unique set of specific bits in the data word. Therefore, no dependency exists between the outputs of the hamming code encoder. Hence, it is an ideal problem to explain the no-output variable sharing concept as well as the performance of MG-GE on such problems.
4.3. Grammars
The grammars for the adder and hamming code encoder problems are shown in Listings 4 and 5, respectively. Both grammars are shown in a compressed form to save space, with certain repetitive rules, production choices and symbols compressed. By repetitive, we mean rules with very similar, but not identical, definitions.
A repetitive rule with a similar definition has been compressed using the syntax as shown in Listing 4. The same compression syntax has been applied to repetitive production choices and symbols and enclosed with curly braces where appropriate.
Both grammars have been designed to use bitwise operators (i.e., gate-level design), which makes the circuit problems more challenging to evolve from scratch. Each grammar is divided into two:
upper and
lower sections, separated by dashed lines. The upper section of the grammar contains the rules that need to be expanded. The lower section contains rules that define the fixed part of the circuit problem, such as the circuit interface. An expanded form of the grammar for the 5-bit + 5-bit Adder with Output and No-Output sharing are shown in Listings A1 and A2 respectively in the
Appendix A.
| Listing 4. N-bit + N-bit Adder Grammar. |
![Algorithms 16 00365 i007 Algorithms 16 00365 i007]() |
| Listing 5. Hamming Code (N,M) Encoder. |
![Algorithms 16 00365 i008 Algorithms 16 00365 i008]() |
4.4. Experimental Parameters
The experimental parameters for conducting the experiment are shown in
Table 1. Preliminary experiments were conducted to tune these parameters. A population size of 1000 is used for all other experiments except the 10-bit + 10-bit Adder, which is a more challenging circuit to evolve. Down-sampled lexicase selection is used for each selection event. Down-sampled lexicase sub-samples training cases during the selection event, thereby reducing the total number of evaluations [
28].
5. Results and Discussions
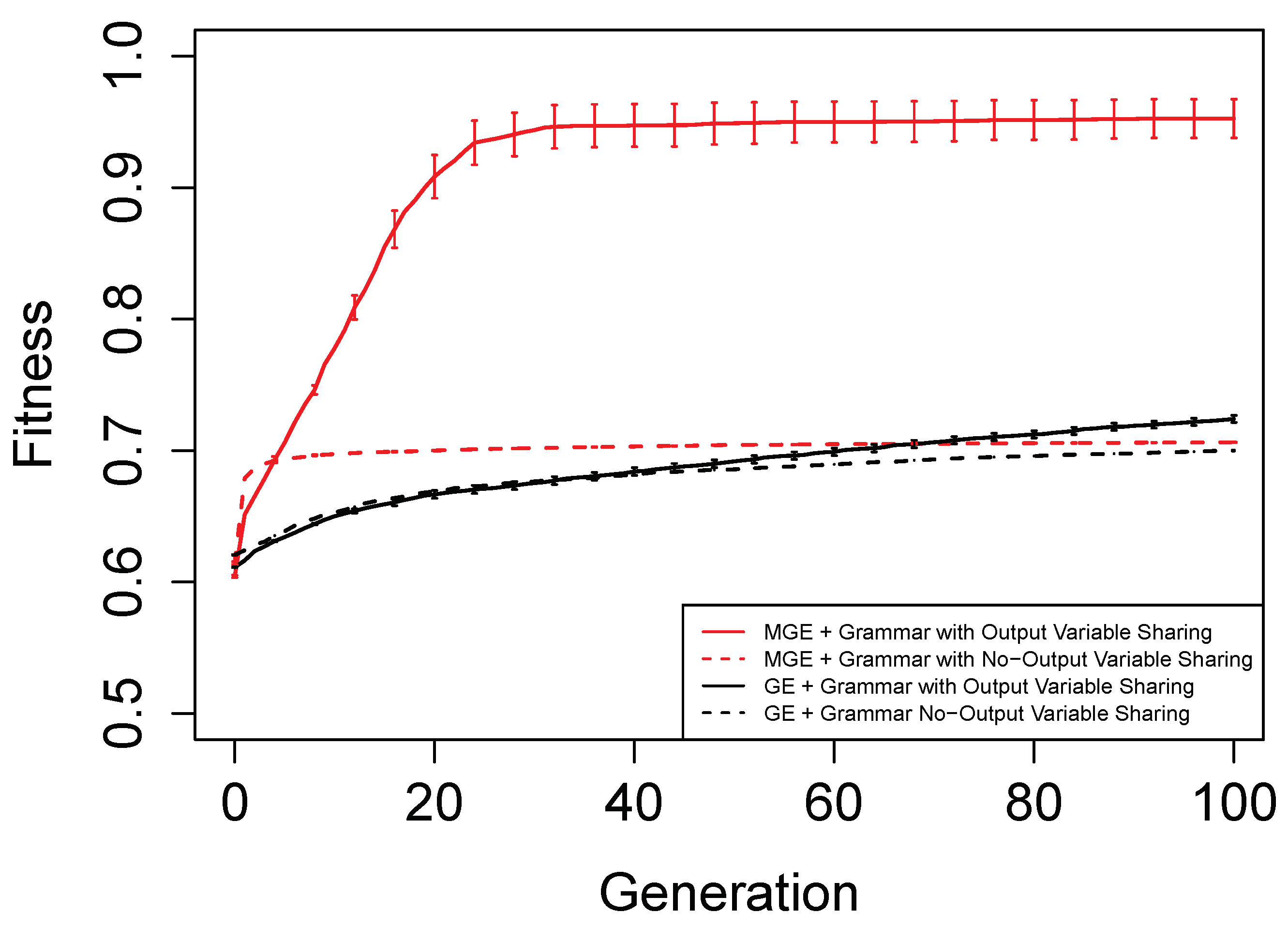
Figure 6,
Figure 7,
Figure 8 and
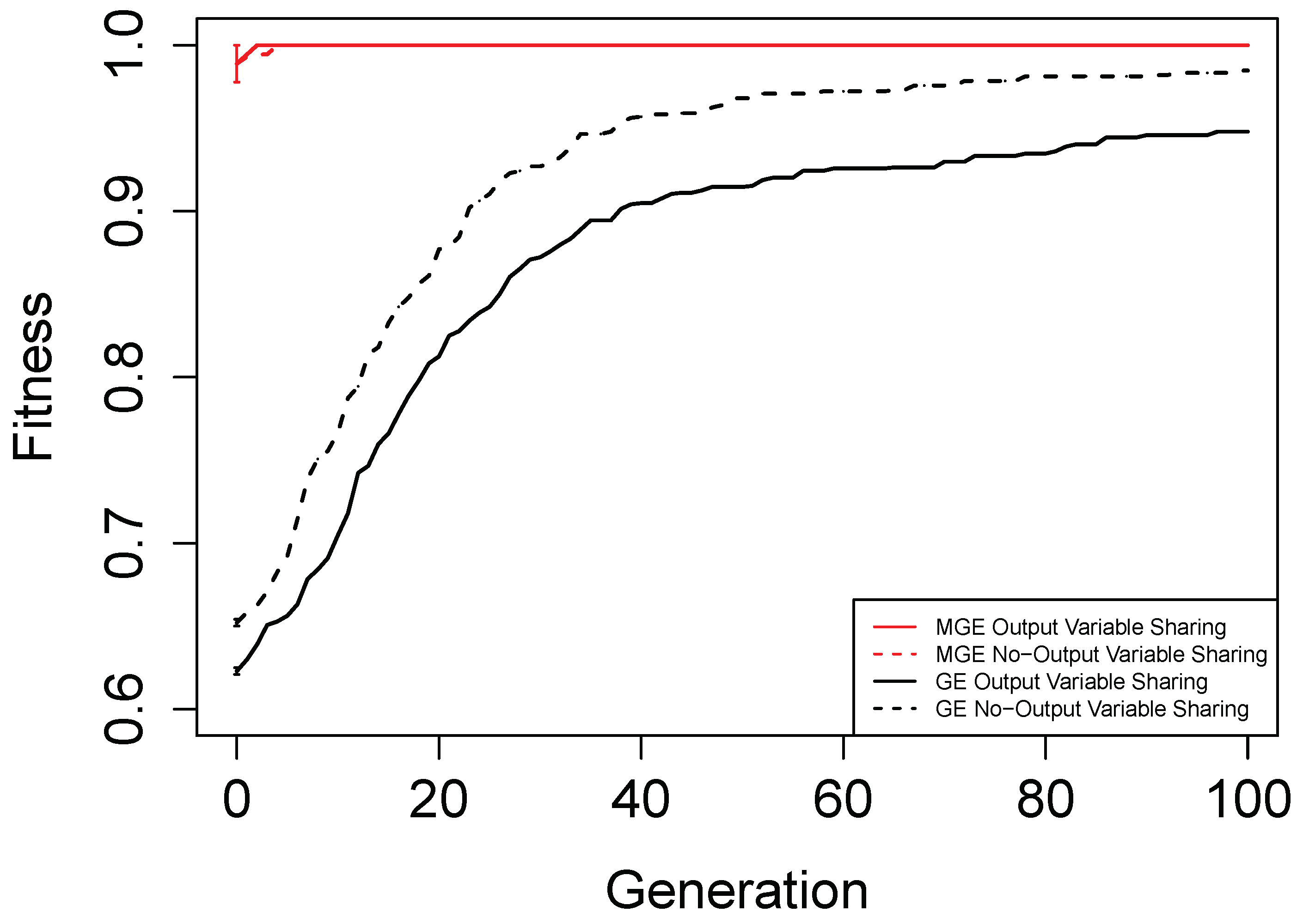
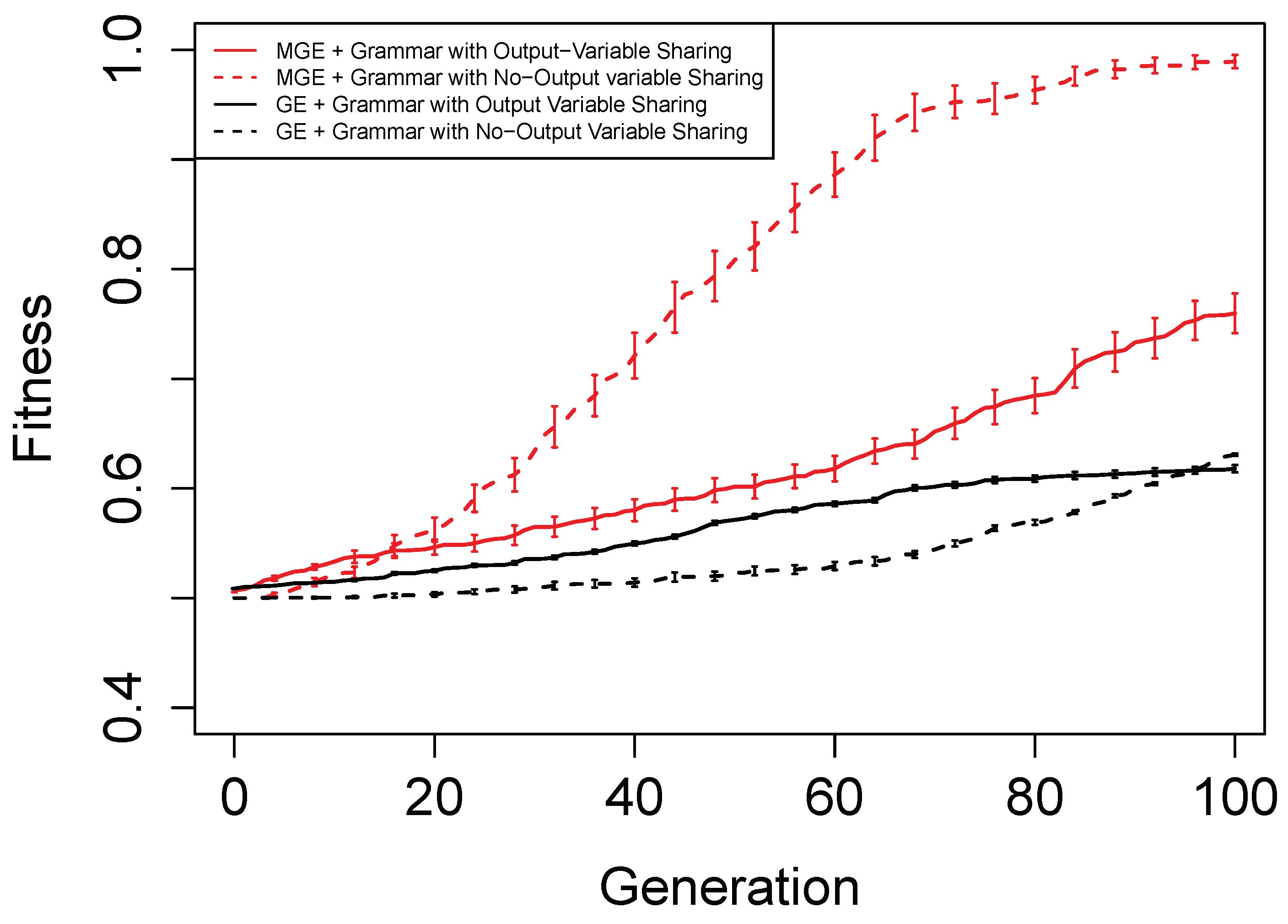
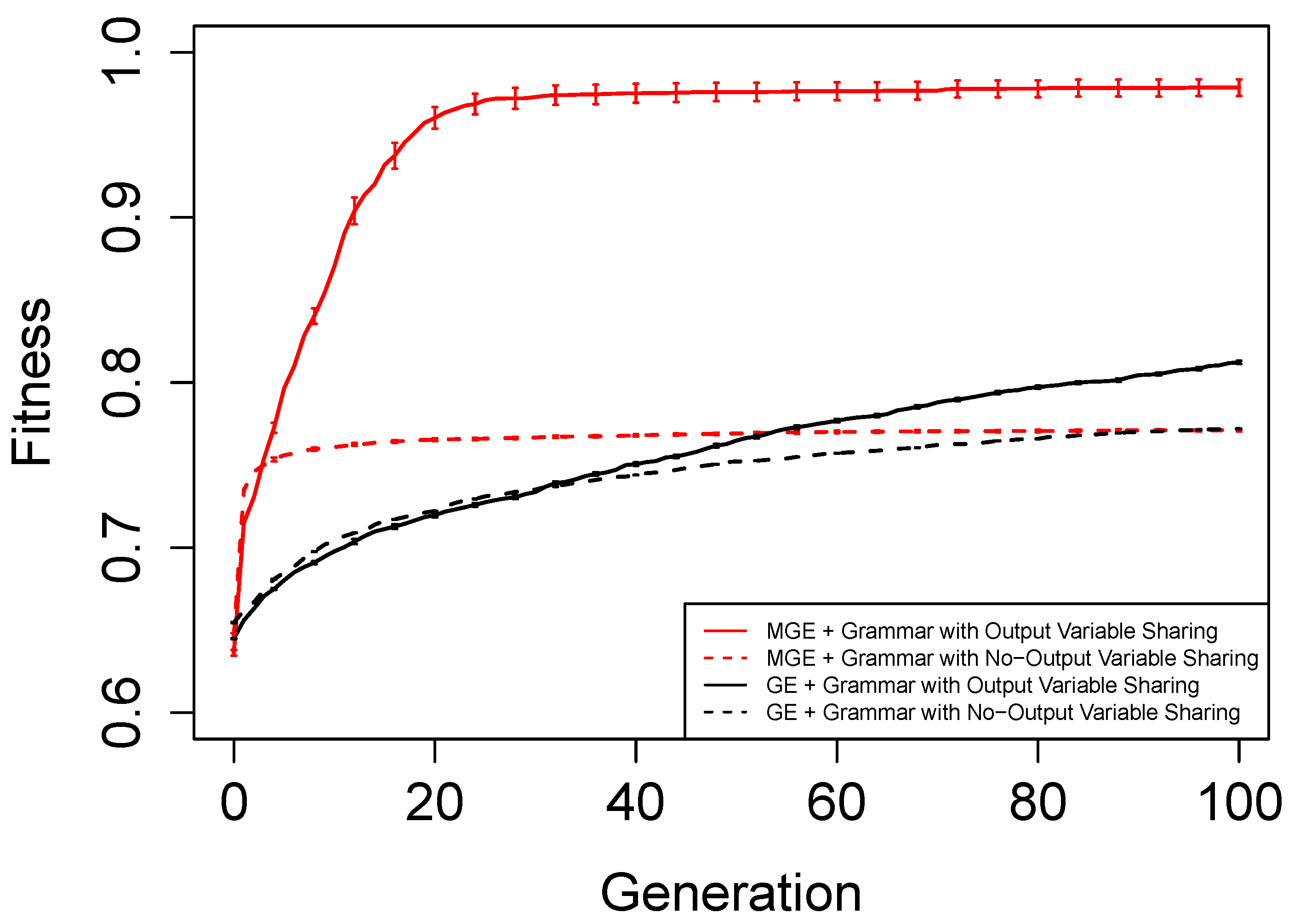
Figure 9 show the evolutionary performance for Hamming Code (7,4) Encoder, Hamming Code (15,11) Encoder, 5-bit and 10-bit adders using both grammar versions, respectively. The solid red line, dashed red line, solid black line, and dashed black line, are the mean best fitness across 30 independent runs for MG-GE using the Grammar with Output Variable Sharing, MG-GE using grammar with No-Output Variable Sharing, GE using Grammar with Output Variable Sharing, GE using grammar with No-Output Variable Sharing respectively. In
Table 2, we summarise the number of independent runs for each experimental setup.
The benefits of the new genome representation can be observed from
Figure 6,
Figure 7,
Figure 8 and
Figure 9. The experimental setups using MG-GE outperform GE when the same grammar variants are used except for the 5-bit + 5-bit adder in
Figure 8, where both MG-GE and GE using Grammar with No-Output Variable Sharing converge to similar final mean best fitness. However, MG-GE Grammar with No-Output Variable Sharing attains the final mean best fitness after a few generations. We also observe both MG-GE setups for the Hamming Code (7,4) Encoder in
Figure 6 attain their final mean best fitness after a few generations. This suggests evolution can perform quite well on relatively easier problems with no inter-output dependencies when the least appropriate grammar is used (Grammar with Output Variable Sharing). Furthermore, MG-GE outperforms GE on all problems using the most appropriate grammar variant.
We observe the experimental setup for MG-GE using the Grammar with Output-Variable Sharing for the 5-bit + 5-bit and 10-bit + 10-bit adders recorded a success rate of 16/30 and 21/30, respectively, while all other setups recorded zero successful runs. This is because the ripple-carry adder, which operates like elementary addition, propagates the carry bits from the previous bit addition stages to the last stage of bit addition. Hence, designing the grammar to allow output variable sharing while ensuring no cyclic dependency between output variables is formed ensures correct carry outputs are available for the summation stages to use. As a result, the Grammars without Output Variable Sharing will require evolution to evolve the carry-out bit from the previous summation stage for the current summation stage, rendering the problem more challenging to deal with.
On the Hamming Code (7,4) and Hamming Code (15,11) Encoder problems, MG-GE with the Grammar with No-Output Variable Sharing obtained a success rate of 30/30 and 27/30, respectively. Using the Grammar with Output Variable Sharing, MG-GE obtained zero successful runs. This is due to the fact that for the hamming code encoders, there exist no dependencies between the output variables. Therefore, using the grammar with Output Variable Sharing for a problem with non-existing inter-output dependencies impedes evolutionary performance.
5.1. Limitations and Drawbacks of The Proposed Approach
Though MG-GE outperforms GE on multi-output problems, it is not without some limitations and drawbacks. Firstly, the Substitution Operator described in
Section 3.11 may not be universally applicable. Therefore, depending on the problem at hand, a new or a modification of the substitution operator may be required. Secondly, the current output variable dependency feature (also known as output variable sharing) is very strict. The output variables are only useful as dependencies to other output variables only when they completely solve their respective objective. In other words, an output variable is not used as input by another output variable if it has not attained the maximum fitness value. This may not be so beneficial for certain problems such as symbolic regression problems. Lastly, the custom grammar syntax rules introduced require strict adherence and consequently some minor errors may result in semantic errors which may be challenging to deal with.
6. Conclusions and Future Work
In this work, we presented a Multi-Genome Grammatical Evolution implementation and demonstrated that it is better suited for solving multi-output (or multi-target) problems than standard Grammatical Evolution. Genetic operators, mappers and initialisation routines have been adapted to work with the new genome representation. Custom grammar syntax rules, together with a cyclic dependency-checking algorithm, have been developed to facilitate the evolution of inter-output dependencies. A new wrapping operator called Perfect Wrapping has been developed to ensure every single Multi-Genome Grammatical Evolution mapping event creates a valid executable object.
Despite the success of Multi-Genome Grammatical Evolution on the benchmark circuit problems used, there are several open questions and further experiments that need to be conducted. For example, the best mutation and crossover events for the genetic operators adapted for Multi-Genome Grammatical Evolution need to be investigated. We need to develop more intelligent algorithms to help Multi-Genome Grammatical Evolution evolve very complex-output dependencies that may exist in other multi-output benchmark problems.
Furthermore, the limitations of output variable dependency feature mentioned in
Section 5.1 needs to be improved to allow output variables that, when used by other output variables, contribute to increasing their fitness value.
Finally, Multi-Genome Grammatical Evolution has the potential to be applied to application domains other than the digital circuit domain. First, Multi-Genome Grammatical Evolution can be used to evolve the single dependent variable and several independent variables before performing multiple regression analysis to combine these variables to predict the target variable. Second, Multi-Genome Grammatical Evolution can be applied to multi-output classification problems. Finally, Multi-Genome Grammatical Evolution was applied to single-output problems that can be decomposed, however, Multi-Genome Grammatical Evolution should be applicable to multi-output problems. However, certain application domains may require several features of Multi-Genome Grammatical Evolution to be customised, such as the substitution operator and mapping mechanism.
Author Contributions
Conceptualization, M.T.; methodology, M.T. and C.R.; software, M.T. and A.d.L.; validation, M.T., C.R., A.M. and D.M.D.; formal analysis, M.T. and A.M.; investigation, M.T. and C.R.; resources, C.R.; data curation, M.T.; writing—original draft preparation, M.T., A.d.L. and J.M. writing—review and editing, C.R., D.M.D. and A.M.; visualization, M.T.; supervision, C.R.; project administration, M.T. and C.R.; funding acquisition, C.R. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are supported by Research Grant 16/IA/4605 from the Science Foundation Ireland and by Lero, the Irish Software Engineering Research Centre. The fourth author is supported, in part, by Science Foundation Ireland grant 20/FFP-P/8818.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Listing A1. 5-bit + 5-bit Adder Grammar with Output Variable Sharing. Output variable sharing is enabled by making an output variable rule non-terminal a production of rules as highlighted in the grammar. |
![Algorithms 16 00365 i009 Algorithms 16 00365 i009]() |
| Listing A2. 5-bit + 5-bit Adder Grammar without Output Variable Sharing. |
![Algorithms 16 00365 i010 Algorithms 16 00365 i010]() |
References
- Kalganova, T. Bidirectional incremental evolution in extrinsic evolvable hardware. In Proceedings of the Second NASA/DoD Workshop on Evolvable Hardware, Palo Alto, CA, USA, 15 July 2000; pp. 65–74. [Google Scholar] [CrossRef]
- Stomeo, E.; Kalganova, T.; Lambert, C. Generalized Disjunction Decomposition for the Evolution of Programmable Logic Array Structures. In Proceedings of the First NASA/ESA Conference on Adaptive Hardware and Systems (AHS’06), Istanbul, Turkey, 15–18 June 2006; pp. 179–185. [Google Scholar] [CrossRef][Green Version]
- Hodan, D.; Mrazek, V.; Vasicek, Z. Semantically-Oriented Mutation Operator in Cartesian Genetic Programming for Evolutionary Circuit Design. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, GECCO ’20, Cancún, Mexico, 8–12 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 940–948. [Google Scholar] [CrossRef]
- Tetteh, M.K.; Mota Dias, D.; Ryan, C. Evolution of Complex Combinational Logic Circuits Using Grammatical Evolution with SystemVerilog. In Proceedings of the Genetic Programming, Lille, France, 10–14 July 2021; Hu, T., Lourenço, N., Medvet, E., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 146–161. [Google Scholar]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Rothlauf, F.; Oetzel, M. On the Locality of Grammatical Evolution. In Proceedings of the EuroGP, Budapest, Hungary, 10–12 April 2006. [Google Scholar]
- Castle, T.; Johnson, C.G. Positional Effect of Crossover and Mutation in Grammatical Evolution. In Proceedings of the Genetic Programming, Istanbul, Turkey, 7–9 April 2010; Esparcia-Alcázar, A.I., Ekárt, A., Silva, S., Dignum, S., Uyar, A.Ş., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 26–37. [Google Scholar]
- Nicolau, M.; Agapitos, A. Understanding Grammatical Evolution: Grammar Design. In Handbook of Grammatical Evolution; Springer International Publishing: Cham, Switzerland, 2018; pp. 23–53. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C.; Keijzer, M.; Cattolico, M. Crossover in Grammatical Evolution. Genet. Program. Evolvable Mach. 2003, 4, 67–93. [Google Scholar] [CrossRef]
- Zhen, X.; Yu, M.; He, X.; Li, S. Multi-Target Regression via Robust Low-Rank Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Shaker, N.; Nicolau, M.; Yannakakis, G.N.; Togelius, J.; O’Neill, M. Evolving levels for Super Mario Bros using grammatical evolution. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 304–311. [Google Scholar] [CrossRef]
- O’Neill, M.; McDermott, J.; Swafford, J.M.; Byrne, J.; Hemberg, E.; Brabazon, A.; Shotton, E.; McNally, C.; Hemberg, M. Evolutionary design using grammatical evolution and shape grammars: Designing a shelter. Int. J. Des. Eng. 2010, 3, 4–24. [Google Scholar] [CrossRef]
- Grammatical Evolution. In Biologically Inspired Algorithms for Financial Modelling; Springer: Berlin/Heidelberg, Germany, 2006; pp. 73–88. [CrossRef]
- de la Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic Composition of Music by Means of Grammatical Evolution. SIGAPL APL Quote Quad 2002, 32, 148–155. [Google Scholar] [CrossRef]
- Mariani, T.; Guizzo, G.; Vergilio, S.R.; Pozo, A.T. Grammatical Evolution for the Multi-Objective Integration and Test Order
Problem. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, GECCO ’16, Denver, CO, USA, 20–24 July 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1069–1076. [Google Scholar] [CrossRef]
- Osojnik, A.; Panov, P.; Džeroski, S. Multi-label classification via multi-target regression on data streams. Mach. Learn. 2017, 106, 745–770. [Google Scholar] [CrossRef]
- Borchani, H.; Varando, G.; Bielza, C.; Larrañaga, P. A survey on multi-output regression. WIREs Data Min. Knowl. Discov. 2015, 5, 216–233. [Google Scholar] [CrossRef]
- Harris, S.; Harris, D. Digital Design and Computer Architecture: ARM Edition, 1st ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2015. [Google Scholar]
- LaMeres, B.J. Introduction to Logic Circuits & Logic Design with Verilog; Chapter Verilog (Part 1); Springer International Publishing: Berlin/Heidelberg, Germany, 2019; p. 157. [Google Scholar] [CrossRef]
- Sutherland, S. RTL Modeling with SystemVerilog For Simulation and Synthesis: Using SystemVerilog for ASIC and FPGA Design; Sutherland HDL, Inc.: Tualatin, OR, USA, 2017. [Google Scholar]
- Slowik, A.; Białko, M. Evolutionary Design and Optimization of Combinational Digital Circuits with Respect to Transistor Count. Bull. Pol. Acad. Sci. Tech. Sci. 2006, 54, 4. [Google Scholar]
- Walker, J.A.; Völk, K.; Smith, S.L.; Miller, J.F. Parallel Evolution Using Multi-Chromosome Cartesian Genetic Programming. Genet. Program. Evolvable Mach. 2009, 10, 417–445. [Google Scholar] [CrossRef]
- Coimbra, V.; Lamar, M.V. Design and Optimization of Digital Circuits by Artificial Evolution Using Hybrid Multi Chromosome Cartesian Genetic Programming. In Proceedings of the Applied Reconfigurable Computing, Mangaratiba, Brazil, 22–24 March 2016; Lecture Notes in Computer Science. Bonato, V., Bouganis, C., Gorgon, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 195–206. [Google Scholar] [CrossRef]
- Baine, N. A Simple Multi-Chromosome Genetic Algorithm Optimization of a Proportional-plus-Derivative Fuzzy Logic Controller. In Proceedings of the NAFIPS 2008—2008 Annual Meeting of the North American Fuzzy Information Processing Society, New York, NY, USA, 19–22 May 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Reyes, O.; Moyano, J.; Luna, J.; Ventura, S. A gene expression programming method for multi-target regression. In Proceedings of the International Conference on learning and optimization algorithms: Theory and applications, LOPAL ’18, Rabat, Morocco, 2–5 May 2018; ACM: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Ryan, C.; Azad, R.M.A. Sensible Initialisation in Grammatical Evolution. In Proceedings of the GECCO 2003: Bird of a Feather Workshops, Genetic and Evolutionary Computation Conference, Chicago, IL, USA, 12–16 July 2003; Barry, A.M., Ed.; AAAI: Chigaco, IL, USA, 2003; pp. 142–145. [Google Scholar]
- Miller, F.P.; Vandome, A.F.; McBrewster, J. Hamming Code: Parity Bit, Two- out- of- Five Code, Hamming(7,4), Reed-Muller Code, Reed-Solomon Error Correction, Turbo Code, Low- Density Parity-Check Code, Telecommunication, Linear Code; Alpha Press: Lagos, Nigeria, 2009. [Google Scholar]
- Hernandez, J.G.; Lalejini, A.; Dolson, E.; Ofria, C. Random Subsampling Improves Performance in Lexicase Selection. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO ’19, Prague, Czech Republic, 13–17 July 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2028–2031. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).