Abstract
Wireless Sensor Networks (WSNs) have a wonderful potential to interconnect with the physical world and collect data. Data estimation, long lifespan, deployment, routing, task scheduling, safety, and localization are the primary performance difficulties for WSNs. WSNs are made up of sensor nodes set up with minimal battery power to monitor and reveal the occurrences in the sensor field. Detecting the location is a difficult task, but it is a crucial characteristic in many WSN applications. Locating all of the sensor nodes efficiently to obtain the precise location of an occurrence is a critical challenge. Surveillance, animal monitoring, tracking of moving objects, and forest fire detection are just a few of the applications that demand precise location determination. To cope with localization challenges in WSNs, there is a variety of localization algorithms accessible in the literature. The goal of this research is to use various optimization strategies to solve the localization problem. In this work, a modified learning enthusiasm-based teaching–learning-based optimization (mLebTLBO) algorithm is used to cope with a 2D localization problem applying the notion of an exclusive anchor node and movable target nodes. A modified LebTLBO algorithm seeks to increase overall efficiency by assessing the exploration and exploitation abilities. The computational results reveal that this technique outperforms others with respect to localization errors in a 2D environment of WSN.
1. Introduction
Sensor nodes are affordable, extremely small sensing devices made possible by advances in wireless communication technology [1]. These sensor nodes can self-organize and establish a wireless sensor network (WSN) once they are deployed. WSNs can be used to detect inaccessible and hazardous locations where traditional sensors are nearly impossible to deploy. Detecting the location is a difficult task, but it is a crucial characteristic in many WSN applications. Locating all of the sensor nodes efficiently to obtain the precise location of an occurrence is a critical challenge. Surveillance, environment monitoring [2], tracking of moving objects, and forest fire detection [3] are just a few of the applications that demand precise location determination. These applications necessitate the stationing of an abundance of sensor nodes in the field, imposing size and cost limits on sensor nodes. Because of these limitations, all current sensor nodes have limited processing and battery power. Furthermore, due to their deployment in inaccessible places, power sources cannot be replaced or regenerated. This necessitates making the most use of sensor node processing and battery power to extend the WSN’s overall lifespan. A lot of WSN applications necessitate knowing the exact location where data is sensed. Sensor nodes can be manually placed at known locations or all sensor nodes can be equipped with GPS [4,5] or other position-finding hardware to find the location of the sensed data. Due to its deployment in difficult areas, manual placement of sensor nodes is not practical, whereas placing a GPS or location-finding system on each node will increase the cost of WSN deployment, making it economically unviable [6]. A variety of alternative strategies have been proposed in the literature [7,8,9,10], in which a restricted amount of location-aware nodes, termed as anchor nodes or beacon nodes, are randomly distributed throughout the network while location-unaware nodes, called target nodes, use anchor nodes to detect their location. Range-based and range-free localization techniques are two types of anchor-node-based localization systems. Range-based approaches are accurate [11], but they necessitate the installation of additional hardware on sensor nodes, making them an expensive solution. Noise and multipath fading have an impact on these as well.
Range-free techniques, on the other hand, are less expensive because only connectivity information is needed for location prediction. These approaches are widely used due to their inexpensive cost, although they provide poor localization accuracy when compared to range-based techniques. Localization can be precise in the case of stationary nodes, but it is more complicated in the case of movable nodes.
In this research, a modified learning enthusiasm-based teaching–learning-based optimization (mLebTLBO) algorithm [12] is used to deploy a single anchor along with hexagonal projection to project the anchor nodes virtually in six diverse orientations to target the undiscovered nodes. Two of these virtual anchors will be chosen at the time when the targeted node comes inside the span of the anchor node, as a minimum of three anchors is necessary to identify the target node’s 2D positions. These three anchor nodes have preliminary awareness of their co-ordinates, which helps in identifying the unknown target node position.
The mLebTLBO algorithm is used to assess the effectiveness of the 2D WSN localization problem utilizing a variety of meta-heuristics. The primary issue with teaching–learning-based optimization (TLBO) is that during the teacher or learner phases, all learners have an equal opportunity to gain knowledge. In fact, learners are distinct individuals who are passionate about learning. Higher levels of learning excitement make the learners more concentrated while they are studying, which gives them a fantastic chance to learn from others. Conversely, those who are less enthusiastic in learning have a relatively less likelihood of learning from others. The research inspired by this behavior brought about the concept of a learning enthusiasm mechanism using LebTLBO.
The optimization strategy used by LebTLBO can be viewed as a continual conversion of the search space. When the optimal solution enters the local optimum, the search space has a difficult time holding it. Therefore, it is crucial to direct the current approximation of the solution space toward the ideal solution space. It is necessary to attain the right balance between the diversification and intensification processes, which is found to be lacking in LebTLBO. Additionally, a probability that specifies the level of exploration and exploitation is a crucial aspect, but no adequate research has been done to identify this parameter. The algorithm is very good at exploring the search space, but it would require a lot of work to make it less exploitative. Therefore, in this work an improved variant of LebTLBO named mLebTLBO is used, that has better exploration and exploitation properties. LebTLBO uses random alternatives in addition to the local stage’s best solution at the moment to enhance local search. The local neighbourhood search (LNS) paradigm is presented to boost convergence properties while enhancing local search capacity. The main idea behind LNS is to update the current solution using the best solution that has been found in a small neighbourhood. Using this concept of mLebTLBO, the best position of unknown nodes in a 2D WSN environment is calculated. The complete algorithm of WSN localization incorporating the mLebTLBO algorithm is as follows:
| Algorithm 1 WSN localization incorporating mLebTLBO |
then Compute the distance from each anchor node utilizing RSSI method Establish the objective function f(x,y) Call the mLebTLBO algorithm to get the best position Set the localized unknown node i = I + 1 if (i > N) Then calculate the average localization error else Repeat the step no. 4 end if end if end for
|
The paper is organized as follows: Section 2 describes the literature review on 2D localization in WSNs. In Section 3, the LebTLBO algorithm is discussed. Section 4 discussed the mLebTLBO algorithm. Section 5 includes the concept of localization employing an individual anchor node. Simulation results and discussions are presented in Section 6, and finally, Section 7 includes the conclusion and future scope.
2. Literature Review
Many researchers have worked in this area and contended with the matter of localization firmly. Various optimization algorithms like the cuckoo search optimization [13], bat algorithm [14], and butterfly algorithm [15] are applied to deal with finding the co-ordinates of the target node. An efficient global optimization approach [16] was put forward using swarm intelligence to locate sensor nodes in WSNs. The main aim of this algorithm was to lessen the objective function by measuring the average square error of all surrounding anchor nodes. Another optimization technique named cuckoo search optimization [13] was employed to discover the undiscovered nodes deployed in WSNs with a quicker convergence time. Bio-inspired algorithms like particle swarm optimization (PSO) techniques and bacterial foraging algorithms (BFA) were used repeatedly to resolve the multidimensional environment localization difficulties [17]. Both of these strategies have the advantage of reducing the transmissions to the base station while maintaining the node’s energy, but the findings show that the suggested solutions have a trade-off issue. The BFA approach takes longer to locate unknown nodes but it does so more accurately, whereas the PSO algorithm finds them rapidly to a greater extent.
A unique hybrid algorithm was developed using BFA and PSO to improve the accuracy of sensor node positioning [18]. By improving location accuracy and shortening convergence time, this approach overcomes many of the limitations of BFA. The genetic algorithm [19] was developed to lower the overall expenses by taking into account very few anchor nodes required for every sensor inside the network to get located itself. Binary PSO established the concept of using RSSI to evaluate the distance between the target and anchor nodes and hence reduced the power utilization due to faster convergence along with increasing the lifetime of the network. The Bat algorithm was designed as a better way to deal with the problem of localization and improve location accuracy [14]. It works well and addresses both difficulties by improving the accuracy and decreasing the computational time. In comparison to PSO, the Flower Pollination optimization technique [20] was developed to minimize the localization errors as well as time of computation. The Range-Free Firefly Algorithm [21] was introduced to discover the nodes in a three-dimensional environment. The sensor nodes were segregated into three levels with anchor nodes at the top and undiscovered nodes at the middle and lower levels. The edge weights were used to determine the unknown node’s co-ordinates. Using this method, a considerable count of nodes can be located. To detect sensor nodes more perfectly, an upgraded algorithm on the basis of an artificial bee colony (ABC) [22] was suggested. This strategy enhances localization accuracy without increasing computational time. To boost the convergence rate, another approach on the basis of chicken swarm optimization [23] was presented. In comparison to PSO and BPSO, the suggested technique’s findings demonstrate high convergence. The Grey Wolf optimization algorithm [24], which is based on the characteristics of grey wolves, was presented to discover maximal nodes with reduced calculation time. The Butterfly optimization approach [15] was proposed to improve WSN performance with respect to localization errors and decreased computations. By combining the symbiotic organisms search (SOS) algorithm with multi-group communication and quantum behaviour approaches, a novel optimization technique named the Symbiotic Organism Search Algorithm with Multi-Group Quantum Behavior Communication (MQSOS) [25] was implemented, which is fast and convergent and may be applied to solve actual problems with several arguments. The MQSOS is contrasted to several intelligent meta-heuristic approaches, namely, particle swarm optimization (PSO), adaptive PSO (APSO), parallel PSO (PPSO), oppositional SOS in the CEC2013 large-scale optimization test suite (OSOS), and Quasi-Affine Transformation Evolutionary (QUATRE). The findings reveal that the algorithm MQSOS surpassed the other algorithms. An upgraded DV-Hop algorithm [26] was put forward focusing on expanding the communication radius to upgrade the minimum hop-count value of unidentified nodes to a lesser hop-count value to solve the issue of the real distance variation of the same hop-count value to a certain extent. An upgraded parallel whale optimization technique [27] was proposed that outperformed certain existing intelligent computing algorithms in terms of performance. Han et al. [28] modified the average distance per hop using a differential evolution localization approach based on DV-Hop.
For discovering the position of movable target nodes in WSNs, a PSO-based computational intellect approach was introduced. Anchor nodes were placed at the corners of the sensing region, and the algorithm was divided into two segments. The initial phase used distance calculations based on RSSI. Anchor nodes were virtually assumed in six diverse orientations at particular angles (ideally 60° each) in the subsequent step to locate undiscovered nodes. At this point, centroid computations were used in conjunction with a PSO optimization technique, and the results revealed a quicker convergence time. Other strategies take into account creating sensor networks to directly address the localization issue without relying on Global Navigation Satellite System (GNSS) signals. Since the GNSS has its limitations, the Local Positioning Systems (LPS) is adopted as a viable technology. LPS is made up of ad hoc deployments of sensors that specifically adjust according to the features of the application environment. This increases the GNSS’s accuracy and stability, enabling precise localization under challenging circumstances. Power, angle, time, phase, frequency, or even combinations of them are categorized according to the physical attribute measured to determine the target location, lowering the percentage risk of error that each one has individually [29]. A new soft computing technique [30] was developed by combining the Harmony Search Algorithm with a local search procedure that iteratively reduces the previously mentioned non-uniqueness of sparse network deployments. Geometrical restrictions based on connectivity also place boundaries on the possible locations for sensor nodes. The suggested strategy beats previously published soft computing localization algorithms in the majority of the simulated topologies. The majority of meta-heuristic algorithms applied to solve the aforementioned localization complication are competitive, but they have flaws such as delayed convergence and increased localization errors. The comparison of various Meta-heuristic algorithms used for WSN localization is listed in Table 1.

Table 1.
Comparison of meta-heuristic algorithms in WSN Localization.
In this research, a new approach for constructing a virtual anchor node in a 2D situation is used to establish the exact location of movable target nodes in WSNs to increase accuracy and lessen localization mistakes utilizing a mLebTLBO method.
3. Learning Enthusiasm-Based TLBO (LebTLBO) Algorithm
LebTLBO is an enhanced version of the basic teaching–learning-based optimization (TLBO) algorithm [12]. A TLBO modification improves the ability to search for the optimal solution. LebTLBO incorporated two new modules: the learning enthusiasm-based teacher phase and the learner phase. These are added to improve the standard of the poor learners using the poor student tutoring phase and to increase search potency. According to the fundamental TLBO, every learner has the same ability to gain knowledge from others. However, LebTLBO gained its motivation by the learning enthusiasm mechanism where every learner has a unique set of abilities and the enthusiasm to learn.
The initial stage comprises a population of NP learners (where the total population is denoted by , initialized as
where is the solution in the dimension; is a random number between [0, 1]; and are lower and upper bound respectively.
After initializing the learners’ population, each’s learner fitness is computed. The highest fitness learner is called the teacher, denoted as . The phases of the LebTLBO algorithm are described as follows:
3.1. Learning Enthusiasm-Based Teacher Phase
LebTLBO is a learning enthusiasm-based paradigm, in which students with good evaluations are more enthusiastic about learning and are therefore more likely to learn from the instructor. Terribly evaluated students are less motivated to learn and are less likely to hear what the educator has to say.
In this phase, all the learners are sorted according to their fitness value:
The learner’s learning enthusiasm value is defined as:
where denotes maximum learning enthusiasm and is minimum learning enthusiasm, with suggested values of = 1 and [12]. The learning enthusiasm curve is depicted in Figure 1, which shows that the best learner exhibits the highest learning enthusiasm and the worst learner exhibits the lowest learning enthusiasm.
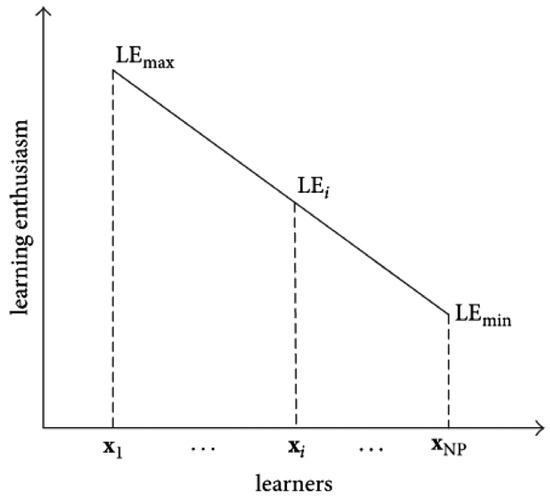
Figure 1.
Learning enthusiasm curve.
On account of the characterization of learning enthusiasm, each student is categorized as either gaining or learning from the teacher or not learning from the instructor, depending on the learning enthusiasm value . We create an irrational number for student ; if , then student will benefit from the educator; otherwise, student will ignore the instructor’s teachings in general. If student can get the knowledge from the teacher, the position is refreshed using a variety of updated showing methodologies under the following conditions:
where are randomly generated integers chosen from ; ; are randomly generated numbers which are uniformly distributed within the range ; and is a scaling factor in range . It is evident from Equation (4) that it can be viewed as a hybrid model of TLBO and DE given by Figure 2.
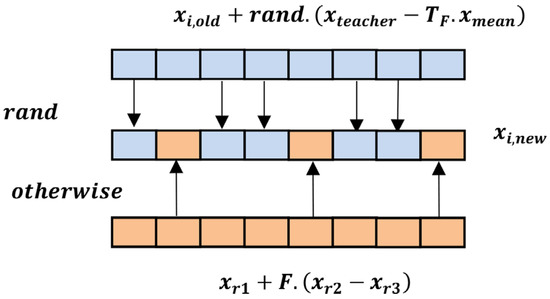
Figure 2.
Diversity-enhanced teaching strategy.
3.2. Learning Enthusiasm-Based Learner Phase
The learner’s approach to learning is also learning enthusiasm-based in LebTLBO. Similar to the teaching strategy, it incorporates higher learning enthusiasm for learners who receive good grades, and they lie in the high probability region for acquiring the knowledge from others and vice versa. In the learning enthusiasm-inspired learner phase, all the learners are ranked based on the performance of grades as defined in Equation (3).
A number is generated randomly between for learner ; if , then the learner will learn from the other learner; otherwise the knowledge of the learner will be neglected by the learner . If learner acquires the knowledge from the teacher, then based on the diversity-enhanced teaching strategy, its position will be upgraded as:
where is the objective function, and is the previous position of the learner. If is fitter than , then is accepted; otherwise remains unchanged.
3.3. Poor Student Tutoring Phase
The fundamental TLBO does not have this phase; the primary goal of this phase is to improve the grades of weak students. The same process is used in this phase as well, with learners ranked from best to worst depending on their grades.
A learner is considered a poor learner if they are in the bottom 10%. This phase will randomly choose learner from each poor student whose rank lies in the top 50%, and the learning is based on the following equation:
If is better than , is accepted; if not, remains the same. Students with poor grades have a lower likelihood of upgrading their position in the category of good students, whereas students with good grades have relatively higher likelihood of upgrading their position. The poor student tutoring phase plays a crucial role in improving the grades of the poor student into that of a good student. This approach is applicable to a real-time teaching–learning process where poor students always need tutorials for their improvement, more than when compared to other good students.
4. Modified LebTLBO (mLebTLBO) Algorithm
LebTLBO has recently attracted the attention of scholars because of its linear character. The refined LebTLBO aims to boost its effectiveness by enhancing its both exploration and exploitation abilities. Exploration would be aided by the use of search equations stimulated by Grey Wolf optimization (GWO) [31], and exploitation would be aided by the use of Local Neighbourhood Search (LNS), which is based on understanding the best result discovered until now in the contemporary solution’s small neighbourhood [32]. The explanation of the LNS concept is discussed below:
In the teacher phase, LebTLBO improves the search space by using the current solution and local data. The local neighbourhood search model has been added to boost the search capabilities and fasten the convergence. The fundamental idea is to refine the contemporary result in the neighbourhood of the current result using the best solution observed so far. The history of the individual’s neighbourhood is analyzed for updating the individual’s location, and the graph of their connectivity is referred to as the neighbourhood structure.
Assume ) in the current LebTLBO population, and is a vector. For any vector, the radius neighbourhood is specified; that is, the neighbourhood is made up of . For examination, we presume that the vectors are grouped into a ring topology based on their indices. The concept of a local neighbourhood model is depicted in Figure 3. As a result, the topology of the neighbourhood and the illustration of the collection of vectors are always static. The LNS model is defined in
where is the best result in the neighbourhood with , with as the scaling factors. In the upgraded model of LebTLBO, the new ideal result is upgraded according to Equation (1) and executes the teacher phase,
where is the ideal solution upgraded by LNS, and and denote arbitrary solutions for thet and learner, respectively, such that and denotes the scaling factor, and .
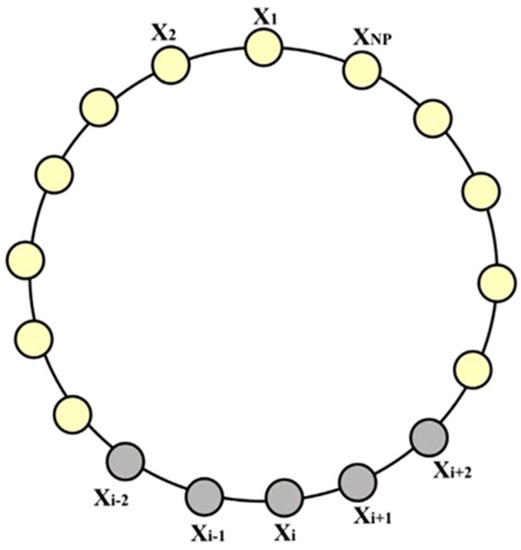
Figure 3.
LNS Model [33].
To strengthen the performance of the current LebTLBO, the learning enthusiasm-based teacher phase is upgraded in the modified LebTLBO [10]. By using the mean of the first three learners’ from the sets of learners, this new search equation is reinforced. These three results are per the best solution available, which is known as . The proposed equations in this regard are:
where and refer to A and , respectively. , are stated as
Here, is a consequentially decreasing random integer with iterations, and and are two uniformly distributed random numbers. These enable the search agents to expand across the search area, enhancing the LebTLBO’s exploratory capabilities.
The main concept for this adjustment has been influenced by GWO search equations [32]. The solution in GWO is built by regulating the parameters to get the ideal search agent location. To obtain a new solution, the same description is employed:
The local neighbourhood search (LNS) paradigm is implemented to increase LebTLBO’s exploitation capacity, as mentioned above. During the teacher phase of basic LebTLBO, the learners upgrade their positions based on local particulars as well as their personal experience.
The number of iterations is divided into two segments in this situation. The learning enthusiasm-based learner phase equation is employed for the first segment of the iterations, and a new search equation is appended for the second segment. The improved ideal solution is revised as per Equation (1) in the enhanced version of the LebTLBO, and the revised result implements the teacher phase as follows:
where is the ideal solution refined by LNS, and denotes the scaling factor such that .
The flowchart of the mLebTLBO algorithm is shown in Figure 4.
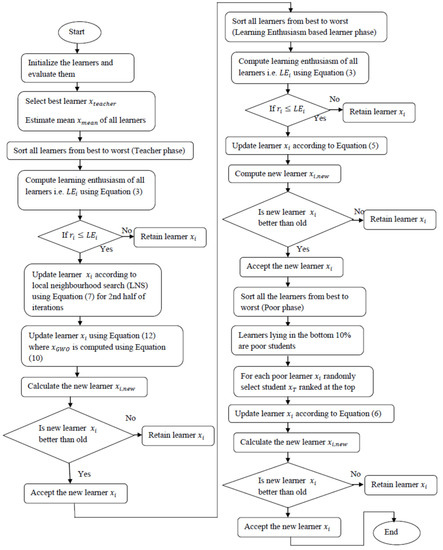
Figure 4.
Flowchart of mLebTLBO.
5. Localization Employing a Single Anchor Node
An individual anchor node is employed to find the locality of movable target nodes, as described above. The unknown target nodes are dispersed in an arbitrary manner. The whole sensor area is partitioned into circles and is inside the span of the anchor node. The anchor node sends out a beacon wave that assists the movable target nodes in locating them separately. When the movable target nodes come inside the span of an anchor node, they first observe the beacon signal and then accumulate the anchor node’s RSS information. After gathering RSS data, the distance between the anchor and target node is calculated. On the basis of these estimations, the anchor node is projected at a 60° angle with six virtual anchors (two of which will be chosen, as at least three reference nodes are necessary) to examine the location of movable target nodes. Every node in this study is considered to have the same hardware specifications and transmission range.
The following steps are involved in locating target nodes:
- (a)
- The region of 15 × 15 m2 is set up including the ‘N’ target nodes and an individual anchor node.
- (b)
- When mobile target nodes drop inside the span of an individual anchor node, each target node keeps a record of distances among the anchor and the target node, as well as two virtual anchors in the vicinity (as at least three reference nodes are needed to discover unknown target nodes). Figure 5 depicts the notion of anchor node, virtual anchor node, and target node.
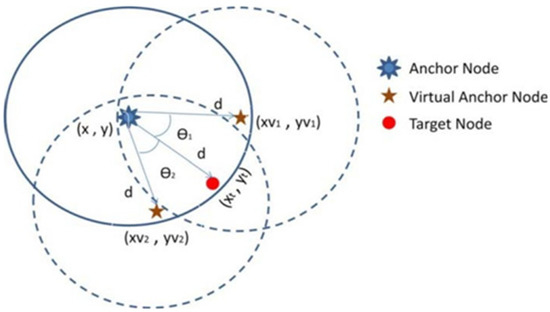 Figure 5. Sensor field representation.
Figure 5. Sensor field representation. - (c)
- The position of unknown nodes is evaluated using mLebTLBO.
The distance between each moving target and the anchor node is illustrated in Figure 5. There are two virtual anchor nodes for each anchor node (as three reference nodes are being taken to compute 2D position).
Here denotes the position of the target node, and denotes the present locality of the anchor node. The centroid calculation (15) along with its representation is illustrated in Figure 6.
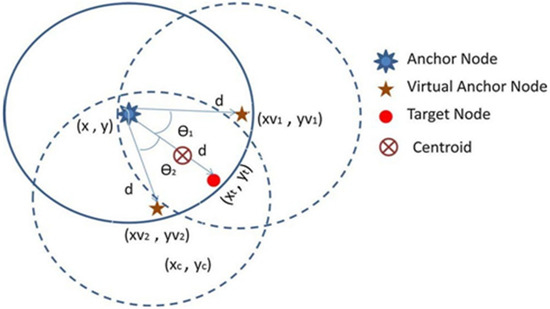
Figure 6.
Centroid calculation.
Figure 7 depicts the use of mLebTLBO to obtain the parameters of a target node denoted by . The goal is to reduce the actual and calculated distance between evaluated and actual node co-ordinates, which is expressed statistically in Equation (16):
where denotes the calculated position of the target node, denotes the position of beacon node in the vicinity of the target node, and is the total count of beacons ( > 3 in this study).
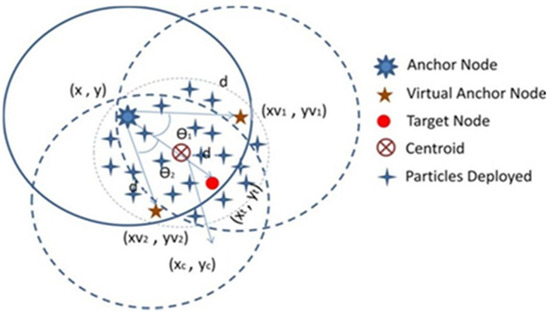
Figure 7.
mLebTLBO implementation around centroid.
The error in localization is estimated using Equation (17) and is illustrated in Figure 8.
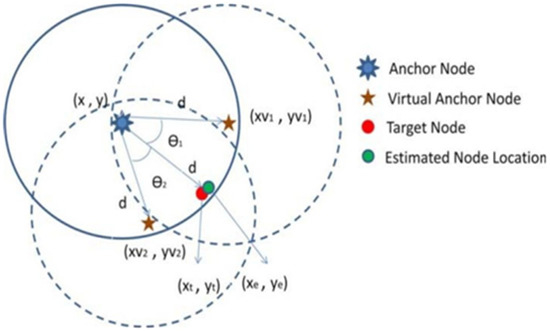
Figure 8.
Error estimation using mLebTLBO.
The optimal positioning of the target node is determined for mLebTLBO until the termination criterion is met.
6. Simulation Results and Discussions
Using the BBO, PSO, FA, HPSO, and mLebTLBO algorithms in MATLAB, simulations were conducted in a WSN field with an individual anchor node and 20 movable target nodes. These were performed on a MacBook Air with an i5 processor and 4 GB of RAM. The target nodes are placed at random throughout the 15 × 15 m2 sensor area, with the anchor node anchored in the center of the sensing area. When the target node drops inside the span of the anchor node, RSS values, as well as two virtual anchor nodes, are taken into account in order to estimate the set of parameters (as at least three anchor nodes are necessary for 2D placement). LOS issues can also be reduced when virtual anchor nodes are used. To determine the efficacy of the mLebTLBO algorithm, numerous simulations must be run. Simulations were carried out on a 15 × 15 m2 sensor area. Although more than six virtual anchors can be projected (Table 2), in our study, six virtual anchors are necessary to meet the requirements of identifying nodes in a two-dimensional environment by choosing the three closest anchors. The simulations were performed to check the effectiveness of the simulation parameters of mLebTLBO; the parameters that give best results are presented in Table 3.

Table 2.
Anchor and Virtual Anchor Nodes Co-ordinates.

Table 3.
Distance between target nodes and anchors deployed in the area.
Each algorithm’s strategic settings, such as those for the BBO, PSO, FA, HPSO, and mLebTLBO algorithms, are listed in Table 4.

Table 4.
Meta-Heuristic Algorithms Parameters Selection.
To locate itself within the recommended structure, each movable target node will use the BBO, PSO, FA, HPSO, and mLebTLBO optimization algorithms. The parameters for mobile node localization are the PSO, HPSO, and mLebTLBO algorithms.
The parameter values of the anchored anchor and virtual anchor are shown in Table 2. The existing distance matrix between the anchor, virtual anchor, and target nodes is shown in Table 3. In this study, the anchor node is employed first, and the mobility of all target nodes is considered in five diverse movements.
The analysis is carried out in a mobility-based scenario using BBO, PSO, FA, HPSO, and mLebTLBO. A fitness function is defined as the mean of the localization error given in Equation (16).
Target nodes are first distributed at random, whereas the anchor node is fixed and situated in the middle of the sensing area. Then, for target nodes, movement is applied, and six virtual anchors at a 60° projection with regard to the anchor node are evaluated. The solutions of localization utilizing numerous optimization techniques such as BBO, PSO, FA, HPSO, and mLebTLBO are shown in the Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.
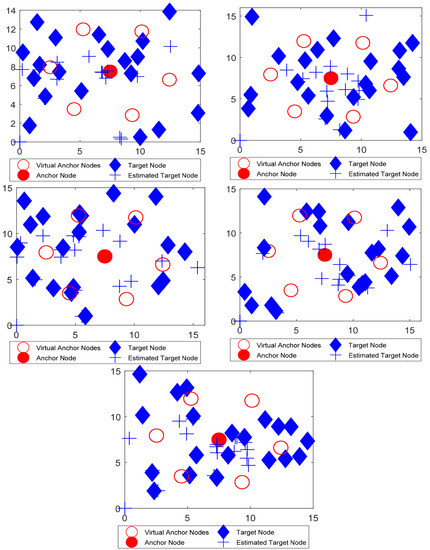
Figure 9.
Localization using BBO algorithm for five distinct movements.
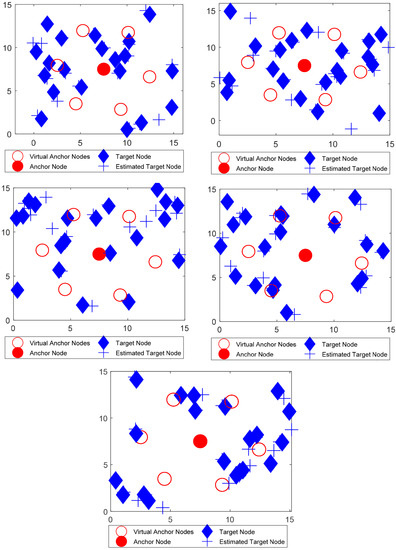
Figure 10.
Localization using PSO algorithm for five distinct movements.
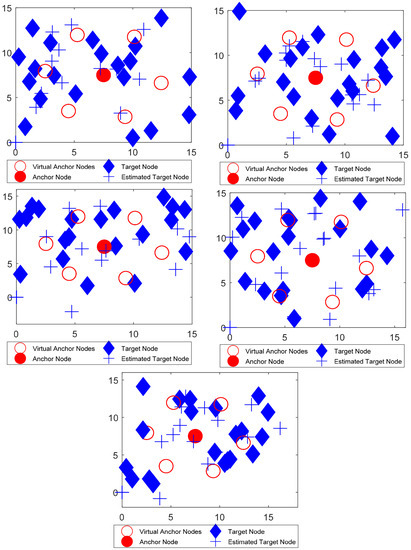
Figure 11.
Localization using FA algorithm for five distinct movements.
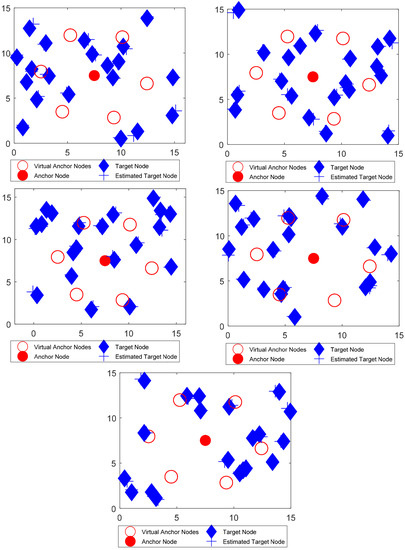
Figure 12.
Localization using HPSO algorithm for five distinct movements.
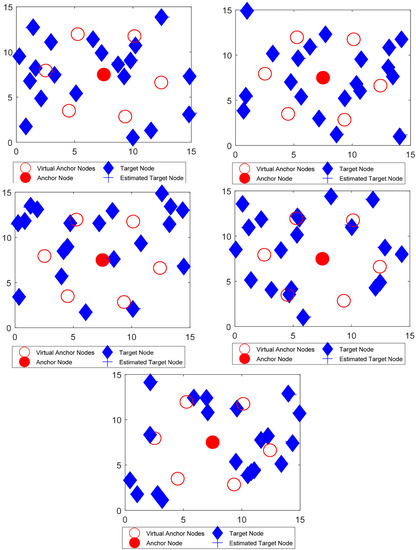
Figure 13.
Localization using mLebTLBO algorithm for five distinct movements.
These optimization methods were simulated for five distinct movements after a specified interval, as shown in the Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, and the entire process repeats itself for each interval. For each optimization strategy, the ‘+’ sign in the fifth movement represents the best predicted localized nodes. As shown in Figure 13, mLebTLBO has a low localization error when contrasted to alternative meta-heuristic strategies.
Table 5 outlines the findings from the mobility of target nodes in the first five locations, demonstrating an enhancement in mean localization error. Localization is done with the use of an individual anchor in this work, which saves energy because no three real anchors are used. The lower localization error is achieved at the cost of higher computational complexity because of the complex mLebTLBO algorithm.

Table 5.
Comparison of localization Algorithms in calculating localization error.
7. Conclusions and Future Scope
One of the most pressing concerns with WSNs is localization. In this research, an individual anchor node is used to conduct localization, with its projection at six different angles within the circle utilizing mLebTLBO. When a target node comes inside the span of the anchor node, two virtual anchor nodes are picked along with the anchor node (as at least three nodes is mandatory to locate the 2D parameters values of the target node). BBO, PSO, FA, HPSO, and mLebTLBO meta-heuristic optimization algorithms are used to compute the localization of 20 randomly deployed target nodes. These algorithms are then run for five iterations to calculate the localization error. In comparison to competitive methods, the Table 4 reveals that the mLebTLBO algorithm outperforms others with respect to average localization error as it has the least average localization error in locating the target nodes. This algorithm can be employed in a diversity of applications, including animal tracking, logistics, personnel tracking in coal mines, and other industrial applications. Another meta-heuristic approach can be implemented in the future for improved accuracy and faster convergence.
Author Contributions
G.K. performed the experimentation and wrote the manuscript. K.J. did the investigation. N.M. designed the methodology, V.M. did the supervision. R.S. did the administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 102–114. [Google Scholar] [CrossRef]
- Fascista, A. Toward Integrated Large-Scale Environmental Monitoring Using WSN/UAV/Crowdsensing: A Review of Applications, Signal Processing, and Future Perspectives. Sensors 2022, 22, 1824. [Google Scholar] [CrossRef]
- Dampage, U.; Bandaranayake, L.; Wanasinghe, R.; Kottahachchi, K.; Jayasanka, B. Forest fire detection system using wireless sensor networks and machine learning. Sci. Rep. 2022, 12, 46. [Google Scholar] [CrossRef] [PubMed]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System. Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Djuknic, G.; Richton, R. Geolocation and assisted GPS. Computer 2001, 34, 123–125. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. Ad hoc positioning system (APS). In Proceedings of the Conference Record/IEEE Global Telecommunications Conference, San Antonio, TX, USA, 25–29 November 2001; Volume 5, pp. 2926–2931. [Google Scholar] [CrossRef]
- Doherty, L.; Pister, K.; Ghaoui, L. Convex position estimation in wireless sensor networks. In Proceedings of the Proceedings-IEEE INFOCOM, Anchorage, AK, USA, 22–26 April 2001; Volume 3, pp. 1655–1663. [Google Scholar] [CrossRef]
- Bulusu, N.; Heidemann, J.; Estrin, D. Gps-less Low Cost Outdoor Localization for Very Small Devices. Pers. Commun. IEEE 2000, 7, 28–34. [Google Scholar] [CrossRef]
- He, T.; Huang, C.; Blum, B.M.; Stankovic, J.A.; Abdelzaher, T. Range-Free Localization Schemes for Large Scale Sensor Networks. In Proceedings of the 9th annual International Conference on Mobile Computing and Networking, MOBICOM, San Diego, CA, USA, 14–19 September 2003; pp. 81–95. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. DV Based positioning in Ad Hoc networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Ababnah, A.; Zghoul, F.; Akter, L. Quantizer design for RSSI-based target localization in sensor networks. Ad-Hoc Sens. Wirel. Netw. 2017, 35, 319–340. [Google Scholar]
- Singh, P.; Mittal, N. Optimized localization of sensor nodes in 3D WSNs using modified learning enthusiasm-based teaching learning based optimization algorithm. IET Commun. 2021, 15, 1223–1239. [Google Scholar] [CrossRef]
- Goyal, S.; Patterh, M. Wireless Sensor Network Localization Based on Cuckoo Search Algorithm. Wirel. Pers. Commun. 2014, 79, 223–234. [Google Scholar] [CrossRef]
- Goyal, S.; Patterh, M. Modified Bat Algorithm for Localization of Wireless Sensor Network. Wirel. Pers. Commun. 2015, 86, 657–670. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Node Localization in Wireless Sensor Networks Using Butterfly Optimization Algorithm. Arab. J. Sci. Eng. 2017, 42, 3325–3335. [Google Scholar] [CrossRef]
- Gopakumar, A.; Jacob, L. Localization in wireless sensor networks using particle swarm optimization. In Proceedings of the 2008 IET International Conference on Wireless, Mobile and Multimedia Networks, Beijing, China, 12–15 October 2008; pp. 227–230. [Google Scholar] [CrossRef]
- Kulkarni, R.; Venayagamoorthy, G.; Cheng, M. Bio-Inspired Node Localization in Wireless Sensor Networks. In Proceedings of the Conference Proceedings-IEEE International Conference on Systems, Man and Cybernetics, Antonio, TX, USA, 11–14 October 2009; pp. 205–210. [Google Scholar] [CrossRef]
- Tamizharasi, A.; Rengaraj, A.; Murugan, K. Bio-inspired algorithm for optimizing the localization of wireless sensor Networks. In Proceedings of the 2013 4th International Conference on Computing, Communications and Networking Technologies, ICCCNT 2013, Tiruchengode, India, 4–6 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Assis, A.F.; Vieira, L.F.M.; Rodrigues, M.T.R.; Pappa, G.L. A genetic algorithm for the minimum cost localization problem in wireless sensor networks. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 797–804. [Google Scholar] [CrossRef]
- Goyal, S.; Patterh, M.S. Flower pollination algorithm based localization of wireless sensor network. In Proceedings of the 2015 2nd International Conference on Recent Advances in Engineering Computational Sciences (RAECS), Chandigarh, India, 21–22 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Kumar, A.; Karampal. Optimized range-free 3D node localization in wireless sensor networks using firefly algorithm. In Proceedings of the 2015 International Conference on Signal Processing and Communication (ICSC), Noida, India, 16–18 March 2015; pp. 14–19. [Google Scholar] [CrossRef]
- Kulkarni, V.R.; Desai, V.; Kulkarni, R.V. Multistage localization in wireless sensor networks using artificial bee colony algorithm. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Al Shayokh, M.; Shin, S.Y.K. Bio Inspired Distributed WSN Localization Based on Chicken Swarm Optimization. Wirel. Pers. Commun. 2017, 97, 5691–5706. [Google Scholar] [CrossRef]
- Rajakumar, R.; Amudhavel, J.; Dhavachelvan, P.; Vengattaraman, T. GWO-LPWSN: Grey Wolf Optimization Algorithm for Node Localization Problem in Wireless Sensor Networks. J. Comput. Netw. Commun. 2017, 2017, 7348141. [Google Scholar] [CrossRef]
- Chu, S.-C.; Du, Z.-G.; Pan, J.-S. Symbiotic Organism Search Algorithm with Multi-Group Quantum-Behavior Communication Scheme Applied in Wireless Sensor Networks. Appl. Sci. 2020, 10, 930. [Google Scholar] [CrossRef]
- Li, T.; Wang, C.; Na, Q. Research on DV-Hop improved algorithm based on dual communication radius. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 113. [Google Scholar] [CrossRef]
- Chai, Q.-W.; Chu, S.-C.; Pan, J.-S.; Hu, P.; Zheng, W.-M. A parallel WOA with two communication strategies applied in DV-Hop localization method. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 50. [Google Scholar] [CrossRef]
- Han, D.; Yu, Y.; Li, K.-C.; de Mello, R.F. Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks. Sensors 2020, 20, 343. [Google Scholar] [CrossRef]
- Verde, P.; Díez-González, J.; Ferrero-Guillén, R.; Martínez-Gutiérrez, A.; Perez, H. Memetic Chains for Improving the Local Wireless Sensor Networks Localization in Urban Scenarios. Sensors 2021, 21, 2458. [Google Scholar] [CrossRef]
- Manjarres, D.; Del Ser, J.; Gil-Lopez, S.; Vecchio, M.; Landa-Torres, I.; Lopez-Valcarce, R. A novel heuristic approach for distance- and connectivity-based multihop node localization in wireless sensor networks. Soft Comput. 2013, 17, 17–28. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Chakraborty, U.; Konar, A. Differential Evolution Using a Neighborhood-Based Mutation Operator. EComput. IEEE Trans. 2009, 13, 526–553. [Google Scholar] [CrossRef]
- Singh, P.; Mittal, N. Efficient localisation approach for WSNs using hybrid DA-FA algorithm. IET Commun. 2020, 14, 1975–1991. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).