Abstract
The Interior layout model is to optimize the arrangement position of each room to maximize the comfort and quality of life of residents. Due to the complexity of the Interior layout problem, the computation of fitness function costs lots of time. To reduce the high computational cost while maintaining the solution performance. An interactive differential evolution algorithm based on Backtracking operator (IDE-BO) is proposed as the solver of the Interior layout model. The human-computer interaction mechanism of IDE benefits the automatic adjustment of fitness parameters that best meet the user’s subjective preferences to achieve the optimal solution. At the same time, the backtracking strategy can also help jump out when the algorithm falls into local optimization. The IDE is compared to other two conventional optimization methods based on two different layout scenarios. The experimental results show that in interior layout model IDE-BO is better than conventional interactive genetic algorithm (IGA) and IDE which do not use BO strategy, the super-performance of IDE-BO in complex situations in terms of execution time and convergence rate.
1. Introduction
With the rapid development of the real estate industry, the demand for house interior design has experienced remarkable growth in the past several decades. Given certain house type and height of storey, indoor space arrangement is the main factor affecting house comfort. Different areas and spaces determine the quality of furniture functions, people’s work and rest life is also closely related to a good spatial layout. Thus, it is important to determine the location of the room to maximize the quality of people’s life, which is usually referred to as layout optimization problem.
In the traditional interior design, the designer understands the user’s needs in advance, draws the floor plan based on a fixed structure, and finally provides the design plan for the user to choose. In the floor plan design process, the user cannot participate in it. Unfortunately, the vast majority of users are lack of professional domain knowledge, they cannot accurately describe their preferences or describe their favorite design styles. They can only use relatively colloquial, vague, and emotional language to describe them, such as “atmosphere”, “warm”, “western”, These abstract terms represent their desired decorating style, but they are unable to give specific requirements or standards. In the end, there will often be situations where the designer spends a lot of energy in designing several sets of solutions, but they do not meet the requirements of the users, and the users cannot tell where they are not satisfied with. The design need to be adjusted in time. This has caused a great waste of social resources. Therefore, in the early stage of house design, especially during the interior floor plan design stage, it is necessary to consider users’ individual needs. Encouraging users to timely participate in the interior floor plan design process is the key to solving this problem.
Interior graphic design can be regarded as a spatial layout problem, which is a typical optimization problem. Early literature results can be divided into two major research areas: space scheduling and site layout planning. Thabet et al. [1] developed the SCaRC (Space Constraint and Resource Constraint) scheduling system to quantify the workspace parameters, and the workspace availability during the scheduling process was defined and merged. Heng Li [2] et al. used genetic algorithms to transform the construction site-level facility layout problem into a problem of assigning scheduled facilities to scheduled locations. The latest methods for automated interior-space design, such as [3,4], relied on custom mathematical formulations of geometry rules, which are implemented and compiled by using general-purpose programming languages. Merrell mainly studies the baseline of automated interior layout based on design guidelines. The empirical weighted sum of the criteria for each mathematical expression is used [3]. When each rule is implemented in the software process, a large amount of user input is required to define object relations and properties. Other methods are used to generate internal layout, such as have centered around learning relations based on existing interior layouts [4].
In this paper, we propose a method for easily creating indoor space layout only through the user’s selection operations. The proposed method uses the cost functions and interactive differential evolution algorithm (IDE), establish a man-machine collaborative work mode. The algorithm is responsible for generating layout map, and the user is responsible for online evaluation. The evaluation information is fed back to the algorithm, and a new generation of drawings are generated again. In this way, it can effectively solve the defects of the previous design model that users are not able to participate in the design process due to their lack of professionalism, reasonably introduce users’ subjective preferences, the template that meets the needs is finally obtained, providing blueprints for users and designers.
Section 1 introduces the background and significance of the research in the field of interior layout, analyzes the existing design defects in the field of interior layout, illustrates the urgent need to improve the existing design methods in the context of “high demand” and “low efficiency”, and finally proposes Finally, a new design approach combining interior layout and interactive differential evolution algorithm is proposed. Section 2 presents a detailed introduction to the layout field, illustrates the current state of contemporary research in the layout field, and points out the shortcomings of modern design software. Section 3 proposes the interactive evolutionary algorithm, introduces the interactive genetic algorithm and the interactive differential evolutionary algorithm, focuses on the relevant contents of the interactive differential evolutionary algorithm, and proposes a backtracking strategy to help the algorithm get rid of the local optimum dilemma in view of the shortcoming that the traditional heuristic algorithm is easy to fall into the local optimum. Section 4 introduces the application model of the algorithm in indoor layout. According to the demand conditions of population in different household stages, the corresponding design framework is given, and the constraint function as well as the model of genetic coding are designed according to the relevant rules, the algorithm design process is introduced in detail, and the whole operation process from inputting parameters to generating the final target solution is completed through the user interaction interface. Section 5 tests the convergence effect of the algorithm and the satisfaction of users using this system through simulation experiments and subjectivity experiments, and it can be seen that it is indeed feasible to apply the interactive differential evolution algorithm in the field of indoor layout.
2. Related Work
2.1. Layout Problem
The problem of layout design is the research on the reasonable arrangement and placement of specific objects. There are a large number of layout design problems in modern industry and engineering, such as container placement and shipment in marine terminal [5], equipment and material flow in warehouse [6] and workshop scheduling [7], architectural layout design in construction industry, etc. Layout design has strong demand and huge market space. The research on its layout design has extensive and profound practical significance. Most layout design problems are inseparable from space, such as the division of one-dimensional space, the indoor plan design of two-dimensional space, and the cockpit layout of three-dimensional space [8,9]. Therefore, the space layout problem accounts for the main part of the layout design.
Interior spatial layout is not only the main problem involved in interior design, but also an important research direction in layout design. Compared with other types of layout problems, interior spatial layout has more research value and prospect interior design [10], virtual reality [11], computer games [12] and other fields have been widely used in indoor space layout in the field of architecture, interior space layout includes layout graphic design (space division) and scene optimization layout (home decoration). Traditional interior design often lacks personalized needs due to the differences in communication between designers and users, resulting in the consumption of a lot of human resources.
In the early research, a large number of restrictive research methods were proposed for the interior graphic design of residential buildings [13,14]. Shami and Mirahmadi [15] designed an evolutionary system to generate multiple groups of configurations according to the given constraints, and rank their priorities according to the evaluation indicators to find the best configuration in the indoor layout. A semi-automatic modeling system was proposed by Rosser [16] to integrate building plan and real-time map data to generate building model. In addition, the expert system (Expert System) [17] implementation plan layout has also been the focus of scholars. Rio-Cidoncha [18] integrated the idea of artificial intelligence and expert system to design a kind of layout design model. Ocheol and Kwon [19] encapsulated the architectural design knowledge and relevant design specifications into the expert system, referenced and deduced the spatial layout based on the given BIM spatial information and existing knowledge, and compared the spatial layout schemes with the expert system to determine the best choice under different accessibility conditions.
Unfortunately, due to the complexity of the combinatorial problem, the traditional constraint methods and evolutionary algorithms can not fully match the constraints and evaluation indicators in the layout problem, such as room adjacent comfort, different indoor styles, natural factors, Feng Shui layout and other factors that can not be formulated [20,21,22]. In the user evaluation mode in IDE, the user’s subjective evaluation replaces the complex data evaluation, so that ordinary people who lack professional knowledge can also replace the designer’s perspective. Compared with others, users can understand their own needs, simplify complexity and improve efficiency.
2.2. Auxiliary Design Tools
Although the style of interior design will change with the fashion trend or social atmosphere, the work done by designers in the design layout has not changed much. They collect materials and on-site investigation according to the requirements of the owners, and design the corresponding sketch, and negotiate with party A to analyze and rectify the good sketch scheme, and finally make the final effect drawing and construction drawing. In recent years, with the development and popularization of computer field, more and more design software is gradually applied to people’s daily life and work. The famous computer design software AutoCAD, 3dsmax and Archicad can be well applied to interior design and greatly reduce the workload.
However, the above aided design systems provide great convenience to the design industry, but they are only one-way operation tools, they are lack of communication platform between users and designers, and the degree of user participation is limited. Moreover, the use of these tools requires professional design basis and software use knowledge, which is difficult for non-professionals to master, so it has certain limitations in the use process.
3. Interactive Evolutionary Algorithm
As a traditional multi-objective optimization problem, interior spatial layout can be solved by evolutionary algorithm. However, the user demand is subjective and difficult to be described by explicit mathematical functions, which is a typical implicit optimization problem. As a representative method to solve implicit optimization problems, interactive evolutionary algorithm does not solve many non-inferior solutions first, but works out the final solution step by step through the dialogue between analysts and decision-makers, which has attracted the attention of many scholars.
3.1. Interactive Genetic Algorithm
Early IEA applications were mostly implemented using interactive genetic algorithms [23,24,25], individual evaluation scores are given by users as a bridge to interact with the algorithm [26]. The iterative process of the algorithm is shown in Figure 1. Evolutionary individuals are provided by the interactive interface in explicit form for users to score, using a purely numerical or hierarchical system. The disadvantage of this evaluation method is that the scores given by users can only be relative results which need to be mapped to absolute fitness values, increasing the complexity of the algorithm.
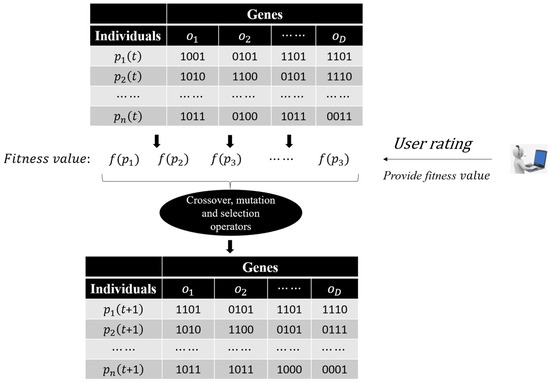
Figure 1.
An iteration of IGA.
3.2. Interactive Differential Evolution Algorithm
Although the introduction of “human-computer interaction mode” can produce better solutions, it also produces fatigue related problems, with the increase of the number of iterations. The user’s fatigue will gradually increase, and the given evaluation score will also be distorted. Therefore, it is difficult to find a balance between the number of iterations and fatigue. Compared with the genetic algorithm, the interactive differential evolution algorithm replaces the scoring mechanism with the selection operation. The user only needs to select a more satisfactory individual between two individuals, which simplifies a series of comparison scoring operations in the mind, which reduces the difficulty of the user’s operation and helps to reduce the degree of fatigue in the operation process. The iterative process of the algorithm is shown in Figure 2. In recent years, interactive differential evolution algorithm has been applied in image retrieval [27], image enhancement [28], image filter [29] and other aspects.
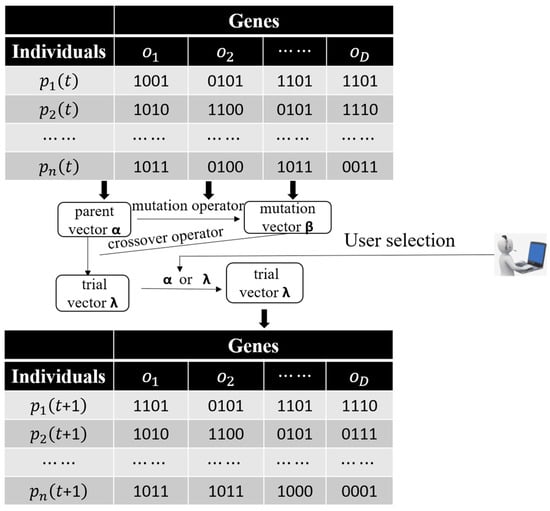
Figure 2.
An iteration of IDE.
3.2.1. Initialization
At the start of the algorithm, a specific method is used to generate the initial population, the method is expressed using the following formula:
where represents the ith component of the jth individual in the initial population, is the lower bound of the ith component, is the upper bound of the ith component, and rand is a random number that follows a uniform distribution [0,1].
3.2.2. Mutation Operation
During each iteration, a mutation vector is generated by the mutation operation. Mutation operation plays an significant role in the performance of differential evolution algorithm. Therefore, since the differential evolution algorithm was first proposed, a great deal of researchers have conducted research on mutation operators and proposed a large number of mutation operators. The most classic mutation operators are as follows.
- (1)
- DE/rand/1:
- (2)
- DE/best/1:
- (3)
- DE/current-to-best/1:
- (4)
- DE/current-to-pbest/1:
The three randomly selected individuals , and in the mutation operator are sorted from good to bad, corresponding to fitness , and . Where = 0.1 and = 0.9.
3.2.3. Crossover Operation
Then cross operation is carried out on the mutation vector and the parent vector to get the trial vector. The crossover operator is generally represented by the following formula:
where is the ith component of the trial vector of the jth individual at tth iteration. CR is the crossover rate of jth individual, is a random number from {1, 2, …, D}.
3.2.4. Selection Operation
After the test vector is obtained, the selection operator is used to select a better one from the parent vector and the trial vector to make it survive to the next generation. The selection operator is expressed by the following formula:
3.3. Interactive Differential Evolution Algorithm Based on Backtracking Strategy
As a kind of heuristic algorithm, differential evolution algorithm is a greedy strategy in essence, which objectively determines that the optimal solution that does not conform to the greedy rule will miss, and the local optimal solution will inevitably fall into.
Generally, the greedy selection operator is excellent. However, when the individual is in a locally optimal state, if the greedy selection operator continues to be used, a better vector from the trial and parent vectors will be selected to survive to the next generation. Since the parent vector is a locally optimal value, the newly generated trial vector is likely to continue further in the locally optimal direction. When an individual falls into a local optimal value, it is characterized by stagnation and is difficult to evolve to a better solution [30]. Literature [31] also proposed that greedy selection is difficult to help individuals to jump out of the local optimal value, so it is necessary to develop a new selection operator to help individuals jump out of the local optimal value.
To solve the above problems, an interactive differential evolution algorithm based on backtracking strategy is proposed, which helps the algorithm to return to a previous state by gradually returning to the upper layer, so as to jump out of the local optimal state. This method has been applied to differential evolution algorithm [32] and particle swarm optimization algorithm [33] respectively, and good experimental results have been obtained in high-dimensional problems.
As the greedy selection operator performs well when individuals do not fall into local optimum, greedy selection operator is used when individuals do not fall into local optimum, a new selection operator based on backtracking strategy is used when the individual falls into the local optimum. The first step is to determine whether the individual is trapped in a local optimum. An individual is considered to be in a stagnant state when its data is slowly updated within a certain range [34]. Although this method may have a subtle failure rate, it is an effective way to determine whether a target individual is stuck in a local optimum, and a strategy can be developed to reduce the impact of misclassification. The new selection operator borrows the idea of the backtracking algorithm, as shown in Figure 3. A spatial warehouse is set up at each iteration to store the individuals Rx (x denotes the number of layers of the current iteration) that failed to compete and were discarded in this round of comparison. When an individual is detected to be trapped in the local optimum at iteration y, vectors Ry−1, Ry−2, and Ry−3 are successively removed from the storage space and one of them is randomly selected to survive to the next generation, and if the individual still does not jump out of the local optimum, vectors Ry−4, Ry−5, and Ry−6 are successively removed from the storage space and removed from [Ry−1, Ry−2, Ry−3, Ry−4, Ry−5, Ry−6] to choose a random vector to survive to the next generation, and so on. If the parent vector is replaced with a randomly generated vector, it is difficult to guarantee the adaptation value of the random vector and the adaptation value must be calculated, which increases the computational complexity. Therefore, replacing the parent vectors with discarded trial vectors is considered. Since these discarded trial vectors are not passed on to the next generation, individuals evolving based on these vectors are more likely to help individuals jump out of local optima, and Figure 4 shows the complete iterative process of the algorithm. where √ represents the better individual who wins in each selection.
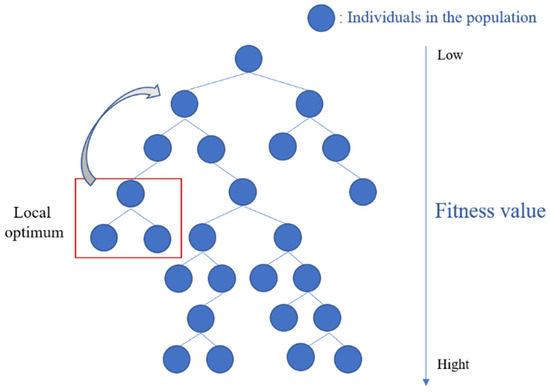
Figure 3.
Backtracking strategies.
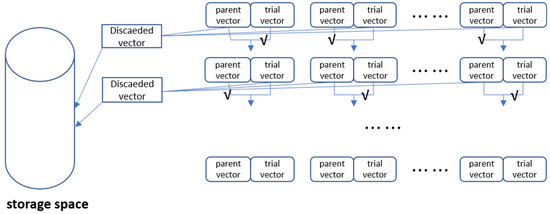
Figure 4.
Iterative process of IDE-BO.
4. Generation Method of Indoor Plan
The interior layout of houses can be solved as a multi-objective optimization problem [35]. Therefore, the relative importance of different objective functions should be considered. In the traditional multi-objective weighting method, each objective function is multiplied by a customized weight and integrated as a single objective, which is transformed into a single-objective optimization algorithm to obtain the optimal solution [36]. In interior design, multi-objective optimization is a big problem that perplexes decision makers. Some factors, such as orientation, daylighting, adjacency and feng shui, are generally difficult to set in advance. A set of Pareto optimal solutions without preference can be obtained by using genetic algorithm, and decision-makers can choose according to their own preferences. However, it will undoubtedly intensify decision-makers’ sense of fatigue and greatly reduce the effect to select the appropriate results from the numerous feasible solutions, and it is difficult to determine the adaptive value with specific functions in design and art industries. The “human-computer interaction” mode in this paper can replace the complex adaptive value function with the subjective choice of the user in a more complex situation, then evolve to the individual that the user is satisfied with, and gradually search to obtain the solution that meets the requirements.
4.1. Exterior Frame
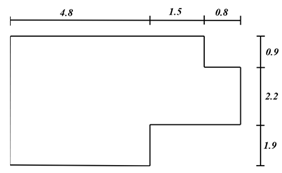
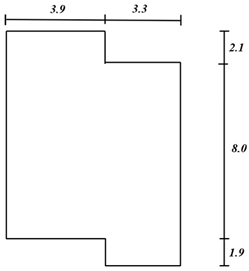
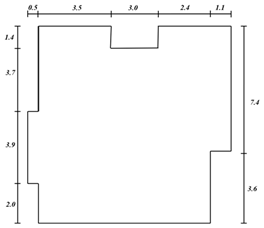
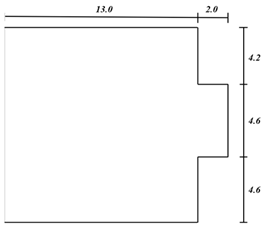
Interior layout refers to the overall framework of the house and the internal space distribution, usually based on the external overall framework fixed in the case of interior design. At different stages of family development, the composition of family members and living functions are characterized by stages [37]. According to the research results, the number of family members and space demand of current home buyers are shown in Table 1. According to the structural design of the house, the house type map presents a variety of forms, which can be divided into one-bedroom, two-bedroom, three-bedroom, multi-bedroom, etc. Table 2 shows a schematic representation of the different types of frameworks.

Table 1.
The spatial needs of the family at different stages.

Table 2.
Model framework.
4.2. Coding Mode
There are many encoding forms of chromosomes in differential evolution algorithm [38]. In this paper, binary coding is adopted, and the parameters of distribution space are expressed in the form of chromosome bit string based on character set {0,1}. In this paper, taking block diagram ④ as an example, the plan is divided into seven parts: room β1–β6 and information of distribution location of each room, the chromosomes of the population are composed of the coding arrangement of all variables (as shown in Figure 5), A-F correspond to 6 rooms respectively, and G represents the position information of their arrangement. The process of gene corresponding to individual is explained in detail (Figure 6). When generating and arranging rooms, the proportion needs to meet certain constraints, but this relationship is by no means specific, and can only be determined according to the design style, room type and user requirements. The result of this algorithm is only the preliminary blueprint of the design, which provides the possibility for users and designers to discuss. Therefore, there may be small errors between the parameters and the actual situation.
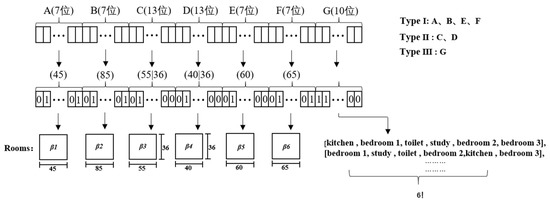
Figure 5.
Coding of chromosomes.
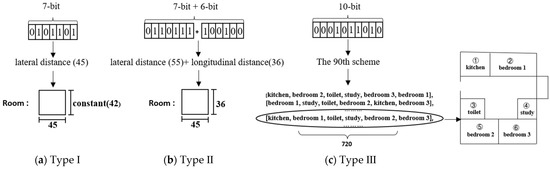
Figure 6.
Detailed explanation of coding.
4.3. Algorithm Flow
The specific idea of this interior layout design is as follows: according to the number of users’ housing needs, choose the external frame of the house with suitable space size, according to the given external frame of the house, choose the regular space area to allocate the functional space required by the users, the shape of the functional space is chosen to represent the most common rectangle in the residential building in life, and the irregular polygon composed of multiple rectangular spaces constitutes the basic interior space layout room unit, the horizontal and vertical distances of functional spaces as well as the location and neighboring relationships are disassembled into the genetic algorithm population individual genetic display, and specific spatial rule constraints are organized according to the survey of a large number of layout maps in the market to prevent a large number of invalid solutions, which affect the efficiency of the algorithm.
The specific process of the algorithm is described as shown in Algorithm 1.
| Algorithm 1 The algorithm flow of IDE with the proposed selection operator |
|
4.4. Interactive Interface
The user interaction interface is shown in Figure 7. According to the principle of simplicity and ease of use the interface can be roughly divided into three parts, the left part is the dominant display of individual genes of the population, from which the user can observe the individuals generated by each iteration of evolution and score them to give adaptation values, the upper half of the right part is the parameter setting area, where the user can adjust parameters such as algorithm crossover and variation probability by himself before the algorithm starts, and select the suitable furniture style, the lower half of the right half of the right side is the individual genetic details, you can select a layout drawing in the left population, and the detailed parameters of the drawing’s room will be displayed on the interface. When the experiment starts, first enter the interface, the user selects the item “home style” in the parameter setting section, such as “Simplicity”, “European”, etc. Afterwards, the user can modify the values of the scale factor (default 0.65) and cross ratio (default 0.2) according to their wishes, and click the “Start” button. Wait until the initial population is generated on the left interface, then the user selects the individual, checks the detailed parameters of the individual and clicks the “Next” button. The algorithm evolves itself to generate the next generation of populations according to the user’s choice, and so on, until we get a layout map that matches the user’s subjective preference.
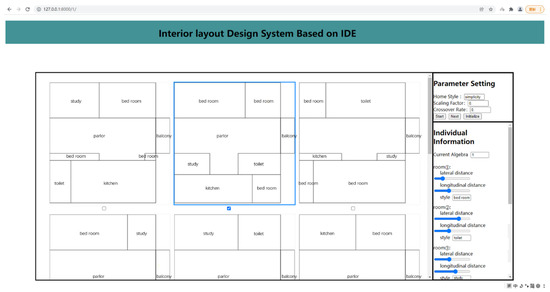
Figure 7.
Human-Machine Interaction Interface.
5. Experimental Test
5.1. Test in Simulated Environment
In order to quickly verify the feasibility of the algorithm, it is assumed that the user’s final satisfactory solution is the plan view shown in Figure 8, that is . The distance between the evolutionary individual and the satisfactory solution is used as the fitness function instead of user evaluation. It is assumed that the user has obtained a satisfactory solution (as shown in Figure 8), the optimization objective has been determined, by the distance between the candidate solution and the target solution as the individual adaptation value. This represents to some extent the gap between the candidate solution and the user’s expectation. The simulation experiments are mainly designed to verify the feasibility of user evaluation in the IDE algorithm framework and that the algorithm converges properly.
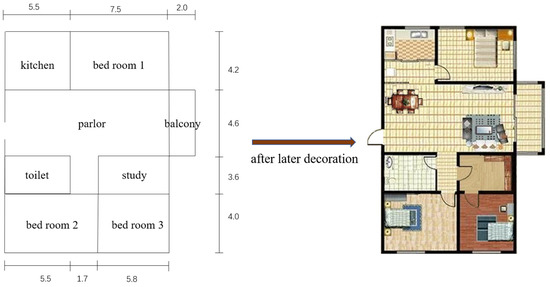
Figure 8.
Experiment template and parameter value.
The euclidean distance between evolutionary individual and target feature vector can help users participate in simulation evaluation. The distance calculation formula is expressed as:
5.1.1. Comparison of Mutation Operators
An excellent mutation operator has quite a significant impact on the performance of the algorithm. In this experiment, four classical mutation operators are compared in order to select the operator that best fits the interior layout model (Figure 9). Meanwhile, the traditional differential evolutionary algorithm uses the adaptation value function to calculate the population individual scores, and selects the top p% of individuals from the highest to the lowest according to the score ranking, from which individuals are randomly selected as the random vector in the variation operator DE/current-to-pbest/1, while the adaptation value function is replaced by the human selection operation in IDE, and the traditional adaptation value ranking is no longer applicable, in order to minimize the error, time of choice is used as the index of individual quality ranking, when the individuals of the population are compared two by two, the individuals that meet the user satisfaction and have higher scores are more likely to be selected by the users in the shortest time, although the time index may misjudge a few good target individuals in the high quality population, the error caused by such misjudgment is almost negligible in the case of having a large number of high quality target individuals.
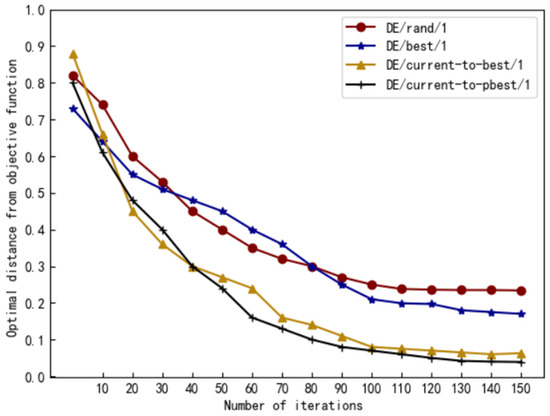
Figure 9.
Result of the comparison.
We set a final satisfactory solution (Figure 8), and set the corresponding fitness function, taking the Euclidean distance between the experimental individual and the final satisfactory solution as the evaluation criteria. The faster the distance decreases or the smaller the gap, the better the effect of the strategy in practical application. The experiment was divided into four control groups with different difference strategies. In order to make the experimental data more accurate, the experiment was conducted in 5 times, and the average value was finally selected as the data of the experiment. From the comparison results listed in Figure 9, we can observe that DE/current-to-pbest/1 and DE/current-to-best/1 attain the best performance since they show better results in convergence. At the same time, compared with DE/current-to-best/1, DE/current-to-pbest/1 is better in convergence speed and convergence, followed by DE/rand/1 and DE/best/1.
5.1.2. Experiment of Parameter Sensitivity
After comparative experiments, it can be found that DE/current-to-pbest/1 is more suitable for the model in this paper than the other three mutation operators. Therefore, in the following experiments, we compare the effects of different values of mutation parameter p on the experimental results, from the two aspects of convergence speed and convergence, the experiment was conducted in 5 times, and the average value was taken as the data of the experiment at the end.
As can be seen from Figure 10, in terms of convergence speed, when p there will be a better result. However, if p is too small, the mutation operator will degenerate into DE/current-to-best/1 and lose convergence. From the two aspects, we can know that when p is 15, the algorithm not only has good convergence, but also has fast convergence speed.
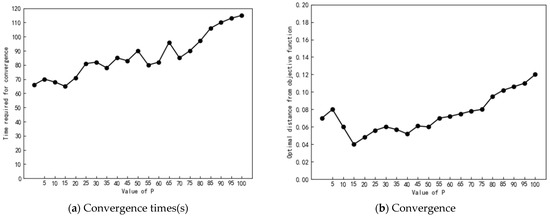
Figure 10.
Simulation experiment of testing p value.
5.1.3. Comparison of Algorithms
In IGA algorithm, in order to solve the requirement of non-negative probability in roulette selection, the calculation formula of adaptive value is revised as follows:
where .
Figure 11 shows the average convergence curve variation of the three algorithms in finding the target value in ten simulation experiments. When t = 20, there is no significant difference between the three algorithms in the initial stage of iteration. In the later stage of iteration, IGA converges in advance, and IDE and IDE-BO have better effects. When t = 60, the convergence speed and convergence accuracy of IDE-BO are obviously better than the other two algorithms. In order to obtain accurate comparison results, the number of iterations in the simulation experiment is t = 150. In the real human-computer interaction environment, in order to avoid user fatigue, t ≤ 30 is generally appropriate.
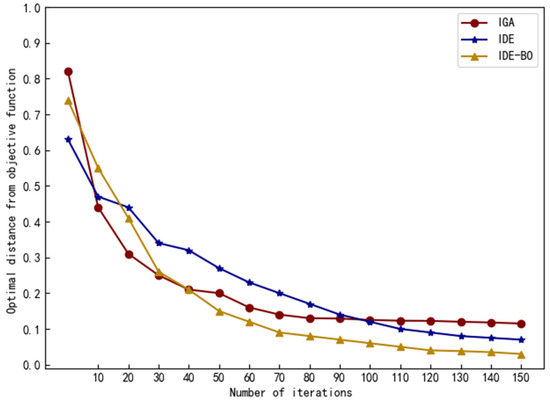
Figure 11.
Result of the simulation evaluation.
Table 3 shows the number of iterations required to reach convergence for IDE-BO and the other two traditional algorithms in 10 simulation experiments, and it can be seen that IDE-BO has reached the convergence condition most of the time at around t = 125, while the number of iterations required to reach around 133 in IDE. Although IGA can converge significantly faster than IDE-BO, its convergence is not good as can be seen in Figure 11. To statistically compare the performance difference in convergence speed between IDE-BO and its competitors, a Wilcoxon signed-ranks test with a 0.05 significance level is conducted. Table 4 shows the p-values of the results when comparing IDE-BO with the other two algorithms. From the table, it can be seen that the p-value of IDE-BO is much lower than 0.05 for IDE which has a small difference in convergence and has a much better convergence than IGA which has a faster convergence. In general, the performance difference between IDE-BO and the other two algorithms is significant.

Table 3.
Number of iterations for the three algorithms to reach convergence.

Table 4.
Statistical comparison results of Wilcoxon test.
5.2. Subjective Test
In interactive algorithms, besides the influence of parameters on convergence, the subjective choice of users plays a key role. The purpose of the subjective test is to test the satisfaction and usefulness of the system by users in real-world effects, and to investigate the influence of users’ subjective choice on convergence during the evolutionary process. Since the characteristics of the design and art industry make quantitative description of convergence difficult, 25 testers were chosen to use this system in this experiment, setting the maximum number of iterations to 40 and investigating user satisfaction with individual members of the population. Given that the purpose of the system is to eventually produce user-satisfied solutions, the system can be deemed to achieve the design purpose as long as a few high-quality solutions can eventually be evolved. In each iteration, the testers selected the individuals in the population that best met their preferences and scored them on a scale from 0 to 100, and the average score given by the 25 testers in each iteration was calculated. The higher the score of the two indexes, the stronger the convergence ability of the algorithm. When the score of the final solution reaches 75 or more, the system can be considered to generate the final satisfactory solution for the users. Figure 12 shows how the satisfaction level varies with the user’s subjective choice and the algorithm.
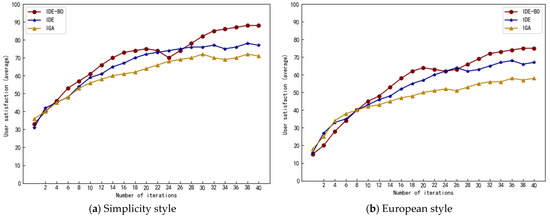
Figure 12.
Subjective test.
It can be seen from the Figure 12 that the three algorithms have no obvious effect on the result when the iteration number t ∈ [0,12]. When t > 14, IDE will show stronger convergence than IGA, and the improved IDE is easier to jump out after falling into local optimization, so it will have higher satisfaction in the end. At the same time, we know that different subjective needs of users will have an important impact on the convergence of the algorithm, and different style choices will also have an impact on users’ subjective judgment, and then affect the convergence of the algorithm. In this test, compared with “Simplicity”, the word “European” has more complex meaning and thinking, which is difficult for users to judge. Therefore, the “Simplicity” style shows better results.
To statistically compare the performance difference between IDE-BO and traditional evolutionary algorithms, a Wilcoxon signed-ranks test with a 0.05 significance level is conducted. Table 5 shows the p-values of the results when comparing IDE-BO with the other two algorithms at different numbers of iterations. The p-values below 0.05 are shown in bold. According to the number of iterations, the experiments were divided into three stages: pre, intermediate, and post. From Table 4, it can be seen that there is little difference in the performance of the three algorithms at the pre stage, at the intermediate stage, comparing IGA, IDE-BO has a significant advantage, and at the post stage, comparing both algorithms, the p-value is less than 0.05. Overall, the difference between IDE-BO and the other two algorithms is remarkable.

Table 5.
Statistical comparison results of Wilcoxon test.
6. Summary and Future Work
In this paper, the interactive differential evolution algorithm is used to generate the interior layout plan, and the backtracking strategy is introduced to reduce the influence when the population falls into local optimum. The interior design mentioned is a local design adjustment (user’s psychological expectation layout) under the satisfaction of certain constraints (domain expert’s reasonableness assessment). The interior design discussed in this paper is not a question of the rationality of the interior layout, but whether the interior layout design meets the user’s expectations. This adjustment of house interior design varies from person to person, and the psychological expectations of different users vary. The interactive algorithm and its related strategies are introduced to realize the individual pursuit of different users, thus effectively bridging the gap between the “professionalism” of design software and the “unprofessionalism” of ordinary users. However, the number of iterations and population range of the algorithm should not be too large due to user interaction during algorithm execution, which limits the breadth of search space. Otherwise, it will aggravate user fatigue and aesthetic fatigue, thus affecting the final results. Therefore, if a screening mechanism is added in subsequent studies to select representative solutions from each generation and present them to users, user evaluation fatigue will be alleviated. How to maintain a balance between slowing down user fatigue and expanding search space can be further discussed in the follow-up research.
Author Contributions
Conceptualization, B.L.; methodology, F.Y.; formal analysis, B.T. and H.W.; writing—original draft preparation, B.L.; writing—review and editing, F.Y.; visualization, B.T.; supervision, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China, grant number 62106092; the Natural Science Foundation of Fujian Province, grant number 2022J01916; and the Research Teaching Reform Project of Minnan Normal University, grant number JG202107.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thabet, W.Y.; Beliveau, Y.J. SCaRC: Space-constrained resource constrained scheduling system. J. Comput. Civ. Eng. 1997, 11, 48–59. [Google Scholar] [CrossRef]
- Li, H.; Ped, L. Genetic search for solving construction site-level unequal-area facility layout problems. Autom. Constr. 2000, 9, 217–226. [Google Scholar] [CrossRef]
- Merrell, P.; Schkufza, E. Interactive furniture layout using interior design guidelines. ACM Trans. Graph. 2011, 30, 1–10. [Google Scholar] [CrossRef]
- Yu, L.F.; Yeung, S.K. Make it home: Automatic optimization of furniture arrangement. ACM Trans. Graph. 2011, 30, 86. [Google Scholar] [CrossRef]
- He, D.Y.; Cha, J.Z. Research on solution to complex container-loading problem based on genetic algorithm. J. Softw. 2001, 12, 1380–1385. [Google Scholar]
- Yang, W.; Liu, J. Integrated optimization of location assignment and job scheduling in multi-carrier automated storage and retrieval system. Comput. Integr. Manuf. Syst. 2019, 25, 251–259. [Google Scholar]
- Xia, Z.C.; Liu, F. Memory based lamarckian evolutionary algorithm for job shop scheduling problem. J. Softw. 2010, 21, 3082–3093. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z. Adapted particle swarm optimization algorithm based layout design optimization of passenger car cockpit for enhancing ergonomic reliability. Adv. Mech. Eng. 2019, 11, 1687814019837808. [Google Scholar] [CrossRef]
- Pang, G.; Pang, L.P. Simulation and optimization of air supply system layout for special vehicle cabin. CIESC J. 2020, 71, 335–340. [Google Scholar]
- Tang, X. Research on interior design strategy based on optimization of computer renderings production process. J. Phys. Conf. Ser. 2021, 1992, 032104. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z. Virtual reality game level layout design for real environment constraints. Graph. Vis. Comput. 2021, 4, 200020. [Google Scholar] [CrossRef]
- Ma, C.; Vining, N. Game level layout from design specification. Comput. Graph. Forum 2014, 33, 95–104. [Google Scholar] [CrossRef]
- Donath, D.; Bohme, L.F.G. Constraint-based design in participatory housing planning. Int. J. Archit. Comput. 2008, 6, 97–117. [Google Scholar] [CrossRef]
- Zawidzki, M.; Tateyama, K. The constraints satisfaction problem approach in the design of an architectural functional layout. Eng. Optim. 2011, 43, 943–966. [Google Scholar] [CrossRef]
- Mirahmadi, M.; Shami, A. A novel algorithm for real-time procedural generation of building floor plans. arXiv 2012, arXiv:1211.5842. [Google Scholar]
- Rosser, J.F.; Morley, G. Modelling of building interiors with mobile phone sensor data. JSPRS Int. J. Geo-Inf. 2015, 2, 989–1012. [Google Scholar] [CrossRef]
- Kamol, K.; Krung, K. Optimizing architectural layout design via mixed integer programming. In Proceedings of the International CAAD (Computer Aided Architectural Design) Futures Conference, Vienna, Austria, 20–22 June 2005. [Google Scholar]
- Martinez, J.; Iglesias, J.E. A multidisciplinary model for floorplan de-sign. Int. J. Prod. Res. 2007, 45, 3457–3476. [Google Scholar]
- Ocheol, K. BIM space layout optimization by space syntax and expert system. Korean J. Comput. Des. Eng. 2017, 22, 18–27. [Google Scholar] [CrossRef]
- Mak, M.Y.; Ng, S.T. The art and science of Feng Shui—A study on architects’ perception. Build. Environ. 2005, 40, 427–434. [Google Scholar] [CrossRef]
- Wu, W.P.; Feng, Y. Interior Space Design and Automatic Layout Method Based on CNN. Math. Probl. Eng. 2022, 2022, 8006069. [Google Scholar] [CrossRef]
- Wu, Y. Architectural Interior Design and Space Layout Optimization Method Based on VR and 5G Technology. J. Sens. 2022, 2022, 7396816. [Google Scholar] [CrossRef]
- Garcia-Hernandez, L.; Pierreval, H. Handling qualitative aspects in unequal area facility layout problem: An interactive genetic algorithm. Appl. Soft Comput. 2013, 13, 1718–1727. [Google Scholar] [CrossRef]
- Koga, S.; Fukumoto, M. A creation of music-like melody by interactive genetic algorithm with user’s intervention. In Proceedings of the International Conference on Human-Computer Interaction, Heraklion, Greece, 22–27 June 2014. [Google Scholar]
- García-Hernández, L.; Arauzo-Azofra, A. Facility layout design using a multi-objective interactive genetic algorithm to support the DM. Expert Syst. 2015, 32, 94–107. [Google Scholar] [CrossRef]
- Lai, C.C.; Chen, Y.C. A user—Oriented image retrieval system based on interactive genetic algorithm. IEEE Trans. 2011, 60, 3318–3325. [Google Scholar] [CrossRef]
- Yu, F.; Li, Y. Interactive differential evolution for user—Oriented image retrieval system. Soft Comput. 2016, 20, 449–463. [Google Scholar] [CrossRef]
- Lee, M.C.; Cho, S.B. Interactive differential evolution for image enhancement application in smart phone. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Piscataway, Australia, 10–15 June 2012. [Google Scholar]
- Liu, G.; Peng, J.Z. Image spatial filtering method based on interactive differential evolution strategy. J. Chin. Comput. Syst. 2015, 36, 2090–2095. [Google Scholar]
- Yang, M.; Li, C. Differential evolution with auto-enhanced population diversity. IEEE Trans. Cybern. 2015, 45, 83–89. [Google Scholar] [CrossRef]
- Zhao, F.; Zhao, L. An ensemble discrete differential evolution for the distributed blocking flow shop scheduling with minimizing make span criterion. Expert Syst. Appl. 2020, 160, 113678. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, M. A new selection operator for differential evolution algorithm. Knowl. -Based Syst. 2021, 226, 107150. [Google Scholar] [CrossRef]
- Yu, J.; You, X. Dynamic density clustering ant colony algorithm with filtering recommendation backtracking mechanism. IEEE Access 2020, 8, 154471–154484. [Google Scholar] [CrossRef]
- Guo, S.M.; Yang, C.C. Improving differential evolution with a successful parent-selecting framework. IEEE Trans. Evol. Comput. 2015, 19, 717–730. [Google Scholar] [CrossRef]
- Coello, C.A.C. Evolutionary multi-objective optimization. Eur. J. Oper. Res. 2008, 181, 1617–1619. [Google Scholar] [CrossRef]
- Cai, C.S.; Chen, S.R. Chen. Framework of vehicle-bridge-wind dynamic analysis. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 579–607. [Google Scholar] [CrossRef]
- Wen, Z.; Qi, P. Establishing public service system of indemni catory housing. Archit. J. 2013, 4, 106–109. [Google Scholar]
- Zhibo, E.; Shi, R. Multi-satellites imaging scheduling using individual reconfiguration based integer coding genetic algorithm. Acta Astronaut. 2021, 178, 645–657. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).