Abstract
This paper presents a new hybrid algorithm that combines genetic algorithms (GAs) and the optimizing spotted hyena algorithm (SHOA) to solve the production shop scheduling problem. The proposed GA-SHOA algorithm incorporates genetic operators, such as uniform crossover and mutation, into the SHOA algorithm to improve its performance. We evaluated the algorithm on a set of OR library instances and compared it to other state-of-the-art optimization algorithms, including SSO, SCE-OBL, CLS-BFO and ACGA. The experimental results show that the GA-SHOA algorithm consistently finds optimal or near-optimal solutions for all tested instances, outperforming the other algorithms. Our paper contributes to the field in several ways. First, we propose a hybrid algorithm that effectively combines the exploration and exploitation capabilities of SHO and GA, resulting in a balanced and efficient search process for finding near-optimal solutions for the FSSP. Second, we tailor the SHO and GA methods to the specific requirements of the FSSP, including encoding schemes, objective function evaluation and constraint handling, which ensures that the hybrid algorithm is well suited to address the challenges posed by the FSSP. Third, we perform a comprehensive performance evaluation of the proposed hybrid algorithm, demonstrating its effectiveness in terms of solution quality and computational efficiency. Finally, we provide an in-depth analysis of the behavior of the hybrid algorithm, discussing the roles of the SHO and GA components and their interactions during the search process, which can help understand the factors contributing to the success of the algorithm and provide insight into potential improvements or adaptations to other combinatorial optimization problems.
1. Introduction
Combinatorial problems [1] involve finding the optimal arrangement, selection or sequencing of a finite set of elements based on specific constraints and objectives. They are prevalent in various fields, such as mathematics, computer science, engineering, operations research, economics and biology. The importance of solving combinatorial problems stems from their practical applications in decision-making, resource allocation and optimization tasks critical for the efficiency and effectiveness of real-world systems.
Examples of combinatorial problems include the traveling salesman problem [2], which seeks the shortest route for a salesman visiting a set of cities once before returning to the starting point; the knapsack problem, which aims to select items with different weights and values to maximize the total value without exceeding a given weight limit; and the graph coloring problem, which assigns colors to graph vertices so that no two adjacent vertices share the same color. These problems, although seemingly different, share common challenges in terms of computational complexity, as they often require exploring an extensive solution space to identify the optimal solution.
One specific combinatorial problem of significant practical importance is the Flow Shop Scheduling Problem (FSSP) [3]. In this problem, a set of jobs must be processed on a collection of machines in a specific order, with each job consisting of multiple operations executed sequentially. The objective is to find a schedule that minimizes the makespan or the total time required to complete all jobs. Due to the combinatorial nature of this problem, finding an optimal solution becomes increasingly difficult as the number of jobs and machines increases.
Swarm intelligence algorithms [4] have emerged as effective approaches for tackling the optimization of makespan in the FSSP. These algorithms are inspired by the collective behavior of social organisms such as birds, fish, and insects, and their ability to solve complex problems through decentralized and self-organizing processes. Some widely used swarm intelligence algorithms for solving the FSSP include Particle Swarm Optimization (PSO) [5], Ant Colony Optimization (ACO) [6], Whale Swarm Algorithm (WOA) [7] and Rat Swarm Optimization [8].
In the context of the FSSP [9], these algorithms encode potential solutions as particles, ants or bees and iteratively explore the solution space by updating the position or path of these agents based on their own experiences and the collective knowledge of the swarm. The agents collaborate and compete, allowing the swarm to converge towards an optimal or near-optimal solution for the makespan. The effectiveness of swarm intelligence algorithms in solving the FSSP has been demonstrated in various industrial applications, such as manufacturing, transportation and logistics, where efficient job scheduling is critical for reducing production costs, improving resource utilization and enhancing overall performance.
In this article, we propose a novel hybrid algorithm that combines the Spotted Hyena Optimizer (SHO) [10] and Genetic Algorithm (GA) [11] to solve the Flow Shop Scheduling Problem (FSSP). The FSSP is a particular case of the Flow Shop Scheduling Problem (FSSP), in which jobs are processed on a set of machines in a specific order, and all jobs follow the same sequence of operations on the machines. The primary objective is to minimize the makespan, which is the total time required to complete all jobs.
The Spotted Hyena Optimizer (SHO) is a nature-inspired optimization algorithm based on the unique hunting behavior of spotted hyenas. It incorporates four main mechanisms: searching, encircling, attacking and mobbing. These mechanisms help explore the solution space efficiently and exploit the best solutions found during the search process.
The Genetic Algorithm (GA) is a widely-used, population-based optimization method inspired by the principles of natural selection and genetics. It operates on a population of candidate solutions and evolves them over generations using genetic operators, such as selection, crossover and mutation. GAs have been successfully applied to solve numerous combinatorial optimization problems, including the FSSP.
In our hybrid approach, we combine the strengths of both SHO and GA to improve the overall search efficiency and solution quality. The proposed algorithm starts with an initial population generated by the SHO. During the search process, the SHO mechanisms are employed to explore the solution space and to update the hyenas’ positions. After a predefined number of iterations, the GA is integrated into the algorithm to further refine the solutions. The GA takes the current hyena positions as an input population and performs selection, crossover and mutation operations to generate offspring. The offspring then replace some of the least fit hyenas in the population, ensuring the best solutions are retained.
This hybridization of SHO and GA capitalizes on the exploration capabilities of the SHO and the exploitation abilities of the GA, resulting in a more robust and efficient algorithm for solving the FSSP. The proposed hybrid method is tested on a set of benchmark instances from the literature, and the results demonstrate its effectiveness in finding near-optimal solutions with competitive computational times. The successful application of the hybrid spotted hyena and genetic algorithm to the FSSP indicates its potential for addressing other complex combinatorial optimization problems in various domains.
The main contributions of this paper can be summarized as follows:
- -
- Development of a Hybrid Algorithm: We propose a new hybrid algorithm that effectively integrates the exploration capabilities of SHO and the exploitation capabilities of GA. This combination ensures a more balanced and efficient search process, allowing the algorithm to find near-optimal solutions for the FSSP.
- -
- Adaptation of SHO and GA to FSSP: We adapt the SHO and GA methods to the specific requirements of FSSP, including encoding schemes, objective function evaluation and constraint handling. This adaptation ensures that the hybrid algorithm is well-suited to address the challenges posed by the FSSP.
- -
- Comprehensive Performance Evaluation: We perform a thorough performance evaluation of the proposed hybrid algorithm using a set of benchmark instances from the literature. The results are compared with those obtained by state-of-the-art algorithms, demonstrating the effectiveness of our hybrid approach in terms of solution quality and computational efficiency.
- -
- Hybrid Algorithm Behavior Analysis: We provide an in-depth analysis of the behavior of the hybrid algorithm, discussing the roles of the SHO and GA components and their interactions during the search process. This analysis helps to understand the factors contributing to the success of the algorithm in solving the FSSP and offers insights into potential improvements or adaptations to other combinatorial optimization problems.
This article is organized into six sections: 1. Introduction, which provides an overview of the combinatorial optimization problem and the motivation for developing the hybrid algorithm; 2. Related Works and Literature Review, where we discuss existing research on swarm intelligence algorithms and their application to the FSSP; 3. Flow Shop Scheduling Problems (FSSP), which offers a detailed description of the FSSP, its challenges and its significance in real-world applications; 4. Methodology, where we present the design and implementation of the proposed hybrid algorithm, combining the Spotted Hyena Optimizer (SHO) and Genetic Algorithm (GA); 5. Experimental Outcomes, where we analyze the performance of the hybrid algorithm using benchmark instances and compare the results with existing state-of-the-art approaches; and finally, 6. Conclusion, where we summarize the main findings of the study, discuss the implications of the results and suggest future research directions in the field of combinatorial optimization.
2. Related Works
In recent years, swarm intelligence has been increasingly applied to solve Flow Shop Scheduling Problems (FSSP) due to its ability to effectively explore and exploit the solution space. The following studies have made significant contributions to this area:
- Tang et al., (2016) [12] proposed an energy-efficient dynamic scheduling approach for a flexible flow shop using an improved particle swarm optimization. The algorithm addresses the dynamic scheduling problem while minimizing energy consumption and makespan.
- C. Zhang et al., (2021) [7] presented a discrete whale swarm algorithm for a hybrid flow-shop scheduling problem with limited buffers, considering practical constraints on buffer area resources and alternative process routes. The algorithm’s effectiveness was validated on three groups of instances and a real-world industrial case.
- Li et al., (2022) [13] examined the distributed assembly mixed no-idle permutation flow-shop scheduling problem (DAMNIPFSP) with a focus on minimizing total tardiness. The researchers developed a mixed-integer linear programming model and proposed a Referenced Iterated Greedy (RIG) algorithm, incorporating novel destruction and reconstruction methods as well as local search methods based on a reference. Experimental results demonstrated the effectiveness of the RIG algorithm, positioning it as a state-of-the-art solution for DAMNIPFSP with the total tardiness criterion.
- Mahmud et al., (2022) [14] introduced a bi-objective integrated supply chain scheduling model and developed two new meta-heuristic algorithms based on multi-objective particle swarm optimization (MOPSO) to solve the strongly NP-hard flexible job shop problem.
- Gümüşçü et al., (2022) [15] investigated the impact of local search strategies on chaotic hybrid firefly particle swarm optimization algorithm in flow-shop scheduling, comparing the results of the solutions obtained using different local search strategies.
- Vali et al., (2022) [16] presented a flexible job shop scheduling problem to optimize patient flow and minimize the total carbon footprint. They developed a metaheuristic optimization algorithm called Chaotic Salp Swarm Algorithm Enhanced with Opposition-based Learning and Sine Cosine (CSSAOS) to solve this NP-hard problem
- Hayat et al., (2023) [17] explored the enhancement of Particle Swarm Optimization (PSO) in tackling Permutation Flow-Shop Scheduling Problems (PFSPs) by hybridizing it with Variable Neighborhood Search (VNS) and Simulated Annealing (SA). The authors compared the performance of the developed hybrid PSO (HPSO) algorithm with 120 distinct Taillard instances, demonstrating its robustness and significantly improved makespan optimization compared to other hybrid metaheuristics.
- Sun et al., (2023) [18] investigated production scheduling technology for knitting workshops utilizing an improved genetic algorithm (IGA) with tabu search. The research, conducted at the Key Laboratory of Modern Textile Machinery & Technology of Zhejiang Province, Zhejiang Sci-Tech University and the School of Automation, Zhejiang Institute of Mechanical & Electrical Engineering aimed to enhance production efficiency and reduce costs. Their proposed IGA demonstrated faster convergence and better search capabilities compared to traditional genetic algorithms, offering valuable insights for advancing intelligent development in knitting production.
Some of the state-of-the-art optimization algorithms for FSSP include GA-SHOA, WD [19], GA [19], IHSA [19], PSO [19], CLS-BFO [20], AGGA [20] and SSO [20]. These algorithms were selected and used for comparison with the hybrid algorithm we propose in this paper. GA-SHOA is a new hybrid algorithm that combines the exploration capabilities of SHOA with the exploitation capabilities of GA to efficiently search the solution space. CLS-BFO is a hybrid algorithm that combines the cuckoo search algorithm (CS) with the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method to solve the FSSP. WD is an algorithm that uses differential evolution (DE) to optimize the FSSP. GA is a well-known metaheuristic algorithm that has been widely used to solve the FSSP. IHSA is a hybrid algorithm that combines the improved harmony search (IHS) algorithm and simulated annealing (SA). PSO is a swarm intelligence algorithm that has been applied to FSSP with promising results. AGGA is another hybrid algorithm that combines the genetic algorithm and the gravitational search algorithm (GSA). SSO is an algorithm that mimics the social behavior of the spotted hyena and has been shown to be effective in solving the FSSP.
Table 1 introduces a comparison of these methods.

Table 1.
Comparison of optimization algorithms for the FSSP.
3. Flow Shop Scheduling Problems (FSSPs)
Flow Shop Scheduling Problems (FSSPs) is a class of scheduling problems that arise in manufacturing and production systems, where a set of jobs or tasks must be processed through a series of machines in a specific order. FSSPs is a well-studied optimization problem in the field of operations research and has numerous applications in various industries, such as automotive, semiconductor, food processing and textile production, among others.
In a typical flow shop environment, there are multiple machines or workstations, and each job must be processed on every machine in a predetermined sequence. The main objective of the FSSP is to determine the optimal scheduling of jobs on machines to achieve certain performance criteria, such as minimizing makespan, total completion time, total tardiness or a combination of these objectives.
The importance of flow shop scheduling problems lies in their ability to optimize the utilization of resources, reduce production costs and improve overall efficiency in manufacturing systems. Effective flow shop scheduling can lead to:
- Reduced production lead time: By optimizing the job sequence and minimizing the idle time of machines, flow shop scheduling can significantly reduce the total production time.
- Improved resource utilization: Efficient scheduling ensures that machines are utilized optimally, reducing idle time and maximizing production throughput.
- Enhanced customer satisfaction: Timely delivery of products and shorter lead times can increase customer satisfaction and help to maintain a competitive edge in the market.
- Lower inventory costs: By reducing work-in-process inventory and minimizing production time, flow shop scheduling can help lower inventory holding costs.
- Increased competitiveness: Effective flow shop scheduling allows companies to be more agile and responsive to market demands, thus enhancing their competitive position.
Despite its importance, FSSP is a challenging combinatorial optimization problem known to be NP-hard, meaning that finding an optimal solution becomes increasingly difficult as the problem size increases. As a result, researchers have developed various heuristic and metaheuristic algorithms to find near-optimal solutions for the FSSP in a reasonable amount of time, such as particle swarm optimization, genetic algorithms, simulated annealing and ant colony optimization, among others. These methods have been successfully applied to tackle real-world flow shop scheduling problems, resulting in significant improvements in manufacturing efficiency and cost reduction.
The Fob-Shop Scheduling Problem (FSSP) involves assigning a set of n jobs, each consisting of multiple operations, to a set of m machines. The primary objective is to find a schedule that minimizes the makespan (Cmax), which is the total completion time of all jobs. A solution can be represented as an n × m vector of operation sequences that optimizes the completion time.
where
The constraints are as follows:
- Constraint (2) minimizes the finish time of the operation on machine m + 1 (the makespan).
- Constraint (3) ensures that precedence relationships between operations are maintained.
- Constraint (4) states that each machine can process only one operation at a time.
- Constraint (5) ensures that the finish times are positive.
4. Methodology
The Spotted Hyena Optimizer (SHO) is a metaheuristic, bio-inspired optimization algorithm developed by Dhiman et al. The algorithm is based on the social behaviors of spotted hyenas, which are the largest among the three other hyena species (striped, brown and aardwolf). Spotted hyenas are skillful hunters that typically live and hunt in groups, relying on networks with over 100 members. The SHO algorithm comprises four main steps that emulate the encircling, hunting, attacking and searching behaviors of spotted hyenas (as shown in Figure 1 [10]).

Figure 1.
Spotted Hyena Hunting Behavior [10].
- Encircling prey:
The best solution is considered the target prey, and other search agents update their positions based on the obtained best solution. The mathematical model for this behavior is given by:
- Hunting:
The hunting strategy of the SHO is defined as follows:
- Attacking prey:
The mathematical formulation for attacking prey is given by:
- Searching for prey:
The search for a suitable solution involves evaluating the E and B vectors. The SHO algorithm can solve various high-dimensional problems with low computational efforts and avoid local optimum issues.
In this study, we will focus on using the encircling behavior to solve the flow shop scheduling problem, and the pseudo-code of the SHO algorithm is provided in Algorithm 1.
| Algorithm 1 Spotted Hyena Optimizer (SHO) |
| 1: procedure SHO 2: Input: Spotted hyenas population Pi (i = 1, 2, ..., n) 3: Output: The optimal search agent 4: Initialize parameters h, B, E, and N 5: Evaluate the fitness of each search agent 6: Ph ← Identify the best search agent 7: Ch ← Form a group or cluster of all distant optimal solutions 8: while x < MaxIteration do 9: for each search agent do 10: Update the current agent’s position using Equation (10) 11: end for 12: Update h, B, E, and N 13: Ensure search agents stay within the given search space and adjust if necessary 14: Compute the fitness of each search agent 15: Update Ph if a better solution is found compared to the previous optimal solution 16: Modify group Ch based on Ph 17: x ← x + 1 18: end while 19: return Ph 20: end procedure |
Alterations to mathematical operators for flow shop problems:
The mathematical operators are redefined to accommodate the flow shop problem as follows:
- Dh = |B · P_prey (x) − P(x)|: The subtraction operation between two rat positions is adapted to a list of swaps to be performed on a job sequence P(t) to obtain the best sequence list Pbest(t).
- E · Dh: This operation, involving a real number between [0, 1] and a list of swaps, is redefined to manipulate and decrease the number of swaps generated by the previous equation.
- P_prey (x) − E · Dh: This operation determines the final number of potential swaps to be applied to a job sequence.
- An illustrative example of these modifications is provided below:
- P_prey (x):

- P(x):

- Dh =|P_prey (x) − P(x)|: List of swaps to be performed on a sequence of jobs P(x) to obtain the first sequence list
- P_prey (x) = [ [J5,J1},{J3,J2}]
- E = 0.5
- E · Dh= ½ [J5,J1},{J3,J2}] = {J5,J1}
- p_prey (x)- E · Dh =

The Genetic Algorithm (GA) is a popular metaheuristic technique for solving optimization problems, including the Flow Shop Scheduling Problem (FSSP). The Uniform Crossover and Mutation are two genetic operators used within GA that combine parent solutions to create offspring. Here’s an example of using a Genetic Algorithm with Uniform Crossover and Mutation to solve the FSSP:
Crossover: Perform the Uniform Crossover on the selected parent individuals to create offspring. In the Uniform Crossover, for each position in the parent’s permutation, a random decision is made as to which parent’s gene will be inherited by the offspring. For example:
- Parent 1: [1, 2, 3, 4, 5] =

- A random binary mask: [0, 1, 0, 1, 0]
- Parent 2: [5, 4, 3, 2, 1] =

- Offspring 1: [1, 4, 3, 2, 5] =

- Offspring 2: [5, 2, 3, 4, 1] =

Mutation: Apply a mutation operator to each gene of the offspring with a certain probability. The mutation operator randomly changes the value of the gene to another valid value. In the FSSP case, which is a random permutation of two tasks, the mutation operator may swap the positions of two tasks in the offspring’s permutation.
For example:
- Offspring 1: [1, 4, 3, 2, 5] =

- Randomly select two genes to mutate 1 and 3 (swap tasks 1 and 3):
- Mutated offspring 1: [1, 4, 2, 2, 5] =

The final algorithm is described as follows in Algorithm 2:
| Algorithm 2 Discrete Hybrid Spotted Hyena Optimizer with Uniform Crocgover |
| 1: procedure HYBRID SHO(2) 2: Input: Spotted hyenas population Pi (i = 1, 2, ..., n) 3: Output: The optimal search agent 4: Initialize parameters h, B, E, and N 5: Evaluate the fitness of each search agent 6: Ph ← Identify the best search agent 7: Ch ← Form a group or cluster of all distant optimal solutions 8: while x < MaxIteration do 9: for each search agent do 10: Update the current agent’s position using Equation (7) 11: end for 12: Perform Uniform Crossover on selected parent individuals to create offspring 13: Apply mutation operators to offspring (inversion) 14: Replace some individuals in the population with the newly created offspring 15: Update h, B, E, and N 16: Ensure search agents stay within the given search space and adjust if necessary 17: Compute the fitness of each search agent 18: if a better solution is found compared to the previous optimal solution then 19: Update Ph 20: end if 21: Modify group Ch based on Ph 22: x ← x + 1 23: end while 24: return Ph 25: end procedure |
5. Experimental Outcomes
The performance of the hybrid GA-SHO algorithm was assessed using over 50 instances from the OR library. The evaluation results are presented in Table 2, which include the instance name (“Instance”), the number of jobs (n) and machines (m) for each instance (“n × m”), the best result achieved by other algorithms (“BKS”), the best and worst results obtained through the SHO method (“Best” and “Worst”), the average results (“Average”) and the average execution time in seconds for 20 runs (“Time”). The “PDav(%)” column displays the percentage deviation of the average solution length from the optimal solution length, computed using Equation (12).

Table 2.
Parameters of Discrete GA-SHO.
The “PDav(%)” column emphasizes values of 0.00 in bold when all solutions found in the 20 runs are equal to the length of the best-known solution. If the average of the solutions discovered in all tests is less than the length of the best-known solution, these values are highlighted in bold and blue. This suggests that the GA-SHO algorithm managed to find solutions that either match or surpass the best-known solutions for these instances.
To properly evaluate the effectiveness of the GA-SHO algorithm, it is crucial to compare it with other methods for solving problems.
The comparison is made with the following algorithms: CLS-BFE [20], DEO [19], GA [19], IHSA [19], PSO [19], AGGA [20] and SSO [20].
The initial parameters are described in Table 2:
Figure 2 shows the comparison of the best-obtained results, clearly demonstrating that the GA-SHOA algorithm outperforms other methods (CLS-BFO, IHSA, PSO, DEO, SSO, GA, AGGA) across all instances (REC01 to REC23).
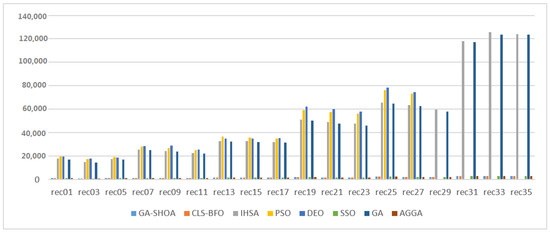
Figure 2.
The comparison of the best-obtained results.
Table 3 and Table 4 clearly demonstrates that the GA-SHOA algorithm outperforms other methods (CLS-BFO, IHSA, PSO, DEO, SSO, GA, AGGA) across all instances (REC01 to REC23). Here’s a more detailed analysis of the data:

Table 3.
Comparison between GA-SHOA, CLS-BFO, IHSA, and PSO.

Table 4.
Comparison between DEO, SSO, GA and ACGA.
- -
- Objective Function Value (Best): For all instances, GA-SHOA consistently attains the most optimal or near-optimal solution. This highlights GA-SHOA’s superior ability to find the most optimal or best solutions compared to the other algorithms.
- -
- Standard Deviation (STD): GA-SHOA exhibits notably lower standard deviation values compared to other methods. This suggests that GA-SHOA’s results are more reliable and exhibit less variation. A low standard deviation implies that the values are close to the mean or expected value, whereas a high standard deviation implies a wider spread of values. In an optimization context, a lower standard deviation is favorable as it indicates consistent solution quality near the optimal.
- -
- Computation Time: GA-SHOA also outshines other methods in terms of computational efficiency, showcasing faster computation times. For instance, in the case of REC01, GA-SHOA takes a mere 0.042 units of time, while other methods, such as CLS-BFO (0.247 units), IHSA (7.750 units) and PSO (6.042 units), require significantly more time.
Conclusively, based on the data provided, GA-SHOA excels over the other algorithms in terms of solution quality (best), solution consistency (std) and computational speed (time). This superior performance is consistent across all instances, positioning GA-SHOA as a more reliable and efficient choice for this specific problem.
To further scrutinize GA-SHOA’s performance against other algorithms, we can conduct an Analysis of Variance (ANOVA) to ascertain if there is a significant difference in the mean objective function values. ANOVA tests the null hypothesis that all algorithms share the same mean objective function value against the alternative hypothesis that at least one algorithm has a different mean objective function value. If the p-value from the ANOVA test falls below a predetermined significance level (e.g., 0.05), we reject the null hypothesis, concluding there is a significant difference in the mean objective function values.
The results of the ANOVA test are described in Table 5:

Table 5.
Anova test comparison.
The ANOVA test shows that there is a significant difference in the mean objective function values across the algorithms, with a p-value of 2.20 × 10−16. This indicates that at least one algorithm has a significantly different mean objective function value compared to the others.
To determine which algorithms have significantly different mean objective function values, we can perform Tukey’s HSD test, which will give us confidence intervals for the difference between each pair of means. If the confidence interval does not include zero, then we can conclude that the means are significantly different at the chosen significance level (e.g., 0.05).
Here are the results of Tukey’s HSD test in Table 6:

Table 6.
The Tukey’s HSD test comparison.
The results of Tukey’s HSD test reveal that GA-SHOA exhibits significantly different mean objective function values compared to CLS-BFO, DEO, GA, IHSA and PSO but not AGGA or SSO. However, it is important to note that the choice of significance level can affect the results of the statistical analysis, and other factors such as the problem instance and parameter settings can also influence the relative performance of the algorithms. Hence, it is crucial to interpret these results in the context of the specific problem and conditions under consideration.
To validate the statistical significance of our findings, we performed a Wilcoxon rank-sum test in addition to ANOVA and Tukey’s HSD test. Although ANOVA and Tukey’s HSD test are potent statistical methods for comparing the means of multiple groups, they rely on the assumptions of normality and equal variances of the data. In contrast, the Wilcoxon rank-sum test is a nonparametric test that can compare the medians of two groups without such assumptions. By conducting the Wilcoxon rank-sum test, we verified our results and ensured the statistical significance of the performance differences between our proposed algorithm and the other methods. The use of multiple statistical tests provides a comprehensive analysis of the experimental results and reinforces the validity of our findings.
Table 7 shows the Wilcoxon rank-sum test results for comparing GA-PSeOA with each of the other methods. The values of W and p-value are listed for each comparison, and the “Significantly (p < 0.05)?” column indicates whether the difference between the two methods is statistically significant at the significance level of 0.05.

Table 7.
The Wilcoxon signed rank test comparison.
Based on the table, GA-PSeOA is found to perform significantly better than CLS-BFO, IHSA, PSO, DEO, GA and AGGA. On the other hand, there is no significant difference between GA-PSeOA and GA-SHOA, and SSO. The p-values for the significant differences are all less than 0.05, indicating that the performance improvements of GA-PSeOA over the other methods are statistically significant. Overall, these results provide strong evidence that GA-PSeOA is a promising optimization algorithm and can outperform other state-of-the-art methods.
6. Conclusions
In conclusion, this study highlights the effectiveness of a new hybrid algorithm, combining genetic and SHOA methods, in solving the shop floor scheduling problem (FSSP). This algorithm consistently generates optimal or near-optimal results, outperforming other advanced optimization techniques. Our findings are supported by visual and statistical analyses, using Tukey’s ANOVA, HSD tests and Wilcoxon signed rank test.
FSSP is a critical and complex problem in many areas of manufacturing. Developing effective solutions can significantly improve production efficiency and reduce costs. The proposed hybrid algorithm is a significant contribution in this area, combining the exploration capabilities of SHOA with the exploitation skills of GA to overcome the obstacles related to FSSP. Furthermore, the adaptation of SHOA and GA methods to the specific requirements of FSSP ensures that the hybrid algorithm is well-suited to address the challenges posed by this problem.
Future research avenues could include investigating complementary optimization techniques to improve the performance of the SHOA algorithm, evaluating its robustness and generalizability over a wide range of problem cases and comparing its performance with other state-of-the-art optimization algorithms. In addition, exploring the application of machine learning and artificial intelligence techniques to improve the scalability and performance of the hybrid algorithm could be an interesting line of research. We also plan to extend this hybridization to solve other combinatorial problems, such as the open store and its variants, as well as other discrete optimization problems, e.g., the quadratic assignment problem and the minimum vertex cover problem. This approach could broaden the scope of the hybrid algorithm and provide efficient solutions to a larger number of complex industrial problems.
Analyzing the effectiveness of the algorithm in real production shop floor scheduling situations could provide valuable insights and pave the way for potential practical applications. In addition, examining the implementation of the hybrid algorithm in various industries and evaluating its scalability in large-scale production environments could make important contributions to the optimization literature.
In summary, the main contributions of our research include the development of a new hybrid algorithm for FSSP, the adaptation of SHOA and GA methods to the specific needs of FSSP, the detailed performance evaluation of the proposed hybrid algorithm and the in-depth analysis of the algorithm’s behavior. Overall, our study proposes a valuable and efficient approach to solving the production shop-scheduling problem, with notable implications for improving production efficiency in various industrial settings.
Author Contributions
Conceptualization, T.M., I.M., M.E.R. and G.D.; methodology, T.M., I.M., M.E.R. and G.D.; software, T.M., I.M., M.E.R. and G.D.; validation, T.M., I.M., M.E.R. and G.D.; formal analysis, T.M., I.M., M.E.R. and G.D.; investigation, T.M., I.M., M.E.R. and G.D.; resources, T.M., I.M., M.E.R. and G.D.; data curation, T.M., I.M., M.E.R. and G.D.; writing—original draft preparation, T.M., I.M., M.E.R. and G.D.; writing—review and editing, T.M., I.M., M.E.R. and G.D; supervision, I.M. and M.E.R.; project administration, T.M., I.M., M.E.R. and G.D funding acquisition, T.M., I.M., M.E.R. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors have no conflict of interest to declare that are relevant to the content of this article.
References
- Grisales-Ramírez, E.; Osorio, G. Multi-Objective Combinatorial Optimization Using the Cell Mapping Algorithm for Mobile Robots Trajectory Planning. Electronics 2023, 12, 2105. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Lin, Y.-D.; Yang, C.-H.; Wang, C.-K.; Chiang, L.-C.; Chiang, P.-J. A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem. Sustainability 2023, 15, 5111. [Google Scholar] [CrossRef]
- Bhongade, A.S.; Khodke, P.M.; Rehman, A.U.; Nikam, M.D.; Patil, P.D.; Suryavanshi, P. Managing Disruptions in a Flow-Shop Manufacturing System. Mathematics 2023, 11, 1731. [Google Scholar] [CrossRef]
- Cao, L.; Chen, H.; Chen, Y.; Yue, Y.; Zhang, X. Bio-Inspired Swarm Intelligence Optimization Algorithm-Aided Hybrid TDOA/AOA-Based Localization. Biomimetics 2023, 8, 186. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kulesz, B.; Sikora, A.; Zielonka, A. The Application of Ant Colony Algorithms to Improving the Operation of Traction Rectifier Transformers. Computers 2019, 8, 28. [Google Scholar] [CrossRef]
- Zhang, C.; Tan, J.; Peng, K.; Gao, L.; Shen, W.; Lian, K. A discrete whale swarm algorithm for hybrid flow-shop scheduling problem with limited buffers. Robot. Comput.-Integr. Manuf. 2021, 68, 102081. [Google Scholar] [CrossRef]
- Mzili, T.; Riffi, M.E.; Mzili, I.; Dhiman, G. A novel discrete Rat swarm optimization (DRSO) algorithm for solving the traveling salesman problem. Decis. Mak. Appl. Manag. Eng. 2022, 5, 287–299. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Liang, S. The circular discrete particle swarm optimization algorithm for flow shop scheduling problem. Expert Syst. Appl. 2010, 37, 5827–5834. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Multi-objective spotted hyena optimizer: A Multi-objective optimization algorithm for engineering problems. Knowl.-Based Syst. 2018, 150, 175–197. [Google Scholar] [CrossRef]
- Keser, M.; Stupp, S.I. Genetic algorithms in computational materials science and engineering: Simulation and design of self-assembling materials. Comput. Methods Appl. Mech. Eng. 2000, 186, 373–385. [Google Scholar] [CrossRef]
- Tang, D.; Dai, M.; Salido, M.A.; Giret, A. Energy-efficient dynamic scheduling for a flexible flow shop using an improved particle swarm optimization. Comput. Ind. 2016, 81, 82–95. [Google Scholar] [CrossRef]
- Li, Y.-Z.; Pan, Q.-K.; Ruiz, R.; Sang, H.-Y. A referenced iterated greedy algorithm for the distributed assembly mixed no-idle permutation flowshop scheduling problem with the total tardiness criterion. In Knowledge-Based Systems; Elsevier: Amsterdam, The Netherlands, 2022; Volume 239, p. 108036. [Google Scholar] [CrossRef]
- Mahmud, S.; Chakrabortty, R.K.; Abbasi, A.; Ryan, M.J. Swarm intelligent based metaheuristics for a bi-objective flexible job shop integrated supply chain scheduling problems. Appl. Soft Comput. 2022, 121, 108794. [Google Scholar] [CrossRef]
- Gümüşçü, A.; Kaya, S.; Tenekeci, M.E.; Karaçizmeli, İ.H.; Aydilek, İ.B. The impact of local search strategies on chaotic hybrid firefly particle swarm optimization algorithm in flow-shop scheduling. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 6432–6440. [Google Scholar] [CrossRef]
- Vali, M.; Salimifard, K.; Gandomi, A.H.; Chaussalet, T.J. Application of job shop scheduling approach in green patient flow optimization using a hybrid swarm intelligence. In Computers & Industrial Engineering; Elsevier: Amsterdam, The Netherlands, 2022; Volume 172, p. 108603. [Google Scholar] [CrossRef]
- Hayat, I.; Tariq, A.; Shahzad, W.; Masud, M.; Ahmed, S.; Ali, M.U.; Zafar, A. Hybridization of Particle Swarm Optimization with Variable Neighborhood Search and Simulated Annealing for Improved Handling of the Permutation Flow-Shop Scheduling Problem. Systems 2023, 11, 221. [Google Scholar] [CrossRef]
- Sun, L.; Shi, W.; Wang, J.; Mao, H.; Tu, J.; Wang, L. Research on Production Scheduling Technology in Knitting Workshop Based on Improved Genetic Algorithm. Appl. Sci. 2023, 13, 5701. [Google Scholar] [CrossRef]
- Chaudhry, I.A.; Elbadawi, I.A.; Usman, M.; Chughtai, M.T. Minimising Total Flowtime in a No-Wait Flow Shop (NWFS) using Genetic Algorithms. Ing. E Investig. 2018, 38, 68–79. [Google Scholar] [CrossRef]
- Kurdı, M. Application of Social Spider Optimization for Permutation Flow Shop Scheduling Problem. J. Soft Comput. Artif. Intell. 2021, 2, 85–97. Available online: https://dergipark.org.tr/en/pub/jscai/issue/66233/1013405 (accessed on 20 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).