A Scheduling Solution for Robotic Arm-Based Batching Systems with Multiple Conveyor Belts ^†

Abstract

In this study, we tackle a key scheduling problem in a robotic arm-based food processing system, where multiple conveyors—an infeed conveyor that feeds food items to robotic arms and two tray lane conveyors, on which trays to batch food items are placed—are implemented. The target scheduling problem is to determine what item on an infeed conveyor belt is picked up by which robotic arm at what position, and on which tray the picked up item will be placed. This problem involves critical constraints, such as sequence-dependent processing time and dynamic item and tray positions. Moreover, due to the speed of the infeed conveyor and latency in the information about entering items into the system, this scheduling problem must be solved in near real time. To address these challenges, we propose a scheduling solution that first decomposes the original scheduling problem into sub-problems, where a sub-problem formulated as a goal program schedules robotic arms only for a single tray. The performance of the proposed solution approach is then tested under a simulation environment, and from the experiments, the proposed approach produces acceptable performance.

1. Introduction

A robotic arm or a machine with a similar feature is an integral part of various autonomous manufacturing and production systems. A robotic arm (or a set of robotic arms) is often placed on or next to a conveyor belt. A conveyor belt brings items to the robotic arm, and the items moving on the conveyor belt are sorted and/or picked by the robotic arm [1]. Figure 1 shows a simplified representation of a robotic arm batching system, where items on a conveyor belt are picked up and put into a tray by a robotic arm.

With a conveyor belt, a robotic arm can significantly improve the throughput of a manufacturing and production system. A robotic arm can also provide flexibility in a system’s item flows by transferring an item from one conveyor belt to another. Compared to batching machines that simply push the items out of a conveyor belt, robotic arms also provide more flexibility in the way the items are handled. If the items to carry are heavy or hazardous, the risk of injury to human operators is further minimized by the robotic arm implementation. Moreover, a robotic arm with a conveyor belt has demonstrated its capability to perform tasks that are simple and repetitive. The tasks that should be performed quickly with quality can also be performed successfully by a robotic arm. Picking, placing and sorting tasks are examples of these tasks [2].

The food processing and packaging business are some of the industrial sectors where such advantages of robotic arms with conveyor belts can improve the profits of the business [3]. Imagine a food batching and packaging process where food items of different sizes are grouped into trays of a predetermined standard size or weight. Here, a robotic arm-based system with a sophisticated control mechanism can identify food items moving fast over a conveyor belt and choose the right pieces of food items from a conveyor belt. In this way, the productivity and efficiency of the process can be dramatically improved, and the need for human labor in the process can be minimized [4]. Moreover, a robotic arm-based system is easy to maintain and provides a high level of hygiene and food quality.

It should be noted that the benefits of a robotic arm-based system will not be achieved by simply equipping and implementing the system. An operating system that controls the robotic arm’s motion and action is essential for fully exploiting the capability of the robotic arm-based system.

The core of the operating system is to address the scheduling problem involved in a robotic arm-based system operation, which addresses a number of nested decision-making problems. For example, given a target weight of a food package, a robotic arm should determine which item would be picked up and put into which package tray in what order so that the productivity of the system (e.g., the number of food items packed per time unit) is maximized and give-away (additional weights given over a target weight) in a tray is minimized. However, such decision making is complex by its nature and should be made in a very short time to keep the throughput of the system as fast as the speed of a conveyor belt. The relevant decision-making problem contexts and challenges can be found in a container crane scheduling problem, where the interference between cranes and the sequence-dependent container (un)loading time are critical to consider [5], as well as a flow shop scheduling problem with real-time order acceptance [6].

Motivated by the decision-making challenges in a robotic arm-based system and the expected impact of a well-designed scheduling algorithm on the performance of the system, this study addresses a scheduling problem involved in a specific but common robotic arm-based system, where multiple robotic arms operate over a conveyor belt system, in which two types of conveyor belts—an infeed conveyor for food items delivery and a tray lane conveyor for food item trays—are operated. We first identify the key decisions and constraints of the target scheduling problem. A decomposition-based scheduling approach is then proposed to solve the resulting scheduling problem within an available computation time. The performance of the proposed solution approach is finally evaluated in a simulation environment, where items with random weights enter into the robotic arm-based system as a stochastic process.

2. Related Work

2.1. Scheduling Problems for Robotic Arms in Automated Systems

As highlighted in the introduction, robotic arms have been applied to various industrial sectors, including manufacturing and production systems due to their contribution to the overall productivity, reliability, and quality of a target system. A key element for a successful implementation of robotic arms into such systems is to schedule movements of a robotic arm to perform atomic tasks, such as welding, drilling, and spray painting. This scheduling problem is known as the robotic task sequencing problem (RTSP) [7].

Given that a robotic arm has a single configuration to perform a task, the RTSP can be formulated as the traveling salesman problem (TSP) [8]. However, a robotic arm could have multiple configurations especially to avoid collisions during operations and to reduce the duration of the movement, which is known as inverse kinematics solutions. With inverse kinematics, the RTSP can be formulated by the generalized TSP (GTSP), where a location for a task is represented as a bin with multiple nodes, and a travel time between two tasks depends on what nodes in the corresponding bins are visited. Given this setting, a robotic arm should visit all the bins for the target tasks, visiting only a single node within the bins [9]. Please refer to [10,11] for a detailed review on the RTSP.

The extended RTSP can be found in a flexible manufacturing system (FMS), where a robotic arm is often installed to transport items from an input station to multiple workstations and from the workstations to an output station. In this case, not only the robotic arm but also the workstations should be scheduled so that the overall system performance (e.g., workstation utilization and throughput of the system) can be optimized. To address this scheduling complexity, Petri nets are often applied to represent a target system as a discrete-event system [12,13].

The RTSP can also be extended for multiple robotic arms. Here, a goal is to operate robotic arms to move objects to available slots with a minimum total travel distance. The resulting multiple robotic arm scheduling problem can be formulated as a parallel machine scheduling problem for a single-stage production [14]. Note that the multiple robotic arm scheduling problem is in general solved for static task positions; therefore, a solution to the problem is often adjusted by a model predictive control (MPC) planning algorithm that addresses dynamic collision avoidance constraints of the robotic arms [15,16].

2.2. Scheduling Problems for Robotic Arms with Conveyor Belts

Here, we review scheduling problems for robotic arms with conveyor belts especially in food processing systems.

Table 1. Related work for a robotic arm-based batching system.

Study	Target System/Problem	Decision	Tray/Bin Lane Number
[17]	A meat processing system	Batch or trim pieces? (with respect to weights)	1
[18]	A fillet batching operation in a poultry processing plant	Which tray? (with respect to weights)	1
[19]	Batching food items for a specific weight target	Which bin? (with respect to weights)	2
[20]	Poultry processing plants with batchers	Which tray? (with respect to weights)	1
[21]	Bin covering with a target weight for a poultry processing plant	Which tray? (with respect to weights)	1
[22]	Packing in a conveyor-based automatic sorting system	Which action? - Do {stay, put, pick} - For {current box, buffer}	1
[23]	A robotic arm system with multiple conveyor belts	Which tray? (with respect to weights and conveyor belt track)	2

and

Table 2. Related work for a robotic arm-based batching system (cont’).

Study	Conveyor Belt Type	Buffer	Machine Type
[17]	Two conveyor belts	Yes	Grader (diverter)
[18]	4 track line conveyor belt	Yes	Grader
[19]	1 track line conveyor belt	Yes	Grader
[20]	1 track line conveyor belt	Yes	Batcher (drop)
[21]	1 track line conveyor belt	Yes	Batcher (drop)
[22]	Unidirectional 1 track conveyor belt A circular conveyor for boxes	Yes (for unused product)	Robotic arm
[23]	2 track line conveyor belt	Yes	Robotic arm

summarize the scheduling problems, batching problems in particular, addressed for a robotic arm-based food processing system in the literature. As comparison criteria, Table 1 considers (1) on what basis the decision was made and (2) the number of conveyor belts, and Table 2 considers (3) the type of conveyor belts, (4) whether there is a buffer between batches, and (5) the characteristics of the robots addressed.

From the literature review shown in the summary tables, it can be highlighted that the existing scheduling mechanisms generally tackle a single decision variable with a single conveyor belt track. On the other hand, our study addresses a robotic arm-based system with multiple conveyor tracks—one track for moving food items and two additional tracks on each side of the food track for trays—which introduces additional decision-making dimensions and constraints to the corresponding robotic arm scheduling problem.

2.3. Solution Algorithms for Scheduling Robotic Arm-Based Batching Systems

Multiple solution approaches have been proposed to solve and analyze various robotic batching systems. Peeters et al. [18] took a wider view of the system and analyzed the layout of the batching process, determining the size and number of batching machines, the flexibility of different setups, as well as introducing solution approaches. Ásgeirsson [24] proposed an algorithm to be used in an online bin covering problem representing a system that pushes the items into trays instead of picking-and-placing. Furthermore, the authors investigated and proposed algorithms for the semi-online problem. Van Sprang [25] investigated the application of condition-based maintenance strategies. A selection method was proposed to choose the most relevant parts of a machine. Among others, it is based on failure rate and downtime costs and consequences. Raaijmakers [26] analyzed different types of batching machines, modeled the machines mathematically (including an online bin covering variant), and proposed solution strategies for each. Finally, the performance of the batching machines is compared with different types of problem features.

Soft computing methods have been also proposed to tackle robotic batching problems. Hundscheid et al. [21] proposed a hybrid genetic algorithm for a more simple batching machine. The problem is formulated as a k-bounded semi-online bin covering problem, which is a frequent model for these types of problems. Hildebrand et al. [23] investigated a deep reinforcement learning approach in the decision process of a robotic batching system and showed promising results.

It should be noted that the robotic arm-based system addressed in Hildebrand et al. [23] has the same system setting as our target system. However, our study tackles the scheduling problem involved in the system by applying a deterministic approach as will be explained in the following sections. The proposed approach has an advantage over the work of Hildebrand et al. [23] in terms of the effort needed to develop and implement a solution approach and the degree of understanding to the solutions derived by the approach.

Based on the reviews presented, we conclude that our target robotic arm scheduling problem with multiple conveyor belts has been rarely addressed in the literature, and the proposed solution approach for the problem is unique from the methodological and implementation perspectives.

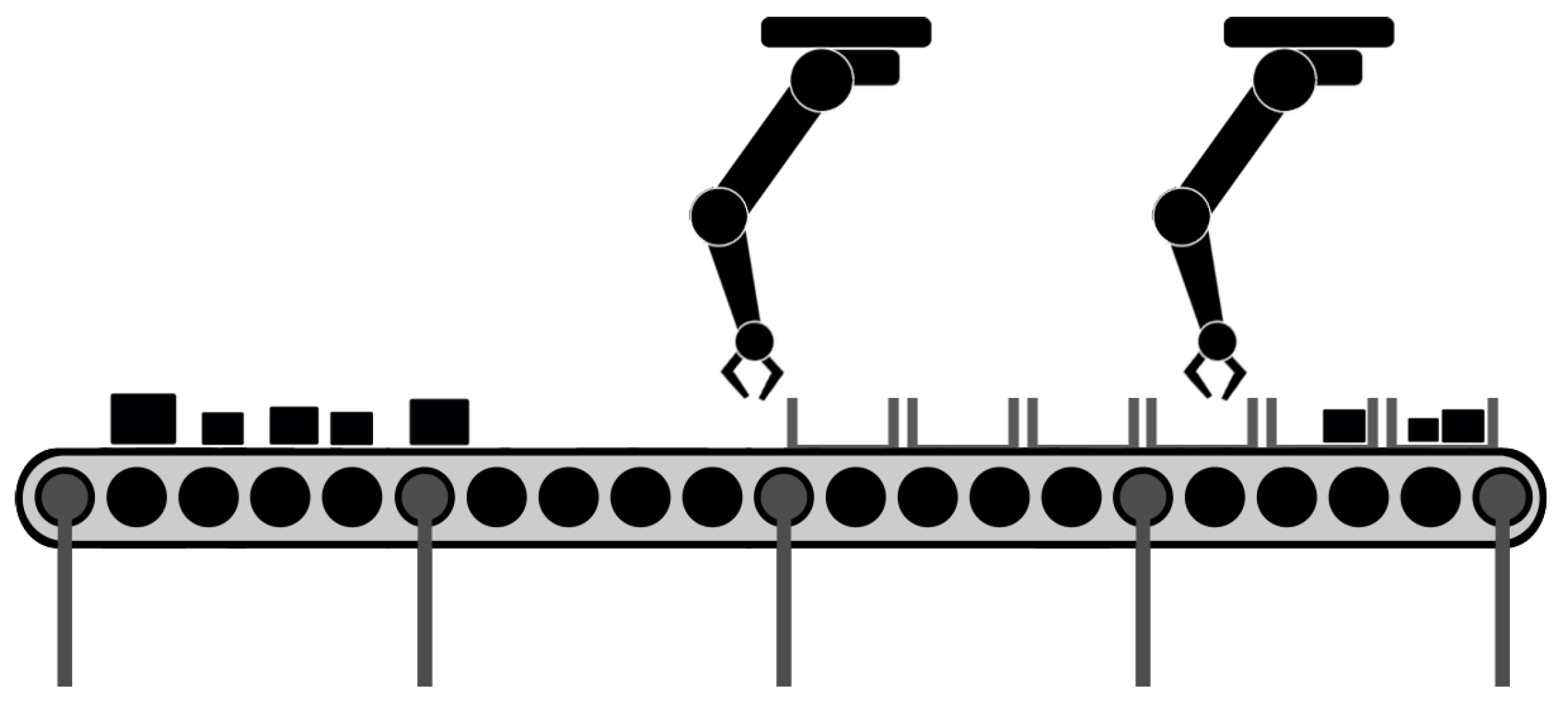
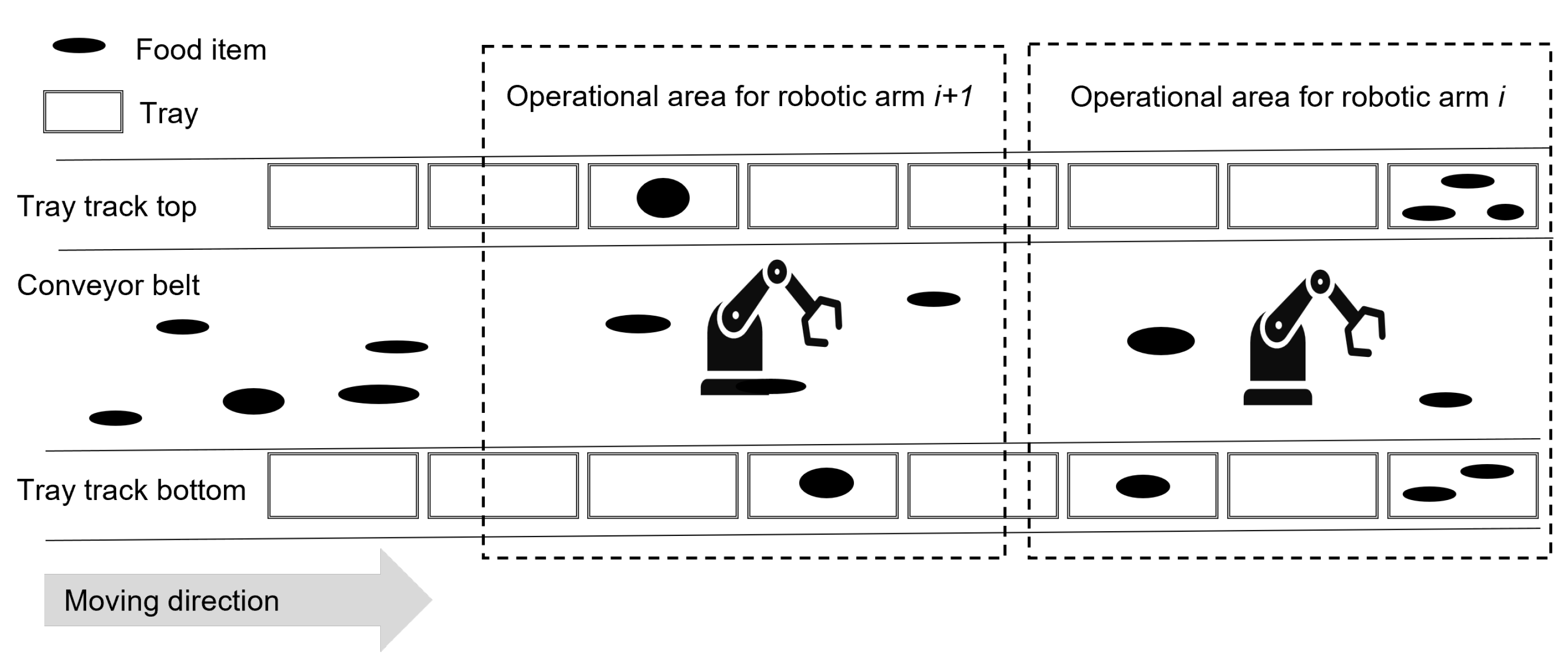
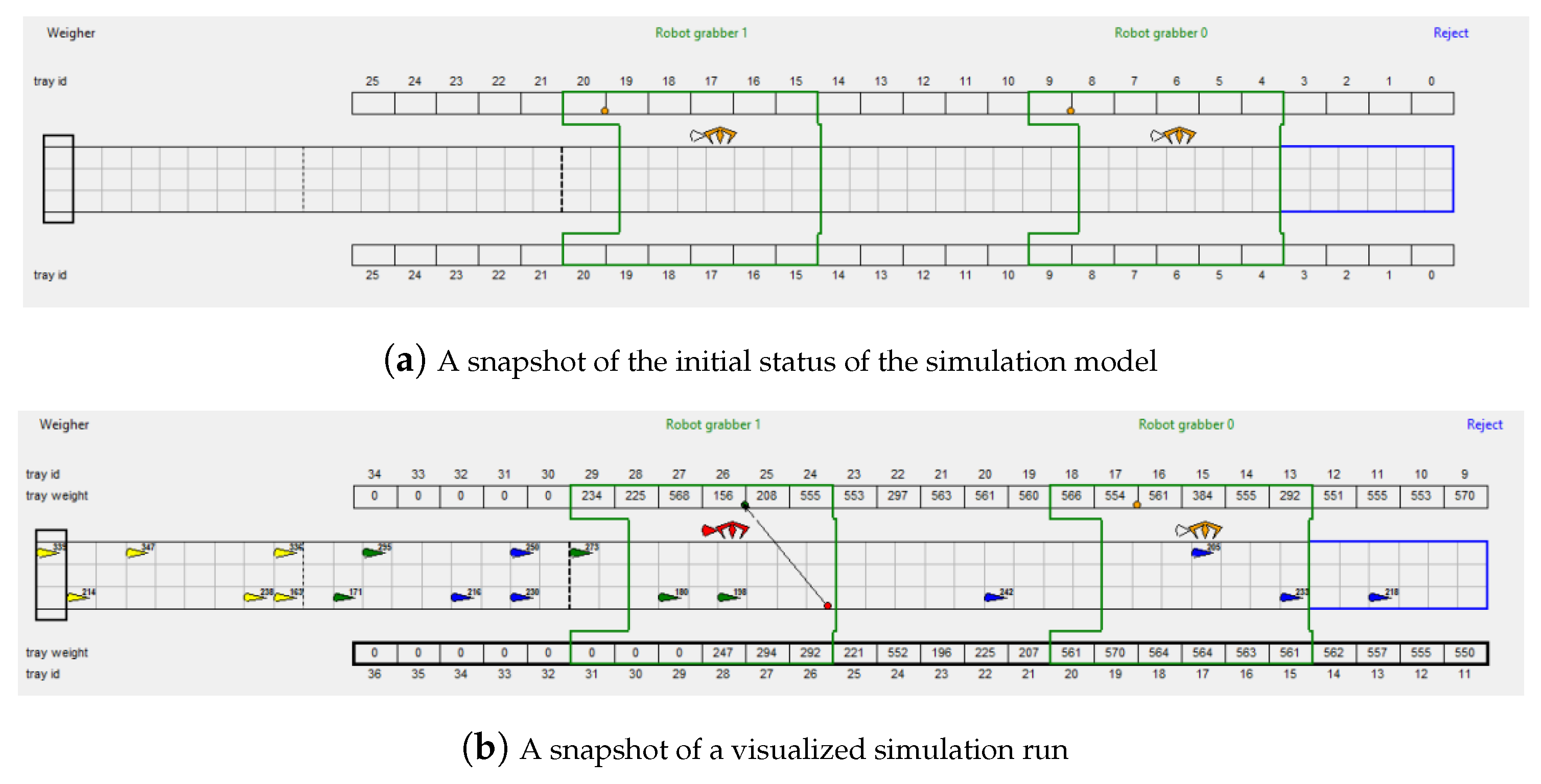
3. A Robotic Arm-Based Food Processing System

3.1. Problem Descriptions

The target system of this study is inspired by a completely autonomous robotic arm-based food batching system, which consists of three main components: an infeed conveyor belt, tray lanes next to the infeed conveyor belt and robotic arms. The conveyor belt moves continuously at a fixed speed. It transports food items with different weights arriving from a preceding food production cell. On each side of the conveyor belt, there is a single moving lane and trays, in which food items picked from the conveyor belt are batched in a tray on the lane. The tray lane can both move and stop. When it advances, it moves incrementally and the tray at the end of the lane will be disposed of from the system, being handled by a following package cell. Usually, the advancement will automatically be triggered when the weight of the last tray exceeds a threshold. The third component is the robotic arms. Each one can reach a specific area of the conveyor belts and the tray lanes. Figure 2 illustrates the target robotic arm-based food batching system.

Given the description of the target robotic arm-based system, the following decision variables can be identified:

• Which robotic arm will pick up an item;
• When and where an item on a conveyor belt will be picked up;
• On which tray on which side of the conveyor belt an item will be placed.

The identified decisions will be made to minimize the give-away of the food items. Give-away is the positive deviation from the target tray weight. Suppose that an order requires trays with target weigh 500 g and the contract will contain a fixed price per tray delivered. If a tray comes to weigh 510 g, then 10 g (or 2%) as a free product is given away.

3.2. The Complexity of the Target Scheduling Problem

Figure 3 shows a simplified flow chart of the basic logic in the robotic batching system with a single robotic arm, a single conveyor lane and a single tray lane. It shows that all the operating parts are mutually interrelated in a highly nested way. Making one decision will affect all the other parts, and they have to be considered in order to ensure feasibility.

Among the interrelationships between the components of the robotic arm-based system and relevant decision variables, the following are highlighted as the key factors that make the target scheduling problem hard to solve:

• The initial position and weight of items are unknown until they enter the conveyor belt;
• The position of an item on a conveyor belt is continuously moving;
• Processing time of a robotic arm depends on (1) the position of an item to pick up and (2) the position of the tray where the robotic arm placed the previous item picked up before the current one;
• A tray track is advanced only when the tray at the end of the track exceeds the target weight, affecting the positions of the entire trays in the system;
• Each robotic arm can handle items in a designated operational area.

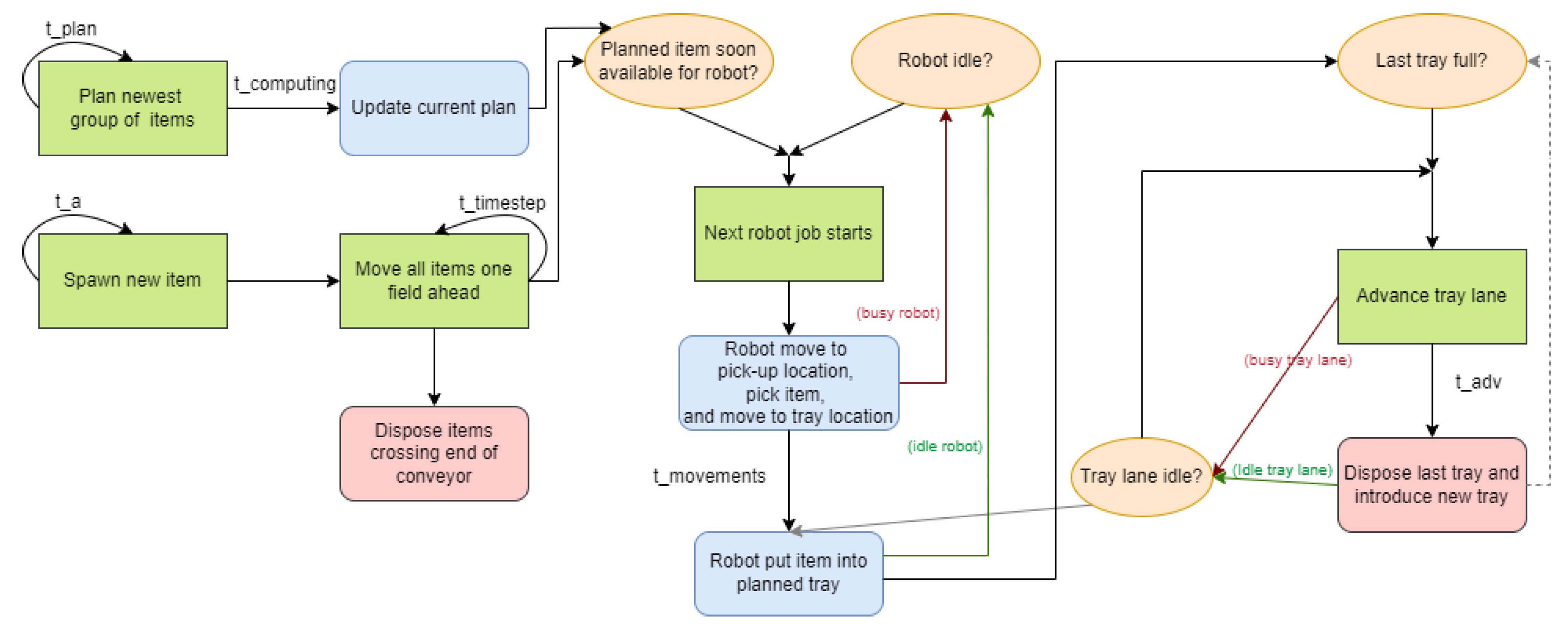
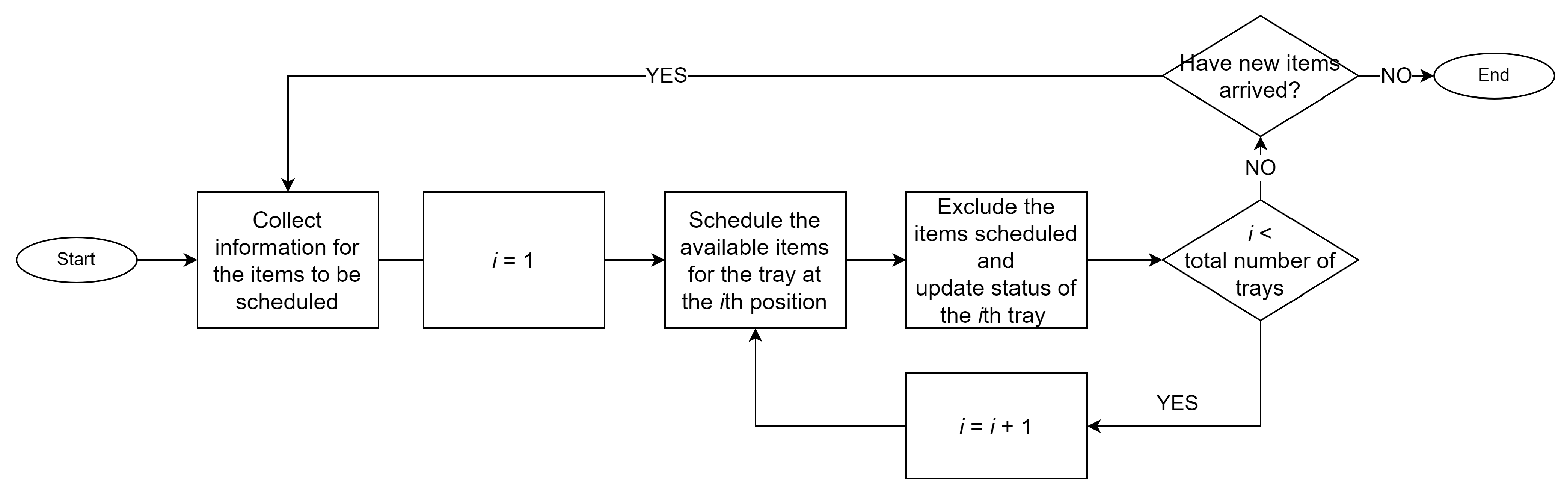
4. The Proposed Solution Approach

To the best of our knowledge, no standard optimization model seems to cover the target robotic batching problem of this paper in its entirety. While knapsack variations, such as the bin covering or subset sum problem, can be considered to address the target problem [27,28], the subset sum model does not allow filling past the target, and the bin covering only seeks to fill as many trays as possible without considering the level of overfill, likely resulting in trays with high give-away.

To address the complexity of the target scheduling problem, we propose a decomposition approach that sequentially solves a simplified scheduling problem for a single tray. Specifically, the original problem is decomposed into a series of sub-problems. Each sub-problem is to assign items to multiple robotic arms only for a specific tray, while making the tray reach a target weight. This sub-problem is formulated using a goal programming approach based on the nature of the objective of the scheduling, i.e., to minimize the deviation of a food tray from the target weight of the tray. A series of sub-problems is solved to find schedules for all trays in the system.

In our decomposition approach for the original scheduling problem, a sub-problem for a tray (let us say, A) on a tray track will be solved after solving the sub-problems for the trays placed in the tray track ahead of tray A, based on the dynamics of a conveyor belt. Recall that a tray track will be advanced only when the tray at the end of the track exceeds or meets a target weight, and therefore, it is natural to sequentially solve the sub-problems according to the positions of the corresponding trays so that the dependency between the sub-problems becomes uni-directional and tractable. Under this decomposition scheme, the outcome of a sub-problem solving—what items are scheduled to be picked up and when a tray track will be advanced—will be used to form the following sub-problems.

Finally, once all the sub-problems are solved following the sequence (meaning that all trays are considered for placing the items entered into the robotic arm-based batching system), the same process will begin as a new set of food items enters the system, while keeping the solutions from the previous sub-problem solving. The proposed decomposition-based solution approach is illustrated in Figure 4.

A Goal Program for a Sub-Problem: Scheduling Robotic Arms Only for a Single Tray

Let us suppose that there are candidate items to be batched by multiple robotic arms into a specific tray on a specific tray lane. These items are included in set V. The weight of item $i\in V$ is denoted by $w_i$. We also introduce the concept of a field, a specific area of an infeed conveyor belt. For the sake of simplicity, we divide the conveyor belt into a set of the same-sized multiple fields and assume that only a single item can be place on a field at a time. Given this, the arrival time of item i at field f, $A{T}_{i,f}$ is then calculated based on the speed of the conveyor belt and the spawn time of item i in the system. We also assume that the operational areas (i.e., a set of consecutive fields) of multiple robotic arms are independent and do not overlap. By this assumption, field index $f\in F$ identifies a responsible robotic arm for the field. The set of fields where the robotic arm responsible for field f operates is denoted by $O{A}_f$.

It should be noted that the schedules from the previous sub-problems solving are the input to the current sub-problem solving, and these schedules identify the following constraints: when the tray for the current sub-problem should advance, and when the robotic arms are unavailable. Given the constraints and the fact that the processing time of a robotic arm depends on the destination tray where an item will be placed by the robot, the timing for the tray advancement serves as a reference point to compute a robotic arm’s processing time. Specifically, we denote the travel time of a robotic arm from field f to the target tray’s position after its nth advancement by ${\tau }_{f\to n}$. Likewise, ${\tau }_{n\to f}$ denotes the travel time for the opposite movement. Similarly, whether a robotic arm can reach the target tray or not also depends on the tray’s advancement and corresponding position. Based on this, we define set $Ad{v}_f$ that includes all the advancement steps, after which a robotic arm working at field f can reach the target tray.

We also compute whether item i will arrive at field f after the nth advancement of the tray, and based on the computation, we create $V_{f,n}$, a set of items that can be handled at field f between the $(n-1)$th and nth tray advancements. Lastly, from the previous sub-problem solutions, we create set $V_{i,f}^{-}$ and $V_{i,f}^{+}$, which include the items that are scheduled by the previous sub-problems and should be placed at a predetermined tray before and after item i arrives at field f (i.e., $A{T}_{i,f}$), respectively.

With the notation, we define the principle decision variable $x_{i,f,n}$ that indicates if item $i\in V$ will be picked up at field $f\in F$ after the nth advancements of the target tray of the sub-problem. Two deviation variables, $d^{+}$ and $d^{-}$, are also defined to measure the gap between the tray’s weight and a target weight.

With the decision variables, the objective function of a sub-problem for the robotic arm scheduling problem that is to minimize the give-away on a tray can be written by

$$\begin{array}{cc}\hfill min& d^{+}\hfill \end{array}$$

(1)

This objective function is then minimized subject to the following constraints. First, we link the primary decision variable to the deviation variables by

$$W_{target}-\sum _{i\in V}\sum _{f\in F}\sum _{n=0}^N{w}_i·x_{i,f,n}=d^{+}-d^{-}$$

(2)

where $W_{target}$ is the target weight of the tray. Next, an item can be picked up at most once by a robotic arm, which can be written by

$$\sum _{f\in F}\sum _{n=0}^N{x}_{i,f,n}\le 1\forall i\in V.$$

(3)

Additionally, in order to pick up item i at field f, a robotic arm for the field should be available. In other words, there should be enough of a time gap for the robotic arm to move from its last position (i.e., the tray where the last previous item is placed on) to field f. This constraint can be written by

$$M+\sum _{n\in Ad{v}_f}\left(A{T}_{i,f}-M\right)·x_{i,f,n}-\sum _{m\in Ad{v}_g}\sum _{g\in O{A}_f}\left(A{T}_{j,g}+{\tau }_{g\to m}+{\tau }_{m\to f}\right)·x_{j,g,m}\ge 0,$$

(4)

for all $i,j\in \left\{V\right|i\ne j\}$ and $f\in F$. ${\tau }_{g\to m}+{\tau }_{m\to f}$ is the total time needed for a robotic arm to move item j from field g to the tray’s position after the mth advancement and to return to field f to grasp an item.

Next, to schedule item i to be picked up at field f and placed to the tray after the nth advancement (i.e., $x_{i,f,n}=1$) in the current sub-problem, the following conditions should be met:

• There is enough time for a robotic arm to move to field f after completing all the tasks scheduled to be done before the time when item i arrives at field f;
• Placing item i on the tray after the nth advancement does not delay any following tasks scheduled by upstream sub-problems.

The constraints for these conditions are formulated by

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}M+\sum _{n\in Ad{v}_f}\left(A{T}_{i,f}-M\right)·x_{i,f,n}-{\tau }_{j\to a}\ge 0& \forall i\in V,f\in F,j\in V_{i,f}^{-}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill A{T}_{j,f_j^{*}}-\sum _{n\in Ad{v}_f}\left(A{T}_{i,f}+{\tau }_{f\to n}+{\tau }_{n\to f_j^{*}}\right)·x_{i,f,n}\ge 0& \forall i\in V,f\in F,j\in V_{i,f}^{+}\hfill \end{array}$$

(6)

where $f_j^{*}$ is the field where item j is scheduled to be picked up by a previous sub-problem solution.

In addition, an item can be placed in the tray only when the tray lane is not moving. With the set $V_{f,n}$, this constraint can be formulated by

$$\begin{array}{cc}\hfill x_{i,f,n}\le 1& \forall i\in V_{f,n},f\in F,0\le n\le N\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}{x}_{i,f,n}=0& \forall i\in V\backslash V_{f,n},f\in F,0\le n\le N.\hfill \end{array}$$

(8)

Lastly, we have binary and positive value constraints for the primary and deviation variables, respectively, which are shown below:

$$\begin{array}{cc}\hfill x_{i,f,n}\in \{0,1\}& \forall i\in V,f\in F,0\le n\le N\hfill \end{array}$$

(9)

$$d^{+},d^{-}\ge 0$$

(10)

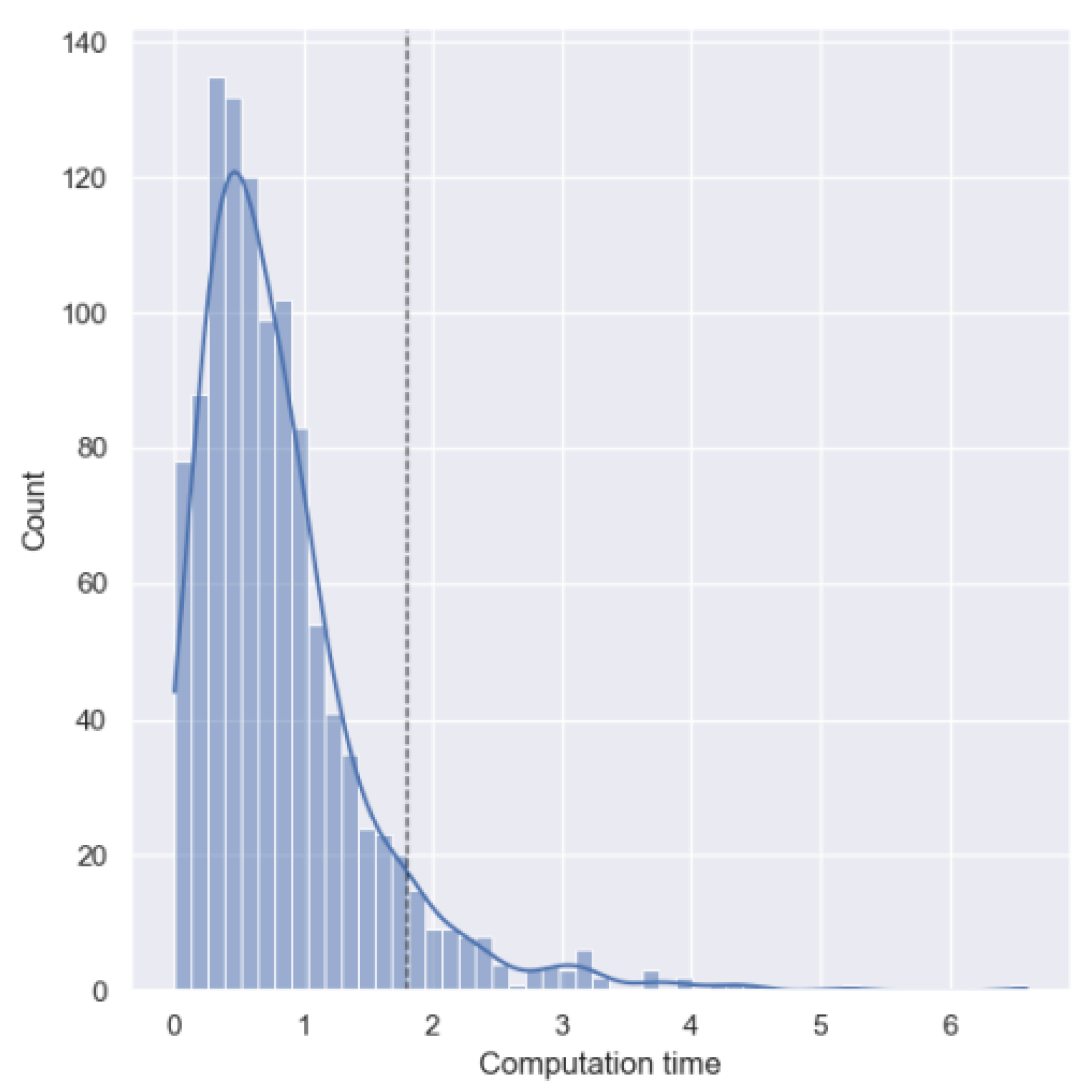
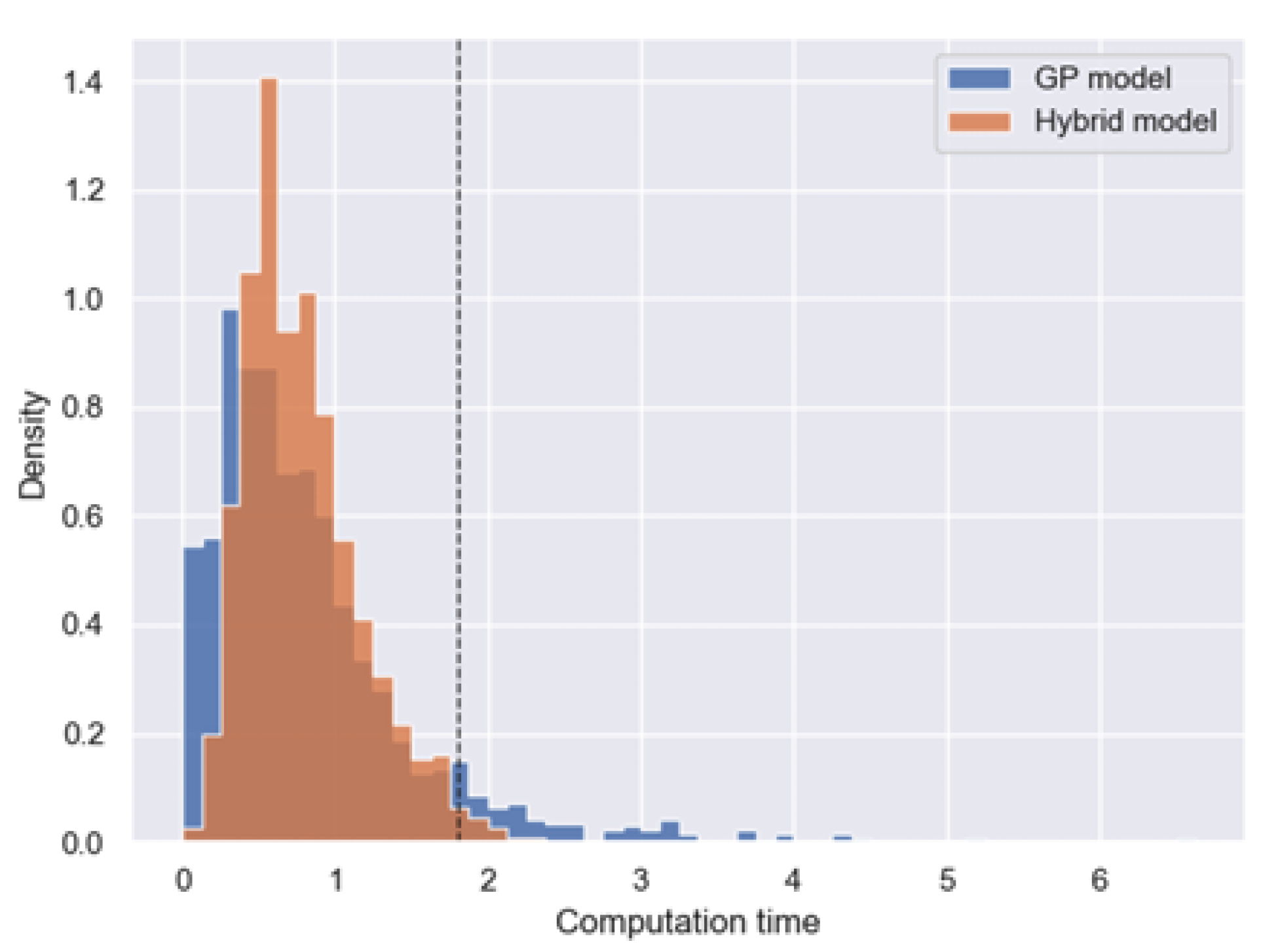
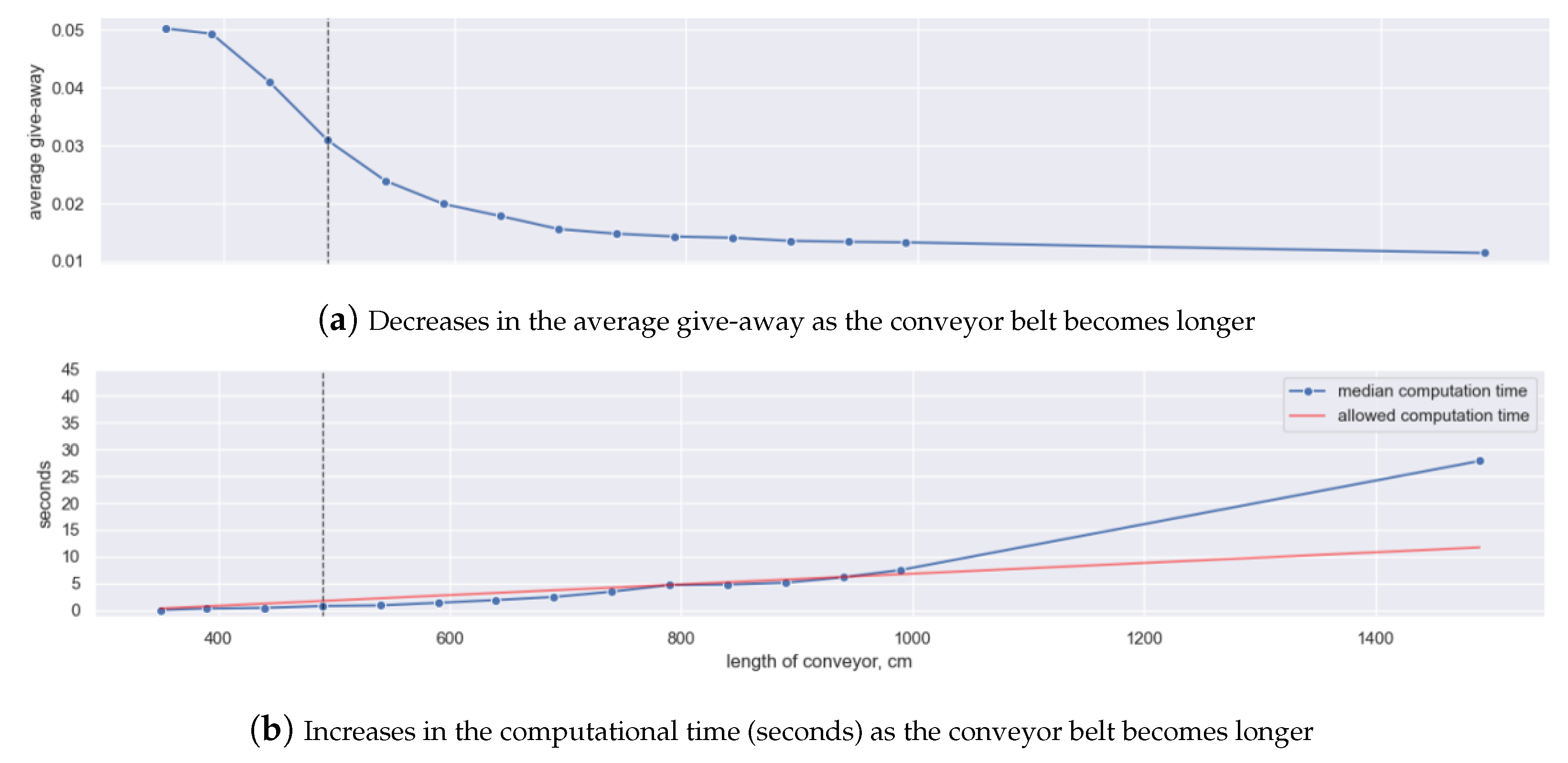
5. Computational Burden of the Proposed Solution Approach

Recall that a conveyor belt moves fast, feeding items to robotic arms at the same speed. Therefore, considering the fact that it is almost infeasible to know when and how food items enter into a robotic arm-based batching system, solving the robotic arm scheduling problem should be done in (near) real time.

To understand the practical scale of a food processing system and the corresponding computational requirements for the proposed solution approach, we took a field trip to a food processing company in Denmark and conducted interviews with employees of the company. From the activity, we conclude that a schedule for an item should be derived before the item passes the buffer zone that spans from the entry point of the conveyor belt to the entry point of the robotic arms’ operational area. The travel time for an item to pass the buffer zone is set as $3.6$ s based on the interview. Because items keep entering into a conveyor belt, making it difficult for a scheduling algorithm to fully use the $3.6$ s to solve the problem, we assume that only half of the buffer passing time, $1.8$ s, is allowed for the scheduling algorithm to solve the scheduling problem. In other words, a series of sub-problems, each of which schedules multiple robotic arms for a specific tray, should be solved within $1.8$ s.

To examine the feasibility of the proposed solution approach in the above mentioned context, we develop a simulation model for a food batching system with two robotic arms. The layout of the target food batching system is illustrated in Figure 5a, which is also used to visualize the simulation as shown in Figure 5b. In the figure, the operational area for the robotic arms is colored in green. The buffer zone, consisting of 18 fields, starts from the left side of the conveyor belt, and an item just registered takes $3.6$ s to pass the buffer zone. Considering a practical arrival rate of food items at the system, the mean inter-arrival time of items is set as $1.2$ s, sampled from exponential distribution. The simulation runs for 30 min in a single replication, and a sub-problem is solved using CPLEX. The experiments are run on a Windows 10 machine with an Intel Core i5-8265U 4-core CPU @ 1.6 GHz with 8 GB RAM.

Figure 6 shows a histogram of the computation time spent to solve a series of the sub-problems for a food item batch (i.e., the items in the first half of the buffer zone). In the chart, 1116 batches are considered. The figure shows that 92% of schedules are derived in less than 1.8 s (the dotted line). The median computational time is $0.66$ s with a standard deviation of 0.69.

It should be pointed out that the success rate of 92% is satisfactory, but it tells us that one out of ten scheduling attempts will require more time than allowed, degrading the performance of the robotic arm-based system. A potential approach to tackle this issue is to consider local search heuristics, which are simple but effective for many combinatorial decision-making problems [29].

6. Discussion

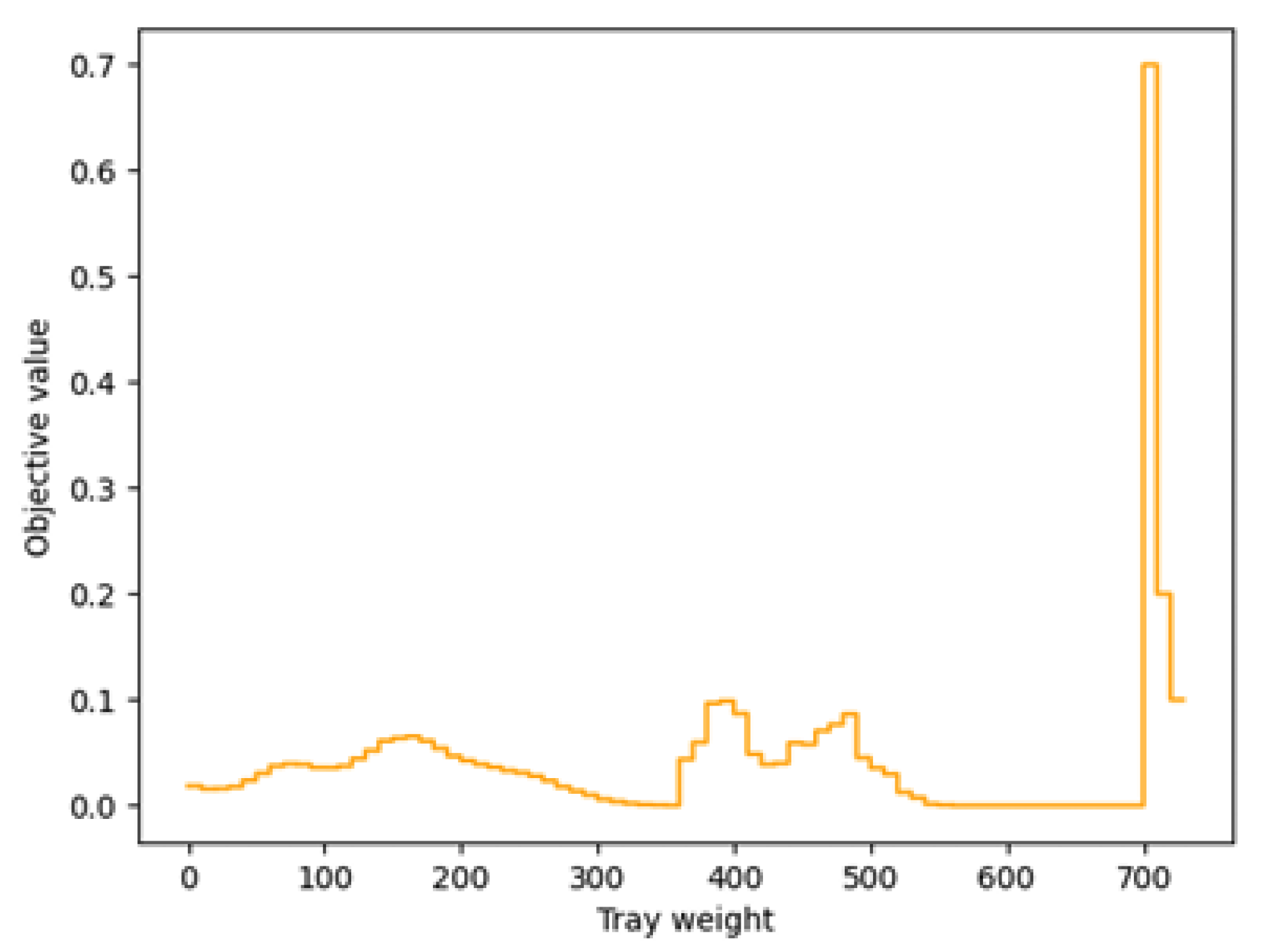
6.1. The Objective Function of the Sub-Problem

Note that a tray does not necessarily need to be filled by currently available items. In other words, if there is no item suitable to fill the tray with a target weight, leaving the tray not fully filled would be a good strategy such that items which will arrive later can be considered to fill the tray with the target weight. However, the proposed objective function in the previous section, which is to minimize solely the positive deviation variable, cannot reflect this idea.

As a solution to this issue, one may tune a profit function as a function of a tray’s weight in a way that a tray with a room for additional items has a profit if it is likely to find items from the next arrivals that make the tray full with the target weight. For example, if a mean weight of entering items is known as 300 g and it is difficult to find items to fill a tray with a target weight (say 700 g), leaving the tray with 400 g would be beneficial, rather than filling the tray up to 600 g. Figure 7 shows an example of such a profit function.

To test this idea, we tune the profit function as a piecewise linear function based on an arbitrary item weight distribution and reformulate the sub-problem’s objective function as a maximization of the profit function. From our experiments, the reformulated problem makes the computation time needed to solve the problem more stable and feasible (meaning that the total computational time needed to solve a series of sub-problems was within 1.8 s in 98% of our test problem instances). Figure 8 shows the histograms of the computational time of the proposed goal program (denoted by GP model) and the reformulated problem (denoted by Hybrid model). The overall give-away level was also lowered by the reformulated problem. However, it is difficult to tune the profit function properly since a distribution of items’ weight is hard to know in advance and keeps changing mainly because items are often provided by multiple suppliers. Therefore, we believe the proposed goal programming formulation would be more preferable than the reformulated one in practice.

6.2. A Robotic Arm-Based Batching System Configuration

One way to increase the time budget allowed for the scheduling problem solving is to have a long buffer zone or slow down the conveyor belt. Importantly, by this managerial solution, more items can be considered for a single run of a series of sub-problem solving, and thus efficient tray utilization can be achieved. On the other hand, having more items to schedule means a larger scale of scheduling problem solving. Note that the number of decision variables and constraints are exponentially increased as the number of items to schedule increases. Additionally, slowing down a conveyor belt obviously reduces the productivity of the system.

Using the simulation model, we can test the impact of such managerial decisions on the performance level of a robotic arm-based system. As an example, we evaluate the impact of the buffer zone length on the performance of the robotic arm-based batching system and the computational feasibility of the proposed solution approach. With 15 different conveyor belt length settings, keeping the rest of the simulation setting as described in the previous section, we run simulations for this trade-off analysis, and the results are summarized in Figure 9.

From the figure, where the current conveyor belt setting is represented by a dotted line, it can be first observed that give-away, the key performance measurement of the target food batching system, is decreased as the buffer zone becomes longer and more items are considered at the moment of the scheduling. On the other hand, one can observe that the computational time for solving the scheduling problem increases as the buffer zone becomes longer and, importantly, this makes the proposed solution approach with a commercial optimization solver no longer feasible.

As observed, it is clear that there is a trade-off between the quality and computational burden of the proposed solution approach. Importantly, this observation implies that the configuration of a robotic arm-based batching system (e.g., the number of robotic arms on a conveyor belt and the length of a buffer zone) should be set carefully, considering not only the physical performance of the system but also the performance of a scheduling solution to the system that actually determines the system performance.

7. Concluding Remarks

The challenge presented in this paper is to schedule robotic arms to fill trays with items with minimal give-away. Compared to similar problems in the literature, our problem has two different conveyor belts, one for food item transition and the other for trays. Importantly, the tray lane conveyor moves only when the last tray of the tracks exceeds the target weight, introducing an additional decision to the robotic arm batching problem. This is a complex but novel problem, especially as it provides a diverse range of research fields through its system structure, allowing for various comparative analyses in terms of the investigated problem, solution approach, and main concern.

To address the target scheduling problem, we proposed a decomposition approach that divides the main robotic arm scheduling problem into smaller sub-problems of each tray. It has computational advantages as it reduces the number of decision-making dimensions, and thus decreases the solution space to search. However, by its nature, a global optimum to the original problem cannot be reached by the proposed solution approach.

We also applied a deterministic solution approach. Instead, a stochastic approach that considers the distribution of incoming items to a conveyor belt can be applied to the problem. In this way, the uncertainties and randomness in a food batching system can be addressed based on knowledge of the system, and thus a more realistic and better solution could be obtained. For this, deep reinforcement learning [23] and other machine learning algorithms can be considered for both batching and food quality and safety [30,31].

Lastly, it is worth noting that other types of conveyor belts in the literature, such as U-shape, loop, and bi-directional [32], together with the corresponding scheduling problems, can be addressed to improve the performance of robotic arm-based batching systems.