A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV
Abstract
:1. Introduction
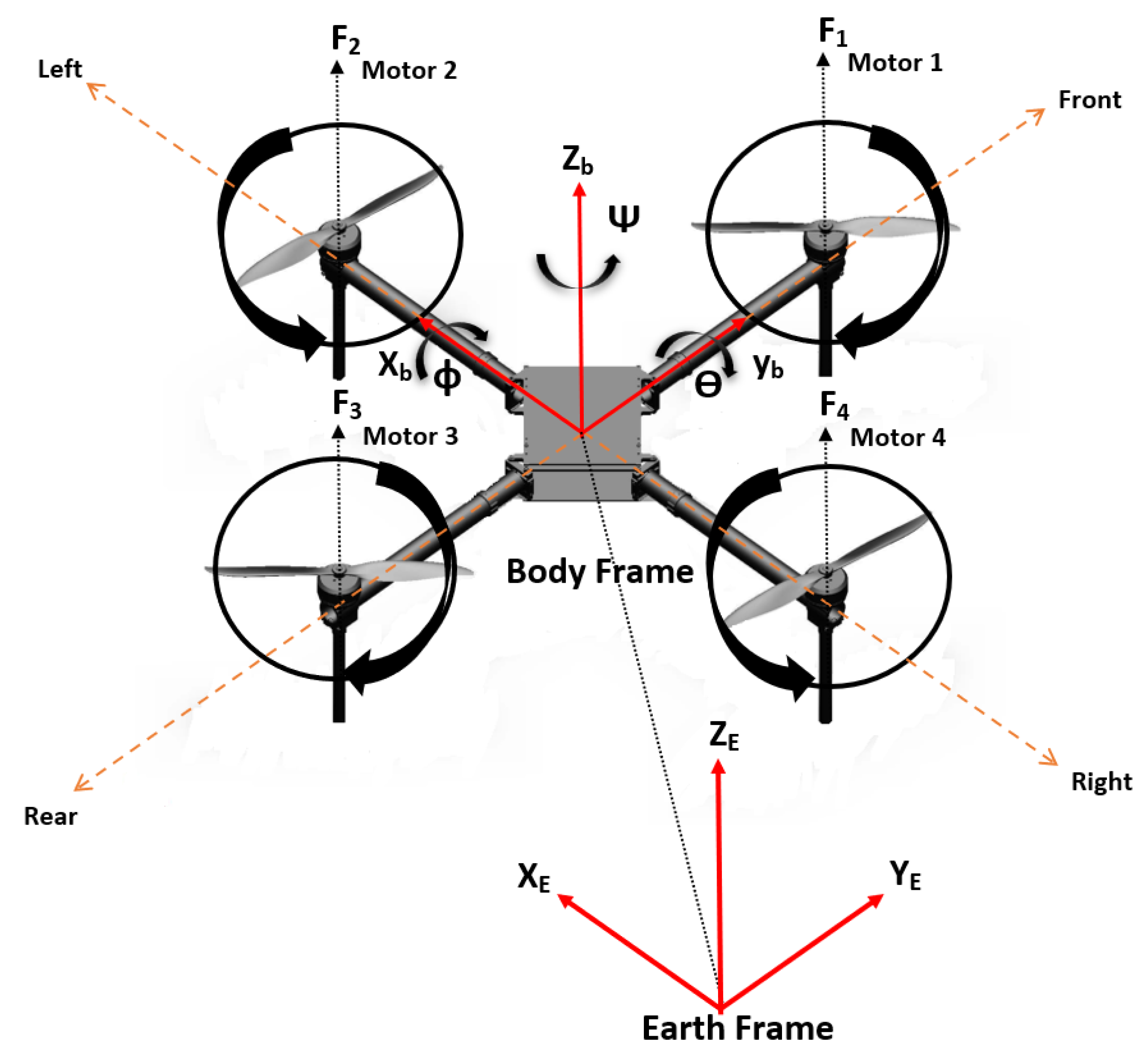
2. Quadrotor Aircraft Modelling
3. Robust Stabilization
3.1. Desired Modes for the y-Axis Dynamics of the Vertical Displacement
3.2. Desired Modes for the x-Axis Dynamics of the Horizontal Displacement
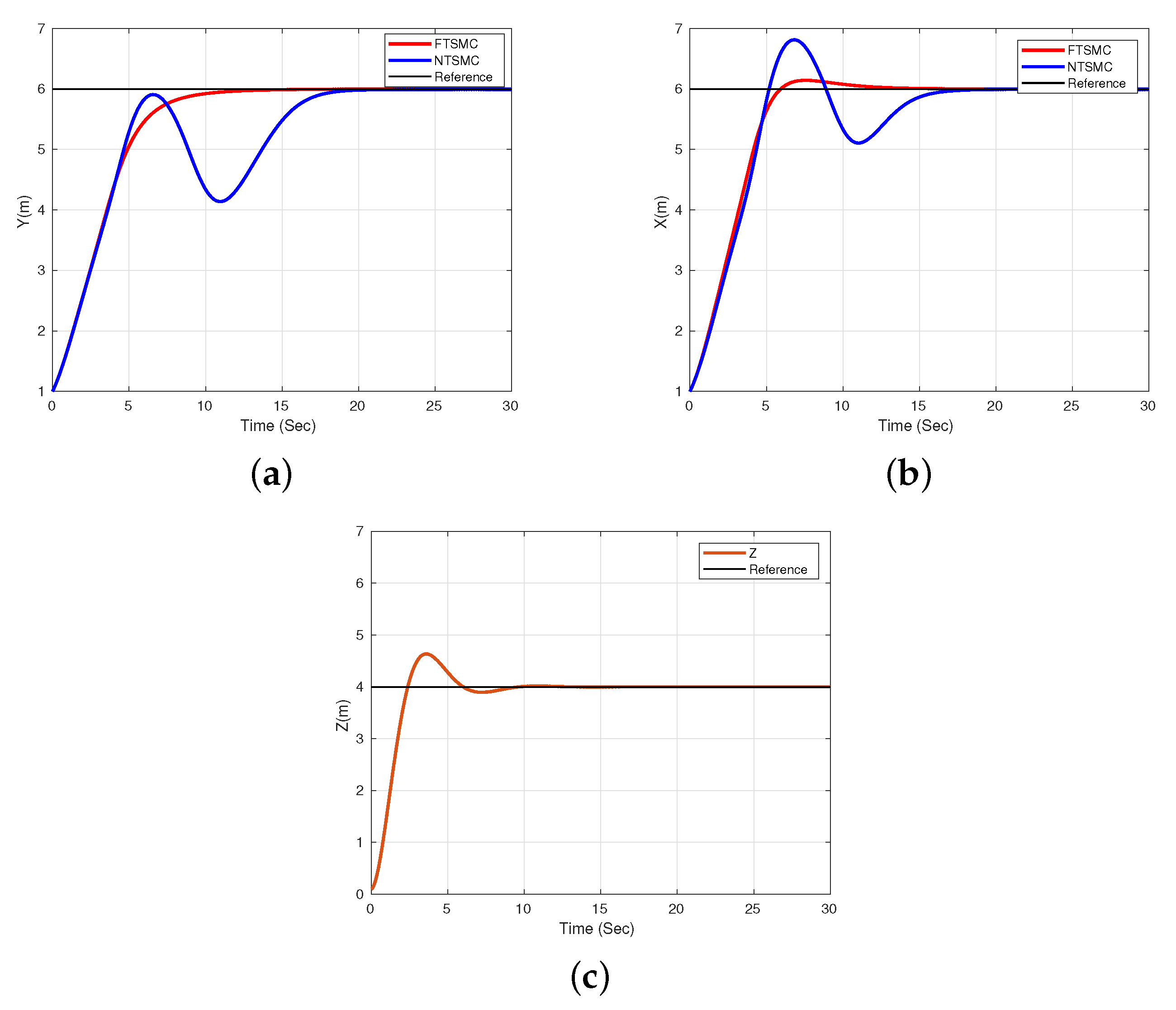
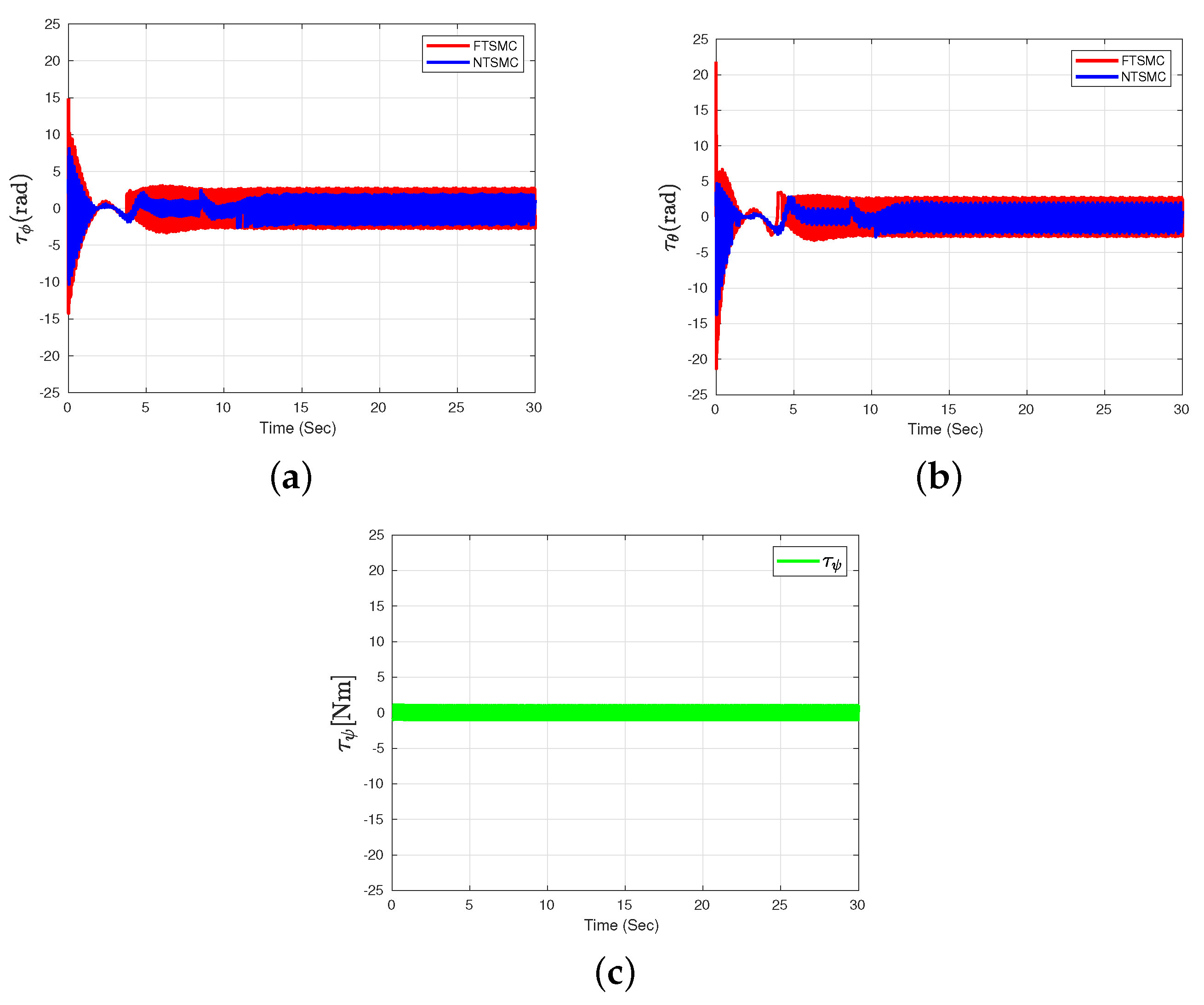
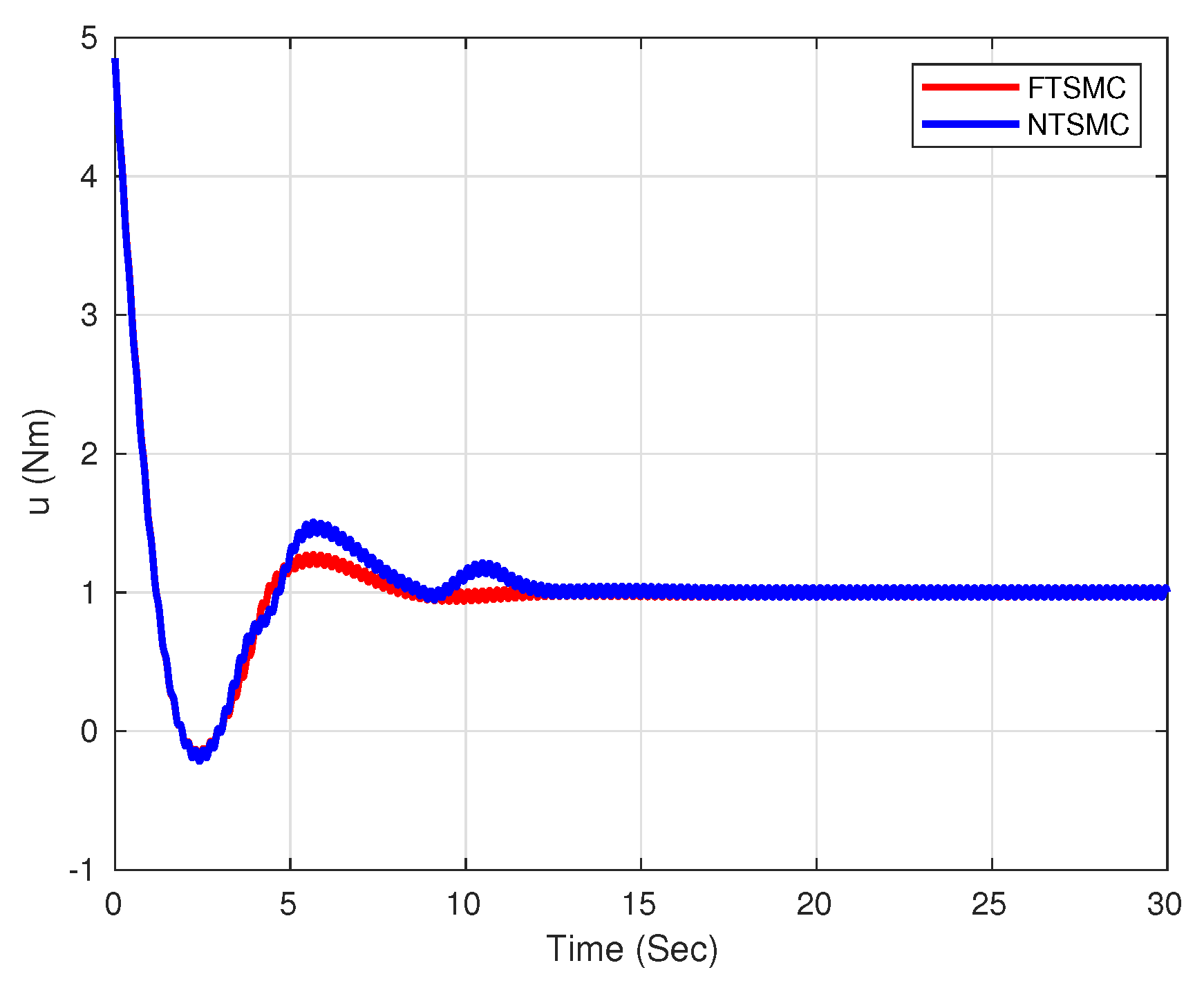
4. Numerical Simulation Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Alotaibi, E.T.; Alqefari, S.S.; Koubaa, A. LSAR: Multi-UAV Collaboration for Search and Rescue Missions. IEEE Access 2019, 7, 55817–55832. [Google Scholar] [CrossRef]
- Daponte, P.; Vito, L.D.; Glielmo, L.; Iannelli, L.; Liuzza, D.; Picariello, F.; Silano, G. A review on the use of drones for precision agriculture. IOP Conf. Ser. Earth Environ. Sci. 2019, 275, 012022. [Google Scholar] [CrossRef]
- Singh, C.; Mishra, R.; Gupta, H.P.; Kumari, P. The Internet of Drones in Precision Agriculture: Challenges, Solutions, and Research Opportunities. IEEE Internet Things Mag. 2022, 5, 180–184. [Google Scholar] [CrossRef]
- Arjomandi-Nezhad, A.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M.; Aminifar, F. Budget-constrained drone allocation for distribution system damage assessment. IET Smart Grid 2022, 5, 42–50. [Google Scholar] [CrossRef]
- Andrade, S.D.; Saltos, E.; Nogales, V.; Cruz, S.; Lee, G.; Barclay, J. Detailed Cartography of Cotopaxi’s 1877 Primary Lahar Deposits Obtained by Drone-Imagery and Field Surveys in the Proximal Northern Drainage. Remote Sens. 2022, 14, 631. [Google Scholar] [CrossRef]
- Wu, B.; Fu, R.; Chen, J.; Zhu, J.; Gao, R. Research on Natural Disaster Early Warning System Based on UAV Technology. IOP Conf. Ser. Earth Environ. Sci. 2021, 787, 012084. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Roy, S.; Baldi, S. Aerial Transportation of Unknown Payloads: Adaptive Path Tracking for Quadrotors. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25 October 2020–24 January 2021; pp. 7710–7715. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Yadav, R.D.; Swayampakula, R.K.; Ganguly, S.; Roy, S. Robustifying Payload Carrying Operations for Quadrotors Under Time-Varying State Constraints and Uncertainty. IEEE Robot. Automat. Lett. 2022, 7, 4885–4892. [Google Scholar] [CrossRef]
- Ganguly, S.; Sankaranarayanan, V.N.; Suraj, B.V.S.G.; Dev Yadav, R.; Roy, S. Efficient Manoeuvring of Quadrotor under Constrained Space and Predefined Accuracy. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 6352–6357. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Roy, S. Introducing switched adaptive control for quadrotors for vertical operations. Opt. Control Appl. Meth. 2020, 41, 1875–1888. [Google Scholar] [CrossRef]
- Golnaraghi, F.; Kuo, B.C. Automatic Control Systems; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Castillo-Zamora, J.J.; Camarillo-Gomez, K.A.; Perez-Soto, G.I.; Rodriguez-Resendiz, J. Comparison of PD, PID and sliding-mode position controllers for V–tail quadcopter stability. IEEE Access 2018, 6, 38086–38096. [Google Scholar] [CrossRef]
- Svečko, R.; Gleich, D.; Sarjaš, A. The Effective Chattering Suppression Technique with Adaptive Super-Twisted Sliding Mode Controller Based on the Quasi-Barrier Function; An Experimentation Setup. Appl. Sci. 2020, 10, 595. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, D.; Li, G.; Wu, T. Adaptive Chattering-Free PID Sliding Mode Control for Tracking Problem of Uncertain Dynamical Systems. Electronics 2022, 11, 3499. [Google Scholar] [CrossRef]
- Ullah, I.; Pei, H.L. Fixed Time Disturbance Observer Based Sliding Mode Control for a Miniature Unmanned Helicopter Hover Operations in Presence of External Disturbances. IEEE Access 2020, 8, 73173–73181. [Google Scholar] [CrossRef]
- Parsa, A.; Kalhor, A.; Atashgah, M.A. Backstepping-Sliding mode Control Performance Enhancement using Close Loop Identification for Quadrotor Trajectory Tracking. In Proceedings of the 2017 5th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 25–27 October 2017; pp. 286–291. [Google Scholar] [CrossRef]
- González-Hernández, I.; Salazar, S.; Rodríguez-Mata, A.E.; Muñoz-Palacios, F.; López, R.; Lozano, R. Enhanced Robust Altitude Controller via Integral Sliding Modes Approach for a Quad-Rotor Aircraft: Simulations and Real-Time Results. J. Intell. Robot. Syst. Theory Appl. 2017, 88, 313–327. [Google Scholar] [CrossRef]
- Abci, B.; Zheng, G.; Efimov, D.; Najjar, M.E.B.E. Robust Altitude and Attitude Sliding Mode Controllers for Quadrotors; Elsevier B.V.: Amsterdam, The Netherlands, 2017; Volume 50, pp. 2720–2725. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Cao, H.; Shen, C.; Wang, H. Robust dynamic surface trajectory tracking control for a quadrotor UAV via extended state observer. Int. J. Robust Nonlin. Control 2018, 28, 2700–2719. [Google Scholar] [CrossRef]
- Huang, T.; Huang, D.; Wang, Z.; Shah, A. Robust tracking control of a quadrotor uav based on adaptive sliding mode controller. Complexity 2019, 2019, 7931632. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2020, 99, 290–304. [Google Scholar] [CrossRef]
- Hassani, H.; Mansouri, A.; Ahaitouf, A. A new robust adaptive sliding mode controller for quadrotor UAV flight. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, K.; Kim, S.; Kwak, S.; You, K. Quadrotor Stabilization and Tracking Using Nonlinear Surface Sliding Mode Control and Observer. Appl. Sci. 2021, 11, 1417. [Google Scholar] [CrossRef]
- Eltayeb, A.; Rahmat, M.F.; Basri, M.A.M.; Mahmoud, M.S. An Improved Design of Integral Sliding Mode Controller for Chattering Attenuation and Trajectory Tracking of the Quadrotor UAV. Arab. J. Sci. Eng. 2020, 45, 6949–6961. [Google Scholar] [CrossRef]
- Shiravani, F.; Alkorta, P.; Cortajarena, J.A.; Barambones, O. An Enhanced Sliding Mode Speed Control for Induction Motor Drives. Actuators 2022, 11, 18. [Google Scholar] [CrossRef]
- González-Hernández, I.; Salazar, S.; Lozano, R.; Ramírez-Ayala, O. Real-Time Improvement of a Trajectory-Tracking Control Based on Super-Twisting Algorithm for a Quadrotor Aircraft. Drones 2022, 6, 36. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B.; Ran, D. Appointed Fixed Time Observer-Based Sliding Mode Control for a Quadrotor UAV Under External Disturbances. IEEE Trans. Aerosp. Electr. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Hassani, H.; Mansouri, A.; Ahaitouf, A.; Fortuna, L. Robust Finite-Time Tracking Control Based on Disturbance Observer for an Uncertain Quadrotor under External Disturbances. J. Robot. 2022, 2022, 4581165. [Google Scholar] [CrossRef]
- Yu, L.; He, G.; Wang, X.; Zhao, S. Robust Fixed-Time Sliding Mode Attitude Control of Tilt Trirotor UAV in Helicopter Mode. IEEE Trans. Ind. Electr. 2022, 69, 10322–10332. [Google Scholar] [CrossRef]
- Zheng, J.; Song, L.; Liu, L.; Yu, W.; Wang, Y.; Chen, C. Fixed-time sliding mode tracking control for autonomous underwater vehicles. Appl. Ocean Res. 2021, 117, 102928. [Google Scholar] [CrossRef]
- Lozano, R. (Ed.) Unmanned Aerial Vehicles: Embedded Control, 1st ed.; ISTE: London, UK, 2010. [Google Scholar]
- Wang, B.H.; Wang, D.B.; Ali, Z.A.; Ting, B.T.; Wang, H. An overview of various kinds of wind effects on unmanned aerial vehicle. Meas. Control 2019, 52, 731–739. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]

| Gain | Value | Gain | Value | I. C. | Value | Perturbation | Value |
|---|---|---|---|---|---|---|---|
| FTSMC | NTSMC | ||||||
| 1 | 1 | ||||||
| 1 | 1 | ||||||
| 1 | 2 | ||||||
| 1 | 1 | ||||||
| 1 | 1 | ||||||
| 2.5 | 2 | ||||||
| 1 | 1 | 4 | |||||
| 1 | 1 | 6 | |||||
| 1 | 2 | 6 | |||||
| 2.5 | 1 | ||||||
| 1 | 1 | ||||||
| 1 | 2 | ||||||
| 1 | |||||||
| 1.5 | |||||||
| 0.5 | |||||||
| 1.5 | |||||||
| 0.5 | |||||||
| 0.35 | |||||||
| 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olguin-Roque, J.; Salazar, S.; González-Hernandez, I.; Lozano, R. A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV. Algorithms 2023, 16, 229. https://doi.org/10.3390/a16050229
Olguin-Roque J, Salazar S, González-Hernandez I, Lozano R. A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV. Algorithms. 2023; 16(5):229. https://doi.org/10.3390/a16050229
Chicago/Turabian StyleOlguin-Roque, Jairo, Sergio Salazar, Iván González-Hernandez, and Rogelio Lozano. 2023. "A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV" Algorithms 16, no. 5: 229. https://doi.org/10.3390/a16050229
APA StyleOlguin-Roque, J., Salazar, S., González-Hernandez, I., & Lozano, R. (2023). A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV. Algorithms, 16(5), 229. https://doi.org/10.3390/a16050229









