Toward Explainable AutoEncoder-Based Diagnosis of Dynamical Systems
Abstract
1. Introduction
1.1. Autoencoders in Diagnosis
1.2. Contributions
- 1.
- We define an explainable autoencoder in terms of a gap metrics, whose induced subspace generates a principal angle [7] to best distinguish the nominal and failure modes of the system.
- 2.
- We show how an autoencoder can diagnose linear time-invariant (LTI) dynamical systems. We extend the application of AE-based approaches to time-series data and dynamical systems, and we provide a clear semantics (and hence explainability) for such approaches.
- 3.
2. Related Work
2.1. Gap Metrics and AE-Based Diagnosis
2.2. Diagnosis Applications of AEs
2.2.1. Diagnosis of Individual Machines
2.2.2. Data-Driven Diagnosis of Complex Dynamical Systems
2.3. Other Applications
3. Preliminaries
3.1. LTI System
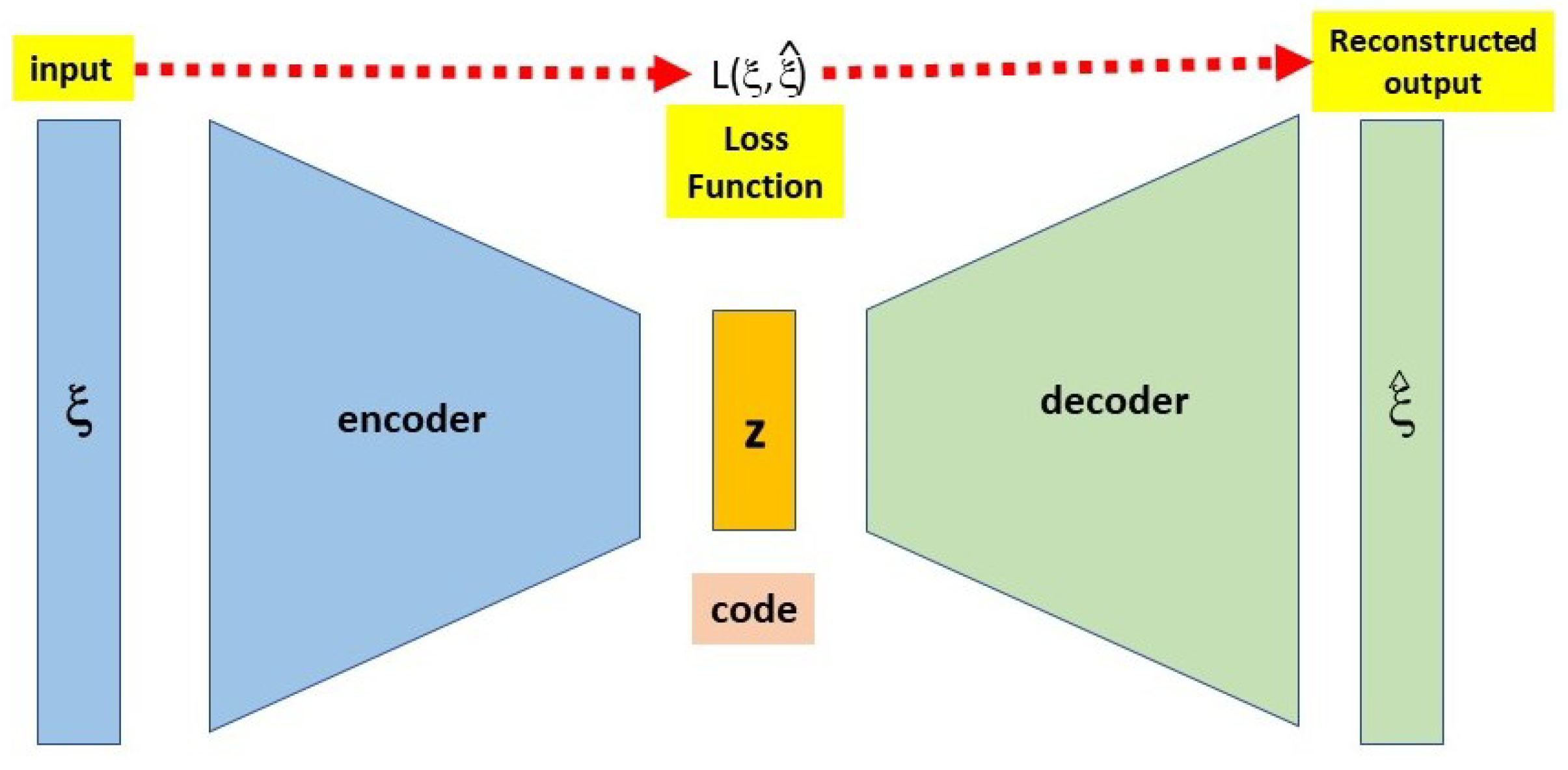
3.2. AutoEncoders
3.3. Temporal Sequence Representation
4. Gap Distance Metric
4.1. Diagnosis via Sub-Space Analysis
4.2. Metrics for Temporal Sequences
4.3. SVD of Hankel Matrix
5. Approach
- 1.
- Encode the input data as a Hankel matrix.
- 2.
- Compute, from the SVD of the corresponding Hankel matrix , the principal angles .
- 3.
- Compute subspace distance in terms of SPA.
- 4.
- Output the loss as the minimum SPA.
6. Empirical Analysis
6.1. Experimental Design
6.2. Data
6.3. Architecture
6.4. Loss Function
- Input : a T-length time-series vector of data.
- Transform into a Hankel matrix .
- Apply an SVD projection of ([44] describes a kernel SVD algorithm for such a task).
- Compute the SPA metric to maximize distance between the modes in this subspace.
6.5. Results
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| AE | Autoencoder |
| SVD | Singular Value Decomposition |
| SPA | Smallest Principal Angle |
| LTI | Linear Time Invariant |
| LSTM | Long Short-Term Memory |
| Symbol | Meaning |
| x | state variable |
| y | output variable |
| u | input variable |
| time-series vector | |
| Hankel matrix | |
| subspace angle |
References
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Chen, J. Robust Residual Generation for Model-Based Fault Diagnosis of Dynamic Systems. Ph.D. Thesis, University of York, York, UK, 1995. [Google Scholar]
- Chen, R.T.; Li, X.; Grosse, R.B.; Duvenaud, D.K. Isolating sources of disentanglement in variational autoencoders. arXiv 2018, arXiv:1802.04942. [Google Scholar]
- Li, J.; Wang, Y.; Zi, Y.; Zhang, H.; Wan, Z. Causal Disentanglement: A Generalized Bearing Fault Diagnostic Framework in Continuous Degradation Mode. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef] [PubMed]
- Knyazev, A.V.; Zhu, P. Principal angles between subspaces and their tangents. arXiv 2012, arXiv:1209.0523. [Google Scholar]
- El-Sakkary, A. The gap metric: Robustness of stabilization of feedback systems. IEEE Trans. Autom. Control 1985, 30, 240–247. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 104. [Google Scholar]
- Lavin, A.; Ahmad, S. Evaluating real-time anomaly detection algorithms—The Numenta anomaly benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; IEEE: New York, NY, USA, 2015; pp. 38–44. [Google Scholar]
- Singh, N.; Olinsky, C. Demystifying Numenta anomaly benchmark. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 1570–1577. [Google Scholar]
- Li, L.; Ding, S.X. Gap metric techniques and their application to fault detection performance analysis and fault isolation schemes. Automatica 2020, 118, 109029. [Google Scholar] [CrossRef]
- Jin, H.; Zuo, Z.; Wang, Y.; Cui, L.; Li, L. An integrated model-based and data-driven gap metric method for fault detection and isolation. IEEE Trans. Cybern. 2021, 52, 12687–12697. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Zhao, Z.; Zhou, J.; Liu, R. Fault detection via data-driven K-gap metric with application to ship propulsion systems. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 6023–6027. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Zhang, Y.; Qiao, L.; Zhao, Z.; He, Z. A Comparison Study of K-gap Metric Calculation Based on Different Data-driven Stable Kernel Representation Methods. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 1335–1340. [Google Scholar] [CrossRef]
- Prasad, G.M.; Rao, A.S. Evaluation of gap-metric based multi-model control schemes for nonlinear systems: An experimental study. ISA Trans. 2019, 94, 246–254. [Google Scholar] [CrossRef]
- González-Muñiz, A.; Díaz, I.; Cuadrado, A.A.; García-Pérez, D. Health indicator for machine condition monitoring built in the latent space of a deep autoencoder. Reliab. Eng. Syst. Saf. 2022, 224, 108482. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A survey on deep learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Yang, D.; Karimi, H.R.; Sun, K. Residual wide-kernel deep convolutional auto-encoder for intelligent rotating machinery fault diagnosis with limited samples. Neural Netw. 2021, 141, 133–144. [Google Scholar] [CrossRef]
- Shen, C.; Qi, Y.; Wang, J.; Cai, G.; Zhu, Z. An automatic and robust features learning method for rotating machinery fault diagnosis based on contractive autoencoder. Eng. Appl. Artif. Intell. 2018, 76, 170–184. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, Y.; Xiang, J.; Chen, B.; Feng, W. Hankel Matrix-Based Condition Monitoring of Rolling Element Bearings: An Enhanced Framework for Time-Series Analysis. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Willems, J.C.; Rapisarda, P.; Markovsky, I.; De Moor, B.L. A note on persistency of excitation. Syst. Control. Lett. 2005, 54, 325–329. [Google Scholar] [CrossRef]
- Markovsky, I.; Dörfler, F. Behavioral systems theory in data-driven analysis, signal processing, and control. Annu. Rev. Control 2021, 52, 42–64. [Google Scholar] [CrossRef]
- Chen, J.; Xie, B.; Zhang, H.; Zhai, J. Deep autoencoders in pattern recognition: A survey. In Bio-Inspired Computing Models and Algorithms; World Scientific: Singapore, 2019; pp. 229–255. [Google Scholar]
- Pratella, D.; Ait-El-Mkadem Saadi, S.; Bannwarth, S.; Paquis-Fluckinger, V.; Bottini, S. A Survey of Autoencoder Algorithms to Pave the Diagnosis of Rare Diseases. Int. J. Mol. Sci. 2021, 22, 10891. [Google Scholar] [CrossRef]
- Zemouri, R.; Lévesque, M.; Boucher, É.; Kirouac, M.; Lafleur, F.; Bernier, S.; Merkhouf, A. Recent Research and Applications in Variational Autoencoders for Industrial Prognosis and Health Management: A Survey. In Proceedings of the 2022 Prognostics and Health Management Conference (PHM-2022 London), London, UK, 27–29 May 2022; pp. 193–203. [Google Scholar]
- Nguyen, T.K.; Ahmad, Z.; Kim, J.M. A Deep-Learning-Based Health Indicator Constructor Using Kullback–Leibler Divergence for Predicting the Remaining Useful Life of Concrete Structures. Sensors 2022, 22, 3687. [Google Scholar] [CrossRef]
- Glad, T.; Ljung, L. Control Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zhai, J.; Zhang, S.; Chen, J.; He, Q. Autoencoder and its various variants. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 415–419. [Google Scholar]
- Michelucci, U. Autoencoders. In Applied Deep Learning with TensorFlow 2; Springer: Berlin/Heidelberg, Germany, 2022; pp. 257–283. [Google Scholar]
- Sontag, E. Nonlinear regulation: The piecewise linear approach. IEEE Trans. Autom. Control 1981, 26, 346–358. [Google Scholar] [CrossRef]
- Presti, L.L.; La Cascia, M.; Sclaroff, S.; Camps, O. Hankelet-based dynamical systems modeling for 3D action recognition. Image Vis. Comput. 2015, 44, 29–43. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace algorithms for the stochastic identification problem. Automatica 1993, 29, 649–660. [Google Scholar] [CrossRef]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Pillonetto, G.; Dinuzzo, F.; Chen, T.; De Nicolao, G.; Ljung, L. Kernel methods in system identification, machine learning and function estimation: A survey. Automatica 2014, 50, 657–682. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, L.; Hu, W. Bridging deep and multiple kernel learning: A review. Inf. Fusion 2021, 67, 3–13. [Google Scholar] [CrossRef]
- Ding, S.X.; Li, L.; Zhao, D.; Louen, C.; Liu, T. Application of the unified control and detection framework to detecting stealthy integrity cyber-attacks on feedback control systems. arXiv 2021, arXiv:2103.00210. [Google Scholar] [CrossRef]
- Zames, G. Unstable systems and feedback: The gap metric. In Proceedings of the Allerton Conference, Monticello, IL, USA, 8–10 October 1980; pp. 380–385. [Google Scholar]
- Vinnicombe, G. Uncertainty and Feedback: H [Infinity] Loop-Shaping and the [nu]-Gap METRIC; World Scientific: Singapore, 2001. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, ML, USA, 2013. [Google Scholar]
- Zhao, H.; Luo, H.; Wu, Y. A Data-Driven Scheme for Fault Detection of Discrete-Time Switched Systems. Sensors 2021, 21, 4138. [Google Scholar] [CrossRef]
- Padoan, A.; Coulson, J.; van Waarde, H.J.; Lygeros, J.; Dörfler, F. Behavioral uncertainty quantification for data-driven control. arXiv 2022, arXiv:2204.02671. [Google Scholar]
- Ljung, L. Characterization of the Concept of ‘Persistently Exciting’ in the Frequency Domain; Department of Automatic Control, Lund Institute of Technology (LTH): Lund, Sweden, 1971. [Google Scholar]
- Park, C.H.; Park, H. Nonlinear discriminant analysis using kernel functions and the generalized singular value decomposition. SIAM J. Matrix Anal. Appl. 2005, 27, 87–102. [Google Scholar] [CrossRef]




| Model | Loss Function | Remarks |
|---|---|---|
| fully connected | MAE | deep network with 2 hidden dense |
| fully connected | PA | layers in encoder/decoder |
| LSTM | MAE | deep network with 2 LSTM |
| LSTM | PA | layers per encoder/decoder |
| Model | Loss Function | Accuracy |
|---|---|---|
| fully connected | MAE | 73 |
| fully connected | SPA | 79 |
| LSTM | MAE | 86 |
| LSTM | SPA | 92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Provan, G. Toward Explainable AutoEncoder-Based Diagnosis of Dynamical Systems. Algorithms 2023, 16, 178. https://doi.org/10.3390/a16040178
Provan G. Toward Explainable AutoEncoder-Based Diagnosis of Dynamical Systems. Algorithms. 2023; 16(4):178. https://doi.org/10.3390/a16040178
Chicago/Turabian StyleProvan, Gregory. 2023. "Toward Explainable AutoEncoder-Based Diagnosis of Dynamical Systems" Algorithms 16, no. 4: 178. https://doi.org/10.3390/a16040178
APA StyleProvan, G. (2023). Toward Explainable AutoEncoder-Based Diagnosis of Dynamical Systems. Algorithms, 16(4), 178. https://doi.org/10.3390/a16040178





