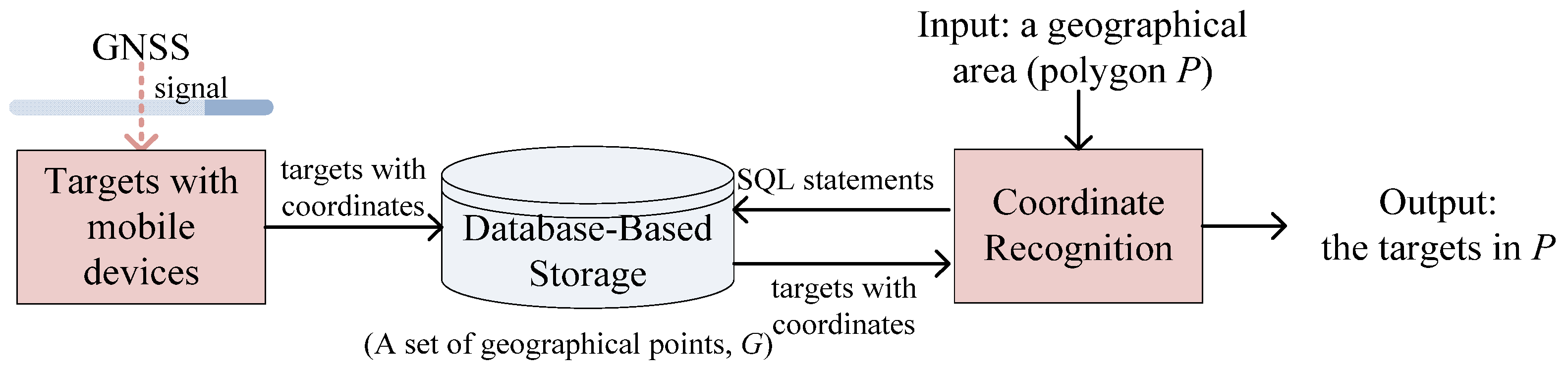
This section describes the recognition algorithm and uses a city as the range to show the steps of the algorithm. The purpose of our research is to assist the epidemic control. Therefore, we use pseudocode style to describe our method, which is to make this method easier to implement.
4.1. The Proposed Algorithm
In this section, a coordinate recognition algorithm will be introduced. We also assume that there is a large number of geographical points (targets) that are stored in table ‘G’ of a unique database, and there is also a unique polygon
P = {
p0,
p1, …,
pn} that refers to a targeted area. This algorithm will be used to calculate the inner points of polygon
P from table ‘G’, and several functions (SegSegInt, PtInPy, SqrInPy, RectOfPy, and RectPtnToSqr) are used. These functions are listed in
Table 1.
The input required by this method is a polygon, a set of geographical points, and the side length of a square. Because the size of geographical points is very large, these geographical points are stored in a database and can be retrieved through the query command of the database. Our method will first define a rectangle that can cover this polygon. Then, it will partition the range of this rectangle into several squares whose side length is SL. Then, for each square, it will calculate the space–overlap status between the square and the polygon. When the range of the square is inside the polygon or is intersected with the polygon, it will retrieve the geographical points within the square range from the database. In the inner status, the retrieved points are the polygon’s inner points without being confirmed through PtInPy. In the intersected status, these points must be confirmed again through PtInPy.
Algorithm 1 is the SegSegInt algorithm. It is a segment–segment intersection algorithm whose input comprises four points:
ga,
gb,
gc, and
gd. The four points compose the segment from
ga to
gb and the segment from
gc to
gd. Applying it will result in a value of 1 or 0 to represent that the two segments intersect or do not intersect.
| Algorithm 1. SegSegInt(point ga, point gb, point gc, point gd) |
- 1.
α:= (ga.x − gb.x) × (gc.y − gd.y) − (ga.y − gb.y) × (gc.x − gd.x); - 2.
if α = 0 then return 0; - 3.
else - 4.
κ1 := ((ga.x − gc.x) × (gc.y − gd.y) − (ga.y − gc.y)×(gc.x − gd.x))/α; - 5.
κ2 := ((ga.x − gb.x) × (ga.y − gc.y) − (ga.y − gb.y)×(ga.x − gb.x))/α; - 6.
if (κ1 ≥ 0 and κ1 ≤ 1) and (κ2 ≥ 0 and κ2 ≤ 1) then return 1; - 7.
else return 0; - 8.
end if - 9.
end if
|
Algorithm 2 is the PtInPy algorithm. It is a point-in-polygon algorithm whose inputs are a point
g and a polygon
P = {
p0,
p1, …,
pn}. This algorithm is used to evaluate whether a point
g is an inner point of polygon
P or if that point
g is an outer point of polygon
P. Applying it will result in a value of 1 or 0, which will indicate if
g is an inner point of
P or if
g is an outer point of
P. In this algorithm, the
count variable is used to count the number of intersections between the rays of
g and the
n edges of
P. Here, mod(
count, 2), which is a modulo operation that returns the remainder after
count is divided by 2, is used. It combines each edge (
pi,
pi+1) of
P, where
i = 0, 1, …,
n−1, and point
g into the segment (
ga,
gb) and the segment (
gc,
gd). If the two segments intersect, the value of
count is increased by 1. Finally, if the value of
count is even (i.e., mod(
count, 2) = 1), it returns 0. Otherwise, it returns 1.
| Algorithm 2. PtInPy(point g, polygon P) |
- 1.
count := 0; - 2.
for i := 0 to n − 1 do - 3.
ga := pi; gb := pi+1; gc := g; gd.x := 0; gd.y := g.y; - 4.
if (SegSegInt (ga, gb, gc, gd) = 1) then - 5.
count := count + 1; - 6.
end if - 7.
if (mod(count, 2) = 1) then return 1; - 8.
else return 0; - 9.
end if - 10.
end for
|
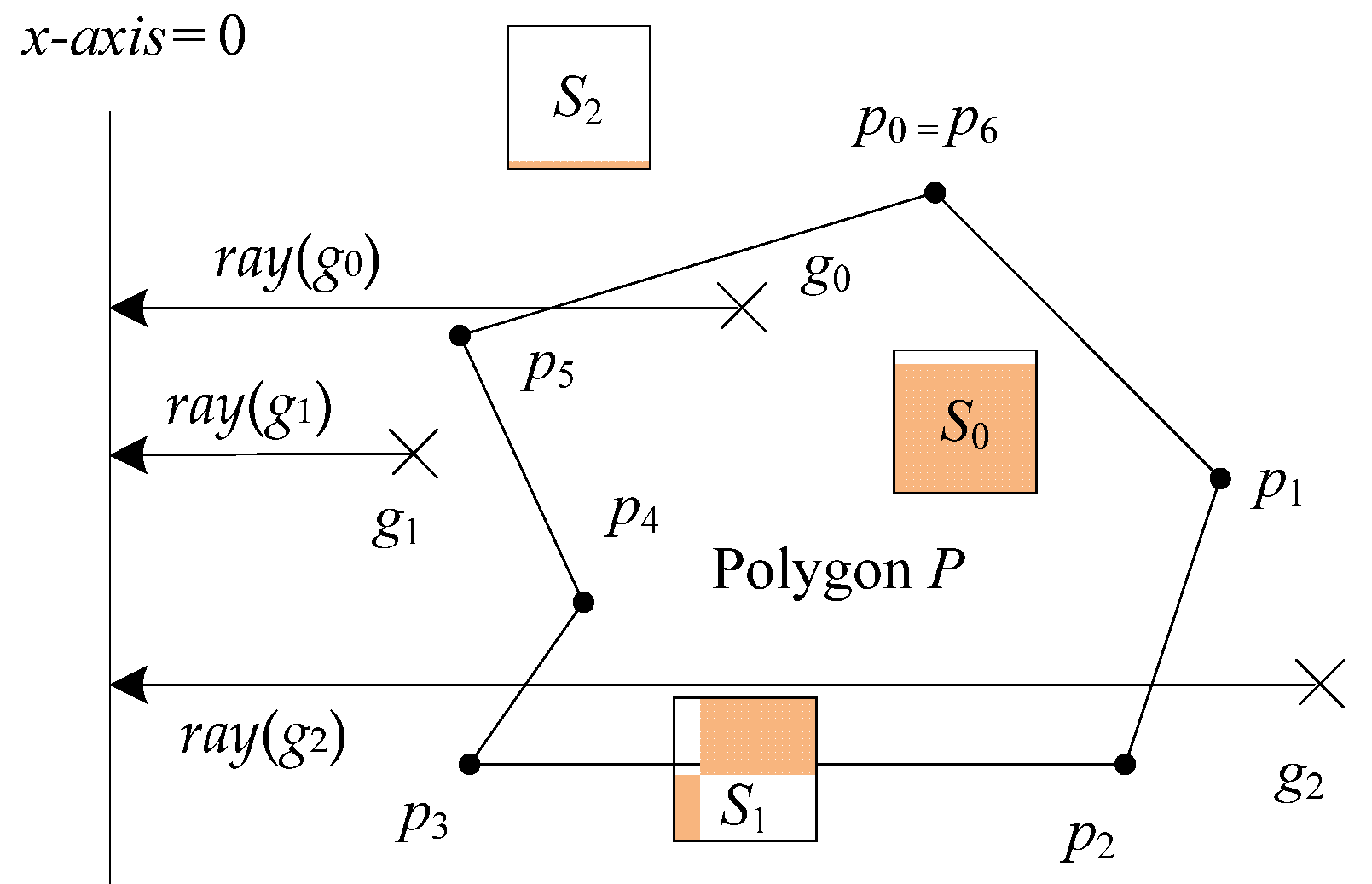
Algorithm 3 is the SqrInPy algorithm. It is a square-in-polygon algorithm whose inputs are a square S = {s0, s1, …, s4} and a polygon P = {p0, p1, …, pn}. This algorithm is used to evaluate the space–overlap relationship between square S and polygon P. Applying it will result in a value of 0, 1, or 2, representing that S is an inner square of P, S is square intersecting with P, or S is an outer area of P. Lines 1 to 6 are used to calculate how many points of S are inner points of P, which is where PtInPy is applied, and the count_pt variable is used to count the number of inner points. Lines 7 to 18 are used to count the intersections between S and P, which is where SegSegInt is applied, and count_edge is used to count the number of intersections.
Lines 19 to 22 are used to evaluate the coverage relationships between the square
S and polygon
P. If the four vertices of square
S are all outer points of polygon
P (i.e.,
count_pt = 0) and the four edges of
S and
n edges of the polygon do not intersect (i.e.,
count_edge = 0), square S is an outer square of polygon
P. On the other hand, if all four vertices of square S are inner points of polygon
P (i.e.,
count_pt = 4) and the four edges of square
S and
n edges of the polygon do not intersect (i.e.,
count_edge = 0), square
S is an inner area of polygon
P. Otherwise,
S intersects with polygon
P.
| Algorithm 3. SqrInPy(square S, polygon P) |
- 1.
count_pt := 0; - 2.
fori := 0 to 3 do - 3.
if (PtInPy(si, P) = 1) - 4.
then count_pt := count_pt + 1; - 5.
end if - 6.
end for - 7.
count_edge := 0; - 8.
forj := 0 to n − 1 do - 9.
for i := 0 to 3 do - 10.
ga := pj; - 11.
gb := pj+1; - 12.
gc := si; - 13.
gd := si+1; - 14.
if(SegSegInt(ga, gb, gc, gd) = 1) - 15.
then count_edge := count_edge+1; - 16.
end if - 17.
end for - 18.
end for - 19.
if (count_pt = 4 and count_edge = 0) then status := 0; - 20.
else if (count_pt = 0 and count_edge = 0) then status := 2; - 21.
elsestatus := 1; - 22.
end if - 23.
returnstatus;
|
Algorithm 4 is the RectOfPy algorithm. It is a rectangle-of-polygon algorithm whose input is a polygon
P = {
p0,
p1, …,
pn}. This algorithm is used to evaluate a minimal rectangular space that completely covers polygon
P. Applying it will result in four values, i.e.,
xmin,
xmax,
ymin, and
ymax. The dataset
R contains these four values, and
R[0],
R[1],
R[2], and
R[3] represent these values. In this algorithm, these values are stored in the variables
xmin,
xmax,
ymin, and
ymax. The algorithm first assigns the coordinate values of point
p0 to these variables. Then, in lines 2 to 7, the values of
pj.x and
pj.y of each point
pj are compared with the values of these variables. If the value of
pj.x is smaller (or larger) than the value of
xmin (or
xmax), the value of
xmin (or
xmax) is assigned as the value of
pj.x. Similarly, if the value of
pj.y is smaller (or larger) than the value of
ymin (or
ymax), the value of
ymin (or
ymax) is assigned as the value of
pj.y. Finally, the values of these four variables are assigned to dataset
R. The values of
xmin,
xmax,
ymin, and
ymax can define a minimal rectangle that can completely cover polygon
P.
| Algorithm 4. RectOfPy(polygon P) |
- 1.
xmin := p0.x; xmax := p0.x; ymin := p0.y; ymax := p0.y; - 2.
for j := 1 to n do - 3.
if pj.x < xmin then xmin := pj.x; end if - 4.
if pj.x > xmax then xmax := pj.x; end if - 5.
if pj.y < ymin then ymin := pj.y; end if - 6.
if pj.y > ymax then ymax := pj.y; end if - 7.
end for - 8.
R := {xmin, xmin, ymin, ymax}; - 9.
return (R);
|
The application of Algorithm 4 results in a dataset
R. The values of dataset
R define the range of a polygon. The dataset
R contains four values, and
R[0],
R[1],
R[2], and
R[3] represent these values. Algorithm 5 is used to divide this polygon into several squares of equal size, where the side length of each square is
sl. Algorithm 5 is the RectPtnToSqr algorithm. It is a rectangle-partition-to-square algorithm, and its inputs are the five values of
xmin,
xmax,
ymin,
ymax, and
sl. It uses the values of
xmin,
xmax,
ymin, and
ymax to define the range of a rectangle into its length and width, respectively ((
xmax −
xmin) and (
ymax −
ymin)). It then partitions the range into a set
SS of
numx×numy squares, where ceiling() is applied. The ceiling() function is a least-integer function. Its input is a real number, and its output is an integer that is not smaller than the input value. This set defines each square
S by using its upper-left vertex (
s0.x,
s0.y). Accordingly, square
S can be defined by using
s0 and the side length s
l.
| Algorithm 5. RectPtnToSqr(xmin, xmax, ymin, ymax, sl) |
- 1.
numx := ceiling ((xmax − xmin)/r); - 2.
numy := ceiling ((ymax − ymin)/r); - 3.
SS := ∅; - 4.
fori := 0 to numx − 1 do - 5.
for j := 0 to numy − 1 do - 6.
s0.x := xmin + i ×sl; - 7.
s0.y := ymin + j ×sl; - 8.
SS := SS∪{s0}; - 9.
end for - 10.
end for - 11.
return (SS)
|
Algorithm 6 is the CoordRecognit algorithm. It is a coordinate recognition algorithm, and its inputs are a polygon
P, a point set
G, and the side length
r of a square. Applying it will return all inner points of polygon
P. This algorithm first defines a rectangle
R, which can cover polygon
P, through RectOfPy. Next, this rectangle
R is partitioned into
SS, a set of squares
SS with a side length
sl, through RectPtnToSquare. For each square
s0 of
SS, where s
0 is the upper-left vertex of the square, its vertices are composed of a square
S = {
s0,
s1,
s2,
s3,
s4(=
s0)}. Then, the space–overlap status between square
S and polygon
P is evaluated through SqrInPy. If
S is an inner square of or a square intersecting with polygon
P, i.e.,
status = 0
or status = 1, the SQL statement is queried in order to retrieve the inner points from table ‘Q’, and they are stored in set
GT. If
S is an inner square of
P, i.e.,
status = 0, set
GT is directly stored in set
GP. If
S is a square intersecting with
P, i.e.,
status = 1, each point
g of
GP must be confirmed through PtInPy. If point
g is an inner point of
P, incrementally, point
g is stored in
GP. Finally,
GP is the set of all inner points of
P.
| Algorithm 6. CoordRecognit (polygon P, point set G, side length sl) |
- 1.
R := RectOfPy(P); - 2.
xmin := R[0]; xmax := R[1]; ymin := R[2]; ymax := R[3]; - 3.
SS := RectPtnToSqr (xmin, xmax, ymin, ymax, sl); - 4.
GP := ∅; GT := ∅; - 5.
for each s0 in SS do - 6.
s0 := (s0.x, s0.y); - 7.
s1:= (s0.x + sl, s0.y); - 8.
s2 := (s0.x − sl, s0.y − sl) ; - 9.
s3 := (s0.x, s0.y − sl); - 10.
s4 := s0; - 11.
S :={s0, s1, s2, s3, s4}; - 12.
status := SqrInPy(S, P); - 13.
if status = 0 or status = 1 then - 14.
GT:={SELECT * FROM ‘G’ WHERE ‘x’ ≥s0.x AND ‘y’ ≥ s0.y AND ‘x’ > (s0.x + r) AND ‘y’ > (s0.y + r);}; - 15.
end if - 16.
if status = 0 then - 17.
GP:= GP ∪ GT; - 18.
end if - 19.
if status = 1 then - 20.
for each g in GT do - 21.
if PtInPy(g, P) = 1 then GP:= GP ∪ {g}; end if - 22.
end for - 23.
end if - 24.
end for - 25.
return (GP);
|
4.2. Example
As an example, we took an area with a longitude ranging from 120.6 to 122.9 East and a latitude ranging from 24.8 to 25.4 North. We collected 267,858 geographic points, which were check-in places obtained from a well-known social network service platform, in this area [
25]. This range also contained the capital of Taipei City. We used the city as the targeted area and the check-in places as the targets to calculate the inner points of this city.
Figure 4 provides the distribution of 10,000 targets that were randomly selected from the 267,858 points. The results related to the layouts of target distributions in this study, such as those shown in
Figure 4 and
Figure 5, and others, were obtained by using Ajax and the Google Maps API [
31]. The city’s polygon
P had 2054 points that were selected along the outermost area, as shown in
Figure 5a. A dataset
R was obtained by using RectOfPy with the polygon P as input, where
R contained an
xmin value of about 121.457, an
xmax value of about 121.666, a
ymin value of about 24.960, and a
ymax value of about 25.210.
Figure 5b provides the corresponding shape, which formed four points (
r0(=(
xmin,
ymin)),
r1(=(
xmax,
ymin)),
r2(=(
xmax,
ymax)), and
r3(=(
xmin,
ymax))) that were the four vertices of a rectangle, i.e., the minimal rectangle covering polygon
P.
Figure 5b provides the shape of this rectangle.
Then, by using RectPtnToSquare, this rectangle could be divided into a set SS of squares.
Figure 6 shows that rectangle
R was divided into a square set
SS with 7×6 squares. For each square
S of
SS, the space–overlap status of
P was calculated through SqrInPy. When square
S was an inner square of or a square intersecting with polygon
P, the inner points of square
S were calculated through the corresponding SELECT statement. If
S was an inner square, the inner points of square
S were also the inner points of polygon
P and were directly stored in the set
GP without confirmation through PtInPy. If
S was a square that intersected, the points that PtInPy confirmed as inner points of
P were stored in the set
GP. Finally, the set
GP contained all inner points of
P. In this example, there were 89,209 inner points in the targeted city.
Figure 7 provides the distribution of the 10,000 inner points that were randomly selected from 89,209 points.