Abstract
We developed a methodology for the neural network boosting of logistic regression aimed at learning an additional model structure from the data. In particular, we constructed two classes of neural network-based models: shallow–dense neural networks with one hidden layer and deep neural networks with multiple hidden layers. Furthermore, several advanced approaches were explored, including the combined actuarial neural network approach, embeddings and transfer learning. The model training was achieved by minimizing either the deviance or the cross-entropy loss functions, leading to fourteen neural network-based models in total. For illustrative purposes, logistic regression and the alternative neural network-based models we propose are employed for a binary classification exercise concerning the occurrence of at least one claim in a French motor third-party insurance portfolio. Finally, the model interpretability issue was addressed via the local interpretable model-agnostic explanations approach.
1. Introduction
The past decade has seen an emergence of a range of new technologies and big data analytics which have begun to reshape the landscape of predictive modeling in many enterprises. The highly data-driven insurance sector not only has to cover the risks which usually fall within its remit but it also needs to continuously adapt and evolve to cover new risks which may result from a combination of traditional data with new data collected from various sources called “big data” which consist of structured, unstructured and semi-structured data. Examples include, but are not limited to, analyzing information from telematics and usage-based insurance for computing insurance premiums, consumer analytics focusing on preferences for certain insurance products, insurance fraud detection, catastrophe modeling, automatic diagnosis of disease from images, crop insurance and weather monitoring and variable annuity products.
Therefore, it can be clearly understood why machine learning (ML) approaches are increasingly being considered in actuarial literature research, as can be seen in [1,2,3,4]. The ML methods which have been used so far for efficiently addressing alternative regression and classification problems in insurance include, for example, XGBoost, random forest (RF), decision trees (DTs), naïve Bayes, K-nearest neighbor (K-NN) model, AdaBoost (AB) model, stochastic gradient boosting (SGB) model, support vector machine (SVM) model and NNs. Additionally, a very interesting and novel research direction, which follows in this study, is the combined actuarial neural network (CANN) approach of [5,6]. Under this approach, every classical actuarial model can be embedded in an NN. In particular, the CANN approach can be interpreted as an NN boosting of the classical actuarial regression model. Therefore, the CANN models can be used to address all kinds of regression and classification tasks with the latter being the main research focus of this study. For more details regarding the use of ML methods in insurance, as can be seen, for instance, in Refs. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].
The aim of this paper was to present alternative ways in which the predictive performance of the classical logistic regression model can be enhanced using neural networks (noting that the methods which are explored herein can be used for any binary response model). The neural network boosting of logistic regression allows us to explore missing interactions of nonlinear type that cannot be captured by generalized linear models such as logistic regression. Following the fundamental approach in the ML process, the generic algorithms which we employ for all the classification models we develop split the input data into a learning or training dataset and a test dataset. Subsequently, the proposed models are fitted on the learning dataset and evaluated on the test dataset in order to demonstrate their ability to make more accurate predictions than the logistic regression, which is used as a benchmark. We compare their predictive performance and investigate whether they generalize well to external data, which in this case, are unseen insurance policies concerning a particular classification task. This procedure is in line with the concept of the so-called “algorithmic modelling culture” according to [38].
In particular, the main contributions we make are as follows:
- We bring the statistical and ML algorithmic cultures concerning binary classification problems into a more integrated relationship by describing how the logistic regression model can be fitted or “trained” by either maximizing its log-likelihood or by minimizing the deviance loss, i.e., the difference between the log-likelihood of the “optimal” model and the learned model.
- The logistic regression model is represented as a shallow dense neural network with one hidden layer which takes in any number of explanatory variables, or input examples in ML jargon, and constrains the output to be between 0 and 1. This approach enables us to consider several extensions of the logistic regression model and utilize methods for optimization and regularization that come as part of platforms for neural network training. Specifically, we consider the following variants of the logistic regression:
- The one-layer, or shallow, perceptron neural network (NN) model. This is the representation of the logistic regression model as a neural network with one hidden layer.
- The one-layer perceptron NN model using embeddings for features. Embedding learning is a more advanced method than one-hot encoding for treating categorical feature components with many nominal levels and it is useful for dealing with categorical variables with many levels in the context of regression analysis. It works by replacing instances of categorical variables by real-valued vectors of fixed size such that the vectors reflect similarity between nominal levels, for different notions of similarity. The embedding technique has its origins in natural language processing (NLP), as can be seen in [39,40,41], but it has also been used in other fields, as can be seen, for example, in Ref. [42]. Regarding actuarial applications, the use of embedding learning has recently been proposed by [3,4,43]. The approach we adopt is novel and slightly different since we aim at receiving a better predictive model by utilizing precomputed embeddings. More precisely, we replace the categorical variables for the one-layer perceptron NN model representation of the logistic regression with a low-dimensional continuous vector representation that was trained by a deep neural network model in order to cluster labels that are more similar to each other with respect to the given classification problem.
- The one-layer perceptron NN model with frozen NN weights on the next-to-last layer. Since the balance property holds true under the canonical link choice for the logistic regression model, see, for example, Ref. [37], a deep neural network can learn feature representations from data. Thus, we partition the training dataset into two sub-datasets of equal size. The deep neural network is trained on the first sub-dataset, and then we feed the second sub-dataset into the pretrained model and we extract the weights of the last hidden layer. In this way, we obtained a new, augmented dataset with new features of different dimensionality. These new features represent nonlinear interactions between the original features. Finally, the one-layer perceptron NN model representation of the logistic regression is fitted on the augmented dataset.
- The one-layer perceptron NN model with transfer learning. The idea is to use embeddings for categorical variables that are obtained from a deep neural network which has been pretrained either on the same or another dataset for another problem which nonetheless shares certain characteristics with the current setting. There are several benefits of using transfer learning. Firstly, one can benefit from other neural network-based models without the need to have access to the data they were trained on. This way, we can convert any regression type problem into a classification type problem and vice versa. Secondly, one can improve the training time for larger datasets. Thirdly, the one-layer perceptron NN model representation of the logistic regression can be updated with new observations, for instance, we can have new insurance policies with new risk characteristics entering the portfolio. Finally, the one-layer perceptron NN model representation of the logistic regression becomes more robust since transfer learning can be seen as a form of regularization.
- In addition to the one-layer perceptron NN model extensions of the logistic regression, we construct alternative feedforward neural network-based models with many hidden layers for addressing the same classification problem. Each layer can be thought of as a possibly nonlinear function whose output is the output to the last layer. The last layer computes the prediction of the model, which, in the setup we adopt herein, is the probability that is associated with the desirable objective for a certain classification task. In particular, we consider the following deep neural network-based models:
- The multilayer perceptron NN model. This is the feed-forward neural network with multiple hidden layers consisting of several neurons.
- The multilayer perceptron NN model with embeddings. The embedding layers which embed categorical features into low-dimensional Euclidean spaces have weights which are learned during the representation learning phase, i.e., the calibration of the model, thus enabling us to investigate the proximity of such features to the classification task.
- The combined multilayer perceptron NN–logistic regression model. Following the CANN approach of [5,6], the logistic regression can be interpreted as a skip connection which is added to the neural network directly connecting the input with the output layer. The logistic regression predicts the probability of an outcome related to a specific classification task and the neural network learns nonlinear transformations and interactions between variables from the data that the logistic regression cannot capture.
- Furthermore, this study investigates how the predictive performance of the proposed models can be improved for addressing the complexity of all sorts of binary classification problems in insurance and special analysis tools are introduced in order to establish their interpretability:
- –
- Neural network architecture. The multilayer perceptron NN-based models, as it can be clearly understood, are more difficult to train and more prone to overfitting to the training data than the one-layer perceptron NN model extensions of the logistic regression.
- –
- The choice of activation functions. Regarding the one-layer perceptron NN model extensions of the logistic regression, the chosen activation function has to be nonlinear in order to capture the stylized characteristics of the data. There are several options for nonlinear activation functions that we discuss later in the paper and the appropriate choice of suitable activation functions at each layer are crucial steps when designing a neural network architecture. Furthermore, we outline the procedure that must be followed for selecting a sufficiently large number of neurons for the one-layer perceptron NN model extensions of the logistic regression for receiving the required accuracy for a particular classification task.
- –
- Loss function. Configuring the loss or cost function for the one-layer perceptron NN model extensions of the logistic regression and the multilayer perceptron NN-based models is an important step for ensuring that the models will perform well in the intended manner since it is a measure of error between what outcome or value the models predict and what the outcome actually is.
- –
- Regularization procedures to prevent overfitting due to the complexity of the multilayer perceptron NN-based models. We consider the following regularization methods:
- Dropout regularization which goes over all the layers in a neural network and randomly setting the probability of keeping or removing some nodes together with all of their incoming and outgoing connections, except the input and output layers which are kept the same.
- Early stopping which is a cross-validation approach. We divide the learning data into training and validation datasets. The models are trained on the learning data and evaluated on the validation data after each training epoch. An arbitrarily large number of training epochs is specified and the training of the model is stopped when it is observed that its performance on the validation dataset does not improve (note that the validation data is part of the learning dataset and thus different from the test dataset used for evaluation of the final model).
- –
- Parameter initialization. For non-convex functions, different parameter initialization strategies can lead to different results. As a result, a unique best model does not exist, as can be seen in [44]. This issue was explored by [45]. Thus, parameter initialization is a very important step.
- –
- Embedding representation and feature prepossessing. For expository purposes, we consider the problem of predicting the probability that an insurance claim will be filed in a French motor third party liability (MTPL) insurance portfolio consisting of features describing the vehicle, the driver and the geographic area of the car registration and the number of insurance claims observed during one accounting year. We discuss in detail the embedding representation for categorical features and feature preprocessing for the continuous and ordered features in the data.
- –
- Hyperparameter tuning. The architectures of the neural network-based models were chosen based on rigorous hyperparameter tuning, i.e., the process of determining the right combination of hyperparameters that allows the model to maximize performance.
- –
- Interpretability. As is well known, for insurance claim predictions, it can be of crucial importance to be able to analyze the reasons behind a certain prediction. For this purpose, we will apply a model that locally approximates the function learned by the NN model with a linear function. The coefficients of this linear approximation function will then show the importance of the original features for the output of the advanced NN model.
The rest of this paper proceeds as follows: in Section 2, we present the classical logistic regression model and how it generalizes to a neural network model. In particular, the Newton–Raphson and the gradient descent algorithms for the logistic regression model are described and the maximum likelihood (ML) estimation, goodness-of-fit and model evaluation are discussed. Then, we discuss how NNs can be used for predicting claim occurrence in the French MTPL data.In Section 3, a detailed description of insurance claims prediction using the neural network boosting of logistic regression is given and the LIME approach is utilized for providing local model interpretability. Finally, concluding remarks can be found in Section 4.
2. Notation and Overview of Techniques
In this section, we present the details of the main techniques used in our paper, and how they apply to the problem at hand. We first introduce logistic regression and then discuss how it can be generalized to feed-forward neural networks.
2.1. Logistic Regression
In logistic regression, the response is a Bernoulli variable with a probability mass function (pmf) given by
where if the i-th claim is observed with probability and with probability otherwise, for .
Furthermore, we assume that the i-th claim will be observed or not using covariate information X, with corresponding to the intercept component.
As is well known, has an exponential dispersion family (EDF) representation with canonical link function given by
where and where the design matrix is of full rank . The use of the canonical link function implies that we receive unbiased estimates on a portfolio level, as can be seen in [46].
Additionally, from Equation (2), we obtain the sigmoid, or the inverse of the logit, function of the prediction
The sigmoid function has the advantage that the predicted values are probabilities which yield more easily interpretable results. Furthermore, the individual coefficients in the vector can be treated as feature importance weights which result in explainable models.
Finally, it is worth noting that in addition to the logistic sigmoid function, which is given by Equation (3), there are several other sigmoid functions, such as the hyperbolic tangent and the arctangent which are also monotonic and have a bell-shaped first derivative. Sigmoid functions were inspired by the activation potential in biological neural networks and have been widely used when designing ML algorithms, particularly as activation functions in artificial neural networks.
2.2. Training a Logistic Regression Model
Let be a set of examples where is the binary response and are explanatory variables, or input examples, such that each example is represented by d real valued features and augmented with the constant 1 that represents the intercept component. Let be the parameters that define the model and be a loss function that evaluates how well the model fits the response Y for input X. We want to optimize the loss with respect to the parameters , and thus, in the following, for brevity, we will denote by . We will present later appropriate choices for the loss function. Let us for now only assume that the first and second derivatives and with respect to the parameters are well defined and nonzero.
Unfortunately, the logistic regression model does not admit a closed form of the optimal solution (for a reasonable choice of the loss function) and we cannot directly compute an optimal solution. Instead, the solution has to be numerically estimated using an iterative process. Below we present two widely used approaches to finding an approximation of the optimal solution: namely the Newton–Raphson algorithm for the logistic regression model, which is outlined in Algorithm 1, and the gradient descent approach, which is presented in Algorithm 2.
| Algorithm 1 Newton–Raphson algorithm |
|
 |
| Algorithm 2 Gradient descent algorithm |
|
 |
Both algorithms use the gradient descent approach that iteratively approximates a local optimum by a starting at a randomly selected point and moving in the opposite direction to the gradient. For a convex loss function, this is also the global optimum. The difference between the approaches is that, if we use a small predefined constant learning rate that moves in the direction of the (local) optimum, we use the second derivative of the loss function that guarantees the convergence with a smaller number of steps. The reduced number of iterations of the Newton–Raphson algorithm comes at the price that we need the second derivative of the loss function. We will later discuss why computing the second derivative can be a computational bottleneck for neural network optimization.
2.3. The Loss Function
We present two different approaches to defining a loss function that measures the quality of a candidate solution for . The first one is based on the ML estimation of the probability mass function of the logistic regression model, and the second one compares the quality of the candidate model to the solution of a saturated model.
2.4. Maximum Likelihood Estimation
Assume that we have a set of data points and we want to calculate the ML estimate of the -dimensional parameter of the logistic regression model in Equations (1) and (2).
The log-likelihood function of the model is given by
for .
To find MLE of , one has to solve the score equation
The negative likelihood thus defines the cross-entropy loss:
However, since there is no analytic solution for Equation (8), the solution has to be numerically estimated using an iterative process as the one described in the previous section. Next, we show how to employ the Newton–Raphson method which is the most popular method for solving systems of nonlinear equations (note that the MLE of the logistic regression model can be obtained by calling the glm() function in programming language whilst setting the family argument to “binomial”).
The Newton–Raphson algorithm for the logistic regression model can be described in matrix form as follows:
- Let be the estimate of obtained after the r-th iteration. The matrix representations of the first and the second derivative of the log-likelihood in (6)–(9) are given byandwhere is the design matrix and where , with , where is the pointwise product . Furthermore, let be an diagonal matrix where the i-th diagonal entry is given by .
- Then, the r-th update is given by
The description of a gradient descent algorithm is straightforward from the above discussion, the difference being that we need to replace the second derivative with a constant learning rate . In order to obtain good quality, we will need to set a sufficiently small , and thus the gradient descent will converge in more iterations than the Newton–Raphson method. However, we avoid the computation of the second derivatives in the Hessian matrix which has a computational complexity of , whereas computing the first derivative can be performed in steps The big O notation denotes asymptotic growth. Formally, it holds iff for all for some constants and .
2.5. Goodness of Fit
In the context of logistic regression, the maximum number of parameters that can be fitted is given by n, i.e., one for each observation. In this case, we have and as the optimal solution obtained from a saturated model. Let denote the vector . One way to assess the goodness of fit of a model is to compare its log-likelihood with that of a saturated model. The relevant test statistic, called the deviance, is defined by:
It can be calculated explicitly, as follows:
where is the sigmoid function.
Note that the first and the second derivatives of the deviance loss are the double of the derivatives of the cross-entropy loss as it holds
and the derivative is computed with respect to . Thus, we can use the same approach to approximate the optimal solution as for the cross-entropy loss.
2.6. Model Evaluation
We split the available dataset into a learning set and a test set . We train the models only on and report results for the performance of the models on both and . We would like the quality of prediction on both datasets to be comparable, since in this case, the model’s performance is likely to be representative for new unseen datasets. This will be particularly important when training neural network models which have higher capacity, i.e., they can represent more complex functions than GLMs. In fact, one of the main results on neural networks is that they can represent arbitrary continuous functions. On the other hand, for this reason, such models are prone to overfitting the training data. Thus, it is of crucial importance to show results of comparable quality on a dataset that was not used for training.
More precisely, we perform the parameter estimation on the learning set to achieve a minimal deviance loss as follows:
This enables the calculation of the in-sample deviance loss
and the out-of-sample deviance loss
This out-of-sample loss is then our main measure of interest when comparing the prediction performance between models. Note that the model is fit only on the learning data and thus we optimize the in-sample loss but evaluate the quality of the model on the out-of-sample loss. The expressions for in-sample and out-of-sample cross-entropy loss can be derived in a straightforward way from the above and Equation (6).
2.7. Neural Networks
In this section, we give an overview of neural networks and we discuss how they can be used in our setting for the prediction of insurance claims in the French MTPL data we consider for our numerical illustration in Section 4.
The design of advanced neural network architectures is a very active research area, with applications ranging from speech recognition to drug design. We refer the reader to [47] for an overview of different neural architectures.
A feed-forward neural network consists of several layers such that each layer consists of a number of neurons. The first layer is the input layer and the last layer computes the output of the function. The layers between the input and the output layers are called hidden layers. In Figure 1, we show a neural network with three hidden layers. This is the network that we are using for our model, as more details are provided in the following sections. Each neuron computes a linear combination of all inputs from the previous layer. We can think of the output of a layer as a matrix multiplication with the input from the previous layer where the entries in the matrix should be learned by training the model. A neuron corresponds to a row in this matrix. In order to represent nonlinear functions, we apply a nonlinear activation function to the output of each layer.
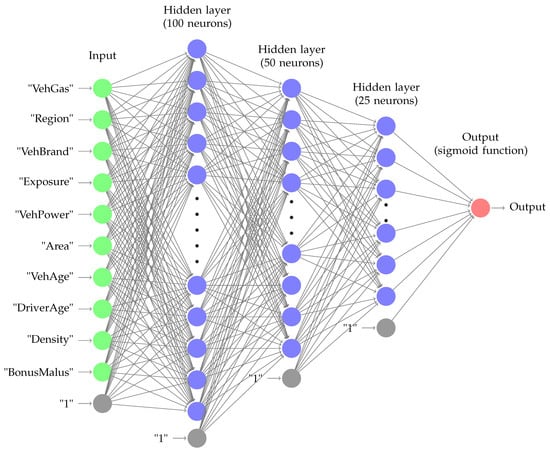
Figure 1.
A multilayer perceptron neural network with three hidden layers. The last neuron in each layer is the intercept term.
More precisely, a neural network computes a function f mapping the features to the response :
As the neural network consists of several hidden layers, and each layer can be expressed as a mapping, we see that f is composed of several functions. In particular, let be the input to the k-th hidden layer with neurons. Then, the function in the k-the layer is given by where for a matrix and a nonlinear activation function that is applied entry-wise to the vector . Thus, the i-th neuron is represented by the i-th row in the matrix W. Summarizing the above, the k-th layer computes the function
The hidden neurons are given by
with . For , the input is simply the design matrix x and is equal to the dimension of the feature space .
The last layer computes a predicted value for the problem at hand. In our setting, we consider a binary classification problem. Thus, to take into account the exposure of every insurance policy, just as in logistic regression, the output layer is given by
where is the sigmoid function which computes the probability that a given example will be an insurance claim. That is equivalent to adding a layer with and a sigmoid activation function. This basic architecture of the neural network then has a depth of K with parameters to be learned.
As a concrete example, we consider the neural network shown in Figure 1. The input comprises 11 variables provided in the insurance claim dataset. There are hidden layers with , , and neurons. Thus, there are 5100 parameters for .
2.7.1. Logistic Regression as a Single Layer Neural Network
We can view logistic regression as a single layer network. In particular, for , and , the network implements the logistic regression model.
2.7.2. Neural Network Training
Given a dataset with examples and a target variable (where for regression problems, and for classification), we want to learn the parameters or the weights of the layers of a neural network that computes a function . This is usually achieved by choosing a particular neural network architecture and a loss function that helps us achieve a given objective, e.g., high accuracy for classification or a small absolute error for regression. In our setting, the desired objective is to reflect the probability for an insurance claim.
The loss function should be well defined and differentiable such that an optimal solution can be found. As neural networks represent complex functions, an optimal solution will not exhibit a closed form in the general case. Instead, a local optimum is found using numerical optimization methods. It is standard to use the gradient descent method. The approach starts with randomly assigned values for the weights for all neurons. The values are random but sampled from some distribution. Empirically, it was observed that sampling from a 0-mean normal distribution where the variance is a function of the number of input and output neurons at the layer guarantees the fast convergence of training.
The examples are processed in batches. For example, let be the output of a neural network for a given regression problem. For a batch with n examples , the loss is defined as where is the response we want to learn. For regression problems, a commonly used loss function is the mean squared error, thus we have to optimize the parameters of F, i.e., the weights of the layers in the neural network, such that is minimized. In the binary classification setting, appropriate choices for the loss function are cross-entropy and deviance, as discussed in the previous section.
The method of choice for neural networks is gradient descent, as described in Algorithm 2. Weights are updated such that the weight values move in the negative direction of the gradient of :
where denotes neural network evaluated at x with weights and is the learning rate. For sufficiently small , gradient descent is guaranteed to converge to a local optimum. Thus, for a convex function, it will probably find an optimal solution.
As discussed, a neural network implements a composition of functions. Thus, the loss function can be written as
Using the chain rule for computing the derivative of a composite function, gradient descent is applied to a neural network using back propagation. Remember that and . In order to compute the derivative of the loss function with respect to the weight of the neurons in the t-th layer, for , we apply the chain rule as
In each layer, we compute the derivative at each layer with respect to the output of the previous layer. In the above, it holds that
Note that, in the above, the design matrix values, i.e., the feature values in the training dataset, are considered to be constants.
Of course, neural networks are not supposed to only model convex functions but even the local optima of non-convex loss functions yield good enough solutions in practice.
2.7.3. More on Gradient Descent Optimization
Gradient descent has become the ubiquitous approach to training neural networks, and is the method of choice in literally all platforms for neural network training. As discussed in Section 2.1, we can apply the Newton–Raphson algorithm which converges in fewer iterations. However, this would require the computation of the second derivative with respect to the parameters at each layer, i.e., we need the Jacobian matrix of the layer parameters . For larger networks with many parameters, this is unfeasible as the Jacobian will have parameters, where and is the number of input and output neurons at the k-th layer. Even for our relatively small neural network from Figure 1, this would mean a Jacobian matrix with 25 million entries.
However, gradient descent comes with many challenges that need consideration:
- We can get stuck in a local optimum which might result in a solution which is not good enough. Furthermore, for a non-convex function there might exist a saddle point where, in one dimension, the function has a positive slope, and a negative slope in other dimension. The derivative of a function at a saddle point is 0 but the saddle point is not a local optimum.
- A small learning rate would lead to very slow convergence, and a large learning rate might lead to oscillation around the optimum.
- Computing the gradient with respect to the whole training dataset might result in very slow updates.
- For certain loss functions, we might encounter the problem of vanishing gradients. Consider the sigmoid function , for large or small values of z the gradient will be close to 0, and thus we will need many iterations until we reach an optimum.
- The learning rate needs to be adapted in order to address changes in the curvature for complex functions. In particular, the gradients in different directions might be of largely different magnitudes, and thus using a constant learning rate might lead to oscillations.
Researchers have approached the above issues using various techniques such as
- In particular, the choice of activation function is of critical importance. We discuss different activation functions and how we use them in our architecture in greater detail in the next subsection.
- Mini-batch training. Compute the gradients not for the whole dataset but for a batch of examples.
- Adaptive learning rate. The idea is that the learning rate is not a constant but a function of the gradients of the past iterations of the optimization process. A popular choice in practice is the Adam approach (adaptive moment estimation) where the learning rate is adjusted after each iteration by using an exponentially decreasing average of past gradients. We refer to [48] for more details on the approach.
- Parameter initialization. We start to train the neural network model by initializing the parameters with random values. However, the magnitude of these random values has to be carefully selected as it might lead to slower training or even vanishing or exploding gradients.
Note that the above list is not exhaustive since, unfortunately, neural network optimization relies on heuristic techniques and trial-and-error-based hyperparameter tuning, and is thus often characterized as being more of an art than science. Regarding the classification problem we consider herein, we provide more details in the next section wherein we discuss the results of our models.
2.7.4. Activation Functions
When the activation function is nonlinear, a deep neural network computes complex nonlinear functions. In fact, the universal approximation theorem states that any continuous function can be approximated with an arbitrarily small error by a neural network with a single hidden layer and a nonlinear activation. However, such functions are unlikely to generalize well as the hidden layer might need to be very large, and thus they will not be useful for learning a model that generalizes well to new data. Instead, one prefers multilayer networks where each layer computes certain patterns which are then combined by the next layer in order to form more complex patterns. In the context of computer vision, one can think of the first layers of a neural network of detectors of basic image features such as edges and contours, while the latter layers combine these basic shapes into more complex patterns that represent object parts.
Below, we list the most widely used activation functions.
- Sigmoid.The sigmoid function is widely used for binary classification as it returns a value in which can be treated as the probability that a given example belongs to one of two classes. For multi-classification problems, the function is generalized to the softmax function which returns the probability for each of k classes. However, the derivative of the sigmoid function is . Therefore, the maximum possible value of the derivative is 0.25. It is not advisable to use the sigmoid as the activation function for several layers as it is likely to encounter the problem of vanishing gradients: by the chain rule, we multiply the derivatives at each layer and thus the gradient will converge to 0 and updating the weights by gradient descent will converge very slowly towards an optimal solution. For this reason, the sigmoid is usually used as an activation function only for the output layer.
- Hyperbolic functions.This is an alternative to the sigmoid function where the range of values is between −1 and 1 which might yield more insights, especially regarding the impact that certain features have on the output. Observe that , and thus the derivative is at most 1 and is close to 1 only for . Thus, stacking several layers with a hyperbolic activation function might again lead to the vanishing gradient problem, and thus it is recommended to use it only for layers close to the output layer.
- ReLU.This is a nonlinear function that can be used to obtain a piecewise linear approximation of arbitrary functions. As long as the weights are positive, gradient descent quickly converges towards the optimal solution. However, an obvious problem of the ReLu activation function is that if the input to a neuron is negative, then the derivative will always be 0, which is the so-called “dying” ReLUs problem. Alternatives have been proposed, such as the LeakyReLU with , where is a small constant, or the eLU for some .
In our setting, we found that the eLU activation function yields the best results, slightly outperforming the ReLU. We will comment more on this in the next section.
2.7.5. Embedding Layer
A common technique for the preprocessing of categorical features is to convert them into numeric vectors. The standard choice is to represent a feature x, with values over c possible categories , by a binary c-dimensional vector x with a single nonzero coordinate such that iff . This is the so-called “one-hot encoding”.
Neural networks offer an important alternative, namely that categorical features are represented by numerical vectors and these vectors are learnt just like we learn the weights of the individual layers. This is achieved by the so-called embedding layer that maps each feature value to its corresponding embedding, i.e., its vector representation. This is implemented by a simple hash table that keeps the corresponding representation for each feature value and loads it when required. All modern neural network frameworks such as Keras, PyTorch, etc., offer embedding layers.
One major advantage is that the learnt feature representations capture the intrinsic characteristics of the features. For example, embeddings are very popular in natural language processing where the semantic similarity between words is reflected in the embeddings. A notorious example is that .
3. Prediction Models and Numerical Illustration
3.1. Data Description
The freMTPL2freq data which we consider for the application of the proposed models are a French MTPL claim count dataset which was included in the R package CASdatasets, as can be seen in [49]. This dataset consists of 678,013 insurance policies, or examples in ML terminology. An in-depth exploratory data analysis of this dataset is given in the tutorials of [6,23,50] for the Swiss Association of Actuaries (SAA). Furthermore, to ensure that the heavily parameterized neural network-based models do not overfit the data, we split the data at random into a learning dataset consisting of 90% of all examples and a test dataset comprising the remaining 10%. Each example consists of 12 features, which are described in Table 1. We used 10 features for the design matrix, and one for the target variable (the unique identification number of the policy is clearly useless for prediction). Each feature is transformed as described in the last column. We converted the number of claims feature into a binary label. This is justified by the data as only 0.278% of examples have a claim number of more than one, as can be seen in Table 2 for the exact numbers. We normalize numeric features to be normally distributed around their mean using the variance in the data. In particular, we use the learning dataset mean and standard deviation of each feature for normalization. Categorical variables were converted into ordinal ones, the order being arbitrarily decided and then normalized. Normalization is important as we bring the features to be on a comparable scale, which is helpful for the gradient descent algorithm. One of the major advantages of deep learning is that, as mentioned earlier, it can be seen as an approach to learning feature representations from data. This is why we chose relatively simple techniques for feature preprocessing.

Table 1.
Summary of the data features and the corresponding preprocessing methods.

Table 2.
Number of examples with a given number of claims.
3.2. Models Overview
At a high level, the algorithms work by following the machine learning paradigm. First, we choose a model that will predict the probability that an insurance claim will be made. The model represents a hypothesis space, namely a family of functions that classify examples into claims and non-claims based on a given input. Our goal is to select an optimal function from this family where optimality is defined with respect to the input data and a given loss function. More precisely, we want to find the optimal function parameters. We provide specific details in the next section.
Optimization
As discussed, we used gradient descent to detect a local minimum with respect to a given loss function using the gradient descent approach. In the case of logistic regression, these are the optimal weights that model the importance of individual features and the algorithm is guaranteed to detect the global minimum. For the neural network models, we want to find the optimal values in the weight matrices at different levels. As discussed, neural networks model non-convex functions and gradient descent is not guaranteed to detect the global minimum.
3.3. Implementation
All models we developed were implemented in the programming language . For the neural network-based models, we used the keras package. In Table 3, we listed all models implemented in the paper. The name of a model is given as , denoting whether this is a logistic regression or a neural network model, and the loss function is either cross-entropy (CE) or deviance (Dev).

Table 3.
List of models evaluated on the MTPL dataset.
In our setting, we found that optimal results for the one-layer perceptron NN model representations of the logistic regression are attainable by using a learning rate of for the Adam algorithm which was run over 100 epochs on random mini-batches of size 10,000 from the training data. We used He initialization [51] for initializing the parameters of the network as this approach is known to guarantee the faster convergence of the gradient descent training algorithm.
Furthermore, regarding the multilayer perceptron NN models, optimal results were obtained from the model returned by early stopping, i.e., the model that performs best on the validation dataset.
In the next subsections, we present more details about each of the models including the architecture neural network-based models, the loss functions, the regularization methods of dropout and early stopping that we employ, as well as details on the evaluation and results for all the proposed models.
3.4. Neural Network Architecture
The architecture for the feed-forward neural network is shown in Figure 1. The 10 input variables are fed into a hidden layer with 100 neurons. The next two hidden layers have 50 and 25 neurons, respectively. The activation after the hidden layers is the eLU function and the output is computed by the sigmoid function. As discussed, we can treat the three hidden layers as computing a new feature representation, and then applying a logistic regression model on the new features. The architecture was designed by careful hyperparameter tuning. The intuition behind the decreasing number of neurons in the hidden layers is that we want to first create combinations of the original features, and then only detect the most significant combinations such that we avoid overfitting.
In Listing 1, we show the implementation of a logistic regression model using a single layer neural network, and in Listing 2, the implementation of the neural network from Figure 1.
| Listing 1. Logistic regression by a neural network. |
|
| Listing 2. Neural network of Figure 1. |
|
3.5. The Loss Functions
We consider the two loss functions defined in Section 2.2 as (i) binary cross-entropy which optimizes the prediction function with respect to an ML estimator
and (ii) deviance loss, which approximates the quality of predictions by a saturated model:
For both of the loss functions we used, the gradient descent method was applied using Adam optimizer with a learning rate set to 0.001. We used a mini-batch of 1000 examples.
In Listing 3, we show the implementation of the custom-defined deviance loss. The cross-entropy loss is one of the default classification loss functions in Keras but we need our own implementation of deviance loss.
| Listing 3. Deviance loss. |
|
3.6. Regularization
As already mentioned, the first step in order to avoid overfitting is to have a smaller number of neurons in the layers.
- Dropout. During learning, when processing different batches of data, a subset of neurons selected at random are not used for training. This forces other neurons to take over their function and this prevents the “overspecification” of neurons and thus yields models with a lower variance. In the network in Figure 1, we randomly dropped 20% of the neurons from the first and second hidden layers, and 10% of the last hidden layer. These values were found by manual hyperparameter tuning.
- Early stopping on a validation dataset. When training a model, we divided the learning data into 80% purely training and 20% validation data. The model is only trained on the training data and the loss function is evaluated on the validation dataset. Training using gradient descent continues until the loss for the given loss function decreases on the validation dataset. Once we observed that the loss on the validation has not decreased for a certain number of iterations, we return the model which has the smallest loss on the validation dataset. The intuition is that the validation dataset is representative for the performance of the model on new data. In Figure 2 (top), we show that, while the loss on the training data (in red) continues to decrease over epochs, it starts to slowly increase on the validation data (in green) indicating that the model overfits. In the plot, we observe that the optimal model, as evaluated on the validation dataset, is achieved after roughly 60 epochs.
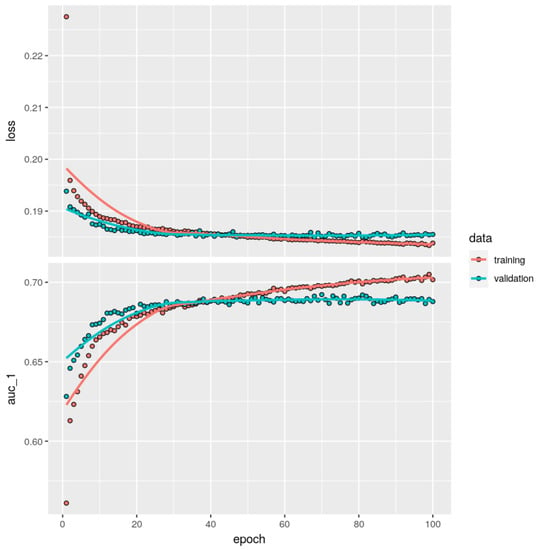 Figure 2. Improvements of deviance loss and AUC metrics over epochs.
Figure 2. Improvements of deviance loss and AUC metrics over epochs.
3.7. Evaluation and Results
The loss can be mathematically optimized but it does not really provide any insights with regard to how useful the proposed model is. For a highly imbalanced classification problem, the accuracy metrics is not a suitable choice. In our case, we can achieve 95% accuracy by simply predicting “no claim” for all inputs. A standard choice is the use of the receiver operating characteristic (ROC) curve which evaluates the prediction quality of a binary classifier by varying the discrimination threshold. Essentially, it shows the true positive rate for various thresholds of the false positive rate. For example, by accepting a 20% rate for false positive claims, we can detect 50% of the real claims. As we want high true positive rates with corresponding low false positive rates, we want most of the area to be under the ROC curve. The area under curve (AUC) metrics is thus widely used to evaluate the quality of a binary classifier. In Figure 2, we show that the decrease in deviance loss reflects an improvement in AUC scores. The results are presented in the Figure 3, Figure 4 and Figure 5 and the Table 4 and Table 5 at the end of this subsection.
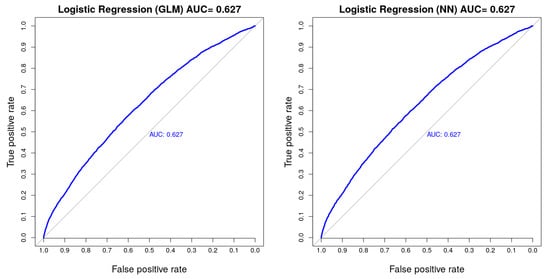
Figure 3.
AUC values on the test set achieved using R’s logistic regression function (left) and logistic regression by a shallow neural network (right).
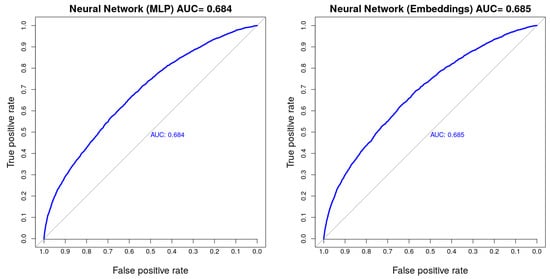
Figure 4.
AUC values on the test set achieved using a neural network with feature normalization (left) and feature normalization + categorical embeddings (right).
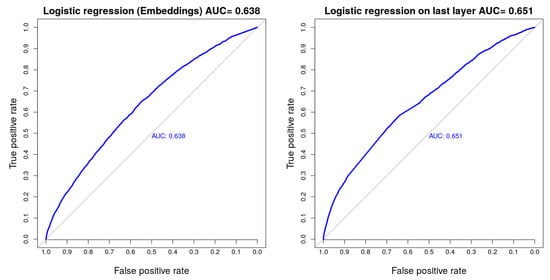
Figure 5.
AUC values on the test set achieved using logistic regression with embeddings (left) and frozen weights learned by a neural network (right).

Table 4.
The deviance loss and the corresponding AUC values on the training and test datasets.

Table 5.
The cross-entropy loss and the corresponding AUC values on the training and test datasets.
3.7.1. Logistic Regression Results
The results for the different variants of logistic regression are in Panel A in Table 4 (deviance as a loss function) and Table 5 (cross-entropy as a loss function).
Logistic Regression Using Embeddings for Features
We discuss how to compute embeddings for the categorical variables VehicleBrand, Region and Area in the next section. We replace the categorical values for these features by the corresponding vector representation that was trained by a neural network model. The values for the entries for in Table 4 and Table 5 show that we improve the results for standard logistic regression.
Training a Logistic Regression Model on the Next-to-Last Layer
Given that that the balance property holds, we have the unbiasedness of the estimated logistic regression on the portfolio level and we can treat the neural network as a model that learns a new feature representation. In particular, we split the training data D into two equal partitions and . Then, we train a neural network model on and call this model . Then, we convert the features of by running on it and extracting the weights of the last hidden layer. In the network from Figure 1, this creates new features of dimensionality 25. Then, we fit a logistic regression model to the newly created dataset. As evidenced from the values in Table 4 and Table 5, we considerably improve upon the standard logistic regression model (the entries for ).
3.7.2. Multilayer Perceptron Results
This is the classical setting for NN training using, in our case, the architecture from Figure 1. In Table 3, the models are denoted by for deviance loss and for the cross-entropy loss. The training of the network follows the approaches discussed above. In particular, we use: He initialization, which is one of the methods one can use to bring the variance of the layer outputs to approximately one; the Adam algorithm with learning rate for gradient descent optimization, with a dropout of 20% for the first two hidden layers and the eLU activation function for all hidden layers. Finally, the activation function for the output layer is the sigmoid.
3.7.3. Advanced Approaches
In addition to the above approaches, we designed several extensions that aim to improve the models.
A Skip-Layer Connection Approach
Following the CANN approach of [5,6], Listing 4, we train a neural network and, in addition to that, we feed the input layer directly into the output layer, i.e., the sigmoid layer. This is a combined model that has, as an input, the features learned by the neural network as well as the original features. The intuition is that, in this way, we can combine more complex features which can improve the model but also lead to overfitting, and thus we also have the original features on which we learn a more basic model such as logistic regression.
More precisely, the model looks as follows
This means that we concatenate the original input (the first “blue” entry) to the output of the k-th layer (the second “red” entry) and train a logistic regression model on the new feature space.
Listing 4. CANN model. |
|
Embeddings
In Listing 5, we show how to compute embeddings for three categorical variables: the vehicle brand, the area and the region in France. Each embedding is a 5-dimensional vector that corresponds to a given categorical values. In Figure 6, we show the distribution of embeddings computed by the network for regions in France. Some of the regions are considered to be more similar to each other and are grouped together. Such a representation is useful as it yields more insight into the features and can be used to improve the performance of other models.
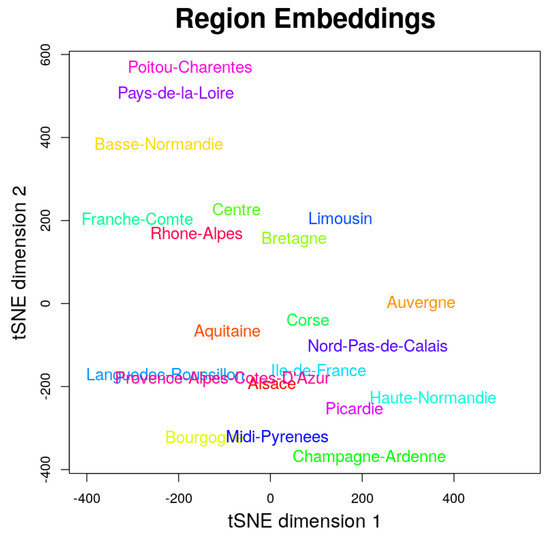
Figure 6.
A tSNE visualization of the 10-dimensional embeddings for the different regions.
| Listing 5. Embedding layers. |
|
Transfer Learning
A widely used approach to training more robust learning models is the so-called transfer learning technique. For example, there are powerful computer vision or natural language processing models that have been trained on massive datasets. For example, the VGG16 classification model [52] was on trained on a dataset consisting of more than 14 million images, and each image belonged to 1 of 1000 classes. If we have to design a new image classifier for a smaller and more specific dataset, e.g., for the classification of dog breeds, it is challenging to train a new model from scratch if we have a smaller dataset with just a few thousand dog images. Instead, we can use the VGG16 neural network but replace some of the top layers with new layers. As such, the neural network will detect certain shapes in the image, e.g., the shape of the ears or the tail, and we will learn how to combine these shapes in order to correctly predict the dog breed.
More precisely, we will apply transfer learning to our setting as follows. Let represent a Poisson regression model. Let be a logistic regression model implemented by a neural network. Let be a set of categorical features that are used as input to an embedding layer in , that are also used as input to the network. After training a model for Poisson regression on , the weights of the embedding layers will then be used in .
We followed this approach and retrained the GAM2 model from [6]. We then extracted the embeddings for the variables VehBrand, Area and Region. The corresponding function implementation is shown in Listing 6. The input is a data frame and a pretrained model with embedding layers from which we extract the embedding for each feature using the get_layer function.
Using these embeddings, instead of the embeddings trained by our architecture, as described in the previous section, we again trained a logistic regression and a neural network model. As we see, the results are essentially identical. This is not really surprising as, in both cases the embeddings capture the information about the relationships between different objects in each category.
| Listing 6. Transfer learning function. |
|
3.8. Interpretability of Results
Deep learning models are notoriously difficult to interpret. By creating new features at each hidden layer, we lose the information provided in the original input. However, we can use approaches that explain the prediction of any black-box model. A well-known approach is the local interpretable model-agnostic (LIME), see [53], which fits a linear model to the original input features that approximates the prediction of the nonlinear model at each point. Note that the LIME is one of the only interpretation methods that can be used with tabular, text and image data.
Figure 7 shows the prediction for a positive and negative test example by a logistic regression (left) and a neural network model (right). Note that both models predict that no claims will be made but the neural network model assigns a lower probability, which is reflected in the better AUC scores we obtain by neural network models. The features are ordered in decreasing order of importance. The colors show that if a larger feature value supports the class assignment, then we see that older cars and young drivers are more likely to make insurance claims. Note that we observed the very same patterns across different test examples. However, neural networks assigned much higher importance to the variable “area”. Most likely, there are different driving habits in different areas but these only become evident in combination with other features.
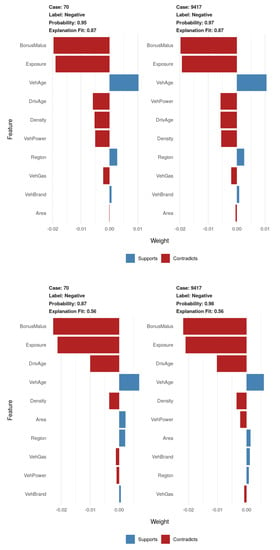
Figure 7.
Feature importance for predicting a positive and negative example for logistic regression (top) and neural networks (bottom).
4. Concluding Remarks
With the advent of “big data” over the last decade, the steady expansion in methodological innovation has focused on the use of actuarial learning methods for boosting classical actuarial models. In this study, we developed a methodology for enhancing the predictive performance of the classical logistic regression model based on NNs. The proposed approach enables us to model nonlinear relationships that were not captured by the simpler logistic regression model. In particular, at a high level, one can think of our approach as comprising two stages: (i) learning new, more complex, features from the original input data which are the explanatory variables related to a certain classification problem; and (ii) fitting a logistic regression model which is implemented by an NN with a single hidden layer and fitting deep NN-based models with multiple hidden layers. Note that these two stages are not necessarily separate from each other but rather intertwined. In particular, the new, more complex features were learned by an NN-based model with several hidden layers, and the output layer of the NN used a sigmoid activation function, just like in logistic regression. Furthermore, both the deviance and the cross-entropy loss functions were used with the proposed models. Additionally, the adopted modeling framework was complemented by skip connections, following the setup of [5,6], regularization procedures, embedding layers and transfer learning. For demonstration purposes, the logistic regression, one-layer perceptron NN model extensions of the logistic regression and the alternative neural network-based models with multiple hidden layers which we constructed were fitted to French MTPL insurance data for which the integer-valued claims counts were replaced by a binary indicator variable which indicates whether at least one claim was made for a given policy. Finally, the LIME model agnostic interpretation method was utilized for investigating feature importance for predicting the occurrence of insurance claims.
In a forthcoming paper, we will consider the neural network embedding of the multinomial logistic regression model for carrying out multiclass classification tasks. Finally, an interesting possible line of further research would be to consider boosting the logistic and/or multinomial logistic regression models using convolutional neural networks and/or recurrent neural networks. The former type of NNs can be used for addressing image classification problems or for modeling time series of constant length. The latter type of NNs can be employed for modeling sequential time series data, such as telematics trips or claim payments.
Author Contributions
Conceptualization, G.T. and K.K.; methodology, G.T. and K.K.; software, G.T. and K.K.; validation, G.T. and K.K.; formal analysis, G.T. and K.K.; writing—original draft preparation, G.T. and K.K.; writing—review and editing, G.T. and K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset which we used in this study is included in the R package CASdatasets.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parodi, P. Pricing in General Insurance; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Wüthrich, M.V.; Buser, C.; Data Analytics for Non-Life Insurance Pricing. Swiss Finance Institute Research Paper 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2870308 (accessed on 30 January 2023).
- Richman, R. AI in actuarial science—A review of recent advances—Part 1. Ann. Actuar. Sci. 2020, 15, 207–229. [Google Scholar] [CrossRef]
- Richman, R. AI in actuarial science—A review of recent advances—Part 2. Ann. Actuar. Sci. 2020, 15, 230–258. [Google Scholar] [CrossRef]
- Wüthrich, M.V.; Merz, M. Yes, we CANN! ASTIN Bull. J. IAA 2019, 49, 1–3. [Google Scholar] [CrossRef]
- Schelldorfer, J.; Wüthrich, M.V. Nesting Classical Actuarial Models into Neural Networks. 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3320525 (accessed on 30 January 2023).
- Quan, Z.; Valdez, E.A. Predictive analytics of insurance claims using multivariate decision trees. Depend. Model. 2018, 6, 377–407. [Google Scholar] [CrossRef]
- Gabrielli, A.; V Wüthrich, M. An individual claims history simulation machine. Risks 2018, 6, 29. [Google Scholar] [CrossRef]
- Yang, Y.; Qian, W.; Zou, H. Insurance premium prediction via gradient tree-boosted Tweedie compound Poisson models. J. Bus. Econ. Stat. 2018, 36, 456–470. [Google Scholar] [CrossRef]
- Lee, S.C.; Lin, S. Delta boosting machine with application to general insurance. N. Am. Actuar. J. 2018, 22, 405–425. [Google Scholar] [CrossRef]
- Wüthrich, M.V. Neural networks applied to chain–ladder reserving. Eur. Actuar. J. 2018, 8, 407–436. [Google Scholar] [CrossRef]
- Wüthrich, M.V. Machine learning in individual claims reserving. Scand. Actuar. J. 2018, 2018, 465–480. [Google Scholar] [CrossRef]
- Richman, R.; von Rummell, N.; Wüthrich, M.V. Believing the Bot-Model Risk in the Era of Deep Learning. 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3444833 (accessed on 30 January 2023).
- Albrecher, H.; Bommier, A.; Filipović, D.; Koch-Medina, P.; Loisel, S.; Schmeiser, H. Insurance: Models, digitalization, and data science. Eur. Actuar. J. 2019, 9, 349–360. [Google Scholar] [CrossRef]
- Trufin, J.; Denuit, M.; Hainaut, D. Effective Statistical Learning Methods for Actuaries—Tree-Based Methods; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Gabrielli, A. A neural network boosted double overdispersed Poisson claims reserving model. ASTIN Bull. J. IAA 2020, 50, 25–60. [Google Scholar] [CrossRef]
- Lopez, O.; Milhaud, X.; Thérond, P.E. A tree-based algorithm adapted to microlevel reserving and long development claims. ASTIN Bull. J. IAA 2019, 49, 741–762. [Google Scholar] [CrossRef]
- De Felice, M.; Moriconi, F. Claim watching and individual claims reserving using classification and regression trees. Risks 2019, 7, 102. [Google Scholar] [CrossRef]
- Baudry, M.; Robert, C.Y. A machine learning approach for individual claims reserving in insurance. Appl. Stoch. Model. Bus. Ind. 2019, 35, 1127–1155. [Google Scholar] [CrossRef]
- Duval, F.; Pigeon, M. Individual loss reserving using a gradient boosting-based approach. Risks 2019, 7, 79. [Google Scholar]
- Gao, G.; Wüthrich, M.V. Convolutional neural network classification of telematics car driving data. Risks 2019, 7, 6. [Google Scholar] [CrossRef]
- Grize, Y.L.; Fischer, W.; Lützelschwab, C. Machine learning applications in nonlife insurance. Appl. Stoch. Model. Bus. Ind. 2020, 36, 523–537. [Google Scholar] [CrossRef]
- Noll, A.; Salzmann, R.; Wüthrich, M.V. Case Study: French Motor Third-Party Liability Claims. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3164764 (accessed on 30 January 2023).
- Zhou, H.; Qian, W.; Yang, Y. Tweedie gradient boosting for extremely unbalanced zero-inflated data. Commun. Stat.-Simul. Comput. 2020, 51, 5507–5529. [Google Scholar] [CrossRef]
- Subudhi, S.; Panigrahi, S. Use of optimized Fuzzy C-Means clustering and supervised classifiers for automobile insurance fraud detection. J. King Saud-Univ.-Comput. Inf. Sci. 2020, 32, 568–575. [Google Scholar] [CrossRef]
- Antonio, K.; Henckaerts, R.; Côté, M.P. Boosting insights in insurance tariff plans with tree-based machine learning methods. N. Am. Actuar. J. 2020, 25, 255–285. [Google Scholar]
- Abdelhadi, S.; Elbahnasy, K.; Abdelsalam, M. A proposed model to predict auto insurance claims using machine learning techniques. J. Theor. Appl. Inf. Technol. 2020, 98, 3428–3437. [Google Scholar]
- Śmietanka, M.; Koshiyama, A.; Treleaven, P. Algorithms in future insurance markets. Int. J. Data Sci. Big Data Anal. 2021, 1, 1–19. [Google Scholar] [CrossRef]
- Hanafy, M.; Ming, R. Machine learning approaches for auto insurance big data. Risks 2021, 9, 42. [Google Scholar] [CrossRef]
- Gao, G.; Wang, H.; Wüthrich, M.V. Boosting Poisson regression models with telematics car driving data. Mach. Learn. 2021, 111, 243–272. [Google Scholar] [CrossRef]
- Delong, Ł.; Lindholm, M.; Wüthrich, M.V. Collective reserving using individual claims data. Scand. Actuar. J. 2021, 2022, 1–28. [Google Scholar]
- Lopez, O.; Milhaud, X. Individual reserving and nonparametric estimation of claim amounts subject to large reporting delays. Scand. Actuar. J. 2021, 2021, 34–53. [Google Scholar] [CrossRef]
- Gabrielli, A. An individual claims reserving model for reported claims. Eur. Actuar. J. 2021, 11, 541–577. [Google Scholar] [CrossRef]
- Blier-Wong, C.; Baillargeon, J.T.; Cossette, H.; Lamontagne, L.; Marceau, E. Rethinking Representations in P&C Actuarial Science with Deep Neural Networks. arXiv 2021, arXiv:2102.05784. [Google Scholar]
- Blier-Wong, C.; Cossette, H.; Lamontagne, L.; Marceau, E. Machine learning in P&C insurance: A review for pricing and reserving. Risks 2021, 9, 4. [Google Scholar]
- Wüthrich, M.V. The balance property in neural network modelling. Stat. Theory Relat. Fields 2021, 6, 1–9. [Google Scholar] [CrossRef]
- Wüthrich, M.V.; Merz, M. Statistical Foundations of Actuarial Learning and Its Applications; Springer Nature: Berlin, Germany, 2023. [Google Scholar]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Janvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Bengio, Y.; Schwenk, H.; Senécal, J.S.; Morin, F.; Gauvain, J.L. Neural probabilistic language models. In Innovationsin Machine Learning; Springer: Berlin, Germany, 2006; pp. 137–186. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Guo, C.; Berkhahn, F. Entity embeddings of categorical variables. arXiv 2016, arXiv:1604.06737. [Google Scholar]
- Perla, F.; Richman, R.; Scognamiglio, S.; Wüthrich, M.V. Time-series forecasting of mortality rates using deep learning. Scand. Actuar. J. 2021, 2021, 572–598. [Google Scholar] [CrossRef]
- Wüthrich, M.V. From Generalized Linear Models to Neural Networks, and Back. 2019. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3491790 (accessed on 30 January 2023).
- Richman, R.; V Wüthrich, M. Nagging predictors. Risks 2020, 8, 83. [Google Scholar] [CrossRef]
- Wüthrich, M.V. Bias regularization in neural network models for general insurance pricing. Eur. Actuar. J. 2019, 10, 1–24. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 30 January 2023).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Charpentier, A. Computational Actuarial Science with R; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ferrario, A.; Noll, A.; Wüthrich, M.V. Insights from Inside Neural Networks. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3226852 (accessed on 30 January 2023).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).