The performance testing of the NDARTS algorithm and its comparison with other algorithms will be divided into two main parts for experimentation.
First, we will conduct performance experiments of the NDARTS algorithm within the DARTS search space. Subsequently, we will compare the obtained experimental results with those of other algorithms operating within their respective search spaces.
3.1.1. Dataset
1. CIFAR-10 Dataset.
The CIFAR-10 [
35] dataset is one of the most popular public datasets in current neural network architecture search work. CIFAR-10 is a small-scale image classification dataset proposed by Alex in 2009. As shown in
Figure 1, there are 10 categories of data, namely aircraft, automobile, bird, cat, deer, dog, frog, horse, ship, and truck. Each category has 6000 images, each of which is a
sized RGB image. The entire CIFAR-10 dataset consists of 60,000 images, among these images, 50,000 images were classified for training and 10,000 images for testing.
2. CIFAR-100 Dataset.
As shown in
Figure 2, the CIFAR-100 [
35] dataset is similar to the CIFAR-10 dataset, except that it has 100 classes. The 100 categories in CIFAR-100 are divided into 20 major categories. Each image comes with a “fine” label (the class it belongs to) and a “rough” label (the large class it belongs to).
During the experiment, the training set of CIFAR-10 and CIFAR-100 is randomly divided into two groups: one group will be used to update weight parameters while the other will serve as a validation set for updating schema parameters. This division is conducted for each category within the samples of the training set.
3. ImageNET Dataset.
ImageNet [
36] is an image dataset organized according to a WordNet hierarchy, where each node in the hierarchy is described by hundreds or thousands of images. The examples of the ImageNet dataset are shown in
Figure 3. At present, there is an average of over 500 images per node, with a total number of images exceeding 10 million and a total of 1000 types of recognition. Compared to the CIFAR-10 and CIFAR-100 datasets, the ImageNet dataset has a larger number of images, higher resolution, more categories, and more irrelevant noise and changes in the images. Therefore, the recognition difficulty far exceeds that of CIFAR-10 and CIFAR-100.
3.1.3. Search Space
1. DARTS search space.
The DARTS algorithm, serving as a fundamental neural network architecture search approach based on gradient descent, encompasses a substantial quantity of nodes and operation types within the building block (unit). The resulting network structure is achieved by stacking two structural units, thus leading to a high architectural complexity. Consequently, the DARTS search space has the potential to produce network models with superior performance. Currently, the majority of gradient-based methods undergo performance evaluation within the DARTS search space and are subsequently compared with other algorithms.
The unit structure of the DARTS search space shown in
Figure 4,
represents the outputs of units
,
, and
k, respectively. In the
k-th unit, there are four nodes between the outputs of the first two units and the output of the
k-th unit. Each edge represents a candidate operation, with eight types of operations including extended separable convolutions of
and
, deep separable convolutions of
and
, average pooling of
, maximum pooling of
, identity operation, and zero operation. Zero operation indicates that there is no connection between two nodes, while identity operation indicates that the data from the previous node is directly transferred to the next node.
The entire network structure is composed of eight units, which are divided into standard units and down-sampling units. In the down-sampling unit, the first two nodes are connected to other nodes through pooling operations. The network consists of six standard units and two down-sampling units, which are located at one-third and two-thirds of the entire network.
2. NAS-Bench-201 Search space.
In current research, a growing number of NAS algorithms have been proposed. Despite their theoretical groundwork, many aspects of these algorithms display significant differences, including distinct search spaces, training strategies for architecture evaluation, and methods used to split validation sets. These differences lead to considerable challenges when comparing the performance of various NAS algorithms. As a result, researchers devote substantial computational resources to traverse and evaluate the performance of different search spaces and neural network structures, as well as their architectures within the designed network structure search space and producing datasets. Subsequent experiments on the NAS-Bench-201 search space [
34] can obtain evaluation results through tabular queries without the need for retraining.
The structural units used in NAS-Bench-201 are shown in
Figure 5. Each structural unit contains four nodes and five operation types (
convolution,
convolution,
average pooling, identity operation, zero operation), totaling
= 15,625 types of unit structures.
3.1.4. Ablation Experiment
We first conducted ablation experiments on the NAS-Bench-201 search space to investigate the impact of parameters on the performance of NDARTS and determine the optimal experimental parameters. The ablation experiment used CIFAR-10 as the training dataset, and a pre-trained model was used to reduce computational complexity. The effects of different parameters were analyzed through 30 epochs of results.
1. T.
Parameter T is the number of steps for updating the weight parameter during the update interval of the architecture parameter . In theory, the larger the T, the more steps the updates during each time is updating, and the is closer to the optimal value . The better the performance of , the better the performance of the super-network when evaluating the architecture, and the more accurate the evaluation results of the subnetwork architecture, which helps the algorithm achieve a more approximate super-gradient estimation. However, the computational cost of the algorithm also increases with an increase in T. According to the experimental results, achieved a good balance between computational cost and model performance.
The experimental results indicate that as T increases, the performance of the algorithm gradually improves. When , both NDARTS and DARTS only optimize the weight parameter once within the update interval of the architecture parameter , with the only difference being that NDARTS uses , while DARTS uses to update the parameter .
The experimental results are shown in
Figure 6 and
Figure 7; it can be seen that NDARTS at
can search for a better framework with faster convergence speed and higher stability compared to the benchmark algorithm DARTS. When
T increased from 1 to 4, the algorithm achieved better convergence speed and stability.
2. K.
The parameter K represents the number of truncated approximations utilized in the optimization formula. The larger the K, the smaller the error is, which is between the approximate gradient value and the true gradient . Therefore, in theory, as K increases, the performance of the neural network should also increase.
From the experimental results in
Figure 8 and
Figure 9, it can be seen that when
K increases from 0 to 2, the accuracy of the model searched by the algorithm increases from
to
, and the stability of the search increases with an increase in
K. Another conclusion is that
is already large enough, so that when
is used, the algorithm performance cannot be further improved. But when
continues to increase, the stability of the algorithm still shows an increasing trend, and when
, the algorithm has already reached a good stability.
3. and .
The calculation of NDARTS is based on the approximation of using the Neumann series, with the potential condition that the learning rate should be small enough to make .
As shown in
Figure 10, when
and
, the algorithm can maintain a good accuracy and stability. When
, the algorithm performance slightly decreases, and the accuracy decreases from
to
, indicating good stability. When
, the accuracy of the algorithm is
, but the stability of the model begins to decrease. When
, the performance of the algorithm decreases again, with a model accuracy of
, and the stability of the algorithm is significantly reduced.
In NDARTS, the parameter
should take a small value to make the coefficient
. As shown in
Figure 11, when
increases from
to
. The performance of the algorithm decreases from
to
, with relatively small stability changes. But when
increases from
to
and
, the performance and stability of the algorithm are significantly reduced.
In summary, NDARTS has strong sensitivity to parameters and , chooses smaller , and can help maintain the performance and stability of NDARTS. The dependence of NDARTS on parameters T and K is relatively small. Larger T and K can improve the convergence speed and performance of the algorithm, but also increase computational costs. Choosing the appropriate T and K can reduce computational costs while maintaining good performance of the NDARTS.
3.1.5. Performance Experiment
The ablation experiment determined the optimal parameters of NDARTS. Subsequently, we tested the performance of NDARTS in the DARTS search space and NAS-Bench-201 search space under the optimal parameters and compared it with other algorithms at similar model scales. Because of the limited computational resources, we mainly tested gradient-based algorithms, and other results are compared using the results of the original paper, marked with * in Tables. The algorithm tested in this article will provide a reference for the accuracy of the validation set as an additional condition, and the program list will be provided in
Appendix A.
DARTS search space.
Comparing the results of the NDARTS algorithm in the DARTS search space with other NAS algorithms, the results on the CIFAR-10, CIFAR-100, and ImageNet datasets are shown in
Table 1,
Table 2 and
Table 3, respectively.
Overall, compared with other types of methods, such as random search and RL, NDARTS has a significant increase in performance. And methods based on random search, RL, and EA have longer computational time, and NDARTS can achieve better performance in a short period. Although the PNAS [
9] algorithm based on sequential models also requires smaller computational resources, the cost is to reduce the accuracy of the model.
Compared with the baseline algorithm DARTS, which is based on gradient descent, NDARTS improves the performance of the algorithm while reducing a certain computational cost. FairDARTS [
38] relaxes the choice of operations to be collaborative, where the authors let each operation have an equal opportunity to develop its strength, but our algorithm performed better than FairDARTS. PDARTS [
24] searches for neural network architecture progressively, achieving good accuracy at a higher computational cost, while NDARTS achieves better performance at a lower computational cost. PC-DARTS [
25] reduces computational costs by sampling channels, and can quickly obtain models with better performance. Although NDARTS has a slightly slower speed than PC-DARTS, it has better performance. In the DARTS search space, NDARTS achieved optimal performance on all three datasets.
Table 1.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the CIFAR-10 dataset.
Table 1.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the CIFAR-10 dataset.
| Algorithm | Val Error (%) | Test Error (%) | Param (m) | Search Space | Search Method |
|---|
| RandomNAS [39] * | —— | 2.65 | 4.3 | DARTS | Random search |
| AmoebaNet * | —— | 3.34 | 5.1 | NASNet | EA |
| NASNet * | —— | 2.65 | 5.3 | NASNet | RL |
| PNAS * | —— | 3.41 | 5.1 | DARTS | Sequential |
| ENAS * | —— | 2.89 | 4.6 | NASNet | RL |
| GDAS * [40] | —— | 2.93 | 3.4 | DARTS | Gradient |
| SETN * [41] | —— | 2.69 | 4.6 | DARTS | Gradient |
| FairDARTS [38] | 3.82 | 2.54 | 2.83 | DARTS | Gradient |
| PDARTS | 3.99 | 2.50 | 3.4 | DARTS | Gradient |
| PC-DARTS | 3.88 | 2.57 | 3.6 | DARTS | Gradient |
| DARTS | 4.38 | 2.76 | 3.4 | DARTS | Gradient |
| NDARTS | 3.98 | 2.37 | 3.8 | DARTS | Gradient |
The results on the CIFAR-10 dataset are shown in
Table 1. This article ran some algorithms and displayed the accuracy of the test set in
Figure 12 (truncated to 50 epochs due to different algorithm settings). It can be seen that the performance of models searched based on gradient methods is generally better than those searched by algorithms based on random search, RL, and other methods. Among gradient-based methods, NDARTS achieved the best performance on the CIFAR-10 dataset, with a test set error of only
, which is superior to other gradient methods such as FairDARTS, PDARTS, PC-DARTS, and DARTS with
,
,
, and
. And, it can be seen from the iteration curve in
Figure 12 that even if the initial state is worse, NDARTS can still quickly optimize to a better model.
Table 2.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the CIFAR-100 dataset.
Table 2.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the CIFAR-100 dataset.
| Algorithm | Val Error (%) | Test Error (%) | Param (m) | Search Space | Search Method |
|---|
| RandomNAS * | —— | 17.63 | 4.3 | DARTS | Random |
| NASNet-A * | —— | 17.81 | 3.3 | NASNet | RL |
| PNAS * | —— | 17.63 | 3.2 | DARTS | Sequential |
| GDAS * | —— | 18.38 | 3.4 | DARTS | Gradient |
| SETN * | —— | 17.25 | 4.6 | DARTS | Gradient |
| PDARTS | 19.97 | 17.4 | 3.4 | DARTS | Gradient |
| PC-DARTS | 20.25 | 17.11 | 3.6 | DARTS | Gradient |
| DARTS | 21.42 | 17.54 | 3.4 | DARTS | Gradient |
| NDARTS | 16.17 | 16.02 | 3.8 | DARTS | Gradient |
Table 3.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the ImageNet dataset.
Table 3.
Results of NDARTS (based on DARTS search space) and other NAS algorithms on the ImageNet dataset.
| Algorithm | Top1 Test Error (%) | Top5 Test Error (%) | Param (m) | Search Space | Search Method |
|---|
| RandomNAS * | 27.1 | —— | 4.3 | DARTS | Random |
| AmoebaNet-A * | 25.5 | 8.0 | 5.1 | NASNet | EA |
| NASNet-A * | 26.0 | 8.4 | 3.3 | NASNet | RL |
| PNAS * | 25.8 | 8.1 | 3.2 | DARTS | Sequential |
| GDAS * | 26.0 | 8.5 | 3.4 | DARTS | Gradient |
| SETN * | 25.7 | 8.0 | 4.6 | DARTS | Gradient |
| SharpDARTS [42] | 25.1 | 7.8 | 4.9 | DARTS | Gradient |
| PDARTS * | 24.4 | 7.4 | 3.4 | DARTS | Gradient |
| PC-DARTS * | 25.1 | 7.8 | 3.6 | DARTS | Gradient |
| DARTS | 26.9 | 8.7 | 3.4 | DARTS | Gradient |
| NDARTS | 24.3 | 7.3 | 3.8 | DARTS | Gradient |
The results on the CIFAR-100 dataset are shown in
Table 2, and the 50 epoch iteration curves of some algorithms are plotted in
Figure 13. The results showed that NDARTS outperforms other gradient-methods with an error of
, while the performance of GDAS on the CIFAR-100 dataset drops to a Test Error of
. In addition, gradient-based methods are generally superior to other algorithms based on random search, RL, and other methods. From the iteration curve, it can be seen that NDARTS, PDARTS, and PC-DARTS have similar search speeds, they have faster search speeds and better performance than DARTS.
The results on ImageNet are shown in
Table 3. When extended to big data, the gradient method can no longer maintain its superiority over other methods in performance, but the NDARTS algorithm still achieved optimal performance with
and
TOP1 and TOP5 Test ERROR, respectively.
Figure 14 and
Figure 15 showed the structures of Normal Cells and Reduction Cells searched by NDARTS in the DARTS search space. As we can see, there are four nodes between the outputs of units
and the output of unit
k. There are some operations on each edge. There are also some pooling operations in the Reduction cell, which can reduce the feature map height and width by a factor of two.
NAS-BENCH-201 search space.
The performance of the NDARTS algorithm and other NAS algorithms was tested in the NAS-Bench-201 search space. The results on CIFAR-10, CIFAR-100, and ImageNet datasets are shown in
Table 4,
Table 5 and
Table 6, respectively. Among them, each algorithm searches for the optimal structural unit on the CIFAR-10 dataset and evaluates its performance on the CIFAR-100 and ImageNet datasets.
Due to the simpler unit search space of NAS-Bench-201 than the DARTS search space, the algorithm performance generally decreases in the NAS-Bench-201 search space. Overall, due to the omission of a large amount of training and evaluation calculations in the NAS-Bench-201 search space, the RL- and EA-based methods have shown good performance. The architecture search algorithm using random search as the baseline still exhibits certain search capabilities in the NAS-Bench-201 search space. The gradient-based method exhibits adaptive differences in the NAS-Bench-201 search space, while the GDAS algorithm, which performs poorly in the DARTS search space, exhibits good performance in the NAS-Bench-201 search space. The model searched by the NDARTS algorithm achieves optimal performance or approaches optimal performance on the three datasets.
The results of the CIFAR-10 dataset are shown in
Table 4, and the results of 50 epochs intercepted using gradient-based methods are plotted in
Figure 16. It can be seen that the methods based on RL and EA have shown good performance in the NAS-Bench-201 search space. DARTS experienced severe performance degradation, while GDAS, which performed poorly in the DARTS search space, maintained good model performance, while NDARTS had a slightly better test set accuracy of
than the
of GDAS. From
Figure 16, it can be seen that DARTS is difficult to search for good architectures in the NAS-Bench-201 search space. The SETN [
30] algorithm with good initial model performance has an unstable search process, while the GDAS and NDARTS algorithms can effectively search for better architectures.
The results of the CIFAR-100 dataset are shown in
Table 5, and the results of intercepting 50 epochs using gradient-based methods are plotted in
Figure 17. It can be seen that on the CIFAR-100 dataset, NDARTS performed with an accuracy of
, almost approaching the optimal performance of
achieved by EA, while GDAS also maintained a good performance of
. However, DARTS and ENAS [
14] methods even have poorer performance compared to methods based on random search. In
Figure 17, when comparing the results of the gradient method, GDAS and NDARTS have similar performance and are superior to DARTS and SETN.
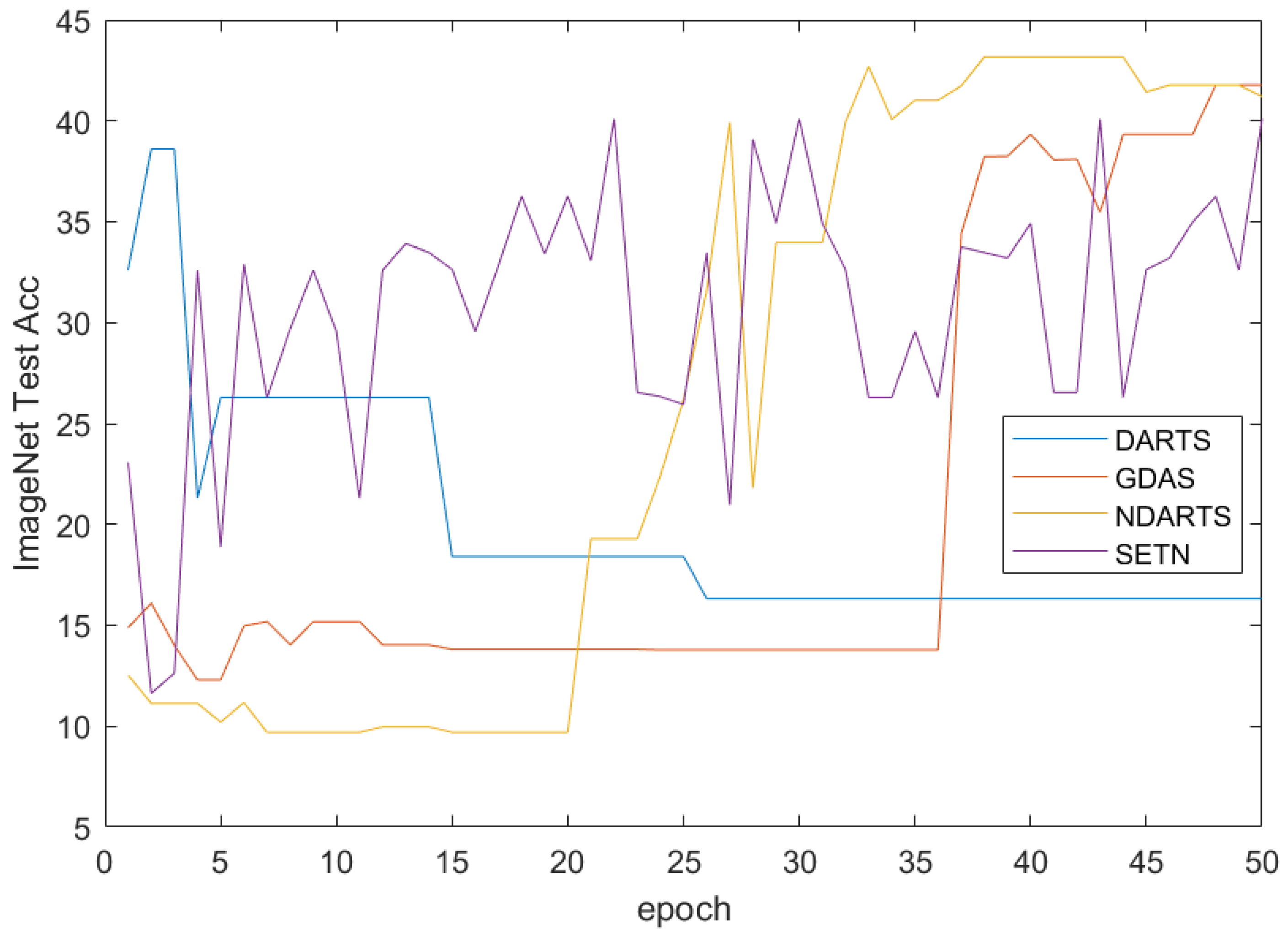
The results of the ImageNet dataset are shown in
Table 6, and the results of intercepting 50 epochs using gradient-based methods are plotted in
Figure 18. It can be seen that on the ImageNet dataset, the evolutionary algorithm-based method achieved the best performance with an accuracy of
, while the reinforcement learning-based method also achieved an accuracy of
. In gradient-based methods, GDAS achieves the best accuracy with
, while NDARTS performs slightly worse with
. The methods based on evolutionary algorithms and reinforcement learning can achieve good performance with the support of a large amount of computing resources. The NAS-Bench-201 search space uses a table query form for performance evaluation, especially on large datasets such as ImageNet, which saves a lot of computation. Therefore, the methods based on EA and RL have shown good performance on the NAS-Bench-201 search space and ImageNet dataset. The gradient-based methods has significant performance differences in the NAS-Bench-201 search space and ImageNet dataset. Specifically, as shown in
Figure 18, GDAS and NDARTS perform better than SETN and DARTS. Although GDAS and NDARTS have poor initial states, they can still quickly optimize to better models, while SETN has a slower search speed and unstable search process, DARTS makes it difficult to search for better models in the NAS-Bench-201 search space.
To compare the performance of NDARTS and GDAS in detail, the results of all epochs on the three datasets were plotted as shown in
Figure 19. It can be seen that NDARTS has a faster search speed than GDAS. When approaching stability, NDARTS and GDAS search for the same model for a long time but ultimately stop at different architectures. At this time, NDARTS has better performance than GDAS on CIFAR-10 and CIFAR-100 datasets, but slightly worse performance on ImageNet datasets.
The model cell structure searched by the NDARTS algorithm is shown in
Figure 20. As we can see, there is just one kind of cell in the NAS-Bench-201 search space. And there are just three intermediate nodes between the input and output. Finally, we can obtain the network by stacking the searched cell.