You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Algorithms
Download PDF
  • Article
  • Open Access

15 November 2023

An Intelligent Injury Rehabilitation Guidance System for Recreational Runners Using Data Mining Algorithms

,
,
,
,
and
1
Department of Physical Education & Sports Sciences, Democritus University of Thrace, 69100 Komotini, Greece
2
Department of Informatics, University of Western Macedonia, 52100 Kastoria, Greece
3
Department of Informatics and Telecommunications, University of Ioannina, 47100 Arta, Greece
*
Authors to whom correspondence should be addressed.
Algorithms2023, 16(11), 523;https://doi.org/10.3390/a16110523
This article belongs to the Special Issue Algorithms in Data Classification
Version Notes
Order Reprints

Abstract

In recent years the number of people who exercise every day has increased dramatically. More precisely, due to COVID period many people have become recreational runners. Recreational running is a regular way to keep active and healthy at any age. Additionally, running is a popular physical exercise that offers numerous health advantages. However, recreational runners report a high incidence of musculoskeletal injuries due to running. The healthcare industry has been compelled to use information technology due to the quick rate of growth and developments in electronic systems, the internet, and telecommunications. Our proposed intelligent system uses data mining algorithms for the rehabilitation guidance of recreational runners with musculoskeletal discomfort. The system classifies recreational runners based on a questionnaire that has been built according to the severity, irritability, nature, stage, and stability model and advise them on the appropriate treatment plan/exercises to follow. Through rigorous testing across various case studies, our method has yielded highly promising results, underscoring its potential to significantly contribute to the well-being and rehabilitation of recreational runners facing musculoskeletal challenges.

1. Introduction

Running constitutes a widely adopted modality of physical activity that confers significant contributions to a health-conscious way of life. Moreover, running has emerged as a prominent global pursuit in the domain of exercise, characterized by substantial engagement rates [1], encompassing a heterogeneous and diversified cohort [2]. Additionally, it offers significant health-related advantages, encompassing musculoskeletal robustness, cardiovascular amelioration, the optimization of bodily composition, and the promotion of psychological equanimity [3].
Unfortunately, many recreational runners suffer injuries [4]. The number of injuries is difficult to identify as there are numerous studies that have provided results on the prevalence and incidence of running-related injuries using a variety of measures of association. In recent years, recreational runners have increasingly used technology to record their performance. However, a study [5] of a group of recreational runners in Ireland reported a high incidence of musculoskeletal injuries due to running. Nevertheless, these injuries were not found to be detectable with the available exercise monitoring technology (e.g., smart watches, smart phones) used.
Clinical reasoning refers to the systematic approach employed by a therapist when engaging with a patient. This approach involves gathering information, formulating and testing hypotheses, and ultimately arriving at the most suitable diagnosis and treatment plan based on the gathered data. It has been characterized as “an inferential process utilized by healthcare practitioners to gather, assess data, and make informed decisions regarding the diagnosis and management of patients’ issues” [6,7]. This process of clinical reasoning assists healthcare professionals in making well-informed judgments to establish an effective strategy for addressing each patient’s injury [8] while also aiding the patient in identifying meaningful goals [9]. Essentially, clinical reasoning is the recording of information given by the patient about his/her injury, after being asked questions by the healthcare professional (the physician, physiotherapist, or rehabilitation trainer) in order to obtain a history at the present moment of the session, in the form of an interview or questionnaire.
The integration of informatics [10] into clinical decision-making systems, while still in its early stages in the United States, is an ever-evolving process that has gained widespread acceptance from both physicians and patients. This integration empowers patients by offering them resources to learn about their health status and actively engage in their healthcare, and it provides easy access to health information. The clinical decision-making system favors reducing the cost of care by seeking alternatives to the evolution of patients’ health status. Health-related informatics can facilitate the transition from a disease prevention model centered on the care system to a patient-centered health-promotion approach.
The article presents an intelligent system [11] that relies on clinical reasoning to collect information from recreational runners and uses data mining algorithms [12] to classify people. Finally, the system provides advice/guidelines according to the category each person belongs to.
The rest of the article is structured as follows: Section 2 outlines prior research related to clinical reasoning and clinical decision-making systems. Section 3 provides details on the dataset and the pre-processing steps taken. In Section 4, we delve into the methodology and showcase the results achieved through the implementation of data mining algorithms, while Section 5 presents the intelligent system. Lastly, Section 6 offers concluding remarks for the article.

3. Dataset and Data Pre-Processing

3.1. Dataset

For our study, we relied on data gathered through an online questionnaire regarding recreational runners who felt musculoskeletal discomfort. The online questionnaire included 14 questions. Each question was included in the dataset with a corresponding feature name.
  • The age of the recreational runner (Age).
  • The height of a recreational runner (Height).
  • The weight of the recreational runner (Weight).
  • The gender of the recreational runner (Gender).
  • The experience of the recreational runner (Experience).
  • Whether the recreational runner feels any musculoskeletal discomfort (e.g., pain, tightness, heaviness) related to running activity (Musculoskeletal Discomfort)
  • If there is any discomfort, specify the area of the body in which it occurs (Symptom Area). The possible choices are:
    (a)
    Lower back
    (b)
    Knee
    (c)
    Calf muscle
    (d)
    Hip
    (e)
    Sole
    (f)
    Thigh
  • The intensity of the pain felt by the discomfort (Pain Intensity). The possible values are on a scale of one to ten:
    (a)
    0–3—No pain or slight pain.
    (b)
    4–6—Moderate pain.
    (c)
    7–8—Intense pain.
    (d)
    9–10—Insufferable pain.
  • The occasion on which the discomfort occurs (Irritability—WHEN). The possible choices are:
    (a)
    When the recreational runner starts running.
    (b)
    When the recreational runner stops running.
    (c)
    During running.
  • The duration of the discomfort (Irritability—DURATION). The possible choices are:
    (a)
    The discomfort does not stop until the next training session.
    (b)
    The discomfort lasts for one or two hours after the running session but stops until the next session.
    (c)
    The discomfort lasts while running but stops later on.
  • The intensity of the discomfort (Irritability—INTENSITY). The possible choices are:
    (a)
    Increases by three degrees (according to the Pain Intensity Scale).
    (b)
    Increases one or two degrees.
    (c)
    Remains constant.
  • The effect the discomfort has on running (Severity—RUNNING). The possible choices are:
    (a)
    No significant effect.
    (b)
    Affects the running distance or the rhythm of running.
    (c)
    Halts the running session.
  • The effect the discomfort has on everyday life (Severity—LIFE). It is a yes-or-no question.
  • The effect the discomfort has on everyday functional activities (Severity—MOBILITY). It is a yes-or-no question.
Based on the answers given by the recreational runners, a dataset was built through which we sought to classify the category that a recreational runner belongs to. There are six categories, each with its own set of advice/guidelines. These advice/guidelines are:
  • Reduce the training load by 30%; complete musculoskeletal functional release exercises, stretching, strengthening exercises, and functional exercises.
  • Reduce the training load by 50%; complete musculoskeletal functional release exercises, stretching, strengthening exercises, and functional exercises.
  • Cessation of training for one week followed by musculoskeletal functional release exercises, stretching, and strengthening exercises.
  • Cessation of training for two weeks followed by musculoskeletal functional release exercises and stretching exercises.
  • Cessation of training for three weeks followed by musculoskeletal functional release exercises and stretching exercises.
  • Seek medical advice and cease training for at least three weeks, followed by musculoskeletal functional release exercises and stretching exercises.
The last seven questions on the questionnaire can be amalgamated into three main factors named:
  • PAIN—Involves question (8), and its values are based on the scale value of the Pain Intensity.
  • IRRITABILITY—Involves questions (9), (10), and (11), and its values are low, moderate, and high.
  • SEVERITY—Involves questions (12), (13), and (14), and its values are low, moderate, and high.

3.2. Data Pre-Processing

Before we employ classification algorithms on the data, some data pre-processing steps are required.
The initial step involved renaming the dataset’s features, which were originally long and incomprehensible. This was done to ensure more comprehensive and descriptive references. Subsequently, we conducted a thorough assessment and determined that the feature indicating musculoskeletal discomfort among recreational runners was redundant as each recreational runner invariably reported such discomfort. In the event that this condition was not met, specifically, if there existed at least one instance of a recreational runner who did not experience musculoskeletal discomfort, it would render the responses they provided to the subsequent questions invalid. This is because, according to the premise, all runners are expected to report some degree of musculoskeletal discomfort. Thus, it was excluded from the dataset. Furthermore, we identified three samples with missing values, which were subsequently removed. Among all the features in the dataset, only the “Experience” feature contained missing values. While our classification process primarily relied on a subset of features, it is worth noting that our analysis encompassed several tests involving various features within the dataset. Consequently, it became imperative to exclude those samples that contained incomplete values to ensure the integrity of our findings. Last but not least, many of the features represented categorical string values, making them unsuitable for classification, as the classification algorithms are only compatible with categorical numerical feature values. To address this issue, we mapped every categorical string value of a feature to a numerical value. Finally, by counting the number of samples in each category, their inherent imbalance was revealed.
Table 1 demonstrates that not only is the data imbalanced but the ratio of the total number of samples to the number of categories is relatively low, implying that there are very few samples per category, thereby making the classification process a challenge.
Table 1. Samples in each category.

4. Methodology

For classifying the condition of each recreational runner, we employed the following algorithms:
  • Decision Trees—A decision tree [27] is a common data mining algorithm that breaks down difficult decisions into a succession of simpler options in order to show a decision-making process visually. The “root” represents the initial choice or query, and the “branches” indicate other potential outcomes or directions. The decision tree resembles an inverted tree structure. A decision or characteristic is assessed at each branch, which leads to other branches until a conclusion or result is obtained in the end.
  • Random Forests—Multiple decision trees are combined using the strong ensemble learning method known as Random Forests [27] in data mining to provide a more reliable and precise predictive model. It works very well for classification [28].
  • Naive Bayes Classifier—A popular probabilistic data mining algorithm for classification tasks [29,30] is the Naive Bayes algorithm [27]. It is based on the Bayes theorem, which determines the likelihood that an event will occur given the likelihood that related events will also occur.
For each algorithm, we conducted numerous experiments with varying sets of features in each run. However, through the utilization of the decision tree classifier, we arrived at the conclusion that the pivotal features for discerning the condition of a recreational runner were those encompassed within the compilation of the main factor list. Thus, the categorical features considered for classification are the:
  • Pain Intensity
  • Irritability—WHEN
  • Irritability—DURATION
  • Irritability—INTENSITY
  • Severity—RUNNING
  • Severity—LIFE
  • Severity—MOBILITY
Before applying any of the aforementioned classifiers on the above features of the dataset, we used the Synthetic Minority Over-sampling TEchnique (SMOTE) [31] to overcome the challenge posed by the category imbalance. As an outcome of implementing this technique, it follows that categories 1, 4, and 6 will incorporate new synthetic samples.
The limited support is inherent to our problem due to imbalanced class distributions. We have chosen evaluation metrics like precision, recall, and F1-score to address this. Additionally, we applied data augmentation techniques, such as SMOTE, solely to the training data. Furthermore, we conducted multiple experiments to strengthen our method’s validity, a common practice for small datasets. For reference, please see [32] on fetal heart rate recordings, where similar practices were employed with just 44 cases.

4.1. SMOTE

As the authors of [31] clearly explain, SMOTE is an over-sampling technique in which the minority class (a class that has fewer instances or samples compared to the majority class) is over-sampled by generating synthetic samples from the already existing ones.
Through the process of oversampling the minority class, synthetic samples are generated by examining each minority class sample within the dataset. These synthetic samples are inserted along the line segments that connect either some or all of the k nearest neighbors belonging to the minority class. The selection of random neighbors from the k nearest neighbors is based on the specific level of oversampling required (the current implementation of SMOTE uses k = 5 nearest neighbors as a default value of k). The process of generating synthetic data samples (Figure 1) begins by selecting a random sample from the minority class and its nearest neighbor. Subsequently, the distance between these two samples is computed and scaled by a random number (gap), which falls within the range of 0 to 1. This calculation is used to create a new sample positioned along the line segment at the determined distance. The synthetic data generated by SMOTE can cause a classifier like the decision tree, or the Naive Bayes, to generalize better.
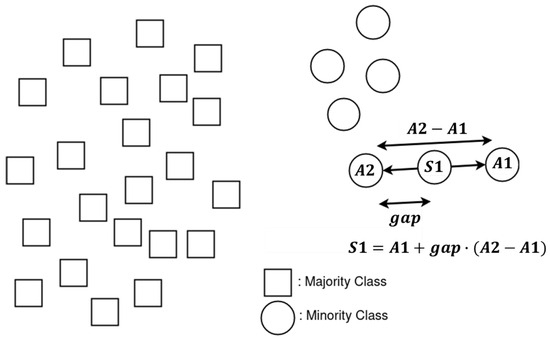
Figure 1. A SMOTE example in a 2D feature space. A1 is the randomly selected sample from the minority class, and A2 is its nearest neighbor. S1 is the generated synthetic sample along the line segment of their calculated distance.
Although SMOTE is restricted to only continuous features, the Synthetic Minority Over-sampling TEchnique-Nominal Continuous (SMOTE-NC) [31] and the Synthetic Minority Over-sampling TEchnique-Nominal (SMOTE-N) [31] are extensions of the original, allowing for the use of a combination of categorical and continuous features.
SMOTE-NC starts by calculating the median standard deviation of all continuous features within the minority class. This calculation serves to account for any disparities in the categorical features between two samples. Then, the Euclidean distance is calculated between a minority class sample and its k nearest neighbors. Finally, new synthetic minority class samples are created using the same methodology as described earlier for SMOTE. The new synthetic samples are populated by new values for the continuous features of the minority class, and as for the categorical features, a value is given based on the values of the majority’s k nearest neighbors.
SMOTE-N discovers the nearest neighbors using the modified value difference metric (MVDM) [33] to measure the dissimilarity or similarity between categorical feature values of the minority class samples, taking into account the class distribution. MVDM addresses some limitations of the original metric (VDM) by incorporating additional features to handle missing values and small sample sizes more effectively. VDM (the traditional version of MVDM) calculates a distance value that represents how different two categorical values are based on their distribution within different classes. Thus, for each class in the dataset, VDM calculates the probability distribution of each categorical value within that class. This involves counting the occurrences of each categorical value within the class and dividing by the total number of instances in that class. Subsequently, for each unique categorical value, VDM calculates the probabilities of occurrence across all classes by calculating the average probability of that value occurring in each class, weighted by the proportion of instances in each class. Finally, for a pair of categorical values from different samples, VDM is calculated as the sum of the absolute differences between their value probabilities across all classes. This accounts for the dissimilarity of the values’ distributions with respect to the classes.

4.2. Decision Tree Classifier

We tested the classifier using:
  • Data from the original dataset.
  • Data subjected to resampling through the utilization of SMOTE and its extensions, with the aim of equalizing the distribution among categories.
Due to the close similarity between the original data and the synthetic data, coupled with the augmented representation of minority categories, it is anticipated that the performance of the data mining algorithms will exhibit an unusually high level of accuracy should the resampled dataset be utilized as the training set, while the original dataset is designated for the testing set. Consequently, this amalgamation of training and testing data would render it unfeasible to assess the efficiency of the algorithms because the test data should ideally differ significantly from the training data but now shares notable similarities. In order to effectively mitigate this issue, it is imperative that we adhere to the practice of segregating the original dataset into distinct training and testing sets. Subsequently, we should apply SMOTE and its associated extensions exclusively to the training set.
We partitioned the dataset into two distinct subsets: a training set, encompassing 70% of the total data, and a testing set, comprising the remaining 30%. Following this partition, the training set consisted of 68 samples, while the testing set contained 28 samples. Subsequently, we applied SMOTE to the training set. This resampling procedure resulted in a noteworthy alteration of the training data’s dimensions, increasing it to a total of 192 samples.
The execution results of the decision tree classifier for a split of 70% (training set) and 30% (testing set) are shown in Table 2. This is a commonly used split ratio in the machine learning community [12] ensuring that a larger training set (70%) allows the model to learn from a substantial portion of the data, reducing bias. While the smaller testing set (30%) helps estimate the model’s generalization performance with a diverse but independent subset, the ”Support” value indicates the number of samples that exist in each category. We also present the decision tree as it was build in Figure 2.
Table 2. Decision tree classifier results.
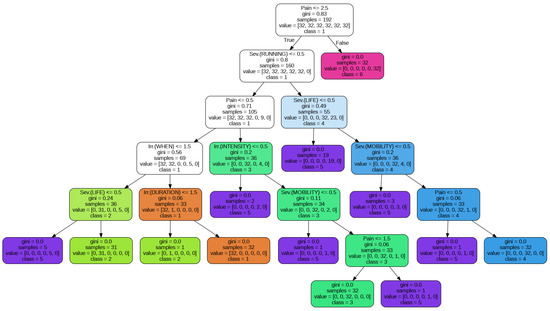
Figure 2. Decision tree classifier for a 30% test set splitting. The gini value [34] at each node evaluates how well a decision tree node separates the data into different categories. Its values range from 0 to 1. A value of 0 indicates a perfect separation, meaning all the samples at one node belong to one category. A value of 1 indicates an even distribution of samples among the different categories.
It is worth underscoring that the partitioning of the dataset into distinct training and testing sets has been accomplished through the application of stratified sampling. This method is predicated on the principle that the distribution of categories within the testing and training sets mirrors the original data’s category distribution. This meticulous approach ensures an equitable representation of all categories, thus preventing any insufficiencies in either set. For elucidation, in our specific case, the composition of category samples, as shown in Table 2, reveals a hierarchy with respect to sample prevalence: category 5, followed by category 2, and subsequently category 3, among others. Consequently, this distribution of sample quantities in the stratified sets maintains parity with that observed in the original dataset, as elucidated in Table 1.
Furthermore, it is imperative to note that the classifier’s performance is profoundly contingent upon the splitting applied to the original dataset. This is because an expansion of the test set results in a diminished quantity of distinct samples within the training set, thereby impinging upon the classifier’s performance, which is predicated on the diversity of the sample pool. This deduction derives from the inherent characteristics of the original dataset, which predominantly consists of unique samples. Consequently, when partitioned, a portion of these unique samples from the training set migrates to the test set. In such circumstances, the application of SMOTE assumes significance, augmenting both the sample count within the dataset and diversifying the dataset itself by introducing synthetic data.
In Table 2, we observe the following performance metrics: precision, recall, F1 score, accuracy, and both weighted and unweighted (macro) mean, which compute the average of precision, recall, and F1 score. Notably, in the case of the weighted sum, this computation incorporates the support, representing the sample count, for each category. The classifier accurately predicts only the samples belonging to categories 1 and 6. Category 1 exhibits uniform categorical values across its samples, facilitating the classifier’s ability to discern the underlying pattern within this category. On the other hand, category 6 samples share a common value for the attribute “Pain Intensity”.
Figure 2 refers to the root node of the decision tree in Figure 2; samples are categorized as category 6 when the “Pain Intensity” attribute value exceeds 2.5. Conversely, category 4 exhibits the lowest F1 score among the categories due to limited diversity among its samples, resulting in an inadequate number of distinct training samples for the classifier. In contrast, the remaining classes benefit from an adequate sample size, resulting in commendable classifier performance, with the potential for further enhancement.

4.3. Random Forests

Prior to deploying the classifier, a random search was conducted within a predefined parameter range to identify optimal hyperparameters. The randomized search will randomly search parameters within a range per hyperparameter. We define the hyperparameters to be used and their ranges in a dictionary of key-value pairs. In our case, we used a hyperparameter to describe the number of estimators (decision trees) and the maximum depth of each estimator. This endeavor was undertaken to enhance the efficiency of the decision tree construction and elevate the classifier’s predictive performance across categories. The execution results of the Random Forests classifier for a splitting of 70% (training set) and 30% (testing set) are shown in Table 3.
Table 3. Random Forest classifier results.
The classifier’s performance remains consistent for categories 1 and 6, as previously discussed in the context of the decision tree classifier. Conversely, we observe a noticeable improvement in the performance of classes 2 and 5. This enhancement is anticipated, given that Random Forests generate multiple decision trees, each utilizing different sets of features. When combined with optimal hyperparameters, this diversity in the ensemble leads to improved performance. However, the challenge persists with category 4 samples because they continue to lack sufficient data for the classifier to discern their inherent pattern.

4.4. Naive Bayes Classifier

The execution results of the Naive Bayes classifier for a splitting of 70% (training set) and 30% (testing set) are shown in Table 4.
Table 4. Naive Bayes classifier results.
The performance of the Naive Bayes classifier remains consistent for classes 1, 6, and 4, showing no significant change compared to the other two classifiers. In contrast, there is a notable and substantial performance improvement for categories 2 and 3, reaching the maximum achievable performance. Additionally, category 5 has also exhibited significant improvement in its classification accuracy.
Because it naturally computes probabilities based on category frequencies, which is essential for the dataset containing categorical features, the Naive Bayes classifier handles categorical data with proficiency, which contributes to its improved performance. Additionally, by using SMOTE to handle the class imbalance in the training set, the possibility of predictions being biased towards the majority class was reduced, a problem that decision trees and Random Forests might still experience. Due to its resistance to overfitting, Naive Bayes may also perform well in rather small datasets, which can be a significant benefit in situations where resources are limited. When relationships among features are not clearly established, its simplicity and reliance on the independence assumption between features can be useful.

5. The Intelligent System

The system follows the 3-tier architecture [35]. The typical structure for 3-tier architecture deployment has the presentation tier deployed to a desktop, laptop, or tablet via a web browser utilizing a web server. The presentation tier has been implemented with the use of web technologies like HTML, CSS, and JavaScript. The underlying application tier (middleware) is hosted on an application server and implements the business logic of the whole application. The application layer has been developed as two components: one responsible for the storage/retrieval of data into/from the database and another for performing the process of categorizing the user based on the answers provided and providing a set of videos that include exercises to repair the damage that has occurred up to that point. Finally, the data layer includes a database. The system architecture is depicted in Figure 3.
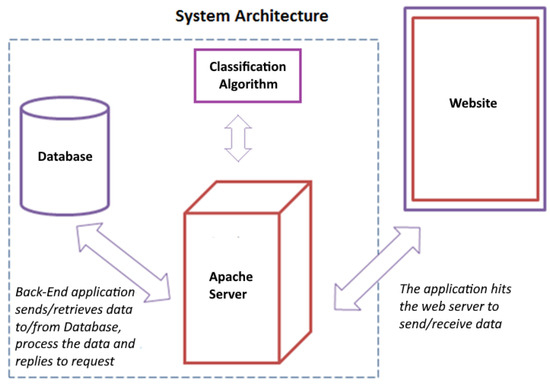
Figure 3. The intelligent system architecture.
First, the user will have to fill in/answer the questions (Figure 4) asked by the system. Then, by pressing the submit button, the server-side application receives the data and provides it to the classification algorithm component, which is executed, and the user is assigned to one of the six categories. Based on the category, the user is taken to a new web page where a set of videos is presented. A group of experienced academics/researchers in the prevention (exercise specialist) and rehabilitation (physical therapist and medical doctor) of sports injuries coming from different scientific fields (exercise science, physical therapy, and medical science) suggest the exercises presented in the videos. Thus, the system can identify the user’s category and suggest exercises and guidelines based on it, see Figure 5.
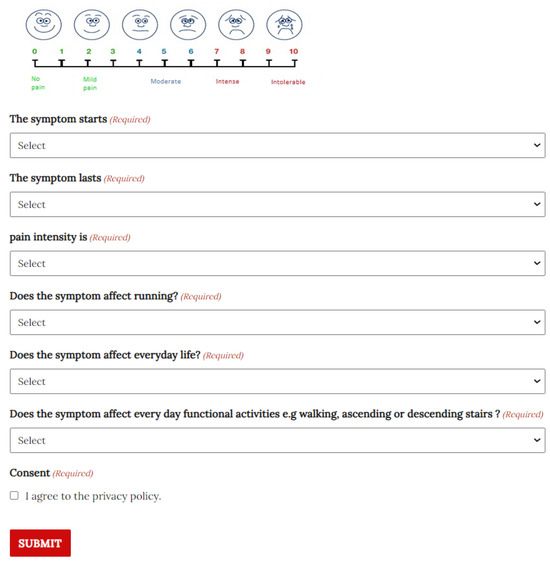
Figure 4. The questionnaire web page.
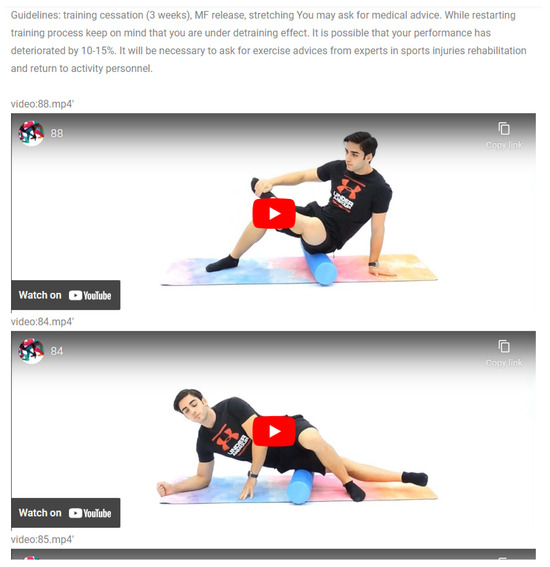
Figure 5. The results web page.

6. Conclusions

In conclusion, our study presents an intelligent rehabilitation guidance system for recreational runners who experience musculoskeletal discomfort. The system can offer specific recovery and rehabilitation exercises tailored to the type of the musculoskeletal discomfort. It can also help recreational runners adjust their training and rest appropriately, preventing more serious injuries. By helping runners recover more effectively, the system can potentially reduce healthcare costs associated with sports-related injuries. This could be beneficial for both individuals and healthcare systems. Moreover, the data collected by the system can also be used to better understand the factors contributing to running-related injuries and how they can be mitigated.
The system employs a diverse set of data mining algorithms, including decision trees, Random Forests, and the Naive Bayes classifier, complemented by SMOTE and its associated extensions to address the inherent challenges in the data. We acknowledge the category imbalance inherited in the data, the small dataset size, and the limited diversity in the samples, which are common issues in real-world injury prediction scenarios.
Despite these challenges, it is noteworthy that the decision tree, Random Forests, and Naive Bayes classifiers have demonstrated their considerable potential in effectively classifying the musculoskeletal condition of a recreational runner. This underscores the adaptability and versatility of these classifiers in addressing real-world classification tasks within the realm of recreational running, where data quality and quantity may be constrained. While there is room for further research to improve the model’s performance, our work highlights the feasibility of leveraging data mining techniques to enhance injury rehabilitation strategies for recreational runners and emphasizes the importance of selecting appropriate algorithms that can address the unique characteristics of the data.

Author Contributions

Conceptualization, N.D., T.T. and P.K.; methodology, N.D., P.K., P.M. and A.B.; software, G.M. and T.T.; validation, T.T. and G.M.; formal analysis, G.M., T.T., P.M. and A.B.; investigation, T.T. and N.D.; resources, T.T.; data curation, G.M. and T.T.; writing—original draft preparation, G.M., T.T., N.D. and P.K.; writing—review and editing, N.D., P.K., P.M. and A.B.; visualization, G.M.; and supervision, N.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The resources used in this study can be found here: https://drive.google.com/drive/folders/1JNRiEHYZOV4pNhtmoui27fhCrRKrVkR5?usp=sharing, accessed on 13 September 2023.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Scheerder, J.; Breedveld, K. Running across Europe: The Rise and Size of One of the Largest Sport Markets; Palgrave Macmillan: Hampshire, UK, 2015. [Google Scholar]
  2. Cook, S.; Shaw, J.; Simpson, P. Jography: Exploring meanings, experiences and spatialities of recreational road-running. Mobilities 2016, 11, 744–769. [Google Scholar] [CrossRef]
  3. Hespanhol, L.C., Jr.; Pillay, J.D.; van Mechelen, W.; Verhagen, E. Meta-analyses of the effects of habitual running on indices of health in physically inactive adults. Sports Med. 2015, 45, 1455–1468. [Google Scholar]
  4. Videbæk, S.; Bueno, A.M.; Nielsen, R.O.; Rasmussen, S. Incidence of running-related injuries per 1000 h of running in different types of runners: A systematic review and meta-analysis. Sports Med. 2015, 45, 1017–1026. [Google Scholar]
  5. Mayne, R.S.; Bleakley, C.M.; Matthews, M. Use of monitoring technology and injury incidence among recreational runners: A cross-sectional study. BMC Sports Sci. Med. Rehabil. 2021, 13, 116. [Google Scholar]
  6. Higgs, J.; Jones, M.A. Clinical decision making and multiple problem spaces. Clin. Reason. Health Prof. 2008, 3, 3–17. [Google Scholar]
  7. Petersen, E.J.; Thurmond, S.M.; Jensen, G.M. Severity, irritability, nature, stage, and stability (SINSS): A clinical perspective. J. Man. Manip. Ther. 2021, 29, 297–309. [Google Scholar]
  8. Gummesson, C.; Sundén, A.; Fex, A. Clinical reasoning as a conceptual framework for interprofessional learning: A literature review and a case study. Phys. Ther. Rev. 2018, 23, 29–34. [Google Scholar] [CrossRef]
  9. Atkinson, H.L.; Nixon-Cave, K. A tool for clinical reasoning and reflection using the international classification of functioning, disability and health (ICF) framework and patient management model. Phys. Ther. 2011, 91, 416–430. [Google Scholar] [CrossRef]
  10. Nimkar, S. Promoting individual health using information technology: Trends in the US health system. Health Educ. J. 2016, 75, 744–752. [Google Scholar]
  11. Safe Run. Available online: https://saferun.eu/ (accessed on 13 September 2023).
  12. Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann Publishers: Burlington, MA, USA, 2016. [Google Scholar]
  13. Smart, K.; Doody, C. The clinical reasoning of pain by experienced musculoskeletal physiotherapists. Man. Ther. 2007, 12, 40–49. [Google Scholar]
  14. Baker, S.E.; Painter, E.E.; Morgan, B.C.; Kaus, A.L.; Petersen, E.J.; Allen, C.S.; Deyle, G.D.; Jensen, G.M. Systematic clinical reasoning in physical therapy (SCRIPT): Tool for the purposeful practice of clinical reasoning in orthopedic manual physical therapy. Phys. Ther. 2017, 97, 61–70. [Google Scholar] [CrossRef]
  15. Barakatt, E.T.; Romano, P.S.; Riddle, D.L.; Beckett, L.A. The reliability of Maitland’s irritability judgments in patients with low back pain. J. Man. Manip. Ther. 2009, 17, 135–140. [Google Scholar] [CrossRef]
  16. Kareha, S.M.; McClure, P.W.; Fernandez-Fernandez, A. Reliability and concurrent validity of shoulder tissue irritability classification. Phys. Ther. 2021, 101, pzab022. [Google Scholar] [CrossRef]
  17. Spanjersberg, W.R.; Bergs, E.A.; Mushkudiani, N.; Klimek, M.; Schipper, I.B. Protocol compliance and time management in blunt trauma resuscitation. Emerg. Med. J. 2009, 26, 23–27. [Google Scholar] [CrossRef]
  18. Baur, D.; Gehlen, T.; Scherer, J.; Back, D.A.; Tsitsilonis, S.; Kabir, K.; Osterhoff, G. Decision support by machine learning systems for acute management of severely injured patients: A systematic review. Front. Surg. 2022, 9, 924810. [Google Scholar] [CrossRef] [PubMed]
  19. Wilkinson, S.G.; Chevan, J.; Vreeman, D. Establishing the centrality of health informatics in physical therapist education: If not now, when? J. Phys. Ther. Educ. 2010, 24, 10–15. [Google Scholar] [CrossRef]
  20. Daley, K.N.; Krushel, D.; Chevan, J. The physical therapist informatician as an enabler of capacity in a data-driven environment: An administrative case report. Physiother. Theory Pract. 2020, 36, 1153–1163. [Google Scholar] [CrossRef]
  21. Lopes, L.C.; de Fátima F Barbosa, S. Clinical decision support system for evaluation of patients with musculoskeletal disorders. In MEDINFO 2019: Health and Wellbeing e-Networks for All; IOS Press: Amsterdam, The Netherlands, 2019; pp. 1633–1634. [Google Scholar]
  22. Qin, Z.; Armijo-Olivo, S.; Woodhouse, L.J.; Gross, D.P. An investigation of the validity of the Work Assessment Triage Tool clinical decision support tool for selecting optimal rehabilitation interventions for workers with musculoskeletal injuries. Clin. Rehabil. 2016, 30, 277–287. [Google Scholar] [CrossRef] [PubMed]
  23. Farzandipour, M.; Nabovati, E.; Saeedi, S.; Fakharian, E. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review. Comput. Methods Programs Biomed. 2018, 163, 101–109. [Google Scholar] [CrossRef] [PubMed]
  24. Halson, S.L. Monitoring Training Load to Understand Fatigue in Athletes. Sports Med. 2014, 44, 139–147. [Google Scholar] [CrossRef]
  25. Peterson, K.D.; Evans, L.C. Decision Support System for Mitigating Athletic Injuries. Int. J. Comput. Sci. Sport 2019, 18, 45–63. [Google Scholar] [CrossRef]
  26. Ghahramani, Z. Learning dynamic Bayesian networks. In Adaptive Processing of Sequences and Data Structures; Giles, C., Gori, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 168–197. [Google Scholar]
  27. Tan, P.N.; Steinbach, M.; Karpatne, A.; Kumar, V. Introduction to Data Mining, 2nd ed.; Pearson: London, UK, 2018. [Google Scholar]
  28. Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
  29. Karvelis, P.; Kolios, S.; Georgoulas, G.; Stylios, C. Ensemble learning for forecasting main meteorological parameters. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 3711–3714. [Google Scholar] [CrossRef]
  30. Georgoulas, G.; Kolios, S.; Karvelis, P.; Stylios, C. Examining nominal and ordinal classifiers for forecasting wind speed. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 504–509. [Google Scholar] [CrossRef]
  31. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
  32. Georgoulas, G.; Karvelis, P.; Spilka, J.; Chudáček, V.; Stylios, C.D.; Lhotská, L. Investigating pH based evaluation of fetal heart rate (FHR) recordings. Health Technol. 2017, 7, 241–254. [Google Scholar] [CrossRef] [PubMed]
  33. Cost, S.; Salzberg, S. A weighted nearest neighbor algorithm for learning with symbolic features. Mach. Learn. 1993, 10, 57–78. [Google Scholar] [CrossRef]
  34. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
  35. Bass, L.; Clements, P.; Kazman, R. Software Architecture in Practice, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Relational Fisher Analysis: Dimensionality Reduction in Relational Data with Global Convergence
Previous
Utilizing Mixture Regression Models for Clustering Time-Series Energy Consumption of a Plastic Injection Molding Process
Next