Abstract
Energy demand and consumption have, in recent times, witnessed a rapid proliferation influenced by technological developments, increased population and economic growth. This has fuelled research trends in the domain of energy management employing tri-generation systems such as combined cooling, heating and power (CCHP) systems. Furthermore, the incorporation of renewable energy, especially solar energy, to complement the thermal input of fossil fuels has facilitated the effectiveness and sustainability of CCHP systems. This study proposes a new approach to improve the overall efficiency of CCHP systems and to compute optimal design parameters in order to assist decision makers to identify the best geometrical configuration. A multi-objective optimization formulation of a solar-assisted CCHP system was adopted to maximize the net power and exergy efficiency and to minimize the CO2 emission using the greywolf optimization technique. In addition, the effects of the decision variables on the objective functions were analysed. The proposed optimization approach yielded 100 set of Pareto optimal solutions which would serve as options for the decision maker when making a selection to choose from when seeking to improve the performance of a solar-assisted CCHP system. It also yielded higher exergy efficiency and lower CO2 emission values when compared with a similar study. The results obtained indicate that a system with high net power output does not necessarily translate to a highly efficient system. Additionally, minimal CO2 emissions were recorded for a system with low compression ratio, low combustion chamber inlet temperature and high inlet turbine temperature. This study demonstrates that the proposed approach is potentially suitable for the optimization of a solar-assisted CCHP system.
1. Introduction
Energy is pivotal to the economic growth of any country and its increased demand/production in recent times, triggered by increasing population, has led to the extreme usage of fossil fuels such as petroleum, natural gas, coal, etc. The utilization of fossil fuels as prime sources has drawbacks, especially in the area of global warming caused by greenhouse gas emission. This is in addition to the cost-intensiveness and depletion of its reserves [1,2]. Environmental deterioration caused by these greenhouse gas emissions from power plants is seen as a significant threat to societies that are concerned by the consequences of global warming. According to an IEA 2022 report [3], CO2 emission increased by 0.9% in 2022, peaking to an all-time high value of about 36.8GT. Spahni et al. [4] have reported that electricity generation accounts for about 32% of CO2 emissions followed by heating and cooling sources, which account for 33%, and transportation media, which account for 35%. This demonstrates that about 65% of CO2 emission are due to power generation, heating and cooling, which are necessities for human survival. It justifies the need for efficient systems to manage and improve energy conservation as well as renewable energy sources that could complement or replace fossil fuels.
An energy management system that has gained research interest due to its fuel efficiency and reduced greenhouse emission rate is the combined cooling, heating and power (CCHP) system. The CCHP system involves the integration of various thermodynamic systems to produce two or more forms of energy in such a way that a ‘top system’ can be employed to drive a ‘bottom system’. A ‘top system’ in this context refers to systems such as gas turbines that require a high degree of energy for their operation while a ‘bottom system’ such as the Rankine cycle, Kalina cycle, absorption chiller, etc., require a lower amount of energy [5]. Wu and Wang conducted an analysis to compare a usual energy system with the CCHP system [6]. Their study established that efficiency improved by about 33%, owing to the cascade energy application of the CCHP system.
The inclusion of renewable energy, either as an adjunct to or as a replacement, for fossil fuels is another energy management idea that is under consideration. According to the 2023 BP Energy Outlook [7], wind and solar power would account for about two-thirds of the global power generation by 2050 and their rapid adoption would be fuelled by a fall in their costs. The solar energy source is predominately employed in CCHP systems—though, due to its variability and the volatility of its radiation, not necessarily as a standalone energy source—to decrease the amount of fossil fuel expended. In CCHP systems, thermal energy is generated from the sun via solar thermal collectors which are either concentrating or non-concentrating. Several pieces of literature have discussed the CCHP systems integrated with solar energy for multiple applications. The effectiveness of a solar energy-integrated CCHP system over one powered by an internal combustion engine has been confirmed by Yousefi et al. [8], who configured a solar-assisted CCHP system. Similarly, Zhang et al. [9] have proposed a hybrid CCHP system that yielded a 30.4% fuel saving with a 26% solar energy input.
CCHP systems offer a sustainable solution to improve energy conservation by reducing greenhouse emissions, heat loss and operation cost, and by improving the overall energy efficiency while ensuring the presence and reliability of several energy generation options [10]. However, the search for more optimal thermodynamic performance indicators is on-going. The CCHP system’s performance can be enhanced through optimization [11]. Optimization advancements in the 1960 and 1970s saw the advent of a meta-heuristic approach, known as evolutionary algorithms. A predominant example of this approach is the genetic algorithm optimization proposed by Holland [12]. This approach is inspired by Charles Darwin’s principles of mutation, crossover and survival of the fittest. Another fundamental metaheuristic method that came into the limelight in the 1990s was the swarm intelligence algorithm spearheaded by Dorigo et al. [13], while Kennedy and Eberhart [14] proposed the ant colony optimization (ACO) and the particle swarm optimization techniques, respectively. Real engineering problems are typically multi-objective in nature, and this implies that the mathematical formulation involves more than one objective function in general [15]. Multi-objective functions are solved by arbitrarily assigning weights in a weighted-sum problem formulation and were employed by Zeng et al. [16] and Song et al. [17] to effectively improve the objectives of a CCHP system. The weight-based optimization or a priori method, however, has the drawback of requiring multiple runs and the need to always seek counsel from an expert/decision maker [18]. These can also be solved using the posteriori method, which involves retaining the multi-objective formulation and obtaining the Pareto optimal solutions in a single run. However, these are computationally intensive. There are a handful of optimization techniques in the literature, namely the response surface method (RSM) [19], non-dominated sorting genetic algorithm-II (NSGA-II) [20], particle swarm optimization (PSO) [21], Harris hawk optimization (HHO) [22], grasshopper optimization (GOA) [23], ant-lion optimization [24], moth flame optimization (MFO) [25], and greywolf optimization(GWO) [26], etc. This research illustrates how GWO could be used to formulate and solve a problem related to a solar-assisted combined cooling, heating and power system. A breakdown of the optimization algorithms is displayed in Figure 1.
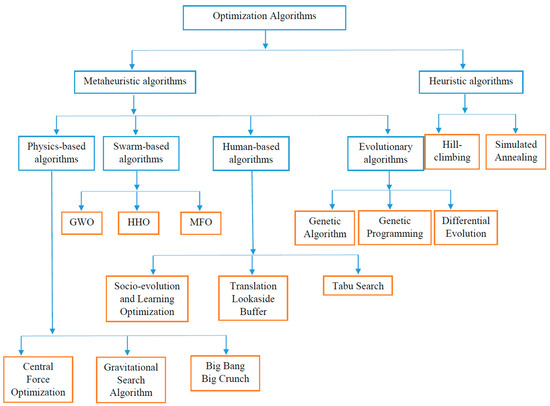
Figure 1.
Optimization algorithms.
Existing optimization studies have revealed that there are typical evaluation criteria that informs CCHP systems optimization and these are the exergetic, economic and environmental factors [27]. The exergetic factors comprise the exergy efficiency, energy efficiency, primary energy saving ratio, etc. The economic factors include, the product unit cost, total cost saving, net present value, etc. while the environmental factors are CO2 emission and integrated performance. This manuscript is structured as follows: Section 2 presents the literature review; Section 3 describes the tri-generation system to be optimized, the greywolf optimization technique and the mathematical formulation of the problem; and Section 4 reports and discusses the results obtained from the optimization and sensitivity analysis. In the light of the above, the proposed research sets out to achieve the following objectives:
- to propose a new approach for the optimization of a solar-assisted CCHP system;
- to maximize the net power and exergy efficiency while minimizing the CO2 emission of a solar energy-integrated CCHP system using the multi-objective greywolf optimization technique;
- to perform an analysis to ascertain the effect that the decision variables have on the objective functions.
2. Literature Review
The struggle to continuously improve CCHP systems with various optimization techniques represents a progressive research trend in the domain of energy conservation/management. Therefore, this section reviews the relevant pieces of literature that seek to optimize certain performance criteria of the solar-based CCHP system.
An extensive review revealed that a greater number of researchers employed the genetic algorithm for optimization applications in solar-assisted CCHP systems. Cao et al. [28] proposed a modified solar-integrated CCHP system and optimized the amount of electricity it generated, its exergy efficiency, and its total cost per unit exergy via the genetic algorithm approach. They also carried out a parametric study to ascertain how their decision variables (oil mass ratio, Rankine inlet pressure, temperature, etc.) affect the objective functions. The proposed approach improved results in terms of the above mentioned performance criteria thus outperforming conventional methods. The thermodynamic analysis and performance optimization of a solar energy- and natural-gas-integrated CCHP system has been presented by Wang et al. [29]. They employed the genetic optimization algorithm with the purpose of maximizing the energetic and exergetic capacities of the CCHP system. Furthermore, a multi-objective optimization model via a genetic algorithm has been developed by Wang et al. [30], who proposed an operational flexibility approach determined by the sizes of the photovoltaic (PV) solar panels and gas turbine to improve the CCHP system’s energy savings, cost savings, CO2 emission and grid integration level. The results obtained illustrate that, although the operational flexibility, as selected by the entropy weighting method, improved the system’s ability to adjust to variable conditions, corresponding decreases in grid interaction level and exergetic, economic and environmental factors were recorded. Song, Liu and Lin [31] employed the NSGA-II for the multi-objective optimization of a solar-based CCHP system modelled on three operational modes. Utilizing the gas turbine capacity, PV area and solar collector area as decision variables, an optimal solution that maximized the cost saving and energy saving ratio was obtained. The study confirmed that the CCHP system was significantly affected by energy prices and by the efficiencies of the PV, solar collector and gas turbine. The NSGA-II optimization approach was presented by Yousefi, Ghodusinejad and Kasaeian [8], with the aim of achieving the best microgrid capacities necessary to provide the needed tri-generation loads for a specified structure. They compared the results obtained from an internal combustion engine-based CCHP system and a solar energy-integrated CCHP system. This revealed that the latter had a better performance in terms of primary energy saving and CO2 emission, though at the expense of a slightly increased net present cost.
The application of the multi-objective greywolf technique has been employed for the optimization of various multi-generation systems. Shakibi et al. [32] proposed a new solar-assisted CCHP system utilizing the heliostat generation unit and employed the RSM and the greywolf optimizer for the multi-objective optimization of exergy performance and unit cost via six selected decision variables. They utilized the three weight-based methods to determine the optimal exergy efficiency, unit cost and performance coefficient. Asgari et al. [33] proposed a heliostat solar-based CCHP system incorporated with a phase change material to regulate the heat rate, thus ensuring a constant temperature input to the gas turbine. They employed the multi-objective greywolf optimization in a bid to further increase the exergy efficiency and power generated while reducing the unit product cost. The optimization results show an increase in exergy efficiency, exergy and environmental impact index as well as a decrease in the unit cost and cooling loads when compared with a similar study. Haghghi et al. [34] employed the greywolf multi-objective technique, coupled with an ANN-based procedure for the optimization of a geothermal-operated poly-generation system. Based on the energy, exergy and economic point of views, the study made use of four distinct approaches that involved the optimization of energy efficiency, investment cost, exergy efficiency and levelized cost. The study achieved its optimization objective of maximizing the energy efficiency and exergy efficiency while minimizing the investment and levelized costs. Habibollahzade and Houshfar [35] remodelled an ORC-based power generation system in a bid to reduce the emission of CO2. This was achieved by incorporating a membrane separator to harness an appreciable amount of the CO2 into a gasifier. Utilizing the greywolf optimizer, the proposed model yielded relatively lower CO2 emission rates and higher exergy efficiency and cost when compared with a similar study. Furthermore, Zhang and Sobhani [36] proposed the analysis and multi-objective optimization of a power and freshwater generation system based on the geothermal and gas turbine cycles. The greywolf optimizer was employed to maximize the net power, freshwater production, exergy efficiency and total emission while minimizing the payback period. The conducted sensitivity analysis confirmed that the air-preheater effectiveness on the system performance criteria is predominant. A solar-based system that produces power, cooling capacity, freshwater and hydrogen has been presented by Azizi, Nedaei and Yari [37]. A thermodynamic analysis of the proposed model was carried out to ascertain the base conditions of the generated electricity, drinking water, cooling capacity and hydrogen. Thereafter, the greywolf optimizer was applied, using two different scenarios, to optimize the unit cost, exergy efficiency and rate of freshwater production. Chen Huang and Shahabi [26] developed a hybrid CCHP system to reduce the primary energy consumption, CO2 emission and cost. The study employed a modified version of the greywolf optimizer that is based on the non-dominated sorting theory, variable detection, memory-based strategy selection and fuzzy theory. The obtained optimization results were validated using the multi-objective particle swarm optimization technique.
Behzadi et al. [38] presented a methanol-fuelled co-generation system consisting of a solid oxide fuel cell (SOFC), heat recovery unit and absorption power cycle (APC). The greywolf multi-objective technique was used to optimize the exergy efficiency and total cost implemented on three different systems, the SOFC, SOFC-ORC and SOFC-APC. The optimization results indicate a better optimal result from the SOFC-APC due to its non-thermal evaporator, condensation process and temperature glide matching. Zhang et al. [39] conducted an investigation on the feasibility of a biomass-based co-generation system. The investigations were carried out using four biomass fuels, with the best fuel—municipal solid waste—subsequently becoming the subject of the multi-objective optimization and parametric analysis of the system. Optimum results were generated and these maximized the total cost and minimized the CO2 emissions. Nedaei, Azizi and Farshi [40] developed a heliostat solar-based multi-generation system comprising the Brayton cycle, absorption refrigeration cycle, humidification, dehumidification, etc. In addition to the conducted thermodynamic exergetic and economic analysis, the greywolf technique was used to compute optimum values for the exergy efficiency, freshwater production rate and unit product cost. Finally, Mahdavi et al. [5] developed a new, solar-based CCHP system and utilized the RSM for the multi-objective optimization of its net power, CO2 emission and exergy efficiency. In the developed system, waste heat between the compressors was harnessed by an intercooler to power an absorption chiller. By means of interaction effects between the four decision variables, six optimal solutions were obtained and the technique for order preferences by similarity to ideal solution (TOPSIS) method was used to determine the best solution. Optimal results corresponding to the net power, CO2 emission and exergy efficiency were obtained. Table 1 gives a summary of some of the reviewed pieces of literature.

Table 1.
Summary of some related works.
The GWO has been applied successfully in many studies. However, no existing study has used this approach for the CCHP system. Hence, this paper illustrates how the greywolf optimizer could be employed to improve the performance of a solar-based CCHP system.
3. Materials and Methods
3.1. Description of the System
This study considers the solar-integrated CCHP system described by Mahdavi et al. [5]. The system comprises three gas turbines, two compressors, a Kalina cycle, absorption chiller, solar collectors, heat recovery steam generator unit (HSRG) and a hot water generator (Figure 2).
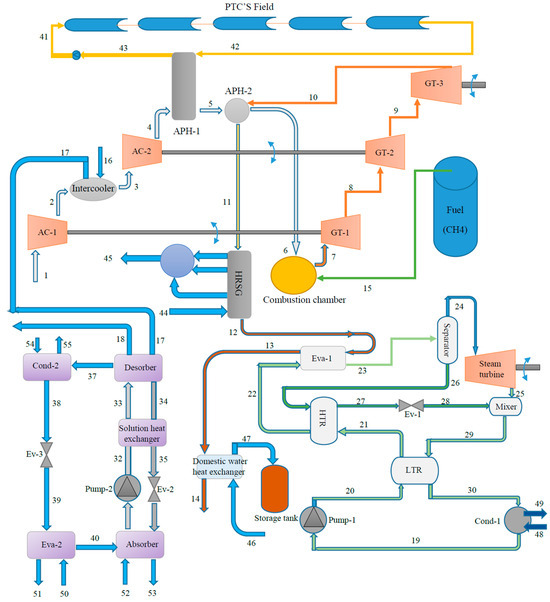
Figure 2.
Diagram illustrating the solar-integrated CCHP system.
The system is operated in such a way that air is compressed by two two-stage compressors (AC-1 and AC-2) with an intercooler in between them. Waste heat from the intercooler is used to drive the absorption chiller via transfer of heat in a desorber. Following that, the air leaving the second compressor is heated through air preheater 1 (APH-1) and air preheater 2 (APH-2), powered by solar energy and exhaust combustion gases from gas turbine 3 (GT-3), respectively. Once the air warms up to the required temperature and pressure, it is reacted with combustion fuel (methane) to produce hot gases in the combustion chamber. The hot gases flow into three consecutive gas turbines, where the first two turbines supply the power needed to drive the compressors while the third is responsible for rotating the shaft of a generator to generate electrical power. Furthermore, exhaust gases from GT-3 are recovered back to the APH-2 and are used to provide heating power to the HSRG, the Kalina cycle through evaporator 1 (Eva-1), and to the domestic water heat exchanger, before being released to the environment.
In the Kalina cycle, pump 1 increases the pressure of its working fluid (ammonia water mixture), which is then passed into two successive heat exchangers (low temperature recuperator (LTR) and high-temperature recuperator (HTR)) to improve its thermal energy and reduce the energy input to Eva-1 subsequently. The resulting two-phase mixture at Eva-1 is sent to the separator where separation into saturated vapour and saturated liquid occurs. The saturated vapour is supplied to the steam turbine to generate further work output while the saturated liquid is sent back to the HTR to recover some thermal energy before being passed to expansion valve 1 (Ev-1) where its pressure is reduced. Subsequently, the low-pressure saturated liquid enters the mixer where it is combined with the output from the steam turbine. This mixture is passed through the LTR to dissipate its energy before being discharged to the atmosphere through the condenser (cond-1), thus completing the cycle.
A series of processes is employed in the single-effect absorption chiller to acquire energy at the desorber (provided by rejected gases from the intercooler) used to supply cooling capacity at the associated evaporator (Eva-2). The working fluid (saturated LiBr-H2O liquid) is pumped into pump 2 before its entrance into the solution heat exchanger (SHE) where it gains thermal energy. In water vapour state, the working fluid enters the condenser (cond-2) from the desorber and condenses into saturated liquid before being throttled from the expansion valve (Ev-3) into Eva-2. At Eva-2, it gains energy to become a saturated vapour before being absorbed into the solution in Ev-2, where it transforms back into the saturated liquid specified at the start of the cycle.
The following assumptions were made—that the system operates in a steady state; kinetic and potential energy changes are negligible; and heat losses from component systems, except the combustion chamber, are insignificant.
Response Surface Method
This is a mathematical and statistical approach that aims to determine the design factor settings in order to enhance the accurate implementation of a procedure [41]. The regression models generated portray the relationship between a certain response variable and the associated design factors. The general procedures undertaken are:
- Design of experiments: This is carried out to establish the experimental conditions. It involves selecting the relevant input factors that would affect the response variable. This is followed by the determination of the constraints used to evaluate the design factors during the experiment.
- Experimental tests: Here, the necessary experiments are performed employing an already prepared experimental plan and the response variable data are collected according to the various fusion of the design factor levels. These tests are arbitrarily conducted to reduce the influence of unimportant design factors.
- Fitting the Regression models: The regression models are fitted employing the data obtained from the experiments using methods such as the least squares or the maximum likelihood estimation. The resulting regression models are evaluated for their goodness-of-fit to inspect for any discrepancies from the initial model presumptions.
- Validation of the regression model: After the model is successfully fitted, it is validated through prediction using further experimental test with unused data.
Based on the system described in Section 3.1, the response surface methodology was utilized to develop regression models capable of predicting its net power, CO2 emission and exergy efficiency. The decision variables and their maximum/minimum values, as well as the equations, are shown in Table 2 and Table 3 and Equations (10)–(12) respectively [5].

Table 2.
Decision variables.

Table 3.
Decision variables and their values.
This study considers three objective functions namely:
- Net Power Output: The net power, which is a function of the energy analysis, is the summation of the work outputs from the gas turbine and Kalina cycle. Mathematically, it can be expressed as [5]:
- = net power output;
- = net power from the gas turbines and the Kalina cycle, respectively;
- = net power from gas turbine 1, 2, and 3, respectively;
- = net power to compressor 1 and 2, respectively;
- = net power from steam turbine and pump 2 of the Kalina cycle;
- = specific enthalpies at state 7, 8, 9, and 10, respectively;
- = mass flow rate of the combustion gases from the combustion chamber.
- 2.
- Exergy Efficiency: According Kumar [42], this is a practical and effective criterion for determining the type, extent and positions of irreversibility in a thermodynamic system. Mathematically, it can be defined as the quotient obtained by dividing the output exergy by the input exergy [5].
- = Exergy at state 44, 45, 46, 47, 50 and 51, respectively;
- = Input exergy;
- = Exergy of fuel;
- = Exergy of solar collector.
- 3.
- CO2 Emission: The ejection of CO2 into the atmosphere has detrimental effects on the environment and its continuous mitigation should be the goal in thermal energy systems. The measure of the production level of CO2 is called emission and is defined as the ratio of the mass flow rate of CO2 to the total output energy [43].
- = Heating and cooling loads of the CCHP system, respectively;
Mahdavi et al. have pointed out that these three regression models exhibit remarkable accuracy in estimating the outputs, with errors measuring less than 1% [5].
3.2. Greywolf Optimization
The optimization technique employed in this study, called the greywolf optimization (GWO), is a swarm-intelligence algorithm proposed by Mirjalili, Mirjalili, and Lewis [44]. It draws inspiration from the behaviour, attacking method, social leadership and encircling process of the wolf to determine the best solution for an optimization problem. The structuring of the GWO is such that the fittest solution is named the alpha (α) in order to reflect the social ranking of wolves. As a result, beta (β) and delta (δ) refer respectively to the next best solutions while the remaining solutions are called omega (ꞷ) wolves. The α, β and δ wolves pilot the hunting activity, with the ꞷ wolves trailing them, in their search for the global optimum. The following mathematical equations are used to initiate the encircling of a prey by the greywolves during hunting [44],
where,
- t = current iteration;
- = coefficient vector;
- = position vector;
- = position vector of the prey.
Furthermore, the coefficient vectors, are calculated as thus:
where the components of decline from 2 to 0, in a linear manner, across the iterations while are randomly selected vectors in [0, 1].
The GWO algorithm commences optimization by producing a random solution set. The top three solutions generated are saved by the algorithm, which requires the other search agents to adjust their locus in relation to the optimum solutions. After the end condition has been met, the location and value of the alpha solution becomes the optimum solution. The following Equations are adopted, during the optimization process, for each search agent to initiate the hunting process and identify potential areas of the search space. The general optimization methodology used in this study and flowchart for the GWO technique is given in Figure 3 and Figure 4.
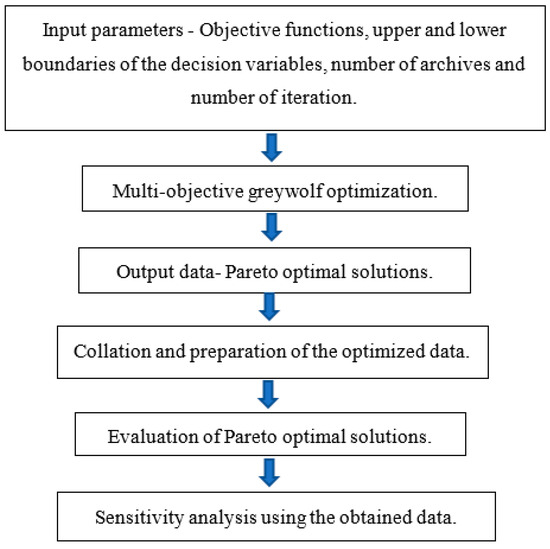
Figure 3.
Optimization methodology.
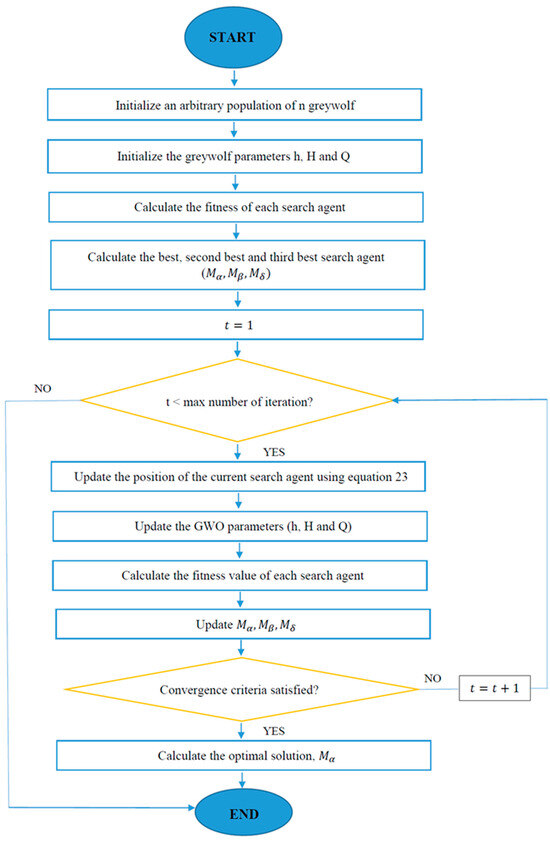
Figure 4.
Flowchart for single-objective greywolf optimization.
When a problem is defined by multiple objective functions and these functions are conflicting, a multi-objective optimization formulation is adopted. Multi-objective optimization involves the simultaneous optimization of more than one objective function to generate a set of alternative solutions that are feasible, with a compromise between the solutions known as the Pareto optimal or non-dominated solutions. The flowchart for the multi-objective GWO technique is given in Figure 5. In order to carry out optimization using a multi-objective greywolf optimizer (MOGWO), two additional components are incorporated into the conventional GWO algorithm, and they are:
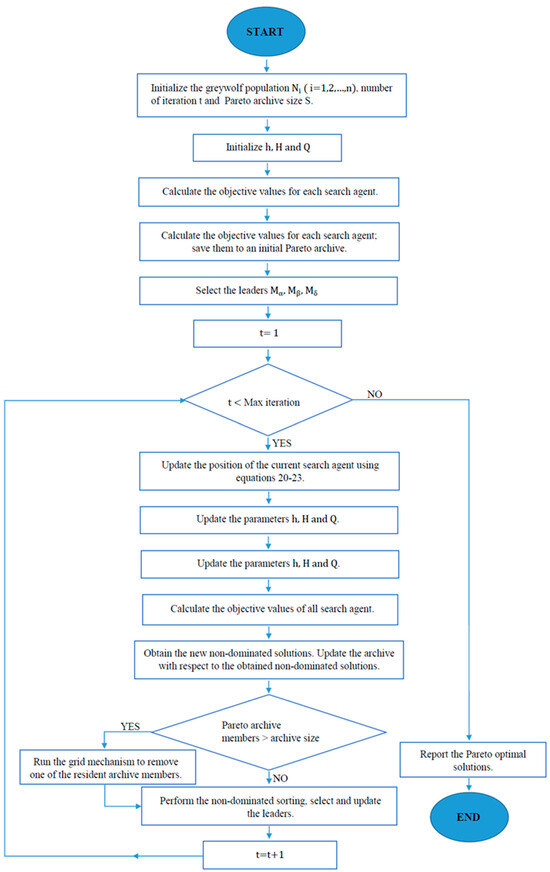
Figure 5.
Flowchart for multi-objective greywolf optimization.
- The archive—for keeping the non-dominated Pareto optimal solutions.
- The leader selection approach—this assists the selection of the alpha and beta as heads of the search activity from the archive.
3.3. Mathematical Formulation
Mathematically, the single optimization of net power can be formulated as follows:
In the same vein the single-objective optimization of CO2 can be formulated as follows:
The single-objective optimization of exergy efficiency can be formulated as follows:
The multi-objective optimization problem is formulated as follows:
Equations (24)–(27) are subject to variable restrictions:
10 ≤ Cr ≤ 15
10 ≤ Pp ≤ 30
1420 ≤ Gt ≤ 1520
850 ≤ Ct ≤ 950.
4. Results
4.1. Single-Objective Optimization
The single-objective greywolf optimization was performed on each of the objective functions for 100 iterations using a search agent number of 100. This was implemented on the MATLAB platform using an 8GB RAM Intel(R) Core(TM) i3-5005U CPU @ 2.00GHz laptop after editing the codes readily available online [45].
4.1.1. Net Power Optimization
This is carried out by solving Equation (24), using the decision variables and their values shown in Table 2 and Table 3, respectively, on the GWO algorithm. The results obtained as shown in Table 4 depict how, in order maximize net power, the following should take place:

Table 4.
Optimal solutions maximizing the net power.
- Minimize the compression ratio, pinch point temperature difference and inlet combustion chamber temperature;
- Maximize the inlet turbine temperature.
4.1.2. CO2 Emission Optimization
This was carried out by solving Equation (25), using the decision variables and their values shown in Table 2 and Table 3, respectively, on the GWO algorithm. The results obtained as shown in Table 5 depict how, in order minimize the CO2 emission, the following should take place:

Table 5.
Optimal solutions maximizing the net power.
- Minimize the compression ratio, pinch point temperature difference and inlet combustion chamber temperature;
- Maximize the inlet turbine temperature.
4.1.3. Exergy Efficiency Optimization
This was carried out by solving Equation (26), using the decision variables and their values shown in Table 2 and Table 3, respectively, on the GWO algorithm. The results obtained as shown in Table 6 depict how, in order to maximize the exergy efficiency, the following should take place:

Table 6.
Optimal solutions maximizing the exergy efficiency.
- Minimize the compression ratio, pinch point temperature difference and inlet turbine temperature;
- Maximize the inlet combustion chamber temperature.
4.1.4. Analysis of the Single-Objective Optimization Results
A summary of the results obtained in Section 4.1.1, Section 4.1.2 and Section 4.1.3 is shown in Table 7. It highlights the behaviour of the optimal solutions obtained where ↑ represents an increasing trend, ↓ represents a decreasing trend while ≠ signify a conflict between parameters.

Table 7.
Optimal solutions maximizing the exergy efficiency.
Table 7 illustrates the conflicting nature of the objective functions, thus requiring the simultaneous optimization of the three objectives to determine the Pareto optimal solutions.
4.2. Multi-Objective Optimization
The multi-objective greywolf optimization was performed on the objective functions. One hundred iterations were adopted and the MATLAB codes, implemented on an 8 GB RAM Intel(R) Core(TM) i3-5005U CPU @ 2.00GHz laptop, were edited and adapted from Mirjalili [46]. The set values of the hyperparameters are given in Table 8.

Table 8.
Set values of the hyperparameters.
The optimization algorithm generated 100 sets of non-dominated solutions. The Pareto front of all three objective functions are shown in Figure 6. Despite the conflicting nature of the objective functions, the sets of optimal solutions obtained proffer the best trade-off solutions. Each of the solutions on the Pareto front are potential optimal solutions and the best optimal can be selected based on the discretion of the decision maker.
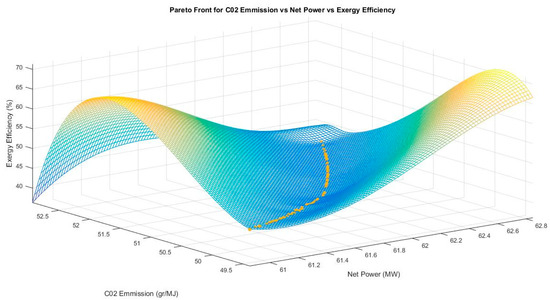
Figure 6.
Pareto front CO2 emission vs. net power vs. exergy efficiency.
In order to obtain further insight into the relation between each objective function, three cases describing the relation CO2 emission and net power output, exergy efficiency and net power output, and exergy efficiency and CO2 emission were considered. Figure 6 shows the global results representing the Pareto front of all three objective functions. This will be simplified into two two-dimensional Pareto fronts in order to point out some important aspects.
The Pareto front in Figure 7 clearly depicts a conflict in the decision-making process because the propensity to maximize net power will increase the emission of CO2, which in turn will negatively affect the environment. The net power of the CCHP system being investigated is significantly dependent on the power output from the GT-3, in addition to the extra power produced by the Kalina cycle. With this in mind, the system may be structured in such a way that combustion gases entering the unfired HRSG from APH-2 are forced to increase in temperature compared with those entering the combustion chamber. Additionally, the heating power from the photovoltaic thermal collectors may be boosted and the fuel consumption rate decreased, all of which is intended to minimize the CO2 emission. This will reduce the net power produced by the GT-3, which as a ‘top’ system generates the larger net power, while boosting the power output from the Kalina cycle which would be ‘cleaner’ (i.e., not requiring combustion) but in smaller amounts. Although this will ultimately reduce the net power generated by the system, its optimization will be achieved together with a minimization in the emission of CO2.
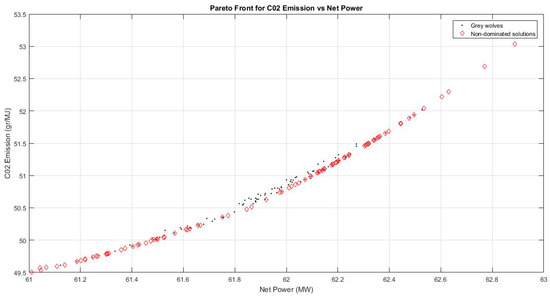
Figure 7.
Pareto front for CO2 emission vs. net power.
The Pareto graph in Figure 8 suggests that the exergy efficiency and the CO2 emission are compatible as a lower value of CO2 emission corresponds with a higher exergy efficiency. It also demonstrates that the CO2 emission value has to be minimized to a certain point in order to achieve a significant increase in the exergy efficiency. Further analysis reveals that reducing the fuel consumption would decrease the input exergy of fuel. With smaller input exergy, together with improved exergy outputs/useful work from the Kalina cycle, the water heat exchanger and absorption chiller are able to significantly maximize the exergy efficiency, which invariably means that the CO2 emission is minimal.
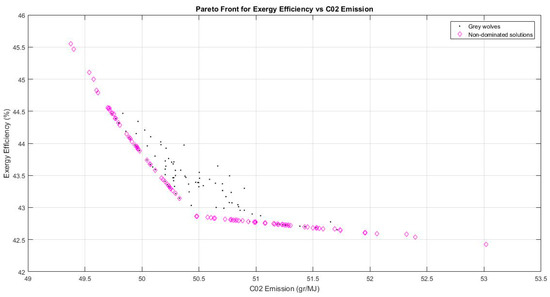
Figure 8.
Pareto front for exergy efficiency vs. CO2 emission.
Furthermore, Figure 9 shows an inverse relationship between the exergy efficiency and the net power. This suggests that a high net power production does not necessarily equate to highly efficient system. However, it is the effective use of the power generated within the CCHP system that determines a system with maximum exergy efficiency. This also suggests that bottom systems (such as the Kalina cycle, absorption chiller) should be operated and designed in such a way as to ensure utilization of maximum waste heat and a reduction in exergy losses.
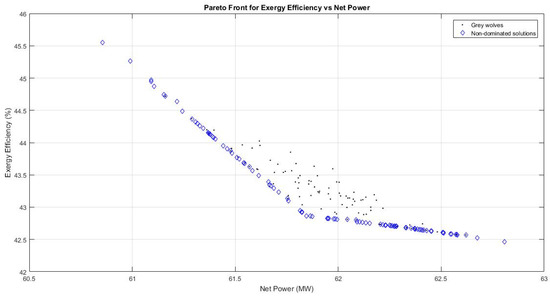
Figure 9.
Pareto front for exergy efficiency vs. net power.
For validation purposes, the MOGWO was structured to generate six optimal solutions to be compared with the six solutions obtained by a similar study. The obtained data, as shown in Table 9, demonstrate that the MOGWO produced an optimized system with lower CO2 emission and higher exergy efficiency values. However, this was at the cost of a reduced net power, though by a small margin.

Table 9.
Validation of optimization results with a related study.
4.3. Sensitivity
The sensitivity analysis was conducted to further understand the dynamics surrounding the multi-objective optimization results. It also helps to ascertain the impact a variation of each parameter would have on the two-dimensional Pareto front of net power, exergy efficiency and CO2 emission. The parameters include the compression ratio, pinch point temperature difference, inlet turbine temperature and inlet combustion chamber temperature. The findings recorded after each analysis are consistent with the research of Mahdavi et al. [5], who employed the RSM for the modelling and optimization of a solar-based CCHP system.
4.3.1. Analysis of the Compression Ratio
In order to perform this analysis, the compression ratio was maintained at values of 10, 12 and 15 while the other variables were left to vary within their range (10–30 for Pp, 1420–1520 for Gt and 850–950 for Ct). Figure 10 shows that at Cr = 15, maximum values for the net power and exergy efficiency are obtained but at the cost of a high emission of CO2. It could also be seen that reducing the value of Cr from 15 to 10 would cause a reduction in the CO2 emission that is more significant than a reduction of the net power and exergy efficiency. This suggests that employing a lower compression ratio will greatly minimize the CO2 emission with negligible effects on the optimal values of the net power and exergy efficiency. It is interesting to note that, in comparison with other decision variables, the Cr produces the greatest change/effect in the CO2 emission and yields the least value.
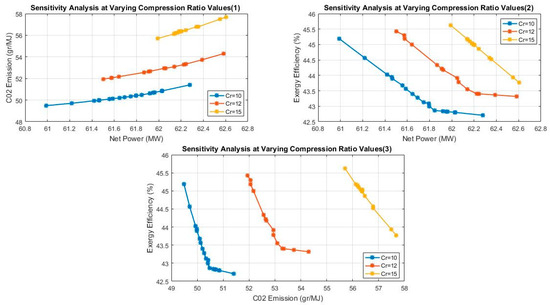
Figure 10.
Effects of compression ratio on the optimal objective functions.
4.3.2. Analysis of the Pinch Point Temperature Difference
The pinch point temperature at air preheater 1 was kept at values of 10, 20 and 30 while the other variables were left to vary within their range (10–15 for Cr, 1420–1520 for Gt and 850–950 for Ct). Figure 11 shows that, at Pp = 30, maximum values for the net power, exergy efficiency and CO2 emission were obtained. It also reveals that a change in the Pp from 30 to 20 yields a greater change in the emission of CO2 (compared with that from 20 to 10) with an associated reduction in the net power and exergy efficiency. This suggests that a fairly average value of Pp would be sufficient to produce good results. In comparison with other decision variables, the Pp has the least effect on the objective functions.
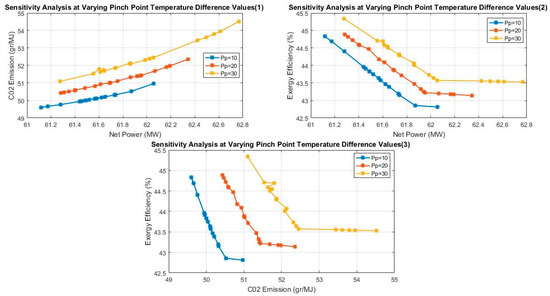
Figure 11.
Effects of pinch point temperature difference on the optimal objective functions.
4.3.3. Analysis of the Inlet Turbine Temperature
The inlet turbine temperature was kept at values of 1420, 1470 and 1520 while the other variables were left to vary within their range (10–15 for Cr, 10–30 for Pp and 850–950 for Ct). Figure 12 shows that, at higher values of Gt (Gt = 1520), maximum values of exergy efficiency are obtained as well as a minimum net power and CO2 emission. This suggests that higher Gt values make for a highly efficient system with minimal emission of CO2, although at the expense of a reduced net power. In comparison with other decision variables, the Gt produces the greatest effect/change on the exergy efficiency.
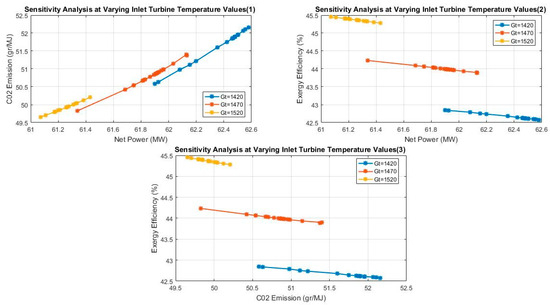
Figure 12.
Effects of turbine inlet temperature on the optimal objective functions.
4.3.4. Analysis of the Inlet Combustion Chamber Temperature
The combustion chamber inlet temperature was kept at values of 850, 900 and 950 while the other variables were left to vary within their range (10–15 for Cr, 10–30 for Pp and 1420–1520 for Gt). As can be seen in Figure 13, a Ct value of 950 yielded maximum net power and CO2 emission as well as a minimum exergy efficiency. This suggests that lower values of Ct are required to obtain minimum values of CO2 emission, maximum exergy efficiency and a minimum net power.
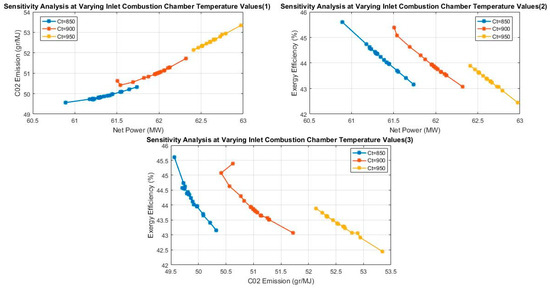
Figure 13.
Effects of combustion chamber inlet temperature on the optimal objective functions.
5. Conclusions
This study set out to employ the greywolf approach for the multi-objective optimization of a solar-assisted CCHP system. This was undertaken in a bid to boost the overall efficiency by maximizing the net power and exergy efficiency of the CCHP system. It also sought to optimally reduce the greenhouse emission that has evidently negative health implications and causes global warming. This research supports the idea that there is a need to reduce fossil fuel depletion rate, as a solar-assisted CCHP was optimized. In so far as related studies have employed other optimization techniques for the multi-objective optimization of a solar-based CCHP system, this study proposes a new optimization approach. The results and findings from this research are outlined as follows:
- A multi-objective optimization approach is used to determine the optimal set of parameters describing the thermodynamic configuration of the solar-based CCHP system: compression ratio, pinch point temperature difference, inlet turbine temperature and inlet combustion chamber temperature.
- The performance of the CCHP system is assessed through the net power, CO2 emission and exergy efficiency that are employed as objective functions to determine how well each set of decision variables complies with all the constraints.
- The greywolf technique is employed for the multi-objective optimization to generate non-dominated Pareto optimal solutions.
- A set of Pareto optimal solutions are computed in this study. The optimal solutions are provided as options for the decision maker to help them make a preferred selection based on their discretion to improve the performance of the CCHP system. A guide, with which to aid this decision-making process, is suggested via the conducting of a sensitivity analysis.
- An interesting finding is the interdependency between the four decision variables. This suggests that a change in one of the decision variables results in respective changes in the other three variables. Hence, a multi-objective optimization technique is pertinent and helpful when evaluating the performance of the CCHP system.
- This study found that there exists a conflict in decision-making processes between net power and CO2 emission as a maximum net power correlates with an undesirable maximum emission of CO2. Another important finding is the compatibility between the exergy efficiency and CO2 emission, which indicates that a system with minimal emission of CO2 is a highly efficient one. This study has shown that a system’s high net power production is not a guarantee of its high efficiency, due to the negative correlation obtained between net power and exergy efficiency.
- The findings from the sensitivity study suggest that a lower compression ratio will significantly reduce CO2 emission while having little impact on the optimal net power and energy efficiency values. It was also found that higher turbine inlet temperature values will result in a system that is highly efficient and emits less CO2, but at the cost of having less net power. This also implies that lower values of combustion chamber inlet temperature are necessary to achieve the minimum CO2 emission values and maximum energy efficiency corresponding with a minimum net power.
- Finally, the study has confirmed the finding of Mahdavi et al. [5] who found that the compression ratio had the most effect on the CO2 emission by virtue of having the highest incremental change. In the same vein, the inlet turbine temperature had the most effect on the exergy efficiency while the inlet combustion chamber had the most effect on the net power.
Author Contributions
Conceptualization, methodology, formal analysis, writing—original draft preparation, U.U.; writing—review and editing, supervision, L.T. and C.W.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the University of Johannesburg research committee and commonwealth scholarship fund for sponsoring this research work.
Data Availability Statement
Data generated during the study are unavailable due to ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nasrin, R.; Rahim, N.A.; Fayaz, H.; Hasanuzzaman, M. Water/MWCNT nanofluid based cooling system of PVT: Experimental and numerical research. Renew. Energy 2018, 121, 286–300. [Google Scholar] [CrossRef]
- Wang, N.; Wang, D.; Xing, Y.; Shao, L.; Afzal, S. Application of co-evolution RNA genetic algorithm for obtaining optimal parameters of SOFC model. Renew. Energy 2020, 150, 221–233. [Google Scholar] [CrossRef]
- IEA. CO2 Emissions in 2022. 2023. Available online: https://www.iea.org/reports/co2-emissions-in-2022 (accessed on 9 May 2023).
- Spahni, R.; Chappellaz, J.; Stocker, T.F.; Loulergue, L.; Hausammann, G.; Kawamura, K.; Fluckiger, J.; Schwander, J.; Raynaud, D.; Masson-Delmotte, V.; et al. Atmospheric methane and nitrous oxide of the late Pleistocene from Antarctic ice cores. Science 2005, 310, 1317–1321. [Google Scholar] [CrossRef] [PubMed]
- Mahdavi, N.; Mojaver, P.; Khalilarya, S. Multi-objective optimization of power, CO2 emission and exergy efficiency of a novel solar-assisted CCHP system using RSM and TOPSIS coupled method. Renew. Energy 2022, 185, 506–524. [Google Scholar] [CrossRef]
- Wu, D.; Wang, R. Combined cooling, heating and power: A review. Prog. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- BP Energy Outlook 2023. Available online: https://www.bp.com/en/global/corporate/energy-economics/energy-outlook.html (accessed on 31 May 2023).
- Yousefi, H.; Ghodusinejad, M.H.; Kasaeian, A. Multi-objective optimal component sizing of a hybrid ICE + PV/T driven CCHP microgrid. Appl. Therm. Eng. 2017, 122, 126–138. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z.; Lior, N.; Han, W. Advancement of distributed energy methods by a novel high efficiency solar-assisted combined cooling, heating and power system. Appl. Energy 2018, 219, 179–186. [Google Scholar] [CrossRef]
- Dincer, I.; Zamfirescu, C. Renewable-energy-based multigeneration systems. Int. J. Energy Res. 2012, 36, 1403–1415. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant algorithms for discrete optimization. Artif. Life 1999, 5, 137–172. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Zeng, R.; Li, H.; Liu, L.; Zhang, X.; Zhang, G. A novel method based on multi-population genetic algorithm for CCHP–GSHP coupling system optimization. Energy Convers. Manag. 2015, 105, 1138–1148. [Google Scholar] [CrossRef]
- Song, Z.; Liu, T.; Liu, Y.; Jiang, X.; Lin, Q. Study on the optimization and sensitivity analysis of CCHP systems for industrial park facilities. Int. J. Electr. Power Energy Syst. 2020, 120, 105984. [Google Scholar] [CrossRef]
- Kim, I.; de Weck, O. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Optim. 2005, 29, 149–158. [Google Scholar] [CrossRef]
- Hasanzadeh, R.; Mojaver, M.; Azdast, T.; Park, C.B. A novel systematic multi-objective optimization to achieve high-efficiency and low-emission waste polymeric foam gasification using response surface methodology and TOPSIS method. Chem. Eng. J. 2022, 430, 132958. [Google Scholar] [CrossRef]
- Ren, F.; Wang, J.; Zhu, S.; Chen, Y. Multi-objective optimization of combined cooling, heating and power system integrated with solar and geothermal energies. Energy Convers. Manag. 2019, 197, 111866. [Google Scholar] [CrossRef]
- Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
- Shehab, M.; Mashal, I.; Momani, Z.; Shambour, M.K.Y.; Al-Badareen, A.; Al-Dabet, S.; Bataina, N.; Alsoud, A.R.; Abualigah, L. Harris Hawks Optimization Algorithm: Variants and Applications. Arch. Comput. Methods Eng. 2022, 29, 5579–5603. [Google Scholar] [CrossRef]
- Sharifian, Y.; Abdi, H. Solving multi-zone combined heat and power economic emission dispatch problem considering wind uncertainty by applying grasshopper optimization algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102512. [Google Scholar] [CrossRef]
- Ji, J.; Wang, F.; Zhou, M.; Guo, R.; Ji, R.; Huang, H.; Zhang, J.; Nazir, M.S.; Peng, T.; Zhang, C.; et al. Evaluation Study on a Novel Structure CCHP System with a New Comprehensive Index Using Improved ALO Algorithm. Sustainability 2022, 14, 15419. [Google Scholar] [CrossRef]
- Xu, L.; Luo, X.; Wen, Y.; Wu, T.; Wang, X.; Guan, X. Energy Management of Hybrid Power Ship System Using Adaptive Moth Flame Optimization Based on Multi-Populations. IEEE Trans. Power Syst. 2023. [Google Scholar] [CrossRef]
- Chen, J.; Huang, S.; Shahabi, L. Economic and environmental operation of power systems including combined cooling, heating, power and energy storage resources using developed multi-objective grey wolf algorithm. Appl. Energy 2021, 298, 117257. [Google Scholar] [CrossRef]
- Wang, J.; Han, Z.; Guan, Z. Hybrid solar-assisted combined cooling, heating, and power systems: A review. Renew. Sustain. Energy Rev. 2020, 133, 110256. [Google Scholar] [CrossRef]
- Cao, Y.; Dhahad, H.A.; Togun, H.; Haghghi, M.A.; Athari, H.; Mohamed, A.M. Exergetic and economic assessments and multi-objective optimization of a modified solar-powered CCHP system with thermal energy storage. J. Build. Eng. 2021, 43, 102702. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Yang, Y.; Mao, T. Thermodynamic performance analysis and optimization of a solar-assisted combined cooling, heating and power system. Energy 2016, 115, 49–59. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ren, F.; Lu, S. Multi-objective optimization and selection of hybrid combined cooling, heating and power systems considering operational flexibility. Energy 2020, 197, 117313. [Google Scholar] [CrossRef]
- Song, Z.; Liu, T.; Lin, Q. Multi-objective optimization of a solar hybrid CCHP system based on different operation modes. Energy 2020, 206, 118125. [Google Scholar] [CrossRef]
- Shakibi, H.; Nedaei, N.; Farajollahi, A.H.; Chitsaz, A. Exergoeconomic appraisement, sensitivity analysis, and multi-objective optimization of a solar-driven generation plant for yielding electricity and cooling load. Process. Saf. Environ. Prot. 2023, 170, 89–111. [Google Scholar] [CrossRef]
- Asgari, A.; Yari, M.; Mahmoudi, S.M.S.; Desideri, U. Multi-objective grey wolf optimization and parametric study of a continuous solar-based tri-generation system using a phase change material storage unit. J. Energy Storage 2022, 55, 105783. [Google Scholar] [CrossRef]
- Haghghi, M.A.; Mohammadi, Z.; Delpisheh, M.; Nadimi, E.; Athari, H. Multi-variable study/optimization of a novel geothermal-driven poly-generation system: Application of a soft-computing intelligent procedure and MOGWO. Process. Saf. Environ. Prot. 2023, 171, 507–531. [Google Scholar] [CrossRef]
- Habibollahzade, A.; Houshfar, E. Improved performance and environmental indicators of a municipal solid waste fired plant through CO2 recycling: Exergoeconomic assessment and multi-criteria grey wolf optimisation. Energy Convers. Manag. 2020, 225, 113451. [Google Scholar] [CrossRef]
- Zhang, L.; Sobhani, B. Comprehensive economic analysis and multi-objective optimization of an integrated power and freshwater generation cycle based on flash-binary geothermal and gas turbine cycles. J. Clean. Prod. 2022, 364, 132644. [Google Scholar] [CrossRef]
- Azizi, S.; Nedaei, N.; Yari, M. Proposal and evaluation of a solar-based polygeneration system: Development, exergoeconomic analysis, and multi-objective optimization. Int. J. Energy Res. 2022, 46, 13627–13656. [Google Scholar] [CrossRef]
- Behzadi, A.; Habibollahzade, A.; Arabkoohsar, A.; Shabani, B.; Fakhari, I.; Vojdani, M. 4E analysis of efficient waste heat recovery from SOFC using APC: An effort to reach maximum efficiency and minimum emission through an application of grey wolf optimization. Int. J. Hydrogen Energy 2021, 46, 23879–23897. [Google Scholar] [CrossRef]
- Zhang, G.; Li, H.; Xiao, C.; Sobhani, B. Multi-aspect analysis and multi-objective optimization of a novel biomass-driven heat and power cogeneration system; utilization of grey wolf optimizer. J. Clean. Prod. 2022, 355, 131442. [Google Scholar] [CrossRef]
- Nedaei, N.; Azizi, S.; Farshi, L.G. Performance assessment and multi-objective optimization of a multi-generation system based on solar tower power: A case study in Dubai, UAE. Process. Saf. Environ. Prot. 2022, 161, 295–315. [Google Scholar] [CrossRef]
- Costa, E.; Almeida, M.; Alvim-Ferraz, C.; Dias, J. Otimization of Crambe abyssinica enzymatic transesterification using response surface methodology. Renew. Energy 2021, 174, 444–452. [Google Scholar] [CrossRef]
- Kumar, R. A critical review on energy, exergy, exergoeconomic and economic (4-E) analysis of thermal power plants. Eng. Sci. Technol. Int. J. 2017, 20, 283–292. [Google Scholar] [CrossRef]
- Mahdavi, N.; Khalilarya, S. Comprehensive thermodynamic investigation of three cogeneration systems including GT-HRSG/RORC as the base system, intermediate system and solar hybridized system. Energy 2019, 181, 1252–1272. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Grey Wolf Optimizer (GWO). MATLAB Central File Exchange. 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/44974-grey-wolf-optimizer-gwo (accessed on 30 May 2023).
- Mirjalili, S. Multi-Objective Grey Wolf Optimizer (MOGWO). MATLAB Central File Exchange. 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/55979-multi-objective-grey-wolf-optimizer-mogwo (accessed on 31 May 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).