Solving of the Inverse Boundary Value Problem for the Heat Conduction Equation in Two Intervals of Time
Abstract
:1. Introduction
2. Materials and Methods Direct Formulation of the Problem on Interval
3. Expansion of the Direct Problem (1)–(5) on
4. Solution of the Inverse BVPs (1)–(5) and (18)–(21)
5. Solution of the Inverse BVP (1)–(5) and (18)–(21) by the Projection Regularization Method
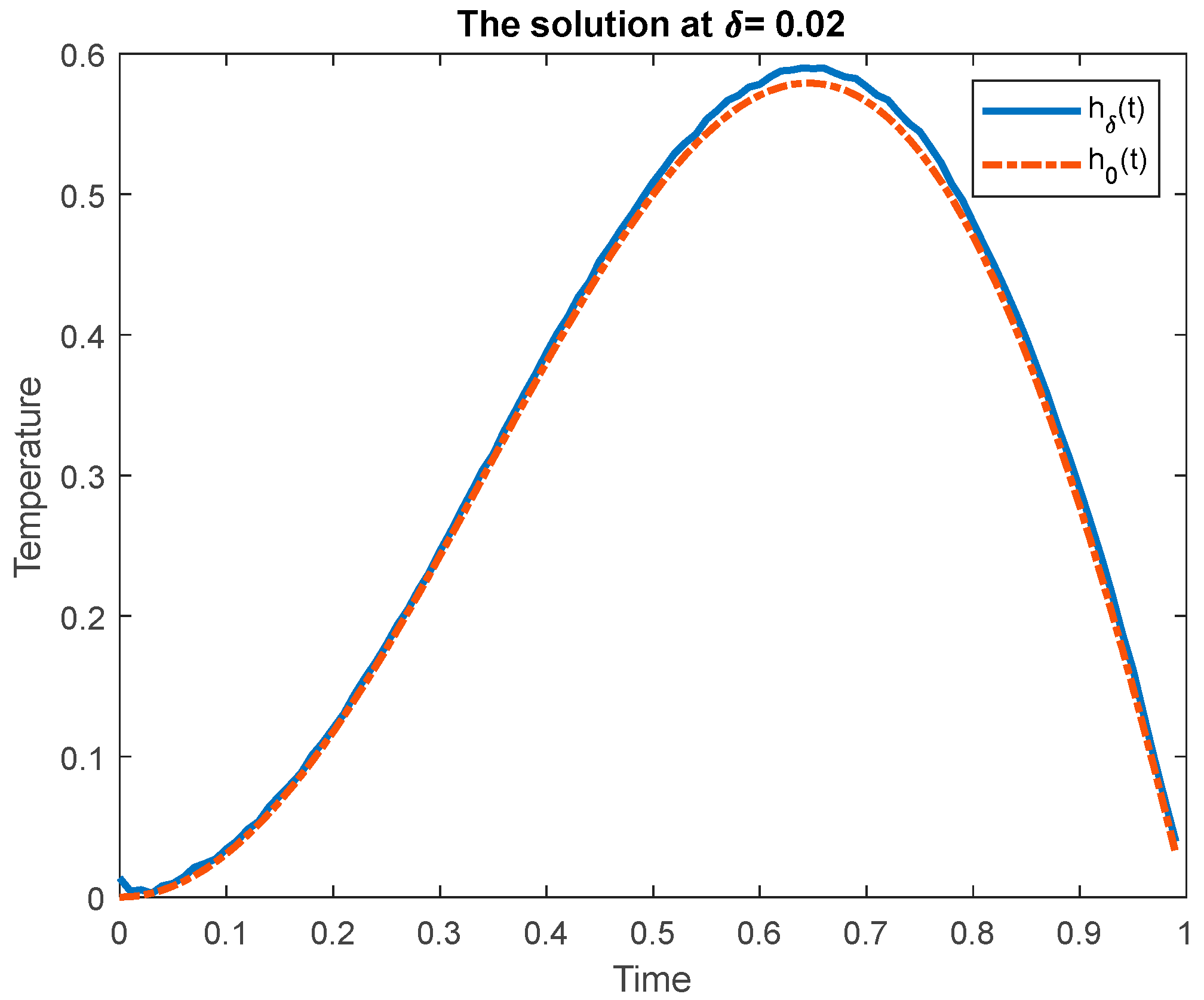
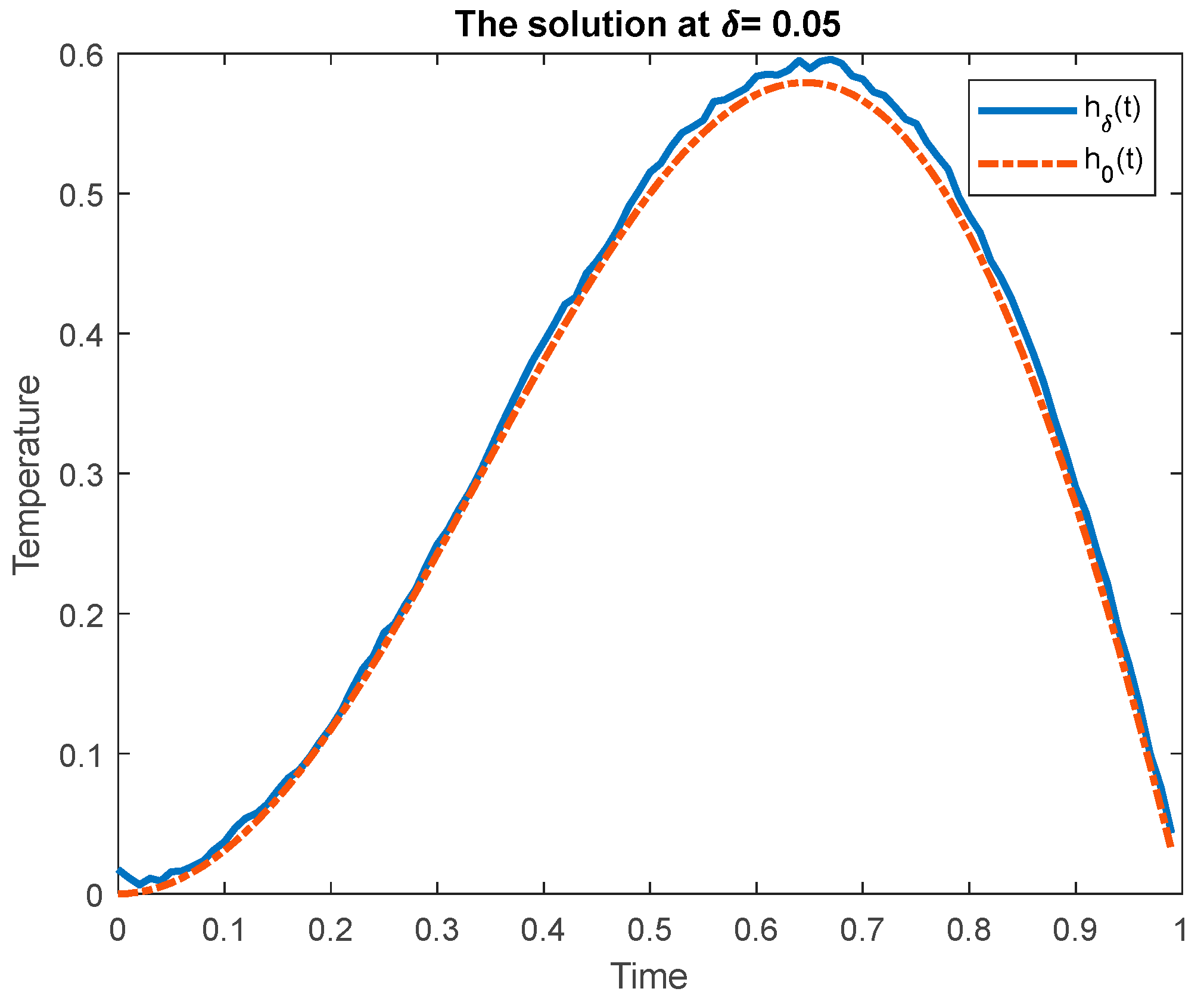
6. Case Study
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tikhonov, A.N. On the Regularization of Ill-Posed Problems. Proc. USSR Acad. Sci. 1963, 153, 49–52. [Google Scholar]
- Lavrent’ev, M.M. On Certain Ill-Posed Problems of Mathematical Physics; Sobolev Division of the USSR Academy Science: Novosibirsk, Russia, 1962. [Google Scholar]
- Ivanov, V.K.; Vasin, V.V.; Tanana, V.P. Theory of Linear Ill-Posed Problem and Application; Nauok: Moscow, Russia, 1978. [Google Scholar]
- John, F. Numerical solution of the equation of heat conduction for preceding times. Ann. di Mat. pura ed Appl. 1955, 40, 129–142. [Google Scholar] [CrossRef]
- Cheniguel, A. Numerical method for the heat equation with Dirichlet and Neumann conditions. Proc. Int. MultiConference Eng. Comput. Sci. 2014, 1, 12–14. [Google Scholar]
- Alifanov, O.M.; Artioukhine, E.A.; Rumyantsev, S.V. Extreme Methods for Solving Ill-Posed Problems with Applications to Inverse Heat Transfer Problems; Begell House: New York, NY, USA, 1995; ISBN 156700038X. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 0470501979. [Google Scholar]
- Dmitriev, V.I.; Stolyarov, L.V. Numerical method for the inverse boundary-value problem of the heat equation. Comput. Math. Model. 2017, 28, 141–147. [Google Scholar] [CrossRef]
- Sidikova, A.I. Approximate Solution of Inverse Boundary Value Problem for Heat Conduction Equation. In Proceedings of the 2018 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 9–16 September 2018; pp. 1–7. [Google Scholar]
- Sidikova, A.I. A Study of an Inverse Boundary Value Problem for the Heat Conduction Equation. Numer. Anal. Appl. 2019, 12, 70–86. [Google Scholar] [CrossRef]
- Tanana, V.P.; Markov, B.A. The control problem for the heat equation in the case of a composite material. J. Phys. Conf. Ser. 2021, 1715, 12049. [Google Scholar] [CrossRef]
- Makhtoumi, M. Numerical solutions of heat diffusion equation over one dimensional rod region. arXiv 2018, arXiv:1807.09588. [Google Scholar]
- Sidikova, A.I.; Al-Mahdawi, H.K. The solution of inverse boundary problem for the heat exchange for the hollow cylinder. AIP Conf. Proc. 2022, 2398, 60050. [Google Scholar]
- Al-Mahdawi, H.K.I.; Abotaleb, M.; Alkattan, H.; Tareq, A.-M.Z.; Badr, A.; Kadi, A. Multigrid Method for Solving Inverse Problems for Heat Equation. Mathematics 2022, 10, 2802. [Google Scholar] [CrossRef]
- Al-Mahdawi, H.K.; Sidikova, A.I. Iterated Lavrent’ev regularization with the finite-dimensional approximation for inverse problem. AIP Conf. Proc. 2022, 2398, 60080. [Google Scholar]
- Al-Mahdawi, H.K.; Sidikova, A.I.; Alkattan, H.; Abotaleb, M.; Kadi, A.; El-kenawy, E.-S.M. Parallel Multigrid Method for Solving Inverse Problems. MethodsX 2022, 9, 101887. [Google Scholar] [CrossRef] [PubMed]
- Al-Mahdawi, H.K.I.; Alkattan, H.; Abotaleb, M.; Kadi, A.; El-kenawy, E.-S.M. Updating the Landweber Iteration Method for Solving Inverse Problems. Mathematics 2022, 10, 2798. [Google Scholar] [CrossRef]
- Glasko, V.B.; Kulik, N.I.; Shklyarov, I.N.; Tikhonov, A.N. An inverse problem of heat conductivity. Zhurnal Vychislitel’noi Mat. I Mat. Fiz. 1979, 19, 768–774. [Google Scholar]
- Belonosov, A.S.; Shishlenin, M.A. Continuation problem for the parabolic equation with the data on the part of the boundary. Siber. Electron. Math. Rep. 2014, 11, 22–34. [Google Scholar]
- Kabanikhin, S.I.; Hasanov, A.; Penenko, A.V. A gradient descent method for solving an inverse coefficient heat conduction problem. Numer. Anal. Appl. 2008, 1, 34–45. [Google Scholar] [CrossRef]
- Yagola, A.G.; Stepanova, I.E.; Van, Y.; Titarenko, V.N. Obratnye zadachi i metody ikh resheniya. Prilozheniya k geofizike. In Inverse Problems and Methods for their Solution: Applications to Geophysics; BKL Publishers: Moscow, Russia, 2014. [Google Scholar]
- Kabanikhin, S.I.; Krivorot’ko, O.I.; Shishlenin, M.A. A numerical method for solving an inverse thermoacoustic problem. Numer. Anal. Appl. 2013, 6, 34–39. [Google Scholar] [CrossRef]
- Tanana, V.P. On the order-optimality of the projection regularization method in solving inverse problems. Sib. Zhurnal Ind. Mat. 2004, 7, 117–132. [Google Scholar]
- Farlow, S.J. Partial Differential Equations for Scientists and Engineers; Courier Corporation: North Chelmsford, MA, USA, 1993; ISBN 048667620X. [Google Scholar]
- Tanana, V.P.; Bredikhina, A.B.; Kamaltdinova, T.S. On an error estimate for an approximate solution for an inverse problem in the class of piecewise smooth functions. Tr. Inst. Mat. I Mekhaniki UrO RAN 2012, 18, 281–288. [Google Scholar]
- Tanana, V.P.; Rudakova, T.N. The optimum of the M. M. Lavrent’ev method. J. Inverse Ill-Posed Probl. 2011, 18, 935–944. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Nuaimi, B.T.; Al-Mahdawi, H.K.; Albadran, Z.; Alkattan, H.; Abotaleb, M.; El-kenawy, E.-S.M. Solving of the Inverse Boundary Value Problem for the Heat Conduction Equation in Two Intervals of Time. Algorithms 2023, 16, 33. https://doi.org/10.3390/a16010033
Al-Nuaimi BT, Al-Mahdawi HK, Albadran Z, Alkattan H, Abotaleb M, El-kenawy E-SM. Solving of the Inverse Boundary Value Problem for the Heat Conduction Equation in Two Intervals of Time. Algorithms. 2023; 16(1):33. https://doi.org/10.3390/a16010033
Chicago/Turabian StyleAl-Nuaimi, Bashar Talib, H.K. Al-Mahdawi, Zainalabideen Albadran, Hussein Alkattan, Mostafa Abotaleb, and El-Sayed M. El-kenawy. 2023. "Solving of the Inverse Boundary Value Problem for the Heat Conduction Equation in Two Intervals of Time" Algorithms 16, no. 1: 33. https://doi.org/10.3390/a16010033
APA StyleAl-Nuaimi, B. T., Al-Mahdawi, H. K., Albadran, Z., Alkattan, H., Abotaleb, M., & El-kenawy, E.-S. M. (2023). Solving of the Inverse Boundary Value Problem for the Heat Conduction Equation in Two Intervals of Time. Algorithms, 16(1), 33. https://doi.org/10.3390/a16010033









