1. Introduction
Medium- and low-voltage distribution networks have undergone important changes in their physical and computational structures that have transformed these passive grids into to active distribution networks [
1,
2]. These changes have been provoked by new regulations regarding the integration of renewable energy resources that have focused on the decabornization of the world’s energy matrix [
3,
4,
5]. The main goal of electricity distribution networks is to transport electricity to end-users with the necessary standards of efficiency, quality, and reliability. This requires minimizing energy losses and improving transport processes in order to achieve more efficient and competitive networks [
6].
To improve the efficiency of electrical distribution networks with regard to reducing power losses, reactive power compensation is one of the most widely recognized methods, given its contribution in this regard and other benefits such as power factor correction, increased transport capacity, improved operation of network lines and devices, voltage stability, and improved voltage profiles. All of these depend on different operating constraints [
7], as it is of great importance to reduce losses and minimize investment costs for current distribution systems.
One of the best options for energy loss reduction is distributed generation (DG). The authors of [
8] presented a decision-making analysis aimed at determining the optimal location and sizes for DG in radial distribution networks, considering the improvement of the voltage profiles and the minimization of the total grid’s active and reactive power losses. However, DG may have very high initial installation costs, especially when compared to strategies such as grid reconfiguration and shunt reactive power compensation with capacitors [
9]. Capacitive compensation can yield the benefits of loss reduction, power factor correction, and voltage profile improvement to the fullest if the location and size are efficiently determined. However, capacitor banks typically inject reactive power in fixed steps [
10], which reduces the positive effect of reactive power injection on reducing energy losses, mainly when daily demand profiles with high variations are considered in the grid operation environment.
In order to improve the advantages of using reactive power to minimize total grid power losses, it is possible to use distribution static compensators (D-STATCOMs). These are regulation devices based on a power electronics voltage source converter that add flexibility to the power distribution network. In comparison with a variable-step capacitor bank, a D-STATCOM is a more flexible device, as it injects the exact amount of reactive power in accordance with the network requirements. This is by means of efficient control techniques [
11]. It is important to mention that D-STATCOMs can inject and absorb reactive power with very fast dynamic responses through the injection of phase-shifted current to the system at the common coupling point, which aids in power factor correction and harmonic filtering, among other benefits [
12]. D-STATCOMs can be located in any of the nodes of the distribution system, so it is important to determine their optimal siting and sizing using efficient optimization techniques for the reduction of energy losses and the minimization of operating costs.
In the specialized literature, there are multiple reports regarding the optimal location and sizing of D-STATCOMs in distribution networks. Some of these approaches are discussed in this document. The authors of [
12] presented a complete way to determine the optimal location and size of D-STATCOMs via analytical and heuristic optimization methods. In addition, they presented the typical objective functions of the specialized literature to improve network performance, i.e., voltage stability and power losses indicators. The work by [
13] proposed a multi-objective particle swarm optimizer to place and size D-STATCOMs while considering simultaneous power grid reconfiguration. As objective functions, the minimization of active power losses, the voltage stability index, and the load capacity factor of the distribution lines were considered. The main feature of this approach is that the optimization process was carried out only under maximum load conditions, which is not considered a suitable scenario given the potential oversizing of the compensating devices, since the consumption of active and reactive power are variable inputs.
The authors of [
14] proposed a multi-objective fuzzy approach based on ant colony optimization in order to solve the simultaneous and proximate reconfigurations (sizing and placement) of PV sources and D-STATCOMs in distribution systems. The objective was to minimize network losses and to improve voltage profiles and feeder load balancing operation characteristics. This methodology was validated in the IEEE 33-bus grid with excellent numerical results. The authors of [
15] presented a heuristic method based on voltage and power loss indexes in order to locate and size D-STATCOMs in radial electrical distribution networks. Numerical validation of this heuristic approach was performed on the IEEE 33-bus test feeder. However, the authors only considered maximum load conditions.
Table 1 summarizes the different algorithms used in the literature to solve the problem concerning the placement and sizing of D-STATCOMs in distribution networks.
The main features of the optimization methods in
Table 1 are the following: (i) the most common function is the minimization of energy losses, and (ii) the studied problems show two tendencies: the first is related to metaheuristics, and the second offers convex formulations or approaches that combine convex and combinatorial methods.
Based on the aforementioned literature review, the problem of reactive power compensation in power systems is still an area of interest for both academia and the industry. Therefore, this research article proposes the following contributions:
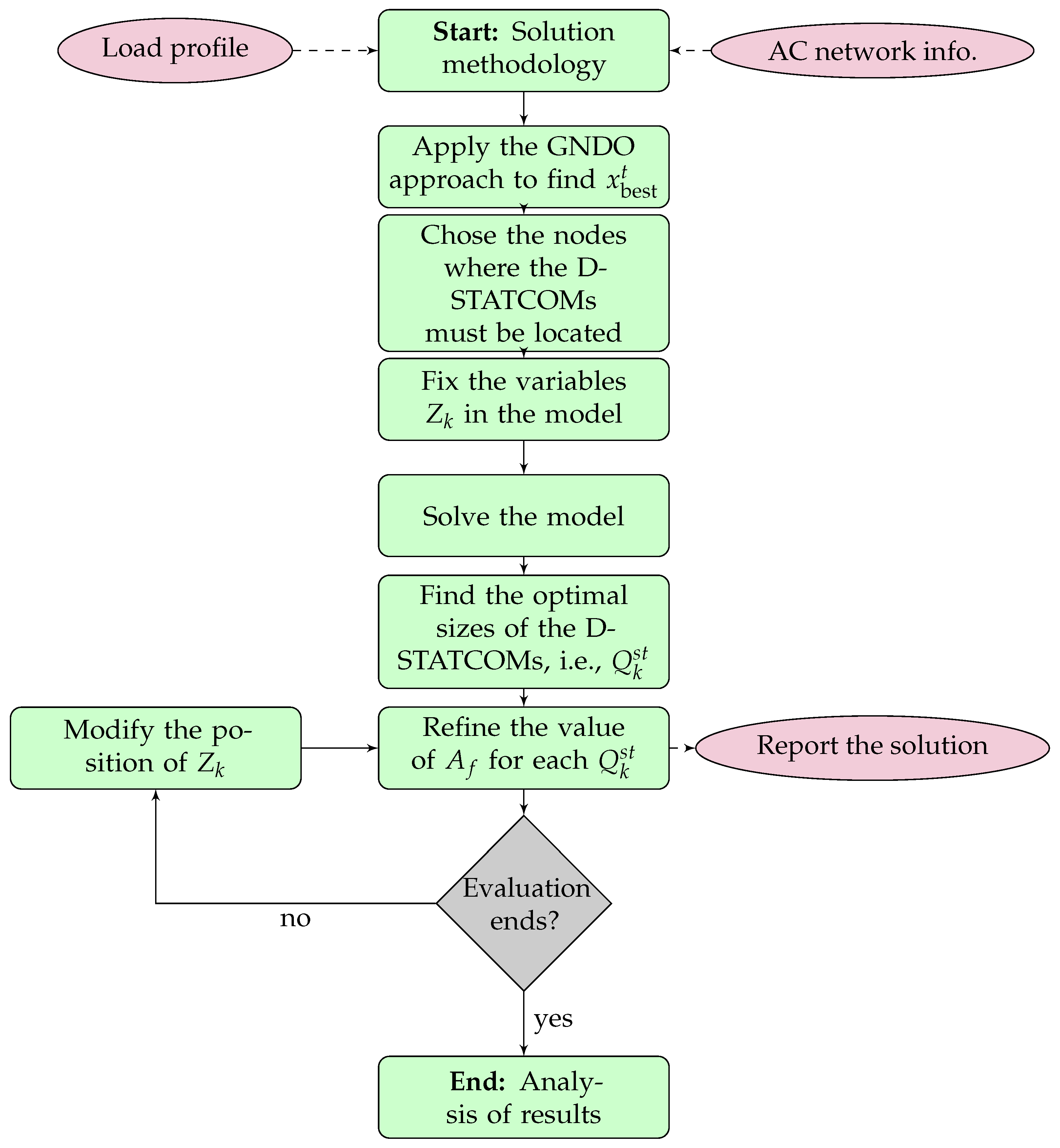
We provide a new solution method based on application of the generalized normal distribution optimizer (GNDO) for locating and sizing D-STATCOMs in distribution networks with radial and meshed topologies while using a discrete–continuous codification.
We combine the GNDO approach with an efficient power flow multi-period approach that allows solving of the technical constraints of the optimization problem, i.e., power balance, voltage regulation, and device capabilities, among others.
We improve the final solution obtained with the proposed master–slave optimizer by using the set of nodes where the D-STATCOMs must be located as inputs for the optimal reactive power flow (ORPF) problem, aiming to further minimize the final expected annual operating costs of the distribution grid.
Note that the selection of the GNDO as a solution technique to address the optimal location and sizing problem for D-STATCOMs in distribution networks is based on three facts:
The GNDO is a metaheuristic method inspired by the classical theory of normal probability distributions. It considers an initial population that evolves throughout the iterative process, considering the means and the standard deviation as advance parameters.
The computational implementation of the GNDO is simple and requires only a few mathematical programming skills to adapt it to any optimization problem that includes binary and continuous variables.
Multiple reports in the specialized literature have confirmed that the GNDO approach is efficient at solving complex optimization problems such as the placement location of renewable energy resources in AC and DC networks [
24,
25] and parameter extraction for photovoltaic models [
26], among other optimization problems.
Note that the proposed solution methodology addressed in this research to locate, size, and operate D-STATCOMs in electrical distribution networks is different from recently published literature reports, since the GNDO approach allows reaching better objective function values with respect to the literature in the case of fixed reactive power injection, and also, with the improvement stage based on the ORPF solution, we find additional profits for the utility company that have not been previously presented by solution methodologies based on combinatorial optimizers available in the current literature. It is important to mention that this work focuses on the optimal design and operation of D-STATCOMS in distribution networks under normal operating conditions and upon the basis of the demand curves provided by utilities. However, as future research, an interesting development could consider the probabilistic nature of the loads and new paradigms regarding the transformation of energy consumption habits with the massive integration of electric vehicles into medium- and low-voltage distribution networks [
27].
The remainder of this work has the following structure presented:
Section 2 presents the mathematical formulation of the D-STATCOM optimal integration problem in power distribution systems via mixed-integer nonlinear programming models.
Section 3 presents the proposed solution method, which is based on the GNDO and the successive approximations power flow approach, with the aim of determining the nodes where the D-STATCOMs must be located as well as their sizes. These nodes are also used as inputs for the ORPF formulation to reach additional reductions in the objective function value.
Section 4 outlines the main characteristics of the test system, which is a 33-node IEEE system that includes demand scenarios for residential, industrial, and commercial users.
Section 5 presents the results of the simulation as well as its analysis and discussion. Finally,
Section 6 describes the main conclusions derived from this study.
4. Test System Characterization
To demonstrate the efficiency and robustness of the proposed optimization, the IEEE 33-bus grid with radial and meshed configurations was employed [
22]. The electrical configuration of this distribution grid is depicted in
Figure 2. Note that this electrical system operates at substation terminals with a nominal voltage of
kV. In addition, the parametric information regarding the peak load consumption and distribution lines is presented in
Table 2.
To consider the effect of load classification in the IEEE 33-bus grid for optimally locating and sizing the D-STATCOMs, the electrical curves of residential, industrial, and commercial users are shown in
Table 3.
To calculate the objective function value regarding component
(see Equation (
2)), all the parameters listed in
Table 4 are used [
19,
35]. Note that the evaluation of this objective function considers that the variable
is defined in Mvar.
In this research, the concept of a benchmark case is assigned to the scenario where the distribution system is operated without considering shunt compensation, i.e., it is the simulation scenario where the total active and reactive power consumptions are always supplied by the generation source, which, in the case of distribution networks, is the substation bus when there is no penetration of distributed energy resources. In the case of the IEEE 33-bus grid with a radial connection, the benchmark case is calculated with the parameters in
Table 4, which corresponds only to an
value of about USD
per year of operation, with
being equal to zero since no D-STATCOMs are considered.
5. Results and Discussion
To validate the proposed solution methodology, the solution of the optimization model for locating and sizing D-STATCOMs in electrical distribution via the AESDC was implemented in MATLAB version R2021b on a computer with an Intel Core i7-10750H @2.6 GHz and 16.0 GB of DDR4 RAM at 2300 MHz on a 64-bit version of Microsoft Windows 10 Home. The validation of the proposed master–slave optimization model in conjunction with the improvement stage was carried out while considering the following facts:
Two configurations are considered for the IEEE 33-bus grid: a radial configuration with the original structure presented in
Figure 2 and a meshed configuration with three tie-lines added to the radial topology, as proposed in [
22].
The GNDO approach, combined with the successive approximations power flow method, is used to obtain the initial nodal locations and sizes for the D-STATCOMs with fixed reactive power injection. Thus, the location of these devices is fixed in the exact MINLP model while aiming for additional gains for operating these reactive power compensators with variable reactive power throughout the day.
For comparison, the MINLP model’s exact solutions obtained with the BONMIN and COUENNE solvers and the recently developed Salp Swarm Algorithm (SSA) [
22] are considered in order to confirm the effectiveness and robustness of the proposed optimization approach.
Note that in order to ensure the effectiveness of the proposed master–slave optimization regarding the solution quality, 100 consecutive evaluations of the complete solution methodology were considered, with 1000 iterations for each of them. With these values, a statistical study of the GNDO performance was conducted considering mean, maximum, minimum, and standard deviation parameters. It is worth mentioning that in order to to make fair comparisons with the SSA approach presented by the authors of [
22] as well as the implementation of the exact model in GAMS software with the BONMIN and COUNNE solvers, all results were obtained with our own implementations that were conducted during this research.
It is worth mentioning that in order to ensure that all the numerical validations presented in this paper were correct, the following validation procedure was followed.
The solution of the multi-period optimal power flow problem for the benchmark case was implemented in MATLAB with our own scripts. However, to ensure the effectiveness of this approach, a comparative analysis with the DIgSILENT software was performed.
The convergence analysis of the power flow problem for the proposed successive approximations power flow method was proven by the authors of [
30], which implies that under the studied conditions this method always converges to the power flow solution.
The solution of the MINLP model with he GNDO approach combined with the successive approximations method was also validated via GAMS and DIgSILENT.
5.1. Radial Configuration Results
Table 5 shows the comparison between the SSA approach, the BONMIN and COUENNE solvers, and to the proposed GNDO approach that considers fixed reactive power injection throughout the day for the IEEE 33-bus system with a radial configuration.
The numerical results presented in
Table 5 allow stating that:
The GAMS solvers (COUENNE and BONMIN) are stuck in locally optimal solutions, with reductions of 11.22 and 16.12%, respectively, with respect to the benchmark case. This can be attributed to the fact that the MINLP structure of the model (
1)–(
8) causes exact solution methods based on Branch and Bound and combined with interior point methods to get stuck in local solutions without the ability to escape from them because of the non-convexity of the solution space.
The proposed GNDO approach improved the best solution reported in the literature, which was obtained with the SSA approach, i.e., by about USD per year of operation. This improvement was reached since the GNDO detected that node 14 is a better location for one of the D-STATCOMs, instead of node 13 as per the SSA approach.
The total installed reactive power obtained with the GNDO approach was 869.84 kvar, while the solution found with the SSA approach installed 891.99 kvar. This implies that the proposed GNDO approach improved the objective function value by selecting a better set of nodes to place the D-STATCOMs, with the main advantage being that less investment is required for these devices.
To demonstrate that the hourly variation of the reactive power injection with D-STATCOMs in distribution networks allows additional gains in the expected annual grid operating costs,
Table 6 compares fixed and variable reactive power injection by fixing the nodes reached by the GNDO approach in the exact MINLP model (
1)–(
8) using the BONMIN solver as a solution method.
The results in
Table 6 show that an additional reduction of USD 1665.25 is obtained when variable reactive power injection is implemented with D-STATCOMs. That is to say, this is in comparison with the fixed injection scenario. This additional profit is reached when the total installed capabilities of the D-STATCOMs increase to 1034.67 kvar, which in turn implies an increase of 164.83 kvar with respect to the fixed injection scenario. With this additional reactive power, the D-STATCOMS have more flexibility to generate variable reactive power, i.e., they gain the ability to follow the demand behavior in order to inject only the needed reactive power for each hour as a function of the total grid requirements.
5.2. Meshed Configuration Results
Table 7 presents the comparison between the SSA approach, the BONMIN and COUENNE solvers, and the proposed GNDO approach that considers fixed reactive power injection throughout the day for the IEEE 33-node grid with a meshed grid topology.
The numerical results shown in
Table 7 imply that:
Once again, the COUENNE and BONMIN solvers got stuck in locally optimal solutions, which is attributed to the nonlinear non-convex nature of the exact MINLP model. The COUENNE solver only reached a reduction of with respect to the benchmark case, while the BONMIN solver yielded a better local solution, with a reduction of with respect to the benchmark.
The proposed GNDO approach found a solution with an expected reduction in the annual operative costs of about 10.45%, i.e., 0.04% better than the solution reported by the SSA approach. However, the main characteristic of both solutions is that these located the D-STATCOMs in the same set of nodes (14, 30, and 32). However, their sizes differ, which explains the difference in the final objective function value.
The total installed size of the D-STATCOMs with the GNDO is 731.83 kvar, whereas the SSA installed 742.90 kvar, which implies that with a better definition of the D-STATCOM sizes it is also possible to reach better final objective function values. Nevertheless, the main characteristic of this behavior is that based on its probability functions, the GNDO explored and exploited the solution space with better sensitivity than the SSA approach.
To confirm that the variable reactive power injections play an important role in reducing the expected annual operating costs of the network with respect to the fixed injection case, the results presented in
Table 8 are employed.
The results in
Table 8 show that the scenario with variable reactive power injection finds additional improvements regarding the final objective function value, i.e., approximately USD 136.89 per year of operation when compared with the fixed reactive power injection case. This result confirms that the main advantage of using D-STATCOMs is that variable reactive power is injected as a function of the network requirements, which justifies the distribution of static compensators instead of capacitor banks in order to support reactive power in distribution grids with variable demand behavior.
5.3. Additional Results
With the purpose of demonstrating the effectiveness and robustness of the GNDO approach in conjunction with the successive approximations power flow method, after 100 consecutive evaluations for the radial and meshed grid structures, the results in
Table 9 show the statistical analysis for both simulation cases.
The difference between the minimum and maximum values reached in the radial configuration was about USD 8776.59, which implies that in the worst simulation case, the expected reductions with respect to the benchmark case would be 10.43%. When compared to the results shown in
Table 5, this is better than both GAMS solutions. Even if the maximum result (worst result of the GNDO method) for the radial simulation case is a local solution, it has better characteristics than the local optimal solutions found with the MINLP BONMIN and COUENNE solvers in GAMS.
As for the meshed configuration, the difference between the maximum and minimum objective function values was USD 2397.22, i.e., the worst solution reached by the GNDO approach reduces the expected annual operating costs by about 7.69%. This result confirms that for the meshed configuration case, the worst solution of the GNDO approach is also better than both solutions found with the GAMS software and with the BONMIN and COUENNE solvers.
The mean values for the radial and meshed configurations are very close to the minimum values, i.e., most of the solutions are closer to each other in a closed ball with a radius equivalent to the standard deviation. These results confirm the effectiveness of the GNDO approach at solving the complex optimization problem involving the optimal location and size of D-STATCOMs in distribution grids via combinatorial optimization, with the main advantage that less than 43 s is required to reach a solution in both simulation cases.
6. Conclusions and Future Work
The optimal reactive power compensation problem via D-STATCOM location and sizing was studied in this research through the application of master–slave optimization methodology that solves its exact MINLP formulation. In the master stage, the GNDO approach was implemented using a discrete codification that decided the nodes where the D-STATCOMs were to be located in conjunction with their optimal sizes. In the slave stage, a power flow method (the successive approximations approach) was used to define the expected energy loss costs for a daily operation horizon. An improvement stage was implemented in the exact MINLP model that involved fixing the location of the D-STATCOMs provided by the master–slave optimizer in order to obtain an NLP model that could vary the reactive power injection on an hourly basis in order to obtain additional profits for the distribution company.
The numerical simulations run in the IEEE 33-bus system with radial and meshed configurations while including residential, industrial, and commercial users demonstrated that:
In the radial configuration scenario, the proposed GNDO approach reached a lower minimum objective function value than the SSA approach. In addition, the improvement stage allowed for an additional reduction of USD 1665.25 regarding the fixed injection case, which confirms that the variable reactive power scenario via the daily control of the D-STATCOMs allows the distribution company to obtain additional profits in the total annual expected operating costs of the network.
In the meshed configuration, the proposed GNDO approach found the same nodal location for the D-STATCOMs as the SSA methodology. However, the sizing was better, which allowed for a better final objective function value. In the variable reactive power scenario, an additional profit of USD 186.39 with respect to the fixed injection scenario was also reached, thus confirming that controlling the reactive power injection as a function of the system’s requirements is the better option to operate D-STATCOMs based on utilities.
The expected annual operative gains for the meshed topology are considerably lower than those of the radial grid, i.e., USD 9080.32 for the meshed cased vs. USD 22,397.96 for the radial case. This is an expected result since in meshed configurations the energy losses are lower when compared to radial configurations, which is attributed to better flow distribution and voltage profiles.
Regarding the processing times, the proposed GNDO approach found the solution for the MINLP model in less than one minute for both topologies, which confirms the effectiveness and robustness of the master–slave optimization methodology to deal with complex electrical engineering problems involving solution spaces with infinite dimensions and complex nonlinear, non-convex constraints.
In future work, the following studies can be conducted: (i) combining the D-STATCOMs with renewable generators in radial and meshed distribution grids by defining their sizes and locations in order to reduce the grid investments and the operating and maintaining costs; and (ii) a comparative study between different reactive power compensators such as D-STATCOMs, Thyristor-controlled series compensators (TCSCs), and Static VAR Compensators (SVCs), as well as their impact on the expected annual grid operating costs.