On the Semi-Local Convergence of Two Competing Sixth Order Methods for Equations in Banach Space
Abstract
1. Introduction
2. Majorizing Sequences
3. Convergence
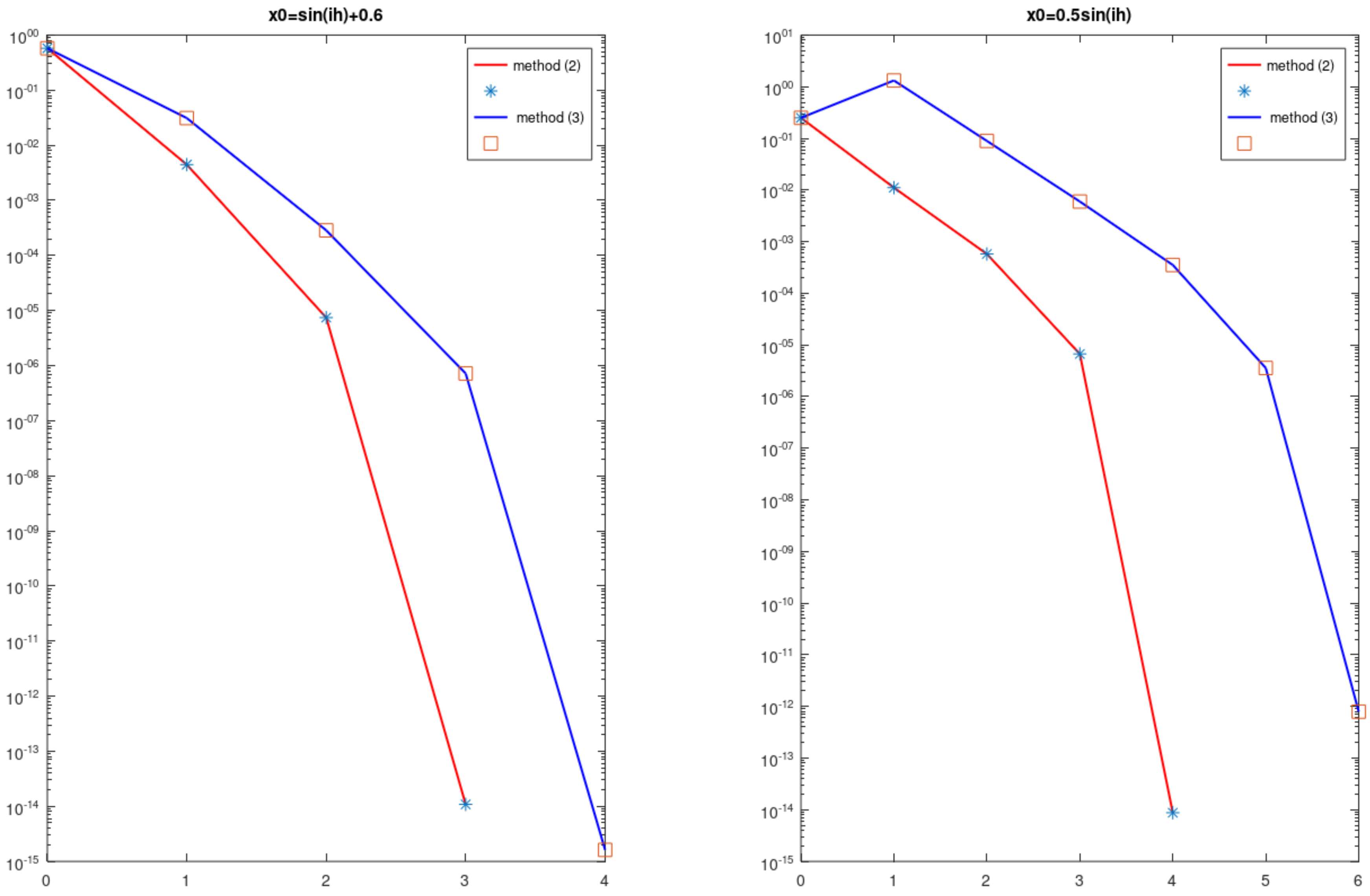
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Argyros, I.K. The Theory and Applications of Iteration Methods, 2nd ed.; Engineering Series; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Shakhno, S.M. Convergence of the two-step combined method and uniqueness of the solution of nonlinear operator equations. J. Comput. Appl. Math. 2014, 261, 378–386. [Google Scholar] [CrossRef]
- Shakhno, S.M. On an iterative algorithm with superquadratic convergence for solving nonlinear operator equations. J. Comput. Appl. Math. 2009, 231, 222–235. [Google Scholar] [CrossRef]
- Argyros, I.K.; Shakhno, S.; Yarmola, H. Two-step solver for nonlinear equation. Symmetry 2019, 11, 128. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. A fourth-order method from quadrature formulae to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 188, 257–261. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Convergence, efficiency and dynamics of new fourth and sixth order families of iterative methods for nonlinear systems. J. Comput. Appl. Math. 2015, 275, 412–420. [Google Scholar] [CrossRef]
- Jarratt, P. Some fourth order multipoint iterative methods for solving equations. Math. Comp. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Kou, J.; Li, Y. An improvement of the Jarratt method. Appl. Math. Comput. 2007, 189, 1816–1821. [Google Scholar] [CrossRef]
- Magrenán, Á.A. Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 2014, 233, 29–38. [Google Scholar]
- Chun, C.; Neta, B. Developing high order methods for the solution of systems of nonlinear equations. Appl. Math. Comput. 2019, 342, 178–190. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newtons method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algor. 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. Efficient Jarratt-like methods for solving systems of nonlinear equations. Calcolo 2014, 51, 193–210. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, H. A simple and efficient method with high order convergence for solving systems of nonlinear equations. Comput. Math. Appl. 2015, 69, 1220–1231. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control. 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, L. Image enhancement based on rough set and fractional order differentiator. Fractal Fract. 2020, 6, 214. [Google Scholar] [CrossRef]
- Ding, W.; Wang, Q.; Zhang, J. Analysis and prediction of COVID-19 epidemic in South Africa. ISA Trans. 2022, 124, 182–190. [Google Scholar] [CrossRef] [PubMed]
| n | ||||||
|---|---|---|---|---|---|---|
| (2) | (3) | (2) | (3) | (2) | (3) | |
| 0 | 3.0000e-01 | 3.0000e-01 | 2.0000e-01 | 2.0000e-01 | 1.0000e-01 | 1.0000e-01 |
| 1 | 1.2680e-01 | 8.3460e-01 | 3.7373e-03 | 2.7441e-02 | 2.3940e-05 | 4.1343e-04 |
| 2 | 2.0491e-05 | 6.6401e-02 | 3.3085e-14 | 6.3708e-07 | 0 | 4.1744e-14 |
| 3 | 0 | 1.6444e-05 | 0 | |||
| 4 | 0 | |||||
| n | ||||||
|---|---|---|---|---|---|---|
| (2) | (3) | (2) | (3) | (2) | (3) | |
| 0 | 1.0000e+00 | 1.0000e+00 | 4.0000e+00 | 4.0000e+00 | 9.0000e+00 | 9.0000e+00 |
| 1 | 8.1192e-02 | 1.0405e-01 | 1.1974e+00 | 1.3057e+00 | 3.3764e+00 | 3.5981e+00 |
| 2 | 1.8507e-06 | 7.5738e-05 | 1.2931e-01 | 1.9303e-01 | 9.3516e-01 | 1.1262e+00 |
| 3 | 0 | 0 | 2.1824e-05 | 6.2796e-04 | 6.7872e-02 | 1.3871e-01 |
| 4 | 0 | 2.2427e-13 | 7.0948e-07 | 2.0438e-04 | ||
| 5 | 0 | 2.6645e-15 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyros, I.K.; Shakhno, S.; Regmi, S.; Yarmola, H. On the Semi-Local Convergence of Two Competing Sixth Order Methods for Equations in Banach Space. Algorithms 2023, 16, 2. https://doi.org/10.3390/a16010002
Argyros IK, Shakhno S, Regmi S, Yarmola H. On the Semi-Local Convergence of Two Competing Sixth Order Methods for Equations in Banach Space. Algorithms. 2023; 16(1):2. https://doi.org/10.3390/a16010002
Chicago/Turabian StyleArgyros, Ioannis K., Stepan Shakhno, Samundra Regmi, and Halyna Yarmola. 2023. "On the Semi-Local Convergence of Two Competing Sixth Order Methods for Equations in Banach Space" Algorithms 16, no. 1: 2. https://doi.org/10.3390/a16010002
APA StyleArgyros, I. K., Shakhno, S., Regmi, S., & Yarmola, H. (2023). On the Semi-Local Convergence of Two Competing Sixth Order Methods for Equations in Banach Space. Algorithms, 16(1), 2. https://doi.org/10.3390/a16010002







