Abstract
In recent years, the development of computer technology has promoted the informatization and intelligentization of hospital management systems and thus produced a large amount of medical data. These medical data are valuable resources for research. We can obtain inducers and unknown symptoms that can help discover diseases and make earlier diagnoses. Hypertensive disorder in pregnancy (HDP) is a common obstetric complication in pregnant women, which has severe adverse effects on the life safety of pregnant women and fetuses. However, the early and mid-term symptoms of HDP are not obvious, and there is no effective solution for it except for terminating the pregnancy. Therefore, detecting and preventing HDP is of great importance. This study aims at the preprocessing of pregnancy examination data, which serves as a part of HDP prediction. We found that the problem of missing data has a large impact on HDP prediction. Unlike general data, pregnancy examination data have high dimension and a high missing rate, are in a time series, and often have many non-linear relations. Current methods are not able to process the data effectively. To this end, we propose an improved bi-LSTM-based missing value imputation approach. It combines traditional machine learning and bidirectional LSTM to deal with missing data of pregnancy examination data. Our missing value imputation method obtains a good effect and improves the accuracy of the later prediction of HDP using examination data.
1. Introduction
1.1. Background
Hypertensive disorder in pregnancy (HDP) is a common kind of obstetric complication that severely threatens the life safety of pregnant women [1,2] and has an adverse impact on the growth and development of the fetus. Hence, it is of great significance to discover and cure HDP in advance. Every pregnant woman will have multiple pregnancy examinations during pregnancy, producing examination data capable of reflecting the dynamic changes of health indicators of pregnant women during pregnancy. A huge number of current prediction models make predictions on the basis of multi-source data [3,4], especially for pregnancy examination data [5,6,7]. However, the pregnancy examination data in the real world always contain different kinds of problems. One of the most common issues is missing data. It exists in almost all kinds of data sets, and the size of the missing data can significantly affect the research outcomes. As more and more studies on HDP are turning into data-driven analysis, the missing data problem is becoming more and more critical in this domain.
1.2. Related Work
Nowadays, several scholars have realized the severity of the missing data problem and explored many approaches to reduce the negative effects of missing data. There are several methods now to process missing data. For instance, the most common method, mean filling, uses the mean value of the sample and prior value filling to fill the missing values with the support of medical experts. In addition, there exist some filling methods that have advantages in effect and applicable scenes. For instance, regression filling [8] develops a regression model on the basis of the relationship between the data of each indicator and the pregnancy week to make interpolations to fill the data. KNN (K-nearest neighbors) [9] filling selects K samples that are most similar to the sample to be filled based on a specific kind of similarity measurement algorithm and fills the data with the weighted mean of the full data of the K samples. The matrix completion algorithm [10] decomposes the original data into two low-rank matrices and then uses the gradient descent method to obtain an approximate value to fill missing data.
Although classical methods of statistics, such as interpolation-like techniques, can be used to approximate the missing data in a time series, the recent developments in deep learning (DL) have given impetus to innovative and much more accurate forecasting techniques. Some researchers use a combination of LSTM and transfer learning to fill in missing data values for water quality, air quality, and energy [11,12,13]. Zhou et al. proposed LSTM-based missing data reconstruction for time-series Landsat images [14]. Sowmya et al. combined LSTM with different activation functions to impute the missing data of a diabetic, breast cancer, and wine quality data set [15]. Kostas Tzoumpas et al. combined a CNN and bi-LSTM to fill the missing data of a sensor [16].
1.3. Contributions
All of the above research results are worthy of study. Pregnancy examination data is of high dimension, has a high missing data rate, is in a time series, and often has many non-linear relations, but the above research work has not enabled a richer and more complete extraction of pregnancy examination data in the data pre-processing stage, which in turn has led to poor results regarding missing value filling.
Therefore, we propose an improved bi-LSTM-based missing value imputation approach for pregnancy examination data. The combined model uses the random forest (RF) model principal component analysis (PCA) and undersampling algorithm in the data preprocessing stage, which can analyze the relationships of the features, balance the dataset and filter out abnormal data. Then, bi-LSTM fills the processed data and significantly improves the already good results from other models. This model, compared with the traditional LSTM model, has forward and backward factors to jointly determine the results of filling missing data, which makes the accuracy of filling missing data effectively improved.
2. Materials and Methods
2.1. Data
The data used by this paper are provided by the Institute of Science and Technology of the National Health Commission of PRC, which is the pregnancy examination data of a hospital from 2008 to 2018 (10 years in total, desensitized). The data contained examination records of 120,396 pregnant women, 7518 of whom suffer from HDP, accounting for about 6.24%. In addition, our data covered the pregnancy examination data of the whole pregnancy cycle from early to late maternal pregnancy examination records. The whole pregnancy cycle is the pregnancy examination data from the 1st week to the 70th week, which is very beneficial to our prediction research on HDP and other diseases. Each pregnant woman will take several examinations during the pregnancy of 70 weeks, with each examination corresponding to a piece of data. Each examination does not include all the examination items, and in different stages of pregnancy, the possibility of taking an examination is also different. Figure 1 shows the distribution of the numbers of examinations taken during pregnancy:
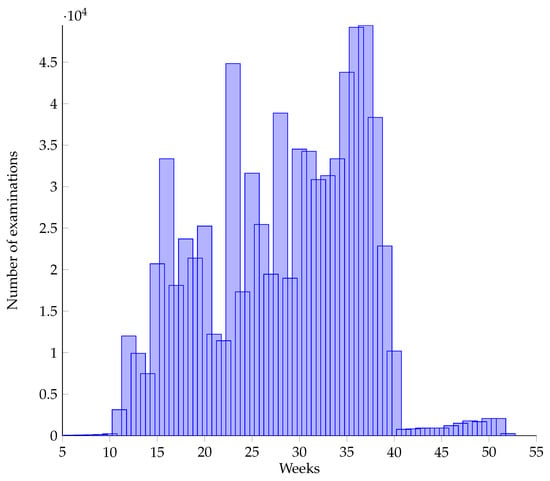
Figure 1.
Distribution of physical examination times during 0–70 weeks of pregnancy.
The data mainly include 4 parts: pregnogram examination data, routine urine data, routine blood data and biochemical D data. The pregnogram examination data contain the results of 10 kinds of pregnancy examinations, including weight, fundal height, diastolic pressure, fetal position, etc. Table 1 lists the name and examples of each indicator. Routine blood data, routine urine data and biochemical D data contain the results of 141 examination indicators, such as platelet count, white blood cell and hemoglobin. Table 1 lists each category and indicator of the 3 examinations. Urine protein (++) means that the urine protein is 1.0–2.0g/L, which is higher than the normal range.Edema ++ indicates a severity level of 2 for edema. All examination indicator can be viewed in Table A1 in Appendix A.

Table 1.
Indicators of pregnogram examination.
2.2. Methods
We propose a method that combines traditional machine learning and bidirectional LSTM to deal with the missing data of pregnancy examination data. First, we use traditional machine learning processing methods to remove redundant or unrelated feature data, analyze relationships among the features, and select important features. Then, we use filling methods to fill missing values. After trying different methods, this paper finally selects the bidirectional LSTM (long short-term memory) method to fill a large number of missing data to optimize the dataset. LSTM and its related variants perform very well in many other experiments [17] and in ours. The data processing flow path is shown in Figure 2.

Figure 2.
The data processing flow path.
2.3. Traditional Machine Learning
2.3.1. Relationship Analysis of the Features
The examination data in this paper are too large and complicated. After removing redundant data, we used the random forest [18] method to analyze relationships among the features.
The random forest (RF) model, developed on the basis of the decision regression tree model, builds multiple classification trees by the bootstrap method. Then, it selects data randomly to carry out training on each classification tree. Features selected for different classification trees are also chosen at random. Finally, we compared the importance of different features based on the training effect of each classification tree.
Table 2 and Table 3 show the top 10 and bottom 10 in terms of importance. It is easy to find that information related to pregnogram data is much more important than information related to biochemical D data, which lays the foundation of our later strategy to fill in missing values and work to reduce the dimension of the data.

Table 2.
Top 10 features of importance.

Table 3.
Bottom 10 features of importance.
2.3.2. Outlier Detection
Outliers are abnormal data that fall outside the cluster. Many fields in medical datasets are manually input, so input errors occur easily. For example, some decimals may be ignored, causing the value to increase 100 times, which obviously leads to abnormal data and results in difficulty in data analysis. This kind of abnormal data will affect the performance of our algorithm if we do not handle it. The concrete method to detect outliers is described as follows.
Detection based on distance measurement [19]: First, we define the distance between samples and then set a threshold distance. Outliers are defined as data points that are far from the others. This method has the advantage of simplicity, which requires low computation and storage costs, but the threshold value is hard to set, and its computation complexity is too big, which is unacceptable for big datasets.
Detection based on clustering algorithms [20]: A clustering model is built, and outliers are defined as data points that are far from all clusters or do not belong to any cluster significantly. This method has an advantage in that there are clustering algorithms that have been developed already, but the method is too sensitive to the selection of the number of clusters.
Detection based on density [21]: The local density of outliers is significantly lower than for neighboring points. The score of an outlier of a sample is the inverse of the density of the area the sample is in. Different definitions of density correspond to different detection methods.
Detection based on statistical methods: A statistical distribution method is built, and outliers are defined as data points with low possibilities. This method has the advantage of the solid foundation of statistics, but it is necessary to obtain the type of distribution of the dataset first; otherwise, it may cause a heavy-tailed distribution.
As this dataset consists of examination indicators, which have relatively fixed ranges, we selected methods based on statistics. For each indicator, we used Matlab to generate a scatter diagram. As the number of outliers was too small, we detected them with a priori knowledge and manually selected them to fix or propose.
2.3.3. Data Filtering
According to the missing mechanism, Rubin [22] divided missing data into 3 categories: completely random missing, random missing and incompletely random missing data. This dataset is of the category of incompletely random missing data. The missing nature of the data depends on the pregnancy week. After analysis, the missing data rate of each pregnancy week is shown in Figure 3. It can be found that data are mainly in the range from week 11 to week 40 (with the ratio of data not missing over 5%), and the later the weeks are, the more pregnancy examination records there are. Therefore, this paper selects data from week 11 to week 40 to be processed and analyzed.
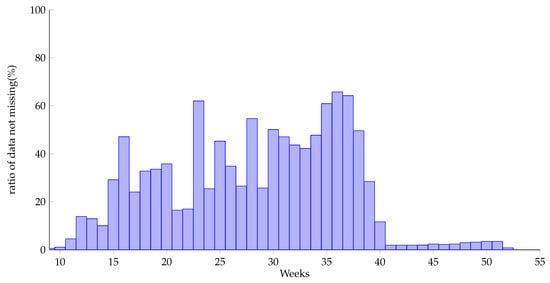
Figure 3.
Ratio of data not missing by pregnancy weeks.
As some pregnant women have relatively few examinations, in the 30 weeks from week 11 to week 40, about 10% of the samples have less than 5 examinations. To improve the quality of the dataset, these data should be removed. However, to utilize the dataset as much as possible, this paper uses the selection method described as follows. We consider the degree of the concentration of the pregnancy weeks of the sample with low examination times. If the pregnancy weeks of the examinations are concentrated in the early or late weeks, the sample is considered to be worthless and removable, but if the weeks are scattered, the sample is considered to have the effect of “supporting” and should be kept. Therefore, this paper calculates the ratio of the range between the pregnancy weeks of each sample and the selected pregnancy week range and selects samples with a ratio greater than 0.8.
This dataset has a large number of complicated indicators, the total number of which is 200. The missing status on each feature is shown in Figure 4. It is shown that that data of most features are severely missing, with only about 10% left. The data of a small number of features are in a good state. Considering the model’s performance and the difficulty of training, we selected features with a missing rate lower than 30% to build the dataset.
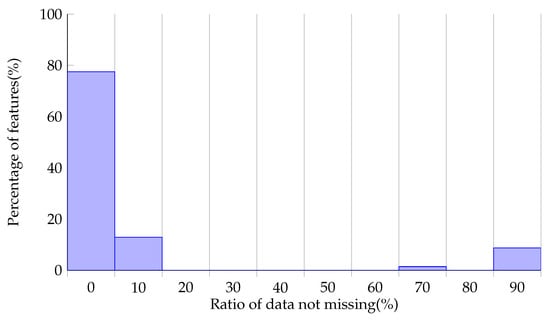
Figure 4.
Missing data status on features.
2.3.4. Feature Extraction
In the previous relationship analysis of features, except for a few kinds of information of pregnograms that are highly related with the disease state of pregnant women, the relationship of a large amount of information of biochemical D, routine blood, and routine urine data is relatively scattered, but they contain a lot of health information regarding the pregnant women. Therefore, methods such as the missing rate ratio, low variance filtering, high relation filtering, and even random forest are not suitable for feature extraction in this paper. The reason is that these methods directly remove a large number of irrelevant features in the dimension reduction process, which greatly damages the richness of the dataset of HDP.
On the other hand, the dataset of HDP is large, containing nearly one million data records. Therefore, the efficiency of feature extraction is also an important factor affecting our decision. Table 4 is a comparison of common feature extraction methods. Reverse feature removal and forward feature construction both need to pre-train the model to select features. The size of the dataset of HDP greatly limits the speed of the model’s training, causing the feature extraction work to consume too much, so they are also not feasible.

Table 4.
Comparison of common feature extraction methods.
After comprehensive consideration, this paper selected principal component analysis (PCA) for the reduction of the dimensions of the data of the HDP dataset [23,24]. Considering the characteristics of the prediction model of HDP, the dataset of HDP after dimension reduction has 32 feature items. Figure 5 shows the process of feature extraction.
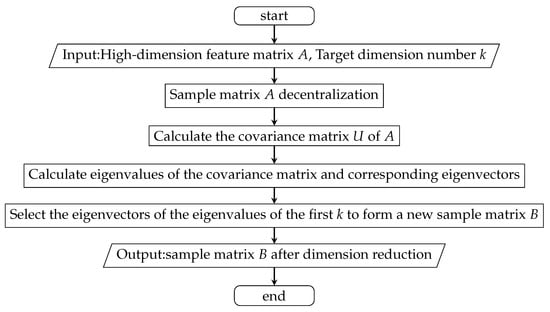
Figure 5.
The process of feature extraction.
2.3.5. Balancing the Dataset
The positive and negative samples are extremely imbalanced in the original dataset, the proportion of which is about 1:10. If original data are used for training directly, the model will not be able to learn the characteristics of positive samples effectively. There are two common methods to balance a dataset: using an oversampling method, such as SMOTE [25], and undersampling. Oversampling will copy or approximate the samples with a small number to supplement the samples so as to balance the number of positive and negative samples. However, such a method to copy or approximate samples will increase the risk of over-fitting, especially in this case of an extreme imbalance of positive and negative samples. Therefore, this paper used the method of random undersampling of negative samples. Negative samples with a number equal to the positive samples were randomly selected to construct the dataset. This method also reduces the difficulty and cost of training effectively.
2.3.6. Processed Data
Table 5 shows the changes before and after data preprocessing. After traditional machine learning processing, redundant and useless data were eliminated. We only retained feature data that were highly relevant to the HDP. The following experiments are based on the processed data.

Table 5.
Changes before and after data processing.
2.4. Strategy to Fill Missing Values—Bi-LSTM
This dataset has severe missing data in the dimensions of time and features, so it is of great significance to discuss the influence of missing data processing on the model’s effect. There are three ways to analyze data with missing values: (1) analyze the data with missing values directly; (2) select methods that are insensitive to missing data for analysis; (3) analyze the missing data after interpolation and filling. Filling missing data has always been a hot topic in various fields. Currently, several effective missing data filling methods have been proposed by experts and scholars. For example, the commonly used mean value interpolation method uses the mean value of sample variables to replace the missing value [26]. Random interpolation, on the basis of the sample distribution, extracts a substitution of missing values with a specific possibility from the population. Regression interpolation uses the linear relationship between auxiliary variables and target variables to predict missing values. Dempster proposed the EM (expectation maximization) algorithm [27] in 1977, which is used to estimate unknown parameters under known variables and can effectively carry out the task of the interpolation of missing data. These methods have high accuracy when filling a small amount of missing data in a static situation but are not satisfactory when processing missing data with a nonlinear relationship, time series characteristics and multiple variables. Recently, with the rapid development of the field of neural networks and the improvement of computing capabilities, neural networks have been widely used in the processing and analysis of missing data, recurrent neural networks (RNN) [28] especially. They are capable of finding long-term time dependences and analyzing time series of variable length, thus playing a very important role in time series analysis.
Figure 6 shows the distribution of the number of pregnancy examinations (i.e., the length of time series) between week 11 and week 40. It can be seen from the figure that the length of the series of most samples is about 11 times. In Figure 1, it can be seen that the data are not uniformly distributed at different time points, and most of the data are concentrated in the later weeks.
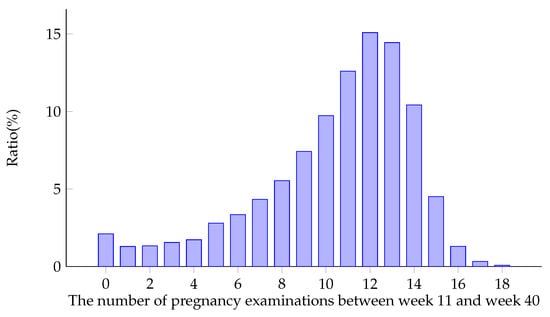
Figure 6.
Distribution of physical examination times during pregnancy after preprocessing.
This paper selected data of a part of time as markers and selected other data as training data. The filling effect was evaluated by the prediction results and symmetric mean absolute percentage error (SMAPE) of markers. Considering the distribution of data at each time point, markers should not be selected randomly in order to prevent losing the data of important time points and severely affecting the results. This paper proposes a method described as follows: let represent the missing state of a series of data:
For ,
represents the “ignorability” of the data of the time point in the series. The less missing data near this value, the more “unimportant” the time point is, and it can be selected from the training set as a marker, where is the decay rate. Table 6 is the result of calculating the missing data state when the sequence length is 10 and the decay rate is 0.5.

Table 6.
Calculation sample of “ignorability” of data in time series.
For ,
represents the data storage rate of time point i in the whole data set. The higher it is, the lower the missing data rate of the time point is, and the lower the possibility it needs to be filled is. Thus, for each series, the possibility that each time point is selected to be a marker , where and are the parameters that adds up to 1, which are used to adjust the influence of the two parts of the possibility. We select data of a certain number of time points in each series as markers to construct the data and markers of the training set. According to distribution of the data, the final parameters used in this paper are , and the data at four time points are selected as markers.
In this paper, we compare several methods of filling missing values, including traditional machine learning methods, such as cubic spline interpolation and KNN filling, and deep learning methods, such as the LSTM model and bidirectional LSTM model.
- 1
- Cubic spline interpolation
Cubic spline interpolation (spline interpolation) [29] is a process of obtaining the curve function group by solving the three-moment equations through a series of value points on the curve. First, we select an interval containing missing values of the dataset, construct a cubic interpolation equation to represent the interval, and then conduct interpolation for the missing values according to the equation.
- 2
- KNN filling
The idea of the KNN method is to identify k spatially similar samples in the dataset. We then use these “k” samples to estimate the value of the missing data points. The missing value of each sample is interpolated using the mean value of the “k” neighborhood found in the data set. In this case, as Figure 7 shows, the missing value is determined by its neighbors. The green point’s neighbors are the orange points in the ellipse. Each pregnant woman’s data are mapped to a vector in a high-dimensional space. To be spatially close means to be physically similar.
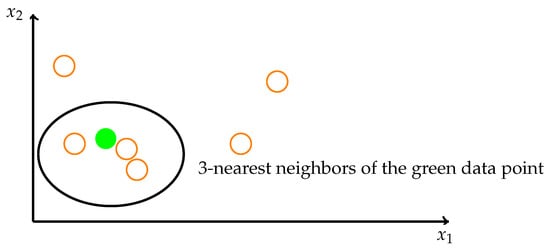
Figure 7.
The theory of KNN algorithm.
- 3
- ST-MVL
ST-MVL is a spatio-temporal multiview-based learning (ST-MVL) method [30] to collectively fill missing readings in a collection of geosensory time series data considering (1) the temporal correlation between readings at different timestamps in the same series and (2) the spatial correlation between different time series. The method combines empirical statistic models, consisting of inverse distance weighting and simple exponential smoothing, with data-driven algorithms, comprised of user-based and item-based collaborative filtering.
- 4
- LSTM Model
The LSTM model is a special kind of recurrent neural network (RNN), which was first proposed by Hochreiter and Schmidhuber [31] in 1997 and solved the problem of the vanishing gradient and long-term dependence (i.e., the inability to integrate dependencies of a series that are too long) of RNNs. As shown in Figure 8, an LSTM consists of a memory unit c and three gates (an input gate i, output gate o, and forgetting gate f).
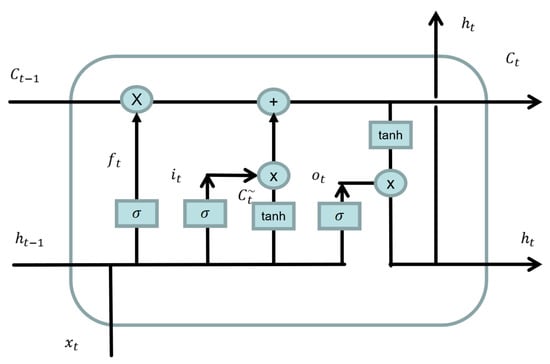
Figure 8.
Unidirectional LSTM unit structure.
The first step of the LSTM is to determine how much of the state of the previous time point will be retained to the current moment . This decision is made by the “forgetting gate”. The forgetting gate uses the output of the previous neural cell and the input of the current cell to calculate a number between 0 and 1, representing how much data from the previous cell was recorded. Here, 1 indicates complete recording, and 0 indicates complete forgetting. The equation is shown as follows, where is the weight matrix of the forgetting gate, is the bias term of the forgetting gate, and is the sigmoid activation function:
The second step of LSTM is to determine what information is to be stored in the current unit state, which is divided into two parts. First, an input gate determines which values to update, and then a new candidate vector is created through the tanh layer and added to the state. The current state of the unit is calculated as follows. First, we forget the data that need to be forgotten by multiplying the state of the last time point by . Then, we add to obtain the value of the current unit:
The third step of the LSTM is to determine the output of the unit. The output is based on the state of previous calculating unit, first through the sigmoid layer to determine which parts of the unit to output, then through tanh to reset the system state (setting the value to between −1 and 1). Then, we multiply it by a sigmoid gate to determine the final output:
- 5
- Bidirectional LSTM Model
The bidirectional LSTM model consists of a forward LSTM structure and a reverse LSTM structure, as is shown in Figure 9. They have the same structure and are independent of each other and only accept input of different word orders. The bidirectional LSTM deep learning network has great advantages, a clear structure, a clear output meaning of the middle layer, and it is easier to find optimization methods for it. The bidirectional LSTM model takes the influence of forward and reverse word order of sentences into account, which can better extract the semantic information of sentence structures. In this task, compared with unidirectional LSTM, the effect of filling missing data with bidirectional LSTM is better.
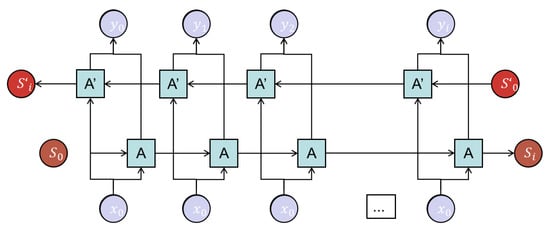
Figure 9.
Bidirectional LSTM structure.
3. Results and Analysis
3.1. LSTM Model Hyperparameters
The hyperparameters of model training are shown in Table 7.

Table 7.
Hyperparameter Settings.
3.2. Analysis of Experimental Results
In this paper, we propose an improved bi-LSTM-based missing value imputation approach for pregnancy examination data. This model, compared with the traditional LSTM model, has forward and backward factors to jointly determine the results of filling miss data, which makes the accuracy of filling missing data effectively improved. This paper selects the results on the validation set after training on 70% of the preprocessed data as the training set. Table 8 shows the comparison of different filling methods. This paper uses SMAPE to evaluate the missing values. It is shown that the bidirectional LSTM model interpolation method has the best filling effect regarding missing data compared with other methods. The experiment found that ST-MVL is not good for filling data columns with serious missing data, so we used data with a missing rate of less than 50% for ST-MVL experiments.

Table 8.
Comparison of different filling methods.
In addition, the lightgBM disease prediction algorithm [32] was used to compare the training model before and after data filling. As is shown in Figure 10, the blue curve represents the training results using the complete data of pregnancy weeks filled by LSTM, and the orange curve represents the training results using unfilled pregnancy week data. It can be seen that the accuracy of the prediction results after filling is higher. In addition, it can be seen that the prediction accuracy is positively correlated with the number of pregnancy weeks. From the figure above, it can be seen that the model has a good prediction effect at just 25–26 pregnancy weeks, and the AUC of the HDP prediction effect can reach more than 0.75. From 25 weeks on, forecasts continuously improve. Data from week 25 to week 40 are more important to model predictions than data before week 25.
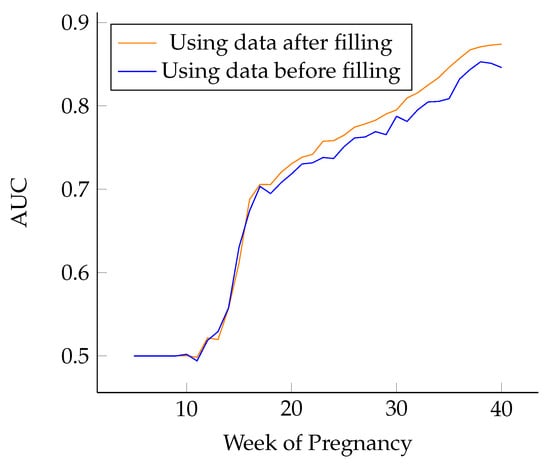
Figure 10.
Prediction effect of different pregnancy weeks.
4. Conclusions and Future Work
HDP is a common obstetric complication that severely threatens the life of pregnant women. Therefore, it is of great significance to detect and prevent HDP in advance. However, pregnancy examination data have the characteristics of high dimensions, large amounts, being in a time series and having a high missing rate, so a good data processing method plays an extremely important role in predicting and preventing HDP. This paper first introduces pregnancy examination data in detail and then proposes a series of data processing strategies, including basic data processing methods such as feature relation analysis, data filtering, feature extraction, balancing the dataset, etc. This paper also puts forward a method of missing value filling based on a bidirectional LSTM model and makes a comparison with cubic spline interpolation, KNN filling and an LSTM model, the results of which show that the bidirectional LSTM model achieves good results in filling missing data. Although this paper has made some progress in data processing, especially in filling missing data, there is still much work to be further studied and explored, including the following aspects:
- In data processing, there are still some factors that are not considered, such as region, age, etc.
- The method of filling missing valuesis relatively simple at present, and the future research direction is to combine multiple algorithms to deal with different features.
- At present, the data preprocessing process is basically manual processing, so it can save a lot of time and stamina to standardize the processing process and build ETL (extract-transform-load) tools automatically.
- After prediction, screening proper drug treatment programs [33] is also important for doctors and patients. Building a complete intelligent medical system is very meaningful.
- At present, the amount of research data in the medical field is very large, but these data are often chaotic. The format of diagnostic data in different medical institutions is not uniform, so it is difficult to use it directly for research. Constructing a complete standardized medical research database is of great significance for disease prevention, drug development, and other research.
Author Contributions
Conceptualization, X.L., L.Y. and R.L.; methodology, X.L., N.Y., R.L. and Z.X.; software, X.L., Z.X., Y.Y. and N.Y.; resources, X.L., R.L., N.Y. and L.Y.; writing—original draft preparation, R.L., Z.X., Y.Y. and N.Y.; writing—review and editing, X.L., R.L., Z.X. and L.Y.; supervision, X.L. and L.Y.; project administration, X.L. and R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable. All data are anonymous and masked. No private information is used.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from the National Research Institute for Health and Family Planning of China.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Each category and indicator of the examinations is shown in Table A1.

Table A1.
Indicators of routine blood, routine urine and biochemical D data.
Table A1.
Indicators of routine blood, routine urine and biochemical D data.
| Routine Urine (UR) | Biochemical D | Routine Blood |
|---|---|---|
| UR_White Blood Cell(centrifuged) | Biochemical D_Calcium | Blood Routine_Lymphocyte Percentage |
| UR_Red Blood Cell(centrifuged) | Biochemical D_Globulin | Blood Routine_Eosinophil Absolute Value |
| UR_Epithelial Cell(centrifuged) | Biochemical D_Albumin: Globulin | Blood Routine_Platlet Count |
| UR_Average RBC Hemoglobin Amount | Biochemical D_Total Bilirubin | Blood Routine_RBC Distribution Width |
| UR_Average Platelet Volume | Biochemical D_Alanine Aminotransferase | Blood Routine_Monocyte Percentage |
| UR_Fungus | Biochemical D_Iron | Blood Routine_Red Blood Cell |
| UR_Granular Cast | Biochemical D_Direct Bilirubin | Blood Routine_Eosinophil Percentage |
| UR_Mucus Strand | Biochemical D_Total Bile Acid | Blood Routine_Monocyte Absolute Value |
| UR_Abnormal RBC | Biochemical D_Phosphorus | Blood Routine_ Average RBC Hemoglobin Amount |
| UR_Red Blood Cell | Biochemical D_Aspartate Aminotransferase | Blood Routine_White Blood Cell |
| UR_Hyaline Cast | Biochemical D_Total Protein | Blood Routine_Basophil Percentage |
| UR_Urate Crystal | Biochemical D_Glutamic-pyruvic Aminotransferase | Blood Routine_Average RBC Volume |
| UR_Sulfa Crystal | Biochemical D_Glutamic-pyruvic:Glutamic-oxalacetic | Blood Routine_RBC Distribution Width-SD |
| UR_Crystal | Biochemical D_Glutamic-oxalacetic Aminotransferase | Blood Routine_Large Platelet Ratio |
| UR_Epithelial Cell | Biochemical D_Indirect Bilirubin | Blood Routine_Average RBC Hemoglobin Concentration |
| UR_RBC Cast | Biochemical D_Total Cholesterol | RBC Distribution Width-CV |
| UR_Normal RBC | Biochemical D_Lactic Dehydrogenase | Glycosylated Hemoglobin |
| UR_Phosphate Crystal | Biochemical D_Kalium | Blood Routine_Large Platelet Count |
| UR_Pyocyte | Biochemical D_Carbon Dioxide Concentration | Blood Routine_Urobilinogen |
| UR_Trichomonad | Biochemical D_Triglyceride | Blood Routine_PH |
| UR_Inorganic Salt Crystal | Biochemical D_Sodium | Blood Routine_Specific Gravity |
| UR_WBC Cast | Biochemical D_Creatine Kinase | Blood Routine_Irregular Antibody Screening(3 cells) |
| UR_Cast | Biochemical D_Creatinine | Blood Routine_Fibrinogen |
| UR_Waxy Cast | Biochemical D_Uric Acid | Blood Routine_Thrombin Time |
| UR_Oxalate Crystal | Biochemical D_Chlorine | Blood Routine_Prothrombin Time |
| UR_Average RBC Volume | Biochemical D_-glutamyl Transpeptidase | Blood Routine_Activated Partial Thromboplastin Time |
| UR_Progesterone | Biochemical D_Alkaline Phosphatase | Blood Routine_PT International Standardized Ratio |
| UR_RBC Distribution Width-SD | Biochemical D_Magnesium | Blood Routine_Sugar Shaker |
| UR_Hemoglobin | Biochemical D_Aspartate:Alanine | Blood Routine_Platelet Distribution Width |
| UR_Lymphocyte Absolute Value | Biochemical D_Creatinine(enzymic method) | Blood Routine_Hematokrit |
| UR_Neutrophil Percentage | Biochemical D_Serum Phosphorus | Blood Routine_Basophil Absolute Value |
| UR_Hematokrit | Biochemical D_Glycated Albumin Ratio | Blood Routine_Average Platelet Volume |
| UR_Lymphocyte Percentage | Biochemical D_PH | Blood Routine_Lymphocyte Absolute Value |
| UR_Average RBC hemoglobin Concentration | Biochemical D_Specific Gravity | |
| UR_Intermediate Cell Percentage | Biochemical D_Serum Thyrotropin | |
| UR_Intermediate Cell Absolute Value | Biochemical D_Low Density Lipoprotein Cholesterin | |
| UR_Large Platelet Ratio | Biochemical D_High Density Lipoprotein Cholesterin | |
| UR_Platelet Count | Biochemical D_Serum Free T4 | |
| UR_Platelet Distribution Width | Biochemical D_Thyroid Peroxidase Antibody | |
| UR_Neutrophil Absolute Value | Biochemical D_Creatine Kinase Isoenzyme | |
| Biochemical D_Lipoprotein(a) | ||
| Biochemical D_Apolipoprotein B | ||
| Biochemical D_Apolipoprotein A |
References
- Vest, A.R.; Cho, L.S. Hypertension in pregnancy. Curr. Atheroscler. Rep. 2014, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Riise, H.K.R.; Sulo, G.; Tell, G.S.; Igland, J.; Nygård, O.; Iversen, A.C.; Daltveit, A.K. Association between gestational hypertension and risk of cardiovascular disease among 617,589 Norwegian women. J. Am. Heart Assoc. 2018, 7, e008337. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Chang, L.; Yu, G. Effective data decision-making and transmission system based on mobile health for chronic disease management in the elderly. IEEE Syst. J. 2020, 15, 5537–5548. [Google Scholar] [CrossRef]
- Yu, G.; Wu, J. Efficacy prediction based on attribute and multi-source data collaborative for auxiliary medical system in developing countries. Neural Comput. Appl. 2022, 34, 5497–5512. [Google Scholar] [CrossRef]
- Ohkuchi, A.; Hirashima, C.; Takahashi, K.; Suzuki, H.; Matsubara, S. Prediction and prevention of hypertensive disorders of pregnancy. Hypertens. Res. 2017, 40, 5–14. [Google Scholar] [CrossRef]
- Ukah, U.V.; De Silva, D.A.; Payne, B.; Magee, L.A.; Hutcheon, J.A.; Brown, H.; Ansermino, J.M.; Lee, T.; von Dadelszen, P. Prediction of adverse maternal outcomes from pre-eclampsia and other hypertensive disorders of pregnancy: A systematic review. Pregnancy Hypertens. 2018, 11, 115–123. [Google Scholar] [CrossRef]
- Hasija, A.; Balyan, K.; Debnath, E.; Ravi, V.; Kumar, M. Prediction of hypertension in pregnancy in high risk women using maternal factors and serial placental profile in second and third trimester. Placenta 2021, 104, 236–242. [Google Scholar] [CrossRef]
- Kassam, S.A. Robust hypothesis testing and robust time series interpolation and regression. J. Time Ser. Anal. 1982, 3, 185–194. [Google Scholar] [CrossRef]
- Kramer, O. K-nearest neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–23. [Google Scholar]
- Candes, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Wang, M.; Zhai, C. A bi-directional missing data imputation scheme based on LSTM and transfer learning for building energy data. Energy Build. 2020, 216, 109941. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H.; Jiang, P.; Yu, S.; Lin, G.; Bychkov, I.; Hmelnov, A.; Ruzhnikov, G.; Zhu, N.; Liu, Z. A transfer Learning-Based LSTM strategy for imputing Large-Scale consecutive missing data and its application in a water quality prediction system. J. Hydrol. 2021, 602, 126573. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Ding, Y.; Lin, C.; Jiang, F.; Wang, M.; Zhai, C. Transfer learning for long-interval consecutive missing values imputation without external features in air pollution time series. Adv. Eng. Inform. 2020, 44, 101092. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Wu, T.; Feng, L.; Wu, W.; Luo, J.; Zhang, X.; Yan, N. For-backward LSTM-based missing data reconstruction for time-series Landsat images. GISci. Remote Sens. 2022, 59, 410–430. [Google Scholar] [CrossRef]
- Sowmya, V.; Kayarvizhy, N. An Efficient Missing Data Imputation Model on Numerical Data. In Proceedings of the 2021 2nd Global Conference for Advancement in Technology (GCAT), Bangalore, India, 1–3 October 2021; pp. 1–8. [Google Scholar]
- Tzoumpas, K.; Estrada, A.; Miraglio, P.; Zambelli, P. A data filling methodology for time series based on CNN and (Bi) LSTM neural networks. arXiv 2022, arXiv:2204.09994. [Google Scholar]
- Jiao, Y.; Qi, H.; Wu, J. Capsule network assisted electrocardiogram classification model for smart healthcare. Biocybern. Biomed. Eng. 2022, 42, 543–555. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, Y.; Miao, D.; Zhang, H. Neighborhood outlier detection. Expert Syst. Appl. 2010, 37, 8745–8749. [Google Scholar] [CrossRef]
- Jiang, S.Y.; An, Q.B. Clustering-based outlier detection method. In Proceedings of the 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinan, China, 18–20 October 2008; Volume 2, pp. 429–433. [Google Scholar]
- Liu, Z.; Pi, D.; Jiang, J. Density-based trajectory outlier detection algorithm. J. Syst. Eng. Electron. 2013, 24, 335–340. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Syms, C. Principal Components Analysis. In Encyclopedia of Ecology, 2nd ed.; Fath, B., Ed.; Elsevier: Oxford, UK, 2019; pp. 566–573. [Google Scholar]
- Omuya, E.O.; Okeyo, G.O.; Kimwele, M.W. Feature selection for classification using principal component analysis and information gain. Expert Syst. Appl. 2021, 174, 114765. [Google Scholar] [CrossRef]
- Li, K.; Zhang, W.; Lu, Q.; Fang, X. An improved SMOTE imbalanced data classification method based on support degree. In Proceedings of the 2014 International Conference on Identification, Information and Knowledge in the Internet of Things, Beijing, China, 17–18 October 2014; pp. 34–38. [Google Scholar]
- Kalton, G.; Kish, L. Some efficient random imputation methods. Commun. Stat. Theory Methods 1984, 13, 1919–1939. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 64–67. [Google Scholar]
- McKinley, S.; Levine, M. Cubic spline interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Yi, X.; Zheng, Y.; Zhang, J.; Li, T. ST-MVL: Filling Missing Values in Geo-Sensory Time Series Data. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems 30 (NIPS 2017); Curran Associates, Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Chang, L.; Wu, J.; Moustafa, N.; Bashir, A.K.; Yu, K. AI-driven synthetic biology for non-small cell lung cancer drug effectiveness-cost analysis in intelligent assisted medical systems. IEEE J. Biomed. Health Inform. 2021, 26, 5055–5066. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).