Abstract
Speaker verification systems use human voices as an important biometric to identify legitimate users, thus adding a security layer to voice-controlled Internet-of-things smart homes against illegal access. Recent studies have demonstrated that speaker verification systems are vulnerable to adversarial attacks such as FakeBob. The goal of this work is to design and implement a simple and light-weight defense system that is effective against FakeBob. We specifically study two opposite pre-processing operations on input audios in speak verification systems: denoising that attempts to remove or reduce perturbations and noise-adding that adds small noise to an input audio. Through experiments, we demonstrate that both methods are able to weaken the ability of FakeBob attacks significantly, with noise-adding achieving even better performance than denoising. Specifically, with denoising, the targeted attack success rate of FakeBob attacks can be reduced from 100% to 56.05% in GMM speaker verification systems, and from 95% to only 38.63% in i-vector speaker verification systems, respectively. With noise adding, those numbers can be further lowered down to 5.20% and 0.50%, respectively. As a proactive measure, we study several possible adaptive FakeBob attacks against the noise-adding method. Experiment results demonstrate that noise-adding can still provide a considerable level of protection against these countermeasures.
1. Introduction
With the advance of the technologies of Internet of things (IoT), smart devices, or virtual personal assistants, such as Google Assistant, Apple Siri, and Amazon Alexa, have been widely used at home to conveniently control and access different objects such as door lock, light blobs, air conditioner, and even bank accounts [2]. These smart home devices can be accessed and controlled through various methods, such as position detection, habit record, and human voice. Because of its convenience and ease of operation, voice control has become the most commonly used interface between users and smart devices.
To make voice control more secure, speaker verification systems apply human voice as an important biometric, in a similar way as fingerprint and iris recognition, to distinguish people. Compared with other verification methods, a speaker verification system has the advantages of being hands free and distance flexible, as it does not require a person to have physical contact with the system and is able to operate within a certain distance.
Speaker verification systems have faced many different attacks that attempt to compromise the integrity of the systems to allow illegal access from attackers [3]. The main attacks include replay attacks [4,5], voice cloning attacks [6], and adversarial attacks [1,7,8]. Among them, adversarial attacks are the most dangerous and especially difficult to detect and defend [7]. In such an attack, small perturbations are well designed and added to a clean audio from an illegal speaker to form the adversarial audio, which is barely perceptible by humans. That is, a person can hardly distinguish between the original clean audio and the adversarial audio when hearing them. However, the adversarial audio can be falsely accepted by the speaker verification system. As shown in [7], FakeBob adversarial attacks can achieve at least 99% targeted attack success rate on both open source and commercial speaker verification systems. This means that more than 99% of generated adversarial audios can be falsely accepted by the speaker verification systems.
Adversarial attacks and defenses have been widely studied in the area of image classification [9]. The defense systems against adversarial images, however, provide limited protection against adversarial audios [7]. Specifically, the defense tools based on the image classification problem, such as local smoothing, quantization, and temporal dependency detection [10], cannot effectively defeat the FakeBob attacks.
As a result, an important research question arises: How can we effectively and efficiently defend against voice adversarial attacks such as FakeBob? The goal of this research is to design and implement a defense system that is simple, light-weight, and effective against adversarial attacks. Specifically, the defense system should be compatible with any existing speaker verification system and should not require any change to the internal structure of the system. Moreover, the proposed system should not substantially increase the computation load of the speaker verification system. Most importantly, the defense system should be able to significantly slow down an attacker to generate a successful adversarial audio and greatly reduce the attack success rate. It is equally important that the defense method should not disturb the normal operations of a speaker verification system.
To achieve the goal, we start with studying the adversarial audio in both the time domain and the Mel spectrogram [11]. We find that the perturbations are similar to white noise, but they are not random and are intentionally designed to fool speaker verification systems. Based on these observations, our intuition is that if the perturbations in an adversarial audio can be removed or modified, adversarial attacks would be less effective against the speaker verification system. That is, before an input audio is taken into a verification system, a plugin function is applied to preprocess this input audio, with the goal to reduce the effect of perturbations from attacks. In this work, we consider two different plugin functions: denoising and noise-adding. The basic idea of the denoising function is to remove or reduce the perturbations or noise in input audios; and the implementation of denoising is based on the work from [12]. The goal of noise-adding is to introduce small noise to input audios to perturb adversarial audios, so that adversarial attacks would lose or reduce the ability to mislead a speaker verification system. Denoising and noise-adding are indeed opposite operations. Through experiments with the state-of-the-art speaker verification systems such as the Gaussian mixture model (GMM) [13] and i-vector [14], we find that both methods, especially the noise-adding method, can significantly reduce the attack success rate of FakeBob.
We summarize our main discoveries and contributions in the following:
- Using the time domain waveform and the Mel spectrogram, we find that the perturbations in an adversarial audio are very small and are similar to white noise. On the other hand, these perturbations are not random, but are intentionally designed to fool speaker verification systems.
- We propose a defense framework that is simple, light-weight, and effective against adversarial attacks in speaker verification systems.
- We find that the denoising function is able to reduce or remove the perturbations. As shown in our experiments based on FakeBob [7] against GMM and i-vector speaker verification systems, denoising can reduce the targeted attack success rate from 100% to 56.05% and from 95% to 38.63%, respectively. A downside of denoising is the added nonnegligible processing time in the GMM system.
- We discover that the noise-adding method performs much better than the denoising function. For example, we show that noise-adding can further reduce the targeted attack success rate of FakeBob to 5.20% in the GMM system and to 0.50% in the i-vector system. Moreover, the speed for FakeBob to generate an adversarial audio is slowed down 25 times in GMM and 5 times in i-vector under the impact of this defense. On the other hand, the processing time of the noise-adding function is very small and can be negligible. Furthermore, noise-adding only slightly increases the equal error rate of a speaker verification system. Therefore, we believe that such a simple solution can be applied to any speaker verification system against adversarial attacks.
- Inspired by adaptive attacks in [15], we study two intuitive strategies that can be used by adaptive FakeBob attacks against the noise-adding defense. One strategy is to bypass the plugin function in the speaker verification system to generate an adversarial audio. The other strategy is to update the objective function of the attack to make the adversarial audio more robust against noise. We show through experiments in a GMM speaker verification system that although these countermeasures reduce the effectiveness of the defense, noise-adding can still provide a considerable level of protection against adaptive FakeBob attacks.
- Through experiments, we find that noise with different probability distribution functions, such as Gaussian [16], uniform [17], logistic [18], Laplace [19], and a variation of the Rademacher distribution [20], has a similar effect on the normal operations of speaker verification systems and the FakeBob adversarial audios.
The remainder of this paper is structured as follows. Section 2 presents the related works, whereas Section 3 provides the background on speaker verification systems and FakeBob adversarial attacks against such systems. Section 4 presents our proposed defense framework and discusses two plugin functions, i.e., denoising and noise-adding. Next, Section 5 studies the possible adaptive FakeBob attacks against the noise-adding method. Section 6 evaluates the performance of our proposed defense system on normal operations of speaker verification systems, and against both original and adaptive FakeBob adversarial attacks. Finally, Section 7 concludes our effort and discusses the future work.
2. Related Work
There have been some works on the detection and defense methods against adversarial attacks in speaker verification systems [21,22,23]. For example, separate neural networks have been proposed to detect the appearance of adversarial samples in [24,25]. Generative adversarial network (GAN) based and variational autoencoders (VAE) based defenses have been studied in [26]. A voting method has been used to defend against adversarial examples in [27]. The implementation of these detection or defense methods, however, is not simple nor light-weight, and requires significant computations. Moreover, it is not clear how these detection and defense methods perform against the state-of-the-art adversarial attacks such as FakeBob.
The most relevant work to our approach was recently presented in [28]. This work also studied how to use small noise to counteract query-based black-box adversarial attacks. There are some key differences between their work and our work: (1) The work in [28] focuses on the image classification problem, whereas we study speaker verification systems. Images and audios are different signals and have distinct characteristics. As shown in [7], many defense systems that perform well for images cannot be applied to audios. (2) Image classification and speaker verification usually apply different machine learning methods. For example, an image classifier uses the classic convolutional neural network (CNN) model, whereas a speaker verification system applies the GMM. The same defense mechanism may have very different performance on distinct machine learning models. (3) The work in [28] aims at untargeted adversarial attacks, whereas our work focuses on targeted adversarial attacks.
3. Background
3.1. Speaker Verification Systems
Speaker verification (SV) systems have been widely used to identify a person through their voice. In our work, we focus on score-based SV systems, which most state-of-the-art SV systems belong to. A score-based SV system contains two phases: speaker enrollment and speaker recognition, as shown in Figure 1.
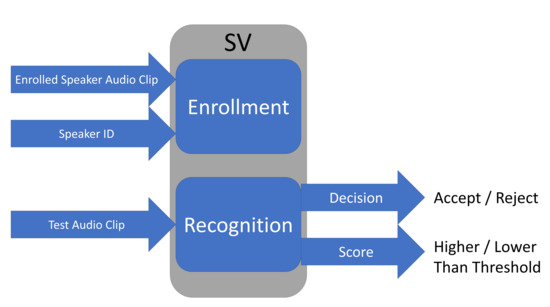
Figure 1.
A score-based speaker verification system.
In the speaker enrollment phase, a speaker needs to provide an identifier and their audio clips. The SV system transfers the speaker’s voice into a fixed length low dimensional vector called speaker embedding. Basically, the speaker embedding represents the features of a speaker’s voice and is used to calculate the level of similarity between two audio clips. Different SV systems use different approaches to obtain speaker embedding. The state-of-the-art SV systems include i-vector [14], GMM [13], d-vector [29], and x-vector [30]. In this work, we focus on GMM and i-vector, since they have been widely used in real life and applied by many as the baseline for comparisons. Here, we use the notation to refer to the vector of speaker embedding of the registered speaker R.
Besides obtaining the speaker embedding, the SV system attempts to find a proper threshold for this speaker during the enrollment phase. Such a threshold is a key consideration for a score-based SV system. To understand the importance of the threshold, we first look at the recognition phrase. As shown in Figure 1, when a test audio clip is provided to the SV system, it abstracts the speaker embedding of this audio, which is referred by . Then, the SV system calculates a similarity score between vector and vector . A higher score reflects more similarity between two vectors of speaker embedding. Finally, the similarity score is compared with the threshold. If the score is higher than or equal to the threshold, the system will accept the test audio clip and treat the speaker as the registered user. Otherwise, the system will reject the access of the speaker.
There are two basic false cases for an SV system: (1) accepting an illegal speaker, i.e., a speaker who is not the registered user, and (2) rejecting the registered speaker. For these two cases, we define two measures to evaluate the performance of an SV system, i.e., the false acceptance rate (FAR) and the false rejection rate (FRR), as follows:
For an ideal SV system, both FAR and FRR are 0. However, in a real SV system, there is a tradeoff between FAR and FRR, which makes it hard to keep both of them at 0. In general, when one decreases, the other will increase. Intuitively, when the threshold increases, it becomes more difficult for an audio clip to be accepted. As a result, FAR will decrease, while FRR will increase. A common practice is to choose a proper threshold that generates the same value for FAR and FRR. Such a value is called the equal error rate (EER) [31].
To find the EER and the corresponding threshold, both registered speaker audio clips and illegal speaker audio clips need to be provided during the enrollment phase. An SV system calculates the similarity scores for all provided audio clips and then finds the threshold that can lead to the EER.
3.2. Adversarial Attacks against Speaker Verification Systems
The study of adversarial attacks rooted from the research of applying machine learning to security-sensitive applications. In their original work, Biggio et al. pointed out that a well-designed adversarial attack can evade the malware detection in PDF files [32]. Moreover, Szegedy and Goodfellow et al. demonstrated that deep learning is particularly vulnerable to adversarial examples attacks [8,33]. For example, after very small perturbations are added, the image of panda can be recognized as gibbon with 99.3% confidence by a popular deep-learning based classifier [33]. Later, researchers realized that adversarial attacks can be applied to many different domains, such as cyber-physical systems [34], medical IoT devices [35], and industrial soft sensors [36]. Interested readers can refer to the paper [9] for a comprehensive survey on adversarial attacks and defenses.
Adversarial attacks and defenses have not yet been comprehensively and systematically studied in the field of SV systems. In the context of an SV system, adversarial attacks attempt to make the SV system falsely accept a well-designed illegal audio, which is called an adversarial audio. Specifically, the adversarial audio is an original illegal clean audio with small perturbations, often barely perceptible by humans. However, such perturbations lead the SV system to falsely accept the audio. Let x be an original audio from an illegal user and p be the perturbation vector with the same length as x. Then, the adversarial audio, , can be written as
If p is designed cleverly, humans may notice no or little difference between x and , but an SV system may be tricked to reject x and falsely accept .
To make sure that the adversarial audio is not noticed or detected by humans, the perturbations are usually very small and constrained by a perturbation threshold, . That is,
Choosing the value of is an important consideration for adversarial attacks. A larger value of makes the attack easier to succeed, but meanwhile causes it to be more perceptible by humans.
In our work, we study the FakeBob attack [7] and how to defend against it, since it is the state-of-the-art adversarial attack against SV systems including GMM, i-vector, and x-vector. Specifically, the FakeBob attack is a black-box attack that does not need to know the internal structure of an SV system. Moreover, as shown in [7], FakeBob achieves at least 99% targeted attack success rate (ASR) on both open source and commercial SV systems, where ASR is defined as follows:
It is noted that both FAR and ASR consider the audios from illegal users. However, the FAR is used for audios without perturbations from adversarial attacks, whereas the ASR is applied for audios with perturbations designed by attackers.
Figure 2 shows the basic process of FakeBob adversarial attacks. Basically, FakeBob applies the basic iterative method (BIM) [37] and the natural evolution strategy (NES) [38] to generate the adversarial audio. The attack takes multiple iterations to produce the final adversarial audio (e.g., ), with the goal of minimizing the following loss function or objective function
where y is an input audio, is the threshold of the SV system, and is the score function that calculates the score of an input audio for SV. FakeBob solves the optimization problem by estimating the threshold and iteratively finding the input audio that reduces , through the method of gradient decent over the input audio. Specifically, it applies the following gradient decent function
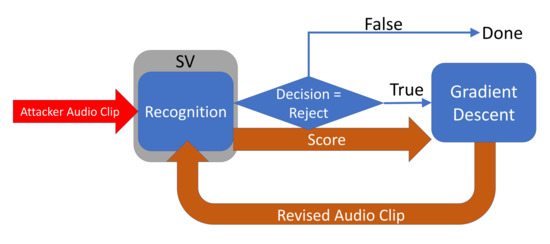
Figure 2.
The process of FakeBob adversarial attacks.
Note that here the gradient decent is different from the back-propagation that is widely used in deep learning, and the differentiation is based on input audios, instead of the weights of the machine learning model.
Define a sign function in the following way: For each element (i.e., ) in the vector y, a sign function gets the sign of the value of each element in the vector, i.e.,
Moreover, assume () is a signal in the original clean audio (i.e., x) from an illegal speaker, () is the corresponding signal in the adversarial audio at k-th iteration (i.e., ), and is the perturbation threshold shown in Equation (4). Based on the assumption in Equation (4), a clip function is defined as follows
Using the above functions, FakeBob updates the input audio through the following iteration
where is the learning rate. The FakeBob attack is summarized in Algorithm 1.
To better understand the FakeBob attack, we look into an example of an adversarial audio in both the time domain and the Mel spectrogram. Specifically, applying the FakeBob with the perturbation threshold of 0.002, we obtained an adversarial audio that is falsely accepted by the GMM SV system. Figure 3 shows the time waveform of the adversarial audio and the perturbations (i.e., p in Equation (3)) in both the time domain and the Mel spectrogram. It can be observed from Figure 3b that the perturbations used in the FakeBob attack are very small, i.e., . Moreover, the perturbations are similar to white noise, i.e., the perturbations are everywhere with the similar color in the Mel spectrogram, as shown in Figure 3c. On the other hand, from FakeBob attacks shown in Algorithm 1, it can be observed that these perturbations are not random, but are intentionally designed to fool the SV system.
| Algorithm 1 FakeBob Attacks |
| 1: Input: an audio signal array, threshold of the SV system |
| 2: Output: an adversarial audio |
| 3: Require: threshold of targeted SV system , audio signal array A, maximum iteration m, score function S, gradient decent function , clip function , learning rate , and sign function |
| 4: |
| 5: |
| 6: for ; ; do |
| 7: |
| 8: if then |
| 9: retun |
| 10: end if |
| 11: |
| 12: end for |
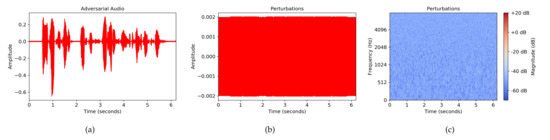
Figure 3.
An adversarial audio in the time domain and its perturbations in both the time domain and the mel spectrogram. (a) Adversarial audio in time domain; (b) perturbations in time domain; (c) perturbations in mel spectrogram.
4. Proposed Defense System
In this section, we propose a defense system against adversarial attacks in SV systems. Specifically, we first introduce the design goals of a defense system. Next, we describe our proposed defense system based on the observations from the adversarial audio. Finally, we provide the implementation details of the defense system in two different approaches: denoising that attempts to remove or reduce the perturbations in adversarial audios and noise-adding that attempts to perturb adversarial audios.
4.1. Design Goals of a Defense System
To counteract the adversarial attacks in an SV system, we attempt to design and implement a defense system that achieves the following goals:
- Simplicity. The defense system is easy to implement and can be compatible with an existing SV system. That is, it does not require any change to the internal structure of the currently used SV system.
- Light weight. It does not significantly increase the computation load of the SV system. The defense method only slightly increases the processing time for an input audio.
- Effectiveness. The defense algorithm should be able to greatly increase the time for an attacker to generate a successful adversarial audio and significantly reduce the ASR of adversarial attacks such as FakeBob. On the other hand, the defense method should minimally affect the normal operations of an SV system, such as slightly increasing the EER of the SV system.
4.2. A Defense System
To achieve these goals, we design a defense system based on the observations from an adversarial audio. As shown in Figure 3 in Section 3, the adversarial audio is simply the clean illegal audio with well-designed perturbations that are similar to white noise. If such perturbations can be removed or modified, adversarial attacks would lose the efficiency against the SV system. Based on this intuition, we propose a defense system as shown in Figure 4. Compared with Figure 1, in Figure 4 we add an additional module, i.e., a plugin function, before the recognition module to an SV system. Such a plugin function is used to preprocess an input audio to either forcefully remove the perturbations or intentionally modify the perturbations. In the following sections we will discuss two options for the plugin function: denoising and noise-adding.
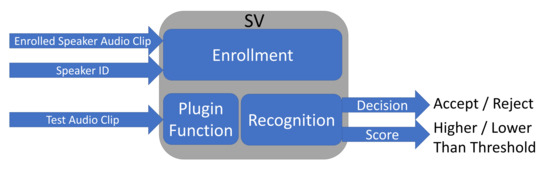
Figure 4.
The proposed defense system.
It can be observed that the proposed defense system is compatible with an existing SV system and can be applied to any SV system. It does not require to change the internal structure of an SV system. Moreover, the overhead of the defense method is only on the plugin function. If such a plugin is light weight, it will not introduce much additional computation to the SV system. Furthermore, the main goal of the plugin function is to modify the input audio, so that the SV system can reject adversarial audios, but can have the similar decisions on normal audios as in the SV system without the plugin. As our first attempt, we study denoising and noise-adding functions in this work. But other functions can be applied here as well.
4.3. Denoising
The basic idea of the denoising function is to remove or reduce perturbations or noise in input audios. Here, we applied the method of noise reducing proposed in [12] as our denoising function.
As indicated in [12], the denoising method uses the spectral gating to reduce noise in an audio. Specifically, given both signal and noise audio clips, it transforms time-domain waveforms into the frequency domain, then removes the noise from the signal in the frequency domain, and finally transforms the modified signal from the frequency domain back to the time domain.
To obtain a noise audio clip, we assume that the noise or the perturbation is white and follows a normal probability distribution, based on the observations of the adversarial audio from Figure 3. That is, we consider that the perturbations are Gaussian noise, and in Equation (4) is assumed to have the following normal distribution with a mean of 0 and a standard deviation of :
The transformation of a signal from the time domain to the frequency domain is based on the short-time Fourier transform (STFT), which is widely applied in digital signal processing [39]. Similarly, inverse STFT (iSTFT) is used to transform the signal from the frequency domain back to the time domain [39]. The algorithm of the denoising function is summarized in Algorithm 2.
| Algorithm 2 Denoising Function |
| 1: Input: an audio clip , noise variance |
| 2: Output: a denoised audio clip |
| 3: Require: normal distribution generator N, short-time Fourier transform , inverse short-time Fourier transform |
| 4: |
| 5: noise clip , size = length of |
| 6: for each signal noise[i] in noise clip do |
| 7: noise[i] |
| 8: end for |
| 9: (noise clip) |
| 10: |
| 11: Remove noise from based on and |
| 12: |
We applied the Librosa tool [40] to plot the mel spectrograms of an adversarial audio and the corresponding denoised adversarial audio with in Figure 5a,b, respectively. The adversarial audio is the one whose waveform was shown in Figure 3a and is with the sampling frequency of 16 kHz. The parameters used in generating the mel spectrograms are the following: the Hann window with the length of 400 for the analysis window, 512 for the length of the fast Fourier transform (FFT), and 160 for the hop length. It can be observed from Figure 5a,b that the background blue color of the denoised adversarial audio is much darker than that of the adversarial audio, indicating that the denoising method can effectively remove or reduce the background noise from an adversarial audio.
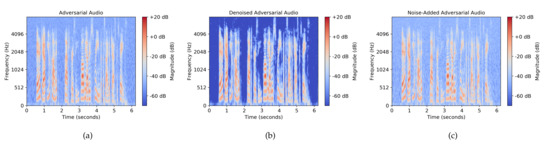
Figure 5.
The mel spectrograms of an adversarial audio, a denoised adversarial audio, and a noise-added adversarial audio. (a) Adversarial audio; (b) denoised adversarial audio; (c) noise-added adversarial audio.
4.4. Noise-Adding
Different from the denoising function, the noise-adding function attempts to perturb adversarial audios so that adversarial attacks would lose or reduce the ability to mislead an SV system.
The noise-adding function introduces some small noise to the input audio. Noise can take many different forms. For example, if we apply Gaussian noise with a mean of 0 and a standard deviation of . That is,
where is the input audio, is the noise-added audio, and
The algorithm of the noise-adding function is shown in Algorithm 3, by applying the Gaussian noise. If a different type of noise is applied, the probability distribution generator at the line 7 of Algorithm 3 would be different.
| Algorithm 3 Noise-Adding Function |
| 1: Input: an audio clip , noise variance |
| 2: Output: a noise-added audio clip |
| 3: Require: normal distribution generator N |
| 4: |
| 5: noise clip , size = length of |
| 6: for each signal noise[i] in noise clip do |
| 7 noise[i] |
| 8: end for |
| 9: noise clip |
We added the Gaussian noise with to the adversarial audio shown in Figure 5a and plotted the mel spectrogram of the resulting noise-added adversarial audio in Figure 5c. Comparing Figure 5a with Figure 5c, we can see that the background blue color of the noise-added audio is slightly lighter than that of the original adversarial audio, indicating that there is more noise in the noise-added audio. Denoising and noise-adding methods are essentially two opposite operations to preprocess input audios: denoising attempts to reduce the noise in an input audio, whereas noise-adding introduces additional noise to it.
5. Adaptive FakeBob Attacks
As pointed out by [15], a defense system against adversarial attacks needs to consider the worst-case scenario that attackers can know about the detailed information of the defense system, and through which they can design a white-box attack to counteract the defense. Such a worst-case attack is called the adaptive attack. In this section, we study some possible strategies that can be applied by adaptive FakeBob attacks.
In Section 6, we demonstrate that the noise-adding defense method performs much better than the denoising method against the FakeBob attack in both GMM and i-vector SV systems. Therefore, we focus on adaptive FakeBob attacks against the noise-adding defense in this section.
It is noted that the noise-adding method introduces randomness through the probability distribution generator so that even for the same input audio, the resulting noise-added audios are different for different runs. Such randomness can cause the gradient decent in adversarial attacks (as shown in Equation (7)) hard to find the correct values. A common technique adopted by adaptive attacks is expectation over transformation (EOT) [15,41,42], which computes the average of gradient decent over multiple runs on the same input sample. However, we found that in the original FakeBob attack, it has applied the natural evolution strategy (NES) [38] that calculates the average of gradient decent over multiple samples of the input audio with Gaussian noise, which is similar to EOT. Therefore, in this section we do not consider EOT, but study two other intuitive strategies that can be used by adaptive FakeBob attacks.
5.1. Bypassing the Plugin Function
As shown in Section 6.3, the noise-adding method can make the FakeBob attack difficult to find the correct values of gradient decent and slow down the attack 25 times and 5 times in GMM and i-vector SV systems, respectively. To speed up the process of obtaining adversarial audios, adaptive FakeBob attacks could bypass the plugin function and feed the input audios directly to the recognition module of an SV system. In such a way, the time required to create an adversarial audio for the adaptive FakeBob attack is the same as the time required for the original FakeBob attack against an SV system without the plugin function. However, the generated adversarial audios are still subject to the noise-adding defense during the test time. In Section 6.4, we will show the performance of such an adaptive attack strategy with different values of the perturbation threshold against an SV system with the noise-adding defense.
5.2. Updating the Objective Function
The adversarial audios generated by adaptive FakeBob attacks proposed in Section 5.1 can still be defeated by noise-adding at the test time, because of the randomness added to the input audios. To reduce such an effect, besides the strategy of bypassing the plugin function, another strategy that an adaptive attack can apply is to update the objective function, in order to make the resulting adversarial audio more robust against noise. Specifically, the adaptive FakeBob attack can change the objective function in Equation (6) to
where . That is, the adaptive attack attempts to generate an adversarial audio with the score of the SV system at least , instead of only . By increasing the targeted score, it becomes more difficult for random noise to change the decision of the SV for the resulting adversarial audios. In the experiments, we consider the cases that
where a is a constant, such as 10%, 20%, etc.
Intuitively, by increasing the targeted score in the object function, it would cause an adaptive FakeBob attack to take a longer time to generate an adversarial audio. In Section 6.4, we will study the tradeoff between the efficiency of generating adversarial audios and the robustness against the noise-adding method for the adaptive FakeBob attacks.
6. Performance Evaluation
In this section, we evaluate the effectiveness and the efficiency of the proposed defense system against adversarial attacks in SV systems. Specifically, we first describe the experimental setup. We then measure the impact of the defense methods on the normal operations of SV systems and against FakeBob attacks. Next, we evaluate the performance of adaptive FakeBob attacks against the noise-adding defense method. By default, the noise-adding method applies Gaussian noise. Finally, we measure the effect of different types of noises for the noise-adding defense method.
6.1. Experimental Setup
The experiments were run through three virtual machines (VMs) provided by Google Cloud Platform [43] and a local GPU server. Two of three VMs are with 8-core Intel Xeon CPU 3.1 GHz and 32 GB memory (i.e., c2-standard-8 machine type), whereas the third VM is with 16-core Intel Xeon CPU 3.1 GHz and 64 GB memory (i.e., c2-standard-16 machine type). The GPU server is with 24-core Intel I9 CPU 2.9 GHz, 128 GB memory, and GeForce RTX 2080 Ti graphic card. All machines are installed with Ubuntu 20.04.
Our experiments focus on GMM and i-vector SV systems. These SV systems are implemented by the Kaldi speech recognition toolkit [44] and use the pre-trained models from VoxCelab 1 [45]. Moreover, the adversarial attacks against these SV systems are implemented through FakeBob attacks [7] with a perturbation threshold of 0.002 (i.e., ) and 1000 maximum iterations (i.e., ). These same parameters were used in [7]. The audio dataset used is from LibriSpeech [46] and contains nine different speakers, which were also applied in FakeBob [7]. These nine speakers have five legitimate users and four illegal users, all speaking English. Legitimate users include three females and two males, whereas illegal users contain two females and two males. All users are native speakers and speak different messages. There are totally 100 audio clips from all illegal users, whereas there are about 100 audio clips from each legitimate user. These illegal audios and legitimate audios can be used to calculate the EER of an SV system. Each audio clip lasts between 4 and 10 s. The experiments on SV systems are through the application programming interface (API) provided by Kaldi GMM or i-vector.
In [7], all legitimate users were fed into the same SV system in experiments. Different from this setup, we put every legitimate user in a stand-alone SV system and thus obtained multiple SV systems in our experiments. The final result is the average over all results from these multiple SV systems. Consequently, our obtained ASR of the FakeBob attack against an SV system without any defense can be lower than that presented in [7]. However, from our view, such a setup with multiple stand-alone SV systems is more realistic.
It is noted that an SV system, either GMM or i-vector, without the proposed defense mechanism, is deterministic. That is, when an input audio is accepted (or rejected) by the SV system, it will be always accepted (or rejected) for future tests in the same SV system. However, an SV system that is installed with our proposed defense mechanism becomes stochastic, because of the randomness introduced by the noise generator. That is, if an input audio is accepted (or rejected) in the current test, it may be rejected (or accepted) next time when it is fed into the same SV system. To address such a stochastic effect, during the test we let an input audio go through an SV system multiple times (e.g., 10 or 100 times) and calculate the average of the performance metrics such as EER and ASR. Specifically, in Section 6.2 and Section 6.3, 100 times are applied; whereas in Section 6.4 and Section 6.5, 10 times are used.
6.2. Performance Evaluation of the Proposed Defense System for the Normal Operations of SV Systems
In our experiments, we first study the impact of the proposed defense methods, i.e., denoising and noise-adding, on the normal operations of an SV system. Here, the noise-adding method applies the Gaussian noise. Specifically, we use the EER as the performance metric. Recall that the EER is the rate of FAR or FRR when they are equal. A smaller EER reflects a better SV system. Moreover, the added plugin function to an SV system would slow down the processing of an input audio. As a result, we also record the processing time in our experiments. Among five legitimate speakers provided, we select two speakers with the identifier of 2830 and 61 as registered users in two separate experiments. To obtain the EER, 100 audio clips from a registered speaker and 100 audio clips from all illegal speakers were tested.
Table 1 shows the average performance of a GMM SV system with or without the denoising or noise-adding function over speakers 2830 and 61, as well as with different values of the standard deviation of noise (i.e., , 0.002, and 0.005). The results in the table are the averages over two speakers. Note that the original GMM SV system, which is without the defense plugin, can be regarded as the special case when for either denoising or noise-adding. It can be observed that for most cases, when increases, the EER increases for both denoising and noise-adding. However, the value of the EER only increases slightly, especially when is not large; for example, . It can also be observed from Table 1 that in a GMM SV system, the denoising function takes much longer time than the noise-adding function to process all 200 testing audios. The overhead of the noise-adding is very light, because the plugin of adding random Gaussian noise does not require too much computation. On the other hand, the denoising function needs to apply both STFT and iSTFT operations, which demand a lot of computation.

Table 1.
Performance evaluation of proposed defense system on normal operations of GMM SV systems.
We further summarize the performance of the proposed defense system for normal operations of an i-vector SV system in Table 2. Similar to the results in Table 1, it can be observed that the EER does not increase too much when increases, especially when or 0.002. Different from the results in Table 1, the processing time of an i-vector SV system with the defense is closer to that without the defense. The reason is that the i-vector SV system requires longer time to test all 200 audios than the GMM SV system, but the overhead of a plugin is fixed.

Table 2.
Performance evaluation of proposed defense system on normal operations of I-Vector SV systems.
From both Table 1 and Table 2, we can conclude that the proposed defense system only slightly degrades the performance of an SV system, especially when is small. Moreover, in a GMM SV system, the noise-adding function is preferred to the denoising function, as it adds on much shorter processing time.
6.3. Performance Evaluation of the Proposed Defense System against FakeBob Attacks
Next, we study the performance of our proposed defense methods against FakeBob attacks presented in Algorithm 1 in an SV system. Specifically, we use the ASR as the performance metric. A smaller value of the ASR indicates a better defense performance. Moreover, FakeBob uses multiple iterations to create an adversarial audio, as shown in Algorithm 1. Therefore, we also measure the average number of iterations and the average running time for FakeBob attacks to find an adversarial audio in our experiments. A larger number of the average iterations and a longer average running time reflect a better defense system. For adversarial attacks, we randomly selected five clean audio clips from each of four illegal speakers. These 20 audios repeatedly went through an SV system for 100 times, in order to obtain the average ASR, the average number of iterations, and the average running time of FakeBob attacks.
Table 3 shows the experimental results of our proposed defense functions, i.e., denoising and noise-adding with Gaussian noise, against FakeBob attacks in a GMM SV system for speakers 2830 and 61, when , 0.001, 0.002, and 0.005. It can be observed that while FakeBob achieves 100% ASR for the original GMM SV system (i.e., ), the ASR of the SV system with the defense is less than 100%. Moreover, when increases, the ASR decreases in general. For example, when , the average ASR is 56.05% for the denoising function, whereas it is only 5.20% for the noise-adding method. It can be clearly observed that noise-adding performs much better than denoising based on the ASR. Moreover, noise-adding leads to a much larger value of the average number of iterations and much longer average running time than denoising and the original SV system. The average number of iterations for denoising is similar to that in the original SV system, whereas the average running time for denoising is slightly larger than that in the original SV system. However, with the noise-adding plugin, the values of these two metrics are much larger. For example, in the original GMM SV system, the average number of iterations is 23.00, and the average running time is 158.68. However, in the defense system with noise-adding and , the average number of iterations and the average running time are 604.95 and 3992.88, respectively. This indicates that noise-adding slows down the attacker’s processing speed more than 25 times and makes FakeBob significantly harder to find the adversarial audios.

Table 3.
Performance evaluation of proposed defense system against FakeBob attacks in GMM SV systems.
Moreover, we have extended our experiments to an i-vector SV system against FakeBob attacks. As shown in Table 4, denoising and noise-adding with are able to reduce the ASR from 95.00% to 38.63% and 0.50%, respectively. Furthermore, the average running time for FakeBob has been significantly increased by applying the noise-adding defense method. For example, when , the noise-adding method slows down the processing speed of the FakeBob attacks more than 5 times.

Table 4.
Performance evaluation of proposed defense system against FakeBob attacks in I-Vector SV systems.
In summary, the experimental results indicate that the noise-adding defense with a reasonable value of the standard deviation of noise (e.g., ) can effectively and efficiently counteract FakeBob attacks. Moreover, such a defense method is simple to implement, is very light-weight, and only slightly degrades the performance of normal operations of an SV system.
6.4. Performance Evaluation of Adaptive FakeBob Attacks against the Noise-Adding Defense
We further study the performance of two strategies that were discussed in Section 5 for adaptive FakeBob attacks against an SV system with the noise-adding plugin function. Here, we focus on GMM SV systems and evaluate both the EER and the ASR over all five legitimate users with the identifier of 1580, 2830, 4446, 5142, and 61. Moreover, during the test time, we let an input audio repeatedly go through an SV system with noise-adding 10 times to address the effect of randomness of Gaussian noise.
6.4.1. Bypassing the Plugin Function
An adaptive attack can bypass the plugin function and generate adversarial audios using an SV system without the defense. The generated adversarial audios were then fed into the SV system with noise-adding during the test time to obtain the ASR. Figure 6 shows the performance of generated adversarial audios with different values of the perturbation threshold, i.e., , 0.001, 0.002, and 0.005, against the proposed noise-adding defense with different values of the standard deviation of noise (i.e., ). It can be observed that when increases from 0 to 0.005, the EER of an SV system slowly increases from 6.20% to 11.57%. When , . Moreover, it can be observed that when is not large (e.g., ), the noise-adding plugin is very effective against adversarial audios. For example, when , the noise-adding defense can reduce the ASR to 9.28%, 14.17%, and 33.45% for adversarial audios with , 0.001, and 0.002, respectively. On the other hand, when is large (e.g., ), the defense with can only reduce the ASR to 72.72%. However, it is noted that an adversarial audio with a higher value of is more perceptible to humans. Therefore, our proposed noise-adding method is still effective against the bypassing-the-plugin strategy by adaptive FakeBob attacks, especially when is not large.
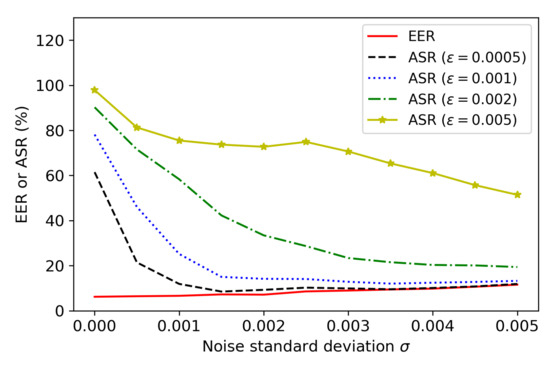
Figure 6.
Performance of the strategy of bypassing the plugin function by adaptive FakeBob attacks with different in GMM SV systems.
6.4.2. Updating the Objective Function
Next, we study the adaptive FakeBob attack that both bypasses the plugin function and updates the objective function to generate adversarial audios against SV systems with noise-adding. Table 5 shows the ASR and the total running time of adaptive attacks with in generating adversarial audios in a GMM SV system without the defense. It can be observed that when the value of a in Equation (15) increases, the targeted score of the SV system for the attack increases, and as a result, it takes longer time for the attack to obtain adversarial audios. Moreover, the ASR in Table 5 is based on the threshold , instead of , so the value of the ASR decreases when a increases. Specifically, when a increases from 0 to 30%, the ASR decreases from 90.24% to 84.03%, whereas the total running time increases from 31 h 3 min to 44 h 47 min.

Table 5.
Performance evaluation of adaptive FakeBob attacks with in generating adversarial audios in GMM SV systems without noise-adding.
Figure 7 shows the performance of adaptive FakeBob attacks with against the noise-adding defense during the test time. It can be observed that when , an SV system is based on the threshold , and adaptive attacks with different values of a have a similar value of the ASR (i.e., about 90%). Moreover, by increasing a, the resulting adversarial audios are more robust against noise when is not large. For example, when , the values of the ASR are 39.40%, 45.36%, and 49.81% for attacks with , 20%, and 30%, respectively. On the other hand, when , the ASR is about 21% for all cases. From Table 5 and Figure 7, it can be observed that an adaptive FakeBob attack with a higher value of a can better mitigate the effect of noise-adding when is not large, but takes longer time to generate adversarial audios, which indicates a tradeoff between the robustness and the efficiency of adaptive FakeBob attacks. On the other hand, the noise-adding defense still provides a considerable level of protection against adaptive FakeBob attacks. For example, the noise-adding method with can reduce the ASR from 89.40% to 49.81% for the adaptive FakeBob attack with .
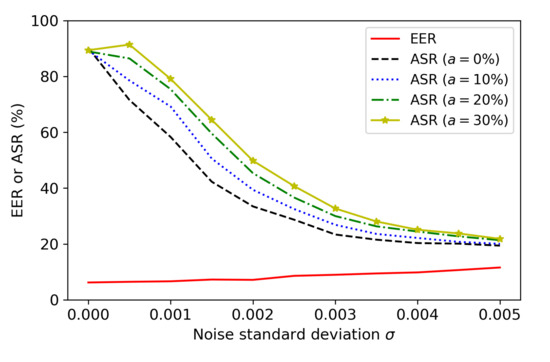
Figure 7.
Performance of the adaptive FakeBob attacks with in GMM SV systems with noise-adding.
6.5. Effect of Different Noise Types for Noise-Adding Defense
In the previous experiments, we applied Gaussian noise for the noise-adding defense method. In this section, we evaluate the effect of different noise types for noise-adding defense. Besides the normal distribution [16] (i.e., Gaussian noise), we consider the following continuous probability distribution functions for generating noise with a mean of 0: uniform [17], logistic [18], and Laplace [19]. Moreover, we study noise with a discrete probability distribution that is a variation of the Rademacher distribution [20]:
Note that and .
Figure 8 and Figure 9 show how the noise-adding defense with different noise types can affect the EER of GMM SV systems for the normal operations and the ASR of FakeBob adversarial audios (with ) for the defense. Here, FakeBob adversarial audios were generated by bypassing the plugin function as described in Section 5.1 and then applied to GMM SV systems with noise-adding defense to measure ASR. It can be observed that the noise-adding defense with the different noise types behaves in a similar way for both EER and ASR. Therefore, the choice of the noise type is not a major consideration for the noise-adding defense method. Moreover, Figure 9 uses an error bar to indicate the standard deviation of ASR when the Gaussian noise is applied. It can be observed that the standard deviation of ASR is relatively small, comparing with the average of ASR.
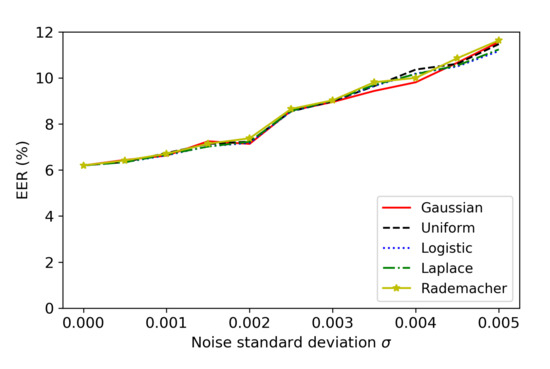
Figure 8.
Performance of the noise-adding defense with different types of noise on the normal operations of GMM SV systems.
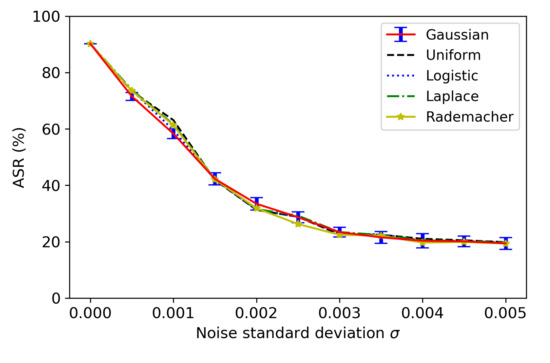
Figure 9.
Performance of the noise-adding defense with different types of noise on FakeBob adversarial audios in GMM SV systems.
7. Conclusions and Future Work
In this work, we have attempted to design and implement a defense system that is simple, light-weight, and effective against adversarial attacks in SV systems. Our designed system is based on the observations that the perturbations in an adversarial audio are very small and similar to white noise, but are not random and intentionally designed to fool SV. We have proposed to add the plugin function to preprocess an input audio so that perturbations can be removed or modified to lose their effectiveness. We have studied two opposite plugin functions, i.e., denoising and noise-adding, and found that noise-adding has much better performance against FakeBob adversarial attacks than denoising. For example, noise-adding with in a GMM SV system is able to slow down the speed of FakeBob to generate adversarial audios 25 times and reduce the targeted ASR from 100% to 5.20%. Moreover, noise-adding with only has a minor effect on normal operations of an SV system and has a slightly higher EER than that in the SV system without the defense. Therefore, we believe that this simple solution, i.e., the noise-adding plugin, should be applied to any SV system to counteract adversarial attacks such as FakeBob. To the best of our knowledge, this is the first attempt in applying the noise-adding method to defend against adversarial attacks in SV systems. The part of source code used in this paper can be found from GitHub [47].
Moreover, we have studied two possible strategies that can be potentially used by adaptive FakeBob attacks against our proposed noise-adding defense. One is to bypass the plugin function, and the other is to update the objective function, when FakeBob generates adversarial audios. We have demonstrated through experiments that under these countermeasures, noise-adding with can still provide a considerable level of protection and reduce the ASR of adaptive FakeBob attacks with from 89.40% to 49.81%.
As our on-going work, we will extend our study to other SV systems such as d-vector [29] and x-vector [30]. Moreover, we plan to research the effect of adding other different types of noise that is not probability based, such as Rustle noise [48], on the normal operations of an SV system and against adversarial attacks. Meanwhile, how to apply other denoising algorithms, which can be more robust than the one we studied in this paper, is a direction of our future work. Furthermore, we are interested in designing a defense system that can counteract adversarial attacks, replay attacks, and voice cloning attacks. From the perspective of adversarial attacks, the perturbations in FakeBob are based on Gaussian noise [38]. Applying different types of noise to generate perturbations is an interesting research problem as well.
Author Contributions
Conceptualization, Z.C., L.-C.C., C.C., G.W. and Z.B.; Formal analysis, Z.C. and L.-C.C.; Funding acquisition, Z.C., G.W. and Z.B.; Investigation, Z.C. and L.-C.C.; Methodology, Z.C. and C.C.; Project administration, Z.C.; Resources, Guoping Wang; Software, Z.C. and L.-C.C.; Supervision, Z.C.; Validation, Z.C., L.-C.C., C.C., G.W. and Z.B.; Writing—original draft, Z.C. and L.-C.C.; Writing—review & editing, C.C., G.W. and Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by 2020 Purdue University Fort Wayne Graduate Research Assistantship and 2020 Purdue University Fort Wayne Collaborative Research Grant.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chang, L.; Chen, Z.; Chen, C.; Wang, G.; Bi, Z. Defending against adversarial attacks in speaker verification systems. In Proceedings of the IEEE International Performance Computing and Communications Conference (IPCCC), Austin, TX, USA, 29–31 October 2021. [Google Scholar]
- Babangida, L.; Perumal, T.; Mustapha, N.; Yaakob, R. Internet of things (IoT) based activity recognition strategies in smart homes: A review. IEEE Sens. J. 2022, 22, 8327–8336. [Google Scholar] [CrossRef]
- Das, R.K.; Tian, X.; Kinnunen, T.; Li, H. The attacker’s perspective on automatic speaker verification: An overview. arXiv 2020, arXiv:2004.08849. [Google Scholar]
- Wang, S.; Cao, J.; He, X.; Sun, K.; Li, Q. When the differences in frequency domain are compensated: Understanding and defeating modulated replay attacks on automatic speech recognition. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security (CCS), Virtual Event, 9–13 November 2020. [Google Scholar]
- Wu, Z.; Evans, N.; Kinnunen, T.; Yamagishi, J.; Alegre, F.; Li, H. Spoofing and countermeasures for speaker verification: A survey. Speech Commun. 2015, 66, 130–153. [Google Scholar] [CrossRef]
- Wu, Z.; Li, H. Voice conversion versus speaker verification: An overview. In APSIPA Transactions on Signal and Information Processing; Cambridge University Press: Cambridge, UK, 2014; Volume 3. [Google Scholar]
- Chen, G.; Chen, S.; Fan, L.; Du, X.; Zhao, Z.; Song, F.; Liu, Y. Who is real Bob? Adversarial attacks on speaker recognition systems. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 24–27 May 2021. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Yuan, X.; He, P.; Zhu, Q.; Li, X. Adversarial examples: Attacks and defenses. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2805–2824. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Li, B.; Chen, P.; Song, D. Characterizing audio adversarial examples using temporal dependency. In Proceedings of the International Conference on Learning Representations, New Orleans, LO, USA, 6–9 May 2019. [Google Scholar]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques. J. Comput. 2010, 2, 138–143. [Google Scholar]
- Sainburg, T. timsainb/noisereduce: V1.0. Zenodo. 2019. Available online: https://github.com/timsainb/noisereduce (accessed on 12 July 2022).
- Reynolds, D.A.; Quatieri, T.F.; Dunn, R.B. Speaker verification using adapted Gaussian mixture models. Digit. Signal Process. 2000, 10, 19–41. [Google Scholar] [CrossRef]
- Dehak, N.; Kenny, P.J.; Dehak, R.; Dumouchel, P.; Ouellet, P. Front-end factor analysis for speaker verification. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 788–798. [Google Scholar] [CrossRef]
- Tramer, F.; Carlini, N.; Brendel, W.; Madry, A. On adaptive attacks to adversarial example defenses. In Proceedings of the Conference on Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020. [Google Scholar]
- Normal Distribution, Wikipedia. Available online: https://en.wikipedia.org/wiki/Normal_distribution (accessed on 12 July 2022).
- Continuous Uniform Distribution, Wikipedia. Available online: https://en.wikipedia.org/wiki/Continuous_uniform_distribution (accessed on 12 July 2022).
- Logistic Distribution, Wikipedia. Available online: https://en.wikipedia.org/wiki/Logistic_distribution (accessed on 12 July 2022).
- Laplace Distribution, Wikipeida. Available online: https://en.wikipedia.org/wiki/Laplace_distribution (accessed on 12 July 2022).
- Rademacher Distribution, Wikipedia. Available online: https://en.wikipedia.org/wiki/Rademacher_distribution (accessed on 12 July 2022).
- Abdullah, H.; Warren, K.; Bindschaedler, V.; Papernot, N.; Traynor, P. SoK: The faults in our ASRs: An overview of attacks against automatic speech recognition and speaker identification systems. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 24–27 May 2021. [Google Scholar]
- Jati, A.; Hsu, C.; Pal, M.; Peri, R.; AbdAlmageed, W.; Narayanan, S. Adversarial attack and defense strategies for deep speaker recognition systems. Comput. Speech Lang. 2021, 68, 101199. [Google Scholar] [CrossRef]
- Villalba, J.; Joshi, S.; Zelasko, P.; Dehak, N. Representation learning to classify and detect adversarial attacks against speaker and speech recognition systems. In Proceedings of the Interspeech 2021, Brno, Czech Republic, 30 August–3 September 2021. [Google Scholar]
- Li, X.; Li, N.; Zhong, J.; Wu, X.; Liu, X.; Su, D.; Yu, D.; Meng, H. Investigating robustness of adversarial samples detection for automatic speaker verification. In Proceedings of the Interspeech 2020, Shanghai, China, 25–29 October 2020. [Google Scholar]
- Wu, H.; Li, X.; Liu, A.T.; Wu, Z.; Meng, H.; Lee, H. Adversarial defense for automatic speaker verification by cascaded self-supervised learning models. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021. [Google Scholar]
- Joshi, S.; Villalba, J.; Zelasko, P.; Moro-Velazquez, L.; Dehak, N. Study of pre-processing defenses against adversarial attacks on state-of-the-art speaker recognition systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4811–4826. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Y.; Wu, Z.; Wang, D.; Lee, H. Voting for the right answer: Adversarial defense for speaker verification. In Proceedings of the Interspeech 2021, Brno, Czech Republic, 30 August–3 September 2021. [Google Scholar]
- Byun, J.; Go, H.; Kim, C. Small input noise is enough to defend against query-based black-box attacks. arXiv 2021, arXiv:2101.04829. [Google Scholar]
- Variani, E.; Lei, X.; McDermott, E.; Moreno, I.L.; Gonzalez-Dominguez, J. Deep neural networks for small footprint text-dependent speaker verification. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014. [Google Scholar]
- Snyder, D.; Garcia-Romero, D.; Sell, G.; McCree, A.; Povey, D.; Khudanpur, S. Speaker recognition for multi-speaker conversations using X-vectors. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Cheng, J.M.; Wang, H.C. A method of estimating the equal error rate for automatic speaker verification. In Proceedings of the IEEE International Symposium on Chinese Spoken Language Processing, Hong Kong, China, 15–18 December 2004. [Google Scholar]
- Biggio, B.; Corona, I.; Maiorca, D.; Nelson, B.; Srndic, N.; Laskov, P.; Giacinto, G.; Roli, F. Evasion attacks against machine learning at test time. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML PKDD), Prague, Czech Republic, 23–27 September 2013; Volume 8190, pp. 387–402. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2015, arXiv:1412.6572. [Google Scholar]
- Li, J.; Liu, Y.; Chen, T.; Xiao, Z.; Li, Z.; Wang, J. Adversarial attacks and defenses on cyber–physical systems: A survey. IEEE Internet Things J. 2020, 7, 5103–5115. [Google Scholar] [CrossRef]
- Rahman, A.; Hossain, M.S.; Alrajeh, N.A.; Alsolami, F. Adversarial examples—Security threats to COVID-19 deep learning systems in medical IoT devices. IEEE Internet Things J. 2021, 8, 9603–9610. [Google Scholar] [CrossRef]
- Kong, X.; Ge, Z. Adversarial attacks on neural-network-based soft sensors: Directly attack output. IEEE Trans. Ind. Inform. 2022, 18, 2443–2451. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Ilyas, A.; Engstrom, L.; Athalye, A.; Lin, J. Black-box adversarial attacks with limited queries and information. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- McClellan, J.H.; Schafer, R.W.; Yoder, M.A. DSP First, 2nd ed.; Pearson Education, Inc.: London, UK, 2016. [Google Scholar]
- Librosa, a Python Package for Music and Audio Analysis. Available online: https://librosa.org/ (accessed on 12 July 2022).
- Athalye, A.; Carlini, N.; Wagner, D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 274–283. [Google Scholar]
- Athalye, A.; Engstrom, L.; Ilyas, A.; Kwok, K. Synthesizing robust adversarial examples. arXiv 2018, arXiv:1707.07397. [Google Scholar]
- Google. Google Cloud Platform. Available online: https://cloud.google.com/ (accessed on 12 July 2022).
- Povey, D.; Ghoshal, A.; Boulianne, G.; Burget, L.; Glembek, O.; Goel, N.; Hannemann, M.; Motlicek, P.; Qian, Y.; Schwarz, P.; et al. The Kaldi speech recognition toolkit. In Proceedings of the 2011 IEEE Workshop on Automatic Speech Recognition and Understanding, Waikoloa, HI, USA, 11–15 December 2011. [Google Scholar]
- Nagrani, A.; Chung, J.S.; Zisserman, A. VoxCeleb2: Deep speaker recognition. In Proceedings of the Interspeech 2018, Hyderabad, India, 27 June 2018. [Google Scholar]
- Panayotov, V.; Chen, G.; Povey, D.; Khudanpur, S. Librispeech: An ASR corpus based on public domain audio books. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015. [Google Scholar]
- defense_FakeBob. GitHub. Available online: https://github.com/zeshengchen/defense_FakeBob (accessed on 12 July 2022).
- Rustle Noise, Wikipedia. Available online: https://en.wikipedia.org/wiki/Rustle_noise (accessed on 12 July 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).