A Data-Driven Fault Tree for a Time Causality Analysis in an Aging System
Abstract
:1. Introduction
2. Time Causality Analysis Methods
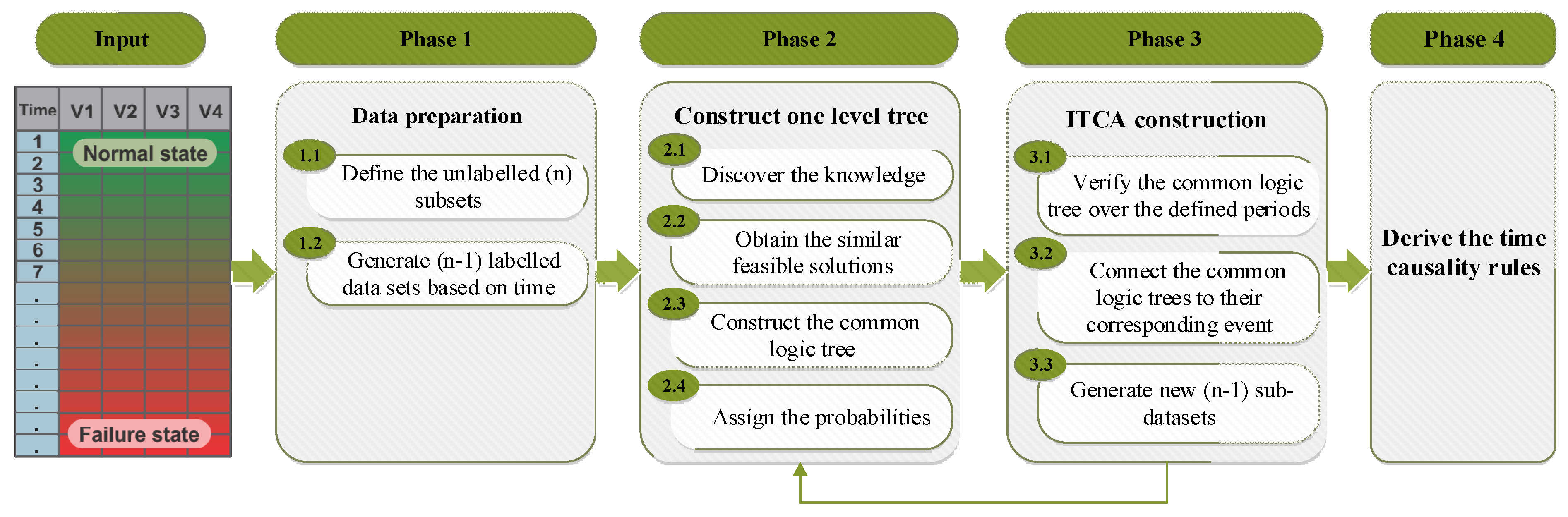
3. The ITCA Methodology
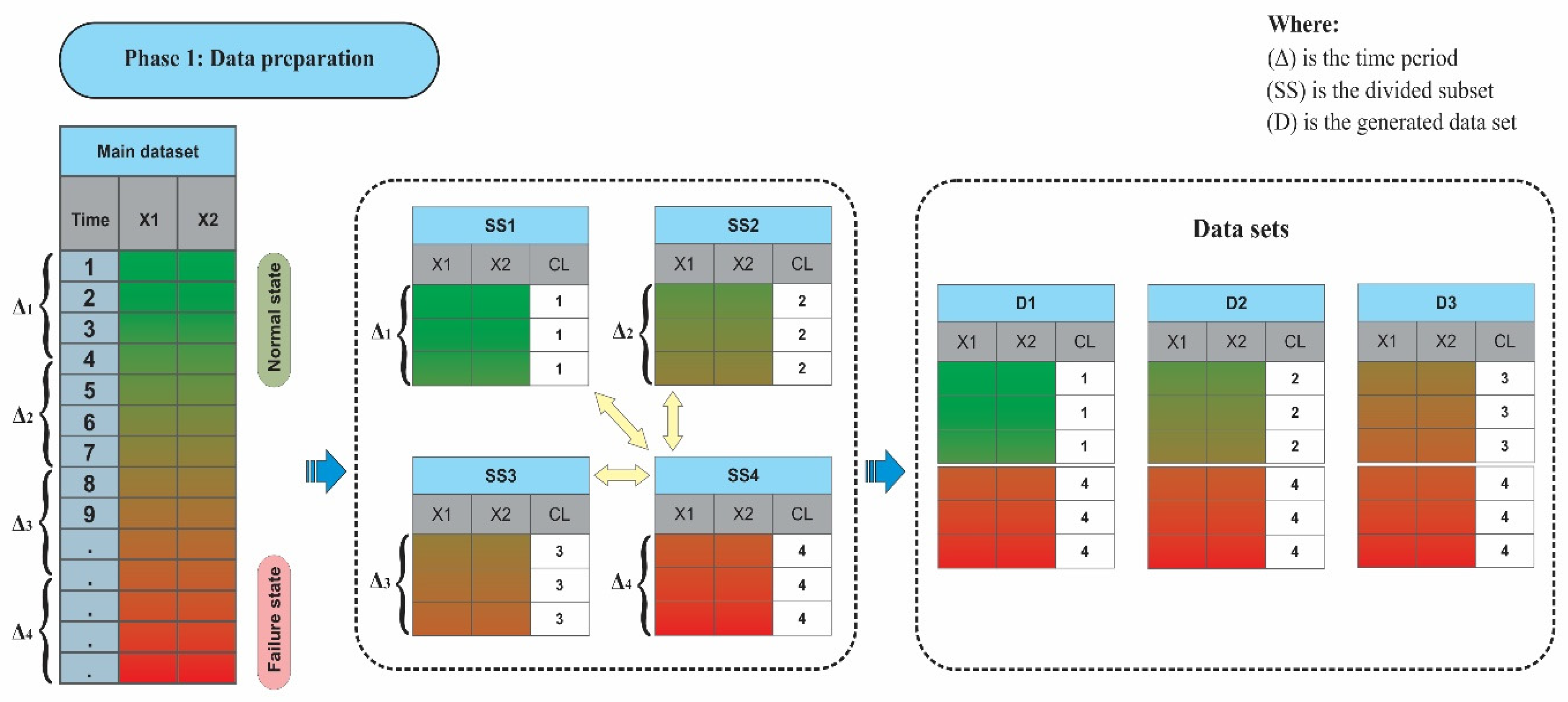
3.1. Phase 1: Data Preparation
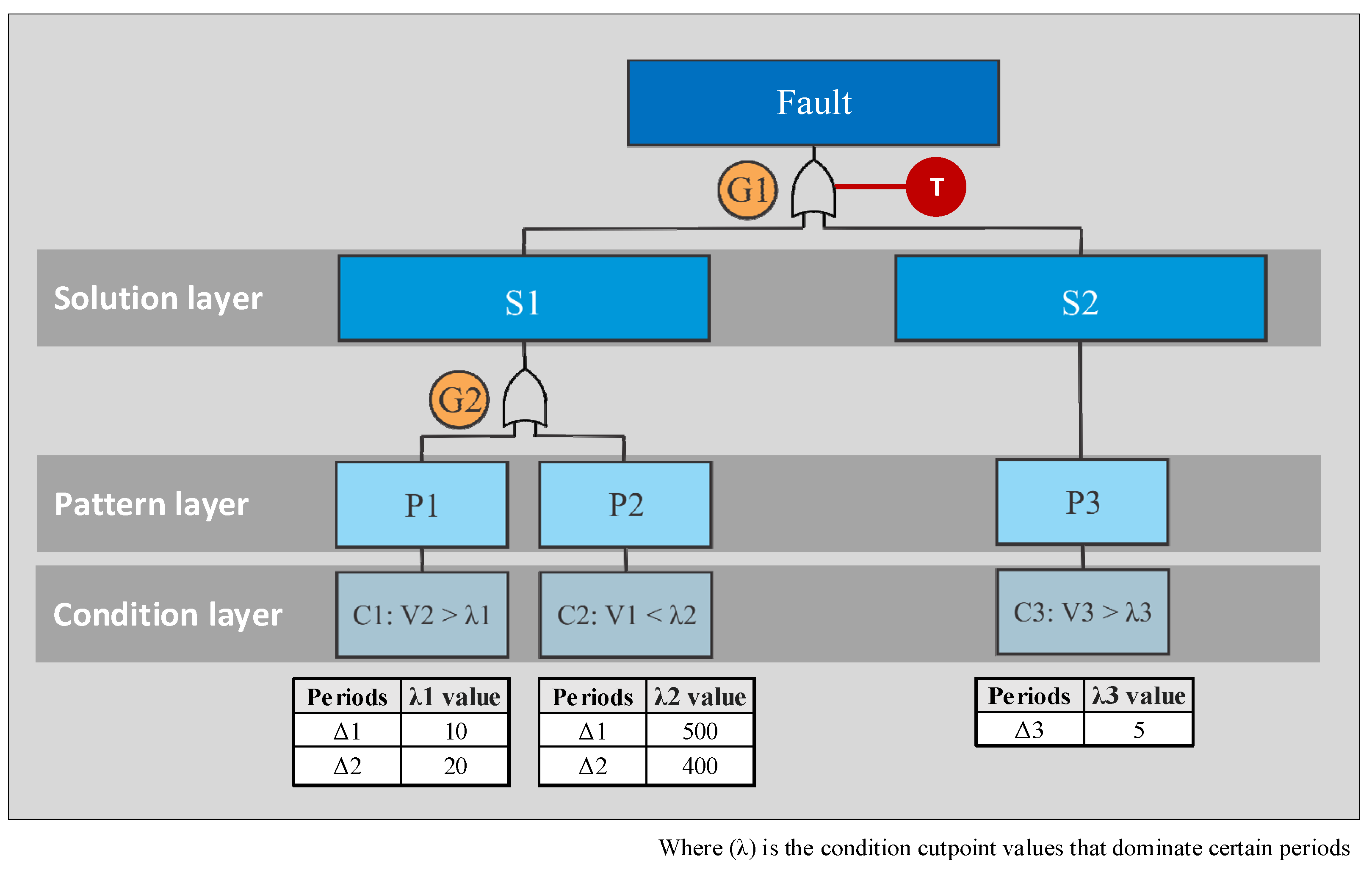
3.2. Phase 2: Build a One Level Fault Tree
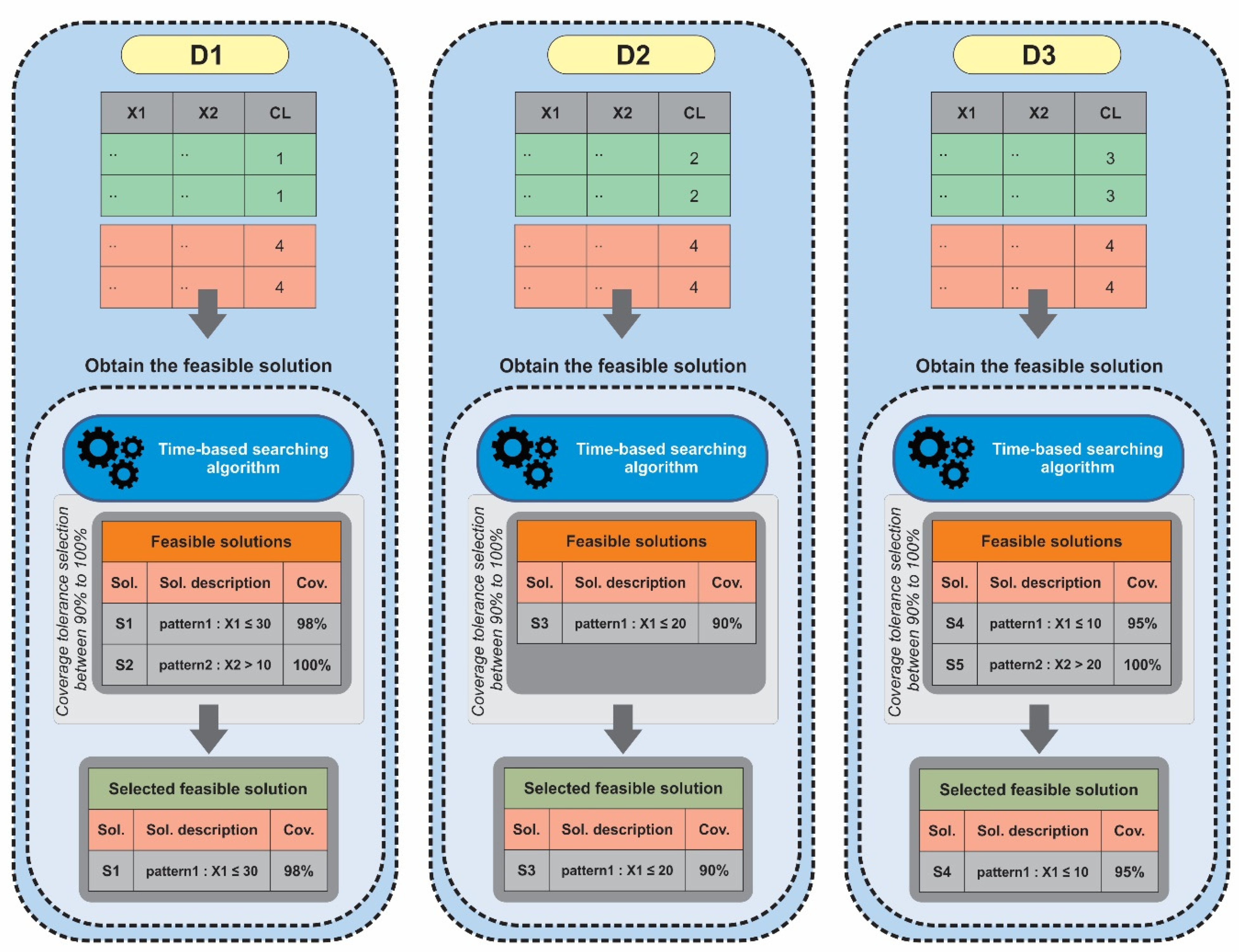
- Stage 1: Discover knowledge. Discovering knowledge from a two-class dataset can be achieved through different pattern generation and extraction techniques, such as the logic analysis of data (LAD) [27] and prediction rule ensembles (PRE) [28]. The pattern is a conjunction of certain conditions that discriminate one class of observations from another class. Each condition includes a variable, an inequality sign, and a cut point value. Furthermore, the percentage of observations covered by a given pattern may characterize the knowledge expanse caught by that pattern. However, when the observations of the same class are covered by more than one pattern, an overlap between those patterns may occur, with a certain percentage leading to redundant knowledge.
- Stage 2: Obtain similar feasible solutions. A solution is defined as a combination of certain patterns that cover the observations of the same class. Each solution can be characterized by its coverage (Cov) and overlap (OL) percentages. The feasible solution is a solution that respects certain criteria. In the ILTA methodology, only the feasible solution that maximizes the class Cov and minimizes the class OL is selected, which leads to maximizing the interpretability and minimizing the redundancy of the discovered knowledge. However, in the ITCA methodology, we need to search for all of the feasible solutions that respect not only the Cov and OL threshold percentages, but also with minimal number of patterns to capture the common knowledge at the same level over time. In other words, the minimal number of patterns having the maximum Cov and the minimum OL allows us to characterize the fault using global knowledge at the first levels of the tree. When this causality is represented in the tree and the related knowledge is removed from the dataset, the subsequent feasible solutions will reveal other knowledge that depicts sub-causalities not yet discovered and represented in the tree. As Stage 2 aims to select similar feasible solutions that characterize knowledge discovery over time, we seek the most frequent patterns over the predefined periods of time. In addition, the frequent pattern involves the same variable and inequality sign in the shared conditions, independent of the cut-point values. Therefore, the initial version of the burn-and-build algorithm proposed in [10] is improved to form a set of feasible solutions instead of only one for each period, using another decision criterion called the solution tolerance selection (STS) threshold. Hence, a time-based searching algorithm is developed in the ITCA methodology to obtain all the similar feasible solutions over time. It is depicted in the following Algorithm 1.
| Algorithm 1. Time-based searching algorithm: Search for similar feasible solutions over time. |
 |
- Stage 3: Construct a common logic tree over time. The similar feasible solutions obtained are visualized in a one-level fault tree through the condition, pattern, and solution layers. At the condition layer, all the involved conditions are connected to their respective patterns using the AND gate. At the pattern layer, all the patterns of the similar feasible solutions are connected to that solution using the OR gate. Similarly, at the solution layer, all the selected similar feasible solutions are connected to the fault event using the OR gate.
- Stage 4: Assign the probabilities. The common logic tree is quantified using the probabilities of the solutions, patterns and conditions involved in similar feasible solutions obtained from the concatenated dataset individually. Let and be the number of observations covered by the condition and the total number of observations in one concatenated dataset, respectively. Equations (1) to (4) calculate the probabilities of the fault class and the involved solutions , patterns , and conditions as follows:
3.3. Phase 3: The ITCA Model Construction
- Stage 1: Verify the common logic trees’ construction over the defined periods. This stage verifies the knowledge representability of the constructed logic tree for each defined period of time and decides whether the further decomposition of its involved condition is required or not. At each decomposition level, verification of the tree knowledge is characterized by the coverage of the common feasible solution, which assists in avoiding decomposing the weak information branches. Therefore, the model construction is verified to sustain the tree at a non-redundant knowledge level based on the pre-set coverage threshold. Meanwhile, the construction phase can be interpreted if there is no common tree that is able to provide sufficient knowledge representability, or if there are no more variables in the dataset for any further root cause explorations.
- Stage 2: Connect the common logic trees to their corresponding causes. The applied relaxation in selecting a common feasible solution over the defined periods is very useful in constructing a common logic tree that easily demonstrates the change in the causality at a given level of decomposition in the ITCA model. However, it could happen if the time-based searching algorithm fails to form only one common logic tree that dominates all the defined periods at a certain decomposition level. This case could happen if there is a lack of extracted knowledge or a tight range in the solution tolerance selection (STS). To solve this situation, different common logic trees may be found by the algorithm, but each period is dominated by only one common feasible solution. Therefore, if such a situation rises, a time–OR gate is proposed to connect the different common logic trees to represent the change in the event causality knowledge over all the defined periods at a given decomposition level. The time–OR gate acts as a time switch that shifts between the common logic trees according to their corresponding periods. Hence, an expert could observe the fault behaviour over time based on the proposed common similar solution trees at a certain decomposition level of the ITCA model.
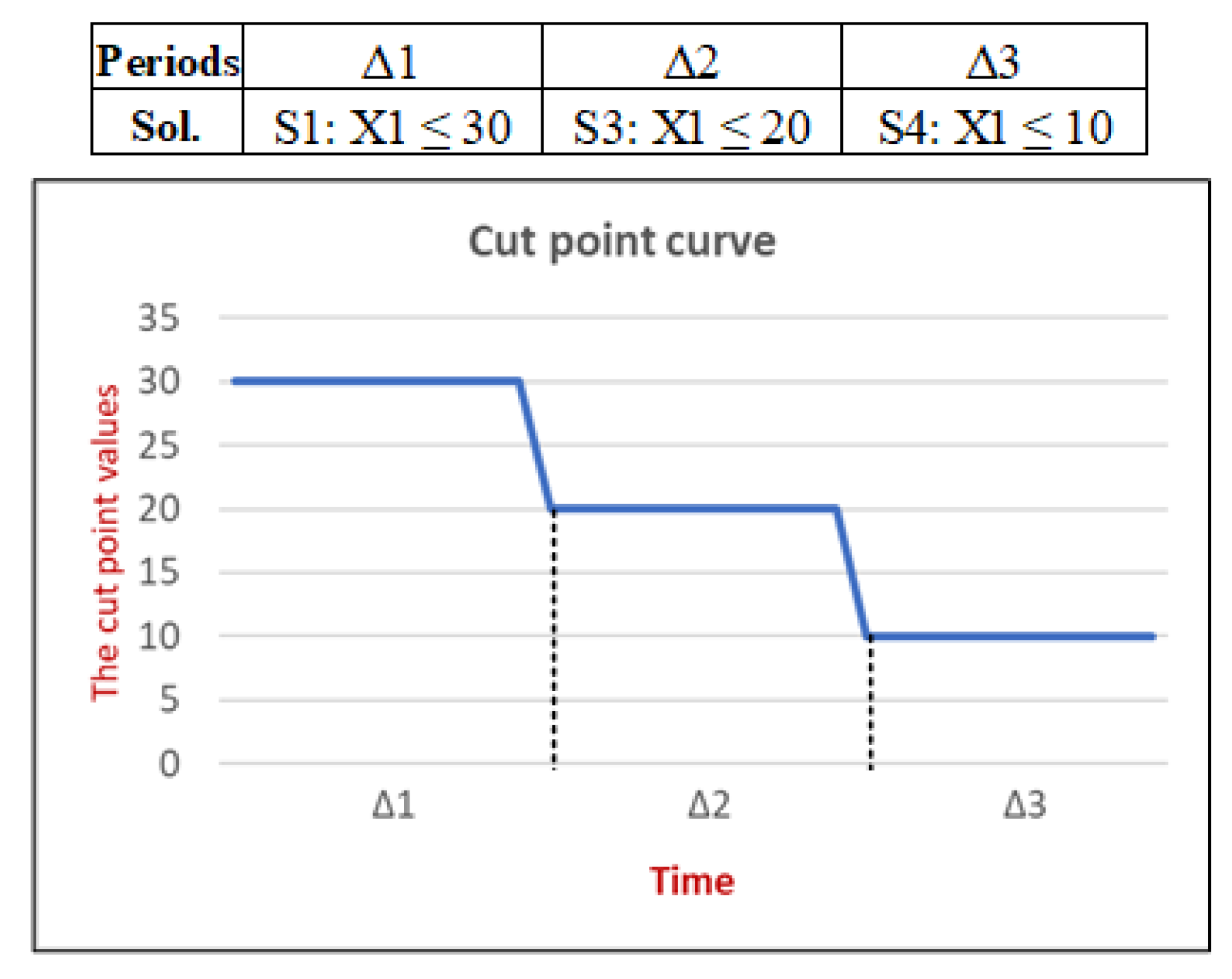
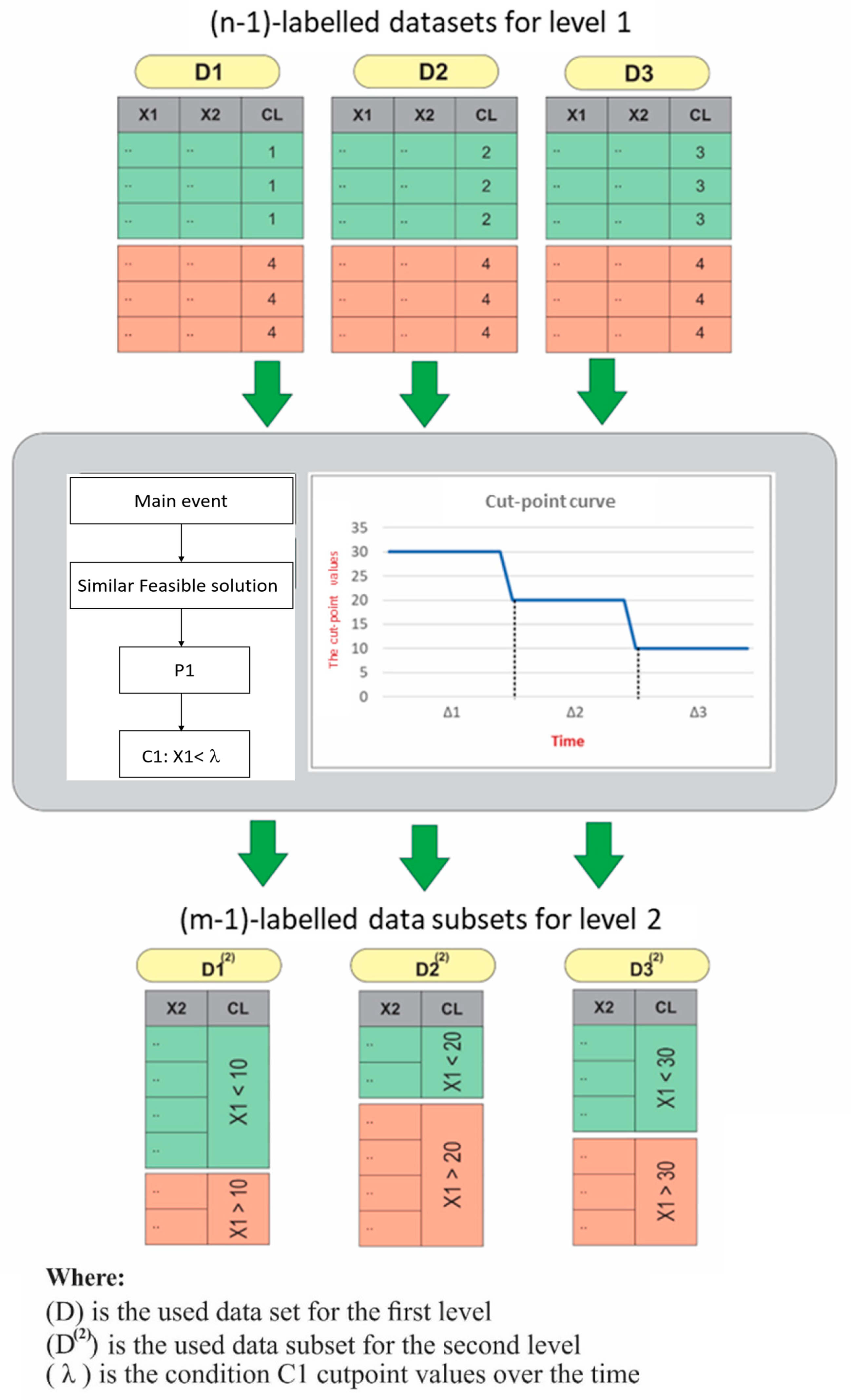
- Stage 3: Generate new (m − 1) sub-datasets. In a case in which the added common logic trees are verified at a certain decomposition level of the ITCA model, each one of the involved conditions in the tree is used to generate new labelled sub-datasets based on the condition variable cut-point values. Figure 6 takes the example of Figure 3. It presents the generation of the three two-class sub-datasets , and at the second decomposition level using the variable cut-point values 10, 20 and 30, respectively. Note that the generated new sub-datasets contain (m − 1) columns each time that a variable is removed from the data.
3.4. Phase 4: Derive the Time Causality Rules
4. Case Study
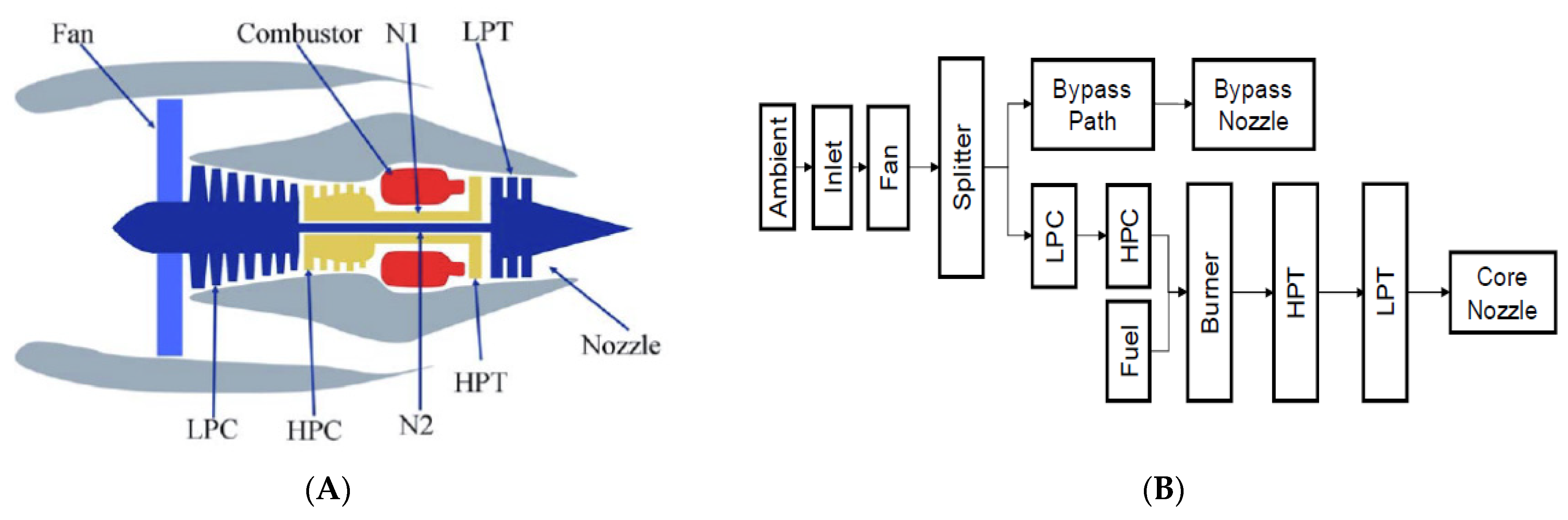
4.1. Dataset Description
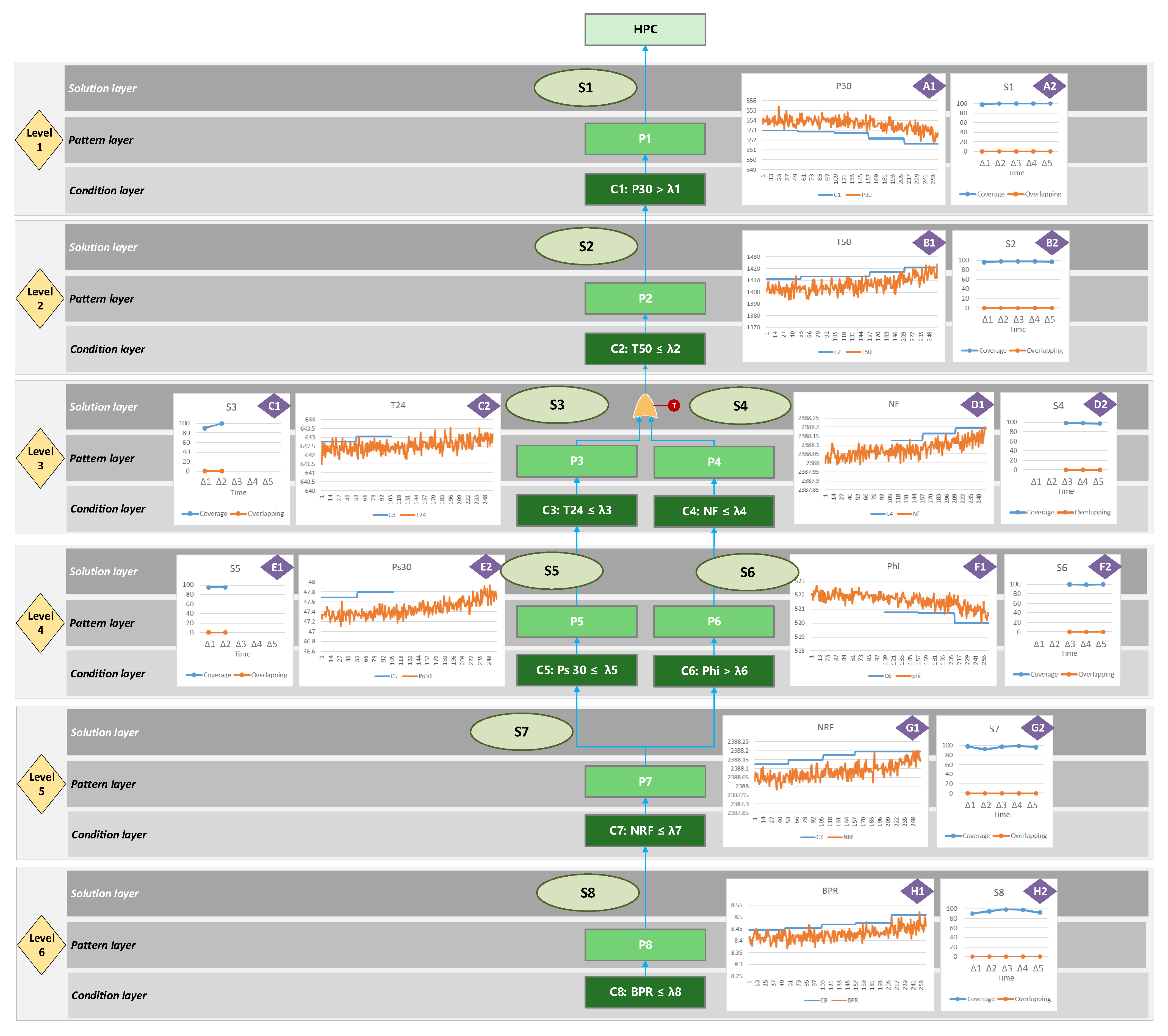
4.2. The HPC Fault Prognosis Using the ITCA Model
4.3. Validation of the ITCA Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vogl, G.W.; Weiss, B.A.; Helu, M. A review of diagnostic and prognostic capabilities and best practices for manufacturing. J. Intell.Manuf. 2019, 30, 79–95. [Google Scholar] [CrossRef] [PubMed]
- Ming, L.; Yan, H.-C.; Hu, B.; Zhou, J.-H.; Pang, C.K. A data-driven two-stage maintenance framework for degradation prediction in semiconductor manufacturing industries. Comput. Ind. Eng. 2015, 85, 414–422. [Google Scholar]
- de Jonge, B. Discretizing continuous-time continuous-state deterioration processes, with an application to condition-based maintenance optimization. Reliab. Eng. Syst. Saf. 2019, 188, 1–5. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.S. Key techniques in intelligent predictive maintenance (IPdM)—A framework of intelligent faults diagnosis and prognosis system (IFDaPS). In Proceedings of the 4th International Workshop of Advanced Manufacturing and Automation (IWAMA 2014), Shanghai, China, 27–28 October 2014. [Google Scholar]
- Bousdekis, A.; Magoutas, B.; Apostolou, D.; Mentzas, G. Review, analysis and synthesis of prognostic-based decision support methods for condition based maintenance. J. Intell. Manuf. 2018, 29, 1303–1316. [Google Scholar] [CrossRef]
- Schwabacher, M.A. A survey of data-driven prognostics. In Proceedings of the Infotech@ Aerospace 2005, Arlington, VA, USA, 26–29 September 2005; p. 7002. [Google Scholar]
- Aggab, T.; Kratz, F.; Avila, M.; Vrignat, P. Model-based prognosis applied to a coupled four tank MIMO system. IFAC PapersOnline 2018, 51, 655–661. [Google Scholar] [CrossRef]
- Schwabacher, M.; Goebel, K. A survey of artificial intelligence for prognostics. In Proceedings of the Artificial Intelligence for Prognostics—Papers from the AAAI Fall Symposium, Arlington, VA, USA, 9–11 November 2007. [Google Scholar]
- Waghen, K.; Ouali, M.-S. Interpretable logic tree analysis: A data-driven fault tree methodology for causality analysis. Expert Syst. Appl. 2019, 136, 376–391. [Google Scholar] [CrossRef]
- Chen, H.-S.; Yan, Z.; Zhang, X.; Liu, Y.; Yao, Y. Root Cause Diagnosis of Process Faults Using Conditional Granger Causality Analysis and Maximum Spanning Tree. IFAC PapersOnLine 2018, 51, 381–386. [Google Scholar] [CrossRef]
- Vania, A.; Pennacchi, P.; Chatterton, S. Fault diagnosis and prognosis in rotating machines carried out by means of model-based methods: A case study. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, IDETC/CIE 2013, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
- Lu, N.; Jiang, B.; Wang, L.; Lü, J.; Chen, X. A Fault Prognosis Strategy Based on Time-Delayed Digraph Model and Principal Component Analysis. Math. Probl. Eng. 2012, 2012, 937196. [Google Scholar] [CrossRef]
- Darwish, M.; Almouahed, S.; de Lamotte, F. The integration of expert-defined importance factors to enrich Bayesian Fault Tree Analysis. Reliab. Eng. Syst. Saf. 2017, 162, 81–90. [Google Scholar] [CrossRef]
- Ragab, A.; El Koujok, M.; Ghezzaz, H.; Amazouz, M.; Ouali, M.-S.; Yacout, S. Deep understanding in industrial processes by complementing human expertise with interpretable patterns of machine learning. Expert Syst. Appl. 2019, 122, 388–405. [Google Scholar] [CrossRef]
- Yunkai, W.; Jiang, B.; Lu, N.; Zhou, Y. Bayesian Network Based Fault Prognosis via Bond Graph Modeling of High-Speed Railway Traction Device. Math. Probl. Eng. 2015, 2015, 321872. [Google Scholar]
- Jin, S.; Zhang, Z.; Chakrabarty, K.; Gu, X. Failure prediction based on anomaly detection for complex core routers. In Proceedings of the 37th IEEE/ACM International Conference on Computer-Aided Design, ICCAD 2018, San Diego, CA, USA, 5–8 November 2018. [Google Scholar]
- Niu, G. Data-Driven Technology for Engineering Systems Health Management: Design Approach, Feature Construction, Fault Diagnosis, Prognosis, Fusion and Decisions; Springer: Singapore, 2016; pp. 1–357. [Google Scholar]
- Zhang, Z.; Wang, Y.; Wang, K. Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network. J. Intell. Manuf. 2013, 24, 1213–1227. [Google Scholar] [CrossRef]
- Wu, Q.; Ding, K.; Huang, B. Approach for fault prognosis using recurrent neural network. J. Intell. Manuf. 2020, 31, 1621–1633. [Google Scholar] [CrossRef]
- Razavi, S.A.; Najafabadi, T.A.; Mahmoodian, A. Remaining Useful Life Estimation Using ANFIS Algorithm: A Data-Driven Approcah for Prognostics. In Proceedings of the 2018 Prognostics and System Health Management Conference, PHM-Chongqing 2018, Chongqing, China, 26–28 October 2018. [Google Scholar]
- Doukovska, L.; Vassileva, S. Knowledge-based Mill Fan System Technical Condition Prognosis. WSEAS Trans. Syst. 2013, 12, 398–408. [Google Scholar]
- Li, Z.; Wang, Y.; Wang, K. A data-driven method based on deep belief networks for backlash error prediction in machining centers. J. Intell. Manuf. 2020, 31, 1693–1705. [Google Scholar] [CrossRef]
- Su, Y.; Jing, B.; Huang, Y.-F.; Tang, W.; Wei, F.; Qiang, X.-Q. Correlation analysis method between environment and failure based on fuzzy causality diagram and rough set of multiple decision classes. Instrum. Tech. Sens. 2015, 100–103. [Google Scholar]
- Kimotho, J.K.; Sondermann-Woelke, C.; Meyer, T.; Sextro, W. Application of Event Based Decision Tree and Ensemble of Data Driven Methods for Maintenance Action Recommendation. Int. J. Progn. Health Manag. 2013, 4 (Suppl. S2), 1–6. [Google Scholar] [CrossRef]
- Medjaher, K.; Moya, J.Y.; Zerhouni, N. Failure prognostic by using Dynamic Bayesian Networks. IFAC Proc. Vol. 2009, 42, 257–262. [Google Scholar] [CrossRef] [Green Version]
- Hammer, P.L.; Bonates, T.O. Logical analysis of data—An overview: From combinatorial optimization to medical applications. Ann. Oper. Res. 2006, 148, 203–225. [Google Scholar] [CrossRef]
- Fokkema, M. PRE: An R package for fitting prediction rule ensembles. arXiv 2017, arXiv:1707.07149. [Google Scholar] [CrossRef] [Green Version]
- May, R.; Csank, J.; Litt, J.; Guo, T.-H. Commercial Modular Aero-Propulsion System Simulation 40k (C-MAPSS40k) User’s Guide. NASA TM-216831. 2010. Available online: https://www.researchgate.net/publication/273755967_Commercial_Modular_Aero-Propulsion_System_Simulation_40k_C-MAPSS40k_User’s_Guide (accessed on 30 September 2021).
- Frederick, D.K.; de Castro, J.A.; Litt, J.S. User’s Guide for the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS): Version 2. 2012. Available online: https://ntrs.nasa.gov/citations/20120003211 (accessed on 30 September 2021).
- National Aeronautics and Space Administration NASA. Turbofan Engine. 2015. Available online: https://www.grc.nasa.gov/www/k-12/airplane/Animation/turbtyp/etfh.html (accessed on 30 September 2021).
- Frederick, D.K.; de Castro, J.A.; Litt, J.S. User’s Guide for the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS). 2007. Available online: https://ntrs.nasa.gov/citations/20070034949 (accessed on 30 September 2021).
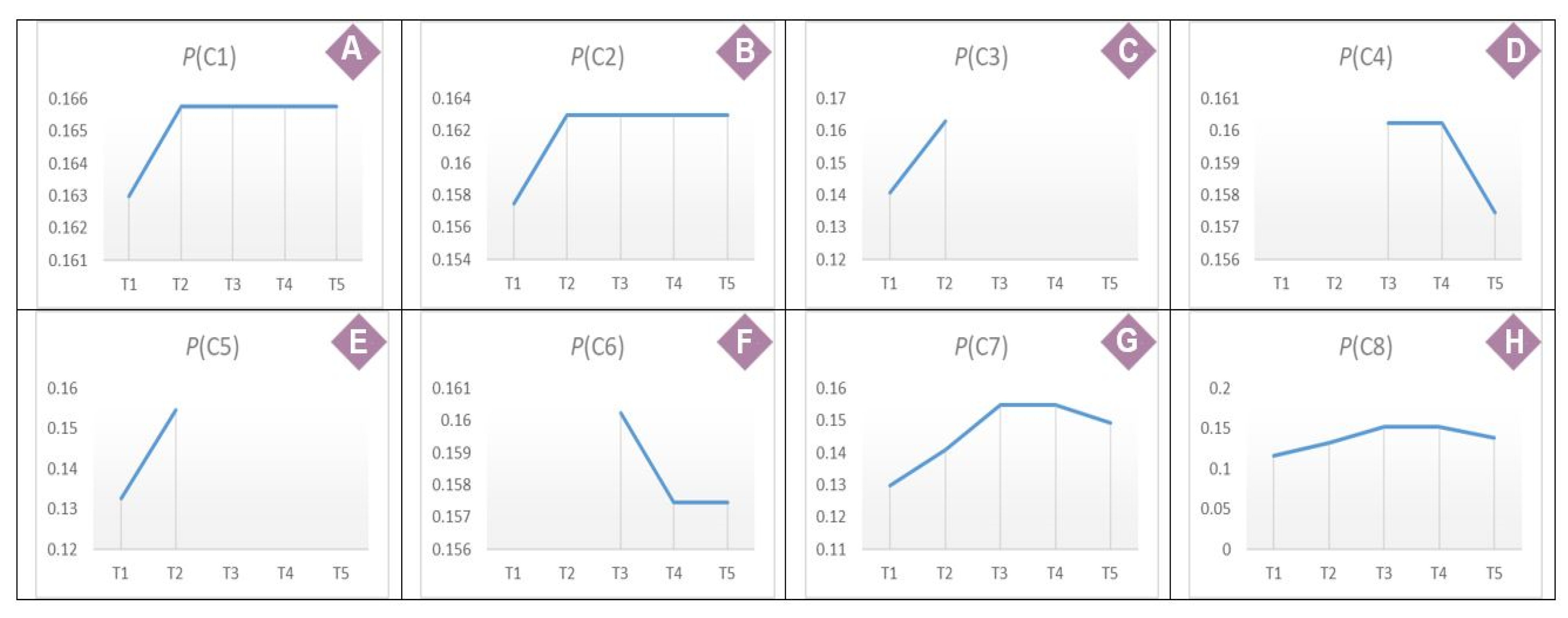
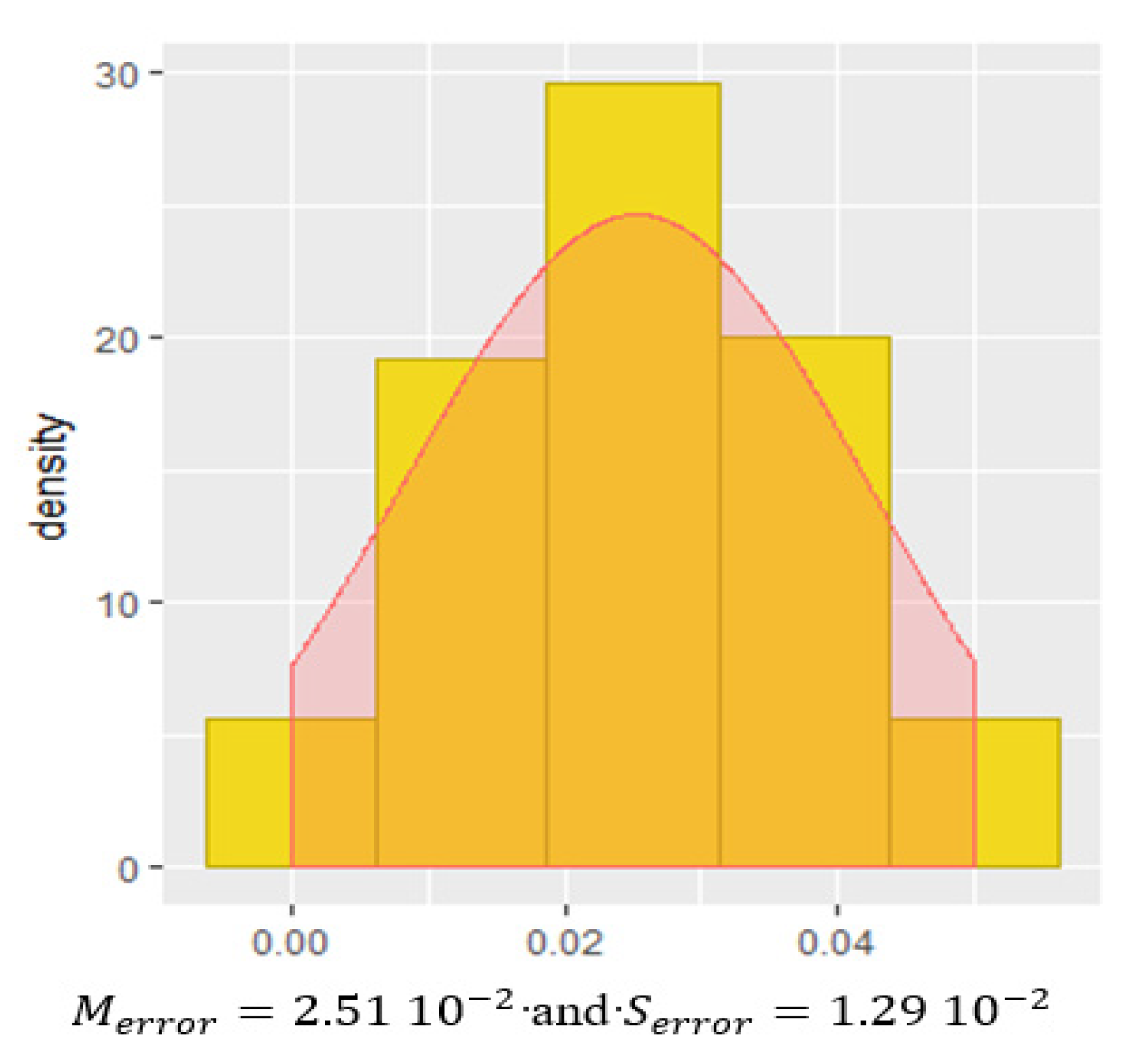
| Variable | Description (Unit) | Trend (—, ↑, ↓) | Variable | Description (Unit) | Trend (—, ↑, ↓) |
|---|---|---|---|---|---|
| T2 | Total temperature at fan inlet (R) | — | phi | Ratio of fuel flow to Ps30 (pps/psi) | ↓ |
| T24 | Total temperature at LPC outlet (R) | ↑ | NRf | Corrected fan speed (rpm) | ↑ |
| T30 | Total temperature at HPC outlet (R) | ↑ | NRc | Corrected core speed (rpm) | ↓ |
| T50 | Total temperature at LPT outlet (R) | ↑ | BPR | Bypass ratio (rpm) | ↑ |
| P2 | Pressure at fan inlet (psia) | — | farB | Burner fuel–air ratio (without unit) | — |
| P15 | Total pressure in bypass duct (psia) | — | htBleed | Bleed enthalpy (without unit) | ↑ |
| P30 | Total pressure at HPC outlet (psia) | ↓ | Nf_dmd | Demanded fan speed (rpm) | — |
| Nf | Physical fan speed (rpm) | ↑ | W31 | HPT coolant bleed (lbm/s) | ↓ |
| Nc | Physical core speed (rpm) | ↓ | W32 | LPT coolant bleed (lbm/s) | ↓ |
| epr | Engine pressure ratio | — | Ps30 | Static pressure at HPC outlet (psia) | ↓ |
| PCNfR_dmd | Demanded corrected fan speed (rpm) | — | |||
| NC | NRc | htBleed | W31 | W32 | |
| T24 | −0.159 | −0.502 | 0.595 | −0.629 | −0.614 |
| T30 | −0.211 | −0.459 | 0.534 | −0.543 | −0.582 |
| T50 | −0.153 | −0.548 | 0.644 | −0.727 | −0.699 |
| P15 | −0.001 | −0.014 | 0.065 | −0.059 | −0.107 |
| P30 | 0.175 | 0.588 | −0.651 | 0.718 | 0.739 |
| Nf | −0.167 | −0.594 | 0.707 | −0.750 | −0.743 |
| Ps30 | −0.171 | −0.594 | 0.689 | −0.761 | −0.742 |
| phi | 0.158 | 0.616 | −0.688 | 0.722 | 0.721 |
| NRf | −0.169 | −0.582 | 0.708 | −0.746 | −0.715 |
| BPR | −0.184 | −0.575 | 0.605 | −0.663 | −0.714 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waghen, K.; Ouali, M.-S. A Data-Driven Fault Tree for a Time Causality Analysis in an Aging System. Algorithms 2022, 15, 178. https://doi.org/10.3390/a15060178
Waghen K, Ouali M-S. A Data-Driven Fault Tree for a Time Causality Analysis in an Aging System. Algorithms. 2022; 15(6):178. https://doi.org/10.3390/a15060178
Chicago/Turabian StyleWaghen, Kerelous, and Mohamed-Salah Ouali. 2022. "A Data-Driven Fault Tree for a Time Causality Analysis in an Aging System" Algorithms 15, no. 6: 178. https://doi.org/10.3390/a15060178
APA StyleWaghen, K., & Ouali, M.-S. (2022). A Data-Driven Fault Tree for a Time Causality Analysis in an Aging System. Algorithms, 15(6), 178. https://doi.org/10.3390/a15060178






