Machine Learning-Based Monitoring of DC-DC Converters in Photovoltaic Applications
Abstract
:1. Introduction
2. Materials and Methods
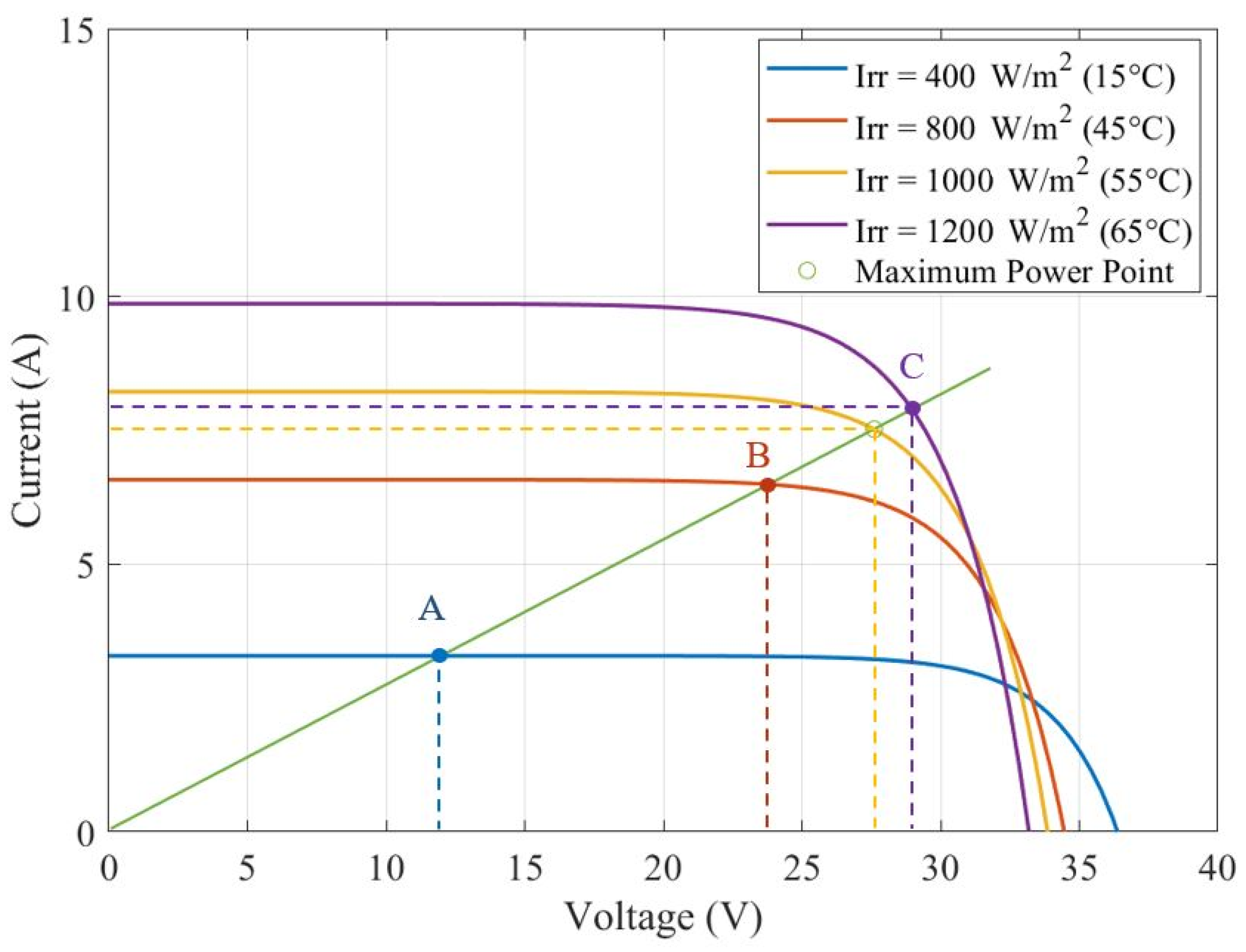
2.1. Photovoltaic Source
2.2. Zeta Converter
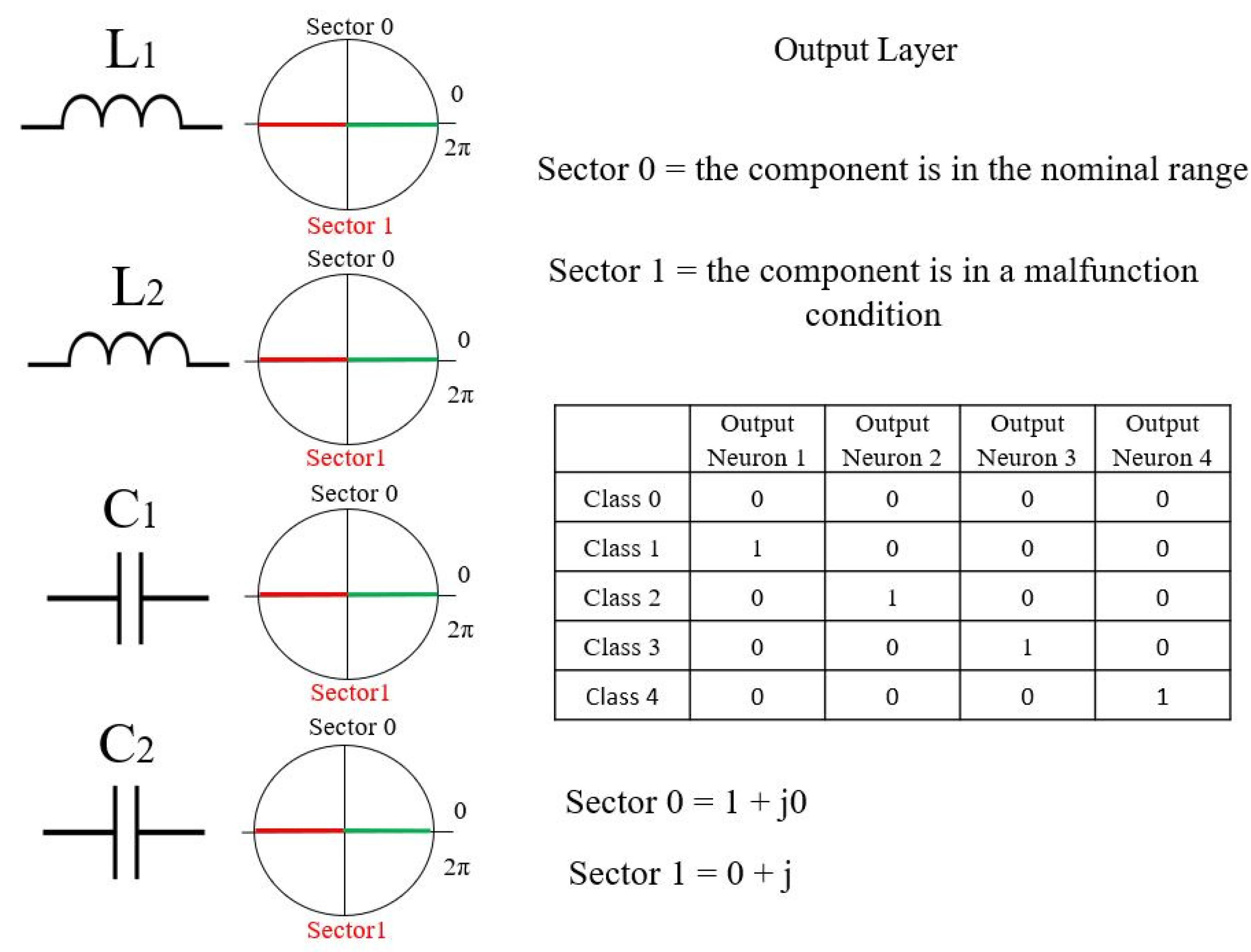
2.3. Fault Classes
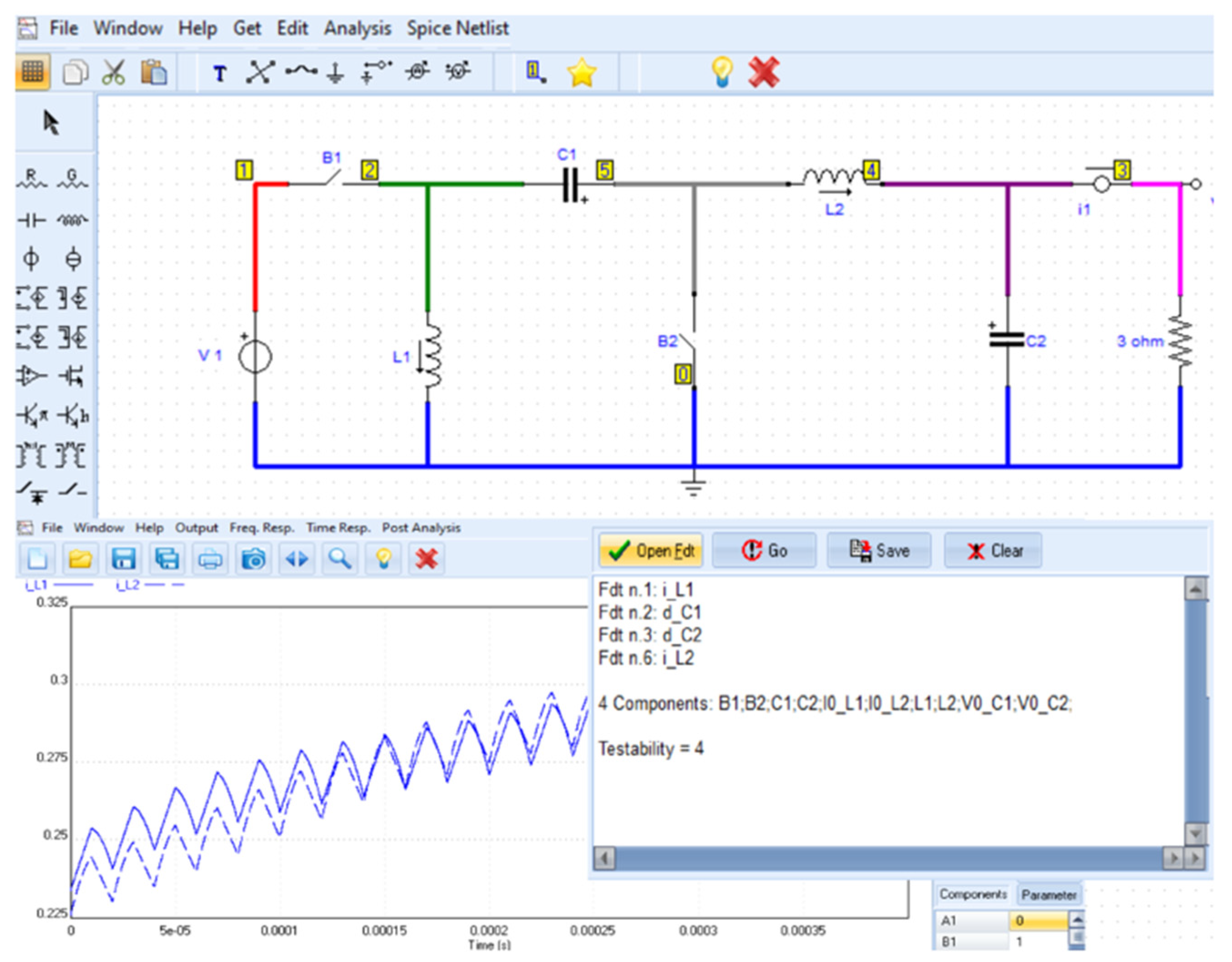
2.4. Testability Analysis
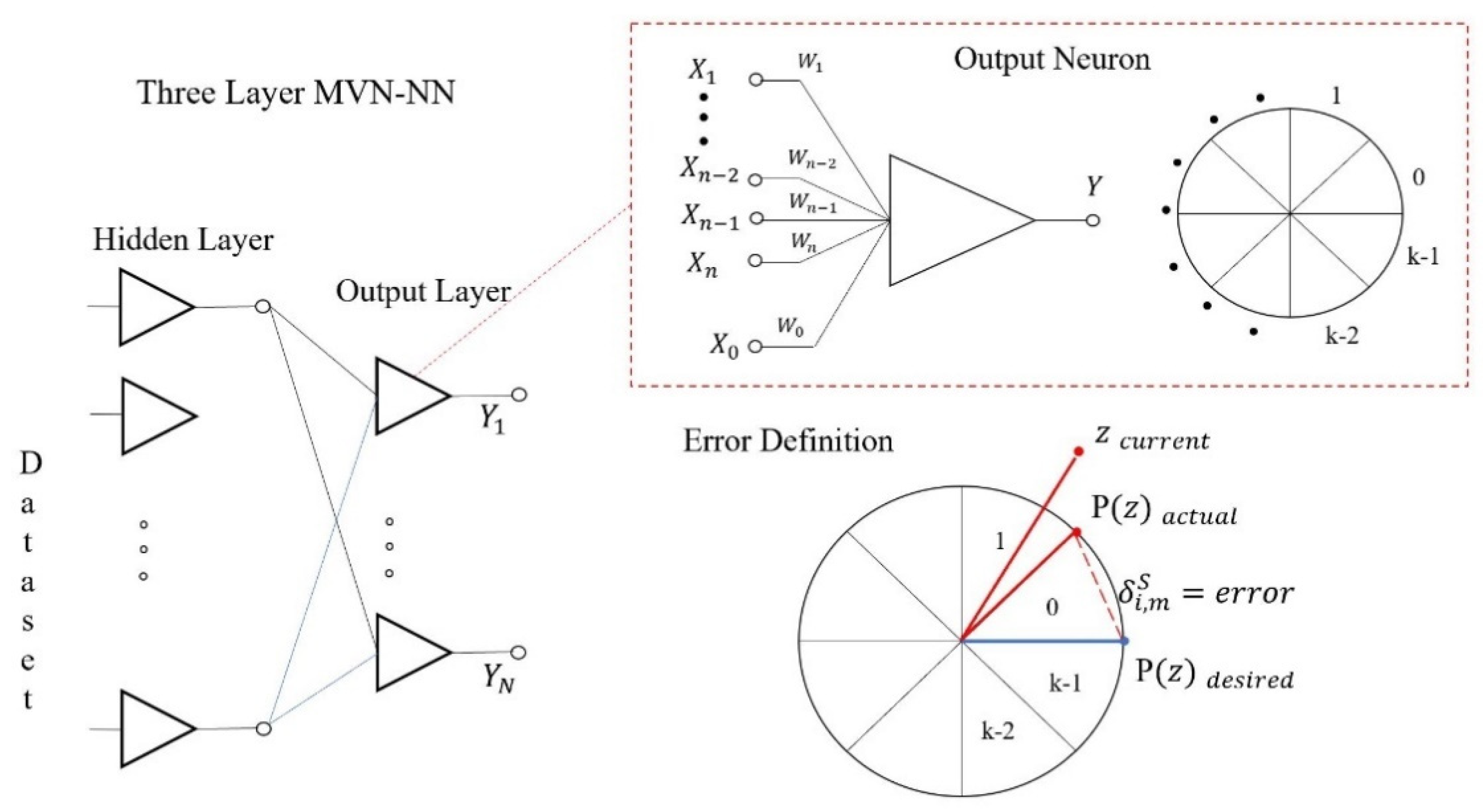
2.5. Multilayer Neural Network with Multi-Valued Neurons (MLMVN) and Its Adaptation to a Zeta Convertor
2.5.1. Main Characteristics
2.5.2. Neural Classifier for Zeta Converter
3. Results
- first selection of measurements;
- testability analysis;
- neural network training.
3.1. First Selection of the Measurements
3.2. Testability Assessment of the Zeta Converter
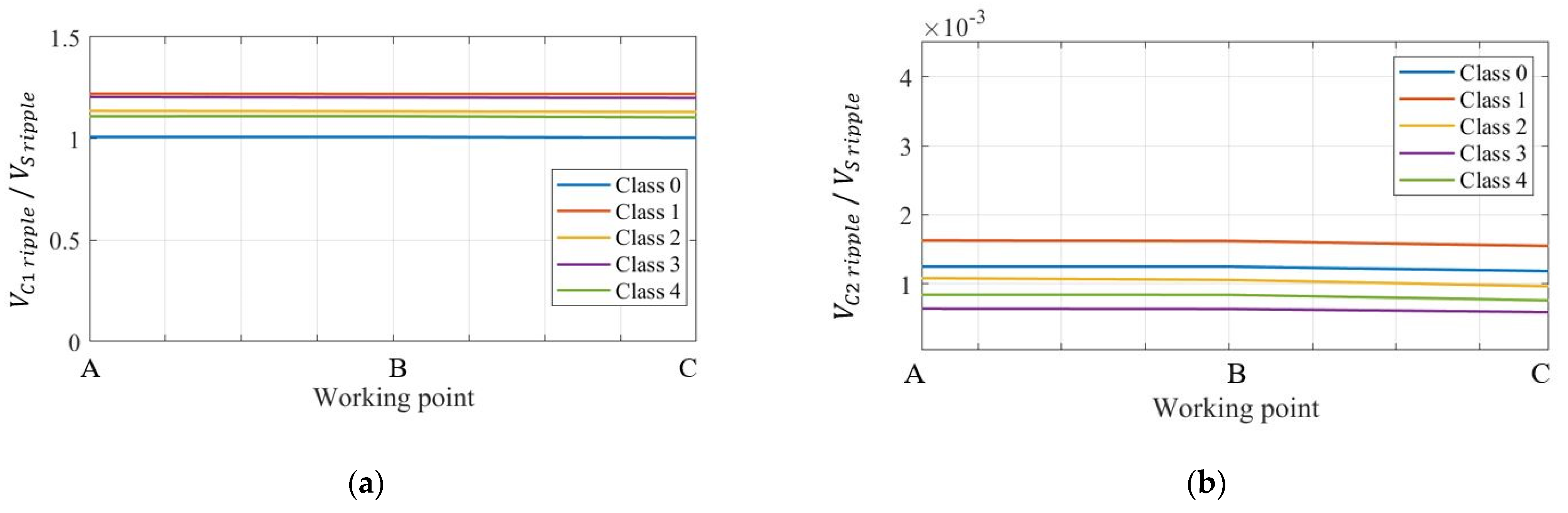
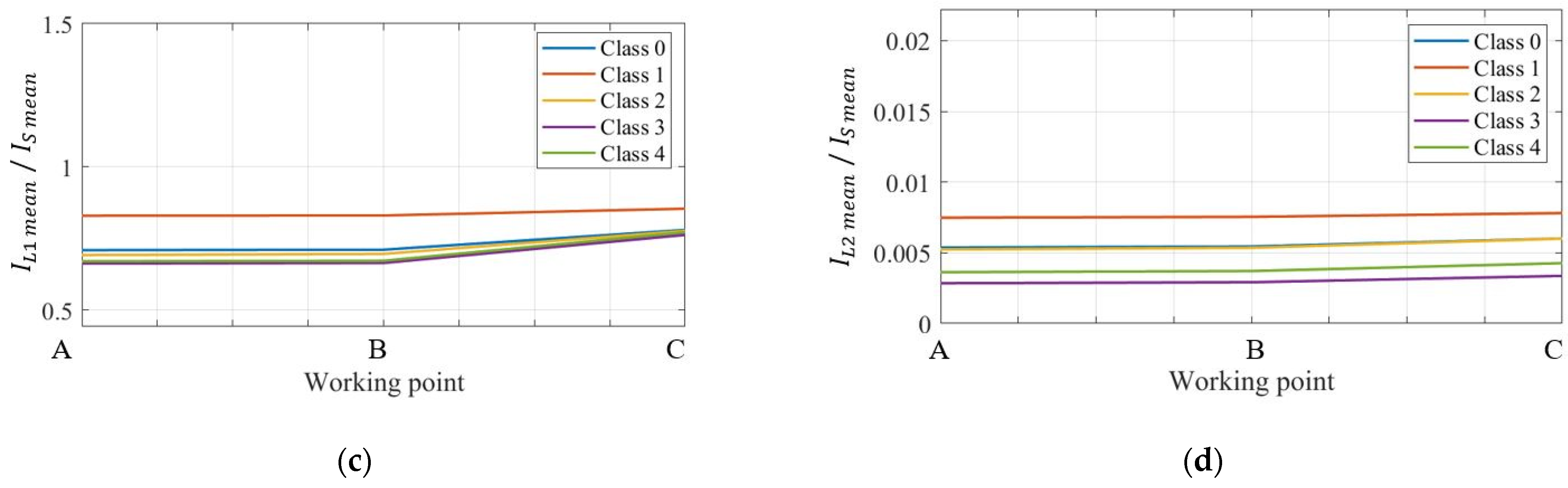
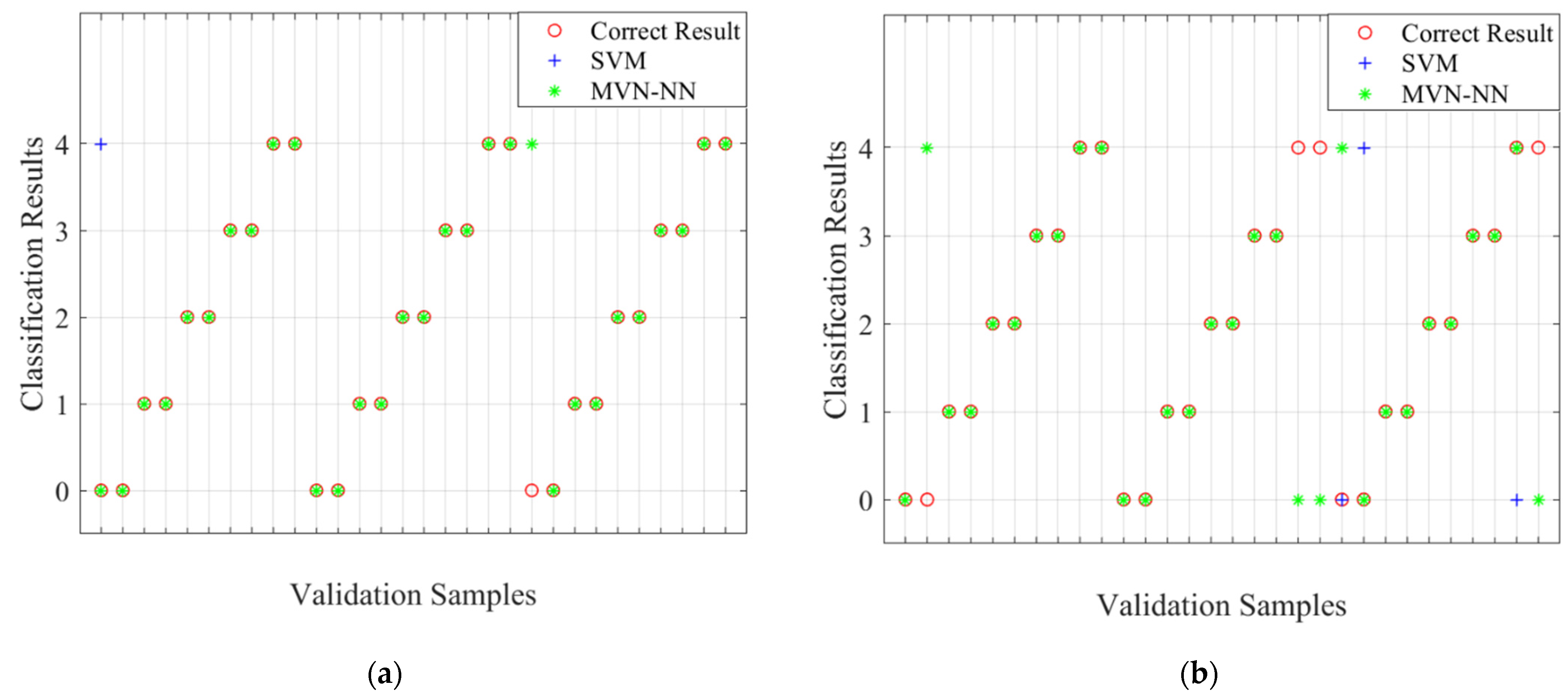
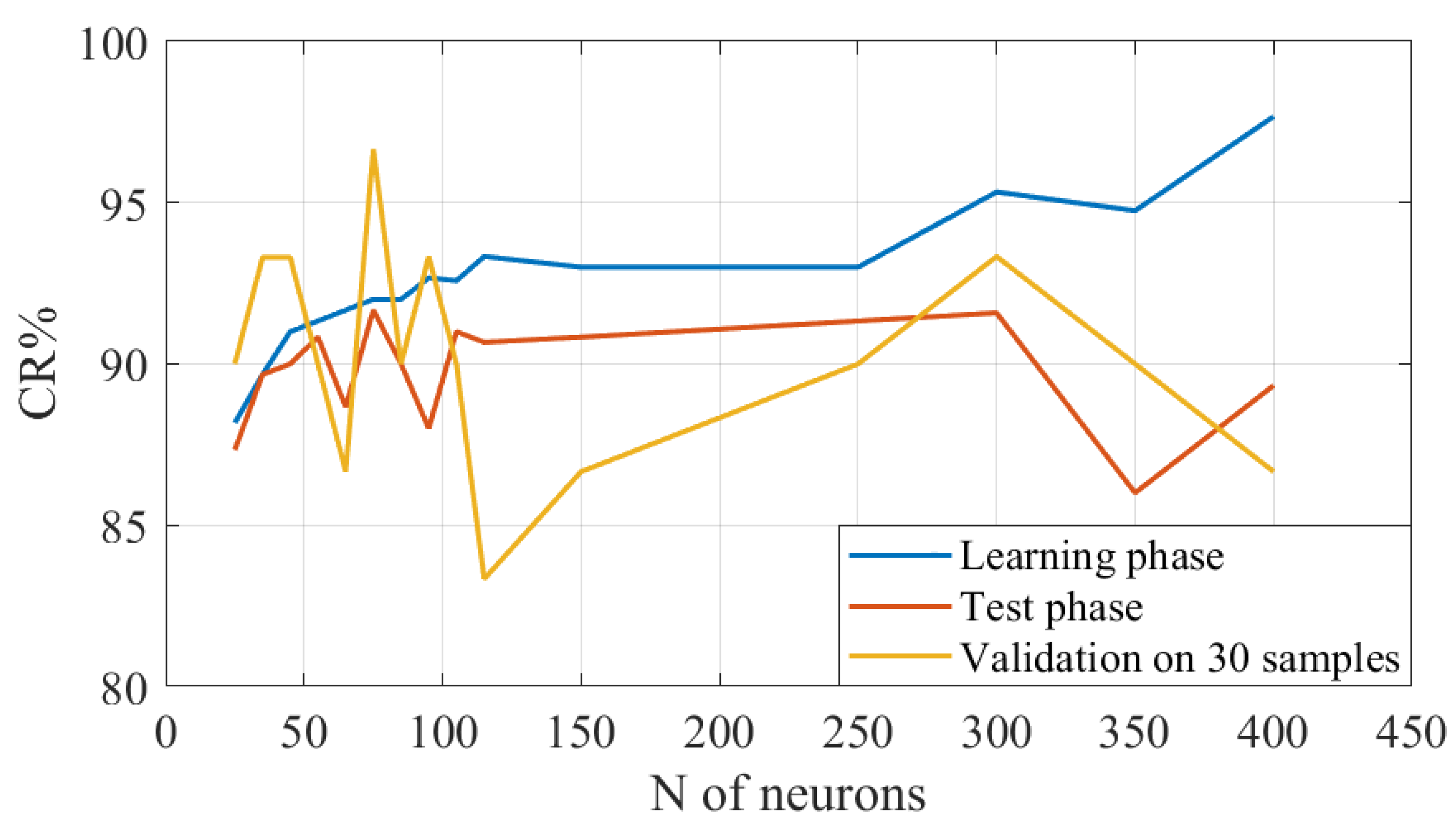
3.3. Neural Network Training and Validation
- the first step is the creation of 400 random values in the nominal range and 100 random values in the malfunction condition for each passive component;
- using these values, 100 samples for each fault class can be obtained in the hypothesis of a single failure;
- the values of the components are used in Simulink to simulate different working conditions and extract the corresponding measurements (voltage ripple on capacitors and mean current values on inductors);
- repeating these steps for three irradiance values (400, 800, and 1200 W/m2), a dataset matrix containing 1500 samples is obtained.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rahbar, K.; Xu, J.; Zhang, R. Real-Time Energy Storage Management for Renewable Integration in Microgrid: An Off-Line Optimization Approach. IEEE Trans. Smart Grid 2015, 6, 124–134. [Google Scholar] [CrossRef]
- Wang, W.; Liu, L.; Liu, J.; Chen, Z. Energy management and optimization of vehicle-to-grid systems for wind power integration. CSEE J. Power Energy Syst. 2021, 7, 172–180. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Ahmed, W.; Ansari, H.; Khan, B.; Ullah, Z.; Ali, S.M.; Mehmood, C.A.A.; Qureshi, M.B.; Hussain, I.; Jawad, M.; Khan, M.U.S.; et al. Machine Learning Based Energy Management Model for Smart Grid and Renewable Energy Districts. IEEE Access 2020, 8, 185059–185078. [Google Scholar] [CrossRef]
- Cardelli, E. A general hysteresis operator for the modeling of vector fields. IEEE Trans. Magn. 2011, 47, 2056–2067. [Google Scholar] [CrossRef]
- Quondam, A.S.; Ghanim, A.M.; Faba, A.; Laudani, A. Numerical simulations of vector hysteresis processes via the Preisach model and the Energy Based Model: An application to Fe-Si laminated alloys. J. Magn. Magn. Mater. 2021, 539, 168372. [Google Scholar] [CrossRef]
- Li, X.; Chen, C.; Xu, Q.; Wen, C. Resilience for Communication Faults in Reactive Power Sharing of Microgrids. IEEE Trans. Smart Grid 2021, 12, 2788–2799. [Google Scholar] [CrossRef]
- Mahmoud, K.; Lehtonen, M. Comprehensive Analytical Expressions for Assessing and Maximizing Technical Benefits of Photovoltaics to Distribution Systems. IEEE Trans. Smart Grid 2021, 12, 4938–4949. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Zheng, R.; Gu, J.; Jin, Z.; Peng, H. Probabilistic Load Forecasting with High Penetration of Renewable Energy Based on Variable Selection and Residual Modeling. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Grasso, F.; Talluri, G.; Giorgi, A.; Luchetta, A.; Paolucci, L. Peer-to-Peer Energy Exchanges Model to optimize the Integration of Renewable Energy Sources: The E-Cube Project. Energ. Elettr. Suppl. 2020, 96, 1–8. [Google Scholar] [CrossRef]
- Lee, W.; Jung, J.; Lee, M. Development of 24-hour optimal scheduling algorithm for energy storage system using load forecasting and renewable energy forecasting. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Dedeoglu, S.; Konstantopoulos, G.C. Three-Phase Grid-Connected Inverters Equipped with Nonlinear Current-Limiting Control. In Proceedings of the 2018 UKACC 12th International Conference on Control (CONTROL), Sheffield, UK, 5–7 September 2018; pp. 38–43. [Google Scholar] [CrossRef] [Green Version]
- Bindi, M.; Garcia, C.I.; Corti, F.; Piccirilli, M.C.; Luchetta, A.; Grasso, F.; Manetti, S. Comparison Between PI and Neural Network Controller for Dual Active Bridge Converter. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Quondam, A.S.; Faba, A.; Rimal, H.P.; Cardelli, E. On the Analysis of the Dynamic Energy Losses in NGO Electrical Steels under Non-Sinusoidal Polarization Waveforms. IEEE Trans. Magn. 2020, 56, 8960638. [Google Scholar] [CrossRef]
- Guarino, A.; Vanel, L.; Scorretti, R.; Ciliberto, S. The cooperative effect of load and disorder in thermally activated rupture of a two-dimensional random fuse network. J. Stat. Mech. Theory Exp. 2006, 2006, P06020. [Google Scholar] [CrossRef] [Green Version]
- Divyasharon, R.; Narmatha Banu, R.; Devaraj, D. Artificial Neural Network based MPPT with CUK Converter Topology for PV Systems Under Varying Climatic Conditions. In Proceedings of the 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 11–13 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, F.L. Luo-converters, voltage lift technique. In Proceedings of the PESC 98 Record, 29th Annual IEEE Power Electronics Specialists Conference (Cat. No.98CH36196), Fukuoka, Japan, 22 May 1998; Volume 2, pp. 1783–1789. [Google Scholar] [CrossRef]
- Woranetsuttikul, K.; Pinsuntia, K.; Jumpasri, N.; Nilsakorn, T.; Khan-ngern, W. Comparison on performance between synchronous single-ended primary-inductor converter (SEPIC) and synchronous ZETA converter. In Proceedings of the 2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Luo, F.L. Double output Luo-converters-voltage lift technique. In Proceedings of the 1998 International Conference on Power Electronic Drives and Energy Systems for Industrial Growth, Perth, WA, Australia, 1–3 December 1998; Volume 1, pp. 342–347. [Google Scholar] [CrossRef]
- Tadeusiewicz, M.; Hałgas, S. A Method for Local Parametric Fault Diagnosis of a Broad Class of Analog Integrated Circuits. IEEE Trans. Instrum. Meas. 2018, 67, 328–337. [Google Scholar] [CrossRef]
- Aizenberg, I.; Belardi, R.; Bindi, M.; Grasso, F.; Manetti, S.; Luchetta, A.; Piccirilli, M.C. A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis. Electronics 2021, 10, 349. [Google Scholar] [CrossRef]
- Bindi, M.; Aizenberg, I.; Belardi, R.; Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. Neural Network-Based Fault Diagnosis of Joints in High Voltage Electrical Lines. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 488–498. [Google Scholar] [CrossRef]
- Li, H.; Yin, B.; Li, N.; Guo, J. Research of fault diagnosis method of analog circuit based on improved support vector machines. In Proceedings of the 2010 The 2nd International Conference on Industrial Mechatronics and Automation, Wuhan, China, 30–31 May 2010; pp. 494–497. [Google Scholar] [CrossRef]
- Ni, Y.; Li, J. Faults diagnosis for power transformer based on support vector machine. In Proceedings of the 2010 3rd International Conference on Biomedical Engineering and Informatics, Yantai, China, 16–18 October 2010; pp. 2641–2644. [Google Scholar] [CrossRef]
- González-Castaño, C.; Lorente-Leyva, L.L.; Muñoz, J.; Restrepo, C.; Peluffo-Ordóñez, D.H. An MPPT Strategy Based on a Surface-Based Polynomial Fitting for Solar Photovoltaic Systems Using Real-Time Hardware. Electronics 2021, 10, 206. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A.; Lozito, G.M.; Mancilla-David, F. Implementation of a neural MPPT algorithm on a low-cost 8-bit microcontroller. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 977–981. [Google Scholar] [CrossRef]
- Available online: https://it.enfsolar.com/tianwei-new-energy (accessed on 11 February 2022).
- Khatab, A.M.; Marei, M.I.; Elhelw, H.M. An Electric Vehicle Battery Charger Based on Zeta Converter Fed from a PV Array. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Fontana, G.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. A Fast Algorithm for Testability Analysis of Large Linear Time-Invariant Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1564–1575. [Google Scholar] [CrossRef]
- Fontana, G.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. A Testability Measure for DC-Excited Periodically Switched Networks with Applications to DC-DC Converters. IEEE Trans. Instrum. Meas. 2016, 65, 2321–2341. [Google Scholar] [CrossRef]
- Aizenberg, I.; Bindi, M.; Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. Testability Analysis in Neural Network Based Fault Diagnosis of DC-DC Converter. In Proceedings of the 2019 IEEE 5th International forum on Research and Technology for Society and Industry (RTSI), Florence, Italy, 9–12 September 2019; pp. 265–268. [Google Scholar] [CrossRef]
- Luchetta, A.; Manetti, S.; Piccirilli, M.C.; Reatti, A.; Corti, F.; Catelani, M.; Ciani, L.; Kazimierczuk, M.K. MLMVNNN for Parameter Fault Detection in PWM DC–DC Converters and Its Applications for Buck and Boost DC–DC Converters. IEEE Trans. Instrum. Meas. 2019, 68, 439–449. [Google Scholar] [CrossRef]
- Aizenberg, I. Complex-Valued Neural Networks with Multi-Valued Neurons; Springer: New York, NY, USA, 2011. [Google Scholar]
- Aizenberg, I.; Luchetta, A.; Manetti, S. A modified learning algorithm for the multilayer neural network with multi-valued neurons based on the complex QR decomposition. Soft Comput. 2012, 16, 563–575. [Google Scholar] [CrossRef]
- Aizenberg, I. MLMVN With Soft Margins Learning. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1632–1644. [Google Scholar] [CrossRef]
- Laudani, A.; Lozito, G.M.; Riganti Fulginei, F. Irradiance Sensing through PV Devices: A Sensitivity Analysis. Sensors 2021, 21, 4264. [Google Scholar] [CrossRef] [PubMed]
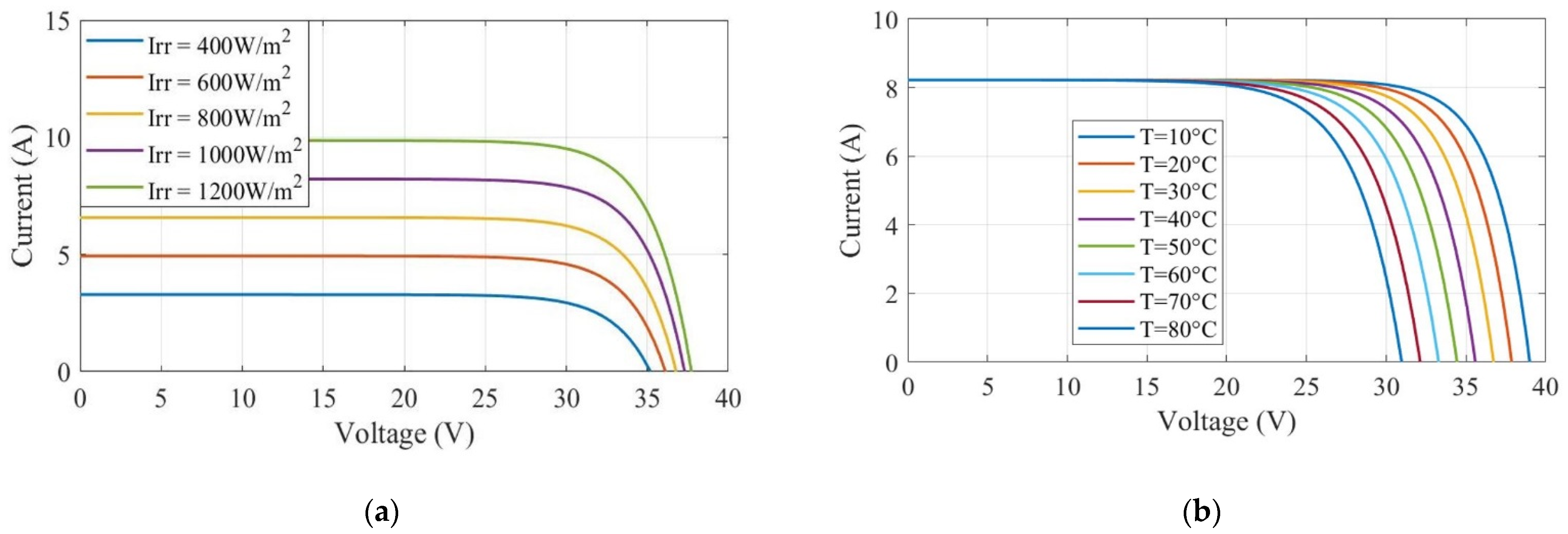
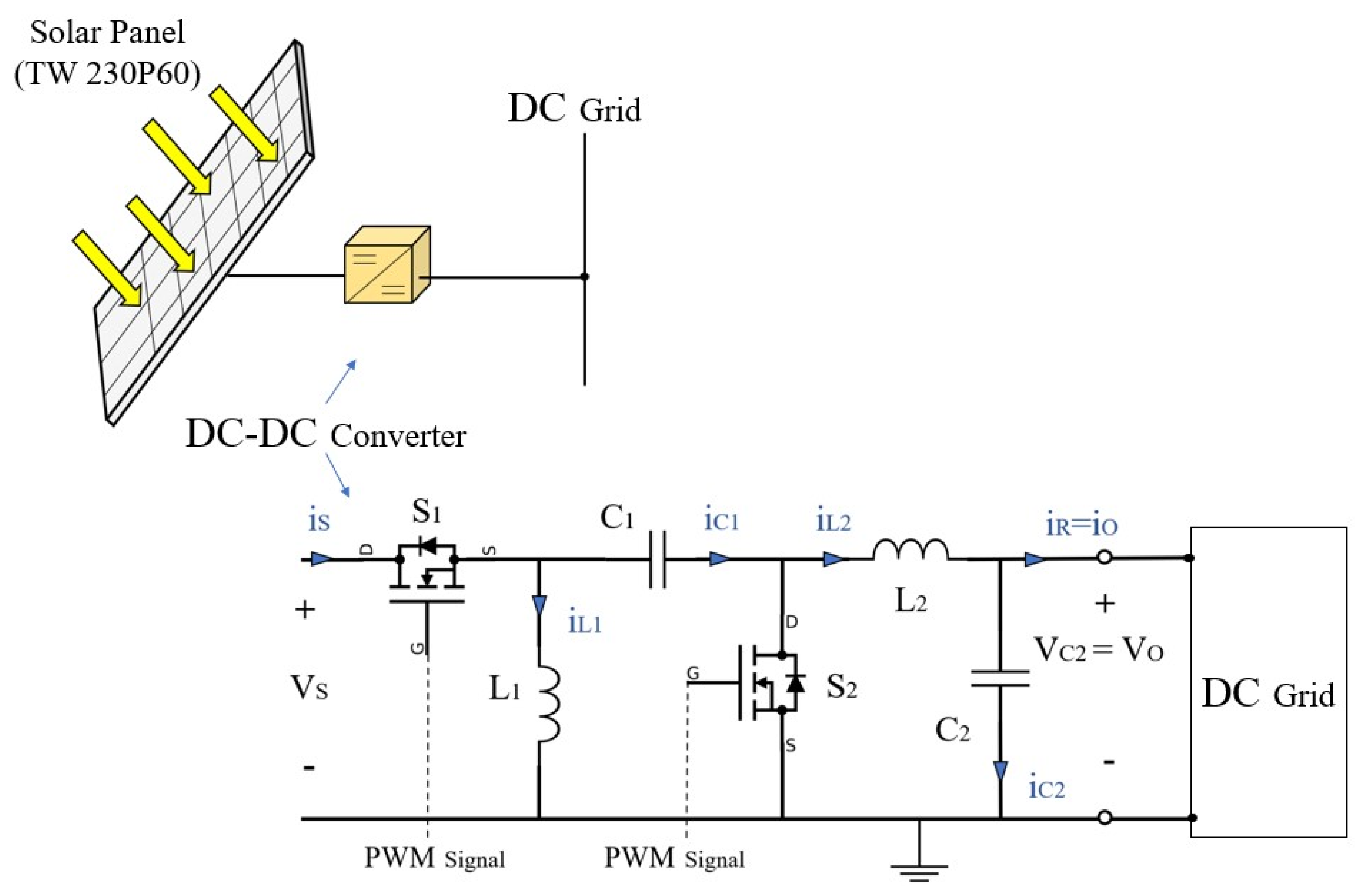
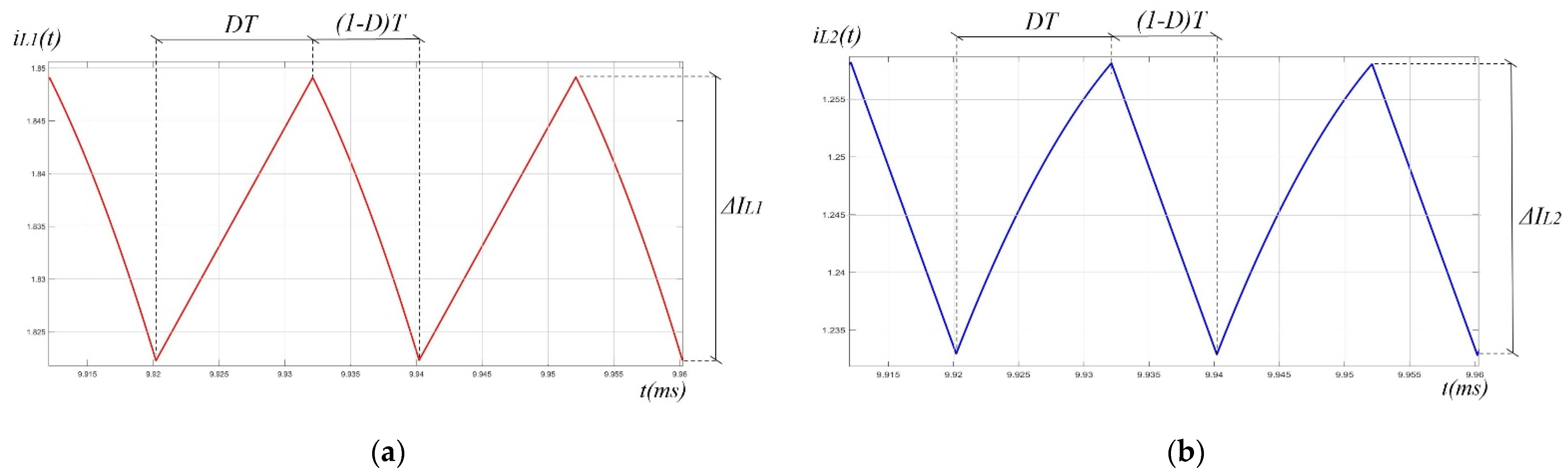

| VMPP | IMPP | VOC | ISC | N Cell | |
|---|---|---|---|---|---|
| 29.4 V | 7.82 A | 37.3 V | 8.22 A | 0.06%/°C | 60 |
| L1 [mH] | L2 [mH] | C1 [μF] | C2 [μF] |
|---|---|---|---|
| 5 | 5 | 2.4 | 2.4 |
| L1 (mH) | L2 (mH) | C1 (μF) | C2 (μF) | |
|---|---|---|---|---|
| Nominal Range | (4.25–5.75) | (4.25–5.75) | (2.04–2.76) | (2.04–2.76) |
| Malfunction Condition | (1.5–4.25) | (1.5–4.25) | (0.72–2.04) | (0.72–2.04) |
| Fault Class | Description |
|---|---|
| 0 | Each component is in the nominal range |
| 1 | Malfunction on L1 |
| 2 | Malfunction on L2 |
| 3 | Malfunction on C1 |
| 4 | Malfunction on C2 |
| Operating Point | Irradiance (W/m2) | Temperature (°C) |
|---|---|---|
| A | 400 | 15 |
| B | 800 | 45 |
| C | 1200 | 65 |
| Irradiance 1 W/m2 | Temperature 1 °C | Irradiance 2 W/m2 | Temperature 2 °C | Irradiance 3 W/m2 | Temperature 3 °C |
|---|---|---|---|---|---|
| 500 | 25 | 705 | 40 | 390 | 19 |
| Classifier | Hyperparameters | Learning Phase | Test Phase | Validation 1 | Validation 2 |
|---|---|---|---|---|---|
| MLMVN | 75 Neurons | 92% | 91.66% | 96.66% | 86.66% |
| SVM | 13 Support Vectors | 88.7% | - | 93.33% | 83.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bindi, M.; Corti, F.; Aizenberg, I.; Grasso, F.; Lozito, G.M.; Luchetta, A.; Piccirilli, M.C.; Reatti, A. Machine Learning-Based Monitoring of DC-DC Converters in Photovoltaic Applications. Algorithms 2022, 15, 74. https://doi.org/10.3390/a15030074
Bindi M, Corti F, Aizenberg I, Grasso F, Lozito GM, Luchetta A, Piccirilli MC, Reatti A. Machine Learning-Based Monitoring of DC-DC Converters in Photovoltaic Applications. Algorithms. 2022; 15(3):74. https://doi.org/10.3390/a15030074
Chicago/Turabian StyleBindi, Marco, Fabio Corti, Igor Aizenberg, Francesco Grasso, Gabriele Maria Lozito, Antonio Luchetta, Maria Cristina Piccirilli, and Alberto Reatti. 2022. "Machine Learning-Based Monitoring of DC-DC Converters in Photovoltaic Applications" Algorithms 15, no. 3: 74. https://doi.org/10.3390/a15030074
APA StyleBindi, M., Corti, F., Aizenberg, I., Grasso, F., Lozito, G. M., Luchetta, A., Piccirilli, M. C., & Reatti, A. (2022). Machine Learning-Based Monitoring of DC-DC Converters in Photovoltaic Applications. Algorithms, 15(3), 74. https://doi.org/10.3390/a15030074













